Wireless Engineering and Technology
Vol.3 No.1(2012), Article ID:16940,5 pages DOI:10.4236/wet.2012.31004
Generalized PIC Detector for Distributed STBC under Quasi-Synchronization
![]()
Department of Electrical Engineering, Islamic University of Gaza (IUG), Gaza, Palestine.
Email: {mtastal, ahdrouss}@iugaza.edu.ps
Received September 23rd, 2011; revised November 2nd, 2011; accepted November 18th, 2011
Keywords: Distributed Space Time Block Coding; Synchronization; Distributed Transmit Diversity; Cooperative Diversity
ABSTRACT
In this paper, we propose a Generalized Parallel Interference Cancelation (G-PIC) approach for the detection of D-STBC under Quasi-Synchronization in the case of any number of relay nodes with just statistical information about time misalignment. While as, most researches assume perfect synchronization between the relay nodes for the detection of D-STBC which is hard to achieve. This approach proved to be very effective to mitigate the degradation in the system performance due to the imperfect synchronization. The numerical simulations, for the proposed approach, showed that in just three iterations we can achieve performance close to the D-STBC with perfect synchronization.
1. Introduction
The cooperative communication techniques can avoid the difficulties of implementing actual antenna arrays by converting a single-input single-output (SISO) system into a virtual multiple-input multiple-output (MIMO) system. Space-Time Block Coding (STBC) are used to improve the transmission reliably and spectral efficiency of MIMO systems. When STBC is applied to cooperative diversity the system termed as Distributed Space Time Block Code (D-STBC). Most of the existing research assumes perfect synchronization among cooperative users in D-STBC. This means that all users are assumed to have the identical timing, carrier frequency, and propagation delay [1].
Unfortunately, perfect synchronization is almost impossible to be achieved. The lack of common timing reference can badly influence the structure of the code matrix [1]. There are different research efforts to overcome this problem [2-4]; most of which has high decoding complexity [5]. In [2,3], the detection scheme is based on Parallel Interference Cancellation (PIC) principle. In [2], a detection scheme proposed for the case of two relay nodes whereas; in [3] a detection scheme has been proposed for three and four relay nodes. These two schemes assume full knowledge about the amount of imperfect synchronization which is unrealistic. In this paper, a PIC detection scheme for any number of relay nodes is proposed. This scheme does not require a full knowledge about imperfect synchronization but instead it uses statistical measures such as the average and standard deviation of the time misalignment.
For the rest of this paper,  represent “transpose”,
represent “transpose”, 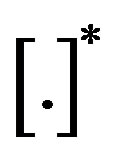 represent “conjugate”, and
represent “conjugate”, and  denotes the set of Gaussian Distributed complex number with the standard variance of
denotes the set of Gaussian Distributed complex number with the standard variance of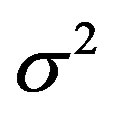 .
.
2. D-STBC under Imperfect Synchronization
Our system model consists of the source node (S), m relay nodes (R1 to Rm), and the destination node (D). As in most cooperative system, there are two phases:
1) Phase 1 (Direct Transmission (DT) phase): In this phase, the transmitter groups the data symbols in to packets (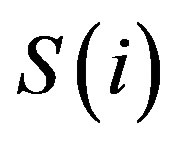 ) each contains k symbols where k is the number of symbols per STBC block (it depends on the code used in Phase 2), and then it will transmit these packets. Both of the relay nodes and the destination will receive the transmission. The destination node has a received signal as shown in Figure 1.
) each contains k symbols where k is the number of symbols per STBC block (it depends on the code used in Phase 2), and then it will transmit these packets. Both of the relay nodes and the destination will receive the transmission. The destination node has a received signal as shown in Figure 1.
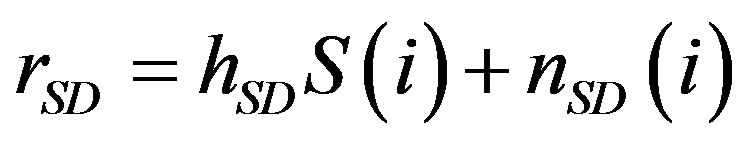 (1)
(1)
where: ,
,  ,
, 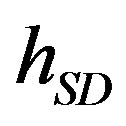 is the channel gain between S and D, and
is the channel gain between S and D, and , since
, since .
.
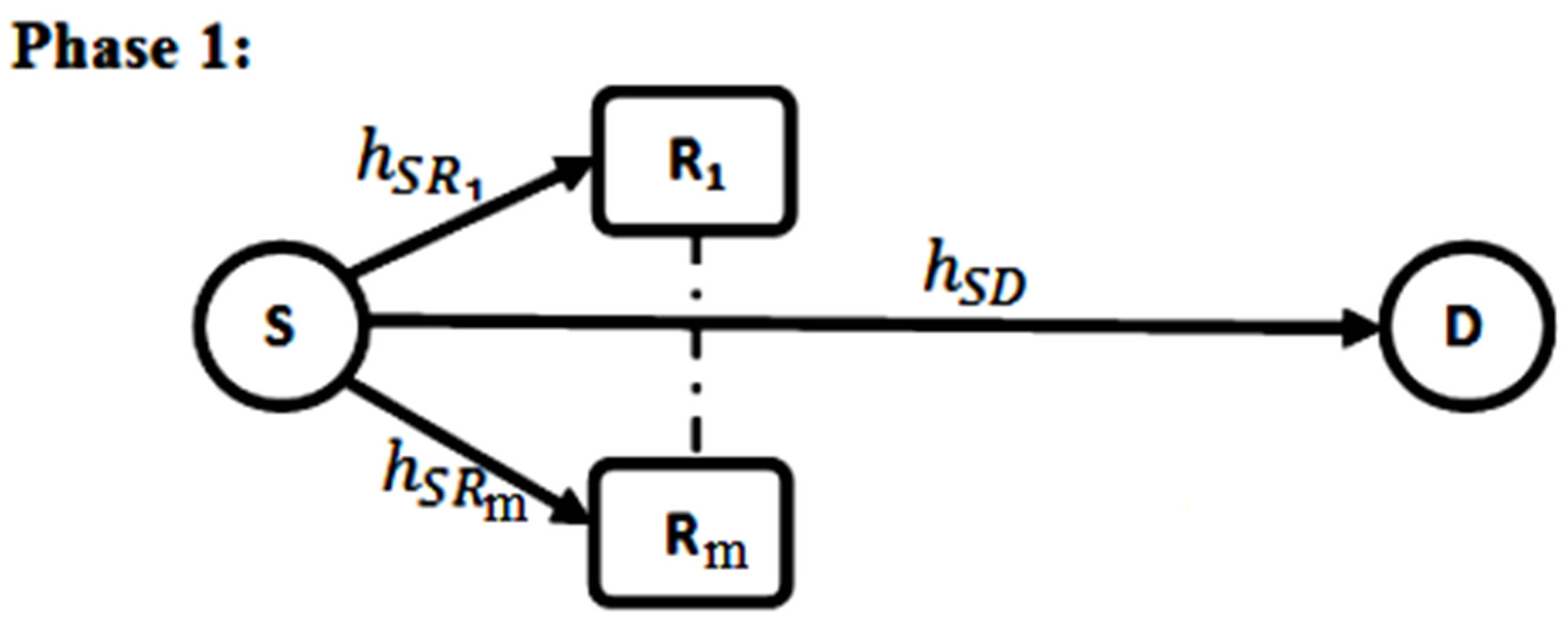
Figure 1. Phase 1 of the system model.
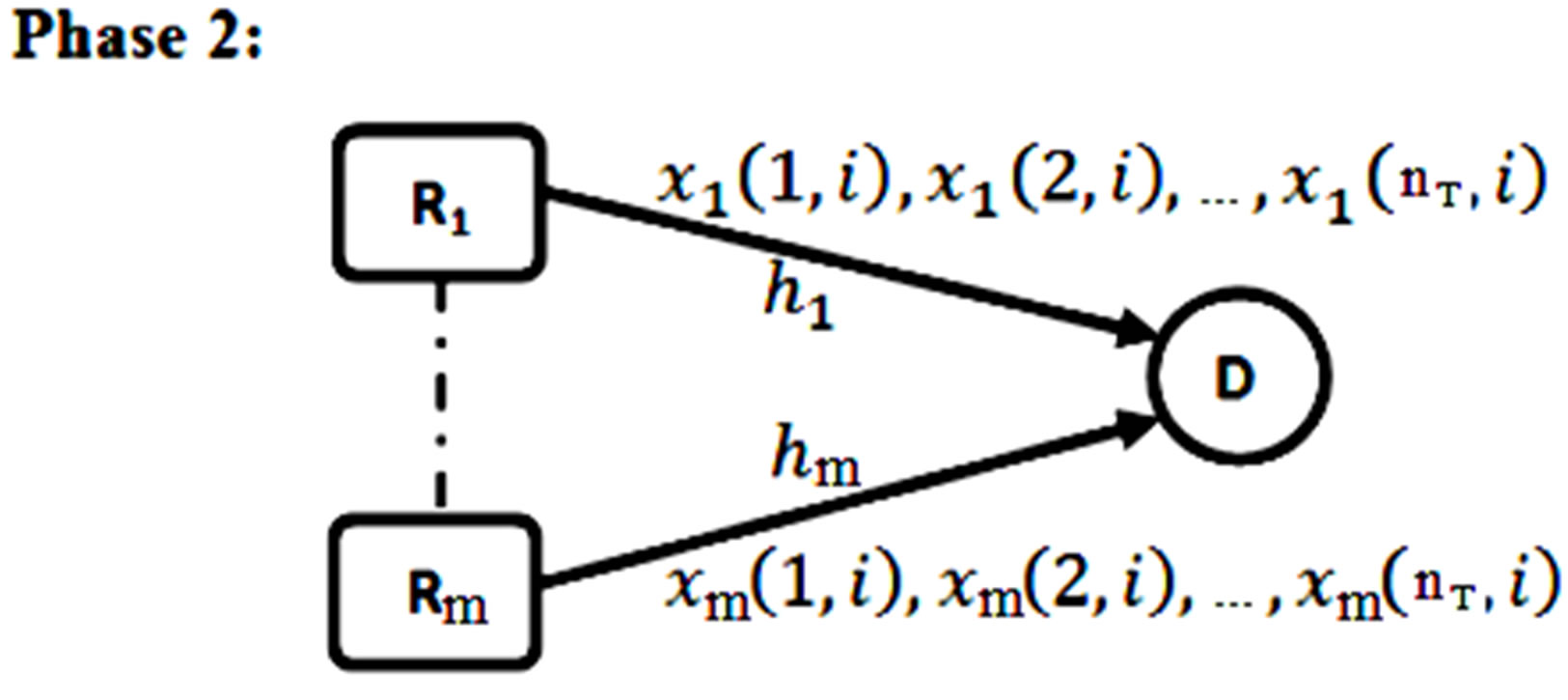
Figure 2. Phase 2 of the system model.
The detection can be determined using Least Square (LS) search:
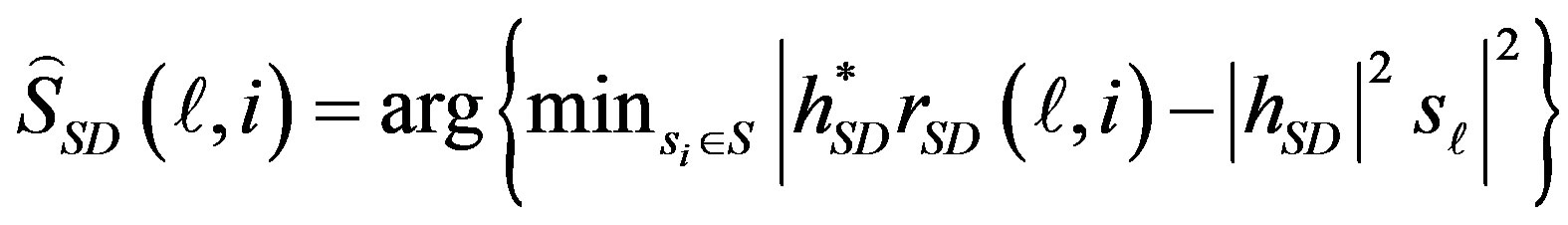 (2)
(2)
for 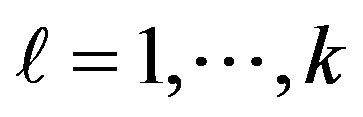 . S is the symbols alphabet depends on modulation type.
. S is the symbols alphabet depends on modulation type.
2) Phase 2 (broadcasting phase) (Shown in Figure 2): Here, we use “selective decode and forward” as relaying protocol [6]. So, at first the relays detect the received symbols, if the detection is correct (can be implemented by adding a sufficient level of cyclic redundancy check (CRC) to the data at node S) then encode it using suitable STBC, and finally every relays transmit their sequence. This system model contains m relay nodes, so Phase 2 requires a STBC code with m columns. In [7], an orthogonal high rate STBC codes to any number of antennas (columns) can be generated through systematic steps. Since these generated codes are orthogonal, the system will have a very simple decoding process at the receiver. Systematic, orthogonal, and high rate are the reasons which attract us to choose these codes. These codes can be modeled by the following general form:
 (3)
(3)
where  is symbol in the column m and the row j of the coding matrix, this symbol will be transmit from the relay node m and at time slot j.
is symbol in the column m and the row j of the coding matrix, this symbol will be transmit from the relay node m and at time slot j.
Because of factors such as different propagation delays, relay’s sequences will arrive at node D at different time instants. An accurate synchronization is difficult or impossible to achieve [8,9], so there is a timing misalignment 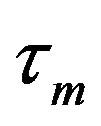 between the received sequences at D from the relays, as shown in Figure 3.
between the received sequences at D from the relays, as shown in Figure 3.
The received signal is a superposition of received sequences, and it is modeled:
 (4)
(4)
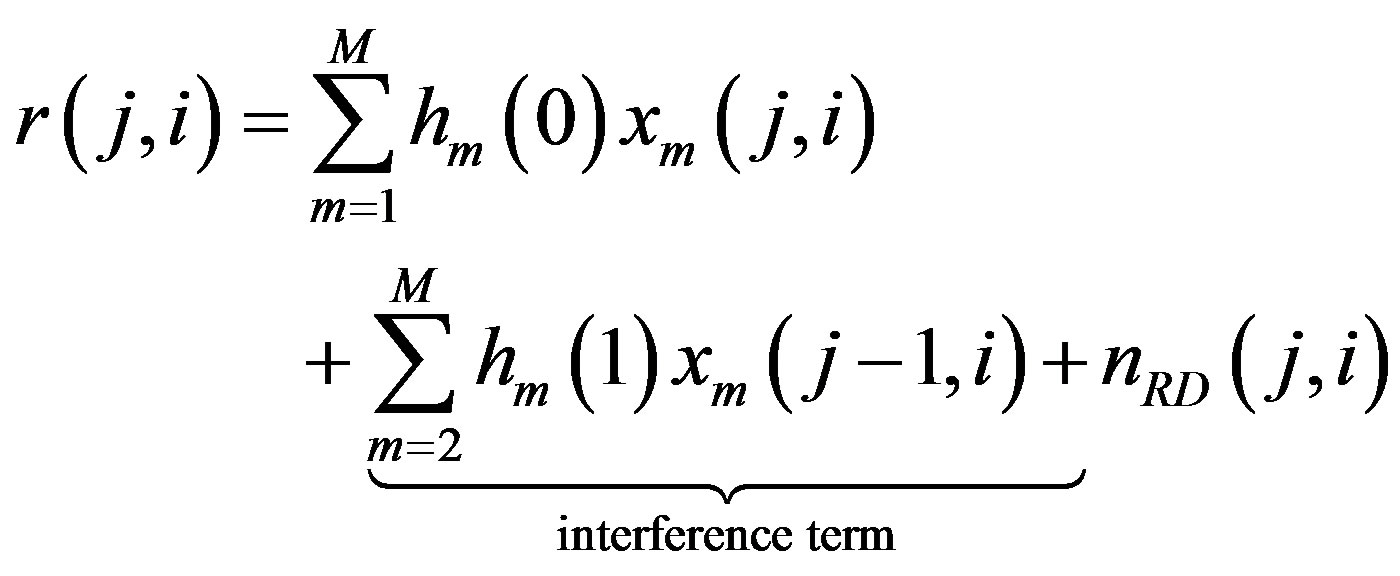 (5)
(5)
since .
.
Here  since
since 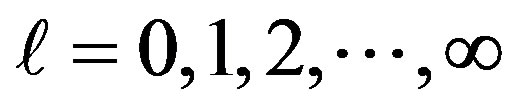 are the channel gains between Rm and D under imperfect synchronization and they are block Rayleigh fading.
are the channel gains between Rm and D under imperfect synchronization and they are block Rayleigh fading.  denotes current time-slot channel gain whereas
denotes current time-slot channel gain whereas 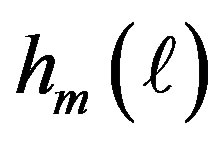 for
for 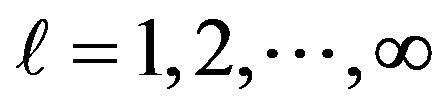 reflects the inter-symbol interference from the previous symbols. For some pulse shaping waveforms
reflects the inter-symbol interference from the previous symbols. For some pulse shaping waveforms 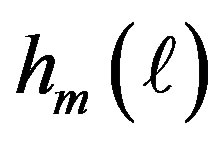 for
for 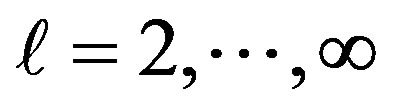 can be truncated since they are much less dominant [2].
can be truncated since they are much less dominant [2].
The condition of quasi-synchronization has been assumed in the above received signal model: 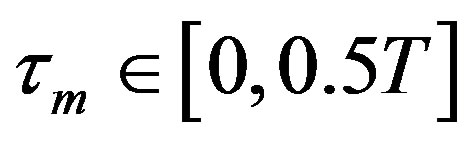 where T is the symbol period. This assumption is much easier to meet in practice. Due to sampling or matched filtering (whatever kind of pulse shaping is used) [2],
where T is the symbol period. This assumption is much easier to meet in practice. Due to sampling or matched filtering (whatever kind of pulse shaping is used) [2],  still causes inter-symbol interference (ISI). The strength of
still causes inter-symbol interference (ISI). The strength of  which represents the amount of time misalignment modeled by ratio:
which represents the amount of time misalignment modeled by ratio:
 (6)
(6)
Its value depends upon time misalignment and the Pulse Shaping Waveform (PSW) used. Whatever PSW is used,  for
for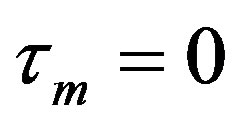 , and
, and 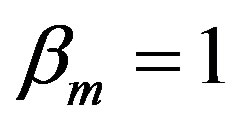 (0 dB) for
(0 dB) for  that’s due to the symmetry of PSW [2].
that’s due to the symmetry of PSW [2].
Rewriting (4,5) in term of the transmitted symbols
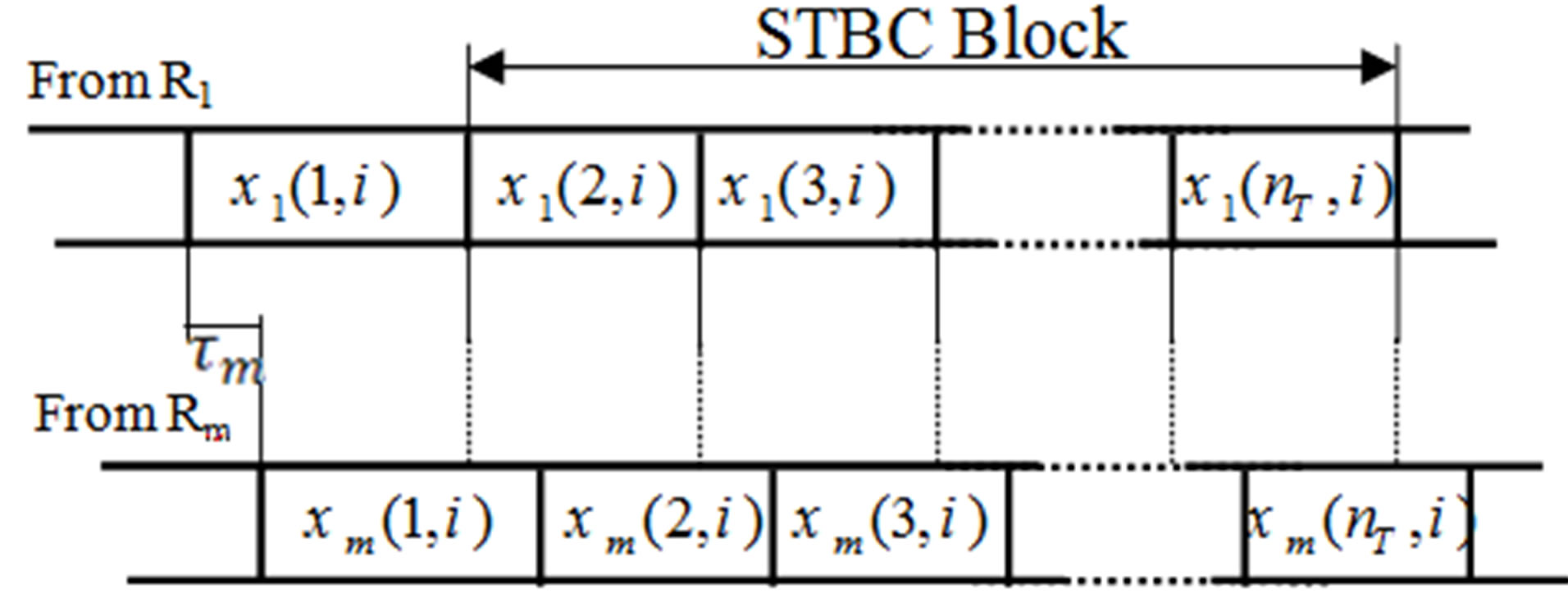
Figure 3. Received signals at node D under Quasi-Synch.
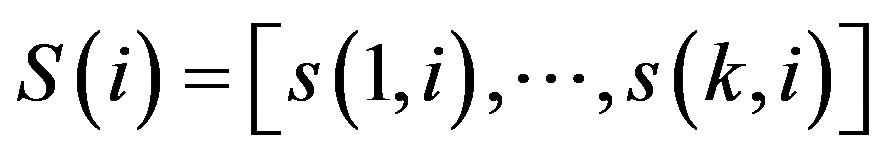 using the coding matrix, and then rearranging the result to get the following form:
using the coding matrix, and then rearranging the result to get the following form:
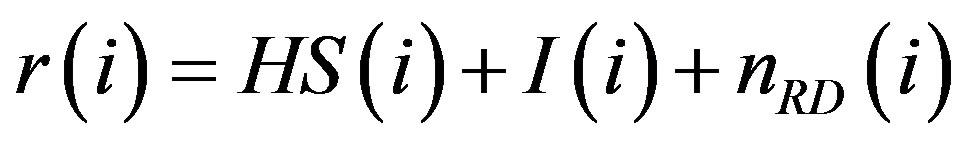 (7)
(7)
where: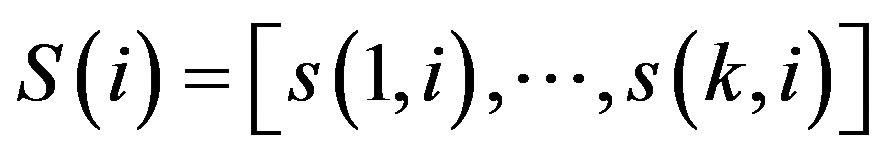 ,
, 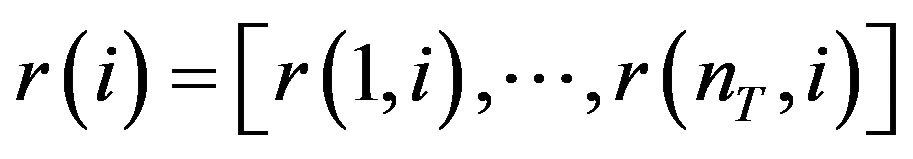 ,
, 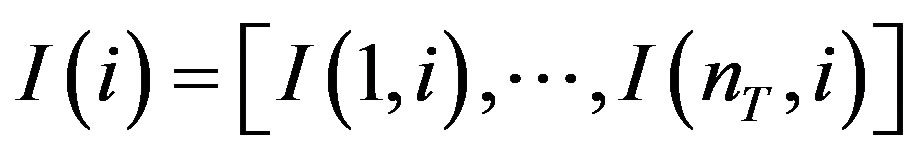 , and
, and 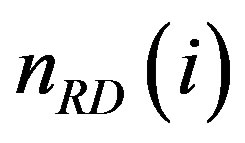 is the Additive Wide Gaussian Noise
is the Additive Wide Gaussian Noise
(AWGN) vector. Also,
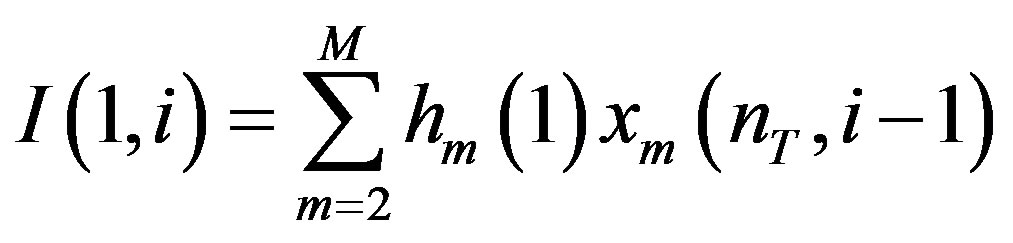 (8)
(8)
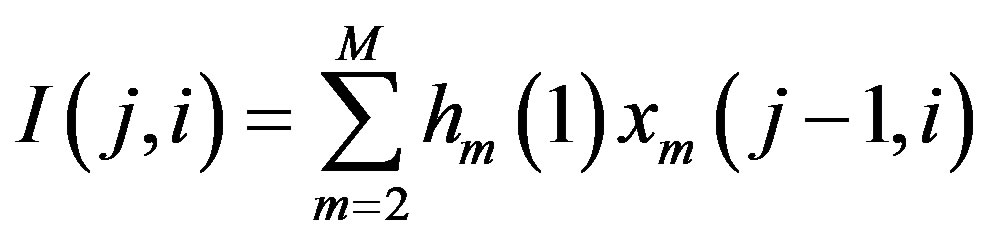 , for
, for 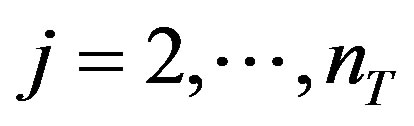 (9)
(9)
As mentioned, these codes which are used in this research are already orthogonal (the matrix manipulations as in [2] aren’t necessary), that’s mean that the decoding process can be done directly using  since
since 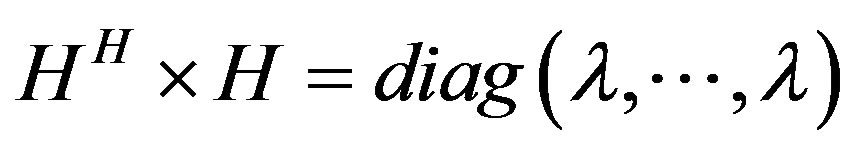 where
where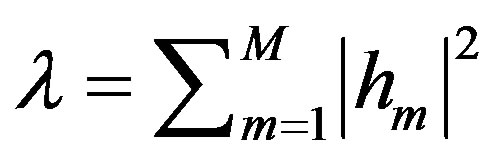 . The detection can be carried as follow:
. The detection can be carried as follow:
 (10)
(10)
The detection for  can be determined using:
can be determined using:
 (11)
(11)
Due to the interference component 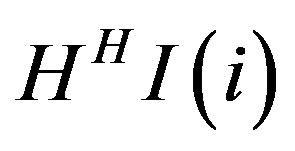 in (10), the orthogonality of STBC is damaged, a great degradation in the performance occurs, unless
in (10), the orthogonality of STBC is damaged, a great degradation in the performance occurs, unless  (the case of perfect synchronization) [2].
(the case of perfect synchronization) [2].
3. PIC Based Detection
The PIC approaches, in [2,3], proposed to mitigate the impact of imperfect synchronization just in the cases of 2, 3, and 4 relay nodes and with assumption of full knowledge of 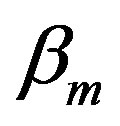 (
( and
and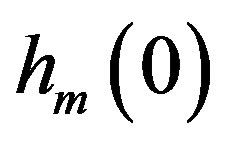 ). Here, we have modified the PIC approach to be suitable for M number of relay nodes. This approach is called as Generalized PIC or GPIC. Also, this generalization form assumes that just the average value of time misalignments is known at the receiver instead of knowing all time misalignments of the relay nodes; this assumption is more realistic than the assumption in [2,3] since step four of that approaches use an instantaneous value of hm(–1) whereas here we will use the average value for all instants. The average value of time misalignment can be determined using statistical data obtained through transmitting training data from the relay nodes over the channels to the destination. The GPIC approach will be illustrated in the following steps:
). Here, we have modified the PIC approach to be suitable for M number of relay nodes. This approach is called as Generalized PIC or GPIC. Also, this generalization form assumes that just the average value of time misalignments is known at the receiver instead of knowing all time misalignments of the relay nodes; this assumption is more realistic than the assumption in [2,3] since step four of that approaches use an instantaneous value of hm(–1) whereas here we will use the average value for all instants. The average value of time misalignment can be determined using statistical data obtained through transmitting training data from the relay nodes over the channels to the destination. The GPIC approach will be illustrated in the following steps:
Initialization
1) Set n = 0.
2) Determine 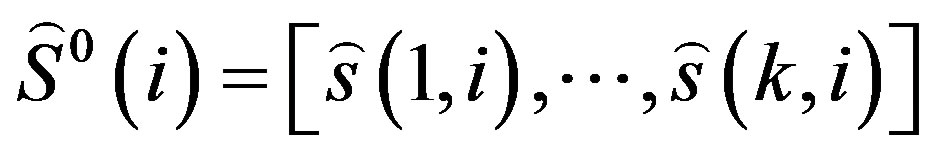 which is the result of LS search of Phase 1 transmission using (2).
which is the result of LS search of Phase 1 transmission using (2).
3) Using , calculate
, calculate 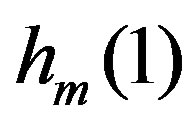 and
and 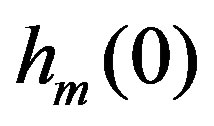 using (6) for all relay nodes.
using (6) for all relay nodes.
Note:
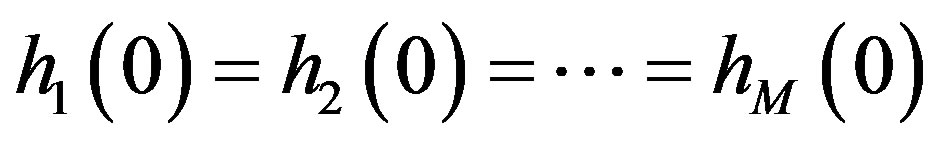 and
and 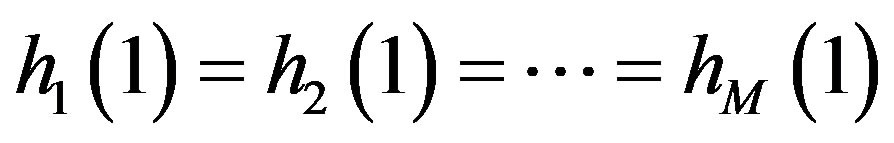
4) Remove ISI from 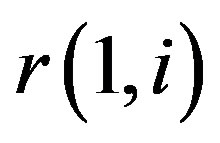 by calculating:
by calculating:

calculate 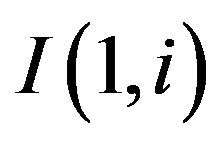 using (8) with the value of
using (8) with the value of  from step (3) and
from step (3) and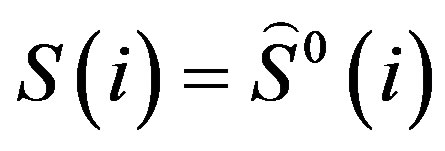 .
.
Iteration n: (n = 1, …, N)
5) Remove more ISI by calculating
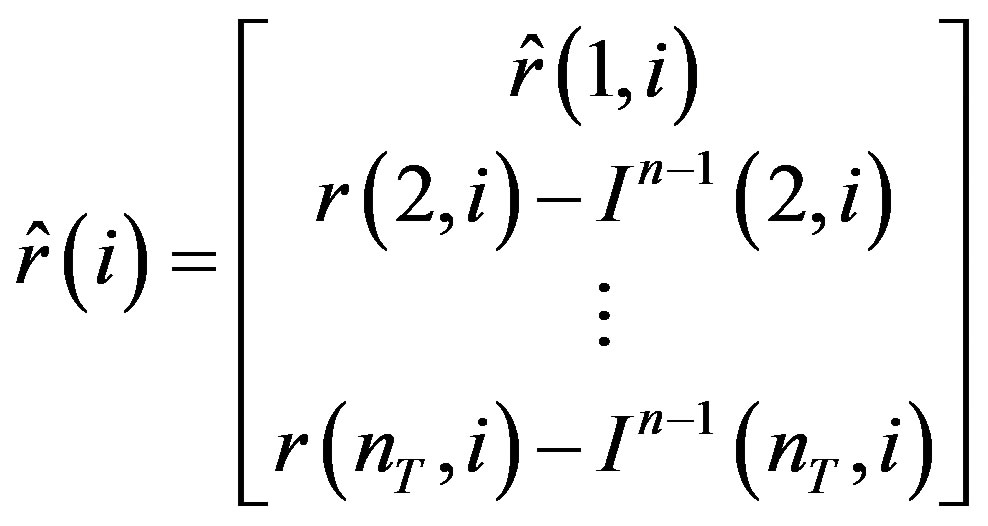 (12)
(12)
calculate 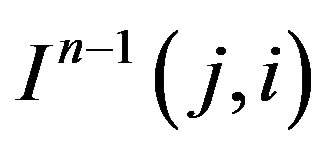 for
for 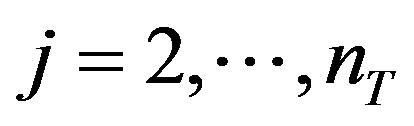 using (9) with the value of
using (9) with the value of  from step (3) and
from step (3) and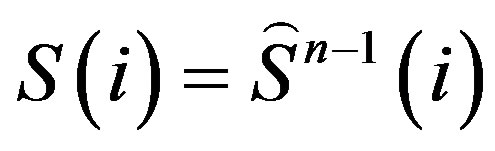 .
.
6) Determine H of (7), using  of step (3).
of step (3).
7) Determine  using (10).
using (10).
8) Apply LS search to detect the transmitted symbols  using (11).
using (11).
4. Simulation Examples
The case of four and six relay nodes will be simulated to test the scheme under Quasi-Synchronization.
Firstly, we want to evaluate our model in the case of four relay nodes to get insight how the process flows.
4.1. Case I: 4 Relay Nodes
Using the steps of [7], the code for four relay nodes is:
 (13)
(13)
Substituting the value of 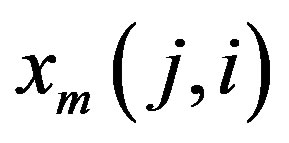 from (13) to (4) and (5) and then rewriting them, (7) become as follow:
from (13) to (4) and (5) and then rewriting them, (7) become as follow:
 (14)
(14)
where:
 ,
, 
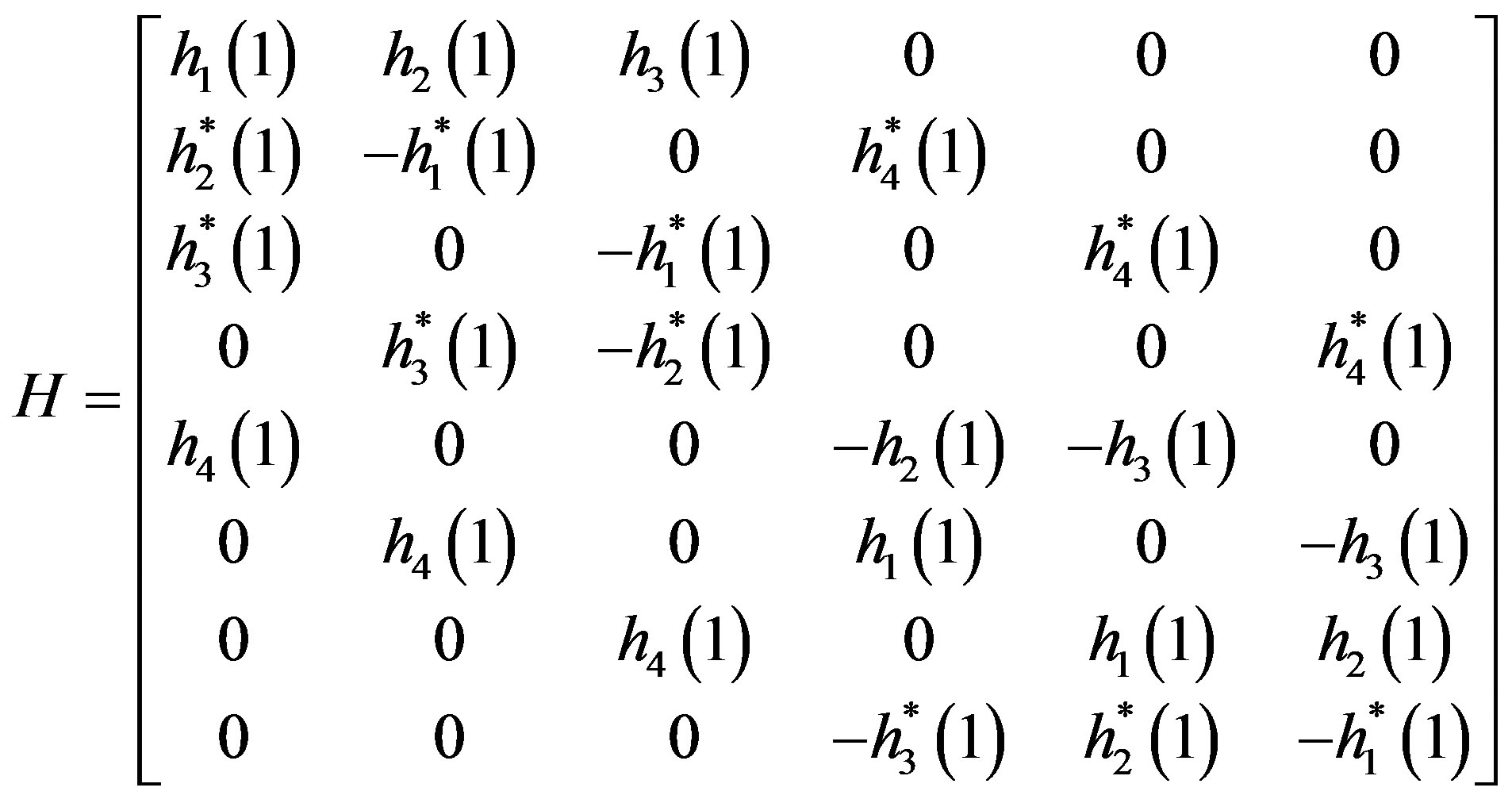
 , and
, and  is the AWGN vector.
is the AWGN vector.
Also,
 (15-a)
(15-a)
 (15-b1)
(15-b1)
 (15-b2)
(15-b2)
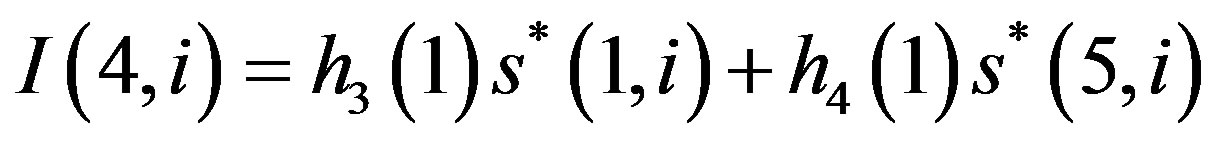 (15-b3)
(15-b3)
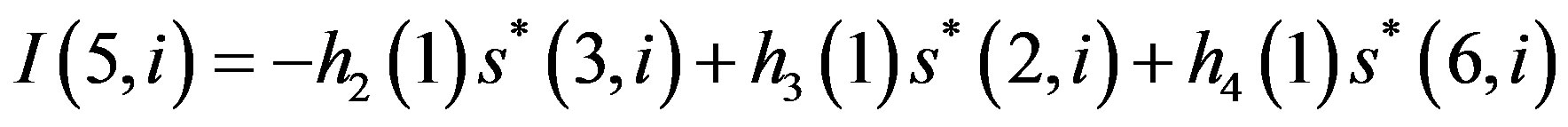 (15-b4)
(15-b4)
 (15-b5)
(15-b5)
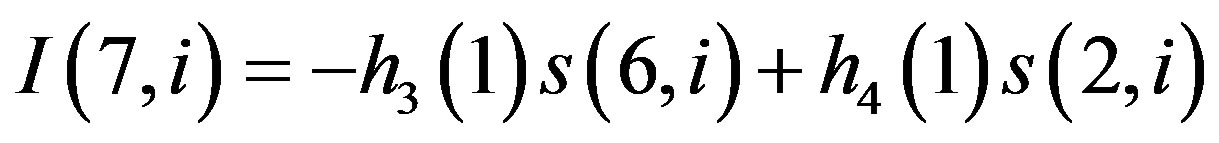 (15-b6)
(15-b6)
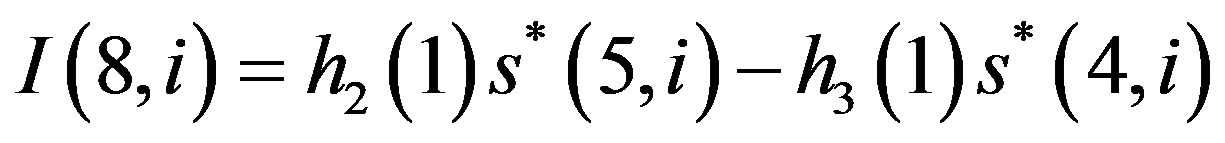 (15-b7)
(15-b7)
Using 8-PSK modulation, k =1, 2, 3 for 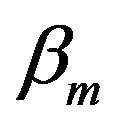 = (–1 to –5) dB with
= (–1 to –5) dB with 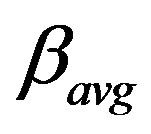 = –3 dB, the bit error rate (BER) performance of the proposed detector (GPIC) are shown in Figure 4. Also, the BER performance of perfect synchronized model, imperfect synchronization model, Direct Transmission (DT) model, and PIC detector with full delay knowledge of [2] is also included in same figures for comparative reasons.
= –3 dB, the bit error rate (BER) performance of the proposed detector (GPIC) are shown in Figure 4. Also, the BER performance of perfect synchronized model, imperfect synchronization model, Direct Transmission (DT) model, and PIC detector with full delay knowledge of [2] is also included in same figures for comparative reasons.
From Figure 4, you can observe that the GPIC approach is very effective to mitigate the impact of imperfect synchronization. Also, you can notice that there is small downgrade in performance of GPIC over PIC, especially in k = 1 and k = 2, but this downgrade is acceptable since it is minute difference (maximum downgrade = 0.7 dB at k = 2 and BER = 10–5) compared to reality addition to the scheme. At final iteration (k = 3), both of GPIC and PIC have nearly same performance even though GPIC uses the average value meanwhile PIC uses the exactly value of .
.
4.2. Case I: 6 Relay Nodes
Here, the BER of GPIC approach will be simulated when

Figure 4. The BER curves of GIC, PIC, Conventional detector, and DT when βm = –1 to –5 dB and m = 4.
there are six relay nodes. Evaluate the general form of Section (2) as what happen in Section (4.1) for the case of 4 relay nodes but use the coding matrix of six relay nodes which presented in [7]. Using the same simulation parameters in (4.2), the BER of GPIC in this case is shown in Figure 5. Even GPIC performance is downgrade when there are six relay nodes, but it still effective when its performance compared with conventional detector under Quasi-Synchronization.
5. Conclusion
The perfect synchronization is very important in DSTBC system and it is very difficult to maintain. In this research, the problem is examined and an effective GPIC approach for symbols detection has been proposed. This approach is a generalized version of already proposed approaches with a realistic conditions assumption. It is
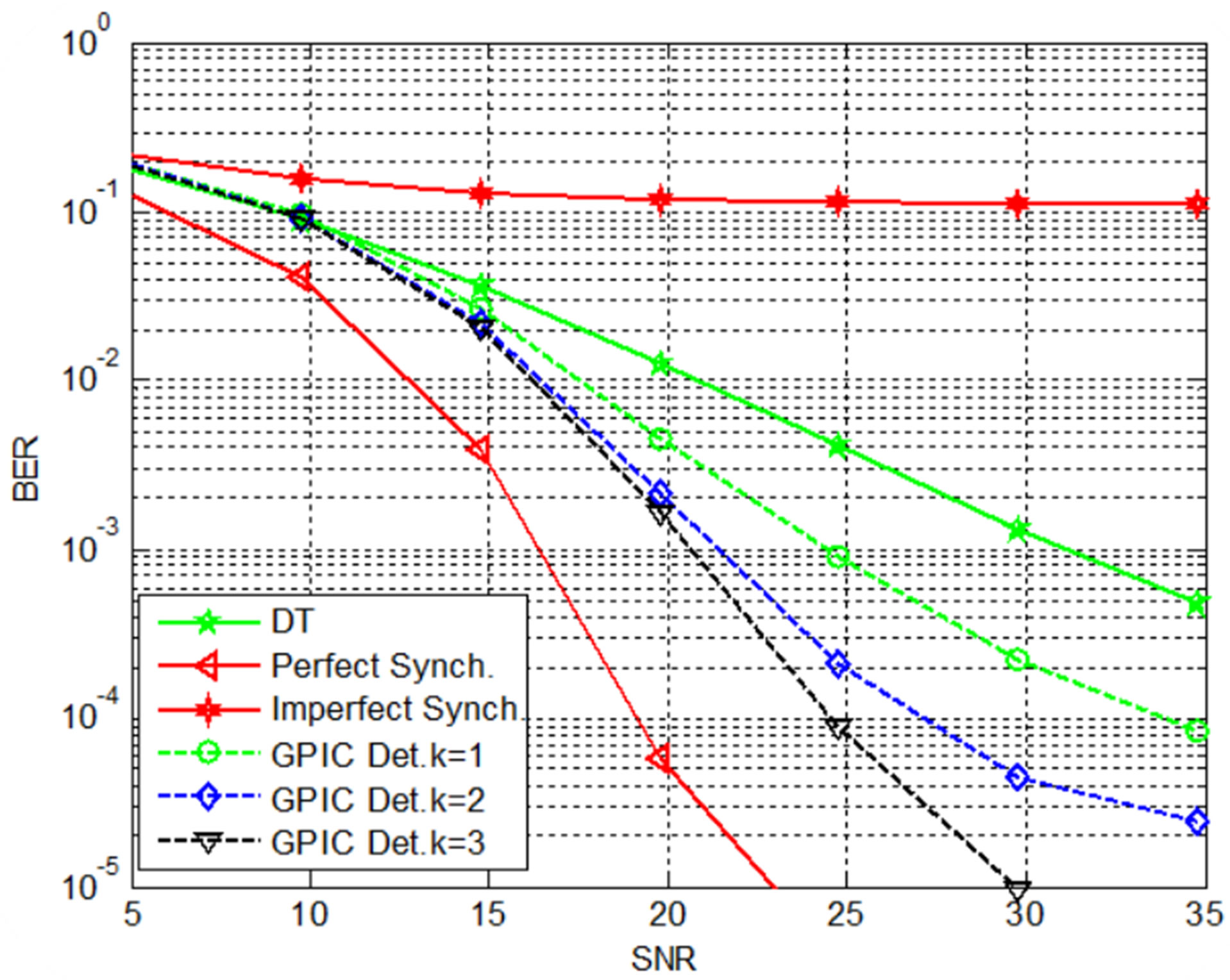
Figure 5. The BER curves of GIC, PIC, Conventional detector, and DT when βm = (–1 to –5) dB and m = 6.
suitable for any number of relay nodes and also it is not assume a full knowledge about the time misalignment. Also, it keeps the decoding in the same level of complexity, or a little bit larger than the conventional one, that is clear if you compare the equations of the approach here with the equations in that approaches of [2] and [3]. Although, it is a little bit complexity larger than conventional one but it has a great performance under imperfect synchronization conditions.
6. Acknowledgements
Authors would like to thank Dr. Hassan S. Ashour for his numerous discussions and suggestions that have found their way into this paper.
REFERENCES
- X. Li, “Space-Time Coded Multi-Transmission among Distributed Transmitters without Perfect Synchronisation,” IEEE Signal Processing Letter, Vol. 11, No. 12, 2004, pp. 948-951. doi:10.1109/LSP.2004.838213
- F.-C. Zheng, A. G. Burr and S. Olafsson, “Distributed Space-Time Block Coding for 3 and 4 Relay Nodes: Imperfect Synchronisation and a Solution,” IEEE 18th International Symposium on Personal, Indoor and Mobile, Radio Communications, Athens, 3-7 September 2007, pp. 1-5.
- F.-C. Zheng, A. G. Burr and S. Olafsson, “Near-Optimum Detection for Distributed Space-Time Block Coding under Imperfect Synchronisation,” IEEE Transactions on Communications, Vol. 56, No. 11, 2008, pp. 1795-1799. doi:10.1109/TCOMM.2008.070006
- F. Ng and X. H. Li., “Cooperative STBC-OFDM Transmission with Imperfect Synchronization in Time and Frequency,” 39th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 28 October 2005-1 November 2005, pp. 524-528.
- Z. Zhong, S. Zhu and A. Nallanathan, “Delay-Tolerant Distributed Linear Convolutional Space-Time Code with Minimum Memory Length under Frequency-Selective Channels,” IEEE Transactions on Wireless Communications, Vol. 8, No. 8, 2009, pp. 3944-3949. doi:10.1109/TWC.2009.081181
- J. N. Laneman, D. N. C. Tse and G. W. Wornell, “Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behaviour,” IEEE Transactions on Information Theory, Vol. 50, No. 12, 2004, pp. 3062-3080. doi:10.1109/TIT.2004.838089
- W. F. Su, X.-G. Xia and K. J. R. Liu, “A Systematic Design of High Rate Complex Orthogonal Space-Time Block Codes,” IEEE Communications Letters, Vol. 8, No. 6, 2004, pp. 380-382. doi:10.1109/LCOMM.2004.827429
- Y. Jia, C. Andrieu, R. J. Piechocki and M. Sandell, “Gaussian Approximation Based Mixture Reduction for near Optimum Detection in MIMO Systems,” IEEE Communications Letters, Vol. 9, No. 11, 2005, pp. 997-999. doi:10.1109/LCOMM.2005.11018
- S. Wei, D. L. Goeckel and M. Valenti, “Asynchronous Cooperative Diversity,” IEEE Transactions on Wireless Communications, Vol. 5, No. 6, 2006, pp. 1547-1557. doi:10.1109/TWC.2006.1638675

