Journal of Environmental Protection
Vol. 3 No. 9A (2012) , Article ID: 22950 , 11 pages DOI:10.4236/jep.2012.329131
Air Pollution Steady-State Advection-Diffusion Equation: The General Three-Dimensional Solution
![]()
1Department of Mathematics and Statistics (IFM/DME), Federal University of Pelotas (UFPel), Pelotas, Brazil; 2Graduate Program in Mechanical Engineering, Federal University of Rio Grande do Sul (UFRGS), Porto Alegre, Brazil; 3Institute of Atmospheric Sciences and Climate (ISAC), National Research Council (CNR), Bologna, Italy.
Email: t.tirabassi@isac.cnr.it
Received June 15th, 2012; revised July 14th, 2012; accepted August 17th, 2012
Keywords: Advection-diffusion equation; Analytical solution; Laplace transform; Air pollution modeling; Atmospheric Boundary Layer; Eulerian models
ABSTRACT
Atmospheric air pollution turbulent fluxes can be assumed to be proportional to the mean concentration gradient. This assumption, along with the equation of continuity, leads to the advection-diffusion equation. Many models simulating air pollution dispersion are based upon the solution (numerical or analytical) of the advection-diffusion equation assuming turbulence parameterization for realistic physical scenarios. We present the general steady three-dimensional solution of the advection-diffusion equation considering a vertically inhomogeneous atmospheric boundary layer for arbitrary vertical profiles of wind and eddy-diffusion coefficients. Numerical results and comparison with experimental data are shown.
1. Introduction
The processes governing the transport and diffusion of pollutants are numerous, and of such complexity that it would be impossible to describe them without the use of mathematical models. Such models therefore constitute an indispensable technical instrument of air quality management.
The theoretical approach to the problem essentially assumes two basic forms. In the Eulerian approach, diffusion is considered, at a fixed point in space, proportional to the local gradient of the concentration of the diffused material and is based on the resolution, on a fixed spatial-temporal grid, of the equation of the mass conservation of the pollutant chemical species. Lagrangian models are the second approach and they differ from Eulerian ones in adopting a system of reference that follows atmospheric motions. Initially, the term Lagrangian was used only to refer to moving box models that followed the mean wind trajectory [1]. Currently, this class includes all models that decompose the pollutant cloud into discrete “elements”, such as segments, puffs or computer virtual particles [1]. In Lagrangian particle models pollutant dispersion is simulated through the motion of computer virtual particles whose trajectories allow the calculation of the concentration field of the emitted substance. The underlying hypothesis is that the combination of the trajectories of such particles simulates the paths of the air particles situated, at the initial moment, in the same position. The motion of the particles can be reproduced both in a deterministic way and in a stochastic way.
In this paper we limited ourselves to the Eulerian approach, and in particular to the K model, where the flow of a given field is assumed to be proportional to the gradient of an appropriate mean variable [2]. K-theory has its own limits, but its simplicity has led to a widespread use as the mathematical basis for simulating pollution dispersion. Most of Eulerian models are based on the numerical solution of the equation of mass conservation of the pollutant chemical species. Such models are most suitable to confronting complex problems, for example, the dispersion of pollutants over complex terrain or the diffusion of non-inert pollutants.
However, a progressive and continuous effort to obtain analytical solutions of the advection-diffusion equation (ADE) has been made in the last years. In fact analytical solutions of equations are of fundamental importance in understanding and describing physical phenomena. Analytical solutions explicitly take into account all the parameters of a problem, so that their influence can be reliably investigated and it is easy to obtain the asymptotic behavior of the solution, which is usually very much more tedious to generate through numerical calculations. Moreover, like the Gaussian solution, that was the first solution of ADE with the wind and the eddy diffusivity coefficients supposed constant in space, they may suggest the construction of operative analytic model. Gaussian models, so named because they are based on the Gaussian solution, are forced to represent real situations by means of empirical parameters, referred to as “sigmas”. Gaussian models are fast, simple, do not require complex meteorological input, and describe the diffusive transport in an Eulerian framework, making easy use of the Eulerian nature of measurements. For these reasons they are still widely employed for regulatory applications by environmental agencies all over the world although their well known intrinsic limits.
A significant number of works regarding ADE analytical solution (mostly two-dimensional solutions) is available in the literature. References [3-16] are considered relevant by the authors. However, the above solutions are valid for very specialized situations: only ground level sources or infinite height of the Atmospheric Boundary Layer (ABL) or specific wind and eddy diffusivities vertical profiles. Vilhena et al. [17] presented an analytical solution, called ADMM (Advection Diffusion Multilayer Method) method, for a limited ABL and general wind and eddy diffusivities vertical profiles, but expressed by a stepwise function (see also [18-20]). Many of the above solutions were utilized in operative air pollution models [21].
Finally a general two-dimensional solution without any restriction in the spatial function of wind and eddy diffusion coefficients was presented in Wortmann et al. [22] and Moreira et al. [23,24]. The solving methodology was the Generalized Integral Laplace Transform Technique (GILTT) that is an analytical series solution including the solution of an associate Sturm-Liouville problem, expansion of the pollutant concentration in a series in terms of the attained eigenfunction, replacement of this expansion in the ADE and, finally, taking moments. This procedure leads to a set of differential ordinary equations that is solved analytically by Laplace transform technique. A complete review of the GILTT method is given in [25].
In this paper we extend these last results and we present a three-dimensional solution for a limited height ABL and without any restriction in the spatial function of wind and eddy diffusion coefficients. Cauchy-Kowalewski theorem [26] guarantees the existence and uniqueness of an analytical solution of the ADE, so we are presenting the general solution of three-dimensional ADE.
2. The Three-Dimensional Solution
The ADE for air pollution in the atmosphere is essentially a statement of conservation of the suspended material and in Cartesian geometry it can be written as [27]:
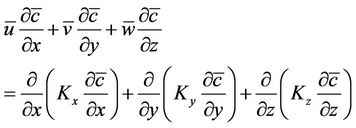 (1)
(1)
Here 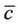 denotes the mean concentration of a passive contaminant (g/m3),
denotes the mean concentration of a passive contaminant (g/m3), 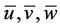 are the Cartesian components of the mean wind (m/s) in the directions x (0 < x < Lx), y (0 < y < Ly) and z (0 < z < h) and
are the Cartesian components of the mean wind (m/s) in the directions x (0 < x < Lx), y (0 < y < Ly) and z (0 < z < h) and 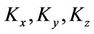 are the eddy diffusivities (m2/s). Equation (1) is subjected to the following boundary and source conditions:
are the eddy diffusivities (m2/s). Equation (1) is subjected to the following boundary and source conditions:
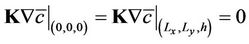 , (2)
, (2)
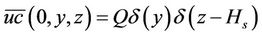 , (3)
, (3)
where 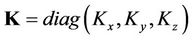 is the diagonal diffusion matrix, Q is the emission rate (g/s), h the height of the ABL (m), Hs the height of the source (m), Lx and Ly are the limits in the x and y-axis and far away from the source (m) and
is the diagonal diffusion matrix, Q is the emission rate (g/s), h the height of the ABL (m), Hs the height of the source (m), Lx and Ly are the limits in the x and y-axis and far away from the source (m) and 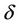 represents the Dirac delta function. The source position is at x = 0, y = y0 and z = Hs.
represents the Dirac delta function. The source position is at x = 0, y = y0 and z = Hs.
In order to solve problem (1), taking advantage of the well-known solution of the two-dimensional problem with advection in the x-direction by the GILTT method [25], we initially apply the integral transform technique in the y variable. To this end, we expand the pollutant concentration as:
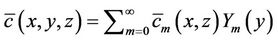 , (4)
, (4)
where 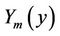 are a set of orthogonal eigenfunctions, given by
are a set of orthogonal eigenfunctions, given by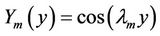 , and
, and 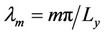 (m = 0, 1, 2, ∙∙∙) are respectively the set of eigenvalues.
(m = 0, 1, 2, ∙∙∙) are respectively the set of eigenvalues.
To determine the unknown coefficient 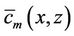 we manipulate equation (1) applying the chain rule for the diffusion terms. After substitute equation (4) in the resulting equation and taking moments, meaning applying the operator
we manipulate equation (1) applying the chain rule for the diffusion terms. After substitute equation (4) in the resulting equation and taking moments, meaning applying the operator , we obtain the result:
, we obtain the result:
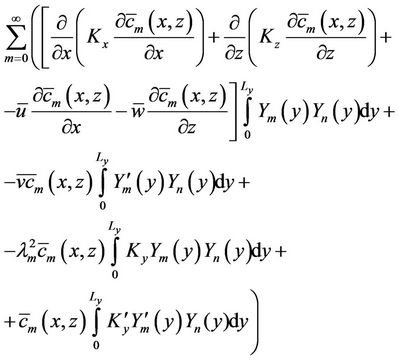 (5)
(5)
Defining the integrals appearing in the above equation like:
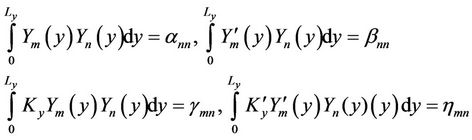
the equation (5) is rewrite as:
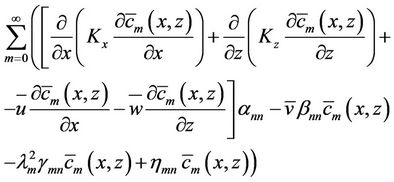 (6)
(6)
Without losing generality, we specialize the application for a pollutant dispersion problem in ABL, assuming that the speeds 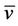 and
and 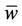 takes the null value. We neglect the diffusion component Kx because we assume that the advection is dominant in the x-direction, i.e.,
takes the null value. We neglect the diffusion component Kx because we assume that the advection is dominant in the x-direction, i.e.,
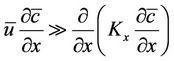 . Further we also consider that Ky has only dependence on the z-direction. After these assumptions, equation (6) is rewritten in matrix fashion as a set of M + 1 two-dimensional diffusion equations:
. Further we also consider that Ky has only dependence on the z-direction. After these assumptions, equation (6) is rewritten in matrix fashion as a set of M + 1 two-dimensional diffusion equations:
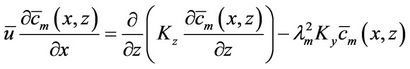 (6)
(6)
The problem (6) is then solved by the GILTT method. Following the work of Moreira et al. [25] and taking advantage of the well known solution for the stationary problem with advection in the x direction, we pose the solution of problem (6) in the form:
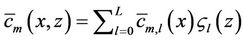 (7)
(7)
where 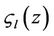 are a set of orthogonal eigenfunctions, given by
are a set of orthogonal eigenfunctions, given by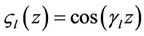 , and
, and 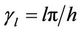 (l = 0, 1, 2, ∙∙∙) are respectively the set of eigenvalues.
(l = 0, 1, 2, ∙∙∙) are respectively the set of eigenvalues.
Replacing equation (7) in Equation (6) and taking moments, we get the first order matrix differential equation:
 (8)
(8)
for m = 0:M, where Pm(x) is the column vector whose components are 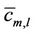 for l = 0:L. The matrix F is defined as
for l = 0:L. The matrix F is defined as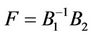 . The entries of matrices B1 and B2 are, respectively, given by:
. The entries of matrices B1 and B2 are, respectively, given by:

Similar procedure leads to the boundary condition of problem (9):
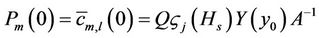 , (9)
, (9)
where A−1 is the inverse of matrix A having the entry
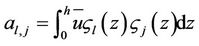 .
.
Problem (9) is solved applying Laplace transform and diagonalization. Firstly, transforming x in s and P em 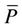 the equation becomes
the equation becomes
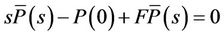 , (10)
, (10)
where the overbar represents the transformed potential.
The matrix F is decomposed in eigenvectors and eigenvalues as F = XDX−1 where X is the matrix of the eigenvectors and D is the diagonal matrix of the eigenvalues of F. Then, the equation (10) became
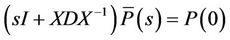 , (11)
, (11)
where I is the matrix identity. After algebraic manipulation we get
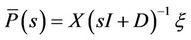 , (12)
, (12)
where 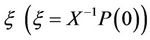 is found from the equation
is found from the equation 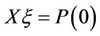 , and their values are calculated by LU factorization. The elements of the matrix (sI + D) have the form
, and their values are calculated by LU factorization. The elements of the matrix (sI + D) have the form 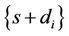 where di are the eigenvalues of the matrix F and the elements of (sI + D)−1 are 1/(s + di) whose inverse Laplace transform is
where di are the eigenvalues of the matrix F and the elements of (sI + D)−1 are 1/(s + di) whose inverse Laplace transform is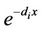 . Let be G(x) the diagonal matrix whose elements are
. Let be G(x) the diagonal matrix whose elements are 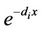 the final solution is then given by
the final solution is then given by
 . (13)
. (13)
Then, using equation (7),
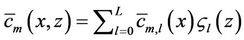 , we obtain the solution of the 2D problem, where
, we obtain the solution of the 2D problem, where 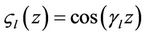 and
and 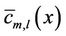 comes from the solution of the transformed problem given by equation (8). Once
comes from the solution of the transformed problem given by equation (8). Once 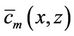 is known we are in a position to write the final three-dimensional solution of problem (1) which is given by equation (4),
is known we are in a position to write the final three-dimensional solution of problem (1) which is given by equation (4),
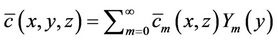 , (14)
, (14)
where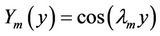 . This solution is named as 3DGILTT (three-dimensional GILTT solution).
. This solution is named as 3DGILTT (three-dimensional GILTT solution).
Since this problem is a special case of the CauchyKowalewsky theorem, existence and uniqueness is guaranteed. Convergence of the solution may be shown by a genuine mathematical convergence criterion. Note that the only numerical error comes from truncation, which is determined from the Sturm-Liouville problem. Recalling that the structure of the contaminant is essentially determined by advection and diffusion, present in form of a velocity vector 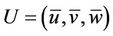 and a diagonal diffusion matrix
and a diagonal diffusion matrix , which define a smoothness length scale by the maximum norm of the expression
, which define a smoothness length scale by the maximum norm of the expression . Thus one may conclude that with decreasing length (
. Thus one may conclude that with decreasing length ( and m an increasing integer number) variations in the solution become spurious.
and m an increasing integer number) variations in the solution become spurious.
Upon interpreting 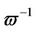 as a sampling density, one may now employ the Cardinal Theorem of Interpolation Theory [28] in order to find the truncation
as a sampling density, one may now employ the Cardinal Theorem of Interpolation Theory [28] in order to find the truncation  in equation (4) that leaves the analytical solution almost exact, i.e. introduces only functions that vary significantly in length scales beyond the mentioned limit. Thus, the Cardinal Theorem of Interpolation theory may be cast in form of a convergence criterion as follows.
in equation (4) that leaves the analytical solution almost exact, i.e. introduces only functions that vary significantly in length scales beyond the mentioned limit. Thus, the Cardinal Theorem of Interpolation theory may be cast in form of a convergence criterion as follows.
The square integrable function 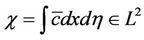
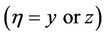 with spectrum
with spectrum  which is bounded by
which is bounded by  has an exact solution for a finite expansion. This statement expresses the Cardinal Theorem of Interpolation Theory for our problem (see Bodmann et al. [29]). Since the cut-off, i.e. the afore mentioned supreme defines some sort of a sampling density, its introduction is an approximation and is related to convergence of the approach and Parseval’s theorem may be used to estimate the error. In order to keep the solution error within a specified order of magnitude, the expansion in the domain of interest has to contain n + 1 terms. For the bounded spectrum and according to the theorem the solution is then exact. In our approximation, if m is properly chosen such that the cut-off part of the spectrum is negligible, then the found solution is almost exact.
has an exact solution for a finite expansion. This statement expresses the Cardinal Theorem of Interpolation Theory for our problem (see Bodmann et al. [29]). Since the cut-off, i.e. the afore mentioned supreme defines some sort of a sampling density, its introduction is an approximation and is related to convergence of the approach and Parseval’s theorem may be used to estimate the error. In order to keep the solution error within a specified order of magnitude, the expansion in the domain of interest has to contain n + 1 terms. For the bounded spectrum and according to the theorem the solution is then exact. In our approximation, if m is properly chosen such that the cut-off part of the spectrum is negligible, then the found solution is almost exact.
3. Model Application to Different Meteorological Scenarios and against Experimental Data
In order to illustrate the behavior of the discussed solution we report a simulation of contaminant dispersion in the ABL for different scenarios. Moreover, we evaluate the performance against experimental ground-level concentration. To do this we first have to introduce a boundary layer parameterization.
3.1. Atmospheric Boundary Layer Parameterization
Define abbreviations and acronyms the first time they are used in the text, even after they have been defined in the abstract. In air pollution diffusion modeling the choice of a turbulence parameterization represents a fundamental aspect for the contaminants dispersion modeling. From a physical point of view a turbulence parameterization is an approximation to nature in the sense that we are putting in mathematical models an approximated relation that in principle can be used as a surrogate for the natural true unknown term [30]. The reliability of each model strongly depends on the way as turbulent parameters are calculated and related to the current understanding of the ABL [31].
The literature reports many, greatly varied formulae, for the calculation of the vertical turbulent diffusion coefficient [2]. As an example of application of our new solution we tested the following vertical and lateral diffusion parameterization suggested by Degrazia et al. [32], derived from Batchelor [33], for convective conditions:
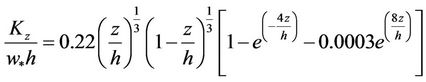 (15)
(15)
 (16)
(16)
with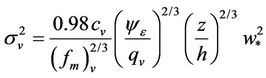 ;
;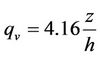 ;
;
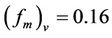 and
and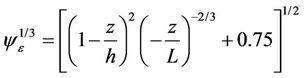 .
.
More, k is the von Karman constant (k = 0.4), 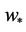 is the convective velocity scale, L is the Monin-Obukhov length,
is the convective velocity scale, L is the Monin-Obukhov length,  is the Eulerian standard deviation of the longitudinal turbulent velocity,
is the Eulerian standard deviation of the longitudinal turbulent velocity, 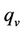 is the stability function,
is the stability function,  is the non-dimensional molecular dissipation rate function,
is the non-dimensional molecular dissipation rate function, 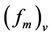 is the peak wavelength of the turbulent velocity spectra and
is the peak wavelength of the turbulent velocity spectra and 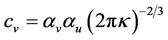 with
with 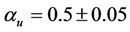 and
and 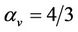 [34,35].
[34,35].
Following Pleim and Chang [36] during convective conditions at 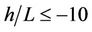 the following relation is used:
the following relation is used:
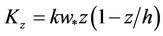 (17)
(17)
During stable and neutral conditions at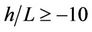 :
:
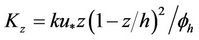 (18)
(18)
where 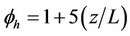 in stable conditions and
in stable conditions and 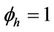 in neutral conditions.
in neutral conditions.
Degrazia et al. [37] proposed for the stable boundary layer an algebraic formulation for the eddy diffusivities in the y-direction. It takes the form:
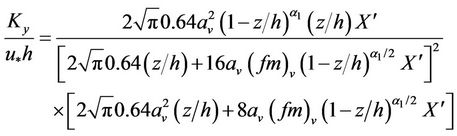 (19)
(19)
where 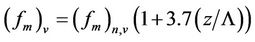 is the frequency of the spectral peak,
is the frequency of the spectral peak,  is the frequency of the spectral peak in the neutral stratification [38],
is the frequency of the spectral peak in the neutral stratification [38], ![]() (
(![]() ;
;![]() [39]) is the local Monin-Obukhov length,
[39]) is the local Monin-Obukhov length, ![]() where
where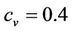 ,
, 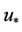 is the friction velocity and
is the friction velocity and  represents the non-dimensional distance.
represents the non-dimensional distance.
The wind speed profile can be described by a power law expressed as follows [40]:
 (20)
(20)
where 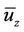 and
and  are the mean wind speeds horizontal to heights z and z1 and n is an exponent that is related to the intensity of turbulence [41].
are the mean wind speeds horizontal to heights z and z1 and n is an exponent that is related to the intensity of turbulence [41].
Thus, in this study we introduce the eddy diffusivities and the wind profile described above in the 3D-GILTT model (Equation (14)) to calculate the ground-level concentration of emissions released from an elevated continuous source point in an unstable/neutral ABL. For the application to different meteorological scenarios the eddy diffusivities (17)-(19) are used, while in the comparisons against experimental data eddy diffusivities (15) and (16) are used.
3.2. Application to Different Meteorological Scenarios
Given the complexity of the solution, it is useful to show the behavior of the solution in different scenarios. It is possible to see a graphical representation in figure 1 of the ground level concentrations predicted by the three dimensional solution for different source heights in convective condition.
Also to show the influence of the atmospheric turbulence we present in figure 2 the non-dimensional concentration in function of the non-dimensional distance from the source (Hs = 0.1 h) for five different meteorological scenarios (exponent of power wind profile α and inverse of Monin-Obukhov length (1/L) values for different meteorological scenarios are showed in Table 1).
In figure 3, the influence of the source height is showed. In fact, the non-dimensional vertical concentrations at three distances, and four different source heights is presented in convective condition.
3.3. Application against Experimental Data
In order to show the performance of the present solution of the ADE and the performance of the proposed ABL parameterizations we have applied the model using the Copenhagen and Kinkaid experimental datasets. The first experiment is carried out in the northern part of Copenhagen, described by Gryning and Lyck [42]. It consisted of tracer released without buoyancy from a tower at a height of 115 m, and collection of tracer sampling units at the ground-level positions at the maximum of three crosswind arcs. The sampling units were positioned at
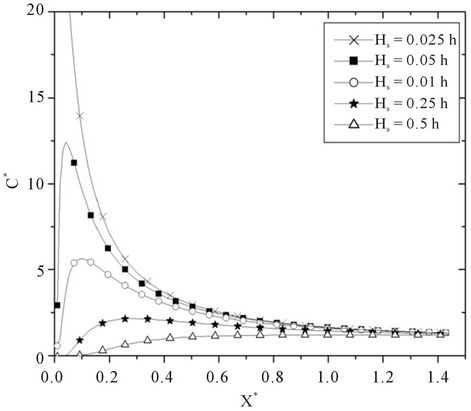
Figure 1. Ground level concentrations predicted by the three dimensional solution for different source heights in convective conditions (1/L = −0.01 m−1).
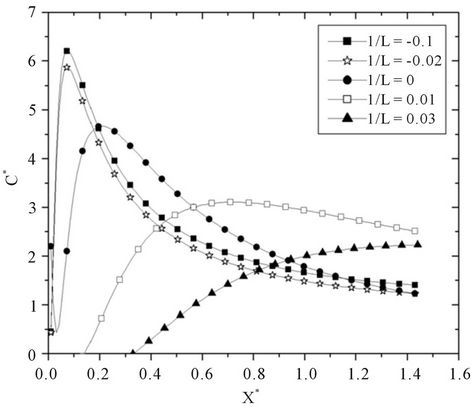
Figure 2. Non-dimensional concentration (C* = cuh2/Q) in function of the non-dimensional distance (X* = xu*/uh) from the source (Hs = 0.1 h) for 5 different meteorological scenarios.

Table 1. Exponent of power wind profile (α) and inverse of Monin-Obukhov length (1/L) values for different meteorological scenarios.
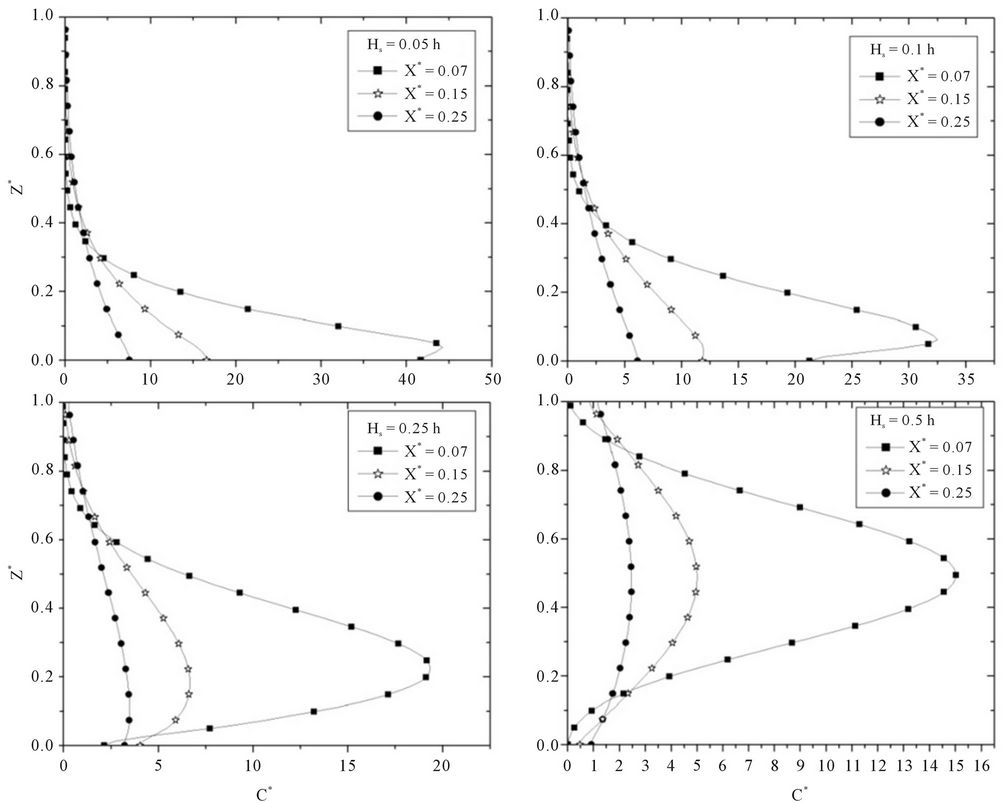
Figure 3. Non-dimensional concentration (C* = cuh2/Q) versus non-dimensional height (Z* = z/h) in convective conditions (1/L = −0.01 m−1) for three different distances from the source (X* = xw*/uh) and four source height (Hs = 0.05 h; 0.1 h; 0.25 h; 0.5 h).
two to six kilometers from the point of release. The site was mainly residential with a roughness length of the 0.6 m.
The Kinkaid experiment was conducted at Illinois, USA, during convective conditions (for −h/L > 10) and is described in the work of Hanna and Paine [43]. The Kinkaid field campaign concerns an elevated release in a flat farmland with some lakes. During the experiment, SF6 was released from 187 tall stacks and recorded on a network consisting of roughly 200 samplers positioned in arcs from 0.5 to 50 km downwind of the source. The data set includes the meteorological parameters as friction velocity, Monin-Obukhov length and height of boundary layer. The measured concentration level is frequently irregular with high and low concentrations occurring intermittently along same arc, moreover there are frequent gaps in the monitoring arcs. For the above reasons a variable has been assigned as a quality factor in order to indicate the degree of readability of data [44]. The quality indicator (from 0 to 3) has been assigned. Here, only the data with quality factor 3 were considered.
Figures 4 and 5 show the comparison of 3D-GILLT predicted concentrations against observed data in the Copenhagen and Kinkaid experiments. We can observe that the obtained concentrations reproduce acceptably the observed data.
In the further we use standard statistical indices in order to compare the quality of the new approach against other models. While the present approach (3D-GILTT) is based on a genuine three dimensional description an earlier analytical approach called GILTTG uses a Gaussian assumption for the horizontal transverse direction [25]. In the GILTTG the crosswind integrated concentration cy(x, z, t) (i.e., two-dimensional) is obtained analytically using the GILTT method. To calculate the three-dimensional concentration c(x, y, z, t) lateral diffusion (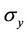 )
)

Figure 4. Observed and predicted scatter diagram of ground-level centerline concentrations using the 3D-GILTT approach for the Copenhagen experiment. Lines indicate a factor of two.
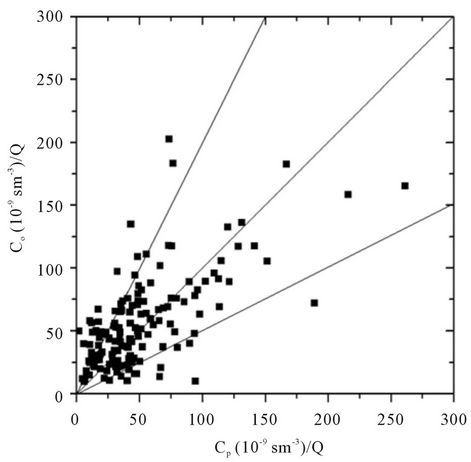
Figure 5. Observed and predicted scatter diagram of ground-level centerline concentrations using the 3D-GILTT approach for the Kinkaid experiment. Lines indicate a factor of two.
needs to be included, that is, it is assumed that the plume has a Gaussian concentration distribution in the lateral. So, to calculate the concentration the following expression is assumed:

Note that we present the two analytical model approaches, since the earlier one was found to be acceptable in comparison to other approaches found in the literature and both give a solution in closed form. For the Copenhagen data set, our results are also compared with the one obtained with the GIADMT method [18]. Basically the GIADMT method consists on the solution of the GITT (Generalized Integral Transform Technique) transformed problem by the ADMM method. The ADMM approach solves the two-dimensional ADE with variable wind profile and eddy diffusivity coefficient [19]. The main idea here relies on the discretisation of the ABL in a multilayer domain, assuming in each layer that the eddy diffusivity and wind profile take averaged values. The resulting ADE in each layer is then solved by Laplace transform.
Tables 2 and 3 present some performances evaluations of the model results using the statistical evaluation procedure described by Hanna [45] and defined in the following way:
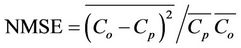 ,
,
 ,
,
 ,
,
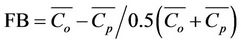 ,
,
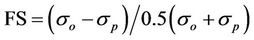 where NMSE is the normalized mean square error, COR the correlation coefficient, FA2 is the fraction of data (%, normalized to 1), FB the fractional bias, FS the fractional standard deviations. Subscripts o and p refer to observed and predicted quantities, respectively, and the overbar indicates an averaged value. The statistical index FB says if the predicted quantities underestimate or overestimate the observed ones. The statistical index NMSE represents the model values dispersion in respect to data dispersion.
where NMSE is the normalized mean square error, COR the correlation coefficient, FA2 is the fraction of data (%, normalized to 1), FB the fractional bias, FS the fractional standard deviations. Subscripts o and p refer to observed and predicted quantities, respectively, and the overbar indicates an averaged value. The statistical index FB says if the predicted quantities underestimate or overestimate the observed ones. The statistical index NMSE represents the model values dispersion in respect to data dispersion.
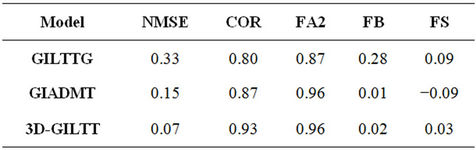
Table 2. Statistical comparison between models using the Copenhagen dataset.

Table 3. Statistical comparison between models using the Kinkaid dataset.
The best results are expected to have values near to zero for the indices NMSE, FB and FS, and near to 1 in the indices COR and FA2. The statistical indices point out that a reasonable agreement is obtained between experimental data and the 3D-GILTT model for both cases.
In order to validate the two models (GILTTG and 3D-GILTT) we fit the predicted versus observed values by a linear regression (see figures 6 and 7) for both experiments, where, the closer they intersect to the origin and the closer the slope is to unity the better is the approach. In order to perform a model validation we introduced an index  with
with

Figure 6. Linear regression for the GILTTG (balls) and 3D-GILTT (stars) using the Copenhagen dataset. The bisector was added as an eye guide.

Figure 7. Linear regression for the GILTTG (balls) and 3D-GILTT (stars) using the Kinkaid dataset. The bisector was added as an eye guide.
 , which if identical zero indicates a perfect match between the model and the experimental findings. Here a is the slope, b the intersection,
, which if identical zero indicates a perfect match between the model and the experimental findings. Here a is the slope, b the intersection,  of the experimental data and
of the experimental data and  its arithmetic mean. Since the experiment is of stochastic character whereas the stochastic properties are hidden in the model parameters, considerable fluctuations are present. Nevertheless, by comparison one observes in Table 4 that the present approach yields the better description of the data for the Copenhagen experiment.
its arithmetic mean. Since the experiment is of stochastic character whereas the stochastic properties are hidden in the model parameters, considerable fluctuations are present. Nevertheless, by comparison one observes in Table 4 that the present approach yields the better description of the data for the Copenhagen experiment.
4. Conclusions
In the present work we developed a novel analytical description of air pollution dispersion in ABL. We solved the steady-state three-dimensional ADE for general vertical profiles of wind and eddy diffusivity. The closed form solution is obtained using an approach set-up by spectral theory together with an integral transform, which in the present case is the Laplace transform. This solution allows simulating dispersion of pollutant substances in a computationally efficient fashion. The advantage of an analytical procedure over the nowadays usual numerical schemes that take advantage of existing computing power is evident from the fact that once an analytical solution to a mathematical model is found one can claim that the problem has been solved, without the necessity for benchmarking. We derived a closed form solution applicable for numerical simulations in principle to any desired precision, since existence and uniqueness are guaranteed by the Cauchy-Kowalewski theorem. The quality of the solution is controlled by a genuine mathematical convergence criterion. For the Laplace inversion only bi-Lipschitz functions are acceptable, which defines then a unique relation between the original function and its Laplace-transform. This makes the transform procedure manifest exact and the only numerical error comes from truncation in the space of orthogonal functions, which may be estimated by a theorem in close analogy to
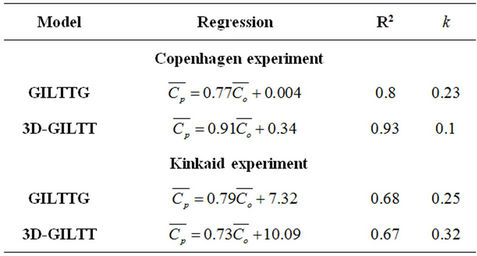
Table 4. Comparison of the linear regressions of GILTTG and 3D-GILTT using the Copenhagen and Kinkaid datasets.
the Cardinal theorem of interpolation theory together with Parseval’s theorem. Once convergence is under control and has no longer heuristic character, a pathway opened for a genuine model validation, differently to numerical approaches where in general it is not straight forward to disentangle model errors from numerical ones.
The performance of the solution together with a parameterization of the ABL was validated against the data from the Copenhagen and the Kinkaid experiments. By comparison the present approach was found to yield an acceptable solution for the three dimensional ADE and moreover predicted tracer concentrations closer to observed values compared to other approaches from the literature. Although K-closure is known to have its limitations, the comparison of measurements and theoretical predictions showed agreement on a satisfactory level and thus supported the usage of such an approach for micro-scale dispersion phenomena.
We outline that an analytical solution can be useful in evaluating the performances of numerical models that solve numerically the ADE by comparing their results, not only against experimental data but with the analytic solution itself in order to check numerical errors without model uncertainties. Finally, the program of providing analytical solutions for close to realistic physical dispersion problems, leads us to future problems with different closure hypothesis considering full space-time dependence in the resulting dynamical equation, which we will approach by a further extension of the proposed methodology.
5. Acknowledgements
The authors thank CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) and FAPERGS (Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul) for the partial financial support of this work.
REFERENCES
- P. Zanetti, “Air Pollution Modelling,” Comp. Mech. Publications, Southampton, 1990.
- J. H. Seinfeld and S. N. Pandis, “Atmospheric Chemistry and Physics,” John Wiley & Sons, New York, 1998.
- O. F. T. Roberts, “The Theoretical Scattering of Smoke in a Turbulent Atmosphere,” Proceedings of the Royal Society A, Vol. 104, 1923, pp. 640-654. doi:10.1098/rspa.1923.0132
- W. Rounds, “Solutions of the Two-Dimensional Diffusion Equation,” Transactions—American Geophysical Union, Vol. 36, 1955, pp. 395-405.
- F. B. Smith, “The Diffusion of Smoke from a Continuous Elevated Point Source into a Turbulent Atmosphere,” Journal of Fluid Mechanics, Vol. 2, No. 1, 1957, pp. 49- 76. doi:10.1017/S0022112057000737
- R. A. Scriven and B. A. Fisher, “The Long Range Transport of Airborne Material and Its Removal by Deposition and Washout-II. The Effect of Turbulent Diffusion,” Atmospheric Environment, Vol. 9, No. 1, 1975, pp. 59-69. doi:10.1016/0004-6981(75)90054-2
- G. T. Yeh and C. H. Huang, “Three-Dimensional Air Pollutant Modeling in the Lower Atmosphere,” Boundary-Layer Meteorology, Vol. 9, 1975, pp. 381-390.
- M. Y. Berlyand, “Contemporary Problems of Atmospheric Diffusion and Pollution of the Atmosphere,” USEPA, Raleigh, 1975.
- C. A. Demuth, “Contribution to the Analytical Steady Solution of the Diffusion Equation for Line Sources,” Atmospheric Environment, Vol. 12, No. 5, 1978, pp. 1255-1258. doi:10.1016/0004-6981(78)90399-2
- A. P. van Ulden, “Simple Estimates for Vertical Diffusion from Sources near the Ground,” Atmospheric Environment, Vol. 12, No. 11, 1978, pp. 2125-2129. doi:10.1016/0004-6981(78)90167-1
- F. T. M. Nieuwstadt, “An Analytical Solution of the Time-Dependent, One-Dimensional Diffusion Equation in the Atmospheric Boundary Layer,” Atmospheric Environment, Vol. 14, No. 12, 1980, pp. 1361-1364. doi:10.1016/0004-6981(80)90154-7
- F. T. M. Nieuwstadt and B. J. de Haan, “An Analytical Solution of One-Dimensional Diffusion Equation in a Nonstationary Boundary Layer with an Application to Inversion Rise Fumigation,” Atmospheric Environment, Vol. 15, No. 5, 1981, pp. 845-851. doi:10.1016/0004-6981(81)90289-4
- W. Koch, “A Solution of the Two-Dimensional Atmospheric Diffusion Equation with Height-Dependent Diffusion-Coefficient Including Ground-Level Absorption,” Atmospheric Environment, Vol. 23, No. 8, 1989, pp. 1729-1732. doi:10.1016/0004-6981(89)90057-7
- C. Chrysikopoulos, L. M. Hildemann and P. V. Roberts, “A Three-Dimensional Atmospheric Dispersion-Deposition Model for Emissions from a Ground Level Area Source,” Atmospheric Environment, Vol. 26A, 1992, pp. 747-757.
- M. Sharan, M. P. Singh and A. K. Yadav, “A Mathematical Model for the Atmospheric Dispersion in Low Winds with Eddy Diffusivities as Linear Function of Downwind Distance,” Atmospheric Environment, Vol. 30, No. 7, 1996, pp. 1137-1145. doi:10.1016/1352-2310(95)00368-1
- J. S. Lin and L. M. Hildemann, “A Generalised Mathematical Scheme to Analytically Solve the Atmospheric Diffusion Equation with Dry Deposition,” Atmospheric Environment, Vol. 31, No. 1, 1997, pp. 59-71. doi:10.1016/S1352-2310(96)00148-3
- M. T. Vilhena, U. Rizza, G. A. Degrazia, C. Mangia, D. M. Moreira and T. Tirabassi, “An Analytical Air Pollution Model: Development and Evaluation,” Contributions to Atmospheric Physics, Vol. 71, No. 3, 1998, pp. 315-320.
- C. P. Costa, M. T. Vilhena, D. M. Moreira and T. Tirabassi, “Semi-Analytical Solution of the Steady ThreeDimensional Advection-Diffusion Equation in the Planetary Boundary Layer,” Atmospheric Environment, Vol. 40, No. 29, 2006, pp. 5659-5669. doi:10.1016/j.atmosenv.2006.04.054
- D. M. Moreira, M. T. Vilhena, T. Tirabassi, C. Costa and B. Bodmann, “Simulation of Pollutant Dispersion in Atmosphere by the Laplace Transform: The ADMM Approach,” Water, Air and Soil Pollution, Vol. 177, No. 1-4, 2006, pp. 411-439. doi:10.1007/s11270-006-9182-2
- M. Vilhena, C. Costa, D. Moreira and T. Tirabassi, “A Semi-Analytical Solution for the Three-Dimensional Advection Diffusion Equation Considering Non-Local Turbulence Closure,” Atmospheric Research, Vol. 90, No. 1, 2008, pp. 63-69. doi:10.1016/j.atmosres.2008.04.002
- T. Tirabassi, “Operational Advanced Air Pollution Modelling,” Pure and Applied Geophysics, Vol. 160, No. 1-2, 2003, pp. 5-16. doi:10.1007/s00024-003-8762-y
- S. Wortmann, M. T. Vilhena, D. M. Moreira and D. Buske, “A New Analytical Approach to Simulate the Pollutant Dispersion in the PBL,” Atmospheric Environment, Vol. 39, No. 12, 2005, pp. 2171-2178. doi:10.1016/j.atmosenv.2005.01.003
- D. M. Moreira, M. T. Vilhena, T. Tirabassi, D. Buske and R. Cotta, “Near Source Atmospheric Pollutant Dispersion Using the New GILTT Method,” Atmospheric Environment, Vol. 39, No. 34, 2005, pp. 6290-6295. doi:10.1016/j.atmosenv.2005.07.008
- D. M. Moreira, M. T. Vilhena, D. Buske and T. Tirabassi, “The GILTT Solution of the Advection-Diffusion Equation for an Inhomogeneous and Nonstationary PBL,” Atmospheric Environment, Vol. 40, No. 17, 2006, pp. 3186- 3194. doi:10.1016/j.atmosenv.2006.01.035
- D. M. Moreira, M. T. Vilhena, D. Buske and T. Tirabassi, “The State-of-Art of the GILTT Method to Simulate Pollutant Dispersion in the Atmosphere,” Atmospheric Research, Vol. 92, No. 1, 2009, pp. 1-17. doi:10.1016/j.atmosres.2008.07.004
- R. Courant and D. Hilbert, “Methods of Mathematical Physics,” John Wiley & Sons, 1989.
- A. K. Blackadar, “Turbulence and Diffusion in the Atmosphere: Lectures in Environmental Sciences,” SpringerVerlag, 1997.
- R. H. Torres, “Spaces of Sequences, Sampling Theorem, and Functions of Exponential Type,” Studia Mathematica, Vol. 100, No. 1, 1991, pp. 51-74.
- B. Bodmann, M. T. Vilhena, L. S. Ferreira and J. B. Bardaji, “An Analytical Solver for the Multigroup Two Domensional Neutron-Diffusion Equation by Integral Transform Techniques,” Il Nuovo Cimento C, Vol. 33, 2010, pp. 199-206.
- C. Mangia, D. M. Moreira, I. Schipa, G. A. Degrazia, T. Tirabassi and U. Rizza, “Evaluation of a New Eddy Diffusivity Parameterisation from Turbulent Eulerian Spectra in Different Stability Conditions,” Atmospheric Environment, Vol. 36, No. 1, 2002, pp. 67-76. doi:10.1016/S1352-2310(01)00469-1
- G. A. Degrazia, “Lagrangian Particle Models,” In: P. Zannetti, Ed., Air Quality Modeling: Theories, Methodologies, Computational Techniques and Available Databases and Software, EnviroComp, 2005, pp. 93-162.
- G. A. Degrazia, H. F. Campos Velho and J. C. Carvalho, “Nonlocal Exchange Coefficients for the Convective Boundary Layer Derived from Spectral Properties,” Contributions to Atmospheric Physics, Vol. 70, 1997, pp. 57- 64.
- G. K. Batchelor, “Diffusion in a Field of Homogeneous Turbulence, Eulerian Analysis,” Australian Journal of Scientific Research, Vol. 2, 1949, pp. 437-450.
- J. C. Kaimal, J.C. Wyngaard, D. A. Haugen, O. R. Coté, Y. Izumi, S. J. Caughey and C. J. Readings, “Turbulence Structure in the Convective Boundary Layer,” Journal of the Atmospheric Sciences, Vol. 33, No. 11, 1976, pp. 2152-2169. doi:10.1175/1520-0469(1976)033<2152:TSITCB>2.0.CO;2
- S. J. Caughey, “Observed Characteristics of the Atmospheric Boundary Layer,” In: F. T. M. Nieuwstadt and H. van Dop, Eds., Atmospheric Turbulence and Air Pollution Modeling, Reidel, Boston, 1982.
- J. E. Pleim and J. S. Chang, “A Non-Local Closure Model for Vertical Mixing in the Convective Boundary Layer,” Atmospheric Environment, Vol. 26A, 1992, pp. 965-981.
- G. A. Degrazia, M. T. Vilhena and O. L. L. Moraes, “An Algebraic Expression for the Eddy Diffusivities in the Stable Boundary Layer: A Description of Near-Source Diffusion,” Il Nuovo Cimento, Vol. 19C, 1996, pp. 399- 403.
- Z. Sorbjan, “Structure of the Atmospheric Boundary Layer,” Prentice Hall, New Jersey, 1989.
- F. T. M. Nieuwstadt, “The Turbulent Structure of the Stable Nocturnal Boundary Layer,” Journal of the Atmospheric Sciences, Vol. 41, No. 14, 1984, pp. 2202- 2216. doi:10.1175/1520-0469(1984)041<2202:TTSOTS>2.0.CO;2
- H. A. Panofsky and J. A. Dutton, “Atmospheric Turbulence,” John Wiley & Sons, New York, 1984.
- J. S. Irwin, “A Theoretical Variation of the Wind Profile Power-Low Exponent as a Function of Surface Roughness and Stability,” Atmospheric Environment, Vol. 13, No. 1, 1979, pp. 191-194. doi:10.1016/0004-6981(79)90260-9
- S. E. Gryning and E. Lyck, “Atmospheric Dispersion from Elevated Source in an Urban Area: Comparison between Tracer Experiments and Model Calculations,” Journal of Applied Meteorology, Vol. 23, 1984, pp. 651- 654.
- S. R. Hanna and R. J. Paine, “Hybrid Plume Dispersion Model (HPDM) Development and Evaluation,” Journal of Applied Meteorology, Vol. 28, No. 3, 1989, pp. 206- 224. doi:10.1175/1520-0450(1989)028<0206:HPDMDA>2.0.CO;2
- H. R. Olesen, “Datasets and Protocol for Model Validation,” International Journal of Environment and Pollution, Vol. 5, 1995, pp. 693-701.
- S. R. Hanna, “Confidence Limit for Air Quality Models as Estimated by Bootstrap and Jacknife Resampling Methods,” Atmospheric Environment, Vol. 23, No. 6, 1989, pp. 1385-1395. doi:10.1016/0004-6981(89)90161-3

