Received 25 March 2015; accepted 28 August 2015; published 31 August 2015

ABSTRACT

In this paper, a multi-objective load shedding framework on the power system is presented. The frame work is useable in any kind of smart power systems; the word of smart here refers to the availability of data transmission infrastructure (like PLC or power line carrier) in the system, in order to carry the system data to the load shedding framework. This is an open framework that means it can optimize load shedding problem by considering unlimited number of objective functions, in other word, the number of objectives can be as much as the operator decides, finally in the end of frame work just one matrix breaker state is chosen in a way of having the most compatibility with the operator ideas which are determined by objectives importance percentage which are one input groups of the framework. A two-stage methodology is used for the optimal load shedding problem. In the first stage, Discrete Multi-objective Particle Swarm Optimization method is used to find a collection of the best states of load shedding (Pareto front). In the second stage, the fuzzy logic is used as a Pareto front inference engine. Fuzzy selection algorithm (FSA) is designed in a way that it can infer according to the operator’s opinion without the expert interference that means rule base is formed automatically by fuzzy algorithm. FSA is consisted of two parts. Membership functions and rules base are formed automatically in the first part, the former in accordance with the costs of Pareto front particles and the latter in correspondence with importance percentage of objectives which are entered to FSA by operator; in other word, decision matrix is formed automatically in the algorithm according to the cost of Pareto front particles and importance percentage of objectives. In the Second part, Mamdani inference engine scrutinizes the Pareto front particles by the use of formed membership functions and rules base to know if they are compatible to operator’s opinion or not. Getting this approach, cost functions of each particle are considered as the inputs of (FSA), then a fuzzy combined fitness (FCF) is allocated to each Pareto front particle by Mamdani inference engine. In other word, FCF shows how much the particle is compatible to the operator’s opinion. Finding minimum FCF, final inference is done. The proposed method is tested on 30-bus, and 118-bus IEEE systems by considering two or three objective functions and the results are presented.

Keywords:

Objective, Load Shedding, Pareto Front, Fuzzy

1. Introduction

One of the desired characteristics of the power network is providing active and reactive power which is required for the consumption in the suitable voltage, frequency, power quality and reliability. But when the level of power consumption in the network exceeds the produced power by the generator, the desired power quality can’t be provided and the probability of instability and complete black out in the network increases. So the operator should disconnect some amounts of the loads which are connected to the network with the aim of preventing the creation of a complete black out or damage to the network. But in a complicated network, selecting one parts of network for load shedding is a complicated, non-linear and important problem which various methods have been proposed to solve that. To this end, in [1] , the genetic algorithm is used to find the optimal load shedding points. In this paper, a combined function of voltage stability index and the amount of disconnected load are used as the objective functions. In [2] , the problem of optimal load shedding is investigated with the use of the combined particle swarm method by taking into account the voltage stability objective function. The objective function in [3] has also been used in several ways including Gomez, Genetic Algorithm and Particle Swarm Optimization Algorithm. Many load shedding techniques have been developed [4] -[10] to optimize the required load curtailment without violating the system security constraints. Most of these techniques [4] -[8] are focused on minimizing load curtailment and increasing the speed of the load shedding process [11] . The available techniques are not generally concerned with customer interruption costs in a given load shedding situation. Some works that have incorporated load shedding with customer interruption costs are presented in [9] [10] . The problem of optimal load shedding in the presence of distributed generation sources in [12] is investigated, which the classic mathematical programming methods are recommended for optimization [13] . A framework is presented to determine a load shedding strategy for the restoration of power flow solvability and improvement of voltage stability margin. Two fuzzy based load shedding algorithms that use a voltage stability indicator for averting voltage collapse are thus proposed in [14] . The first method identifies the most appropriate locations and uses an analytical procedure to compute the disconnected load, while the second directly predicts the amount of load to be shed at the critical buses.

As mentioned, many methods to calculate the optimal load shedding on the power grid are proposed so far. In each of these methods, the author has introduced the operator’s desired objective and he has calculated the optimal load shedding points. It is obvious that many parameters are defined in the operation of power network that one of them will not be sufficient to determine the appropriate operating point. Note that during load shedding, the power system will be in a new steady state that lasts a long time, so it is necessary for this new operating point to be optimized according to the various network parameters. By this approach, the load shedding problem is converted into a multi-objective optimization problem. These objectives can include technical, economical, and even power marketing objectives which are simply not in line with each other. For example, the profit function which is defined by the perspective of the consumer and the producer is unlike to each other. Therefore, in the final solution, fully optimize all objectives simultaneously is impossible; so a response needs to be chosen as a compromise among various objectives. To sum up, previous papers were confined in accepting different objective functions and could not solve the problem of exact decision making as their final inference that means their out-puts is a collection modes of best states, which cannot be practical for the operator because he does not know which collection is better to consider.

In this paper, the framework of the multi-objective load shedding optimization on the power system is presented. In the proposed algorithm, the operator is able to define: the intended targets (as many as he wants, it is an open framework), the importance percentage of each objective and network constraints for load shedding optimization, also he can specify the new system operating point by presenting the proposed load shedding frame work. In the proposed framework after determining objective functions by operator a collection of the best load shedding states (Status of the buses breaker) which have respected the network constraints, are identified by the multi-objective discrete particle swarm optimization algorithm. Then, using the proposed FSA one of the optimization output states is selected as the optimal operating point. In the other word, the multi-objective Particle Swarm Optimization algorithm has been used in order to find the best states of load shedding, and proposed fuzzy selection algorithm (FSA) is designed to specify the global optimum response which is noticeably compatible to operator’s opinion.

This paper is presented in VI Sections that after this chapter, in Chapter II, the required concepts of the proposed framework are presented. Then the proposed framework is described in Chapter III. In Chapter IV the proposed framework on two samples of 30-buses and 118-bus IEEE networks under the two scenarios have been implemented and its results are presented. In Chapter V the results of the simulation are analyzed and deduced.

2. Basic Description

2.1. Load Shedding Problem

The load shedding issue is a non-linear problem which varies throughout the day. During a time of stress on the system such as transient the problem of load shedding should be resolved according to the current situation.

In this paper, the load shedding issue has been expressed as a multi-objective problem which can select the best mode of load shedding according to the network constraints and the importance percentage of each objective function. In the following the objectives and constraints to solve the load shedding problem is described.

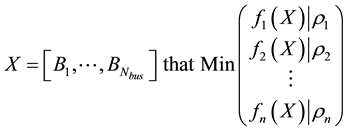
(1)

where the array 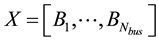is the array of each buses breaker status, f_n represents the objective of load shedding, is the importance percentage of n-th objective and 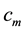indicates the limitations of the network. The following each of these are illustrated in detail.

2.2. Objective Functions (f_n)

As it mentioned before, by defining the load shedding issue as a multi-objective problem the probability of optimization and compromise between the operational objectives is provided. Among these objectives, minimizing the voltage difference of nominal value, minimizing losses in the grid, minimizing the amount of disconnected load and optimizing the network voltage stability can be noted. Needless to say that fulfilling these objectives can’t be implemented simultaneously, because changing the arrangements of load shedding in network each of these goals (objectives) have been changed in a non-symphonic order. In this paper, four parameters: minimizing the voltage difference of nominal value, minimizing losses in the grid, minimizing the amount of disconnected load in the network and maximizing the voltage stability index are targeted, as well as, described in the following:

2.2.1. Total Voltage Variation (f₁)

One of the desired goals in power systems is the Proximity of the buses voltage to the nominal voltage.

The Proximity of the buses voltage to the nominal voltage can reduce the real and reactive power losses in the grid lines; also it can improve the voltage profile and increase the quality of the power which is delivered to the consumers. In [1] , TVV is used as an indicator parameter of the grid which is obtained in the Equation (2).

(2)

2.2.2. Power Losses (f₂)

Minimizing losses is another goal which should be considered, for this purpose the total amount of active power losses in the network which is calculated from Equation (3) is considered as an objective function which should be minimized in the steady state situation after load shedding.

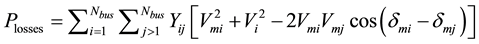(3)

2.2.3. Total Disconnected Load (f₃)

Minimizing the amount of disconnected load is necessary in load shedding management of the system, because the grid operator is obligated to pay penalty to turn off the consumers load. In this paper the total disconnected load is defined as the third objective function. The importance degree of loads can be taken by considering the load shedding cost function in the system in a way that the cost of the more important loads is more expensive than the conventional loads cost.

(4)

2.2.4. Voltage Stability Index (f₄)

Voltage stability index is one of the most important factors which should be considered in load shedding optimization algorithms, in [1] , a stability index for radial networks is presented which can be maximise as an objective function by load shedding optimization algorithm.

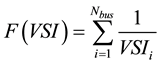
2.3. Network Constrains (c_m)

In the networks, there are some limitations according to the shape and structure as well as the equipment which are used in its design. Constraints such as thermal limits of lines, bus voltages, network frequency and etc, which these limitations are specified by the designer or operator. These constrains should be respected to solve as many issue related to the networks. The following some constrains are mentioned.

2.3.1. Active and Reactive Power (c₁)

In each system the active and reactive generating power in each bus is equal to the consuming and transferring power. This issue is such a constraint on the power grid which should also be considered in solving the load shedding problems. This constraint is written as Equations (5) and (6) [15] .

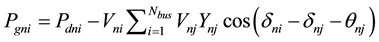(5)

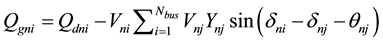(6)

Each power system has a set of constraints which are related to the physical characteristics of its components. These constraints should be respected in the way of finding the best steady state situation. The following, these constrains are explained.

2.3.2. Voltage (c₂)

In a power system the amplitude as well as the phase of buss voltage should not over step in both limits which is shown in the inequalities 5 and 6. These two limits are defined due to the physical characteristics of the network, by operator. Violation of these provisions will cause instability in the system [16] .

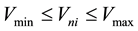(7)

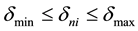(8)

2.3.3. Thermal Limit (c₃)

One of the network constrains is the thermal limits of transmission lines. These thermal limits with the maximum transferring power of line are specified; also they are shown in inequality 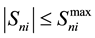9.

(9)

2.4. Optimization Algorithm

2.4.1. Basic Multi Objective Particle Swarm Optimization (MOPSO)

There are many nonlinear problems due to the complexity, non-linearity of the equations and high volume of calculation in the economic and technical issues of the power system which algorithms are used to solve them. But the purpose of solving the problem in many of these issues is to provide multi-purpose simultaneously. Notably, in the majority of these issues, all objectives cannot be at their optimum state due to the failure to align of the objectives. This means that the optimization of one objective may destroy other purpose. Hence in the multi-objective problem rather than finding an optimal response predominates, a set of optimal response is determined which each objective can be the overall optimal solution and this selection depends on the importance of each objective.

One of the proposed methods in solving the multi-objective problems is the multi-objective particle swarm optimization. The method is proposed in [17] and is used to solve continuous multi-objective problems. This method is based on particle swarm motion according to the best individual memory and the best collective memory (leader chosen based).

But some changes are required to solve the problem of finding the load shedding position in a multi objective manner. The discrete nature of load shedding problem and the need to select the specific state with desired criteria by the operator is among these changes. Therefore, the above algorithm is modified according to this issue and it is described in the next section.

2.4.2. Discrete MOPSO for the Load Shedding Problem

Needless to say that generally, there is a breaker for connecting the feeder to the bus and to disconnect the load on the bus by opening and closing the breaker. Because of this, to solve the locational problem of load shedding we have N_bus variables that each of them takes only two Values of zero and one. Due to this problem we need to use discrete multi-objective particle swarms. For this purpose, we have changed the basic algorithm. Figure 1 shows the flowchart of the optimization algorithm which its process is shown the following.

2.5. Fuzzy Selection Algorithm (FSA)

Having ended the above algorithm, a collection of different states of load shedding is obtained. However in order to apply load shedding in the system we need to select a mode between the modes which are available. It is needed to choose an option as the final option according to the importance percentage of each objective. Although, weighting methods were used in previous papers to find the best solution, in this paper a fuzzy selection algorithm is proposed to get a clear-cut solution according to the operator’s comments.

The proposed fuzzy selection algorithm causes objectives to be set in a match exact range, in turn, leading to adjusting final inference to important percentage of each objective. In this paper having formed fuzzy membership functions and fuzzy rules base according to Pareto fronts and important percentage of each objective, the variation range of each membership function from The actual amount of that are mapped to a standard range, then according to the proposed formula of fuzzy rules base, important percentages and cost functions will be turn into a fuzzy combined fitness which its range is always between zero and one.

The proposed fuzzy algorithm is superior to the traditional methods of weighting due to the following reasons:

First, the proposed method forms intervals of the membership functions based on the current position, not on predetermined intervals which change over time.

Second, the fuzzy algorithm lets operator to apply as many as objectives that he wants, without any concern of using weighting methods. This method is shown in the flowchart in Figure 2 and it is described as follow:

1) In the first stage the non-dominated particles of the optimization are considered as the input. At this stage, the parameters such as the number of input membership functions N_mem, the number of objective functions N_Cost and the importance of each objective jρ are also initialized.

2) Investigating the stopping criteria of the intervals formation for each objective function.

3) Sorting j-th objective function value of all non-dominated particles: at this stage the j-th objective function value of all particles has been isolated and these values are sorted by small to large. This step is done to find the maximum and minimum of the j-th objective function among non-dominated particles and it will be used in the next step.

4) Calculating the interval length of input membership functions for the j-th purpose of Equation (10): after obtaining the maximum and minimum values of the objective function among non-dominated particles, by the use of Equation (10), the intervals of the input membership functions base (Figure 3) is calculated for this objective function.

(10)

5) Forming membership functions of the j-th input: After identifying the interval length of input membership functions as well as the minimum and the maximum values for each objective function, the input membership functions are drawn with the use of Equations (11) to (13). Also naming the membership functions to use in Equation (14) and to calculate the fuzzy rules base, is considered as the numbers of 1 to N_mem. In this paper the membership functions 1 and N_mem are considered as the trapezoidal membership functions and the rest of them are considered as the triangular functions.

(11)

(12)

(13)

The output membership functions as well as the input membership functions are calculated from Equations (9) to (12) by considering the minimum and maximum values of zero and one. The number of interval in the output membership functions are specified by N_mem.o.

6) Forming the fuzzy rules based according to the user’s settings: in this section with respect to the importance percentage of each parameters in operator’s view, the fuzzy rules are calculated from Equation (14).

(14)

where ρ_j parameters are the importance percentage of j-th input, m_j is the number of the j-th input membership function, N_mem is the intervals number of the input membership functions; N_mem.o is the intervals number of the output membership functions and is the selected output membership function (FCF membership function).

7) Calculating the objective function value of fuzzy hybrid particles: eventually after forming the base of fuzzy rules and forming the input and output objective functions, we can obtain a value of fuzzy hybrid utility by applying the objective functions value of each members of the Pareto Front to the formed fuzzy system which works by the Mamdani inference method For each member. This value is between zero and one, the smaller the value, the Particle is more desirable.

8) Selection: after calculating the fuzzy objective function value for all non-dominated particles, the particle who obtains the minimum phase have selected as optimal output.

3. Proposed Multi Objective Load Shedding Framework

In this chapter, Multi-objective optimization model is presented to find the best load shedding state in the network. The proposed model is presented to be applicable for any number of the adjectives. In other word the proposed framework is an open framework which can accept infinite number of adjectives and then by the end of algorithm one breaker state (according to the operator priorities which are inputs of the algorithm) will be chosen with the thanks of automatic fuzzy algorithm which its rule base form automatically. The flowchart of Figure 4 shows the general form of the proposed model which its stages are classified in 4 parts, as follows.

3.1. Loading Framework Required Data

Loading the network data: In order to implement the proposed frame work, the basic information is required to be given to the system. This information includes transmission lines data, network buses data and power plants data that are needed to run load shedding.

3.2. Framework Setting

After loading the power system data, the proposed frame work setting is required to be determined by the operation. This configuration is done in the following three sections:

1) Objective Functions: In this episode operator should specify the number and the type of objectives for load shedding. These goals can include technical purposes such as buses voltage, voltage stability index and etc; economic goals such as lines losses, the costs of disconnected loads and etc; or competitive purposes such as the discussion of market power in the power system, which the number of them are mentioned in Section 2.

2) Determining the importance of optimization objectives: After identifying the load shedding objectives, the operator had better determine the importance degree of each goals ρ_n. By the importance degree of each goal it will be specified that how much each objective should be taken into consideration in the final inference.

3) The network constraints adjustment: Any optimization of the power grid network is required to follow the network constrains, as it mentioned in Section 2. There are many restrictions on the network that three of them have been mentioned in Section 2. The numerical limitation of these constrains must be specified Before Optimization by the operator. These limits are usually fixed on the network and they are identified during designing.

3.3. Multi-Objective Optimization Algorithm

1) Initializing the optimization parameters: in This section it is required to initialize the parameters of optimization such as the number of population particles N_par, The number of the ultimate collected solutions (non- dominated particles) N_rep and the coefficients which are defined in the optimization algorithm (β, ω, c₁, c₂, It_max) (stated in Section 2).

2) Optimization and finding the Pareto front: at this stage by using the improved MOPSO optimization algorithm which is discussed in detail in Section 2 (Figure 1), the best load shedding scenarios which have observed the network constrains are specified.

3.4. Selection Algorithm

Selecting the best option in FSA method: After finishing the above steps, using the proposed fuzzy selection method, which is described in Chapter 2 (Figure 2), and also with respect to the importance percentage of objectives, one of the states is selected as the optimal solution.

In the next section the proposed model is tested on two standard IEEE network, 118-bus and 30-bus.

4. Case Study

In this section, the proposed model will be reviewed under two scenarios. In the first scenario, the load shedding is implemented as a two-objective and three-objective on IEEE 30 bus system. These results are presented in two sections of the outcomes of optimization and fuzzy inference results.

In the results of the Fuzzy selection algorithm, the out puts of the system are also explored for various settings by the operators. In the second scenario, the load shedding pattern is tested on 118-bus IEEE standard system and the results are expressed as before.

4.1. 1st Scenario

Network Expression

The tested network in this case, is the standard 30-bus IEEE network which is shown in Figure 5.

4.2. Three Objectives

4.2.1. DMOPSO Results

As mentioned in Section 3, in order to find the best load shedding states, the initial stage is finding a collection of non-dominated articles. This collection is called the Pareto front. Pareto front which is obtained from the tested framework in the first scenario is the form in Figure 6. Each point in this figure represents a load shedding state in the tested network.

4.2.2. Selection Results

After identifying the Pareto front, it is time to choose the best mode which is based on the operator’s setting. Reaching this purpose, the fuzzy selection method is used in the proposed Algorithm. FSA results for the first scenario and for two different modes of operation settings are presented in Table 1. The Selected points are marked in green in Figure 6.

As it can be seen in the Table 1, in the first row that the importance percentage of total disconnected load of the system was less important, the amount of disconnected load from the network is 27% of total loads. While in the second row that the TDL importance percentage has raised to 80 percent, a rate of disconnected loads is reduced to 20% and in exchange the two parameters of TVV and PL were increased. As it is clear in the Pareto fronts, improving one parameter can worsen the other parameters. So it is required to make a compromise and selection according to the operator settings.

The selected load shedding state and buses voltage after load shedding (according to Table 1) are represented in Figure 7. It should be noted that red color represents disconnected loads in the network. As it can be seen from Figure 7, the more the important percentage of TDL, the less the total disconnected load.

4.3. Two Objectives

4.3.1. DMOPSO Results

In this test, the 30-bus system is selected as the plant that two Purpose of TVV and TDL are considered as objective function. The obtained Pareto front in this test is shown in Figure 8.

4.3.2. Selection Results

In this test after obtaining Pareto fronts, the selection algorithm will be run according to the operator’s view. In

the selection process, fuzzy rule base, updated according to the settings and then the final selection is done. Final results of the two modes are shown in Table 2. The Selected points are marked in green in Figure 8. In addition, the formed fuzzy surfaces which are based on the importance percentage of objective functions are specified in Figure 9.

4.4. 2nd Scenario

Network Expression

In this test, the 118-bus system is selected as the plant. The test system is shown in Figure 10.

4.5. Three Objectives

4.5.1. DMOPSO Results

In this test the proposed load shedding algorithm is examined on 118-bus system with 3 objective functions of TVV, Power losses and TDL.

4.5.2. Selection Results

After identifying the optimization algorithm results and setting the importance percentage of each objectives, the fuzzy selection results are obtained and they ate presented in Table 3, As it can be seen in Table 3, increasing the importance percentage of each objective by the operation of the power system, the combination of network load shedding changes in a way that this objective function provides greater desirability. In the table it is clear that by increasing the importance percentage of total disconnected loads from 50 percent to 80 percent, the rate of change of the objective function is not great because of the discrete and non-identical size of the loads which are connected to the buses. Selected points are marked green in Figure 11.

The selected load shedding state and buses voltage after load shedding (according to Table 3) are represented in Figure 12. It should be noted that red color represents disconnected loads in the network. As it can be seen

from Figure 12, the more the important percentage of TDL, the less the total disconnected load.

4.6. Two Objectives

4.6.1. DMOPSO Results

The result of applying the proposed load algorithm on the 118-bus system with two objective functions of TVV and TDL is shown in Figure 13. The shown particles are the different states of load shedding which are plotted according to its objective function values.

4.6.2. Selection Results

In this test the Selection algorithm results with two user settings are given in Table 4 and the formed fuzzy surfaces which are based on the importance percentage of objective functions are specified in Figure 14. The Selected points are marked in green in Figure 13.

5. Conclusion

It is essential to be a balance between power consumption and demand on the power network. In some situations

such as withdrawal a generator of the network, the unbalanced situation occurs. In this situation load shedding is needed in order to prevent blackout in the power system. However, selecting a part of network for load shedding is a complicated, non-linear and important problem. In this paper, a load shedding framework is presented. This framework is practicable for any number of objective functions and network constrains, in other word, this is an open framework which can accept infinite numbers of objectives and constrains. In addition in fuzzy part, rules base are formed automatically without the need of expert, then at the end of algorithm, the out-put will be one best breaker state not a collection of best states which may confuse the operator. The proposed framework has two main parts; in the first part, a collection of the best states of load shedding (Pareto front) is specified by Discrete Multi-objective Particle Swarm Optimization algorithm. In the second part, the proposed fuzzy algorithm is used to find the best selected mode according to the operator’s opinion. The proposed load shedding framework is tested for two systems of 30-bus and 118-bus IEEE in the states of two or three objectives. The results are explained in two sections of optimization results and fuzzy selection results. The results showed that the proposed method can choose the best load shedding mode according to the current conditions of the system, system constraints, objective functions and the importance percentage of each objective.

Cite this paper

AtiehDelavari,MiladNemati,Mohammad H.Moradi, (2015) Multi Objective Load Shedding Framework. Smart Grid and Renewable Energy,06,260-277. doi: 10.4236/sgre.2015.68022

References

NOTES

^*Corresponding author.