Smart Grid and Renewable Energy
 Vol.4 No.4(2013), Article ID:33935,5 pages DOI:10.4236/sgre.2013.44041

Comparison of Different Models for Estimation of Global Solar Radiation in Jharkhand (India) Region

Kumari Namrata1, S. P. Sharma2, S. B. L. Saksena1

1Department of Electrical Engineering, NIT Jamshedpur, Jamshedpur, India; 2Department of Mechanical Engineering, NIT Jamshedpur, Jamshedpur, India.

Email: nirmala_bimal@yahoo.com

Copyright © 2013 Kumari Namrata et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received January 30th, 2013; revised March 5th, 213; accepted March 14th, 2013

Keywords: GSR; sunshine duration; predicted solar radiation; daily global radiation; Jharkhand

ABSTRACT

In this paper with the help of different empirical models we have estimated the value of monthly average global solar irradiation for Ranchi (23.3500˚N, 85.3300˚E), a tropical location. The values of monthly average global solar radiation are calculated using the regression constants in the models (both linear and quadratic) suggested by: AngstromPrescott, Rietveld, Ogleman, Akinoglu, Glover, Gopinathan and Sangeeta et al. All the regression models are investigated, validated and compared. On comparison it was observed that the quadratic models are overall more accurate for calculating the Global Solar Radiation for the Jharkhand region, but the Angstrom-Prescott model as well shows better variance for most of the months. The calculated data from these models is compared with the data provided by MNRE [1]. GSR values are important parameters for designing any Solar Power Systems as the whole solar power generation is directly proportional to the amount of global solar radiation. The calculated and measured data are simulated using MATLAB.

1. Introduction

Solar energy technologies offer a clean, renewable and domestic energy source and are essential components of a sustainable energy future. The amount of global solar radiation and its temporal distribution are the primary variable for the use of solar energy. Development of a solar energy research program must always start with a study of solar radiation data at a site or region of interest [1-20]. Unfortunately, the measurement of these parameters is made only in a few meteorological stations, especially in developing countries, for both historical and economical reasons. For places where it is not directly measured, solar radiation can be estimated by using models and empirical correlations. Therefore, there have been numerous investigations on the examination of the relationship between global radiation and sunshine duration for which data are available in a greater number of meteorological stations [2]. However, the computational complexity and associated time and input data requirements discourage many researchers and users from basing their calculations of energy, irradiation on models which have strong links to the fundamental radiative equations rather they are encouraged by simplicity and expediency of calculations using empirically based methods [3]. It can be observed from

Figure 1 shows that the solar energy potential of India is one of the highest in the world as the tropic of cancer passes through it [4]. But the true potential is yet to be utilized because of lack of data. It is worth pointing that

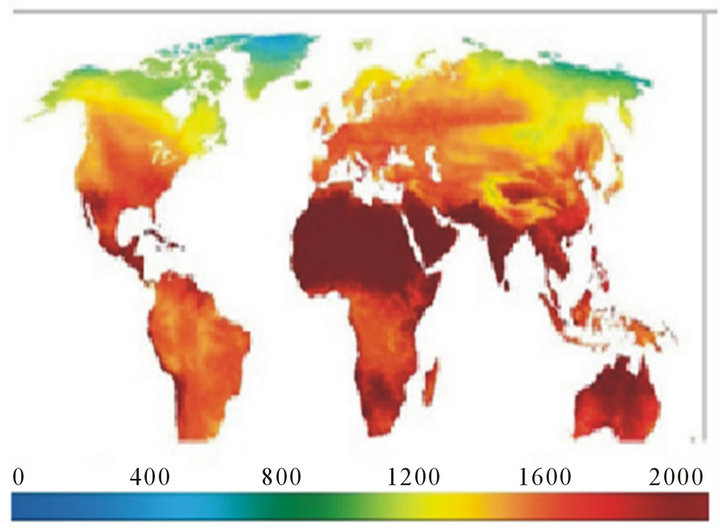
Figure 1. NASA map of world solar energy potential (kW/ m2/year).

regression models are used for prediction or estimation, data description, parameter estimation and control.

2. Model of Analysis (Table 1)

To calculate the monthly mean daily radiation on a horizontal surface in absence of atmosphere Ho a number of approaches had been made here is based on Duffi and Beckman [5]. The value of Ho is thus calculated as shown in equation (1)

(1)

where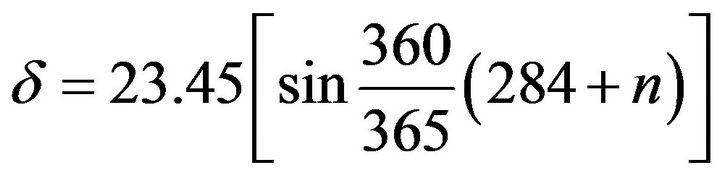

.

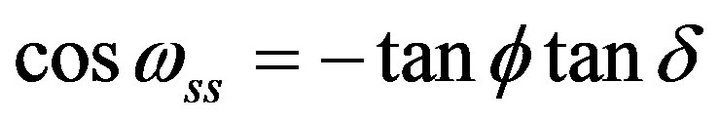2.1. Angstrom-Prescott Model

Among the different empirical models, the most popular is the regression equation of the Angstrom [6,7] type. The regression constant a and b depend on φ (latitude) and seasonal variation.

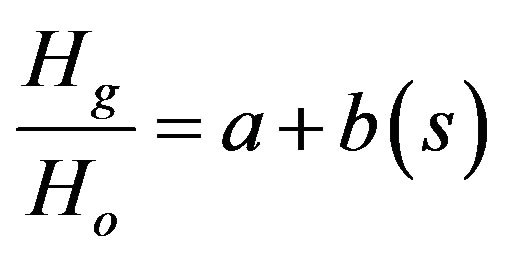(2)

2.2. Rietveld Model

Rietveld [8] examined several published values of a and b and noted that a is related linearly and b hyperbolically to the mean value of S such that this equation is believed to be applicable anywhere in the world and yields superior results for cloudy conditions, for S < 0.4.

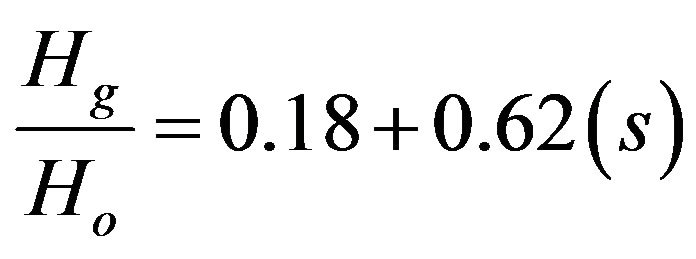(3)

2.3. Ogleman Model

Ogleman [9] et al. proposed the use of a correlation which relates the global solar radiation to S in a quadratic form as

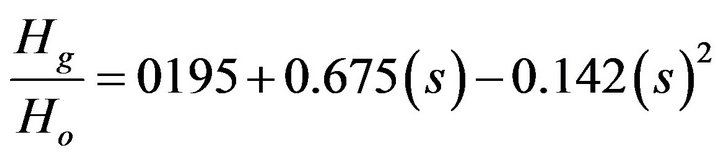(4)

2.4. Akinoglu Model

Akinoglu and Ecevit [10] suggested a quadratic correlation between the ratio of 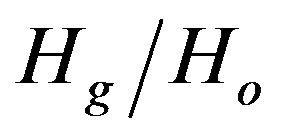and S to estimate the values of global solar radiation for 58 locations displaced in several countries. This equation, whose coefficients have the same values, respectively for all tested locations is

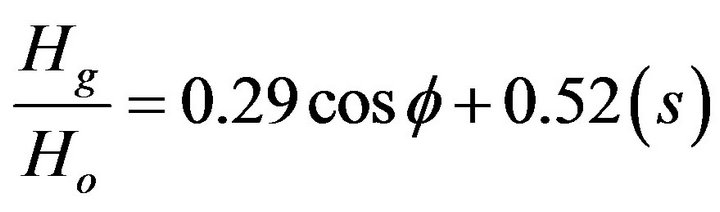(5)

2.5. Glover Model

Glover and McCulloch [11] attempted to introduce latitude dependency to one of the Angstrom-Prescott coefficients and presented the following

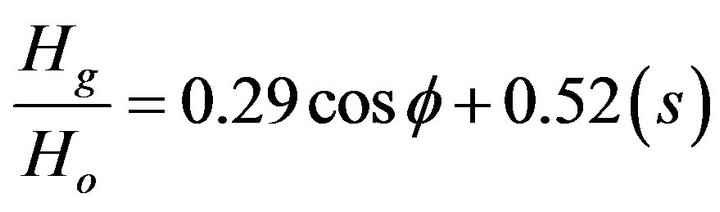(6)

2.6. Gopinathan Model

Gopinathan [12] proposed a and b are related to three parameters, the latitude, the elevation and the sunshine hours.

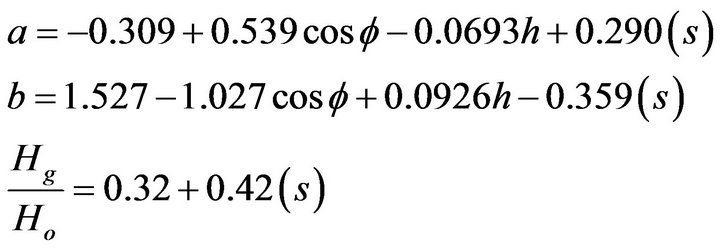(7)

2.7. Sangeeta et al. Model

In this model a and b are related to the parameters, the latitude and the sunshine hours.

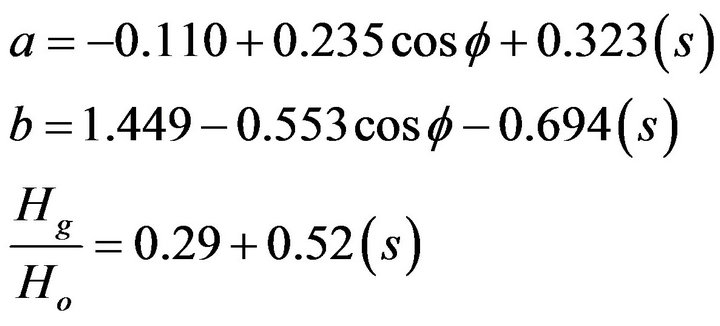(8)

3. Comparison of Models

The various models discussed above are used to calculate the extra-terrestrial radiation and the Global Solar Radiation. The calculated values are show in Table 2" target="_self"> Table 2. In Figure 2 and Table 3, the comparison of different linear models with measured data provided by MNRE for Ranchi for the year 2008 is shown. In Figure 3" target="_self"> Figure 3, the comparison of quadratic models with measured data is shown. In Figure 4, the variation of Hg (GSR) in all proposed models is compared and it is observed that the quadratic models have more accuracy than the linear models with the exception of Angstrom-Prescott and Riveted for the months of June-October.

4. Conclusion

When all the values of Hg for different linear models are compared in figure 2, it is seen that the AngstromPrescott model shows more accuracy than rest of the linear models, while quadratic models are compared in figure 3; it is observed that Ogleman and Akinoglu models have shown more accuracy with respect to other linear

Table 1. Regression models.

Table 2. Calculated values of basic parameters for the city Ranchi.

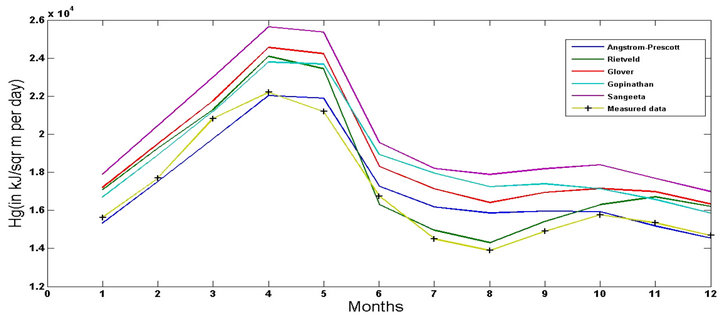
Figure 2. Comparison of different models with measured data.

Table 3. Comparison of different models.

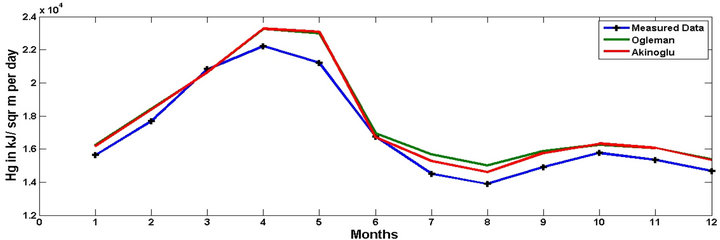
Figure 3. Comparison of quadratic models with measured data.

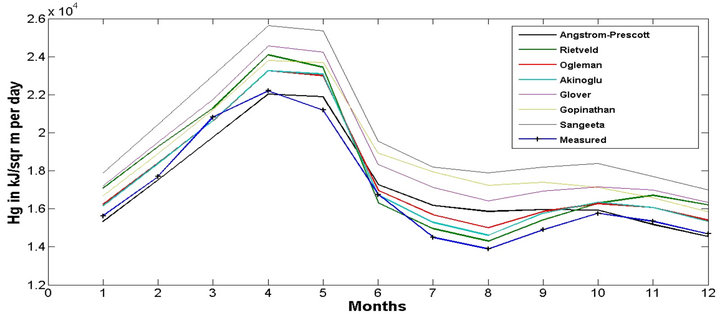
Figure 4. Comparison of all models with measured data.

models. Though it can be seen that Rietveld model show greater accuracy during June-October period i.e. during the monsoon. Thus observing all the factors Ogleman, Akinoglu and Angstrom-Prescott models are proposed for measuring the Global Solar Radiation for the Jharkhand region. Thus we can conclude that the quadratic models are more accurate than the linear models for calculating the Global Solar Radiation in Jharkhand region.

REFERENCES

  1. “Solar Radiation Handbook,” Solar Energy Centre, MNRE, 2008.
  2. M. Chegaar and A. Chibani, “A Simple Method for Computing Global Solar Radiation,” Renewable Energy Reviews, Chemss, 2000, pp. 111-115.
  3. K. Bakirci, “Correlations for Estimation of Daily Global Solar Radiation with Hours of Bright Sunshine in Turkey,” Energy, Vol. 34, No. 4, 2009, pp. 485-501. doi:10.1016/j.energy.2009.02.005
  4. T. Muneer, S. Younes and S. Munawwar, “Discourses on Solar Radiation Modeling,” Renewable and Sustainable Energy Reviews, Vol. 11, No. 4, 2007, pp. 551-602. doi:10.1016/j.rser.2005.05.006
  5. J. A. Duffie and W. A. Beckman, “Solar Engineering of Thermal Processes,” 3rd Edition, John Wiley & Sons, Inc., New York, 2006.
  6. A. Angstromm, “Solar and Terrestrial Radiation,” Quarterly Journal of the Royal Meteorological Society, Vol. 50, No. 210, 1924, pp. 121-126.
  7. J. A. Prescott, “Evaporation from Water Surface in Relation to Solar Radiation,” Transactions of the Royal Society of South Australia, Vol. 64, 1940, pp. 114-118.
  8. M. R. Rietveld, “A New Method for Estimating the Regression Coefficients in the Formula Relating Solar Radiation to Sunshine,” Agricultural Meteorology, Vol. 19, No. 2-3, 1978, pp. 243-252. doi:10.1016/0002-1571(78)90014-6
  9. H. Ogelman, A, Ecevit and E. Tasdemiroglu, “A New Method for Estimating Solar Radiation from Bright Sunshine Data,” Solar Energy, Vol. 33, No. 6, 1984, pp. 619- 625. doi:10.1016/0038-092X(84)90018-5
  10. B. G. Akinoglu and A. Ecevit, “A Further Comparison and Discussion of Sunshine Based Models to Estimate Global Solar Radiation,” Solar Energy, Vol. 15, No. 10, 1990, pp. 865-872.
  11. J. Glover and J. D. G. Mc Gulloch, “The Empirical Relation between Solar Radiation and Hours of Sunshine,” Quarterly Journal of the Royal Meteorological Society, Vol. 84, No. 360, 1958, pp. 172-175. doi:10.1002/qj.49708436011
  12. K. K. Gopinathan and A. Solar, “A Sunshine Dependent Global Insolation Model for Latitudes between 60N and 70N,” Renewable Energy, Vol. 2, No. 4-5, 1992, pp. 401- 404. doi:10.1016/0960-1481(92)90073-C
  13. Y. H. Liu, Y. N. Jiang and X. X. Chen, “Evaluation of Three Models for Calculating Daily Global Solar Radiation at Yushu, Tibet,” 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, 16-18 April 2011, pp. 1252-1255.
  14. J. Almorox and C. Hontoria, “Global solar radiation using sunshine duration in Spain,” Energy Conversion and Management, Vol. 45, No. 9-10, 2004, pp. 1529-1535. doi:10.1016/j.enconman.2003.08.022
  15. N. A. Elagib and M. G. Mansell, “New Approaches for Estimating Global Solar Radiation across Sudan,” Energy Conversion and Management, Vol. 41, No. 5, 2000, pp. 419-434. doi:10.1016/S0196-8904(99)00123-5
  16. H. S. Li, W. B. Ma, Y. W. Lian and X. L. Wang, “Estimating Daily Global Solar Radiation by Day of Year in China,” Applied Energy, Vol. 87, No. 10, 2010, pp. 3011- 3017. doi:10.1016/j.apenergy.2010.03.028
  17. A. Q. Jakhrani, A. K. Othman, A. R. H. Rigit and S. R. Samo, “A Simple Method for the Estimation of Global Solar Radiation from Sunshine Hours and Other Meteorological Parameters,” IEEE ICSET 2010, Kandy, 6-9 December 2010.
  18. B. Y. Liu and R. C. Jordan, “The Interrelationship and Characteristic Distribution of Direct, Diffuse, and Total Solar Radiation,” Solar Energy, Vol. 4, No. 3, 1960, pp. 1-19. doi:10.1016/0038-092X(60)90062-1
  19. M. J. Ahmad and G. N. Tiwari, “Solar Radiation Models: A Review,” International Journal of Energy Research, Vol. 35, No. 4, 2010, pp. 271-290.
  20. K. Bakirci, “Correlations for Estimation of Daily Global Solar Radiation with Hours of Bright Sunshine in Turkey,” Energy, Vol. 34, No. 4, 20009, pp. 485-501.

Journal Menu >>