Smart Grid and Renewable Energy
Vol.1 No.3(2010), Article ID:3326,10 pages DOI:10.4236/sgre.2010.13019
An Approach to Analyse Energy and Exergy Analysis of Thermal Power Plants: A Review
![]()
1Centre for Energy Studies, Indian Institute of Technology Delhi, New Delhi, India; 2School of Infrastructure Technology & Resource Management, Shri Mata Vaishno Devi University, Katra (J&K), India.
Email: drvsr81@gmail.com
Received October 30th, 2010; revised November 25th, 2010; accepted November 30th, 2010
Keywords: Exergy, Energy, Rankine Cycle
ABSTRACT
In this paper, a thermodynamic analysis of a coal based thermal power plant and gas based cogeneration power plant has been carried out. The energy and exergy analysis has been studies for the different components of both power plants. The paper analyses the information available in the open literature regarding energy and exergy analysis on high temperature power plant has been included. A comprehensive literature review on thermal power plants, especially boiler in coal base thermal power plants and combustion chamber in gas-steam cogeneration has been included. Finally, explaining the procedure of analysis of thermal power plant systems by exegetical approach.
1. Introduction
The name thermodynamics comes from the Greek words therme (heat) and dynamis (power), which is most expressive of the conversion from heat into power [1]. Now adays same name is broadly interpreted to include all aspects of energy and energy transformations, including power generation, refrigeration, and relationships among the properties of matter. The First Law deals with the amounts of energy of various forms transferred between the system and its surroundings and with the changes in the energy stored in the system. It treats work and heat interactions as equivalent forms of energy in transit and offers no indication about the possibility of a spontaneous process proceeding in a certain direction. The first law places no restriction on the direction of a process, but satisfying the first law does not ensure that the process can actually occur. This inadequacy of the first law to identify whether a process can take place is remedied by introducing another general principle, the second law of thermodynamics.
The exergy method of analysis is based on the Second law of thermodynamics and the concept of irreversible production of entropy. The fundamentals of the exergy method were laid down by Carnot in 1824 and Clausius in 1865. The energy-related engineering systems are designed and their performance is evaluated primarily by using the energy balance deduced from the First law of thermodynamics. Engineers and scientists have been traditionally applying the First law of thermodynamics to calculate the enthalpy balances for more than a century to quantify the loss of efficiency in a process due to the loss of energy. The exergy concept has gained considerable interest in the thermodynamic analysis of thermal processes and plant systems since it has been seen that the First law analysis has been insufficient from an energy performance stand point.
However it can specify where the process can be improved and therefore, it will signify what areas should be given consideration. The simple energy balance will not sometimes suffice to find out the system defect. In such circumstances the exergy analysis is well thought-out to be significant to locate the systems imperfections.
Recently, we had new technologies for high temperature air combustion and ultra-high temperature combined cycle. In this case, it is necessary to study the exergy analysis on combustion and thermodynamic processes, because ordinary energy analysis does not have any evaluation supported at its temperature level. If we introduce the exergy analysis against energy analysis, which is supported by this temperature level, it is clear that the high temperature energy has a greater evaluation compared with low temperature one. In this particular field of engineering, it is difficult to use the ambient temperature energy of air and water, which are widely available. When we discuss power generation, high temperature energy of 1500°C and above in combined cycle has higher conversion efficiency than that of 500-600°C in steam cycle. In a thermodynamic cycle, it is necessary to consider the combustion, heat transfer and energy conversion processes, which include many kinds of effective and invalid items. So, when considering the above mentioned processes, the exergy analysis must be introduced to analyze power generation and heat pump cycles as against energy analysis. Recently a large number of studies based on exergy analysis have been carried out by many researchers all over the world in various system applications.
2. Cycle Analysis of Coal Fired Thermal Power Plants
Coal based thermal power plant working base on Rankine power cycle. The ideal cycle for vapor power cycles many of the impracticalities associated with the Carnot cycle can be eliminated by superheating the steam in the boiler and condensing it completely in the condenser, as shown schematically on a T-s diagram in Figure 1. The cycle that results is the Rankine cycle, which is the ideal cycle for vapor power plants. The ideal Rankine cycle does not involve any internal irreversibility and consists of the following four processes:
1-2 Isentropic compression in a pump;
2-3 Constant pressure heat addition in a boiler;
3-4 Isentropic expansion in a turbine;
4-1 Constant pressure heat rejection in a condenser.
2.1. Approach to Increase the Efficiency of the Rankine Cycle
The efficiency of Rankine cycle can be improved with considering following points:
2.1.1. Lowering the Condenser Pressure
Inside the condenser steam exists as a saturated mixture at the saturation temperature corresponding to the pressure inside the condenser. Therefore, lowering the operating pressure of the condenser automatically lowers the temperature of the steam. It increases the turbine output. It cannot be lower than the temperature of the cooling medium. Because, it increases the moisture content of the steam at the final stages of the turbine and it erodes the turbine blades. Finely decreases the turbine efficiency. Luckily, this problem can be solved by reheating of steam.
2.1.2. Superheating the Steam to High Temperatures
Superheat the steam to very high temperatures before it enters the turbine. This would be the desirable solution since the average temperature at which heat is added would also increase, thus increasing the cycle efficiency. However, it has the limitation to rise the steam temperature up to metallurgic-ally safe levels.
2.1.3. Increasing the Boiler Pressure
Increasing the boiler pressure increases the thermal efficiency of the Rankine cycle, but it also increases the moisture content of the steam to unacceptable levels.
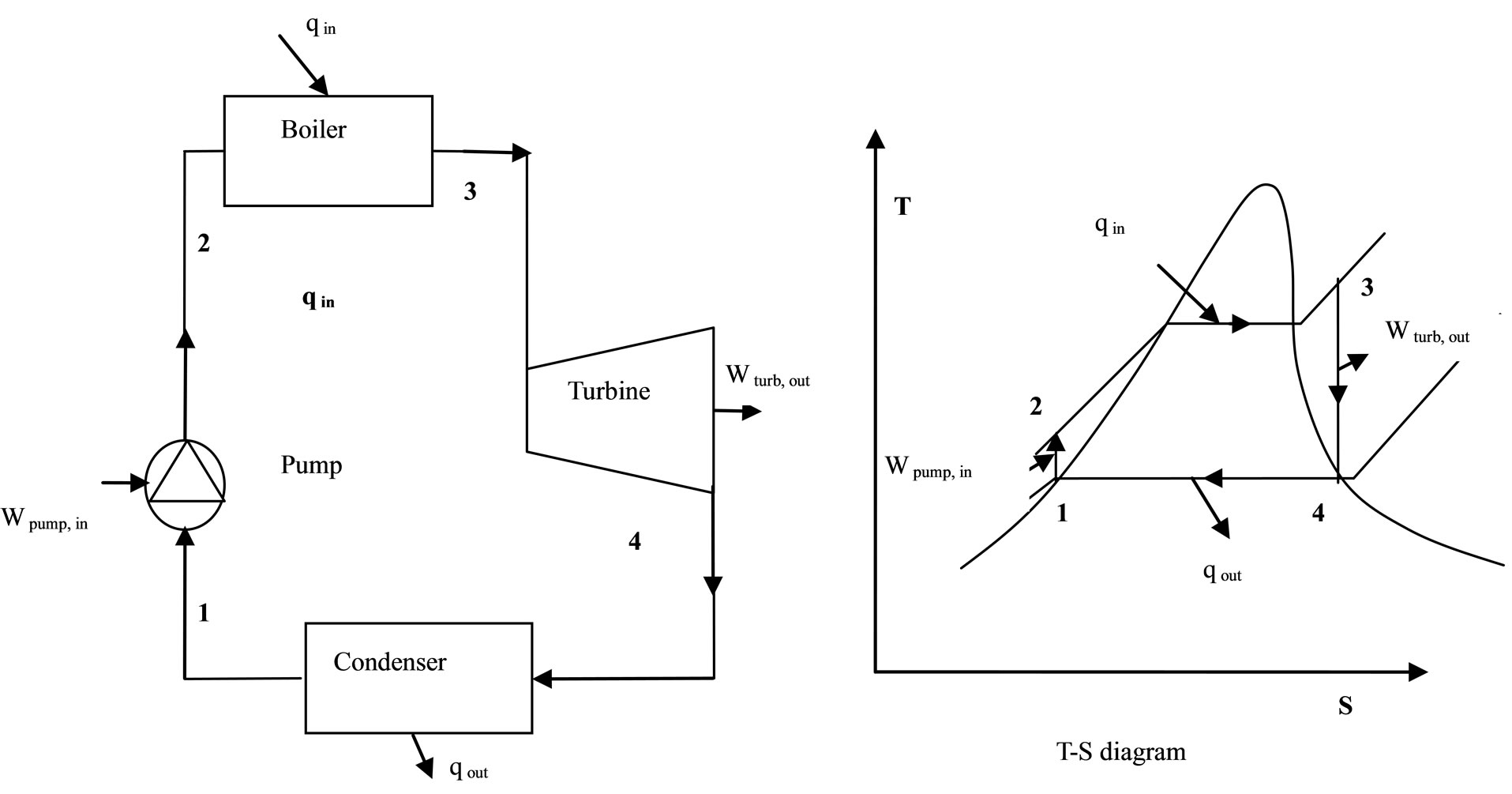
Figure 1. Schematic of rankine cycle.
2.1.4. Reheat Rankine Cycle
Increasing the boiler pressure increases the thermal efficiency of the Rankine cycle, but it also increases the moisture content of the steam to undesirable levels. Expand the steam in the turbine in two stages, and reheat it in between. It can decrease the excessive moisture problem in turbines. The reheat cycle was introduced in the mid-1920s, but it was deserted in the 1930s. It was reintroduces single reheat in the late 1940s and double reheats in the early 1950s because of the operational complexities. The purpose of the reheat cycle is to reduce the moisture content of the steam at the final stages of the expansion process.
2.1.5. Regenerative Rankine Cycle
To transfer heat to the feed-water from the expanding steam in a counter-flow heat exchanger built into the turbine, that is, to use regeneration. A practical regeneration process in steam power plants is accomplished by extracting/bleeding the steam from the turbine at various points. Regeneration not only improves cycle efficiency. It also helps control the large volume flow rate of the steam at the final stages of the turbine (due to the large specific volumes at low pressures).
3. Cycle Analysis of Gas Fired Thermal Power Plants
In this power plants toping cycle base on the Brayton cycle, operated as gas based power cycle and bottoming cycle base on the Rankine cycle. Regarding ranking cycle process we discussed in the above section. [2] The ideal cycle for gas-turbine engines: The Brayton cycle was first proposed in 1870 by George Brayton for use in the reciprocating oil-burning engine. Now a day, it is used for gas turbines only where both the compression and expansion processes take place in rotating machinery. Gas turbines usually operate on an open cycle. Fresh air at ambient conditions is drawn into the compressor; its pressure and temperature are raised. The high pressure air proceeds into the combustion chamber, where the fuel is burned at constant pressure. The resulting high-temperature gases then enter the turbine; they expand to the atmospheric pressure while producing power.
Brayton cycle, which is made up of four internally reversible processes:
1-2 Isentropic compression;
2-3 Constant-pressure heat addition;
3-4 Isentropic expansion;
4-1 Constant-pressure heat rejection.
The total reversible processes cycle shown schematically on a T-s diagram in Figure 2.
4. First and Second (Exergy) Law Analysis
Second law is a generic term for a group of concepts that define the maximum work potential of a system, a stream of matter or a heat interaction; the state of the (conceptual) environment being used as the datum state. In an open flow system there are three types of energy transfer across the control surface namely working transfer, heat transfer, and energy associated with mass transfer or flow. [3] The work transfer is equivalent to maximum work, which can be obtained from that form of energy. The availability (ExQ) of heat transfer Q from the control surface at temperature T is determined from maximum rate of conversion of thermal energy to work Wmax. The Wmax is given by
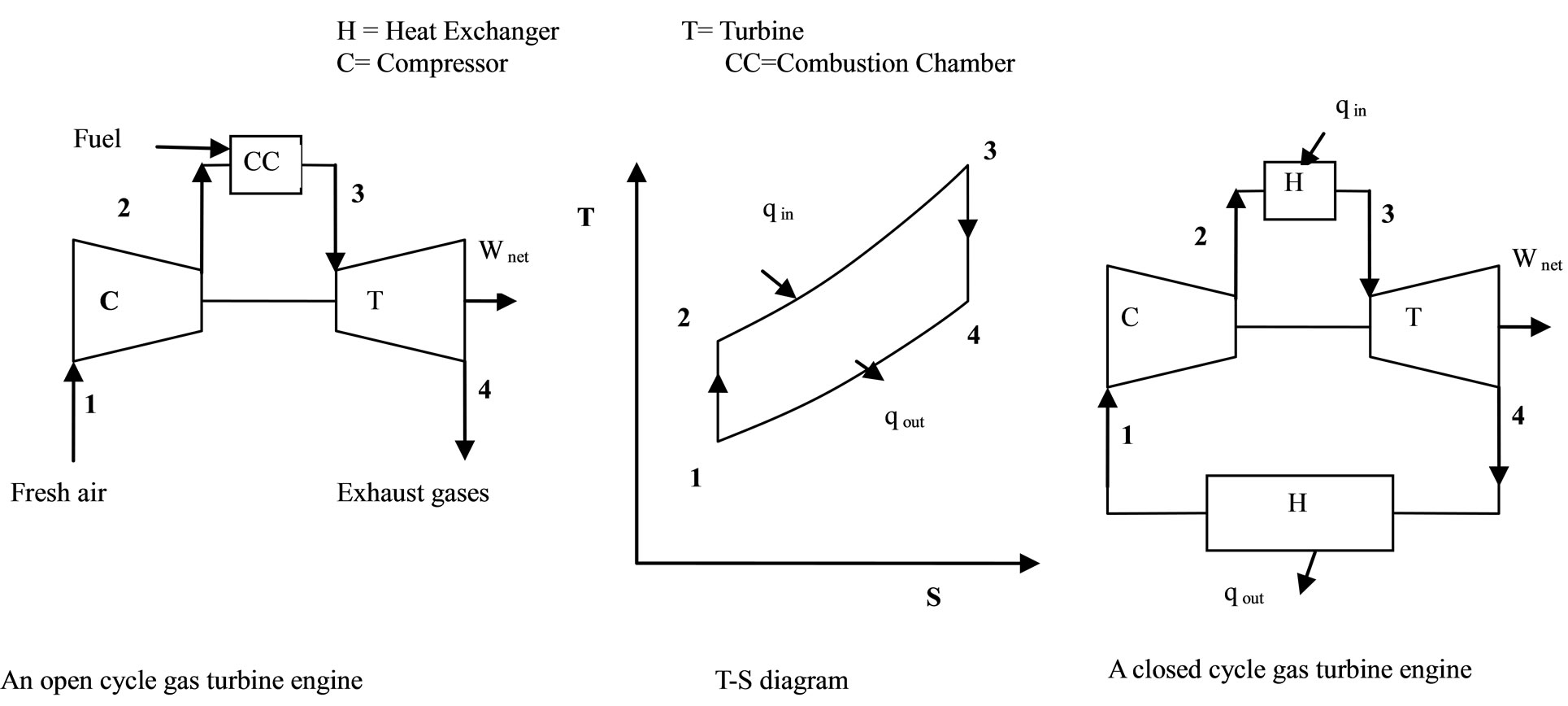
Figure 2. chematic of Brayton cycle.
 (1)
(1)
Exergy of steady flow stream of matter is sum of kinetic, potential and physical exergy Exph. The kinetic and potential energy are again equivalent to exergy. The physical specific exergy 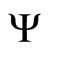 depends on initial state of matter and environmental state.
depends on initial state of matter and environmental state.
Energy analysis is based on the first law of thermodynamics, which is related to the conservation of energy. Second law analysis is a method that uses the conservation of mass and conservation of energy principles together with the entropy for the analysis, design and improvement of energy systems. Second law analysis is a useful method; to complement not to replace energy analysis. The first law of thermodynamics or energy balance for steady flow process of an open system is given by
 (2)
(2)
where 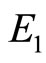 and
and  are respectively the energy associated with mass entering and leaving the system,
are respectively the energy associated with mass entering and leaving the system, 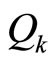 is heat transfer to system from source at Tk, and W is net work developed by the system. The Second law balance for steady flow process of an open system is given by
is heat transfer to system from source at Tk, and W is net work developed by the system. The Second law balance for steady flow process of an open system is given by
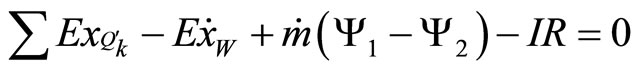 (3)
(3)
where 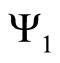 and
and 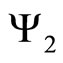 are available energy associated with mass inflow and outflow are respectively,
are available energy associated with mass inflow and outflow are respectively, 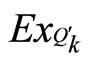 is available energy associated with heat transfer, ExW is available energy associated with work transfer and IR is irreversibility of process. The irreversibility may be due to heat transfer through finite temperature difference, mixing of fluids and mechanical friction. Second law analysis is an effective means, to pinpoint losses due to irreversibility in a real situation. The energy or first law efficiency
is available energy associated with heat transfer, ExW is available energy associated with work transfer and IR is irreversibility of process. The irreversibility may be due to heat transfer through finite temperature difference, mixing of fluids and mechanical friction. Second law analysis is an effective means, to pinpoint losses due to irreversibility in a real situation. The energy or first law efficiency 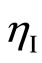 of a system or system component is defined as the ratio of energy output to the energy input of system or system component, i.e.
of a system or system component is defined as the ratio of energy output to the energy input of system or system component, i.e.
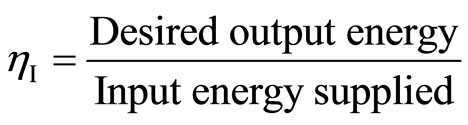 (4)
(4)
The second law efficiency is defined as
 (5)
(5)
5. Studies Conducted on Energy and Exergy Analysis of Thermal Power Plants
Bejan [4] draw outlines the fundamentals of the methods of exergy analysis and entropy generation minimization (or thermodynamic optimization-the minimization of exergy destruction). The paper begins with a review of the concept of irreversibility, entropy generation, or exergy destruction. Examples illustrate the accounting for exergy flows and accumulation in closed systems, open systems, heat transfer processes, and power and refrigeration plants. George and Park [5] discusses how to estimate the avoidable and unavoidable exergy destruction and investment costs associated with compressors, turbines, heat exchangers and combustion chambers. This general procedure, although based on many subjective decisions, facilitates and improves applications of exergoeconomics.
5.1. Coal Fired Thermal Power Plants
Kotas [6] explained in this work the concept of exergy used to define criteria of performance of thermal plant. Ganapathy et al. [7] studied with an exergy analysis performed on an operating 50 MWe unit of lignite fired steam power plant at Thermal Power Station-I, Neyveli Lignite Corporation Limited, Neyveli, Tamil Nadu, India. The distribution of the exergy losses in several plant components during the real time plant running conditions has been assessed to locate the process irreversibility. The comparison between the energy losses and the exergy losses of the individual components of the plant shows that the maximum energy losses of 39% occur in the condenser, whereas the maximum exergy losses of 42.73% occur in the combustor. Kamate and Gangavati [8] studied exergy analysis of a heat-matched bagasse -based cogeneration plant of a typical 2500 tcd sugar factory, using backpressure and extraction condensing steam turbine is presented. In the analysis, exergy methods in addition to the more conventional energy analyses are employed to evaluate overall and component efficiencies and to identify and assess the thermodynamic losses. Boiler is the least efficient component and turbine is the most efficient component of the plant. The results show that, at optimal steam inlet conditions of 61 bar and 475°C, the backpressure steam turbine cogeneration plant perform with energy and exergy efficiency of 0.863 and 0.307 and condensing steam turbine plant perform with energy and exergy efficiency of 0.682 and 0.260.
Datta et al. [9] was presented work on exergy analysis of a coal-based thermal power plant is done using the design data from a 210 MW thermal power plant under operation in India. The exergy efficiency is calculated using the operating data from the plant at different conditions, viz. at different loads, different condenser pressures, with and without regenerative heaters and with different settings of the turbine governing. The load variation is studied with the data at 100, 75, 60 and 40% of full load. Effects of two different condenser pressures, i.e. 76 and 89 mmHg (abs.), are studied. It is observed that the major source of irreversibility in the power cycle is the boiler, which contributes to exergy destruction of the order of 60%. Part load operation increases the irreversibilities in the cycle and the effect is more pronounced with the reduction of the load. Increase in the condenser back pressure decreases the exergy efficiency. Successive withdrawal of the high pressure heaters shows a gradual increment in the exergy efficiency for the control volume excluding the boiler. Aljundi [10] was presented in this study, the energy and exergy analysis of Al-Hussein power plant in Jordan is presented. The primary objectives of this paper are to analyze the system components separately and to identify and quantify the sites having largest energy and exergy losses. In addition, the effect of varying the reference environment state on this analysis will also be presented. Energy losses mainly occurred in the condenser where 134 MW is lost to the environment while only 13 MW was lost from the boiler system. The percentage ratio of the exergy destruction to the total exergy destruction was found to be maximum in the boiler system (77%) followed by the turbine (13%), and then the forced draft fan condenser (9%). In addition, the calculated thermal efficiency based on the lower heating value of fuel was 26% while the exergy efficiency of the power cycle was 25%. For a moderate change in the reference environment state temperature, no drastic change was noticed in the performance of major components. Dai et al. [11] was done exergy analysis for each cogeneration system is examined, and a parameter optimization for each cogeneration system is achieved by means of genetic algorithm to reach the maximum exergy efficiency. The cement production is an energy intensive industry with energy typically accounting for 50-60% of the production costs. In order to recover waste heat from the preheated exhaust and clinker cooler exhaust gases in cement plant, single flash steam cycle, dual-pressure steam cycle, organic Rankine cycle (ORC) and the Kalina cycle are used for cogeneration in cement plant. The optimum performances for different cogeneration systems are compared under the same condition. The results show that the exergy losses in turbine, condenser, and heat recovery vapor generator are relatively large. Rosen [12] reported results were of energyand exergy-based comparisons of coal-fired and nuclear electrical generating stations. A version of a process-simulation computer code, previously enhanced by the author for exergy analysis, is used. Overall energy and exergy efficiencies, respectively, are 37% and 36% for the coal-fired process, and 30% and 30% for the nuclear process. The losses in both plants exhibit many common characteristics. Energy losses associated with emissions (mainly with spent cooling water) account for all of the energy losses, while emission-related exergy losses account for approximately 10% of the exergy losses. The remaining exergy losses are associated with internal consumptions. Dincer and Rosen [13] present effects on the results of energy and exergy analyses of variations in dead-state properties, and involves two main tasks: 1) examination of the sensitivities of energy and exergy values to the choice of the dead-state properties and 2) analysis of the sensitivities of the results of energy and exergy analyses of complex systems to the choice of dead-state properties. A case study of a coalfired electrical generating station is considered to illustrate the actual influences. The results indicate that the sensitivities of energy and exergy values and the results of energy and exergy analyses to reasonable variations in dead-state properties are sufficiently small. Erdem et al. [14] analyze comparatively the performance of nine thermal power plants under control governmental bodies in Turkey, from energetic and exergetic viewpoint. The considered power plants are mostly conventional reheat steam power plant fed by low quality coal. Firstly, thermodynamic models of the plants are developed based on first and second law of thermodynamics. Secondly, some energetic simulation results of the developed models are compared with the design values of the power plants in order to demonstrate the reliability. Thirdly, design point performance analyses based on energetic and exergetic performance criteria such as thermal efficiency, exergy efficiency, exergy loss, exergetic performance coefficient are performed for all considered plants in order to make comprehensive evaluations Vidal et al. [15] analysis exergy method was applied in order to evaluate the new combined cycle proposed by Goswami, using Hasan-Goswami-Vijayaraghavan parameters. This new combined cycle was proposed to produce both power and cooling simultaneously with only one heat source and using ammonia-water mixture as the working fluid. At the irreversible process two cases were considered, changing the environmental temperature. However, in order to know the performance of the new cycle at different conditions of operation, the second irreversible case was analyzed varying the rectification temperatures, the isentropic efficiency of the turbine and the return temperature of the chilled water. Exergy effectiveness values of 53% and 51% were obtained for the irreversible cycles; with heat input requirements at temperatures of 125 and 150˚C. Solar collectors or waste heat are suggested as heat sources to operate the cycle.
5.1.1. Combustion
Arai et al. [3] presents an exergy analysis on combustion and energy conversion processes, which is based on the above-mentioned concept of exergy and energy supported by temperature level. When we discuss high temperature air combustion in furnace, this process shows a higher performance than that of the ambient air combustion.
5.1.2. Throttling
Luo and Wang [16] propose an approach to calculate the efficiency of throttling in which the exergy (available energy) is used to evaluate the energy conversion processes. The compressibility factor is calculated by using Peng-Robinson (P-R) equation. It is found that the largest deviation between the exergies calculated by the real gas equation and ideal gas assumption is about 1%. Because the exergy is a function of the pressure and temperature, the Joule-Thomson coefficients are used to calculate the temperature changes of throttling, based on the compressibility factors of the Soave-Redlich-Kwong (S-R-K) and P-R equations, and the temperature decreases are compared with those calculated by empirical formula.
5.1.3. Waste Emissions
Dincer and Rosen [17] studied in this paper, the concepts of exergy analysis and the linkages between exergy and environmental impact are discussed, and several issues regarding the exergies of waste emissions are addressed. Exergy is a measure of the degree of disequilibrium between a substance and its environment. The relations between several measures of environmental impact potential and exergy are investigated by comparing current methods used to assess the environmental impact potential of waste emissions and the exergy associated with those emissions.
5.2. Cogeneration and Combined Cycle Thermal Power Plants
Khaliq and Kaushik [18] presented thermodynamic methodology for the performance evaluation of combustion gas turbine cogeneration system with reheat. The energetic and exergetic efficiencies have been defined. The effects of process steam pressure and pinch point temperature used in the design of heat recovery steam generator, and reheat on energetic and exergetic efficiencies have been investigated. The power to heat ratio and second-law efficiency increases significantly with increase in process steam pressure, but the first-law efficiency decreases with the same. Results also show that inclusion of reheat provides significant improvement in electrical power output, process heat production, fuel-utilization (energetic) efficiency and second-law (exergetic) efficiency.
5.2.1. Gas Turbine Based Thermal Power Plants
Khaliq and Kaushik [19] were presented theoretical second-law approach for the thermodynamic analysis of the reheat combined Brayton/Rankine power cycle. Expressions involving the variables for specific power-output, thermal efficiency, exergy destruction in components of the combined cycle, second-law efficiency of each process of the gas-turbine cycle, and second law efficiency of the steam power cycle have been derived. It is found that the exergy destruction in the combustion chamber represents over 50% of the total exergy destruction in the overall cycle. The combined cycle efficiency and its power output were maximized at an intermediate pressure-ratio, and increased sharply up to two reheat-stages and more slowly thereafter. Chen and Tyagi [20] were presented parametric study of an irreversible cycle model of a regenerative-intercooled-reheat Brayton heat engine along with a detailed. The power output and the efficiency are optimized with respect to the cycle temperatures for a typical set of operating conditions. It is found that there are optimal values of the turbine outlet temperature, inter cooling, reheat and cycle pressure ratios at which the cycle attains the maximum power output and efficiency. But the optimal values of these parameters corresponding to the maximum power output are different from those corresponding to the maximum efficiency for the same set of operating condition. Kaushik and Tyagi [21] explained in this paper a parametric study of an irreversible regenerative Brayton heat engine with isothermal heat addition has been performed with external as well as internal irreversibilities. The external irreversibility is due to the finite temperature differences between the heat engine and the external reservoirs, while the internal irreversiblities are due to other processes, viz. non-isentropic compression and expansion processes in the compressor and turbine, respectively, and the regenerative heat loss. There is a significant improvement in the thermal efficiency (above 15%) of a Brayton cycle with isothermal heat addition over the conventional one. It is seen that the effect of the isobaric side effectiveness is rather pronounced for the power output and the corresponding thermal efficiency. Zubair [22] was examined the performance of regenerative -reheat power plants in terms of irreversibility analysis. The reduction in the irreversible losses with the addition of backward, cascade-type feed water heaters and/or a reheat option are compared with a conventional energy -balance approach. The results indicate that most of the irreversible losses occur in the boiler and that these losses are significantly reduced by the incorporation of feed water heating. The incorporation of feed water heating results in a reduction of the total irreversibility rate of the cycle by 18%. The corresponding improvement in efficiency is 12%.
5.2.2. Heat Exchangers
Yilmaz et al. [23] presented in his paper, second-law based performance evaluation criteria to evaluate the performance of heat exchangers. First, the need for the systematic design of heat exchangers using a second law-based procedure is recalled and discussed. Then, a classification of second-law based performance criteria is presented: 1) criteria that use entropy as evaluation parameter, and 2) criteria that use exergy as evaluation parameter. Both classes are collectively presented and reviewed, and their respective characteristics and constraints are given.
5.2.3. Combined Cycle Based Thermal Power Plants
The Schematic diagram of gas fired combined cycle thermal power plant is shown in Figure 3. Chen et al. [24] present performance analysis and optimization of an open-cycle regenerator gas-turbine power plant. The analytical formulae about the relation between power output and cycle overall pressure-ratio are derived taking into account the eight pressure-drop losses in the intake, compression, regeneration, combustion, expansion and discharge processes and flow process in the piping, the heat-transfer loss to the ambient environment, the irreversible compression and expansion losses in the compressor and the turbine, and the irreversible combustion loss in the combustion chamber. The power output is optimized by adjusting the mass-flow rate and the distribution of pressure losses along the flow path. Reddy and Mohamed [25] present work, exergy analysis of a natural gas fired combined cycle power generation unit is performed to investigate the effect of gas turbine inlet temperature and pressure ratio on exergetic efficiency for the plant and exergy destruction/losses for the components. For a fixed gas turbine inlet temperature, an optimum pressure ratio exists where the exergy destruction is less [26]. The effect of steam injection on the performance of natural gas fired combined cycle power plant is investigated. For a particular combined cycle power generation configuration, the effect of steam injection on the performance of topping cycle, and carbon dioxide emissions is conducted based on first law of thermodynamics.
Sohn et al. [27] described details of exergy-based performance characteristics of a heavy-duty gas turbine, 150MW-class GE 7F model. Results have shown that a chemical reaction in the combustor of which the exergy destruction ratio is 28.3% at full-load is one of the major sources of exergy destructions in the gas turbine it was discovered that the magnitude of exergy destruction by the cooling air in turbine stages is large enough to influence the overall turbine efficiency. The exergy destruction by the cooling air is more than half of the total exergy destruction of each cooled turbine stage Results have shown that a chemical reaction in the combustor of which the exergy destruction ratio is 28.3% at full-load is one of the major sources of exergy destructions in the gas turbine. Koroneos et al. [28] studied the exergy analysis of solar energy, wind power and geothermal energy. That is, the actual use of energy from the existing available energy is discussed. In addition, renewable energy sources are compared with the non-renewable energy sources on the basis of efficiency. Khaliq [29] was proposed conceptual trigeneration system based on the conventional gas turbine cycle for the high temperature heat addition while adopting the heat recovery steam generator for process heat and vapor absorption refrigeration for the cold production. Combined first and second law approach is applied and computational analysis is performed to investigate the effects of overall pressure ratio, turbine inlet temperature, pressure drop in combustor and heat recovery steam generator, and evaporator temperature on the exergy destruction in each component, first law efficiency, electrical to thermal energy ratio, and second law efficiency of the system.
It also indicates that maximum exergy is destroyed during the combustion and steam generation process; which represents over 80% of the total exergy destruction in the overall system Ivar et al. [30] was investigated a concept for natural-gas fired power plants with CO2 capture using exergy analysis. Natural-gas was reformed in an auto-thermal reformer, and the CO2 was separated before the hydrogen-rich fuel was used in a conventional combined-cycle process. A corresponding conventional combined-cycle power plant with no CO2 capture was simulated for comparison. A base case with CO2 capture was specified with turbine-inlet temperature of 1250˚C and an air-compressor outlet pressure of 15.6 bar. In this case, the net electric-power production was 48.9% of the lower heating value of the Natural-gas or 46.9% of its chemical exergy. The effect of increased turbine-inlet temperature to 1450˚C was investigated. Combining both measures, the net electric power production was increased to 53.3% of the natural-gas lower heating value or 51.1% of the natural-gas chemical exergy. On the other hand, both increased turbine-inlet temperature and the auto-thermal reformer product-feed heat exchange reduced the conversion of hydrocarbons to CO2. Nag and Gupta [31] was down exergy analysis , to reduce thermal irreversibilitys a thermodynamic cycle was conceptualized for the bottoming part of a combined cycle by Kalina, which uses NH3- H2O mixture as the working substance. The effect of one of the key parameter, mixture concentration at turbine inlet on the cycle performance has been studied. Franco and Russo [32] presented in this present particular work point out attention to the optimization of the heat recovery steam generator (HRSG), as a first step in the analysis of the whole plant, according to a hierarchical strategy. He handles this problem adopting both a thermodynamic and
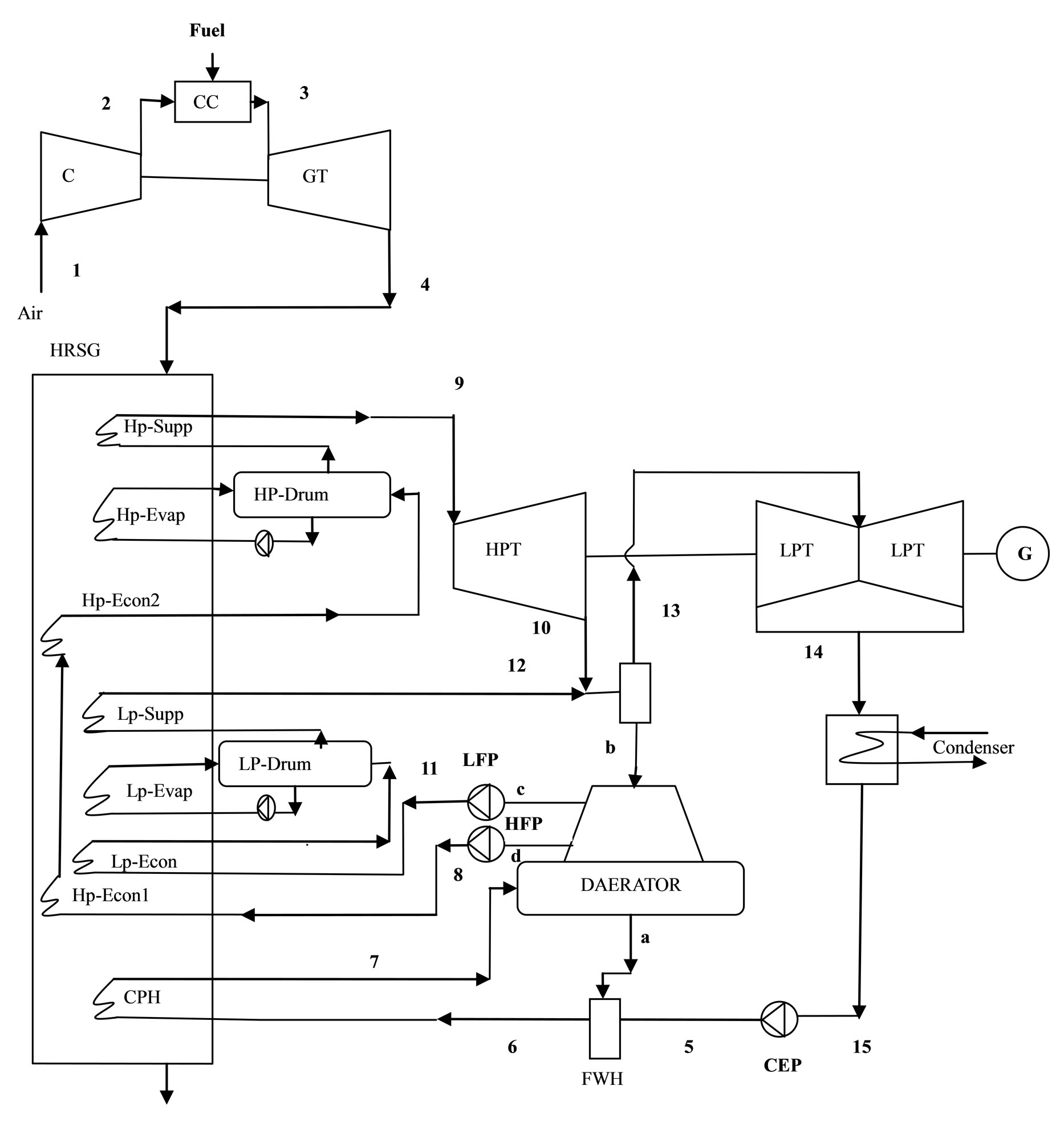
Figure 3. Schematic of gas fired combined cycle thermal power plant.
a thermo economic objective function instead that with the usual pinch point method. Thermodynamic optimization has the purpose to diminish energy losses, expressed on exergy basis, while the aim of the thermo economic optimization is the minimization of a cost function, sum of the cost of exergy inefficiencies and the cost of the HRSG. Bilgen [33] presented exergetic and engineering analyses as well as a simulation of gas turbine-based cogeneration plants consisting of a gas turbine, heat recovery steam generator and steam turbine. The exergy analysis is based on the first and second laws of thermodynamics. The engineering analysis is based on both the methodology of levelized cost and the payback period.
Dincer et al. [34] presented an efficiency analysis, accounting for both energy and exergy considerations, of a design for a cogeneration-based district energy system. A case study is considered for the city of Edmonton, Canada, by the utility Edmonton Power. The energyand exergy-based results differ markedly (e.g., overall energy efficiencies are shown to vary for the three configurations considered from 83% to 94%, and exergy efficiencies from 28% to 29%, respectively). Datta et al. [35] studied thermal performance and sizing of Biomass based decentralized power generation using externally fired gas turbine can be a technically feasible option plants have been analyzed at different cycle pressure ratio (rp = 2-8), turbine inlet temperature (1050-1350 K) and the heat exchanger cold end temperature difference (200-300 K). It is found that the thermal efficiency of the externally fired gas turbine plant reaches a maximum at an optimum pressure ratio depending upon the turbine inlet temperature and heat exchanger. For a particular pressure ratio, thermal efficiency increases either with the increase in turbine inlet temperature or with the decrease in heat exchanger cold end temperature. Sue and Chuang [36] presented in his paper the engineering design and theoretical exergetic analyses of the plant for combustion. The results show the exergy analyses for a steam cycle system predict the plant efficiency more precisely. The plant efficiency for partial load operation is lower than full load operation. Increasing the pinch points will decrease the combined cycle plant efficiency of gas turbine based power generation systems.
6. Conclusions
The worldwide concern about cost, environment and quick availability to meet continuous load growth will continue to enhance the adoption of gas and steam turbine engines in power systems. The escalating interest in efficient use of energy will support the adoption of cogeneration with simultaneous production of power and thermal energy. The first law analysis shows major energy loss has been found to occur in condenser. The second law (Exergy) analysis shows that combustion chamber in both steam and gas turbine thermal power plants are main source of Irreversibility. The Irreversibility in condenser is insignificant, because in the condenser the low quality energy is lost. An Exergy method of optimization gives logical solution improving the power production opportunities in thermal power plants.
REFERENCES
- A. Yunus and A. Michael, “Thermodynamics an Engineering Approach,” Tata McGraw Hill, New Delhi, 2007.
- P. K. Nag, “Power Plant Engineering,” Tata McGraw Hill, New Delhi, 2007.
- N. Arai, H. Taniguchi, K. Mouri and T. Nakahara, “Exergy Analysis on Combustion and Energy Conversion Processes,” Energy, Vol. 30, No. 2-4, 2005, pp. 111-117.
- A. Bejan, “Fundamentals of Exergy Analysis, Entropy Generation Minimization, and the Generation of Flow Architecture,” International Journal of Energy Research, Vol. 26, No. 7, 2002, pp. 545-565.
- G. Tsatsaronis and M. Park, “On Avoidable and Unavoidable Exergy Destructions and Investment Costs in Thermal Systems,” Energy Conversion & Management, Vol. 43, No. 9-12, 2002, pp. 1259-1270.
- T. J. Kotas, “Exergy Criteria of Performance for Thermal Plant: Second of Two Papers on Exergy Techniques in Thermal Plant Analysis,” International Journal of Heat and Fluid Flow, Vol. 2, No. 4, 1980, pp. 147-163.
- T. Ganapathy, N. Alagumurthi, R. P. Gakkhar and K. Murugesan, “Exergy Analysis of Operating Lignite Fired Thermal Power Plant,” Journal of Engineering Science and Technology Review, Vol. 2, No. 1, 2009, pp.123-130.
- S. C. Kamate and P. B. Gangavati, “Exergy Analysis of Cogeneration Power Plants in Sugar Industries,” Applied Thermal Engineering, Vol. 29, No. 5-6, 2009, pp. 1187- 1194.
- A. Datta, S. Sengupta and S. Duttagupta, “Exergy Analysis of a Coal-Based 210 mw Thermal Power Plant,” International Journal of Energy Research, Vol. 31, No. 1, 2007, pp. 14-28.
- I. H. Aljundi, “Energy and Exergy Analysis of a Steam Power Plant in Jordan,” Applied Thrmal Engineering, Vol. 29, No. 2-3, 2009, pp. 324-328.
- Y. Dai, J. Wang and L. Gao, “Exergy Analyses and Parametric Optimizations for Different Cogeneration Power Plants in Cement Industry,” Applied Energy, Vol. 86, No. 6, 2009, pp. 941-948.
- M. A. Rosen, “Energyand Exergy-Based Comparison of Coal-Fired and Nuclear Steam Power Plants,” Exergy, Vol. 1, No. 3, 2001, pp. 180-192.
- I. Dincer and M. A. Rosen, “Effect of Varying Dead-State Properties on Energy and Exergy Analyses of Thermal Systems,” International Journal of Thermal Sciences, Vol. 43, No. 3, 2004, pp. 121-133.
- H. Erdem, A. V. Akkaya., A. Dagdas, S. H. Sevilgen, B. Sahin, I. Tek, C. Gungor and S. Atas, “Comparative Energetic and Exergetic Performance Analyses for CoalFired Thermal Power Plants in Turkey,” International Journal of Thermal Sciences, Vol. 48, No. 11, 2009, pp. 2179-2186.
- A. Vidal, R. Best, R. Rivero and J. Cervantes, “Analysis of a Combined Power and Refrigeration Cycle by the Exergy Method,” Energy, Vol. 31, No. 15, 2006, pp. 3401- 3414.
- Y. X. Luo and X. Y. Wang, “Exergy Analysis on Throttle Reduction Efficiency Based on Real Gas Equations,” Energy, Vol. 35, No. 1, 2010, pp. 181-187.
- I. Dincer and M. A. Rosen, “Exergy Analysis of Waste Emissions,” International Journal of Energy Reserch, Vol. 23, No. 13, 1999, pp. 1153-1163.
- A. Khaliq and S. C. Kaushik, “Thermodynamic Performance Evaluation of Combustion Gas Turbine Cogeneration System with Reheat,” Applied Thermal Engineering, Vol. 24, No. 13, 2004, pp. 1785-1795.
- A. Khaliq and S. C. Kaushik, “Second-Law Based Thermodynamic Analysis of Brayton/Rankine Combined Power Cycle with Reheat,” Applied Energy, Vol. 78, No. 2, 2004, pp. 179-197.
- G. M. Chen, S. K. Tyagi, Q. Wang and S. C. Kaushik, “A New Thermoeconomic Approach and Parametric Study of an Irreversible Regenerative Brayton Refrigeration Cycle,” International Journal of Refrigeration, Vol. 29, No. 7, 2006, pp. 1167-1174.
- S. C. Kaushik, S. K. Tyagi and M. K. Singhal, “Parametric Study of an Irreversible Regenerative Brayton Cycle with Isothermal Heat Addition,” Energy Conversion & Management, Vol. 44, No. 12, 2003, pp. 2013-2025.
- S. M. Zubair and M. A. Habib, “Second-Law-Based Thermodynamic Analysis of Regenerative-Reheat RankineCycle Power Plants,” Energy, Vol. 17, No. 3, 1992, pp. 295-301.
- M. Yilmaz, O. N. Sara and S. Karsli, “Performance Evaluation Criteria for Heat Exchangers Based on Second Law Analysis,” Exergy, Vol. 1, No. 4, 2001, pp. 278-294.
- L. G. Chen, Y. Li, F. R. Sun and C. Wu, “Power Optimization of Open-Cycle Regenerator Gas-Turbine PowerPlants,” Applied Energy, Vol. 78, No. 2, 2004, pp. 199- 218.
- B. V. Reddy and K. Mohamed, “Exergy Analysis of Natural Gas Fired Combined Cycle Power Generation Unit,” International Journal of Exergy, Vol. 4, No. 2, 2007, pp. 180-196.
- B.V. Reddy and I. E. Alaefour, “Performance Simulation of a Natural Gas Fired Combined Cycle Power Generation System,” 19th National & 8th ISHMT-ASME Heat and Mass Transfer Conference, Hyderabad, 2008.
- J. L. Sohn, T. W. Song, J. H. Kim, T. S. Kim and S. T. Ro, “Exergy-Based Performance Analysis of the Heavy-Duty Gas Turbine in Part-Load Operating Conditions,” Exergy, Vol. 2, No. 2, 2002, pp. 105-112.
- C. Koroneos, T. Spachos and N. Moussiopoulos, “Exergy Analysis of Renewable Energy Sources,” Renewable Energy, Vol. 28, No. 2, 2003, pp. 295-310.
- A. Khaliq, “Exergy Analysis of Gas Turbine Trigeneration System for Combined Production of Power Heat and Refrigeration,” Refrigeration, Vol. 32, No. 3, 2009, pp. 534-545.
- I. S. Ertesvag, H. M. Kvamsdal and O. Bolland, “Exergy Analysis of a Gas-Turbine Combined-Cycle Power Plant with Precombustion Co2 Capture,” Energy, Vol. 30, No. 1, 2009, pp. 5-39.
- P. K. Nag and A. V. S. S. K. S. Gupta, “Exergy Analysis of the Kalina Cycle,” Applied Thermal Engineering, Vol. 18, No. 6, 1998, pp. 427-439.
- A. Franco and A. Russo, “Combined Cycle Plant Efficiency Increase Based on the Optimization of the Heat Recovery Steam Generator Operating Parameters,” International Journal of Thermal Sciences, Vol. 41, No. 9, 2002, pp. 843-859.
- E. Bilgen, “Exergetic and Engineering Analyses of Gas Turbine Based Cogeneration Systems,” Energy, Vol. 25, No. 12, 2000, pp. 1215-1229.
- I. Dincer, M. A. Rosen and N. L. Minh, “Efficiency Analysis of a Cogeneration and District Energy System,” Applied Thermal Engineering, Vol. 25, No. 1, 2005, pp. 147-159.
- A. Datta, R. Ganguly and L. Sarkar, “Energy and Exergy Analyses of an Externally Fired Gas Turbine (Efgt) Cycle Integrated with Biomass Gasifier for Distributed Power Generation,” Energy, Vol. 35, No. 1, 2010, pp. 341-350.
- D.-C. Sue and C.-C. Chuang, “Engineering Design and Exergy Analyses for Combustion Gas Turbine Based Power Generation System,” Energy, Vol. 29, No. 8, 2004, pp. 1183-1205.

