Energy and Power Engineering
Vol.07 No.08(2015), Article ID:58909,9 pages
10.4236/epe.2015.78034
Polymer Foam Flow in Porous Media under Different Injection Modes
Wei Zhao, Haiqing Cui, Keliang Wang
Key Laboratory of Enhanced Oil and Gas Recovery of Ministry of Education, Northeast Petroleum University, Daqing, China
Email: zhaoweinepu@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 July 2015; accepted 17 August 2015; published 20 August 2015
ABSTRACT
The mathematical models of the flow of polymer foam in porous media under three injection modes are established and the relevant numerical calculation methods are given. The profiles of the liquid phase saturation, the pressure drop and the number density of the flowing HPAM foam in artificial sandstone cores with the dimensionless distance under three injection modes are numerically calculated and analyzed. The results show that, compared with the injection mode 2 and 3, HPAM foam flows in a piston-like fashion in the artificial sandstone core under the injection mode 1 and produces the biggest pressure drop. Obviously, the flood efficiency is the highest under the injection mode 1.
Keywords:
Injection Mode, Polymer Foam, Porous Media, Mathematical Model, Numerical Calculation

1. Introduction
It can provides the necessary theoretical foundation for polymer flooding engineering design through researching the flow of the polymer foam in porous media under different injection modes. Shan, et al. [1] given an optimal foam-injection strategy in homogeneous reservoirs with a variety of foam models by using simulation. Stevens, et al. [2] presented an overview of the operating plan for CO2 foam injection and the details of the CO2 foam injection schedule and design criteria in the East Vacuum Grayburg San Andres Unit. Hou, et al. [3] compared three main injection modes, including co-injection of gas and solution, alternative injection of gas and solution, and direct injection of foam and pointed that the direct injection of foam was the most effective mode and the alternative injection of gas and solution is the poorest. Li, et al. [4] experimentally studied the use of additives to enhance foam properties and the factors affecting blocking performance such as injection model, gas liquid ratio, and alternate slug, etc. Harsenhorst, et al. [5] illustrated with a model fit by Rossen, et al. [6] to data of Persoff, et al. [7] , a fit specifically designed for a hypothetical surfactant-alternating-gas (SAG) application. The mathematical models of the flow of polymer foam in porous media under three injection modes will be established and the numerical calculation methods will be given in this paper. According to the mathematical models and the numerical calculation methods metioned above, the profiles of the liquid phase saturation, the pressure drop and the number density of the flowing HPAM foam in artificial sandstone core under three injection modes metioned above will be numerically calculated and analyzed.
2. Injection Modes
There are three injection modes for the porous media filled with polymer-surfactant aqueous solution,that is, the injection mode 1 which is the co-injection of polymer surfactant aqueous solution and air into the porous media, the injection mode 2 which is the injection of air into the porous media and the injection mode 3 which is the injection of polymer surfactant aqueous solution into the porous media.
3. Mathematical Models
According to the mass and the population balance principles, the mathematical models of polymer foam flow in porous media under different injection modes can be obtained.
3.1. Injection Mode 1
The mathematical model of the flow of polymer foam in porous media under the injection mode 1 is as follows [8] -[11] .
The mass balance equations
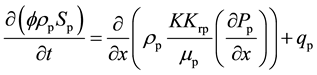 (1)
(1)
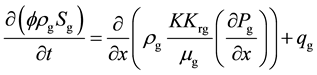 (2)
(2)
the population balance equations
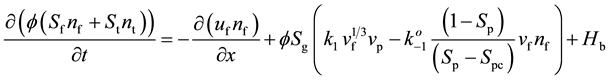 (3)
(3)
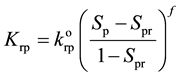 (4)
(4)
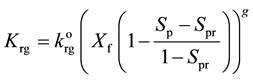 (5)
(5)
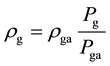 (6)
(6)
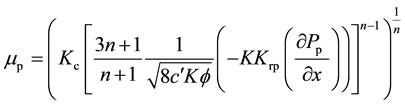 (7)
(7)
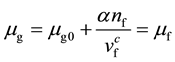 (8)
(8)
the assistant equations
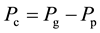 (9)
(9)
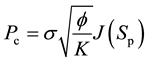 (10)
(10)
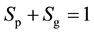 (11)
(11)
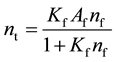 (12)
(12)
the initial conditions
 (13)
(13)
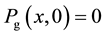 (14)
(14)
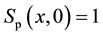 (15)
(15)
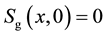 (16)
(16)


the boundary conditions






where
















































































3.2. Injection Mode 2
Under the injection mode 2, where the Formula (19) of the mathematical model of the flow of the polymer foam in porous media under the injection mode 1 changes as follow

the mathematical model of the flow of the polymer foam in porous media consists of Formula (1)-(18), (25), (20)-(24).
3.3. Injection Mode 3
Under the injection mode 3, the mathematical model of the flow of the polymer foam in porous media consists of Formula (1), (13), (15), (19) and (21).
4. Numerical Calculation Methods
The mathematical models of the flow of polymer foam in porous media under three injection modes are numerically calculated by the finite difference method [9] [14] [15] .
For the Injection mode 1 and the injection mode 2, the mass balance Equations (1) and (2) are solved by IMPES (Implicit Pressure Explicit Saturation) method, and the population balance Equation (3) is solved by TVD (Total Variation Diminish) three order method. For the Injection mode 3, the mass balance Equation (1) is solved by IM (Implicit Method).
5. Numerical Calculations and Analyses
The flow of the foam of the 0.015 wt% HPAM, 0.200 wt% FL-605 and 0.830 wt% NaCl HPAM solution and the air under different injection modes in the artificial sandstone core are numerically calculated and analyzed.
5.1. Basic Data
The basic data of the three injection modes are shows as Table 1 [8] [9] .
5.2. Injection Mode 1
Under the injection mode 1, the profiles of the liquid phase saturation


In Figure 1, under the injection mode 1, the liquid phase saturation




In Figure 2, under the injection mode 1, the pressure drop



In Figure 3, under the injection mode 1, there is the flow front of HPAM foam in the artificial sandstone core. The number density

Table 1. Basic data.
Figure 1. Profiles of the liquid phase saturation

Figure 2. Profiles of the pressure drop

Figure 3. Profiles of the number density

number density


5.3. Injection Mode 2
Under the injection mode 2, the profiles of the liquid phase saturation


In Figure 4, under the injection mode 2, the liquid phase saturation



In Figure 5, under the injection mode 2, the pressure drop



Figure 4. Profiles of the liquid phase saturation

Figure 5. Profiles of the pressure drop

Figure 6. Profiles of the number density

downstream of flow front decreases slowly, which is due to the fine foam texture of flow front under injection mode 2.
In Figure 6, under the injection mode 2, the number density



5.4. Injection Mode 3
Under the injection mode 3, the profiles of the liquid phase saturation


In Figure 7, under the injection mode 3, the flow of the HPAM aqueous solution in the artificial sandstone core is a single phase fluid flow. Obviously, the liquid phase saturation

In Figure 8, under the injection mode 3, the pressure drop

Figure 7. Profiles of the liquid phase saturation

Figure 8. Profiles of the pressure drop

Figure 9. Profiles of the number density

In Figure 9, under the injection mode 3, the number density

5.5. Comparisons of Injection Modes
Among the three injection modes mentioned above, the pressure drop


6. Conclusions
1) The mathematical models of the flow of the polymer foam in porous media under the three injection modes are established and the relevant numerical calculation methods are given.
2) The profiles of the liquid phase saturation, the pressure drop and the number density of the flowing HPAM foam with the dimensionless distance in the artificial sandstone core under the three injection modes are numerically calculated and analyzed.
3) Compared with the injection mode 2 and 3, HPAM foam flows in a piston-like fashion in the artificial sandstone core under the injection mode 1 and shows the biggest pressure drop. Obviously, flood efficiency is highest under the injection mode 1.
4) Based on the research results mentioned above, it can choose the better injection mode to reach the best flood efficiency in the polymer flooding engineering design according to the actual situation. Especially, in the injection mode 1, it also needs the future study to continue working and researching for what factor influencing the flood efficiency most, such as the polymer type, concentration and so on.
Cite this paper
WeiZhao,HaiqingCui,KeliangWang, (2015) Polymer Foam Flow in Porous Media under Different Injection Modes. Energy and Power Engineering,07,365-374. doi: 10.4236/epe.2015.78034
References
- 1. Shan, D. and Rossen, W.R. (2002) Optimal Injection Strategies for Foam IOR. SPE Journal, 9, 1-17.
- 2. Steven, J.E., Harpole, K.J., Zornes, D.R. and Martin, F.D. (1992) CO2 Foam Field Verification Pilot Test at EVGSAU: Phase II-Foam Injection Design and Operation Plan. SPE Annual Technical Conference and Exhibition, Washington, DC, 4-7 October 1992, 115-128.
- 3. Hou,Q.F., Zhu, Y.Y., Luo, Y.S. and Weng, R. (2012) Studies on Foam Flooding EOR Technique for Daqing Reservoirs after Polymer Flooding. Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, 14-18 April 2012, 1-11.
http//dx.doi.org/10.2118/151955-ms - 4. Li, Z.Q., Zhou, G.H. and Zhou, Z.M. (2006) The Feasibility Studies of Polymer Foam Flooding in Gudao Oilfield. Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Adelaide, 11-13 September, 1-8.
http//dx.doi.org/10.2118/101189-ms - 5. Harsenhorst, R.M., Dharma, A.S., Andrianov, A. and Rossen, W.R. (2013) Extension of a Simple Model for Vertical Sweep in Foam SAG Displacement. Proceedings of the EAGE Annual Conference & Exhibition Incorporating SPE Europec, London,10-13 June 2013, 1-11.
http//dx.doi.org/10.2118/164891-ms - 6. Boeije, C.S. and Rossen, W.R. (2013) Fitting Foam Simulation Model Parameters to Data. Proceedings of the IOR 2013—17th European Symposium on Improved Oil Recovery, St. Petersburg, 16-18 April 2013, 1-16.
http//dx.doi.org/10.3997/2214-4609.20142604 - 7. Persoff, P., Radke, C.J., Pruess, K, Benson, S.M. and Witherspoon, P.A. (1991) A Laboratory Investigation of Foam Flow in Sandstone at Elevated Pressure. SPE Reservoir Engineering, 6, 365-372.
http//dx.doi.org/10.2118/18781-PA - 8. Kovseck, A.R. (1994) Foam displacement in Porous Media: Experiment and Mechanistic Prediction by the Population Method. University of California at Berkely, Berkely.
- 9. Zhao, W. (2015) Polymer Foam Transient Flow in the Porous Media. Northeast Petroleum University, Daqing.
- 10. Bertin, H.J., Quintard, M.Y. and Castainier, L.M. (1998) Development of a Bubble-Population Correlation for Foam-Flow Modeling in Porous Media. SPE Journal, 3, 356-362.
http//dx.doi.org/10.2118/52596-pa - 11. Garrouch, A.A. (1999) A Viscoelastic Model for Polymer Flow in Reservoir Rocks. Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, 20-22 April 1999, 1-10.
http//dx.doi.org/10.2118/54379-ms - 12. Falls, A.H., Musters, J.J. and Ratulowski, J. (1989) The Apparent Viscosity of Foams in Homogeneous Bead Packs. SPE Reservoir Engineering, 4, 155-164.
- 13. Hirasaki, G.J. and Lawson, J.B. (1985) Mechanisms of Foam Flow in Porous Media: Apparent Viscosity in Smooth Capillaries. Society of Petroleum Engineers Journal, 25, 176-190.
http//dx.doi.org/10.2118/12129-pa - 14. Aziz, K. and Settari, A. (1979) Petroleum Reservoir Simulation. Applied Science Publishers, London, 135-139.
- 15. Leonard, B.P. (1984) Third Order Upwinding as a Rational Basis for Computational Fluid Dynamics. Proceedings of the Computational Techniques and Applications: CTAC-83, Sydney, 1983, 106-120.











