Energy and Power Engineering
Vol.06 No.11(2014), Article ID:50467,8 pages
10.4236/epe.2014.611031
Improving the Power Generation Performance of a Solar Tower Using Thermal Updraft Wind
Masataka Motoyama1*, Kenichiro Sugitani2, Yuji Ohya2, Takashi Karasudani2, Tomoyuki Nagai2, Shinsuke Okada1
1Department of Aeronautics and Astronautics Engineering, Kyushu University, Fukuoka, Japan
2Research Institute for Applied Mechanics, Kyushu University, Fukuoka, Japan
Email: *motoyama74@riam.kyushu-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2014; revised 29 August 2014; accepted 8 September 2014
ABSTRACT
The purpose of this study is to improve the efficiency of the power generation system of a solar tower using fluid dynamics. The power generation system of a solar tower can be designed and constructed at relatively low cost. However, the energy output tends to be low for its physical size compared with other renewable energy production systems. The technical and scientific improve- ment of these types of generation systems has lost its momentum since the shutdown of the well- known Spanish pilot plant “Manzanares Solar Chimney” in 1989, although it still has the potential to play a role in renewable energy in the future. We have focused on the tower component of the system to seek possible enhancements of the power output of the internal turbine. As a result of our fluid dynamic shape optimization, a diffuser-shaped tower was employed to increase the internal flow speed of a scaled model. The results show a remarkable improvement in the power output of the internal wind turbine.
Keywords:
Solar Tower, Thermal Updraft, Wind Turbine, Diffuser

1. Introduction
A solar tower [1] that can generate electricity in a simple structure, and enables easy and less costly maintenance, has considerable advantages. In particular, a tower of the thermal updraft wind type has significant potential as a renewable energy power plant. One of the few problems for this type is the low power electric generation capacity per unit area. Consequently, the solar tower needs to be enlarged to achieve an adequate performance. If we can improve its performance in power generation by some method, the solar tower may become competitive when compared with other renewable energy systems. In this study, we show an example of optimizing the tower shape in terms of its fluid dynamic characteristics to raise its efficiency in generating power.
Power plants that use towers either have a thermal updraft as for the solar tower shown in Figure 1 [2] - [4] or are of another type of tower called an energy tower. For the solar tower the sun’s energy is collected by a heat collector below the tower creating a thermal updraft that passes into the transparent collector and rotates the wind turbine. The power plant mechanism in the energy tower involves spraying the upper part of the tower with water, creating a circulating and increasing downdraft flow within the tower that rotates the wind turbine [5] [6] . The solar tower, which we focus on in this study, is based on the simple structure conducted in the demonstration experiment in Manzanares, Spain, from 1982 to 1989 by the German engineer, J. Schlaich. The concept of the solar tower is not new. Leonardo da Vinci designed a chicken barbecue with a windmill driven by the hot upwind in the chimney [2] . In developing the original idea for the purpose of exploiting solar energy, simple techniques―in this case, the greenhouse, the chimney and the windmill―were combined in an uncomplicated collector and conversion system. Thus the solar tower was born.
However, a thermal updraft wind type of solar tower power plant using thermal updraft wind is, for example, in Manzanares, where the height is 194 m, and the collector is 46,000 m2, a very large scale plant, but generates little power for its size, and remains at 44.19 MWh per annum. On the other hand, for example, if we spread solar panels over the same area of land, 8.5 GWh of power is generated (assumed capacity factor 13%) under conditions of Japan’s greatest annual sunshine (1420 kWh/m2).
Since the pilot plant in Manzanares was completed, further development worldwide has been minimal and any scientific technical research has hardly been carried out, although the Menzanares solar tower still has the potential to play a role in renewable energy in the future. Recently, with priorities such as non-nuclear power generation and CO2 reduction, renewable energy sources have been attracting attention in the search for energy security. Consequently, other renewable energy sources such as wind-generated electricity, where there is adequate wind, and solar cells, where there is adequate sunshine, are generally recognized as the most promising options. Fundamental experiments on how much power is generated depending on the size of the basic component of the solar tower, have not been performed (power generation expectation and the optimization study [7] [8] ). We applied a diffuser shape as the first step in optimizing the tower shape in a trial to increase power generation using fluid dynamics. We performed an experiment to compare the updraft wind velocity flowing through a diffuser-shaped tower with a typical cylindrical form. This experiment was conducted with two large scale models and one small scale model to confirm that the results complied with the scaling law. It demonstrated that when upsizing the scaling law remained valid.
Figure 1.Mechanism of solar tower.
2. Previous Experiments
Preliminary experiments were conducted on mini-models of solar towers [9] [10] . The mini-models consisted of cylindrical and diffuser models with a 0.66 m radius collector and a tower 0.4 m high. If the external flow around the solar tower is assumed to be negligible, the dominant flow is from heat convection. The flow field is approximated by natural convection from the temperature difference between the flow temperature heated by the solar thermal energy and the ambient temperature. In this laboratory experiment, the flow field was the natural convection driven by the temperature difference between the flow temperature Θ2 from the controlled floor surface temperature at the bottom of the tower, and the ambient temperature Θ1. The ambient temperature was defined as the temperature surrounding the exit of the tower Θ1. The temperature difference was ?Θ = Θ2 − Θ1. The flow created by the sun and ambient temperature was simulated as shown above. Figure 2 shows the experimental results from measuring the velocity of the updraft. In the cylindrical tower, the velocity at 70 mm above the heated floor was 0.55 m/s. In the diffuser tower the velocity at the same point was faster at 0.77 m/s. When the temperature difference ∆Θ was approximately 20˚K, 70 mm above the floor, the velocity of the updraft in the diffuser tower exceeded that in the cylindrical tower. If the rotor of a wind turbine is set at this point, a larger power output is expected.
3. Past Numerical Simulation
A computational fluid dynamics analysis was conducted by simulating the experimental model. The state variables, which were the velocity components, pressure and temperature, were computed using Direct Numerical Simulation (DNS) based on the Finite Difference Method (FDM). The time integration algorithm was the variant of the fractional step.
Method [11] [12] : The pressure was determined by computation of the Poisson equation, solved using the Successive Over Relaxation (SOR) method. A second-order central scheme was used to discretize the spatial derivatives except for the convective terms, which were discretized using the modified third-order upwind differencing scheme based on an interpolation method [13] [14] . Figure 3 shows the updraft flow velocity augmentation ratio, which was the updraft flow velocity of the diffuser tower normalized against the updraft flow velocity of the cylindrical tower. The straight line is Least Square Estimate. The augmentation ratios of the numerical and experimental values were almost the same. Even the numerical values showed a maximum augmentation ratio 70 - 90 mm from the floor, which gave the augmentation effect from the diffuser tower.
4. Experiment
The experiment with a larger model was conducted in a room. Figure 4 shows the experimental model. The
Figure 2. Measuring point of cylindrical tower and diffuser tower, right hand side temperature difference and updraft wind velocity along the vertical center line.
Figure 3. Updraft wind velocity distribution of laboratory experiment and computational fluid dynamics (Temperature Difference 30˚C).
Figure 4. Experimental model and the configuration.
towers used were a cylindrical type and a diffuser type with an open angle of 8˚ (4˚ each side). The towers were 2 m high. To exchange the towers, and make it easy to insert or remove the wind turbine, the tower part was easily disassembled. One side of the collector section was 3 m and it was supported by spacers 20 cm from the floor. The collector was made of acrylic sheet. It was divided into three sections. To ensure the thermal updraft wind did not leak from the gaps between the divided collectors, they were covered with a vinyl sheet. The panel unit was 1.5 m × 1.5 m 9 mm thick iron plate with 8 × 375 W heater elements. The heating elements were connected to the four panel unit. A temperature sensor (Pt100) was attached in the center of a unit panel. Using the signals from these sensors, a temperature controller controlled the temperature of the panel unit. In the experiment, the temperatures of the iron plates were controlled by the controller and heaters to maintain the panel units at the required temperatures. The updraft wind velocity was measured by inserting an Ultra Sonic Anemometer into the tower from the top to 5 cm above the blade of the wind turbine. The signal from the Ultra Sonic Anemometer was fed to a PC and monitored using an FFT Analyzer. Figure 5 shows the distribution of flow velocity. The location of the Ultra Sonic Anemometer was 6 to 7 cm between the center and edge of the inside of the tower. Note, as is shown in Figure 5, the distribution of wind velocity was almost uniform, and it was assumed to be the same over the horizontal plane inside the tower.
Figure 5. Velocity measured inside the tower.
5. Results and Discussion
5.1. Without Wind Turbine
The dimensionless parameters which are dominant in the flow field of thermal convection are the Reynolds number Re and Richardson number Ri. When these two dimensionless parameters are equal, dynamic similarity is maintained. It is difficult for Ri and Re to be equal simultaneously. Re had the greatest difference between the real scale and experimental models, but at the tower throat section(radius 0.32 m), the updraft wind was 2.5 m/s, and Re ? 52000. This Reynolds number seemed to be close to real scale flow. On the other hand, Ri and the wind velocity had the following relationship between the real scale and experimental models:
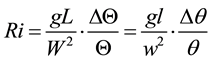 , (1)
, (1)
 , (2)
, (2)
where, L, W, Θ are the reference length, reference velocity and reference temperature for each, capitalized parameters are for the real scale, and lower case parameters, l, w, θ are for the experimental model. Equation (2) is derived from Equation (1) and provides the transform for the expression between the real scale and experimental model. Initially, as stated in Section 3, we compared the result for the wind velocity of a small scale mini-model [9] [10] with that of the experimental model. If l is for the mini-model in the preliminary experiment and L is the present experiment, the scale is l:L = 1:5. Under natural convection, if the Ri of both the experimental and preliminary experimental models is the same, the velocity for the experimental model is evaluated by the root of the scale ratio multiplied by the velocity for the preliminary model.
Figure 6 shows, on the left, a two-way arrow, which is the scaled-up difference of the diffuser tower, and on the right, a two-way arrow, which is the scaled-up difference of the cylindrical tower. From these results, we can draw conclusions: The ratio of the velocity between mini-model and larger model is 2.2 - 2.5 and the values are almost equal to 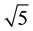 i.e. from the scaling effect. We confirmed the wind velocity increased in proportion to the root of the scale ratio. Figure 6 also shows two measurements of the wind velocity inside the diffuser and cylindrical towers at this time. From this result, the ratio between the wind velocity inside the diffuser and cylindrical towers was almost 1.5 - 1.8 times for a temperature difference ?Θ 20 - 35˚K at this time.
i.e. from the scaling effect. We confirmed the wind velocity increased in proportion to the root of the scale ratio. Figure 6 also shows two measurements of the wind velocity inside the diffuser and cylindrical towers at this time. From this result, the ratio between the wind velocity inside the diffuser and cylindrical towers was almost 1.5 - 1.8 times for a temperature difference ?Θ 20 - 35˚K at this time.
5.2. Case When the Wind Turbine Is Present
5.2.1. Test of Power Generation for the Wind Turbine
The test of power generation was conducted to check the characteristic of the wind turbine for experimental use. Figure 7 shows an experimental model. To investigate the optimal tip speed ratio λ and power coefficient Cp for this small wind turbine (rotor radius 0.15 m), Cp is given by Equation (3) [15] :
Figure 6. Comparison of wind velocity between mini-model (l = 40 mm high) and experimental model (L = 2000 mm high).
Figure 7. Model of wind turbine.
Figure 8. Cp vs. tip speed ratio λ.
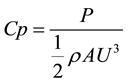 . (3)
. (3)
To find out the optimal tip speed ratio λw the variable resistance is adjusted as in Figure 7. Figure 8 shows the results of the performance test. In the case of a wind velocity of 2.5 - 3.0 m/s as shown in Figure 8, Cp is the maximum at around a tip speed ratio of λw = 2.5 - 2.9.
5.2.2. Influence of the Wind Turbine on the Velocity
Figure 9 shows the relationship between the flow temperature and vertical velocity at 0.05 m above the rotor when it is rotating. Installing the wind turbine creates a resistance. The wind velocity decreases in comparison with the case with no wind turbine. In addition, the vertical wind velocity inside the diffuser tower is 1.7 times greater than that inside the cylindrical tower, i.e. (1) By installing the wind turbine, 1.9 m/s wind velocity (temperature difference 20˚K, diffuser type) was slowed down to 1.7 - 1.8 m/s (Figure 9) whereas the velocity was slightly slowed down to 1.3 m/s in the case with no wind turbine (temperature difference 38˚K, cylindrical). (2) Even if a wind turbine was installed, the ratio between the velocity of the diffuser and cylindrical towers was about 1.7, which is almost the same ratio with or without the wind turbine. As a consequence, the velocities for the diffuser and cylindrical towers are clearly different.
5.2.3. Performance of Power Generation
Next we discuss the power. Figure 10 shows the turbine rotation speed for the diffuser tower was greater than for the cylindrical tower. We measured the speed of rotation of the rotor with a revolution counter. The increasing speed of rotation of the rotor relates directly to the power output. Here, we define power as P, Torque as Tr and number of rotation ω, the relationship is given by Equation (4):
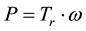 . (4)
. (4)
The power output is expected to increase for the diffuser tower. Figure 11 shows the power output vs. tem-
Figure 9. Temperature vs. velocity.
Figure 10. Temperature difference vs. rotational speed.
Figure 11. Temperature difference vs. power.
perature difference. From the results in Figure 11, whereas the ratio of velocity between the diffuser and cylindrical towers is 1.7, the power output for the diffuser tower turns out to be 6 times greater than for the cylindrical tower. This is because the power output is proportional to the cube of the velocity.
In addition, from the relationship of the output for the diffuser vs. flow temperature, the diffuser output produces power from a lower temperature difference than the cylindrical output. In using the diffuser shape tower for a solar tower, the wind velocity exceeds that for a cylindrical type tower.
Furthermore, even if a wind turbine is installed, the ratio of the speed increase is constant, the speed of rotation of the rotor increases and the power output increases considerably.
6. Conclusions
The purpose of this research is to focus on the shape of the solar tower, and increase the power output by changing the structure from the conventional cylindrical tower to a diffuser type tower, thus increasing the power output.
As a result of previous preliminary experiments conducted by Okada, the mini-model of a diffuser type tower achieved greater wind velocity than a cylindrical tower. In these experiments, we made the size of the model 5 times larger than the mini-model. By installing a wind turbine, we actually measured the obtained power output and verified it.
1) Initially, similar to the mini-model, we measured the wind velocity of the diffuser and cylindrical towers without a wind turbine. As the result, the wind velocity for the diffuser tower was greater than for the cylindrical tower by a factor of 1.5 - 1.8 times. The velocity of this model was almost 
2) Next, by installing a wind turbine, the change in velocity and power output was measured. The ratio of velocity between the diffuser and cylindrical towers was almost 1.7, similar to the case for the temperature difference ?Θ without a wind turbine. Because the power output was proportional to the cube of the velocity, the power output obtained in the diffuser tower was 6 times greater than that for the cylindrical tower.
From these results, we concluded that the diffuser tower, which has the advantage of a larger power output than the cylindrical tower, was the preferred option for a solar tower.
Acknowledgements
This work was supported in part by a grant from the Ministry of Education, Science and Culture (No. 2424161).
References
- Schlaich, J. (1996) The Solar Chimney. Axel Menges, Germany.
- Haaf, W., Friedrich, K., Mayr, G. and Schlaich, J. (1983) Solar Chimneys―Part I: Principle and Construction of the Pilot Plant in Manzanares. International Journal of Solar Energy, 2, 3-20. http://dx.doi.org/10.1080/01425918308909911
- Haaf, W. (1984) Solar Chimneys―Part II: Preliminary Test Results from the Manzanares Pilot Plant. International Journal of Solar Energy, 2, 141-161. http://dx.doi.org/10.1080/01425918408909921
- Schlaich, J., Bergermann, R., Schiel, W. and Weinrebe, G. (2005) Design of Commercial Solar Updraft Tower Systems―Utilization of Solar Induced Convective Flows for Power Generation. Journal of Solar Energy Engineering, 127, 117-124. http://dx.doi.org/10.1115/1.1823493
- Altman, T., Carmel, Y., Guetta, R., Zaslavsky, D. and Doytsher, Y. (2005) Assessment of an “Energy Tower” Potential in Australia Using a Mathematical Model and GIS. Solar Energy, 78, 799-808. http://dx.doi.org/10.1016/j.solener.2004.08.025
- Omer, E., Guetta, R., Ioslovich, I. and Gutman, P.O. (2008) Optimal Design of an “Energy Tower” Power Plant. IEEE Transactions on Energy Conversion, 23, 215-225. http://dx.doi.org/10.1109/TEC.2007.905349
- Gannon, A.J. and von Backström, T.W. (2000) Solar Chimney Cycle Analysis with System Loss and Solar Collector Performance. Journal of Solar Energy Engineering, 122, 133-137. http://dx.doi.org/10.1115/1.1314379
- Koonsrisuk, A. and Chitsomboon, T. (2007) Dynamic Similarity in Solar Chimney Modeling. Solar Energy, 81, 1439- 1446. http://dx.doi.org/10.1016/j.solener.2007.03.003
- Okada, S., Ohya, Y., Uchida, T. and Karasudani, T. (2006) Wind Convergence Performance Evaluation of VT- WCONVS. Proceedings of 19th Wind Engineering Symposium, Tokyo, 29 November 2006, 145-150. (in Japanese)
- Okada, S., Ohya, Y., Uchida, T. and Karasudani, T. (2006) Convergence of Wind Using VT-WCONVS (Vertical Type Wind Convergence Structure). Proceedings of Renewable Energy, Yokohama, 2006.
- Ohya, Y. and Uchida, T. (2008) Laboratory and Numerical Studies of the Atmospheric Stable Boundary Layers. Journal of Wind Engineering and Industrial Aerodynamics, 96, 2150-2160.
- Kim, J. and Moin, P. (1985) Application of a Fractional-Step Method to Incompressible Navier-Stokes Equations. Journal of Computational Physics, 59, 308-323. http://dx.doi.org/10.1016/0021-9991(85)90148-2
- Kawamura, T., Takami, H. and Kuwahara, K. (1986) Computation of High Reynolds Number Flow around a Circular Cylinder with Surface Roughness. Fluid Dynamics Research, 1, 145-162. http://dx.doi.org/10.1016/0169-5983(86)90014-6
- Kajishima, T. (1994) Upstream-Shifted Interpolation Method for Numerical Simulation of Incompressible Flows. Transactions of the Japan Society of Mechanical Engineers B, 60, 3319-3326. (in Japanese)
- Manwell, J., Mcgowan, J. and Rogers, A. (2009) Wind Energy Explained. Wiley, New York.
NOTES
*Corresponding author.
















