Energy and Power Engineering
Vol.6 No.9(2014), Article
ID:49573,20
pages
DOI:10.4236/epe.2014.69022
Thermodynamics of a Shallow Solar Still
Juan Cristóbal Torchia-Núñez1, Jaime Cervantes-de-Gortari2, Miguel Angel Porta-Gándara3
1Independent Energy Consultant, San José, Costa Rica
2Mechanical Engineering Department, National University of Mexico, Mexico City, Mexico
3CIBNOR, La Paz, BCS, Mexico
Email: jgonzalo@unam.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2014; revised 28 July 2014; accepted 10 August 2014
Abstract
A detailed summary of the most relevant aspects of the thermodynamics of a shallow solar still is presented, including historical features not often found in the literature. Solar distillation has grown from applying empirical knowledge to advanced modeling and simulation. Geometrical, environmental and operational parameters of the solar still to heat transfer phenomena including evaporation and condensation, are taken into account in this overview, giving a comprehensive structure and classification to the study of solar stills from the thermodynamic point of view. The article describes global parameters, such as solar radiation, wind speed and thermal insulation among others and how they have been taken into account in the literature. Also, a distinction between internal and external heat transfer phenomena is proposed for clarification. Exergy balance is included to account for thermodynamic imperfections in the several processes inside the solar still.
Keywords:Solar Still, Overview, Thermodynamics, Modeling, Exergy, Heat Transfer

1. Introduction
1.1. History of Solar Distillation
Solar distillation of sea water is without doubt, one of the few possibilities to satisfy the water needs in many regions of the world in a sustainable way. It is an ancient process that human beings have learnt in order to satisfy different needs. Aristotle clearly explained in his writings the evaporation process as part of the water cycle in nature and the ancient Egyptians showed solar distillation in their paintings and hieroglyphics.
Full accounts of solar stills within the context of seawater desalination have been presented [1] where an extensive description of various designs of solar stills, from the single-box still to the sophisticated mutiple-effect distiller and greenhouse-inclusive types are described. These authors mentioned that direct solar desalination systems had low operating and maintenance costs, but required large installation areas and high initial investment. However, this is an appropriate solution for remote areas and small communities in arid and semi-arid regions lacking water. These authors [1] pointed out that the first conventional solar still plant was built in 1872 by Charles Wilson in the mining community of Las Salinas in Northern Chile. This still was a large basin-type still used to supply fresh water from brackish feed water to the community, with a total capacity of about 23 m3/day and lasted 40 years until the mines were exhausted. A notable historical account of this project can be found in [2] , which offers a social and historical background about Wilson, the solar distillation plant and other authors who wrote about it.
Few other historic reviews with different emphases have been reported [3] for designs and experiences during the 50 s to 70 s; and more recently, an extensive account of solar stills has been published [4] .
Solar distillation is one of the oldest methods used to produce fresh water for different basic human needs. According to [5] and [6] , one of the first treatises about solar distillation is De distillationelibri IX, written by G.B. della Porta in 1589. This work describes a solar distillation with glass hemispheres directly exposed to the sun. In [7] mentioned Lavoisier and its method of solar concentrators for heating alembics in 1770. It is also described in [7] , manufacturing and operation advances of conventional basin and portable solar stills during WWII. This author analyzes some isolated elements of the solar still independently, showing different experimental results, such as the efficiency and fresh water production as a function of solar energy.
Perhaps the most important work of the last decades is [8] . This is the first work in which the basis of a complete analysis of the energy balance applied to the different elements of the solar still is presented. The analysis results in a lumped-parameters set of equations for simple and multiple-effect solar stills. The experimental work is based on five “diffusive” solar stills in operation for several months, where an electrical heater supplies energy to the solar still instead of solar radiation. The correspondence between experimental and calculated distillate production results is not good [8] ; however, the model is found as a proper mathematical tool for design purposes. Furthermore, [8] presents a general energy efficiency for the still defined as the ratio of heat used for evaporation in comparison with the amount of energy supplied to the still, reporting an efficiency of 57.7%.
Morse and Read [9] presented an important theoretical and experimental study in the solar distillation literature due to the parametric nature of thermal analysis and the method used to solve it. The method consists of a characteristic chart where the different heat fluxes can be expressed as a function of the glass cover temperature. Parameters involved in this study are wind velocity, ambient temperature and heat losses from the base.
Cooper [10] presents a purely theoretical, finite-difference model for the energy balance of the glass cover and the brine. The influence of several parameters, such as initial mass of brine—with and without thermal insulation under the basin—, is analyzed. Several other later works ([11] -[15] ) have established the lumped-parameter equations for the energy balance, based on the model in [8] with several useful modifications.
In the authors’ opinion, Solar Distillation [6] is one of the most important and complete works in the Solar Distillation field. It describes the heat transfer model of a solar still, the energy balances and the results of distillation yield as a function of time. Also, there is an extensive description of systems, configurations and applications of solar stills along with certain aspects of engineering economics.
1.2. Description of a Single-Basin Solar Still
The simplest design of a solar still consists of a rectangular box with a transparent upper cover as in Figure 1. This cover is usually a glass or a plastic sheet where, in the inner face, condensation is produced. The side walls are often made of an insulating and impermeable material to reduce heat and vapor losses. Solar stills can be mounted above the floor or lying plainly on the ground; either case, the bottom of the still is specially covered with an insulating material to reduce heat losses that can be particularly high along the direction normal to the bottom.
The solar distillation process is as follows: 1) the still is partially filled with brine in the bottom deposit which is a black surface (collector) used to absorb incoming radiation after it passes through the glass cover and the brine; 2) the collector increases its temperature and transfers heat to the brine; 3) water evaporates at the free surface; 4) a natural convection flow of humid air circulating inside the enclosure takes place due to the temperature difference between the free surface of the heated brine and the upper cool cover; 5) this inclined trans-
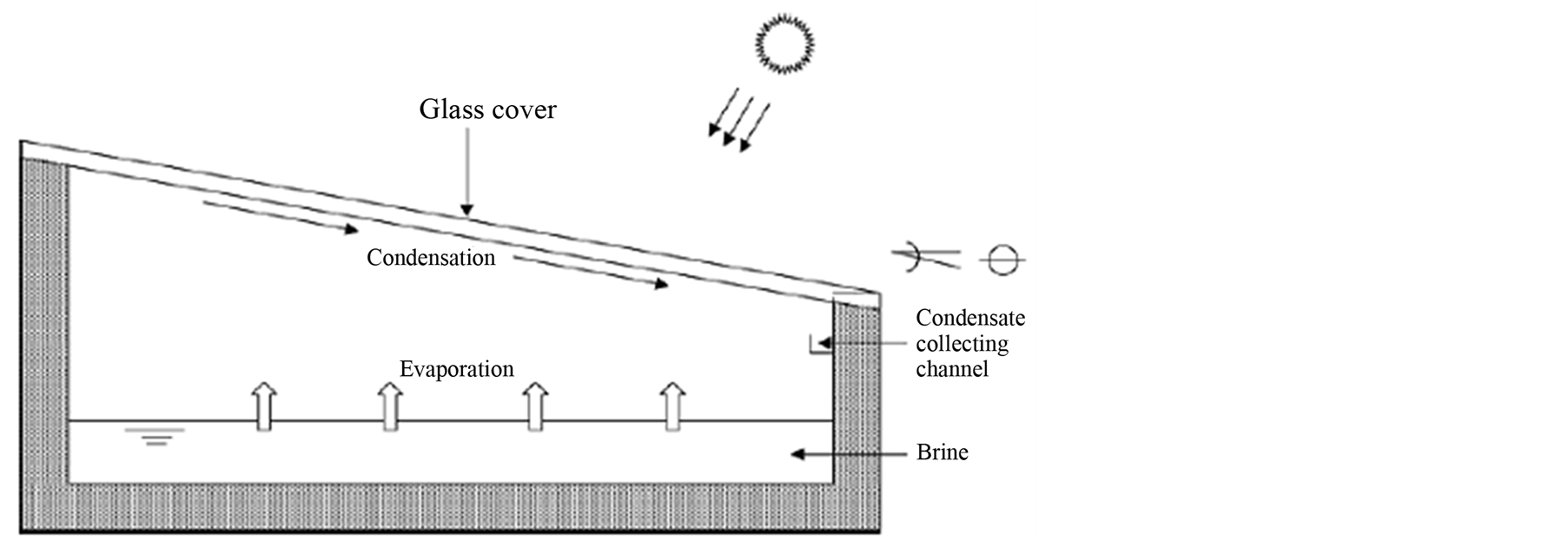
Figure 1. Schematic view of a single-basin solar still.
parent sheet serves as a condensing plate where the distillate water runs by gravity along its internal face to a small collector channel in the shortest sidewall of the arrangement. There are other several designs for solar stills varying in complexity and applications. A thoughtful and extensive review of solar stills designs and their applications can be found in [1] [6] [16] .
2. Global Parameters of a Solar Still
We call Global Parameters to characteristic properties, dimensions and factors that influence the distillation yield sprouting from climate, configuration and designing decisions. These parameters are usually studied by researchers in the solar still field to understand the influence on overall still variables such as distillation yield or efficiency. There are other several parameters that could be taken into account into a list of this type; however, the authors feel that these are representative for introduction purposes in this study.
2.1. Solar Radiation
The Sun is in essence a huge fusion nuclear reactor where the gravity pushes together hydrogen atoms at an enormous pressure and transforms them into heavier helium atoms. This process produces a deficit in the mass balance between hydrogen and helium, and this lost mass is actually the energy produced by the fusion reaction and radiated away. This is what we call solar radiation.
Solar radiation represents the driving force that keeps a solar still running and producing distillate water. Some 1360 W/m2 of radiation power reaches the Earth’s atmosphere. This is a rough value called “The Solar Constant”, which actually is not constant because it varies some 3% due to variations in Sun-Earth distance along the year. Also, there are periodic variations in the power emitted by the Sun as the measurements from Spatial Agencies’ satellites and Observatories around the planet have shown.
Some 30% of this radiation is reflected by the atmosphere so that, let us say, 800 W/m2 reaches the surface of the Earth in a very sunny day near the Equator. This means that, if completely absorbed, 1 m2-surface collector receives the same power than eight 100-Watts light bulbs. In just 12 hours, this 1-m2 device receives almost 10 kWh of solar energy, that is, 10 days of a color TV’s usage. According to the World Bank data [17] in average, a person in the US consumed 36.29 kWh of electricity each day back in 2011. A perfect solar collector would need just 3.5 m2 to satisfy the electricity of one person by using 12 hours of sunlight.
Now, these are optimistic numbers because there are geographical, seasonal and weather variations that reduce the 800 W/m2 down to some 170 W/m2 as an average according to the World Energy Council [18] . This figure is averaged in time (24 hrs) and across regions of the planet. There are places on Earth that far exceed 170 W/m2, especially those near the Equator. Furthermore, no solar device has 100% efficiency; thus, the power output of a device using solar radiation would be lower than 170 W/m2. Solar radiation is a resource that needs more efficient conversion devices and relative large areas in order to compete with fossil and fissile energy sources. Although this work is not dedicated to the resource of solar radiation and its characteristics, it has to be noted that the discussion of solar energy conversion has to be centered on the efficiency of devices, instead of the solar resource. The solar resource is very little negotiable, unless solar concentration steps into the discussion. There is not much to do about the amount of energy reaching the surface of the Earth but there is a lot to do with the amount and the quality of solar devices can be placed in the surface of the Earth. Most of the countries where solar conversion devices are in full development are located in poor solar-radiated zones like Northern Europe which shows that the scarce solar radiation should not be a decisive factor when considering options about the energy supply.
2.1.1. Description of the Radiation Phenomenon
Radiation is a mechanism of heat transfer between two bodies. The main feature of radiation lies in the fact that there is no need of a participating medium between the source of the radiation and a receiver. Radiation can transport heat through vacuum and the main example is solar radiation going through an almost empty space between the Sun and the Earth. As long as radiation travels through space, whether it is empty or not, it can be described accurately as a wave. This wave is produced by vibrations in the particles of the source. Each time a molecule changes its energy levels, radiation is produced [19] . However, radiation also behaves as particles called photons.
In summary, radiation can be both, a wave and a particle. For some particular conditions it will behave like a wave (the interference phenomenon) and for some other conditions it will be described as a particle (the photoelectric phenomenon). This duality has intrigued and mesmerized physicists since it was first proposed.
The nature of radiation is complex and it basically needed a whole new theory just to be completely understood and explained. One part of the knowledge about radiation was given by Electromagnetic Theory, which was completed when James Clerk Maxwell established the link between the laws of electricity and magnetism. However, there was a situation in the theory that was dramatically called Ultraviolet Catastrophe where experiments showed that the mathematical model used to describe the ultraviolet power radiation was wrong for certain frequencies. Planck solved the problem by bringing up something that was later called Quantum Theory [20] .
Radiation is a phenomenon that depends on several parameters:
1) Intensity;
2) Wavelength;
3) Angle of the ray with respect to the normal of the surface of the source;
4) Optical properties of the material;
5) Solid angle described by the bundle of rays;
6) Temperature of the source and the receiver.
So it is easy to note that the modeling of radiation from the viewpoint of heat transfer is complex and multidependent. A unique characteristic of radiation is that the heat transported is proportional to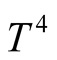 , different from the convection-conduction linear dependence on temperature. That is the reason why radiation becomes the dominant heat transfer mechanism when temperature increases as it can be perceived in incandescent bulbs, furnaces, combustion devices and, of course, the Sun, among others.
, different from the convection-conduction linear dependence on temperature. That is the reason why radiation becomes the dominant heat transfer mechanism when temperature increases as it can be perceived in incandescent bulbs, furnaces, combustion devices and, of course, the Sun, among others.
When it comes to solar conversion technology, the solar radiation values takes into account the solid angle produced by the solar disk in space, the integration of all solar wavelengths, and supposed to reach the solar still at a 90˚ angle from the horizontal. About the optical properties of a solar still, the glass cover is considered a surface with very high transmittance and no absorptance. The brine, if considered as part of the analysis, shares almost the same optical characteristics than the glass cover although care should be taken whenever the level of brine or its brackishness increases. The bottom of the still is considered to be a perfect absorber with zero transmittance and reflectance. The air-vapor mixture within the solar still is simply disregard as a non-participating medium. There is a vast literature about radiation [19] and solar radiation for engineering purposes [21] where the reader can find complete information regarding these topics.
2.1.2. Direct, Diffuse and Global Solar Radiation
Radiation can be classified into three types that are especially important in solar conversion technology: direct, diffuse and global.
Direct solar radiation is the part of the radiation that comes straight from the sun without being scattered by any participating medium. It can be described as a coherent pencil of rays that does not diverge from its original path. It can be measured by a pyrheliometer. A pyrheliometer is a device that uses a collimator tube which is blackened and diaphragmed to receive the ray and drives it into the sensor. The collimator tube allows only an angular acceptance of solar radiation of about 5˚ and 6˚ of the total sky hemisphere [22] . The sensor is a set of thermopiles located at the bottom of the collimator tube. As the thermopiles receive solar radiation, they increase in temperature and produce an electrical current which is a linear function of solar radiation intensity.
Diffuse radiation is constituted by electromagnetic waves that have been scattered by matter within the path of the wave so many times that its intensity, wavelength and directional properties are completely different from those of the radiation leaving the source. It is the radiation coming from the sky hemisphere that is not direct radiation. Pyranometers are instruments that measure diffuse radiation or global radiation depending on how the instrument is set. A pyranometer is a device that uses a transparent hemisphere glass at the top that allows radiation to heat, again, a thermopile that produces an electrical current when radiation lies within 0.3 and 2.8 µm which is 99% of solar radiation [22] . However, some pyranometers might have silicon photovoltaic sensors. For diffuse radiation measurements, no direct radiation is allowed into the pyranometer, therefore, there are disks or shadow bands located above the glass hemisphere to block and then prevent direct radiation reaching the pyranometer’s sensor. Corrections are needed for accurate measurements of diffuse radiation when using a pyranometer due to the blockage.
Global radiation is obtained simply by adding the direct and diffuse radiation components. Global radiation is measured with a pyranometer too, the difference being that there must be no objects between the hemisphere and the instrument. Both pyrheliometers and disks or shadow bands for diffusion radiation pyranometers need a tracking system to follow the sun’s path across the sky both for daily and seasonal variations.
2.1.3. Maps and Units
As any other solar energy conversion technology, solar stills rely on the intensity of solar radiation as the most critical and important parameter. With the advent of solar energy engineering devices and concerns over climatic changes around the world, solar radiation maps have become available in almost every region on the planet. These maps are color or gray tones representations that show the amount of solar resource reaching the ground as a function of space (regions) and time (per day or per year). It can be seen in this maps that the higher intensity radiation is distributed around the Equator and especially on desert areas of the planet such as Australia, Mexico, Middle East and North Africa.
It is important to clarify some of the terms and units employed in solar energy conversion technology since there are many in the literature to describe different concepts interrelated. We suggest following the nomenclature given in [23] . Solar radiation is simply a general way to describe the radiation phenomenon that stems from the sun. Irradiance is the radiation power per unit area and its units are W/m2. Irradiation is the radiation energy per unit area and its units are J/m2. The difference between these two magnitudes is time.
Irradiance is measured instantaneously. Take, for example, that at 6 o’clock in the morning, an instrument measures an irradiance value of, say, 100 W/m2 but two hours and a half later, the instrument reads 345 W/m2. One instant is for only one measure that results in only one value. On the other hand, an instrument that measures irradiation needs an interval of time. From, say, 6:00 a.m. to 8:00 a.m., the accumulated value of energy that arrived as radiation is, let’s say, 1500 J/m2. It is a measurement that needs some time to be taken; it is not possible to have an instantaneous value of irradiation. The difference between the two is simply a matter of the information they provide: an instantaneous measure of the energy in radiation (Power in kW/m2) or the accumulated energy in a certain time interval (Energy in kWh/m2 or J/m2).
When it comes to Solar Maps, units are not the same for all of them since they are arbitrarily chosen by the research group or editorial board of the publication. However, they can be easily transformed between one another and both are clear information about the solar resource. Most of the maps show Irradiance as the variable of study, because they use kWh/m2 per year or per day, that is the time-averaged energy (kWh) falling in some region.
2.2. Thermal Insulation
The goal of thermal insulation is to minimize heat leaks through the side and bottom walls of the solar still. Thermal insulator materials have to fulfill the requirements of a long-life operation while resisting aggressive environments such as humid and saline near the sea coasts or arid and corrosive in desert industrial zones keeping in mind that they should be as cost-effective as possible.
Thermal insulation is a resistance to heat fluxes that depends on the thermal conductivity of the material that surrounds the brine. Definition of thermal conductivity comes along with Fourier’s constitutive relation that models heat transfer phenomenon by conduction through a medium.
If the thermal conductivity is reduced, the temperature difference between the collector and its surroundings will increase, for instance, the still will be better insulated. Insulation is considered an isotropic and independent of temperature in order to be characterized by a constant thermal conductivity. Heat conduction losses through the insulation are reduced if ambient temperature increases or wind speed decreases (for a mounted still).The influence of insulation has been proved to be significant up to some degree. Theoretically [9] and experimentally [24] validate this tendency. It is seen that the usefulness of insulation manifests up to a certain value of thickness. Cooper [10] showed that the absence of a thermal insulator has no significant effect, but a 30% increase of distillate production is obtained for 0.5 to 12 inches of brine-glass cover gap using thermal insulator.
2.3. Wind Speed
Wind speed is the most unpredictable of all solar still parameters due to its very own nature. Solar stills are not necessarily located in regions where charts of wind speed and direction are known or available as is the case for regions where, for example, wind turbines are installed. Therefore, it is a parameter that cannot be controlled or specified with relative good accuracy for solar still operation.
The effect of wind speed is a reduction in the overall temperature of a solar still which would be an undesirable effect. However, if the wind flows over the glass cover it extracts heat from it and promotes an increase in still productivity due to a larger temperature gap between brine and glass cover. Looking into the detail of heat transfer phenomena within the solar still, the more heat we extract from the glass cover, the higher yield we would get out of it.
When the outside surface of the glass cover is blown with colder air, heat is dissipated to the surroundings. This dissipation is increased whenever wind speed increases due to a higher heat transfer coefficient. McAdams [25] presented an expression for the heat transfer coefficient over a surface as a function of speed. This expression have found widespread acceptance in the solar still literature but it has to be noted that the expression is an experimental result [25] found by Jurgesback in 1924 for a parallel airflow at room temperature over a vertical copper plate. These specific experimental conditions are far from representing a solar-still glass cover, however, we think that there wasn’t much information regarding heat transfer coefficients back in the 1960’s and McAdams [25] was a strong reference for heat transfer studies.
Wind speed is a parameter that has been studied with no conclusive results regarding a positive or negative influence on distillation. El-Sebaii [26] has numerically shown that at higher wind speeds, both temperature difference and distillation output increase but only up to a certain value. Its influence on distillation rate has been debated with contradictory results in several articles. Morse and Read [9] in their parametric study conclude that wind speed is not relevant for distillation output. Malik et al. [6] reported a steady increase in daily output as the loss coefficient decreased. Cooper [10] found that wind speed over 5 miles per hour have a marginal augmentation effect on the distillate yield.
2.4. Brine Inlet Temperature
Considering the heat transport phenomena, brine temperature is relevant to all heat fluxes from basin water, that is, evaporation, free convection and radiation. Evaporation rates increase for higher water temperatures due to the fact that less energy is needed to break the barrier from liquid to gaseous form. Another way to look at it: at some specific pressure (atmospheric pressure), water will evaporate at the saturation temperature and the higher brine temperatures are the closer brine is to saturation temperature. Therefore, it is not surprising that some techniques use residual heat to preheat brine ([27] -[29] ).
In fact, solar stills are at the bottom of high temperature requirement for thermal devices needing only some 5˚C to 10˚C above environmental temperature in order to function properly, in contrast with metallurgical furnaces or power plants, for example. Most of the industries that produce residual heat don’t have solar stills to be fed because they have full access to clean water by other means. Nonetheless, it would be interesting to promote the idea, whenever it is cost-effective, that solar stills could be a part of every industry if space or costs are not restricted. Distilled water could be for staff use or distributed to the community as a social benefit for the company or district.
For high latitude regions where cold brine is found and the possibility to preheat it is economically unfeasible, low-level-basin or wick-type solar stills should be considered for higher distillate yields.
2.5. Brine Depth
The amount of brine inside the basin determines the brine depth or the level of brine. This is a parameter that appears only in analyses where the heat transfer between the collector and the brine is considered. There are studies where the brine and the bottom of the still are thought as the same system [8] . This has two consequences: first, this means that radiation doesn’t contribute to heat the brine; and second, that all the performance of the still is independent on the water depth which is arguable, as experimental results in the literature.
Water depth implies the total amount of water in a solar still. The bottom of the solar still has a surface which is fixed. The brackish water or brine that is poured into the basin spreads through all that area and reaches a certain level inside the basin of the solar still. The mass of water is directly proportional to the thermal inertia of a solar still. Thermal inertia is how resistant the brine is to change its temperature. It depends on the heat capacity and the mass of the brine. The higher the thermal inertia, the greater the time it is required for the still to produce distillate.
Tripathi and Tiwari [30] showed that for 0.10 m and 0.15 m of brine depth, higher distillation rates were achieved due to thermal storage effect. They found not only distillation was influenced by brine depth due to thermal storage effect but also due to the modification of the heat transfer coefficient between water surface and inner condensing cover by changing their average spacing.
Tayel et al. [31] studied different configurations and parameters in solar still productivity, one of them being brine depth. The study shows that the highest distillation rate is found for a 2-cm brine depth. Badran [32] experimentally studies enhancement parameters for a solar still. As brine depth increases, productivity decreases due to an increase in heat capacity of the water in the basin which, in turn, reduces evaporation rate for the same solar input. Furthermore, in terms of how solar radiation is affected by a layer of water depending in its depth is reported by Kreider and Kreith [33] .
2.6. Cover Tilt Angle
The cover tilt angle is fundamental for the production of distillate water. It provides the proper inclination for the condensate to flow out of the still: a small angle would produce condensate to drip from the interior face of the glass cover while a large angle would increase still costs and compromise mechanical support.
As Rahbar and Esfahani [34] pointed, the model from [8] has a limitation due to the 10˚-angle value for the cover tilt, which is a small value even for low-latitude locations. This limitation has promoted a considerable amount of studies regarding cover tilt angle in solar stills, whether they are single or double sloped.
A thorough survey of studies where cover tilt angles were examined can be found in Khalifa [35] . This author examined the relationship between cover tilt angle and latitude for optimal distillate production. It seems that for higher productions, cover tilt angle and latitude should be close to each other, which is a rule of thumb for solar water heaters. However, conflicting results can be found about this parameter as the author pointed out.
3. Thermal Balances
Current trends on solar distillation are based on new geometrical designs, evaporative-enhancing materials, its coupling with photovoltaic cells and surfactants supplied into the brine. But in the opinion of the authors, there has been little effort in trying to explain and widen fundamental knowledge on transport phenomena, primarily inside the still, where the useful effect occurs. Evaporation and condensation are critical phenomena for solar distillation and most of the theoretical and experimental relations are simplifications leading to very useful design information. However, in this work emphasis is made in reviewing classical aspects of heat and mass transfer and exploring solutions based on ideas located in other fields of study.
A series of thermal analyses considering the transient operation of the still, are presented, based on the published literature and the author’s own experience. These include physical and mathematical modeling of internal and external transport phenomena that affect the response of the still, as well as thermodynamic balances of the whole equipment and environment coupled systems. The internal analysis comprehends natural convection from basin to brine and from brine to air, and thermal radiation from the basin to the glass cover. The external analysis considers solar radiation from the glass cover to the surroundings and into the basin.
3.1. Internal Transport Phenomena
3.1.1. Natural Convection from Brine to Glass Cover
Convection is the method in which heat flows by the motion of a fluid. Natural convection is the heat flow when the fluid is set in motion by some force inside the fluid. This force is produced by a difference in density within the fluid. Density changes may be produced by a temperature difference or a concentration difference. Natural convection is a critical mechanism inside the still: no water steam evaporating from the brine could reach the condensation surface (glass cover) without the motion of natural convection cells.
For many years it was taught that energy and mass transport in solar stills were mainly accomplished by diffusive transfer in most part of the still, with a little boundary layer type flow close to the glass cover and may be in a small region adjacent to the liquid surface [8] . The reason for this interpretation can be found, perhaps, in that there were no detailed experimental and visualization studies except for the investigation conducted by Baum and Baimarov [36] , showing a physical structure resembling very much to the one described above.
Nevertheless, natural convection in a solar still has been recognized by contemporary authors, as the most important mechanism for heat transport along with evaporation from the surface of the brine to the glass cover ([6] [37] [38] ). The extensively used model for free convection in a solar still, widely referred to in the literature, is the one first proposed in [8] and explained in detail in [6] .
Dunkle [8] proposed that the Nusselt number for free convection could be expressed as:
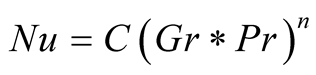 (1)
(1)
where the constants 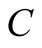 and
and ![]() are obtained from experiments, with different values that depend on the flow regime either, laminar or turbulentLaminar flow
are obtained from experiments, with different values that depend on the flow regime either, laminar or turbulentLaminar flow 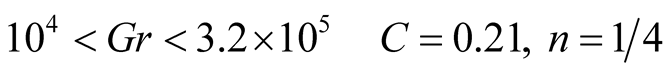
Turbulent flow 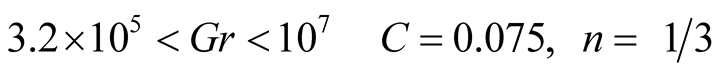
Malik et al. [6] considered a turbulent regime which cancels out the presence of a length scale in the Grash of number and this result is interpreted as if the heat transfer coefficient 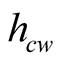 would not depend on the height of the still (the distance between the surface of the brine and the glass cover), contrary to what Porta-Gándara et al. [39] have reported. Hongfei et al. [40] on the other hand, considered a laminar regime in the solar still, based in their own experimental results. To add even more uncertainty in the regime that one would expect, PortaGándara et al. [39] , Rubio et al. [41] and Porta-Gándara et al. [42] presented flow visualization results for a transition regime in the same class of solar still, Figure 2. In addition to the turbulent regime for natural convection within the still, Malik et al. [6] proposed a limited range of temperatures for which the values of the physical properties of the fluid remain constant with the temperature. With the appropriate consideration of mass transport during evaporation they arrive to the generally accepted expressions:
would not depend on the height of the still (the distance between the surface of the brine and the glass cover), contrary to what Porta-Gándara et al. [39] have reported. Hongfei et al. [40] on the other hand, considered a laminar regime in the solar still, based in their own experimental results. To add even more uncertainty in the regime that one would expect, PortaGándara et al. [39] , Rubio et al. [41] and Porta-Gándara et al. [42] presented flow visualization results for a transition regime in the same class of solar still, Figure 2. In addition to the turbulent regime for natural convection within the still, Malik et al. [6] proposed a limited range of temperatures for which the values of the physical properties of the fluid remain constant with the temperature. With the appropriate consideration of mass transport during evaporation they arrive to the generally accepted expressions:
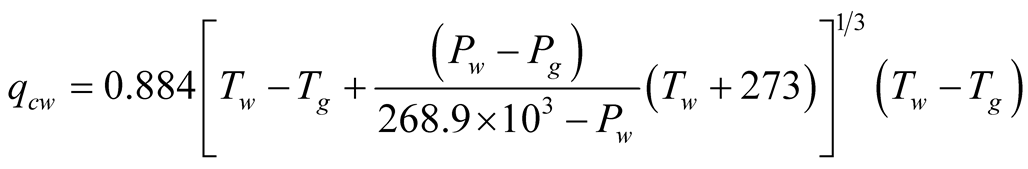 (2)
(2)
and
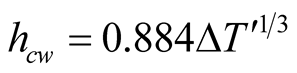 (3)
(3)
where 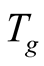 is the temperature of the glass cover.
is the temperature of the glass cover.
Malik et al. [6] used a linear expression for the pressure based on the temperature. There is an exponential approximation of the pressure function in terms of temperature which tends to be more accurate [37] .
When mass transfer occurs between two substances with different molecular masses, such as the case of water into air, a modified Grashof number is required, as described in Malik et al. [6] . The modification of the temperature difference affects the Grashof number in the following way:
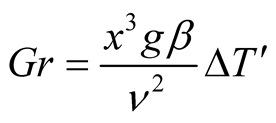 (4)
(4)
where
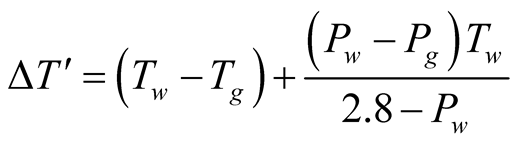 (5)
(5)
Therefore, the Rayleigh number is
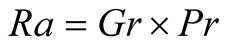 (6)
(6)
where the Prandtl number is defined as
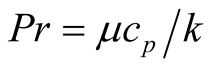 (7)
(7)
In almost every heat transfer study, the Nusselt number is used as ratio of convection and conduction, describing how heat flux is transported between the walls into the fluid region.
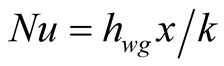 (8)
(8)
3.1.2. Natural Convection from Basin to Brine
Once solar radiation increases the temperature of the basin, typically a black surface, heat is transported to the brine by natural convection. As a result, the brine is heated by convection currents from the inside bottom of the still and brine increases its temperature which, in turn, favors evaporation. In terms of modeling, this particular heat flux is often not taken into account by some authors, noticeably [8] . He establishes that the energy gain by the water is due to the absorption of the radiation of the still’s base. This fraction is due to the high transmittance of, both glass cover and brine layer, and also due the high absorptance of the base. In this case, the solar still base and brine is the same thing for modeling purposes. Therefore, there is no basin-to-brine convection. Furthermore, the amount of water inside the basin may be so low that water convection cells may be inhibited and only conduction is present.
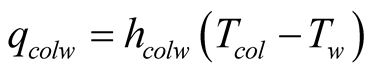 (9)
(9)
3.1.3. Radiation from the Brine to the Glass Cover (or Elsewhere)
Radiation is perhaps the least dominant heat transfer phenomenon within the solar still due to the relative low temperatures of the overall solar still. Radiation from the brine to the glass cover can be divided in short and long wavelength. Short wavelength radiation is the amount of solar radiation that is reflected back from the brine surface or the bottom liner of the still to the glass cover. In most studies this radiation is simply neglected. On the other hand, long wavelength radiation (IR radiation) emitted from the basin to the glass cover is frequently taken into account.
The mathematical expression for heat radiation, in this case, is
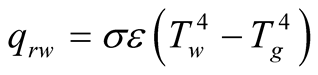 (10)
(10)
Theoretically, using a trial method, Dunkle [8] found that radiation accounted for 10% from the overall energy budget in the still when using a value of 0.9 for water emissivity.
3.1.4. Evaporation
Evaporation is the phase change of the brine or brackish water from liquid to gas and the mechanism that separates salt (or some other dissolved or suspended particles) from water, which is the first goal of any still: the separation process.
In the solar still, once the brine receives a certain amount of heat (enthalpy of evaporation) it changes from a liquid phase to a gaseous phase. Then it flows upward to the glass cover due to convective currents. The driving force for evaporation is a pressure difference. In the vast majority of cases, this pressure difference is produced by a temperature difference which modifies the partial pressure of steam in two regions of the still. In the brine surface, temperature is higher, so the partial pressure of steam, whereas inside the glass cover, partial pressure of steam is lower due to lower temperature.
Evaporation is a complex phenomenon that involves coupled heat and mass transfer, geometry parameters, external forces (gravity) and the properties of substances. From the viewpoint of the Kinetic Theory of Gases, evaporation is born from an unbalanced situation when more particles cross the interphase from the liquid to the vapour region than particles going from the liquid to the vapour region. Kinetic Theory calculates the mass flux from one phase to the other as a function of temperature and pressure [43]
 (11)
(11)
Malik et al. [6] proposed a heat flux coefficient for evaporation in a solar still after the analysis of mass balance between the surface of the water and the glass cover. This coefficient is expressed as a function of the partial pressures of the vapor in the surface of the water and near the glass cover. The difference of partial pressures in these two regions of the still is the driving force that produces evaporation from the surface.
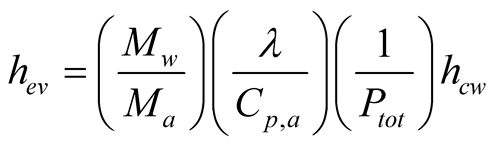 (12)
(12)
After making some assumptions about the numerical values of water and air properties and pressure, the heat transfer coefficient for evaporation is:
 (13)
(13)
After some algebraic manipulation and considerations, it is found:
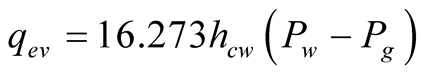 (14)
(14)
In general, heat released from evaporation is expressed by:
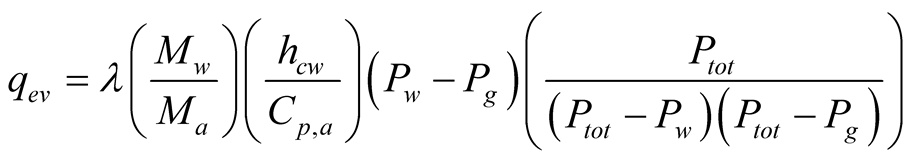 (15)
(15)
3.1.5. Condensation
The condensation process in a solar still is a phase change from gaseous to liquid phase produced in the inside cold surface of the glass cover [44] . Unfortunately, most of the theoretical and experimental studies about solar stills almost completely disregard condensation as a fundamental part of the process of fresh water production. One notable exception is [45] where a model and experiments are developed in a tubular solar still in order to get correlations that take into account the effect of air in steam condensation.
At all lights, condensation is the final step towards distillate output in the sequence of processes within a solar still and it should be considered as a critical part in the distillation process, enhancement techniques and optimization-based design.
This topic has received a lot of attention in the condenser literature for power plants, specially nuclear power plants and refrigeration applications. However, it is important to note that industrial condensers work with just one component or species on its condensation surface (air is avoided, as a rule, due to corrosion problems) whereas the glass cover of the solar still condensates water in the presence of air, a non-condensable gas. In this regard, a great amount of literature has been produced in the nuclear engineering field to study the effect of noncondensable gases in condensation on vertical and horizontal tubes ([46] [47] ).
In any case, condensation inside a solar still occurs in a boundary (interior face of the glass cover) where the fluid has small amounts of water vapor so that it shares this feature with psychrometry applications.
3.1.6. Diffusion
Diffusion is the transport of substance(s) within a region occupied by other substance(s) by means of molecular interactions. These substances are called species and in order to have diffusion, at least two species are needed in the same region. Diffusion is a very important subject of study for chemical engineering, kinetics, electrochemistry and other related analysis such as transport of biological components.
Mathematical modeling of mass transfer by diffusion can be approached in several ways ([43] [48] ). However, most of the analyses use the constitutive relation called Fick’s law to relate concentration gradients to diffusion mass fluxes. Water steam diffusing into air is a commonly known process and data such as diffusivity coefficients are easily available in the specialized literature. In a solar still, diffusion of evaporated water within air is neglected as an influential transport phenomenon inside a solar still in comparison to the mass transported by free convection currents.
Using scale analysis, the diffusion time needed for a particle of water steam to diffuse up to the glass cover is
 (16)
(16)
where 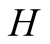 is the distance diffused by species and
is the distance diffused by species and , the diffusivity of the water vapor. Now, a 20-cm height from brine surface to the glass cover and 0.260 cm2/s asthe value of diffusivity of water in air [48] , the diffusion time is approximately 1540 seconds or 26 minutes. On the other hand, the time for transport due to free convection is
, the diffusivity of the water vapor. Now, a 20-cm height from brine surface to the glass cover and 0.260 cm2/s asthe value of diffusivity of water in air [48] , the diffusion time is approximately 1540 seconds or 26 minutes. On the other hand, the time for transport due to free convection is
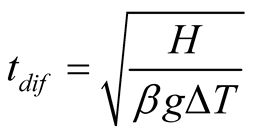 (17)
(17)
Assuming the water vapor as an ideal gas, properties at 40˚C and a temperature difference, 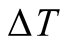 equal to 20˚C, the convective time is 1.64 seconds. In a solar still, diffusion is slow in comparison to convective transport. A 2-mm gap between brine surface and glass cover is needed for diffusion to be as dominant as free convection for mass transport. It is noticeable that [8] and [36] mentioned “diffusion stills” emphasizing diffusive process as the dominant driving force within a still.
equal to 20˚C, the convective time is 1.64 seconds. In a solar still, diffusion is slow in comparison to convective transport. A 2-mm gap between brine surface and glass cover is needed for diffusion to be as dominant as free convection for mass transport. It is noticeable that [8] and [36] mentioned “diffusion stills” emphasizing diffusive process as the dominant driving force within a still.
Rahbar and Esfahani [34] included diffusion transport in their CFD study by adding the buoyancy force due to concentration gradients in the momentum equation. They presented contours of vapor mass fraction inside the solar still showing high concentration gradients near the surfaces and almost constant concentration regions in the bulk fluid along with the traces of convective cells, which is the result of a dominant convective transport.
3.2. External Transport Phenomena
As long as heat flows within the solar still, it is part of the Internal Transport phenomena. External Transport Phenomena are simply heat transfer losses from the solar still to the surroundings. From the efficiency point of view, some of these losses decrease the performance of a solar still so they need to be minimized. However, it is important to recognize that glass cover “needs” to lose heat so that a temperature difference between the brine and the glass cover is established in order to enhance distillate yield and perform properly. Thus, some heat losses should be minimized by design while other heat losses should not.
3.2.1. Conduction from Basin to Surroundings
Heat flows from every wall containing the basin to the surroundings by conduction, which is mathematically modeled by Fourier’s law of conduction:
 (18)
(18)
Typically, cheap, insulating materials are used to build solar stills like wood, cement and fiberglass. For some fixed temperature difference between brine and ambient temperature, the largest surface conducts more heat than the others. This means that the basin bottom should be thicker than the other walls and less exposed to wind whenever possible. Conduction losses account for around 8% of energy input from solar radiation [8] .
3.2.2. Radiation Losses to the Surroundings
Basically there are two sources for radiation from the solar still: 1) Long wavelength radiation emitted from the basin and 2) short wavelength radiation reflected back by the glass cover.
There is a fraction of solar radiation that is reflected back to the surroundings due to the reflectivity of the glass cover and the walls of the still. A good solar still design would require the lowest possible value for reflectivity and absorptivity for the glass cover, so that most of the radiation is transmitted through the glass. Also, glass thickness should be kept as minimum as possible without compromising mechanical strength.
The radiation emitted by the glass cover to the surroundings
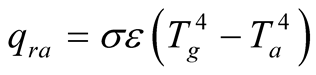 (19)
(19)
Due to the low emissivity of the glass and the low temperature gap between the glass cover and the surroundings, this term is a small fraction in comparison with the other heat fluxes.
3.2.3. Convection from Glass Cover to Surroundings
The dominant heat losses from the outer surface of the glass cover to the surroundings are by convection due to the wind. The expression for heat transfer by convection from glass to the environment is:
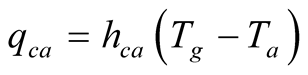 (20)
(20)
It was already mentioned in Section 2.3 that there is an expression widely used in solar still literature for 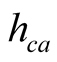 due to McAdams [25] using data of Jurges for a 0.5-m2 copper plate:
due to McAdams [25] using data of Jurges for a 0.5-m2 copper plate:
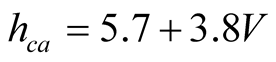 (21)
(21)
Duffie & Beckman [21] mentioned that probably this formula includes the effects of natural convection and radiation. Wattmuff et al. [49] on the other hand, found the expression
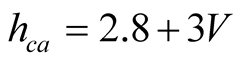 (22)
(22)
which tends to give lower values for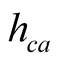 . Glass covers for solar collectors fits properly glass covers used for solar stills regarding materials and inclination angle, so these expressions may be used safely for calculations.
. Glass covers for solar collectors fits properly glass covers used for solar stills regarding materials and inclination angle, so these expressions may be used safely for calculations.
4. Thermodynamic Modeling of a Solar Still
Thermodynamics is the science that studies states and their accessibility. States are a set of conditions (properties and external agents) that establish the description of a system completely. In Thermodynamics, many systems are described only by their pressure, temperature and specific volume. In a solar still, it is often seen that the knowledge of temperature and pressure suffices to characterize the state of any system within it, although more complex analysis should take chemical potential of steam and air into account.
Thermodynamics have proposed four laws that relate the possibility of a system reaching some particular states from an initial state or from a final state, tracking back its possible initial states. The Zeroth law is the recognition of a property called temperature, completely unidentifiable, elsewhere in science. The first law of Thermodynamics states the definition of energy and its consequence is the mathematical expression of the conservation of energy. The second law of thermodynamics was born as the result of the discovery that for a given amount of energy, it was impossible to use the whole of it for useful output.
Thermodynamics describes the evolution of systems in space and time from an initial to a final condition. Using its laws, Thermodynamics provides tools to find a maximum usage of energy to feed processes in order to satisfy several types of commodities, i.e. material, energetic, etc.
In a solar still there are several transport phenomena coupled in order to produce fresh water. Keeping track of each one of these fluxes and studying them under the scope of Thermodynamics, that is, defining systems and describing their processes using its laws, gives the opportunity to design better solar still systems, produce more fresh water or optimize the solar resource for a given solar still. Furthermore, the second law of thermodynamics establishes a limit in the amount of useful energy that can be extracted from every process. Knowing thermodynamics, among other things, equals to know the best theoretical thermal device for a given purpose and compare it with the real device.
4.1. Modeling of a Solar Still
In a solar still, part of the complexity of modeling lies in the fact that the three heat transport mechanisms appear within the solar still. Conduction and convection are proportional to a temperature difference. Meanwhile, radiation heat transfer is directly proportional to the fourth power of temperature. Another part of the complexity is that heat transfer convection mechanism depends highly on geometry, fluid/wall properties and temperature.
In the resulting mathematical model after a first-law analysis, the unknowns of the energy equations are temperatures. Temperatures are obtained once the input functions i.e. solar irradiation and ambient temperature and parameters are set.
The energy equations (see below) of the solar still are nonlinear, time dependent, ordinary differential equations. They are the result of a lumped parameter analysis, that is, variables do not change spatially. The nonlinear character is due to the heat transfer convective coefficients that depend on the temperature. The heat transfer coefficients are brought into the equation in order to model heat fluxes. Thermodynamics is unable to find relations to calculate heat fluxes. Transport phenomena are non-equilibrium phenomena; therefore, Classical Thermodynamics is unable to find a mathematical expression for heat, which is the study of Heat Transfer.
The expressions for solar irradiance and ambient temperature functions for a 24 hour period are, respectively:
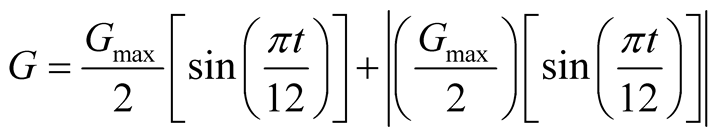 (23)
(23)
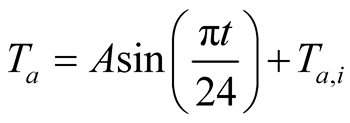 (24)
(24)
where t is the time in hours and  is the ambient temperature at the beginning of the day in ˚C.
is the ambient temperature at the beginning of the day in ˚C.
Equation (23) is the input of the solar still model, the driving force.
Assumed in the model is the following:
• All physical properties of materials are not affected by temperature differences;
• Vapor-air mixture and insulation are not regarded as systems or participating media;
• Brine and glass cover do not interact with incoming solar radiation;
• The shape factor value between the collector and glass cover is 1;
• The solar still is a closed system;
• There are no temperature gradients across brine depth, collector plate or glass cover.
Solar irradiance and ambient temperature are two time-dependent parameters with an important role in the transient energy balance of the still. Malik et al. [6] used Fourier series for modeling the periodic behavior of solar parameters.
4.2. Energy Balance
Energy is an inherent property of matter, so general that it is almost impossible to define. We do not quite perceive it, only its manifestations. There is nothing in the universe happening that cannot be counted as an energy transformation. Every imaginable process has to be with the conversion of one type of energy to another. In Thermodynamics, the First Law is a statement that defines a property called energy. A consequence out of the First Law of Thermodynamics is the Conservation of Energy.
Conservation of energy can be thought as an accounting exercise that basically establishes that what goes in equals what goes out plus the accumulation or minus the lost. The mathematical expression of the conservation of energy is one of the thermodynamic tools to study systems and several of its forms can be found in the vast literature of Thermodynamics.
Applying the conservation of energy to the solar still results on a three-equation system, for the glass cover, brine and collector, respectively, we obtain:
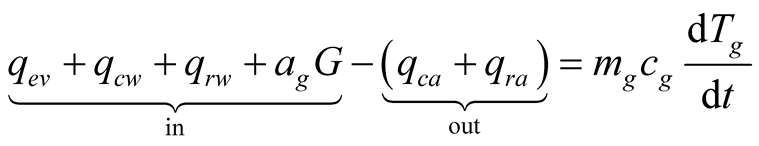 (25)
(25)
 (26)
(26)
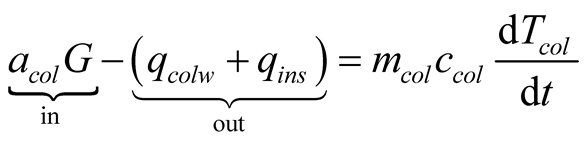 (27)
(27)
where
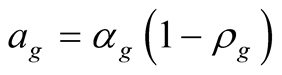 (28)
(28)
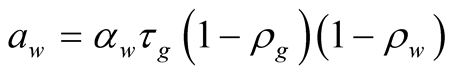 (29)
(29)
 (30)
(30)
The unknowns in this set of equations are glass cover, brine and collector plate temperatures . The equations are presented as the difference between the energy inputs and outputs equal the change of energy (accumulation or loss) in time.
. The equations are presented as the difference between the energy inputs and outputs equal the change of energy (accumulation or loss) in time.
Let us discuss briefly this set of equations. We consider that there are no sources of energy (chemical, electrical fissile, etc.) in any component of the still. The energy flux produced by the diffusion process is neglected. If all heat transfer coefficients, h, are temperature independent, then these differential equations are offirst-order and linear. Thus, analytical solutions can be found although the expressions can be quite complicated due to the time-dependence of solar irradiation,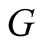 . Notice that these equations would be nonlinear if the expression for heat radiation was used explicitly due to
. Notice that these equations would be nonlinear if the expression for heat radiation was used explicitly due to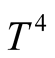 . In this case, Equations (10) and (19) are solved for certain typical still parameters and their numerical values embedded into Equations (25), (26) and (27), so that the set can be solved easily.
. In this case, Equations (10) and (19) are solved for certain typical still parameters and their numerical values embedded into Equations (25), (26) and (27), so that the set can be solved easily.
These equations described lumped-parameter systems where no gradients are taken into account. Glass cover, brine and collector have properties independent of any coordinate direction. In this sense, they are analogous to the unitary operations in chemical and process engineering. These equations, modified dozens of times by researchers, have become the horse work in solar still modeling, providing accurate and useful information about its thermal behavior along a day.
Solar still studies have been, generally speaking, concerned aboutthe energy characterization of the device, putting aside the air-water vapor mixture flow inside the still. Experimentally [39] [41] [42] have discussed the flow structure and its time-dependence on solar stills in a laboratory.
4.3. Exergy Balance
Exergy is the maximum amount of work that can be extracted from a system when it goes from a certain thermodynamic state to a reference state [50] . The reference state is often modeled as the environmental state, although, depending on the type of exergy, some other references have been proposed ([51] -[53] ). Exergy describes the quality of energy instead of its quantity for a given system or a flux; it quantifies how much energy goes directly into work. Simply put, exergy is the useful part of energy.
The term exergy was coined [54] by Zoran Rant in 1956 and its use has spread widely, especially in Europe. However, the concept can be traced back to Gibbs, namely Gibbs’ available work. A detailed history of the exergy concept can be found in [55] .
The exergy balances refer to the account of exergy inputs, losses and the exergy destruction in the various components of the still. In mathematical form a general expression of this balance is:
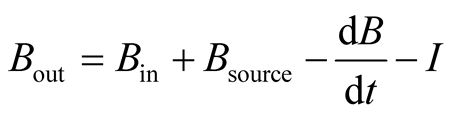 (31)
(31)
It can be seen that the right-hand side of Equation (31) is formed by input exergy flux, 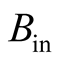 , the exergy from an energy source,
, the exergy from an energy source, 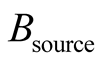 , (chemical, fissile, electrical, fusion, etc.), the local exergy change in time,
, (chemical, fissile, electrical, fusion, etc.), the local exergy change in time, 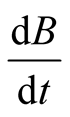 , and the exergy destruction by irreversibilities,
, and the exergy destruction by irreversibilities,![]() . Now, the exergy output may be a useful flux of exergy (work, heating, cooling, etc.) or simply exergy leaving the system with no useful consequence. However it may be, this form of exergy balance (Equation (31)) shows clearly the hindrances for having high values of exergy output. High thermal exergetic inertia and irreversibilities decrease exergy output.
. Now, the exergy output may be a useful flux of exergy (work, heating, cooling, etc.) or simply exergy leaving the system with no useful consequence. However it may be, this form of exergy balance (Equation (31)) shows clearly the hindrances for having high values of exergy output. High thermal exergetic inertia and irreversibilities decrease exergy output.
The exergy balances for glass cover, brine and collector are, respectively:
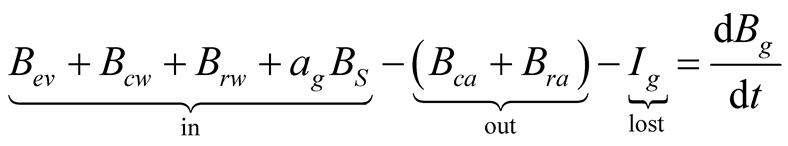 (32)
(32)
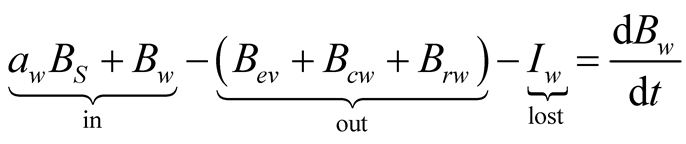 (33)
(33)
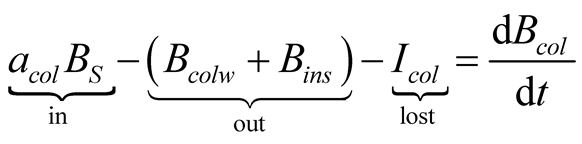 (34)
(34)
No mystery here. All energy terms in Equations (25)-(27) have its correspondent exergy plus the irreversibility that occurs in that component of the still. However, there is a crucial difference between energy and exergy balances. Exergy is a quantity that it is only conserved in a reversible process. When it is not conserved, irreversibility is produced. In an energy balance, no such concept is found because exergy is a concept derived from the 1st (energy) and the 2nd (entropy) law altogether. In this sense, thermodynamically speaking, “balance” is not the most suitable word to describe what happens to the exergy of a system in a process, nonetheless it is used here to describe more clearly in a mathematical sense.
The source for irreversibility can be friction, electrical resistance, accelerations, turbulence in a fluid, a temperature or a concentration difference among several others [56] [57] . Irreversibility is an amount of energy that can never be used to perform work. Eventually, all irreversibilities are dissipated as heat at ambient temperature.
In Equations (32)-(34), not all exergy fluxes have the same expression. For heat radiation, the exergy is expressed as [58] :
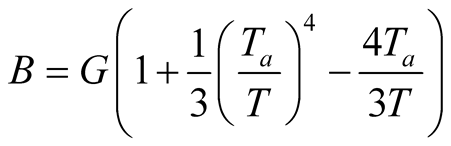 (34)
(34)
For all other heat transfer mechanisms, the exergy is calculated as [50] :
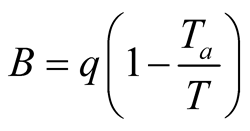 (34)
(34)
Considering that every component of the still is an incompressible substance (the air-water vapor mixture is not included in the balances), the change of exergy in time can have be expressed as:
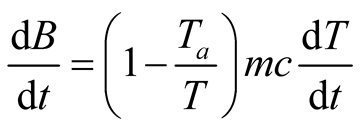 (34)
(34)
or, when considering the possibility of a variable ambient temperature, as [59] :
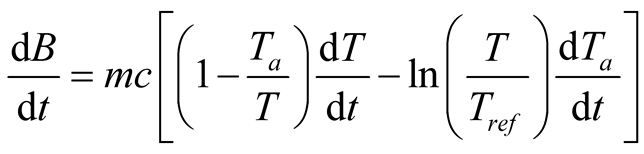 (34)
(34)
Useful exergy is that part of the exergy used to heat the brine and produce distillation. Distillate production can be directly related to the solar exergy input. However, it is difficult to interpret exergy in terms that are not useful work (energy flow) because the amount of exergy from the distillate is not relevant. The fundamental expression for exergy has been established in most modern thermodynamics treatises, essentially as the difference between reversible work and lost work, which corresponds to a power maximization point of view. Thus, a high exergy air-water vapor mixture inside the still will produce more work than a low exergy mixture. The largest irreversibility in a solar still (and in any solar thermal application) occurs at the collector because a significant fraction of the total solar radiation absorbed in this component is poorly employed [59] . The high exergy losses causing the low exergyefficiencies are made up of avoidable and unavoidable contributions. The avoidable contributions can be reduced by improving the corresponding physical components of the system.
It is the opinion of the authors that second law analysis of solar-driven technologies, whether they are based on exergy, entropy generation, emergy, thermoeconomics or irreversible thermodynamics should complete any conventional thermodynamic analysis.
5. Conclusions
An extended overview of solar distillation from the thermodynamic point of view is presented in this work. Solar distillation has been known and applied for several hundreds of years; however, the understanding of physical phenomena behind it has been developed just some decades. A comprehensive and structured discussion is, therefore, necessary to a better understanding of the thermodynamic basis of these devices. Firstly, a concise history of solar distillation engineering is presented, from practice to theory. Relevant aspects of radiation are treated due to the importance of this parameter in solar distillation. The description of typical parameters in a solar still is useful for the identification of trade-offs in the performance of the device when one of them is varying. A considerable amount of literature is presented for each parameter’s subsection.
Internal and external heat transfer phenomena in a solar still are clearly specified, including their definitions, mathematical modeling and a brief discussion of studies in the field for each one of them. One of the most important topics in solar distillation is thermodynamic modeling and the result is the energy balance. The authors have widened the scope of this study by the addition of second law concepts, such as exergy and irreversibilities. Intentionally, no mention is made to the several types of solar stills in the field and even more modifications are made to each of these types in order to increase distillation. In general, with some variations, every solar still performs based on the same phenomena is discussed here.
References
- Chaibi, M.T. and El-Nashar, A.M. (2009) Solar Thermal Processes. In: Cipollina, A., Micale, G. and Rizzuti, L., Eds., Seawater Desalination: Conventional and Renewable Energy Processes, Springer, London, 131-163.
- Arellano, N. (2011) La planta solar de desalación de agua de Las Salinas (1872). Literatura y memoria de una experiencia pionera. Quaderns d’Història de l’Enginyeria, 12, 229-251.
- Nebbia, G. (2005) Early Work on Solar Distillation in Italy, 1953-1970. In: Goswami, D.Y., Vijayaraghavan, S. and Campbell-Howe, R., Eds., Proceedings of the Solar World Congress 2005, American Solar Energy Society, Boulder, 2709-2713.
- Kalogirou, S. (2005) Seawater Desalination Using Renewable Energy Sources. Progress in Energy and Combustion Science, 31, 242-281. http://dx.doi.org/10.1016/j.pecs.2005.03.001
- Maurel, A.(1981) La desalinización del agua de mar. Mundo Científico, 1, 296-305.
- Malik, M.A.S., Tiwari, G.N., Kumar, A. and Sodha, M.S. (1982) Solar Distillation: A Practical Study of a Wide Range of Stills and Their Optimum Design, Construction and Performance. Pergamon Press, Oxford.
- Telkes, M. (1953) Fresh Water from Sea Water by Solar Distillation. Industrial & Engineering Chemistry, 45, 1108-1114. http://dx.doi.org/10.1021/ie50521a062
- Dunkle, R.V. (1961) Solar Water Distilation: The Roof Type Still and a Multiple Effect Diffusion Still. Proceedings of International Heat Transfer Conference,University of Colorado, Boulder, Colorado, Part V, 895-902.
- Morse, R.N. and Read, W.R. (1968) A Rational Basis for the Engineering Development of a Solar Still. International Journal of Solar Energy, 12, 5-17. http://dx.doi.org/10.1016/0038-092X(68)90021-2
- Cooper, P.I. (1969) Digital Simulation of Transient Solar Still Processes. International Journal of Solar Energy, 12, 313-331. http://dx.doi.org/10.1016/0038-092X(69)90046-2
- Ali, H.M. (1993) Effect of Forced Convection inside the Solar Still on Heat and Mass Transfer Coefficients. Energy Conversion and Management, 34, 73-79. http://dx.doi.org/10.1016/0196-8904(93)90009-Y
- Singh, A.K. and Tiwari, G.N. (1992) Performance Study of Double Effect Distillation in a Multiwick Solar Still. Energy Conversion Management, 33, 175-181. http://dx.doi.org/10.1016/0196-8904(92)90127-I
- Sharma, V.B. and Mullick, S.C. (1993) Calculation of Hourly Output of a Solar Still. ASME Journal of Solar Energy Engineering, 118, 1-6.
- Shawaqfeh, A.T. and Farid, M.M. (1995) New Development in the Theory of Heat and Mass Transfer in Solar Stills. Solar Energy, 55, 527-535. http://dx.doi.org/10.1016/0038-092X(95)00069-4
- Mowla, D. and Karimi, G. (1995) Mathematical Modelling of Solar Stills in Iran. Solar Energy Journal, 55, 389-393. http://dx.doi.org/10.1016/0038-092X(95)00041-O
- Tiwari, G.N., Singh, H.N. and Tripathi, R. (2003) Present Status of Solar Distillation. Solar Energy, 75, 367-373. http://dx.doi.org/10.1016/j.solener.2003.07.005
- World Data Bank (2011) World Development Indicators. United States. http://databank.worldbank.org/data/views/reports/tableview.aspx?isshared=true
- World Energy Council (2013) World Energy Resources: Solar. http://www.worldenergy.org/wp-content/uploads/2013/10/WER_2013_8_Solar_revised.pdf
- Modest, F.M. (2003) Radiative Heat Transfer. 2nd Edition, Academic Press, Boston.
- Gearhart, C.A. (2002) Planck, the Quantum and the Historians. Physics in Perspective, 4, 170-215. http://dx.doi.org/10.1007/s00016-002-8363-7
- Duffie, J.A. and Beckman, W.A. (2006) Solar Engineering of Thermal Processes. 3rd Edition, Wiley, Hoboken.
- Garrison, J.D. and Roeder, S.B.W. (1999) Environmental Measurement. In: Webster, J.G., Ed., Measurement, Instrumentation and Sensors Handbook, CRC Press, Boca Raton, pp. 73.1, 1-64.
- Anonymous (2002) Units and Symbols in Solar Energy. Solar Energy, 73, III-V. http://dx.doi.org/10.1016/S0038-092X(02)00081-6
- Aboul-Enein, S., El-Sebaii, A.A. and El-Bialy, E. (1998) Investigation of a Single-Basin Solar Still with Deep Basins. Renewable Energy, 14, 299-305. http://dx.doi.org/10.1016/S0960-1481(98)00081-0
- McAdams, W.H. (1954) Heat Transmission. McGraw-Hill, New York.
- El-Sebaii, A.A. (2000) Effect of Wind Speed on Some Designs of Solar Stills. Energy Conversion and Management, 41, 523-538. http://dx.doi.org/10.1016/S0196-8904(99)00119-3
- Kumar, S. and Tiwari, G.N. (1996) Performance Evaluation of an Active Solar Distillation System. Energy, 21, 805-808. http://dx.doi.org/10.1016/0360-5442(96)00015-1
- Tiwari, G.N., Kumar, S., Sharma, P.B. and Khan, M.E. (1996) Instantaneous Thermal Efficiency of an Active Solar Still. Applied Thermal Energy, 16, 189-192. http://dx.doi.org/10.1016/1359-4311(95)00053-G
- Yadav, Y.P. and Prasad, A.S. (1995) Performance Analysis of a High Temperature Solar Distillation System. Energy Conversion and Management, 36, 365-374. http://dx.doi.org/10.1016/0196-8904(95)98901-X
- Tripathi, R. and Tiwari, G.N. (2005) Effect of Water Depth on Internal Heat and Mass Transfer for Active Solar Distillation. Desalination, 173, 187-200. http://dx.doi.org/10.1016/j.desal.2004.08.032
- Tayel, S.A., El-Nakib, A.A., El-Meseery, A.A. and Badr, M.M. (2009) Solar Energy Utilization in Water Distillation. Misr Journal of Agricultural Engineering, 26, 428-452.
- Badran, O.O. (2007) Experimental Study of the Enhancement Parameters on a Single Slope Solar Still Productivity. Desalination, 209, 136-143. http://dx.doi.org/10.1016/j.desal.2007.04.022
- Keith, F. and Kreider, J.F. (1978) Principles of Solar Engineering. Hemisphere, Washington DC.
- Rahbar, N. and Esfahani, J.A. (2013) Productivity Estimation of a Single-Slope Solar Still: Theoretical and Numerical Analysis. Energy, 49, 289-297. http://dx.doi.org/10.1016/j.energy.2012.10.023
- Khalifa, A.J.N. (2011) On the Effect of Cover Tilt Angle of the Simple Solar Still on Its Productivity in Different Seasons and Latitudes. Energy Conversion and Management, 52, 431-436. http://dx.doi.org/10.1016/j.enconman.2010.07.018
- Baum, V.A. and Bairamov, R. (1964) Heat and Mass Transfer Processes in Solar Stills of Hotbox Type. International Journal of Solar Energy, 8, 78-82. http://dx.doi.org/10.1016/0038-092X(64)90081-7
- Porta-Gándara, M.A., Chargoy, N. and Fernandez-Zayas, J.L. (1997) Extreme Operating Conditions in Shallow Solar Stills. Solar Energy, 61, 465-476.
- Tiwari, G.N., Emran, K.M. and Goyal, R.K. (1998) Experimental Study of Evaporation in Distillation. Desalination, 115, 121-128. http://dx.doi.org/10.1016/S0011-9164(98)00031-9
- Porta-Gándara, M.A., Rubio, E. and Fernandez J.L. (1998) Visualization of Natural Convection inside Shallow Solar Stills. Experiments in Fluids, 25, 369-370. http://dx.doi.org/10.1007/s003480050242
- Zheng, H.F., Zhang, X.Y., Zhang, J. and Wu, Y.Y. (2002) A Group of Improved Heat and Mass Transfer Correlations in Solar Stills. Energy Conversion and Management, 43, 2469-2478. http://dx.doi.org/10.1016/S0196-8904(01)00185-6
- Rubio-Cerda, E., Porta-Gándara, M.A. and Fernandez, J.L. (2000) Cavity Geometry Influence on Mass Flow Rate for Single and Double Slope Solar Stills. Applied Thermal Engineering, 20, 1105-1111. http://dx.doi.org/10.1016/S1359-4311(99)00085-X
- Porta-Gándara, M.A., Cervantes, J.G. and Solorio, F.J. (2004) Periodic Enclosed Natural Convection in a Laboratory Solar Still. Experiments in Fluids, 37, 483-487. http://dx.doi.org/10.1007/s00348-004-0831-1
- Bird, B.R., Edward, W.E. and Lightfoot, E.N. (2007) Transport Phenomena. John Wiley & Sons, New York.
- Lienhard IV, J.H. and Lienhard V, J.H. (2003) A Heat Transfer Textbook. Phlogiston Press, Cambridge.
- Ahsan, A. and Fukuhara, T. (2009) Condensation Mass Transfer in Unsaturated Humid Air inside Tubular Solar Still. Annual Journal of Hydraulic Engineering, 53, 97-102.
- Pong, L. and Moses, G.A. (1986) Vapor Condensation in the Presence of a Noncondensable Gas. Physics of Fluids, 29, 1796-1804. http://dx.doi.org/10.1063/1.865607
- Caruso, G., Di Maio, D.V. and Naviglio, A. (2013) Condensation Heat Transfer Coefficient with Noncondensable Gases inside Near Horizontal Tubes. Desalination, 309, 247-253. http://dx.doi.org/10.1016/j.desal.2012.10.026
- Cussler, E.L. (2007) Diffusion, Mass Transfer in Fluid Systems. Cambridge University Press, New York.
- Watmuff, J.H., Charters, W.W.S. and Proctor, D. (1977) Solar and Wind Induced External Coefficients for Solar Collectors. Revue Internationale d’Heliotechnique, 2, 56.
- Bejan, A. (1998) Advanced Engineering Thermodynamics. Wiley, New York.
- Szargut, J., Morris, D.R. and Steward, F.R. (1988) Exergy Analysis of Thermal, Chemical & Metallurgical Processes. Hemisphere Publishing Corporation, New York.
- Serova, E.N. and Brodianski, V.M. (2004) The Concept “Environment” in Exergy Analysis: Some Special Cases. Energy, 29, 2397-2401. http://dx.doi.org/10.1016/j.energy.2004.03.044
- Pons, M. (2009) On the Reference State for Exergy When Ambient Temperature Fluctuates. International Journal of Thermophysics, 12, 113-121.
- Bosnjakovic, F. (1965) Technical Thermodynamics. Holt, New York.
- Sciubba, E. and Wall, G. (2007) A Brief Commented History of Exergy from the Beginnings to 2004. International Journal of Thermophysics, 10, 1-26.
- Kotas, T.J. (1994) The Exergy Method of Thermal Plant Analysis. Butterworths, London.
- Moran, J.M. (1989) Availability Analysis: A Guide to Efficient Energy Use. ASME Press, New York.
- Petela, R. (1964) Exergy of Radiation. Journal of Heat Transfer, 86, 187-192. http://dx.doi.org/10.1115/1.3687092
- Torchia-Nu?ez, J.C., Porta-Gandara, M.A. and Cervantes-de Gortari, J.G. (2008) Exergy Analysis of a Passive Solar Still. Renewable Energy, 33, 608-616. http://dx.doi.org/10.1016/j.renene.2007.04.001�
Nomenclature
![]() Dimensionless coefficient based on optical properties
Dimensionless coefficient based on optical properties
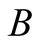 Exergy power (W)
Exergy power (W)
![]() Specific heat capacity (J/mK)
Specific heat capacity (J/mK)
 Diffusivity (m2/s)
Diffusivity (m2/s)
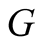 Solar irradiance (W/m2)
Solar irradiance (W/m2)
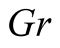 Grashof number
Grashof number
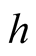 Convection heat transfer coefficient (W/m2K)
Convection heat transfer coefficient (W/m2K)
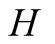 Distance from brine surface to glass cover inside the solar still (m)
Distance from brine surface to glass cover inside the solar still (m)
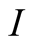 Irreversibility (W/m2)
Irreversibility (W/m2)
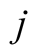 Mass flux per unit of area (kg/m2s)
Mass flux per unit of area (kg/m2s)
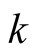 hermal conductivity (W/mK)
hermal conductivity (W/mK)
![]() Mass (kg)
Mass (kg)
 Molecular mass (kg/kmol)
Molecular mass (kg/kmol)
 Nusselt number
Nusselt number
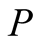 Pressure (kPa)
Pressure (kPa)
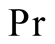 Prandtl number
Prandtl number
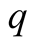 Heat flux (W/m2)
Heat flux (W/m2)
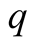 Heat flux (W/m2)
Heat flux (W/m2)
 Universal gas constant (kJ/kmolK)
Universal gas constant (kJ/kmolK)
![]() Temperature (˚C/K)
Temperature (˚C/K)
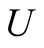 Global heat transfer coefficient (W/m2K)
Global heat transfer coefficient (W/m2K)
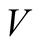 Wind speed (m/s)
Wind speed (m/s)
![]() Thickness (m)
Thickness (m)
![]() Ambient/air within the still
Ambient/air within the still
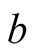 Interior surface of the bottom of the still
Interior surface of the bottom of the still
![]() Forced convective heat transfer from glass cover to surroundings
Forced convective heat transfer from glass cover to surroundings
 Collector (bottom inner part of the still)
Collector (bottom inner part of the still)
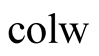 Heat convective transfer from collector to water
Heat convective transfer from collector to water
![]() Free convection
Free convection
![]() Convective heat transfer for water vapor
Convective heat transfer for water vapor
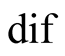 diffusion
diffusion
![]() Evaporation heat transfer
Evaporation heat transfer
![]() Glass cover
Glass cover
 Convective and radiative heat transfer from glass cover to ambient
Convective and radiative heat transfer from glass cover to ambient
 Initial
Initial
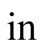 Input
Input
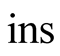 Insulation
Insulation
![]() Maximum
Maximum
 Output
Output
![]() Radiation between glass cover and surroundings
Radiation between glass cover and surroundings
![]() Radiation emission from water to surroundings
Radiation emission from water to surroundings
![]() Solar radiation
Solar radiation
![]() Source
Source
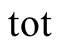 total
total
![]() Water (Brine)
Water (Brine)
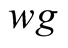 Interaction between brine and glass cover
Interaction between brine and glass cover
Greek Symbols
![]() Absorptance
Absorptance
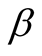 Thermal Expansion coefficient (K−1)
Thermal Expansion coefficient (K−1)
![]() Difference (Operator)
Difference (Operator)
![]() Emissivity
Emissivity
![]() Enthalpy of evaporation
Enthalpy of evaporation
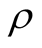 Reflectance
Reflectance
![]() Transmittance
Transmittance
Subscripts
![]() Ambient/air within the still
Ambient/air within the still
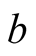 Interior surface of the bottom of the still
Interior surface of the bottom of the still
![]() Forced convective heat transfer from glass cover to surroundings
Forced convective heat transfer from glass cover to surroundings
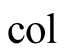 Collector (bottom inner part of the still)
Collector (bottom inner part of the still)
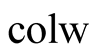 Heat convective transfer from collector to water
Heat convective transfer from collector to water
![]() Free convection
Free convection
![]() Convective heat transfer for water vapor
Convective heat transfer for water vapor
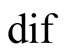 diffusion
diffusion
![]() Evaporation heat transfer
Evaporation heat transfer
![]() Glass cover
Glass cover
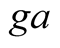 Convective and radiative heat transfer from glass cover to ambient
Convective and radiative heat transfer from glass cover to ambient
 Initial
Initial
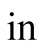 Input
Input
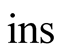 Insulation
Insulation
![]() Maximum
Maximum
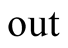 Output
Output
![]() Radiation between glass cover and surroundings
Radiation between glass cover and surroundings
![]() Radiation emission from water to surroundings
Radiation emission from water to surroundings
![]() Solar radiation
Solar radiation
![]() Source
Source
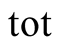 total
total
![]() Water (Brine)
Water (Brine)
 Interaction between brine and glass cover
Interaction between brine and glass cover


