Energy and Power Engineering
Vol. 4 No. 1 (2012) , Article ID: 17047 , 6 pages DOI:10.4236/epe.2012.41004
Reduced Detailed Mechanism for Methane Combustion
1Laboratory of Mechanics, Energetics and Processes, Ecole Nationale Supérieure d’Arts et Métiers, Moulay Ismail University, Meknes, Morocco
2Laboratory of Heat and Mass Transfer, FST of Mohammedia, Hassan II University, Casablanca, Morocco
Email: msaadabdelouahad@yahoo.fr
Received December 2, 2011; revised December 28, 2011; accepted January 10, 2012
Keywords: Detailed Mechanism; Reduced Mechanism; PCAF Method; CSP Algorithm
ABSTRACT
Simulated results from a detailed elementary reaction mechanism for methane-containing species in flames consisting of nitrogen (NOx), C1 or C2 fuels are presented, and compared with reduced mechanism; this mechanism have been constructed with the analysis of the rate sensitivity matrix f (PCAF method), and the computational singular perturbation (CSP). The analysis was performed on solutions of unstrained adiabatic premixed flames with detailed chemical kinetics described by GRI 3.0 for methane including NOx formation. A 9-step reduced mechanism for methane has been constructed which reproduces accurately laminar burning velocities, flame temperatures and mass fraction distributions of major species for the whole flammability range. Many steady-state species are also predicted satisfactorily. This mechanism is especially for lean flames. This mechanism is accurate for a wide range of the equivalence ratio (1, 0.9, 0.8, and 0.7) and for pressures as high as 40 atm to 60 atm. For both fuels, the CSP algorithm automatically pointed to the same steady-state species as those identified by laborious analysis or intuition in the literature and the global reactions were similar to well established previous methane-reduced mechanisms. This implies that the method is very well suited for the study of complex mechanisms for heavy hydrocarbon combustion.
1. Introduction
The primary aim of most recent research in applied and industrial chemistry is to contribute to the protection of the environment. Environmental friendly design and control of chemical processes means that fewer pollutants are produced and fewer by-products are formed. To achieve it, very detailed knowledge of chemical processes is needed. The ultimate level of information is when the process is described by a detailed reaction mechanism. Such reaction mechanisms are available for many important processes and the parameterized temperature and pressure dependence of all rate coefficients. This mechanism is usually utilized in the following three steps. First, the detailed reaction mechanism is created and validated using all available experimental information [1]. The next step should be the analysis of the mechanism and a characterization of the limits of its application. Simulation of a large reaction mechanism might consume too much computer time, when applied for real-time process control or in a computational fluid dynamics (CFD) code that simulates a complex flow field. Therefore, the final step can be the reduction of the reaction mechanism to an almost equivalent smaller computation model [2].
This paper does not deal with the creation of a detailed reaction mechanism, but discusses possible ways for the analysis and reduction of such mechanisms.
The chemical process represented in the reduced mechanism related to the slowest chemical. Inspection of the additional chemical process introduced by increasing the steps in the reduced mechanism will reveal additional features of the flames dynamics.
In this work, we reduced the detailed mechanism of the methane combustion in air by using the PCAF method combined with the CSP algorithm at high pressure 40 atm to 60 atm [3,4]. We consisted to determine and analyses the global reduced mechanism of the methane/air combustion (GRI-3.0) [5].
2. Construction of Global Reduced Mechanisms
Detailed chemistry calculations have been carried out using PREMIX [6,7]. This code was setup to calculate a laminar, freely propagating 1-dimensional adiabatic flame. The code solves transport Equations for the species vector Y and energy E which are given in a transient form below:

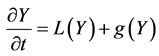 (1)
(1)
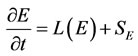 (2)
(2)
The PREMIX solutions are analysed using the CSP-SSTEP code [4,8]. This code indicates the fast and slow modes within the chemical system based on Jacobian analysis and global integrated pointers. A detailed outline of the method can be found in [4]. A short overview is presented here: The conservation Equations for a reacting flow existing of N species and K reactions are given by the same set as for the PREMIX code: part (a) of Equation (1). The left hand side (LHS) is the N dimensional species vector. The right hand side (RHS) of this equation, g is a vector function describing the non-linear chemical kinetics and L is the linear operator for convection and diffusion. The non-linear function g can be written as , in which W is an N × N matrix with the molecular weight of the species divided by the total mass density. S is the stoichiometric matrix that is composed of K stoichiometric vectors Si representing participation of the N species in K reactions. ω is a vector containing the K elementary rates ωi.
, in which W is an N × N matrix with the molecular weight of the species divided by the total mass density. S is the stoichiometric matrix that is composed of K stoichiometric vectors Si representing participation of the N species in K reactions. ω is a vector containing the K elementary rates ωi.
Based on analysis of the Jacobian of each species’ reaction rate and chemical time scales for every grid point of the PREMIX solution from the previous paragraph, it is possible to split the RHS of Equation (1) into a fast domain and slow domain, selecting M slow species and N – M steady-state species:
 (3)
(3)
Looking at Equation (2), the 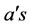 are column basis vectors of respectively N – M and M elements. The fast domain, indicated with subscript r, is driven by the slow domain, subscript s. In other words, the slow domain defines the manifold on which the chemical system moves:
are column basis vectors of respectively N – M and M elements. The fast domain, indicated with subscript r, is driven by the slow domain, subscript s. In other words, the slow domain defines the manifold on which the chemical system moves:
 (4)
(4)
The fast domain is assembled of assumed steady state species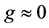 , species which have relatively fast rates and are only present for a fraction of the total domain. In contrast, the slow domain, describing the whole chemical system, is filled with the relatively slow species. The slow species are “rate determining” species in the chemical system.
, species which have relatively fast rates and are only present for a fraction of the total domain. In contrast, the slow domain, describing the whole chemical system, is filled with the relatively slow species. The slow species are “rate determining” species in the chemical system.
3. Reduced Mechanism for Methane
The Algorithm:
The construction of reduced mechanisms by PCAF method and CSP starts with the choice on the desired number of global steps, say S, and follows the steps outlined below [9].
3.1. Identification of Redundant Species
The aim of most kinetic modeling studies is to describe properly the concentration changes of certain species which are considered important. Another objective of a study can be the reproduction of some kinetic features of the reaction, as for instance the maximum concentration of species, the corresponding reaction time, the length of induction period, or the period time of an oscillating reaction.
A consequence of the kinetic law of mass action is that if a species has no consuming reactions, the change of its concentration has no influence on the concentrations of other species. Therefore a species is redundant if the elimination of all of its consuming reactions does not cause significant deviation from the solution of the full model, regarding important species and/or features. This test has to be carried out by investigating each species which is not important. However, a species may be redundant even if the elimination of its consuming reactions causes significant changes. This is the situation, when a species is formed by fast reversible reactions and if the concentration of this species is low and it is therefore not a significant reservoir of mater. If all consuming reactions of this species are eliminated, the concentration of it will increase significantly, maybe causing a simultaneous change of the concentration of important species, hence those species, which were not found to be redundant, have to be reinvestigated by eliminating simultaneously their fast forming and consuming reactions. This second procedure may reveal further redundant species [10,11]. After the elimination of redundant species and all their reactions the mechanism contained 124 irreversible reactions.
3.2. Reference Solution
A numerical solution of the flame structure with a suitable mechanism contained 124 irreversible reactions is obtained, on which the CSP analysis is performed. It is anticipated that the reduced mechanism will be accurate over a range of conditions close to those of the detailed kinetics solution. The exact range of the mechanisms applicability is quantified a posteriori.
3.3. CSP Local Pointers
Given the desired number of global steps, M = N – S steady-state species must be identified, where N is the total number of species in the detailed mechanism. For this purpose, CSP analysis is performed at each point in time providing the CSP pointer of each species i:
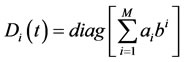 (5)
(5)
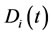 , is a function of time and takes a value between zero and unity. In physical terms, the CSP pointer is a measure of the influence of the M fastest chemical time scales on each of the species. When
, is a function of time and takes a value between zero and unity. In physical terms, the CSP pointer is a measure of the influence of the M fastest chemical time scales on each of the species. When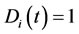 , the ith species are completely influenced by the fastest scales and are the best candidates to be steady-state. In contrast, when
, the ith species are completely influenced by the fastest scales and are the best candidates to be steady-state. In contrast, when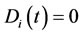 , the fast time scales have no effect on the ith species and cannot be identified as steady-state.
, the fast time scales have no effect on the ith species and cannot be identified as steady-state.
3.4. Intergrated Pointers
The local pointer 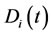 is integrated over the time using the local species net production rate and species mole fraction as a weighting factor, to give
is integrated over the time using the local species net production rate and species mole fraction as a weighting factor, to give
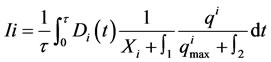 (6)
(6)
where 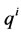 is the net species production rate,
is the net species production rate, 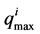 is the corresponding maximum during the time
is the corresponding maximum during the time 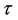 and
and 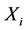 is the species mole fraction and
is the species mole fraction and  and
and  are properly selected small positive numbers used in order to avoid the numerical problems when
are properly selected small positive numbers used in order to avoid the numerical problems when  or
or  equal zero. In contrast to the CSP pointers, the scalars Ii can take any value between zero and infinity. As discussed in Massias [4], the weighting by the mole fraction is consistent with the traditional criterion of taking low-concentration species as the steady-state ones. The quantities Ii for each species are ordered and the N – M species with the lowest values are taken as major (non-steady-state) species. The M species with the largest values are identified as steadystate species.
equal zero. In contrast to the CSP pointers, the scalars Ii can take any value between zero and infinity. As discussed in Massias [4], the weighting by the mole fraction is consistent with the traditional criterion of taking low-concentration species as the steady-state ones. The quantities Ii for each species are ordered and the N – M species with the lowest values are taken as major (non-steady-state) species. The M species with the largest values are identified as steadystate species.
3.5. Fast Reaction Identification
The rate of each elementary reaction is integrated over the time. The reactions which consume the steady-state species (III.4) and exhibit the largest integrated rate are selected and deemed the “fast” reactions (the rest are “slow”). For M steady-state species, M fast reactions are selected.
3.6. Global Reactions
Based on the results of (III.3) and (III.4), the stoichiometry and rates of the global reactions and compiled following [4]. The reduced mechanism consists of the global steps involving the major species and the corresponding global rates, which are expressed as linear combinations of the “slow” elementary rates. The rates depend, of course, on all species, steady-state and nonsteady-state. The former are calculated from the solution of a system of steady-state algebraic relations with the “inner iteration” procedure. In some cases a decoupling of the system of the steady-state algebraic relations is possible and its solution is then straightforward.
According to PCAF and to the CSP algorithm, we obtained the following 9-Step reduced mechanism based on a critical review 325 elementry reaction (GRI-3.0):
1) 
2) 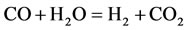
3) 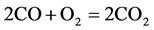
4) 
5) 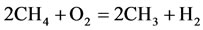
6) 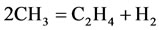
7) 
8) 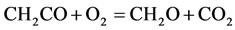
9) 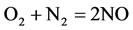
The rate for each reaction in the reduced mechanism is a linear combination of the elementary rates in the detailed mechanism. Note that of the nine steps in the reduced mechanism, the first 1) describe the hydrogen to water, the next two describe the conversions the water and carbon monoxide to the carbon dioxide. Reaction 4) and 5) describes the major fuel breakdown process, in the main zone, to hydrogen, carbon monoxide and methyl. Reactions 6), 7) and 8) describe the methyl to ethyl and ethane conversion, involve C2-chemistry. Reaction 9) describes the thermal NO pathway [12], which is the dominant NO formation path due to the high temperature involved.
4. Results and Discussion
In order to validate the reduced mechanism obtained in the previous sections of this paper, we compare the results obtained with the reduced mechanism (9-Step) to those obtained with the detailed mechanism GRI-3.0. This comparison is done for two different values of the equivalence ratio ( and
and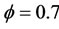 ).
).
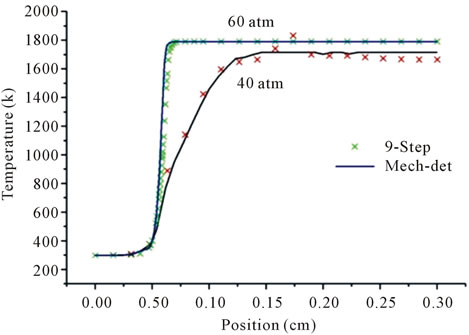
Figure 1 shows the temperature profiles along the flame for different pressures and different richness, Figures 1(a) and (b) at the reaction zone; for the first detailed mechanism GRI-3.0 and the reduced mechanism, the temperature profiles agree well, and the reduced mechanism produces the correct evolution of the temperature.
In this work the reduced mechanism takes into account the formation of the species NOx. In the Figure 2, the concentrations relating to the specie NO across the flame
 (a)
(a)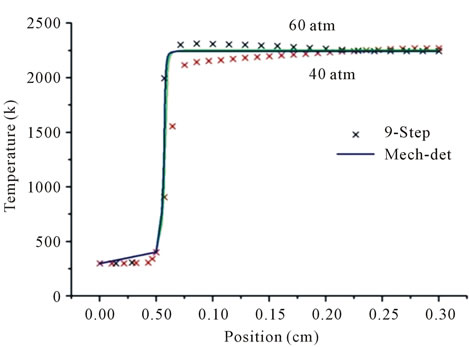 (b)
(b)
Figure 1. Temperature profiles at two pressures 40 atm and 60 atm, resulting from the mechanism GRI-3.0 and 9-Step at richness: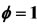 ; (b)
; (b)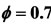 .
.
 (a)
(a) (b)
(b)
Figure 2. Mole fractions of specie NO at two pressures 40 atm and 60 atm, resulting from the mechanism GRI-3.0 and 9-Step at richness: (a)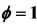 ; (b)
; (b) .
.
obtained with the reduced mechanism are compared with detailed results. According to Figures 2(a) and (b), we can note the existence of initial region of rapid NO growth associated with equilibrium radical concentrations, followed by region of slow growth (mall slope). This difference between the results obtained by reduced mechanism and detailed mechanism explicated by the formation of NO at high temperature. This difference between the two results becomes clearly distinguished in the case of lean flame.
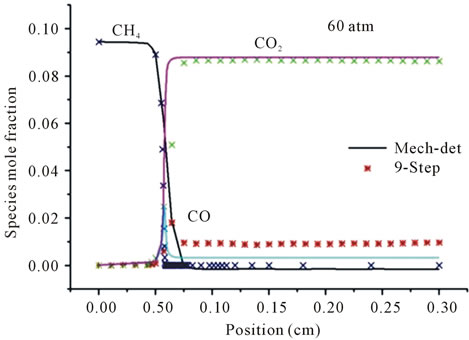
Figure 3 represents the evolution in space of the mole fraction profiles the important species CH4, CO2 and CO for different richness (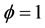 (a) and (b) and
(a) and (b) and 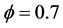 (c) and (d)) at different pressures (40 atm, 60 atm).
(c) and (d)) at different pressures (40 atm, 60 atm).
It is seen that the reduced mechanism produces the correct evolution of the mole fraction the species CH4, CO2 and CO throughout the computational domain with high accuracy of the detailed mechanism for different richness and different pressures.
5. Conclusion
Reduced mechanism for CH4 combustion and NOx are constructed by using PCAF combined with CSP. The analysis was made on solution of adiabatic premixed flames with detailed kinetics mechanism by GRI-3.0. This reduced mechanism involves 9-Step global reaction. A comparative study with the detailed mechanism GRI-3.0 showed that this reduced mechanism reproduces accurately the important parameters of combustion such as flame temperature and mole fraction distributions of major species (CO2, NOx, H2O, H2), intermediate (CH3,
 (a)
(a) (b)
(b) (c)
(c)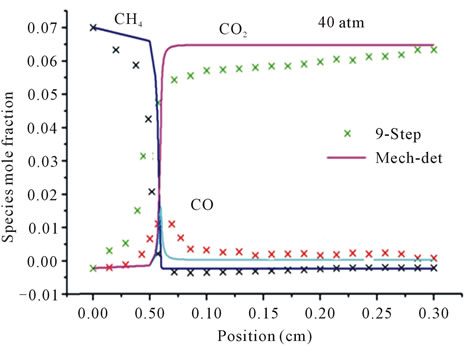 (d)
(d)
Figure 3. Mole fractions of CH4, CO2, CO at two pressures 40 atm and 60 atm, resulting from the mechanism GRI-3.0 and 9-Step at richness: (a) ; (b)
; (b) ; (c)
; (c) ; (d)
; (d) .
.
CH2O, C2H4, C2H6 and CH2CO) and pollutant species such as NO and CO.
REFERENCES
- J. H. Bechtel, R. J. Blint, C. J. Dash and D. A. Weinberger, “Atmospheric Pressure Premixed Hydrocarbon Air Flames,” Theory and Experiment, Combustion and Flames, Vol. 42, No. 2, 1981, pp. 197-213. doi:10.1016/0010-2180(81)90158-9
- T. Lovas, P. Amneus, F. Mauss and E. Mastorakos, “Comparaison of Automatic Reduction Procedures for Ingnition Chemistry,” Proceedings of the Combustion Institute, Vol. 29, No. 7, 2002, pp. 1387-1393. doi:10.1016/S1540-7489(02)80170-5
- T. Turanyi, “Reduction of Large Reaction Mechanisms,” New Journal of Chemistry, Vol. 14, No. 2, 1990, pp. 795- 803.
- A. Massias, D. Diamantis, E. Mastorakos, D. A. Goussis, “An Algorithm for the Construction of Global Reduced Mechanisms with Csp Data,” Combustion and Flame, Vol. 117, No. 1, 1999, pp. 685-708. doi:10.1016/S0010-2180(98)00132-1
- M. Frenklach, H. Wang, M. Goldenberg, G. P. Smith, D. M. Golden, C. T. Bowman, R. K. Hanson, W. C. Gardiner and V. Lissianski, “An Optimized Detailed Chemical Reaction Mechanism for Methane Combustion,” Report No. GRI-95/0058, GRI-Mech, 1995.
- B. de Jager, “Combustion and Noise Phenomena in Turbulent Alkane Flames,” Ph.D. Thesis, University of Twente, Enschede, 2007.
- R. J. Kee, J. F. Grcar, M. D. Smooke and J. A. Miller, “A Fortran Computer Program for Modeling Steady Laminar One-Dimensional Premixed Flames,” Sandia National Laboratories Report, SAND, 1991, pp. 85-8240.
- D. A. Goussis, “On the Construction and Use of Reduced Chemical Kinetic Mechanisms Produced on the Basis of Given Algebraic Relations,” Journal of Computational Physics, Vol. 128, No. 1, 1996, pp. 261-273. doi:10.1006/jcph.1996.0209
- A. Massias, D. Diamantis, E. Mastorakos and D. A. Goussis, “Global Reduced Mechanisms for Methane and Hydrogen Combustion with Nitric Oxide Formation Constructed with CSP Data,” Theory and Modelling, Vol. 3, No. 2, 1999, pp. 233-257. doi:10.1088/1364-7830/3/2/002
- T. Kovacs, I. G. Zsely, A. Kramarics and T. Turanyi, “Kinetic Analysis of Mechanisms of Complex Pyrolytic Reactions,” Journal of Analytical and Applied Pyrolysis, Institute of Chemistry, Vol. 79, 2007, pp. 252-258.
- T. Nagy and T. Turányi, “Reduction of Very Large Reaction Mechanisms Using Methods Based on Simulation Error Minimization,” Combustion and Flame, Vol. 156, No. 3, 2009, pp. 417-428. doi:10.1016/j.combustflame.2008.11.001
- T. Turanyi, T. Berces and S. Vajda, “Reaction Rate Analysis of Complex Kinetic Systems,” International Journal of Chemical Kinetics, Vol. 21, No. 1, 1989, pp. 83-99. doi:10.1002/kin.550210203
Appendix
Figures 3(a) and (b) describe the evolution the mole fraction of species CH4, CO2 and CO at richness , and pressure 40 atm and 60 atm. Resulting from the detailed mechanism GRI-3.0 and reduced mechanism 9-Step obtained by the method CSP.
, and pressure 40 atm and 60 atm. Resulting from the detailed mechanism GRI-3.0 and reduced mechanism 9-Step obtained by the method CSP.
Figures 3(c) and (d) describe the evolution the mole fraction of species CH4, CO2 and CO at richness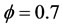 , and pressure 40 atm and 60 atm. Resulting from the detailed mechanism GRI-3.0 and reduced mechanism 9-Step obtained by the method CSP.
, and pressure 40 atm and 60 atm. Resulting from the detailed mechanism GRI-3.0 and reduced mechanism 9-Step obtained by the method CSP.

