Communications and Network
Vol.06 No.04(2014), Article ID:51469,14 pages
10.4236/cn.2014.64025
Development of Global Geographical Coverage Area for Terrestrial Networks Internetworked with Leo Satellite Network
V. O. C. Eke1, A. N. Nzeako2
1Department of computer Science, Ebonyi State University, Abakaliki, Nigeria
2Department of Electronic Engineering, UNN, Enugu State, Nigeria
Email: veke39@yahoo.com, annzeako2005@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 September 2014; revised 20 October 2014; accepted 30 October 2014
ABSTRACT
Network planning, analysis and design are an iterative process aimed at ensuring that a new net- work service meets the needs of subscribers and operators. During the initial start-up phase, cov- erage is the big issue and coverage in telecommunications systems is related to the service area where a bare minimum access in the wireless network is possible. In order to guarantee visibility of at least one satellite above a certain satellite elevation, more satellites are required in the con- stellation to provide Global network services. Hence, the aim of this paper is to develop wide area network coverage for sparsely distributed earth stations in the world. A hybrid geometrical to- pology model using spherical co-ordinate framework was devised to provide wide area network coverage for sparsely distributed earth stations in the world. This topology model ensures Global satellite continuous network coverage for terrestrial networks. A computation of path lengths between any two satellites put in place to provide network services to selected cities in the world was carried out. A consideration of a suitable routing decision mechanism, routing protocols and algorithms were considered in the work while the shortest paths as well as the alternate paths between located nodes were computed. It was observed that a particular satellite with the central angle of 27˚ can provide services into the diameter of the instantaneous coverage distance of 4081.3 Km which is typical of wide area network coverage. This implies that link-state database routing scheme can be applied, continuous global geographical coverage with minimum span, mi- nimum traffic pattern and latency are guaranteed. Traffic handover rerouting strategies need fur- ther research. Also, traffic engineering resources such as channel capacity and bandwidth utiliza- tion schemes need to be investigated. Satellite ATM network architecture will benefit and needs further study.
Keywords:
Network Planning, Global Network Coverage, Visibility Angle, Link-State Database, Orthogonal Route Path, Dijkstra’s Algorithm

1. Introduction
Network planning, Analysis and Design is an iterative process encompassing topological design, network syn- theses and network realization. It is aimed at ensuring that a new network or service meets the needs of sub- scribers and operators [1] . Network planning is done before the establishment of a telecommunication network or service. It has been noted in [2] that during the initial start-up phase of telecommunications systems, coverage is the big issue and traffic demand is minimal to a small network which will require expansion later. [3] states that coverage in telecommunications systems is related to the service area where a bare minimum access in the wireless network is possible. When determining the coverage of a system, both system capacities for handling traffic and radio coverage must be considered. Some areas of the system may need radio ports for capacity while some may need application points (or base stations) for coverage. Also [3] identified mobility and coverage as requirements in the digital cellular networks. It was further stated that in voice and low data networks, compre- hensive coverage and mobility are the dormant design parameters while in WLANS and point-to-point fixed wireless communications, coverage and mobility are restricted. The modeling framework for cellular/PCS net- works can be divided into mobility model, topology model and call model [2] . In line with the above, simple mathematical mobility models were developed in [4] for configuring a Global Network Interconnectivity with LEO satellites. A successful development of the one dimensional satellite mobility models were presented as well as the performance evaluation of the satellite mobility models regarding optimum, global terrestrial net- work coverage, time of geographical earth coverage and coverage angle parameters. Mathematical simulations of their parameters were carried out and it was found that the instantaneous coverage arc lengths were exponen- tially varying with time and continuously distributed within the four zones (quadrants) around one polar orbit. If a contiguous, real-time connection is required between LEO satellites, a system constellation of satellites will be needed.
In this paper, therefore, we extend the idea of one satellite system to the idea of a constellation of satellites in two dimensions. Hence, we aim is to design and develop a geometrical topology model to determine to network coverage of an area. In Section 2, we develop a LEO satellite geometrical constellation network model. In Sec- tion 3, we present a global terrestrial coverage model. In Section 4, we present the implementation of the global network model internetworking LEO satellite network with the terrestrial networks. In Section 5, we conclude with recommendations for future work.
2. Design of the Leo Satellites Geometrical Constellation Network Model
The integration of LEO satellites with the ground-based internet gateway and connection-oriented circuit-switch- ed telephony service also means that the end-to-end system connectivity will be provided transparently using the satellite infrastructures. LEO satellite networks are planned in large constellations to cover large portions of the earth, mainly targeted isolated mobile terminals where ground infrastructure is missing or temporarily unavaila- ble with different geometries [5] as discussed below.
2.1. Types of Satellite Constellations
Two main types of satellite constellations are stated in the literature: 1) walker delta (or Ballard Rosette) con- stellations and 2) Walker star constellations. The Rosette constellation covers a large band around the equator. A ground station is in the footprint of several satellites whose orbital planes overlap several times. The Earth sta- tion traces a sinusoidal shaped orbital track on the flattened surface of the Globe [6] . In contrast, a walker “Star” or polar constellations uses a number of orbits all crossing the polar region. These result to equally distributed orbital planes crossing at the earth’s poles. Several equally distanced Satellites move along the earth orbit path at the same speed. This guarantees that each point on the earth is within a footprint of a satellite at any given time, for example, Iridium [7] and Teledesic, [8] projects.
Irridium is a LEO satellite network, where connection oriented circuit-switched telephony service, and dial-up through satellite to ground Internet-gateway are offered on any spot on the earth. Irridium [9] uses polar orbits and 66 satellites forming a planned grid that covers the whole earth surface. It uses this variation of the Manhat- tan Network topology where satellites can rotate around the earth with equi-distance spacing between each two satellites on the same plane. In comparison, Teledesic, a connectionless network of satellites was initially plan- ned with 840 LEO satellites [10] , scaled down to 288 LEO satellites [9] before being scrapped off the drawing board in October, 2002 14 [11] . Teledesic can provide seamless compatibility with terrestrial broadband (fibre) networks. This network uses fast packet switching technology based on Asynchronous Transfer Mode (ATM) developments [9] .
Two types of intersatellite links (ISLs) are often witnessed: Intra-plane ISLs, the ISLs between satellites on one orbital plane, and the interplane ISLs, the links between satellites on different planes. Both ISLs enable the communication between two users in different footprints with not more than two ground gateways being neces- sary. The interplane ISLs are permanently switched because of the fast change in relative positions of the satel- lite to each other. With the introduction of the advances in smart and adaptive radio [12] , more possibilities for complex meshed ad hoc connectivity between any groups of satellites could be offered.
2.2. Satellite Constellation Design Considerations
It was noted in [13] that for a system designer to develop a LEO satellite constellation that provides continuous global coverage, the following design considerations are required: length of coverage arc on the surface of the earth within an instantaneous earth system; the number of satellites needed to complete a global satellite system; and the gain of the satellite antenna. The following additional requirements were also identified [13] : whether or not to use ISLs, whether to design to operate across the system if ISLs are used selecting an orbital height, number of satellites visible at any instant coverage region, etc. All these requirements interact in the overall sys- tem.
Four important factors that influence the design of any satellite communication system has also been identi- fied in [13] : incremental growth, interim operations (satellite) replenishment options, and end-to-end system im- plementation. Most of the Medium Earth Orbit (MEO) and LEO system operators developed interim operations plans where a reduced number of satellites could provide useful service. The technical planning for interim op- erations includes: relaxing the number of satellites visible to any user at any particular time which lowers the number of satellites required to complete the constellation. The elevation angle minimum for users is usually lowered, the gaps between operational satellites in the same plane are made symmetrical, and the orbits adjusted if possible to maximize coverage over those parts of the day when user service requests are highest. Most LEO constellations have at least four satellites per plane and multiple spacecraft launches are used in the constellation buildup.
Also, the design of a Non-Geosynchronous Satellite orbit system will be heavily influenced by the decision on whether or not to provide services directly to end-users (i.e. end-to-end system implementation). It will also be impacted by the decision on whether or not to include established telephone companies in the delivery of the service. By their very nature, mobile satellite systems have committed to serve the end user directly. However, dif- ferent approaches have been taken with regard to including established telephone companies. Two examples of organizations that took opposite decisions are the Global Star and Irridium. Global Star elected not to bypass the existing telephone companies while Irridium did. These decisions led to a very different architecture for the two systems.
2.3. Theoretical Design of the Leo Satellite Architecture
In this sub-section, we consider the geometrical aspect of developing satellite constellation network model. First of all, we review the analysis of the motion of a satellite body of mass, m, which is at a height, h, above the earth and is revolving round the earth in a circle of radius, rs, as given in [4] [13] and represented here for emphasis as shown in Figure 1.
Using the sine rule to triangle, SEC, we have that
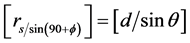
Figure 1. Geometry for calculating coverage area.
which yields
 (1)
(1)
where 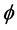 is the elevation angle, rs is the vector from the centre of the earth to the satellite,
is the elevation angle, rs is the vector from the centre of the earth to the satellite, 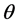 is the central an- gle measured between the rs and re, the radius of the earth, is the angle between the earth station, E and the satel- lite, S; d is the vector from the earth station to the satellite.
is the central an- gle measured between the rs and re, the radius of the earth, is the angle between the earth station, E and the satel- lite, S; d is the vector from the earth station to the satellite.
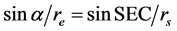 (2)
(2)
But angle 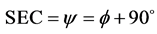
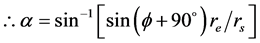 (3)
(3)
where  the angle between two neighbouring satellites of the same orbit,
the angle between two neighbouring satellites of the same orbit, 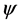 is the angle measured from rc to d.
is the angle measured from rc to d.
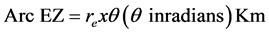 (4)
(4)
The diameter of the instantaneous coverage region is given by:
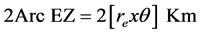 (5)
(5)
And the coverage angle at the centre of the earth is given by:
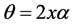 (6)
(6)
The angular displacement, 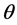 in radians can be given in terms of arc length, l which it subtends on a circular radius, rs by [14] .
in radians can be given in terms of arc length, l which it subtends on a circular radius, rs by [14] .
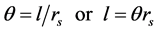 (7)
(7)
where l is the circumferential distance, a satellite body on the circle of rotation has moved (or would roll without slipping) if free to do so. This is Newton’s Law of circular motion.
We extend the above analysis to an idea of a LEO satellite constellation thus:
1) To establish whether a particular satellite location can provide service into a given region, a simple visibil- ity test can be carried out as shown in [13] .
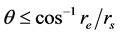 (8)
(8)
This means that the maximum central angular separation between the earth station and sub-satellite point is limited by this value. The central angle 
2) The distance, d, will determine the free space path loss along the propagation path and will be a factor in the link budget design. This is given by:

where rs, re, 
3) The elevation angle 
4) The number of satellites required in one polar orbit. The decision on whether or not to use ISLs, whether to design to operate across the system if ISLs are used, is usually imparted by the number of satellites required to complete one plane with a suitable overlap. The satellites in a plane are separated from each other with an angu- lar distance given by:
5) 
where Ns is the number of satellites required to complete one plane with a suitable overlap. Since the planes are circular, the radii of the satellites in the same plane are the same at all times and so are the distances from each other.
The length Lv of all intra-plane ISLs is fixed and is computed by [15] .

where R is the radius of the plane.
6) Number of planes, M, for complete full global coverage. The Satellite Network is composed of M separate orbits (planes), each with Ns satellites at low distances from the earth. It has been observed that one plane of the satellites, if in the polar orbit, will have satellites on both hemispheres of the earth, some going Northwards (or Eastwards) and some going southwards (or Westwards). Hence, it will be technically necessary to have M planes equal to half of the number of the satellites per plane, Ns That is,

The planes are separated from each other with the angular distance given by:

The length Lh of the inter-plane ISLs is variable and is calculated by [16] .

where
With lat as the latitude at which the iner-plane ISL resides (see Figure 4).
7) Total number of satellites for a global network coverage. Using the same logic as in (10) and (12) above, there will be Ns slots (or slices) around the equator made up of Mp planes of satellites. Therefore, the total mini- mum number of satellites needed for complete global network coverage is given by:

2.4. Computations of the Parameter Values
In this sub-section, we compute the values of the above parameters as follows:
1) Satellite visibility value: This is given in (8) by:
Given:


But we do know that

2) The central angle
We need to find out the central angle, 
where

3) The diameter of the instantaneous coverage
The value 

We now have a situation set-up as shown in Figure 2.
4) The number of satellites required to complete one complete plane with suitable overlap is computed from (10) given by:
5) The number of planes for complete full global coverage is computed from (12) as shown below:
6) The total number, NT of the satellites for the full continuous global satellite network is given by (15) above, i.e.,
2.5. Proposed Satellite Network Topology Model
The choice of the constellation model influences the other aspects of the network architecture such as the topol- ogy organization and routing scheme [9] . Theoretically, our derived satellite network constellation model has shown to comprise 200 satellites with 20 satellites in 10 planes. However, we propose a situation in which the
Figure 2. Geometrical set-up for instantaneous coverage Arc ED.
number of satellites in a constellation at any particular time is relaxed to 8 satellites in 4 planes which will in turn relax a total number of satellites to 32 satellites. This configuration can be arranged in 4 × 4 matrix struc- ture.
We propose a hybrid topology model in [14] to implement our scaled down satellite constellation design as shown in Figure 3 below.
If we consider the hybrid topology model network shown in Figure 3 above, we can see that there exists more than one shortest path from the source, S, to the destination, D. we call all the nodes in the rectangle, where the source is a corner and the destination is the other on the diagonal, a routing set. If there are K-routing sets, we call it K-set, where K is the number of paths between source and destination. All the directions toward the des- tination are located on the shortest path from the source to the destination.
All possible paths are shown in the hybrid mesh topology. And all of the paths using any one of the links with the specified directions are equal and are shortest paths. Also, all the paths using these directions are loop free. Thus, the routing problem for a satellite system becomes the “shortest paths” discovery problem. However, since the network is spherical and there exists many routing set between the source (S) and the destination (D) and most of them pass through the polar region on through the horizontal plane a virtual network has to be con- sidered while finding the right routing set [17] .
The above analysis is fundamental to the determination of the Global Network that covers an earth geographi- cal Network service area if internetworked with the Space Network derived in Sub-Section 2.4 and 2.5 respec- tively.
3. Continuous Global Earth Network Coverage Area
In this section, we intend to develop a continuous global Earth Network Coverage area suitable for a Wide Area Network (WAN). Just as Local Area Network (LAN) provides internal connectivity to a small geographic area, and a Metropolitan Area Network (MAN) extends intermediate coverage to a wider area, wide area networks provide wider area coverage and they go beyond the boundaries of cities and extend globally. The extreme of the WAN is the Global Network. First of all, we model the positions of a location on the earth using the spheri- cal co-ordinates framework in 3.1. Next we compute the distances between the selected locations (cities) in the world.
3.1. Global Earth Coverage Model
We model the position of a satellite location on the earth using the spherical co-ordinate framework where the
Figure 3. 4 × 4 hybrid topology model.
position of a point is considered as being a point in a sphere as depicted in Figure 4 below.
The latitude of a place is measured in degrees North or South of the equator. The latitude of a place lies be- tween 90˚ North or 90˚ South of the equator.
Let G be a position on the earth’s surface as shown in Figure 4 above. We measure the latitude of G as fol- lows:
Let the line NGBS through G be the meridian.


EGHI = the parallel of latitude through G and H
In



Or

Similarly, the longitude of a place is measured in degrees East and West of the Greenwich meridian and it lies between East and West of the Greenwich meridian.
Let H be a position on the earth’s surface as shown in Figure 4 above. The longitude of a position H on the earth’s surface is measured as follows:
Let the Greenwich meridian NGBS
Intersect the parallel of latitude EGHI at G. Let the meridian NHCS through H intersect the equator, ABCD at C and intersect the parallel of latitude EGHI at H.
The angle 
Let H be the position on the earth’s surface of the equator as shown in Figure 4 above. We measure the lon- gitude H as follows:
Let NHCS through H be the meridian;



Hence, by resolution of vectors, the total displacement between location H, G and B respectively is given by:

In general, therefore, the total distance along any parallel of latitude North or South of the equator and then meridian (or Greenwich meridian) East or West of the equator is given by the sum of the arc lengths travelled in x and y directions respectively. This implies two dimensional mobility model.
Figure 4. Spherical earth co-ordinates frame-work.
3.2. Computation of the Routes (Distances) between Locations (Cities) in the World
Suppose we plan to develop a Widea Area Network coverage area for a LEO satellite constellation network de- veloped in Section 2. We arbitrarily select eight satellite locations to represent points of Network access for the Widea Area Network (WAN). We select two satellite locations in each quadrant of the earth surface to cover the whole globe as shown in Table 1 below:
Using Equations (17) to (20) derived in Sub-Section 3.1, we then can compute the total distances travelled between the selected cities in the world as shown in Table 2 below.
4. Determination of the Continuous Global Earth Geographical Network Coverage Area
For widely dispersed users, long paths exist that connect the various parts. Generally, a user at one location will send the desired message to a network entry point. We think of this wide area network as a cloud. That is, we do not know what is going on inside but we know that there are ways to get the messages from here to there either through 3 types of networking technologies [13] : Circuit switching, message switching, and packet switching. The network will determine how the messages pass through all the paths based on the protocol and list of trans- port. The end to end transport of data packets is achieved by routing the data packets through series of data links across the network. This routing decision is taken by the Network layer of the Nodes. The mechanisms deployed for the transport can be connection-oriented or connectionless.
Routing protocols could be divided into [13] static and dynamic routing. Static routing is used in simple net- works that lack redundancy while in dynamic routing the forwarding tables are continuously updated with the information received from other routers. The routers exchange this information using a routing protocol.
Table 1. Satellite locations in each quadrant of the earth surface.
Table 2. Total distances travelled between the selected cities in the world.
Also, the routing protocols are based on one of the following two algorithms namely: Distance vector and link state algorithms. The underlying concepts of distance vectors, link state routing, Dijkstra’s algorithm for the shortest path precede the discussion on any specific routing protocol. Hence, we first discuss the basics of link state routing in Sub-Section 4.1, then proceed to discuss the Dijkstra’s algorithm in 4.2 and finally, demonstrate the application of Dijkstra’s algorithm in the determination of the continuous global earth geographical network coverage area in 4.3.
4.1. Link-State Routing: Basic Operation
Distance vector routing does not work well if there are changes in the internetwork. When two or more networks are interconnected, we refer to such extended network as interwork. The reasons why this routing algorithm does not work well are for the facts that the distance vectors sent to the neighbours do not contain enough in- formation about the topology of the internetwork. That is, every router tell its neighbours its distances to all the networks without knowing the Network topology. No wonder why it was stated in [18] that topology has noth- ing to do with Geographical Coverage. This results to misleading conclusions as can be seen with the count to- infinity problem which could cause congestion for every other routers. However, link state algorithm overcomes this problem because with link state algorithm, every router tells every other router the information it truthfully knows about its neighbours and distances to them. Every router works out from this information: the network topology and the optimal paths.
In a link state routing, every router maintains a database of Network topology. The database contains records of the links of the entire network. Each record consists of source router identification, its neighbouring router identifiers, and the costs associated with the link between them. Each record is called link state. The cost can be defined in terms of distance, hop, delay, inverse of bandwidth or any other parameters [19] .
Identical database is available in all the routers. The database is refreshed at fixed intervals (30 minutes in open shortest path First). For refreshing the database, every router sends updates called link state advertisements [LSAs].
If there is a change in the neighbourhood (e.g. a link/router goes down or a new router is added), LSAs are sent immediately by the routers that detect the change. They do not wait for the regular schedule of advertise- ments for refreshing the records of the database. LSAs are sent using controlled flooding across the internet so that every router receives them.
Each router works out the shortest paths to every other router using the database and the Dijkstra’s algorithm, once the shortest paths are known, the forwarding table can be constructed readily.
An advantage of link-state routing is the availability of alternate paths. If a link goes down, a router can rea- dily work out alternative path from its topology database.
4.2. Dijkstra’s Algorithm
Dijkstra’s algorithm computes the shortest paths from a Node (called the root) to all other nodes from the link- state debatable. The root-node selects one of its neighbours having the least cost. The link costs of neighbours of these two nodes are examined. One of the neighbours having the least cost to the root is selected again. The pro- cess is repeated, and each time a neighbor with the least cost of the root is selected and added to the set of nodes whose link costs have been computed.
4.3. Implementation of the Dijkstra’s Algorithm
To understand the algorithm, let us consider a simple graph consisting of the nodes A, B, C…H that represents the eight cities and the link costs between any pair of interconnected nodes. See Table 3 that shows the link costs associated with each link of the graph shown in Figure 5.
We will first of all define the followings:
Root: The node from which the least cost paths are being determined.
Set (S): Set of those nodes whose least cost paths to the root have been determine.
Set (N): Set of neighbours of set S.
I
We note that since we are to determine the forwarding Table 4 of node A, A is the root. We will use
Figure 5. A graph of interconnected cities with the link costs associated with each link.
Table 3. The link costs associated with each link of Figure 5.
Table 4. Least cost path determination using Dijkstra’s algorithm.
Dijkstra’s algorithm to determine the least paths from A to the rest of the nodes. Table 4 shows the steps of the Dijkstra’s algorithm applied to A as the root.
With Step 8, all the least cost paths to the root A have been determined. Figure 6 shown illustrates the result- ing tree.
4.4. Results and Discussion
It has been stated that an advantage of link state routing is the availability of alternate paths [20] . If a link goes down, a router can easily work out alternate path from its topology database. The Dijkstra’s algorithm computes the shortest paths from a node (called root) to all other nodes from the link state database. An illustration of some city (node) to city (code) distances and their alternate paths are shown in Table 5.
Table 5 shows that:
1) The route from Los Angeles (A) to Churchill (B) (i.e. A ® B) is 1254 km with two other alternate routes: A ® D ® B is 11,928; and A ® C ® D ® B is 16,779 km.
Figure 6. The resulting tree of the Dijkstra’s algorithm applied to A as the root.
Table 5. An illustration of some city (node) to city (code) distances and their alternate paths.
2) The route from Los Angeles (A) to Marcus D (i.e. A ® D) is 5095 km with two other alternate routes: A ® B ® D is 7095 km while route A ® C ® D is 9938 km.
3) The route from Los Angeles (A) to Falkland (C) is 2914 km with other two alternate routes: A ® D ® C is 12,111 km and A ® B ® D ® C is 15,119 km.
4) The route from Los Angeles (A) to Onitsha (E) (i.e. A ® B ® E is 5440 km with five other alternate routes: A ® C ® E is 6799 km, A ® D ® E is 11,413 km, A ® B ® D ® E is 14,421 km, A ® C ® D ® E is 16,264, while A ® C ® F ® E is 16,500 km.
5) The route from Los Angeles (A) to Port Elizabeth (F) (i.e. A ® C ® F is 9168 km with other five alternate routes: A ® B ® E ® F is 12,772 km, A ® C ® E ® F is14,131 Km; A ® D ® E ® F is 18,745 Km; A ® B ® D ® E ® F is 207,753 km while A ® C ® D ® E ® F is 23,596 Km.
6) The route from Los Angeles (A) to Nagasaki (G), A ® C ® F ® G, is 11,091 km with four other alternate routes: A ® B ® E ® G is 11,243 km, A ® B ® E ® F is 14,695 km, A ® C ® E ® F ® G is 16,054 km, A ® B ® D ® E ® F ® G is 22,676.
7) The route from Los Angeles, A to New Plymouth, H (i.e. A ® C ® H) is 9563 km with two other alternate routes: A ® B ® E ® G ® H is 14,818 km while A ® C ® F ® H is 17,590 km.
At times, we want to deviate from the shortest path strategy because the shortest path may not have enough capacity to carry the entire traffic due to its bandwidth limitations. Traffic engineering allows us to provision more traffic flows along the desired path which may not be the shortest path.
· Basic traffic engineering depends on coverage. When determining the coverage of a system both system ca- pacity for handling traffic and coverage must be considered. Hence, based on Equation (5) and (8) derived above, it has been shown that a particular satellite location provides service into a given instantaneous cov- erage region of 4081.3 km with a visibility angle of 37.32˚, and total instantaneous coverage angle of 2δ = 122.68˚ (i.e. 2 × 61.34˚). Hence, the concept of phased array antenna can be used on our satellite system to divide up among a set of receive antennas that provide 360˚ coverage, as in the sectored antenna approach of cellular systems [13] .
· The implication of the instantaneous coverage distance range of 4081 km is that satellites must handover their connections to the earth stations at about this distance. The handover procedure requires a state transfer from one satellite to the next, and will result in a change in the delay characteristics of the connections at least for a short time interval. Considering that the orbital period of a satellite is 100.5 minutes [4] and that an orbit is made of eight satellites (see Figure 3), we then obtain a coverage time for a satellite (the amount of time a fixed point on earth is covered by a satellite) of around 12.6 minutes. This time duration is also the maximum time before a handover to the next satellite on the same orbit (called south handover). Since there are four polar orbits, the time between two handovers to the next Eastern orbit (called East handover) is three hours.
· Also, two commonly used routing efficiency are channel traffic and communication latency. The channel traffic at any time instant (or during any time period) is indicated by the longest path transmission time in- volved. For instance, the route from Los Angeles (A) to New Plymouth (H) has an optimal route A ® C ® H that is 9563 km with two other alternate routes: A ® B ® E ® G ® H that is 14,818 km and A ® C ® F ® H that is 17,590 km. In traffic engineering, the shortest path may not have the required capacity to carry the entire traffic due to its bandwidth limitation; we therefore, choose the longest path transmission that has much more latency. An optimally routed network should achieve both minimum traffic and minimum latency for the communication pattern [20] .
· The concept of virtual networks leads to the network partitions of a given physical network into logical sub- networks for multicast communication. Considering the results of the computed total distances travelled be- tween the selected cities in the world as tabulated in Table 2, one can observe that the pattern divided the Global geographical network coverage area into two sub-networks. The system has the form of Lower tri- angular and upper triangular matrix (8 × 8). The two forms have North-West direction flow of data traffic and South-East direction flow of data traffic. It is also observable that the strictly diagonally travelled path is prohibited as seen by dash values along the line. This is confirmed in Figure 6 as there is no direct route from Los Angeles to New Plymouth. However, short immediate diagonal paths may be allowed. For instance, the route from the source A (Los Angeles) to destination H (New Plymouth) i.e. A ® B ® D ® E ® F ® G ® H is 27,269 km travelled in six hops (links).
But if we consider the orthogonal paths taken between the same source A and destination H, we would have a route from A (Los Angeles) vertically to C (Falkland) and horizontally to the destination H (New Plymouth) giving a total distance of 9563 km in 2 hops (links).
· Equally observable is the minimum span global geographical coverage area as shown in Figure 6. There ex- ist four shortest routes: A ® D, A ® B ® E, A ® C ® F ® G and A ® C ® H that guarantees continuous global geographical earth coverage area. The coverage area spans from A (Los Angeles) to B (Churchill) in the second quadrant of the Earth to C (Falkland) and D (Marcus) in the third quadrant to E (Onitsha) and G (Nagasaki); and then to F (Port Elizabeth) and H (New Plymouth) in the fourth quadrant.
5. Conclusion and Recommendation
An in-depth study for the development of the continuous global geographical coverage are for interworking LEO satellite network and terrestrial networks has been presented in this paper. First, a successful design of the LEO satellite geometric network connectivity is presented, and the analysis and computation of the LEO satel- lite system parameters were evaluated in terms of the satellite visibility, central angle, diameter of the instanta- neous coverage area, number of satellites required to complete plane with suitable overlap, number of planes for complete global coverage as well as the total number of satellites for the full continuous global satellite network through mathematical simulations. The values informed our choice of a hybrid mesh network model that has been configured to a 4 × 4 matrix structure and was implemented with a shortest path routing. Next, analytical equations were developed for computing point-to-point distances between nodes (cities) that were located under the satellite footprints. Eight cities, two in each quadrant were chosen to represent the point-to-pint network ac- cess points for the wide area network coverage of the satellite locations. A discussion of the Dijkstra’s algorithm and its application in the determination of the continuous global earth geographical network coverage area is presented through mathemtical simulation resulting in high but tolerable distance range of 4081 km as well as coverage time delays for a link state database routing scheme. We believe that this link state database routing scheme can smooth very effectively this result as well provide alternate paths with the longest paths that have required capacity and hence enough bandwidth to carry the traffic where traffic congestion (or router failures) exists.
In conclusion, therefore, we have developed an integrated terrestrial/space system that can be implemented with a link state database routing scheme. This scheme is capable of guaranteeing continuous global geographi- cal coverage area with minimum span whereby orthogonal set of paths taken from any source to destination will achieve both minimum traffic pattern and latency. Handover research and re-routing strategies should need fur- ther research. Traffic engineering resources such as channel capacity and bandwidth utilization schemes need to be investigated. Network architecture for implementing the interworking of LEO satellite ATM network and terrestrial networks also needs further research.
References
- Penttinen, A. (1999) Chapter 10-Network Planning and Dimensioing, Lecture Note: S-38, 145-Introduction to Tele- Traffic Theory. University of Technology, Helsink. Sourced at Network Planning and Technology and Design-Wil- kepedia, The Free encyclopedia, 11/12012.
- Garg, V.K. and Wilkes, J.E. (1999) Principles and Applications of GSM. Pearson Education, Inc., India, 294.
- Pahlavan, K. andKrishnamurthy, P. (2003) Principles of Wireless Network—A Unified Approach. Pearson Education Inc. (Singapore), India, 108, 549.
- Eke Vincent, O.C. and Nzeako, A.N. (2013) An Analysis and Computation of Optimum Earth Geographical Coverage for Global Communications. Journal of Communications and Network, 5, 337-343.
- Lo, M.W. (1999) Satellite Constellation Design. Computer Science Engineering, 1, 58-67.
- Wood, L. (2003) Satellite Constellation Networks, Chapter 2 of Internetworking and Computing over Satellite Net- works’ by Zhang. 13-34.
- Irridium (2014). http://www.irridium.com
- Wood, L., Clerget, A., Andri Kopoulos, I., Palvlou, G. and Dabbous, W. (2000) Internet Protocol (IP) Routing Issues in Satellite Constellation Networks. International Journal of Satellite Communications, 18.
- Houyou, A.M., Holzer, R., De Meer, H. and Heindl, M. (2005) Performance of Transport Layer Protocols in LEO Pico- Satellite Constellations. Technical Report MIP-0502.
- Sturza, M.A. The Teledesic Satellite System: Overview and Design Trades.
- Wood, L. (2014) Teledesic News and Information-Maintained. http://www.ee.survey.ac.uk/personal/L.Wood/constellation/teledesic.ht
- Pavlidou, F.N., Annoni, M., Aracil, J., Cruickshank, H., Franck, L., Ors, T. and Papapetrou, E. (1999) Traffic Charac- terization, Routing, and Security Issues in High Speed Networks Interconnected through Low Earth Orbit (LEO) Con- stellations. Joint Workshop COST255/252/253, Touloues.
- Pratt, T., Bostian, C. and Allnut, J. (2003) Satellite Communicaions. 2nd Edition, John Willey and Sons Inc., New York.
- Paxson, V. (1999) End-to-End Internet Packet Dynamics. IEEE/ACM Transactions on Networking, 7, 277-292. http://dx.doi.org/10.1109/90.779192
- Dobosiewicz, W. and Gburzynki, P. (1996) A Bounded-Hop-Count Deflection Scheme for Manhattan Street Network. Proceedings of Institute of Electrical and Electronics Engineering (IEEE), Computer Communications, Vol. 1, 172- 179.
- Ekici, E., Akyildiz, I.F. and Benden, M.D. (2000) Datagram Routing Algorithm for LEO Satellite Networks. Institute of Electrical and Electronics Engineering (IEEE) Information and Communication (INFOCOM).
- Kucukates, R. and Ersoy, C. (2003) High Performance Routing in a LEO Satellite Network. Proceeding of the IEEE ISCC, Antalya, 1403-1408.
- Carr, H.H. and Snynder, C.A. (2003) The Management of Telecommunications. 2nd Edition, McGraw Hill, Irwin, 229.
- Gupta, P.C. (2009) Data Communications and Computer Networks. PHI Learning Private Limited, New Delhi, 30, 611.
- Hwang, K. Advanced Computer Architecture: Parallelism, Scalability, Programmability. 383.




















