Communications and Network
Vol.6 No.2(2014), Article ID:45717,10 pages DOI:10.4236/cn.2014.62010
Markov Model Based Jamming and Anti-Jamming Performance Analysis for Cognitive Radio Networks
Wednel Cadeau, Xiaohua Li, Chengyu Xiong
Department of Electrical and Computer Engineering, State University of New York at Binghamton, Binghamton, USA
Email: wcadeau1@binghamton.edu, xli@binghamton.edu, cxiong1@binghamton.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 29 March 2014; revised 20 April 2014; accepted 30 April 2014
ABSTRACT
In this paper, we conduct a cross-layer analysis of both the jamming capability of the cognitiveradio-based jammers and the anti-jamming capability of the cognitive radio networks (CRN). We use a Markov chain to model the CRN operations in spectrum sensing, channel access and channel switching under jamming. With various jamming models, the jamming probabilities and the throughputs of the CRN are obtained in closed-form expressions. Furthermore, the models and expressions are simplified to determine the minimum and the maximum CRN throughput expressions under jamming, and to optimize important anti-jamming parameters. The results are helpful for the optimal anti-jamming CRN design. The model and the analysis results are verified by simulations.
Keywords:Cognitive Radio, Dynamic Spectrum Access, Jamming, Markov Model, Throughput

1. Introduction
Cognitive radio networks (CRNs) have attracted great attention recently because they can potentially resolve the critical spectrum shortage problem [1] . Under the umbrella of dynamic spectrum access, CRN accesses the spectrum secondarily, i.e., as long as it can guarantee no interference to any primary user (PU) who is using this spectrum at this time in this location [2] . This means that the cognitive radios need to periodically sense the spectrum to detect the PU’s activity. They have to vacate the channel immediately whenever the PU activity is detected.
While cognitive radios can realize more flexible spectrum access and higher spectrum efficiency, malicious users can also exploit them to launch more effective attacks, in particular jamming attacks. As a matter of fact, CRN is extremely susceptible to jamming attacks because of its unique requirements in the physicaland MAC-layers, such as the requirement of channel vacating when detecting any PU signals. On the other hand, it is believed that the capability of hopping among many channels gives CRN a unique advantage in improving their anti-jamming performance.
The anti-jamming performance of CRN is a new and interesting research topic that is critical for the secure and reliable CRN design [2] -[4] .Conventionally, anti-jamming study is conducted in the Physical-layer via some anti-jamming modulations, such as spread spectrum, or in the layers above MAC via channel switching. However, even if the CRN has an anti-jam Physical-layer transmission scheme, it may still be sensitive to jamming attacks because of the unique property of CRN in spectrum sensing and spectrum vacating [5] -[7] . In addition, channel switching in CRN is costly considering the required timing/frequency synchronization, channel estimation, handshaking for information exchange and network setup. In particular, the information about the available channels may not be identical among the CRN nodes because of the asynchronous spectrum sensing and the inevitable sensing errors. Extensive handshaking is necessary, which can be extremely timing/bandwidth consuming. Considering the complexity of jamming and anti-jamming interactions in CRN, game theory has also been adopted in anti-jamming research [8] -[10] . Nevertheless, the cost of channel switching has not been addressed sufficiently in these studies.
In this paper, we study the anti-jamming performance of CRN against jammers that are also equipped with similar cognitive radios. We focus on evaluating quantitatively some best jamming parameters as well as some optimal anti-jamming parameters, in particular the effect of number of white space channels. We conduct a cross-layer analysis of both the jamming capability and the anti-jamming capability. To address the CRN specific properties such as channel switching more accurately, we use a Markov chain to model the CRN operations. This provides us an efficient way to analyze the role of channel switching in mitigating jamming attacks. Although Markov model has been widely used for CRN performance analysis [11] , its application in anti-jamming study is relatively less. In contrast, we addressed them in [12] -[14] , which form the foundation for this paper.
The organization of this paper is as follows. In Section 2, we give the models of the CRN and the cognitive-radio-based jammers. Then in Section 3, we derive the jamming and anti-jamming performance expressions. In Section 4, we analyze and optimize important parameters that are critical for anti-jamming design. Simulations are conducted in Section 5. Conclusions are then given in Section 6.
2. Models of CRN and Jammers
We consider a generic cognitive radio transmission model that includes three states: spectrum sensing, data transmission and channel switching, as illustrated in Figure 1(a). The working sequence of a cognitive radio always begins with the spectrum sensing. If the spectrum sensing indicates that the channel is available for secondary access, then the cognitive radio transmits a data packet, and the model shifts into the data transmission state. If the spectrum sensing indicates the channel is not available, the cognitive radio conducts channel switching, and the model shifts into the channel switching state.
We use the Markov chain in Figure 1(b) to model the operation of the CRN, where 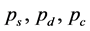 are the probabilities of the CRN in the spectrum sensing, data transmission and channel switching modes, respectively. The transitional probabilities
are the probabilities of the CRN in the spectrum sensing, data transmission and channel switching modes, respectively. The transitional probabilities 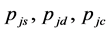 are the probabilities that the spectrum sensing, data transmission and channel switching procedures are jammed, respectively.
are the probabilities that the spectrum sensing, data transmission and channel switching procedures are jammed, respectively.
The durations of spectrum sensing slot, data transmission slot, and channel switching slot are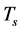 ,
, 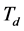 , and
, and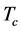 . Usually the spectrum sensing duration
. Usually the spectrum sensing duration 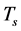 is much smaller than both
is much smaller than both 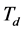 and
and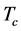 .The CRN has
.The CRN has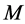 white space channels to select from. The availability of each channel depends on the activity of the PU and the jammers. The large number of channels is one of the primary advantages of CRN to combat jamming.
white space channels to select from. The availability of each channel depends on the activity of the PU and the jammers. The large number of channels is one of the primary advantages of CRN to combat jamming.
We use signal-to-noise-and-interference ratio (SINR) to measure the signal and jamming levels. For the data transmission slot, we assume that the minimum workable SINR is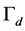 . SINR less than
. SINR less than 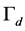 means that the CRN’s data packet transmission is jammed. For the spectrum sensing slot, we assume that if the SINR is larger than the detection threshold
means that the CRN’s data packet transmission is jammed. For the spectrum sensing slot, we assume that if the SINR is larger than the detection threshold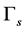 , then the cognitive radio will make a decision that the channel is occupied by the PU, and is thus not available.
, then the cognitive radio will make a decision that the channel is occupied by the PU, and is thus not available. 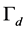 is usually much larger than
is usually much larger than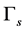 . We also assume that the minimum SINR for the channel switching procedures is
. We also assume that the minimum SINR for the channel switching procedures is , which is usually smaller than
, which is usually smaller than 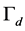 because the CRN may adopt
because the CRN may adopt
 (a)
(a) (b)
(b)
Figure 1. (a) Illustration of cognitive radio transmissions. (b) Markov model for cognitive radio transmissions under jamming.
some more reliable transmission techniques (albeit with lower data rate) such as spread spectrum modulations to increase the reliability of channel switching.
We make the following assumptions about the jammers. 1) There are 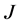 jammers. 2) Each jammer uses devices that have similar capabilities as a CRN node, including spectrum sensing and RF transceiving. 3) The jammers do not know the secret keys that the CRN is using for channel selection and communication. Therefore, the jammers do not know which channel the CRN is using. The only way left for the jammers is to randomly select some channels to jam.
jammers. 2) Each jammer uses devices that have similar capabilities as a CRN node, including spectrum sensing and RF transceiving. 3) The jammers do not know the secret keys that the CRN is using for channel selection and communication. Therefore, the jammers do not know which channel the CRN is using. The only way left for the jammers is to randomly select some channels to jam.
Since the jammers can fastly switch among the channels, they may choose to jam multiple channels simultaneously. In this paper the jamming strategies are described by two parameters: the jamming signal duration 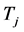 and the number of channels that are jammed simultaneously. We assume that each jammer has the same transmission power
and the number of channels that are jammed simultaneously. We assume that each jammer has the same transmission power 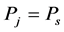 as the CRN, where
as the CRN, where 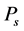 is the CRN node’s transmission power. The demodulation and signal detection of the CRN receiver depend on the average SINR received during the entire slot. If the jamming duration
is the CRN node’s transmission power. The demodulation and signal detection of the CRN receiver depend on the average SINR received during the entire slot. If the jamming duration 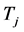 is smaller, the overall jamming signal power in this slot is lower. But the jammers can jam more channels simultaneously with smaller
is smaller, the overall jamming signal power in this slot is lower. But the jammers can jam more channels simultaneously with smaller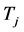 . We assume that all the jammers adopt the same jamming parameter
. We assume that all the jammers adopt the same jamming parameter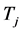 .
.
3. CRN Throughput under Multiple Uncooperative Jammers
3.1. Jamming Probabilities
Consider a CRN where a pair of CRN transmitter and receiver is conducting transmission at unit data throughput. A group of 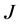 jammers want to jam the CRN transmission so as to reduce the throughput.
jammers want to jam the CRN transmission so as to reduce the throughput.
First, we consider a data packet transmission slot with slot length 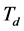 and SINR requirement
and SINR requirement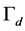 . If there are
. If there are 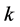 jamming signals falling in this slot, each with duration
jamming signals falling in this slot, each with duration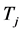 , then the SINR is
, then the SINR is
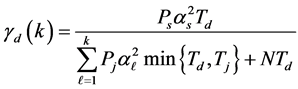 (1)
(1)
where 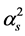 is the power gain of the Rayleigh flat fading channel of the CRN,
is the power gain of the Rayleigh flat fading channel of the CRN, 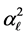 is the power gain of the Rayleigh flat fading channel of the
is the power gain of the Rayleigh flat fading channel of the 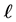 th jamming signal,
th jamming signal,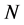 is the power of the additive white Gaussian noise (AWGN). We assume that
is the power of the additive white Gaussian noise (AWGN). We assume that 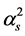 and
and 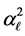 are independent exponential random variables with unit mean. A successful jamming means that
are independent exponential random variables with unit mean. A successful jamming means that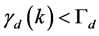 .
.
The number of jamming signals 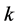 is limited to
is limited to 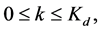 where
where 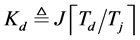 and
and 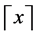 denotes the minimum integer that is no less than
denotes the minimum integer that is no less than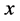 . The probability that there are
. The probability that there are 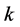 jamming signals in this slot follows the binomial distribution
jamming signals in this slot follows the binomial distribution
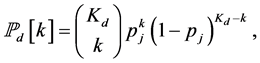 (2)
(2)
where 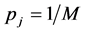 is the probability that a jammer chooses the same channel as the CRN. For simplicity, we do not consider the white space detection errors of the CRN and jammers. White space detection errors may make the available white space channels less for CRN. However, for the jammers, a safer approach might be just to jam every one of the
is the probability that a jammer chooses the same channel as the CRN. For simplicity, we do not consider the white space detection errors of the CRN and jammers. White space detection errors may make the available white space channels less for CRN. However, for the jammers, a safer approach might be just to jam every one of the 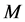 white space channels.
white space channels.
Proposition 1. If there are 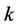 jamming signals with the same jamming duration
jamming signals with the same jamming duration 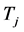 injected into a data transmission slot of duration
injected into a data transmission slot of duration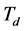 , the probability that the data packet transmission is jammed is
, the probability that the data packet transmission is jammed is
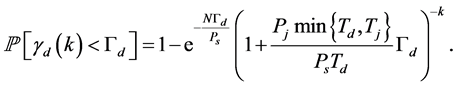 (3)
(3)
Proof. Using (1), we can change 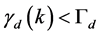 into
into 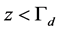 with
with
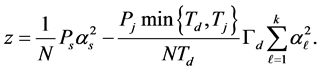 (4)
(4)
Since 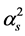 is an exponential random variable with unit mean, its probability density function is
is an exponential random variable with unit mean, its probability density function is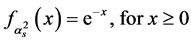 . In addition,
. In addition, 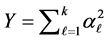 has Erlong distribution with probability density function
has Erlong distribution with probability density function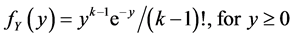 . Due to the independence assumption, their joint distribution is
. Due to the independence assumption, their joint distribution is
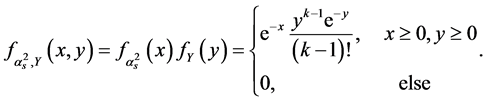 (5)
(5)
Then, the probability 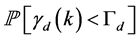 can be evaluated as
can be evaluated as
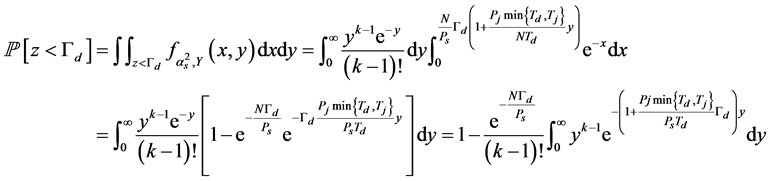 (6)
(6)
The last integration in (6) can be changed to the integration of the Erlong probability density function. According to the property of the Erlong distribution, we can derive (3). ■
Averaging over all possible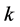 , the probability that the data transmission slot is jammed is
, the probability that the data transmission slot is jammed is
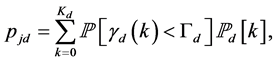 (7)
(7)
which can be evaluated by using (2) and (3).
Proposition 2. For the channel switching slot with duration 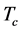 and required SINR
and required SINR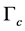 , the probability of being jammed is
, the probability of being jammed is
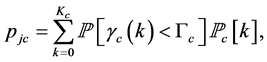 (8)
(8)
where the maximum number of jamming signals in this slot is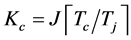 , the jamming probability under
, the jamming probability under 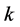 jamming signals is
jamming signals is
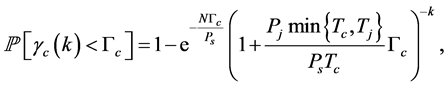 (9)
(9)
and the probability of having 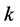 jamming signals is
jamming signals is
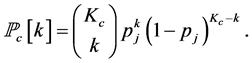 (10)
(10)
Proof. We can derive (8)-(10) by following the proof of the Proposition 1, and by replacing 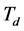 and
and 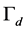 with
with 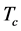 and
and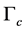 , respectively. ■
, respectively. ■
The spectrum sensing slot is different from either the data packet slot or the channel switching slot because the SINR 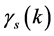 is in fact the interference (jamming) to noise ratio
is in fact the interference (jamming) to noise ratio
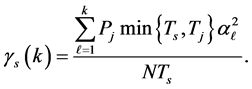 (11)
(11)
Usually the CRN is highly sensitive in PU sensing, which means that there is an extremely small sensing threshold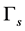 . By making
. By making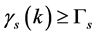 , the jammers disguise the PUs to force the CRN to conduct channel switching, which defines the jamming of the sensing slots.
, the jammers disguise the PUs to force the CRN to conduct channel switching, which defines the jamming of the sensing slots.
Proposition 3. For the channel sensing slot with duration 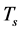 and sensing threshold
and sensing threshold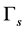 , the probability of being jammed is
, the probability of being jammed is
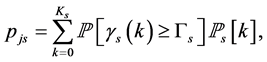 (12)
(12)
where the maximum number of jamming signals in this slot is 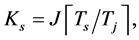 the probability of having
the probability of having 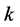 jamming signals is
jamming signals is
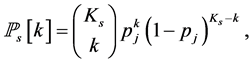 (13)
(13)
and the jamming probability under 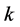 jamming signals is
jamming signals is
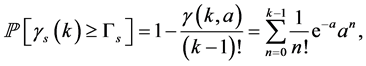 (14)
(14)
where 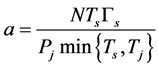 and
and 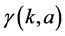 is the lower incomplete Gamma function.
is the lower incomplete Gamma function.
Proof. The equation (13) can be derived similarly as 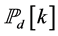 in (2) by replacing
in (2) by replacing 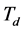 with
with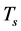 . To derive (14), from the SINR definition (11) and the Erlong distribution of
. To derive (14), from the SINR definition (11) and the Erlong distribution of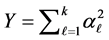 , we have
, we have
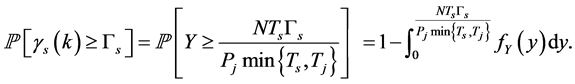 (15)
(15)
From the property of the Erlong distribution, the integration of (15) leads to (14). ■
3.2. Throughput of CRN under Jamming
With the jamming probabilities 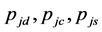 derived in Equations (7), (8) and (12), we can calculate the steady state probabilities of the three states
derived in Equations (7), (8) and (12), we can calculate the steady state probabilities of the three states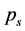 ,
, 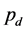 and
and 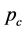 of the Markov model in Figure 1(b) by solving the equation
of the Markov model in Figure 1(b) by solving the equation
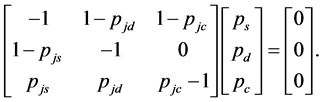 (16)
(16)
We need the constraint 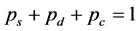 for (16) to have a unique solution.
for (16) to have a unique solution.
From (16) we can find that the system stays in the data packet transmission slots with probability
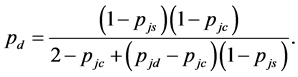 (17)
(17)
However, some of the data packets are lost due to jamming. Considering the jamming probability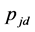 , the data packet transmission is successful with probability
, the data packet transmission is successful with probability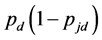 .
.
We define the normalized average throughput of the CRN transmission as
 (18)
(18)
Proposition 4. Considering the throughput definition (18), the throughput of CRN under jamming is
 (19)
(19)
Proof. From (16), we can describe  and
and  by
by 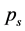 as
as
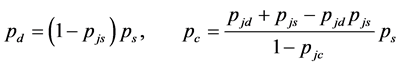 (20)
(20)
Substituting (20) into (18), we can get (19). ■
4. Analysis of Anti-Jamming Performance
4.1. A Closed-Form Throughput Expression
Although (19) can be used to evaluate numerically the anti-jamming performance, further analytical study is difficult. In this section, we first adopt some reasonable simplifications to simplify the jamming probability and the throughput expressions. Then, we analyze the anti-jamming performance by deriving the maximum and minimum throughputs under jamming.
For the jammer model, instead of considering  non-cooperative jammers that randomly inject
non-cooperative jammers that randomly inject  jamming signals with duration
jamming signals with duration 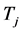 and power
and power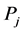 , we assume in this section that they cooperatively inject a single jamming signal of duration
, we assume in this section that they cooperatively inject a single jamming signal of duration 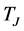 (which equals to the CRN slot lengths without loss of generality). The total power is
(which equals to the CRN slot lengths without loss of generality). The total power is . We assume that the jammers can jam
. We assume that the jammers can jam 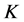 channels simultaneously, and the jamming power sent to each channel is
channels simultaneously, and the jamming power sent to each channel is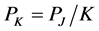 . We define
. We define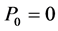 . We also assume that the maximum number of channels that these jammers can jam simultaneously is
. We also assume that the maximum number of channels that these jammers can jam simultaneously is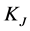 , which means
, which means 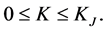
For the data transmission slot, if there is jamming signal, the cognitive radio’s received signal’s SINR is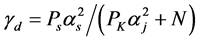 . If there is no jamming signal, the SINR becomes
. If there is no jamming signal, the SINR becomes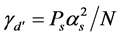 .
.
Since there are  white space channels, if the jammers randomly select
white space channels, if the jammers randomly select channels to jam, then they have probability
channels to jam, then they have probability 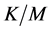 of sending a jamming signal to the channel being used by the CRN. Therefore, the probability that the data transmission is jammed (including the case that the channel gain is too small to transmit data successfully) can be written as
of sending a jamming signal to the channel being used by the CRN. Therefore, the probability that the data transmission is jammed (including the case that the channel gain is too small to transmit data successfully) can be written as
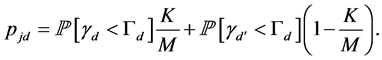 (21)
(21)
Note that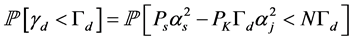 . Similar to the proof of the Proposition 1, we can find
. Similar to the proof of the Proposition 1, we can find
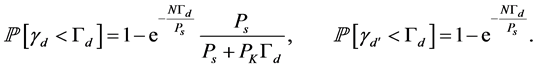 (22)
(22)
Therefore, the probability that the data transmission is jammed can be derived from (21)-(22) as
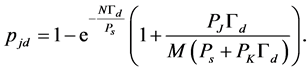 (23)
(23)
Next, we consider the channel sensing slots. In case of absence of PU, if there is jamming signal in this sensing slot, then we have SINR 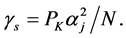 Otherwise, the SINR becomes simply
Otherwise, the SINR becomes simply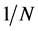 . For jamming probability, we just need to consider
. For jamming probability, we just need to consider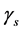 . The probability of having jamming signal in this sensing slot is similarly
. The probability of having jamming signal in this sensing slot is similarly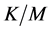 . Therefore, the probability that the sensing slot is jammed can be found as
. Therefore, the probability that the sensing slot is jammed can be found as
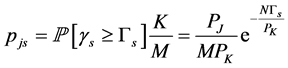 (24)
(24)
because 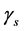 has exponential distribution.
has exponential distribution.
Finally, because channel switching is usually more jamming-resistant than channel sensing and data transmission, we let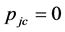 . Furthermore, without loss of generality, we let
. Furthermore, without loss of generality, we let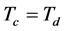 , which means that the CRN waits for a full data slot before switching to a new channel. Then the throughput (19) can be readily deduced into a close-form expression
, which means that the CRN waits for a full data slot before switching to a new channel. Then the throughput (19) can be readily deduced into a close-form expression
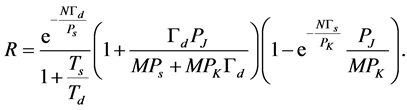 (25)
(25)
4.2. Anti-Jamming Throughput Analysis
One of the major parameters for the jammers to adjust jamming attacks is the jamming signal strength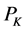 , or equivalently, the number of channels to jam simultaneously
, or equivalently, the number of channels to jam simultaneously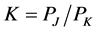 . In contrast, one of the major parameters for the CRN to mitigate jamming is the number of white space channels
. In contrast, one of the major parameters for the CRN to mitigate jamming is the number of white space channels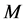 .
.
If considering just 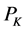 and
and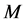 , the optimal anti-jamming performance of CRN can be found from the max-min optimization
, the optimal anti-jamming performance of CRN can be found from the max-min optimization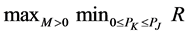 .
.
First, let us analyze the jammer’s best strategy to minimize the CRN throughput. Define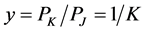 , and rewrite the throughput (25) into
, and rewrite the throughput (25) into
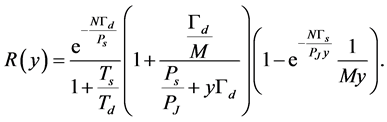 (26)
(26)
Note that the range of  is
is . If
. If 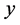 is extremely small, the item
is extremely small, the item 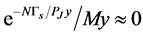 can be omitted from
can be omitted from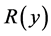 . In this case, the derivative
. In this case, the derivative
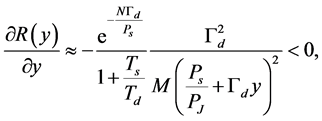 (27)
(27)
which means that 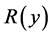 is a monotone decreasing function of
is a monotone decreasing function of 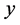 when
when 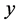 is extremely small.
is extremely small.
When 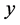 is not so small, because
is not so small, because 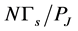 is usually a very small number, we let
is usually a very small number, we let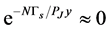 . In this case, by taking the derivative of (26) with respect to
. In this case, by taking the derivative of (26) with respect to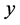 , we can easily find that
, we can easily find that
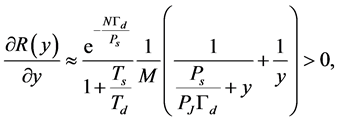 (28)
(28)
which means that the throughput 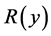 becomes a monotone increasing function for relatively large
becomes a monotone increasing function for relatively large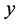 . Therefore, the minimum
. Therefore, the minimum 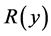 should happen with some extremely small
should happen with some extremely small 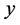 values, whereas the maximum throughput happens either when
values, whereas the maximum throughput happens either when 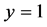 or
or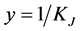 . The former means that the jammers just jam one channel at a time, while the latter means the weakest jamming signal is used. The maximum throughput is thus
. The former means that the jammers just jam one channel at a time, while the latter means the weakest jamming signal is used. The maximum throughput is thus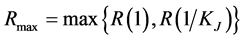 , which can be calculated from (26).
, which can be calculated from (26).
The optimal jamming parameter 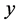 for the jammers to minimize the CRN throughput is shown below.
for the jammers to minimize the CRN throughput is shown below.
Proposition 5. For the jammers, the (approximately) optimal jamming parameter is
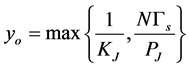 (29)
(29)
which minimizes the CRN throughput into 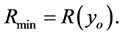
Proof. From (26), we can take the derivative 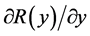 and let it be zero to find the optimal
and let it be zero to find the optimal . After some straightforward deductions, we can get
. After some straightforward deductions, we can get
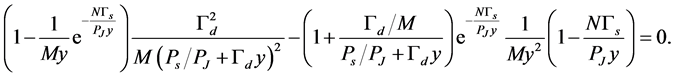 (30)
(30)
Unfortunately, (30) is too complex to find closed-form solutions to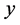 . Therefore, as an approximation, we consider the major items only. Because the minimum
. Therefore, as an approximation, we consider the major items only. Because the minimum 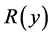 happens when
happens when 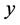 is extremely small, we can consider only those items in (30) involving
is extremely small, we can consider only those items in (30) involving 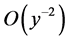 and
and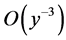 . Then (30) can be approximately simplified to
. Then (30) can be approximately simplified to
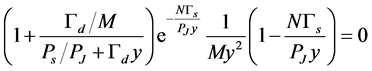 (31)
(31)
which gives solution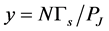 . Considering the practical range of
. Considering the practical range of 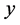 and the monotone property of
and the monotone property of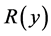 , we can derive (29). The throughput can be obtained by applying
, we can derive (29). The throughput can be obtained by applying 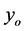 into (26). ■
into (26). ■
If 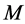 is large and
is large and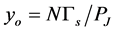 , then the minimum throughput becomes
, then the minimum throughput becomes
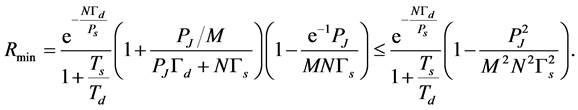 (32)
(32)
On the other hand, if 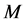 is small so the jammer can jam all the channels with
is small so the jammer can jam all the channels with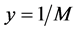 , then the throughput becomes
, then the throughput becomes
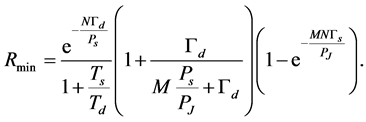 (33)
(33)
From (32)-(33), it can be seen that 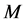 should be extremely large (e.g., several hundreds) for moderately high throughput. The CRN can increase
should be extremely large (e.g., several hundreds) for moderately high throughput. The CRN can increase 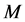 to mitigate jamming. Unfortunately, from (32) we can see that the throughput increases according to
to mitigate jamming. Unfortunately, from (32) we can see that the throughput increases according to 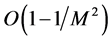 only, which means larger
only, which means larger 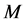 only brings smaller throughput increase, or the throughput increase tends to saturate at large
only brings smaller throughput increase, or the throughput increase tends to saturate at large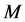 . Alternatively, the CRN may reduce the length of spectrum sensing slot
. Alternatively, the CRN may reduce the length of spectrum sensing slot 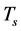 or increase the spectrum sensing threshold
or increase the spectrum sensing threshold 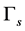 to increase the throughput. But this may increase interference to PUs. Therefore, anti-jamming CRN design is a challenging issue.
to increase the throughput. But this may increase interference to PUs. Therefore, anti-jamming CRN design is a challenging issue.
5. Simulations
In this section, we use simulations to verify the analysis results derived in Sections 3 and 4. Specifically, the normalized average throughput 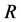 and the probability of transmitting unjammed data packets
and the probability of transmitting unjammed data packets 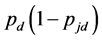 were evaluated. The following parameters were used:
were evaluated. The following parameters were used: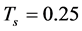
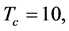
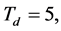
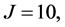
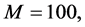 ,
, 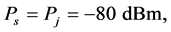
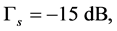
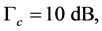
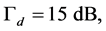 and
and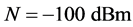 .
.
First, we verify the results in Section 3. For the jammers, we tested the jamming signals with duration 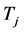 from 0 (jamming-free) up to the duration of
from 0 (jamming-free) up to the duration of 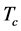 since
since 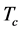 was the longest slot length. For the theoretical results, we used (19) to calculate
was the longest slot length. For the theoretical results, we used (19) to calculate 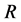 and used (7) and (17) to calculate
and used (7) and (17) to calculate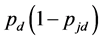 .
.
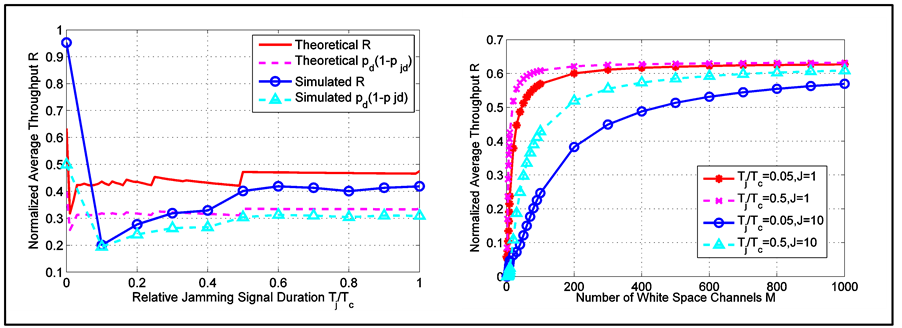
The simulation results are shown in Figure 2. From Figure 2(a), we can see that the theoretical results fit well with the simulated results, which demonstrated the validity of the modelling and analysis. Compared to the jamming-free throughput 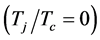 which was near unity, the throughput drastically reduced to just below 0.3 when facing 10 jammers that used small
which was near unity, the throughput drastically reduced to just below 0.3 when facing 10 jammers that used small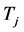 . Even with 100 channels to hop from, the CRN throughput still suffered from detrimental effect of jamming.
. Even with 100 channels to hop from, the CRN throughput still suffered from detrimental effect of jamming.
In Figure 2(b), we evaluated the anti-jamming performance of CRN when the CRN could hop among a large number of white space channels. It can be seen that while increasing the channel number 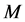 could drastically increase the anti-jamming capability of CRN, such a benefit tended to saturate after tens of channels had been used. Even with 1000 white space channels, the average throughput were still just around 0.6. In contrast, the jammers could reduce this benefit by just using a few more jammers.
could drastically increase the anti-jamming capability of CRN, such a benefit tended to saturate after tens of channels had been used. Even with 1000 white space channels, the average throughput were still just around 0.6. In contrast, the jammers could reduce this benefit by just using a few more jammers.
Next, we use simulations to verify that the analysis results of Section 4. For the jammer, we evaluated the jamming parameters 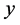 from 0 (jamming-free) up to 0.1. The simulation results are shown in Figure 3. From the
from 0 (jamming-free) up to 0.1. The simulation results are shown in Figure 3. From the
 (a) (b)
(a) (b)
Figure 2. (a) Average throughput and probability of transmitting unjammed data packets under various jamming parameters. (b) Average throughput as function of number of white space channels, under various jamming parameters.
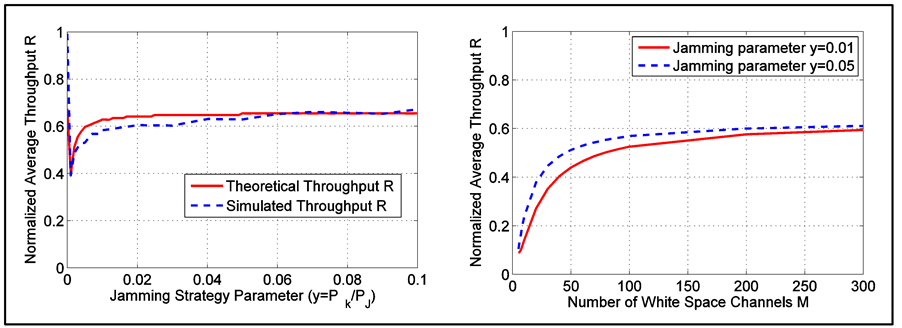
Figure 3. Comparison of simulation results to the analysis results of the average throughput.
results, we can see that the analysis results fit well with the simulated results, which demonstrated the validity of the analysis. It clearly showed that the throughput reduced with 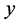 when
when 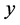 was extremely small, but increased with
was extremely small, but increased with 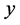 when
when 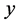 became larger.
became larger.
6. Conclusion
In this paper, with a Markov model of the cognitive radio transmissions, both the jamming performance of the cognitive-radio-based jammers and the anti-jamming performance of the CRN are analyzed. Expressions of the CRN average throughput and jamming probabilities are derived. Some optimal jamming parameters and anti-jamming parameters are analyzed, in particular the number of white space channels, which are verified by simulations. The results indicate that the CRN is extremely susceptible to jamming attacks, and it suffers from a saturation effect when combating jamming attacks by increasing the number of white space channels.
References
- Akyildiz, I.F., Lee, W.-Y., Vuran, M.C. and Mohanty, S. (2006) NeXt Generation/Dynamic Spectrum Access/Cognitive Radio Wireless Networks: A Survey. Computer Networks, 50, 2127-2159. http://dx.doi.org/10.1016/j.comnet.2006.05.001
- McHenry, M., Livsics, E., Nguyen, T. and Majumdar, N. (2007) XG Dynamic Spectrum Access Field Test Results. IEEE Xplore: Communications Magazine, 45, 51-57. http://dx.doi.org/10.1109/MCOM.2007.374432
- Cordeiro, C., Challapali, K., Birru, D. and Shankar, S. (2006) IEEE 802.22: An Introduction to the First Wireless Standard Based on Cognitive Radios. Journal of Communication, 1, 38-47.
- Clancy, T.C. and Goergen, N. (2008) Security in Cognitive Radio Networks: Threats and Mitigation. International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Singapore.
- Chen, R., Park, J.-M. and Reed, J.H. (2008) Defense Against Primary User Emulation Attacks in Cognitive Radio Networks. IEEE Journal on Selected Areas in Communications, Special Issue on Cognitive Radio Theory and Applications, 26, 25-37. http://dx.doi.org/10.1109/JSAC.2008.080104
- Wang, Q., Ren, K. and Ning, P. (2011) Anti-Jamming Communication in Cognitive Radio Networks with Unknown Channel Statistics. 2011 19th IEEE International Conference on Network Protocols (ICNP), 393-402.
- Pietro, R.D. and Oligeri, G. (2013) Jamming Mitigation in Cognitive Radio Networks. IEEE Network, 27, 10-15. http://dx.doi.org/10.1109/MNET.2013.6523802
- Li, H. and Han, Z. (2009) Dogfight in Spectrum: Jamming and Anti-Jamming Inmultichannel Cognitive Radio Systems. Proc. of IEEE GLOBECOM, 1-6.
- Wang, B., Wu, Y., Liu, K.J.R. and Clancy, T.C. (2011) An Anti-Jamming Stochastic Game for Cognitive Radio Networks. IEEE Journal on Selected Areas in Communications, 29, 877-889. http://dx.doi.org/10.1109/JSAC.2011.110418
- Chen, C., Song, M., Xin, C. and Backens, J. (2013) A Game-Theoretical Anti-Jamming Scheme for Cognitive Radio Networks. IEEE Network, 27, 22-27. http://dx.doi.org/10.1109/MNET.2013.6523804
- Tumuluru, V.K., Wang, P., Niyato, D. and Song, W. (2012) Performance Analysis of Cognitive Radio Spectrum Access with Prioritized Traffic. IEEE Transactions on Vehicular Technology, 61, 1895-1906. http://dx.doi.org/10.1109/TVT.2012.2186471
- Li, X. and Cadeau, W (2011) Anti-Jamming Performance of Cognitive Radio Networks. Proceedings of the 45th Annual Conf. on Information Sciences and Systems (CISS), Johns Hopkins Univ., Baltimore.
- Cadeau, W. and Li, X. (2012) Anti-Jamming Performance of Cognitive Radio Networks under Multiple Uncoordinated Jammers in Fading Environment. Proceedings of the 46th Annual Conf. on Information Sciences and Systems (CISS), Princeton Univ., Princeton. http://dx.doi.org/10.1109/CISS.2012.6310843
- Cadeau, W. and Li, X. (2013) Jamming Probabilities and Throughput of Cognitive Radio Communications against a Wideband Jammer. The 47th Annual Conference on Information Sciences and Systems (CISS), Johns Hopkins University.

