Communications and Network
Vol.6 No.1(2014), Article ID:42840,7 pages DOI:10.4236/cn.2014.61004
A Novel Decoding Method for Non-Binary TCM Codes
1College of Engineering Al-Mustansiriyah University, Baghdad, Iraq
2College of Engineering, Basrah University, Basrah, Iraq
3College of Engineering, Al-Mustansiriyah University, Baghdad, Iraq
Email: Ryad_petrol@yahoo.com, kareem134@yahoo.com, raadthaher@yahoo.com
Copyright © 2014 Riyadh A. Al-Hilali et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Riyadh A. Al-Hilali et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received July 1, 2013; revised August 1, 2013; accepted August 8, 2013
KEYWORDS
Convolutional Codes; Coded Modulation (CM); Trellis Code Modulation (TCM); Non-Binary Error Correcting Codes; Groups; Rings of Integers
ABSTRACT
A new non-binary decoding method, which is called Yaletharatalhussein decoding algorithm, is designed and implemented for decoding non-binary convolutional codes which is based on the trellis diagram representing the convolutional encoder. Yaletharatalhussein decoding algorithm outperforms the Viterbi algorithm and other algorithms in its simplicity, very small computational complexity, decoding reliability for high states TCM codes that suitable for Fourth-Generation (4G), decreasing errors with increasing word length, and easy to implement with real-time applications. The proposed Yaletharatalhussein decoding algorithm deals with non-binary error control coding of the convolutional and TCM codes. Convolutional codes differ from block codes in that a block code takes a fixed message length and encodes it, whereas a convolutional code can encode a continuous stream of data, and a hard-decision decoding can easily be realized using the Yaletharatalhussein algorithm. The idea of non-binary codes has been extended for symbols defined over rings of integers, which outperform binary codes with only a small increase in decoding complexity. The simulation results show that the performance of the nonbinary TCM-based Yaletharatalhussein algorithm outperforms the binary and non-binary decoding methods.
1. Introduction
When conventional coding techniques are introduced in a transmission system, the bandwidth of the coded signal after modulation is wider than that of the uncoded signal for the same information rate and the same modulation scheme. In fact, the encoding process requires a bandwidth expansion that is inversely proportional to the code rate, being traded for a coding gain. On the other hand, the available radio spectrum is limited and the communication capacity needs cannot be met without a significant increase in spectral efficiency [1]. Digital signals are more reliable in a noisy communications environment. They can usually be detected perfectly, as long as the noise levels are below a certain threshold. Digital data can easily be encoded in such a way as to introduce dependency among a large number of symbols, thus enabling a receiver to make a more accurate detection of the symbols. This is called error control coding. The design of signal processing algorithms for digital data seems much easier than designing analog signal processing algorithms. The abundance of such digital algorithms, including error control and correction techniques, combined with their ease of implementation in very large-scale integrated (VLSI) circuits, has led to many successful applications of error control coding in practice.
Advances in coding, such as turbo [2] and low density parity check codes [3], made it feasible to approach the Shannon capacity limit [4] in systems with a single antenna link. Significant further advances in spectral efficiency are available through increasing the number of antennas at both the transmitter and the receiver [5-7].
Further performance gains can be achieved by using non-binary codes in the coded modulation scheme, but with an increase in the decoding complexity [8]. Nonbinary codes are the most commonly used error-correcting codes and can be found in optical and magnetic storage, high-speed modems and wireless communications.
Among the various Coded Modulation (CM) schemes, TCM [9] was originally designed for transmission over Additive White Gaussian Noise (AWGN) channels. TTCM [10] is a more recent joint coding and modulation scheme which has a structure similar to that of the family of binary turbo codes, but employs TCM schemes as component codes. Both TCM and TTCM employ set-partitioning-based constellation mapping [11], while using symbol-based turbo interleavers and channel interleavers. Another CM scheme, referred to as BICM [12], invokes bit-based channel interleavers in conjunction with grey constellation mapping. Furthermore, iteratively decoded BICM [13] using set partitioning was also proposed.
2. Rings of Integers
If the two binary operations “+” and “·” are allowed then a ring can be defined. A ring must have the following conditions; associativity, distributivity, and commutativity under addition. The ring is called a commutative ring if it also has commutativity under multiplication. If the ring has a multiplicative identity 1 then it is called a ring with identity. An example of a ring is the ring of integers 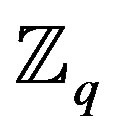 under modulo-q addition and multiplication, where q is the cardinality of the ring. For example,
under modulo-q addition and multiplication, where q is the cardinality of the ring. For example, 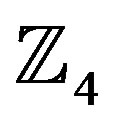 is defined as {0, 1, 2, 3}.
is defined as {0, 1, 2, 3}.
It is easy to see that the elements obey the three definitions of a ring. Also, all the elements commute under multiplication and the multiplicative identity element 1 is present, meaning that 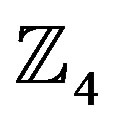 is a commutative ring with identity. Tables 1 and 2 show the addition and multiplication tables respectively of the ring of integers
is a commutative ring with identity. Tables 1 and 2 show the addition and multiplication tables respectively of the ring of integers 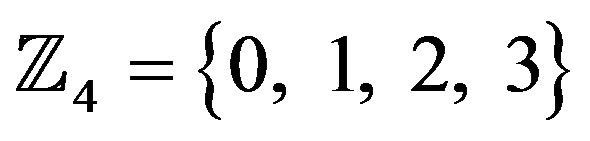 [14].
[14].
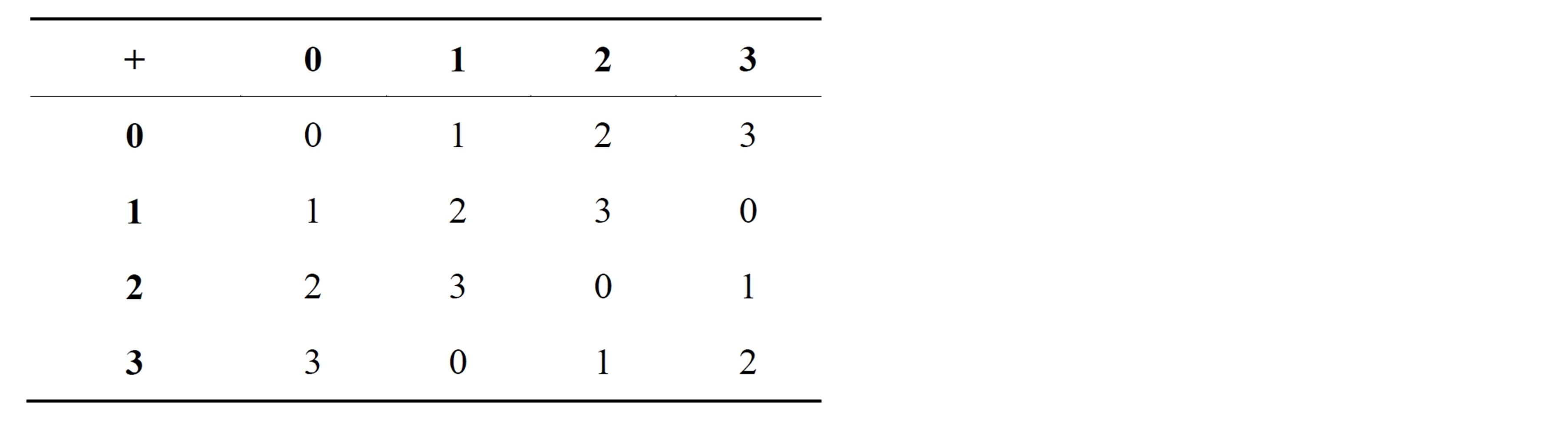
Table 1. Addition table for .
.
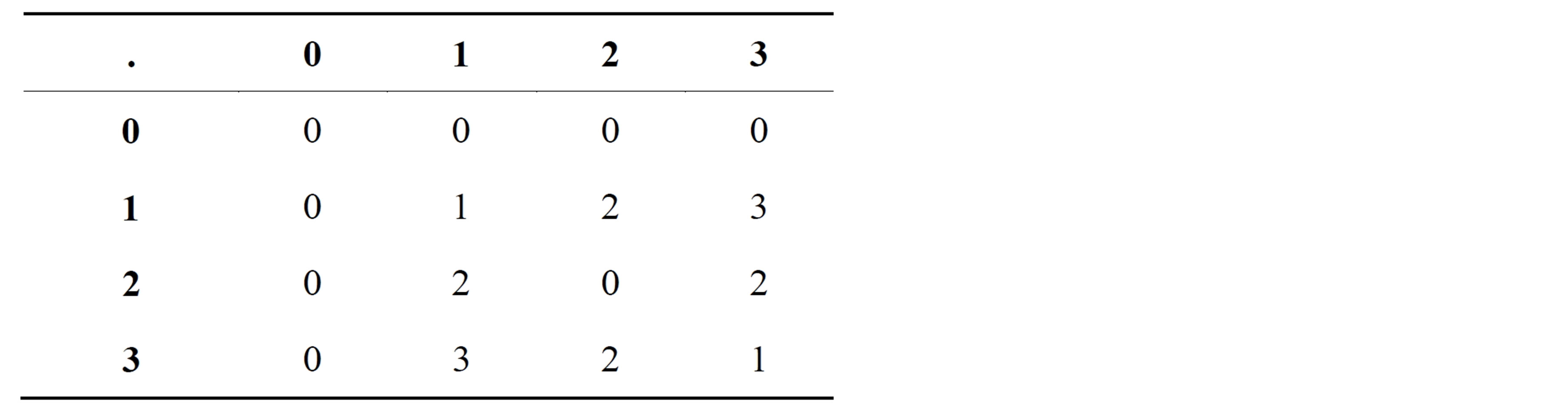
Table 2. Multiplication table for .
.
The set of all polynomials with coefficients defined in 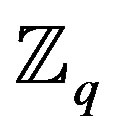 forms a ring under the addition and multiplication operations.
forms a ring under the addition and multiplication operations.
3. Non-Binary TCM
Convolutional codes and TCM codes are based on rings of integers modulo-M. Due to the similarities between M-PSK signal sets and the algebraic structure of rings of integers modulo-M, modulo-M ring-TCM codes are the natural linear codes for M-PSK modulation.
TCM Based on Rings of Integers
The general structure of a ring-TCM encoder suitable for M-PSK modulation, assuming that m information bits are transmitted per baud, with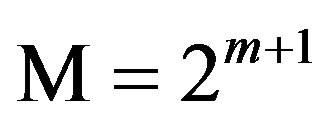 , is shown in Figure 1. This ring-TCM encoder works as follows [15]:
, is shown in Figure 1. This ring-TCM encoder works as follows [15]:
1) First, m + 1 information bits, bi, are mapped into a modulo-M symbol, 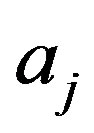 , according to a mapping function f (for instance, f can be a Gray mapping function).
, according to a mapping function f (for instance, f can be a Gray mapping function).
2) Next, m modulo-M 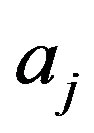 symbols are introduced into a linear multi-level convolutional encoder (MCE), which generates m + 1 modulo-M coded symbols,
symbols are introduced into a linear multi-level convolutional encoder (MCE), which generates m + 1 modulo-M coded symbols,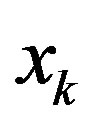 .
.
3) Finally, each one of these coded symbols 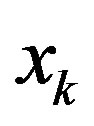 is associated with a signal of the M-PSK signal set and is sent to the channel.
is associated with a signal of the M-PSK signal set and is sent to the channel.
As a total of m + 1 modulo-M coded symbols 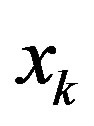 are transmitted per single trellis branch, ring-TCM codes can be considered as
are transmitted per single trellis branch, ring-TCM codes can be considered as 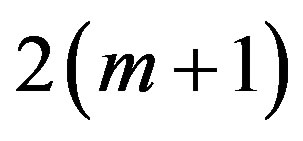 -dimensional TCM codes.
-dimensional TCM codes.
4. A 4-State Ring-TCM Code Defined over 4
A good 4-state ring-TCM code over 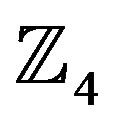 is shown in Figure 2 and this would be used in this research work [16].
is shown in Figure 2 and this would be used in this research work [16].
Where each of the input and output of Figure 2 represent the elements of the ring of integers modulo-4, 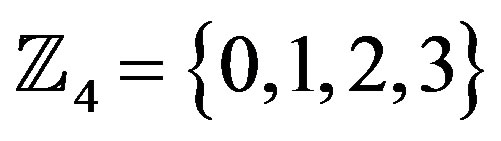 , and all addition arithmetic operations satisfy the properties of the ring of integers modulo-4 addition. The delay block represents the constraint length (number of memory elements, i.e., in this case there is only one memory element).
, and all addition arithmetic operations satisfy the properties of the ring of integers modulo-4 addition. The delay block represents the constraint length (number of memory elements, i.e., in this case there is only one memory element).
5. Yaletharatalhussein Decoding Algorithm
The Yaletharatalhussein non-binary decoding algorithm is proposed in this paper for decoding non-binary convolutional codes. The decoder for the non-binary convolutional code finds the most probable sequence of data bits 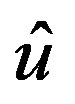 given the received sequence y:
given the received sequence y:
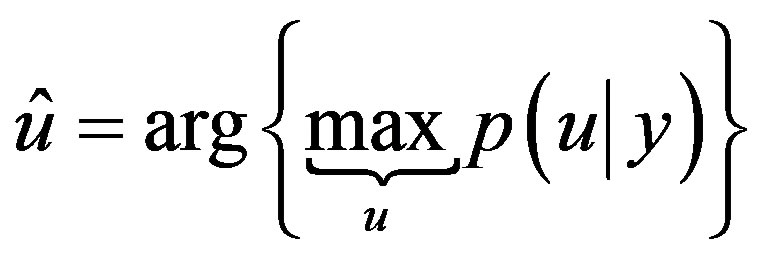 (1)
(1)
where y is the set of code symbols c observed through noise. The above equation can be solved using the Yale-

Figure 1. General structure of a ring-TCM encoder suitable for M-PSK modulation.
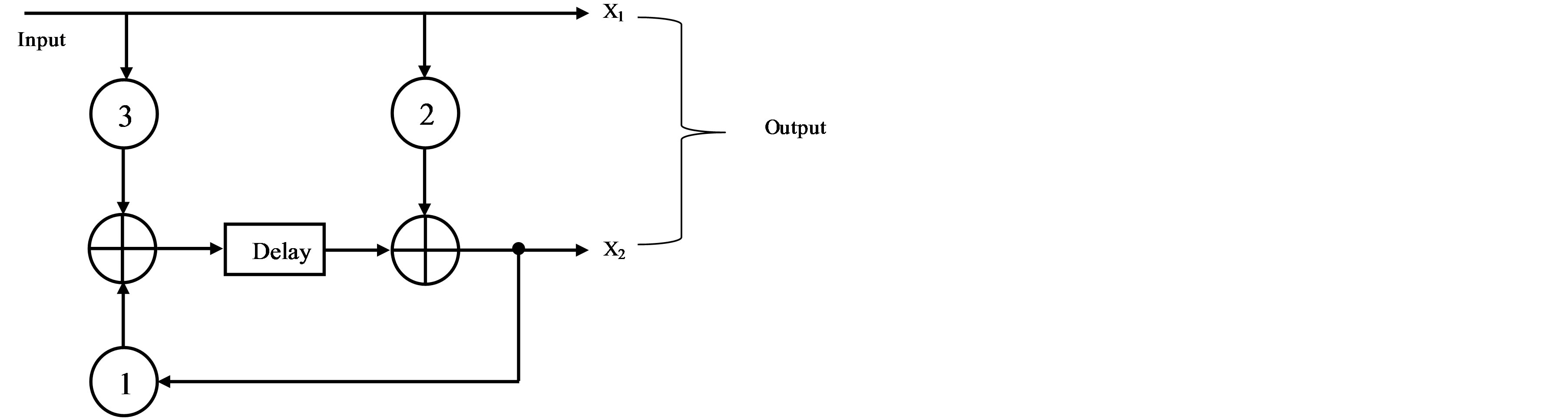
Figure 2. A 4-state ring-TCM Encoder.
tharatalhussein algorithm, explained later.
The application of the Yaletharatalhussein algorithm to decoding non-binary convolutional codes is based on the logic similarities and differences, at each time instant, between the noisy received bits, i.e., y, and the sequence of output data bits, i.e., u, of the non-binary state table that represents the non-binary convolutional encoder sequential logic states.
This principle states that creating a state vector containing binary logic states, which represents the similarities and differences between y symbols associated with each u bits at the current time instant, and then searching for a minimum logic state in this vector to determine the state node number with its order bit for using in the next time instant of searching strategy method, in one hand, and for recovering the transmitted code word in the other hand. In this case, the decoding method is independent on the trellis diagram representing the non-binary convolutional encoder.
The basic steps in the Yaletharatalhussein non-binary decoding algorithm can be described as follows:
1) Determine the logic state vectors that represent the logic similarities and differences between the first block noisy received symbols, y, associated with each output data bits vector of all states, u, at each time instant (i.e., t = 0 to t = K), according to the following condition:
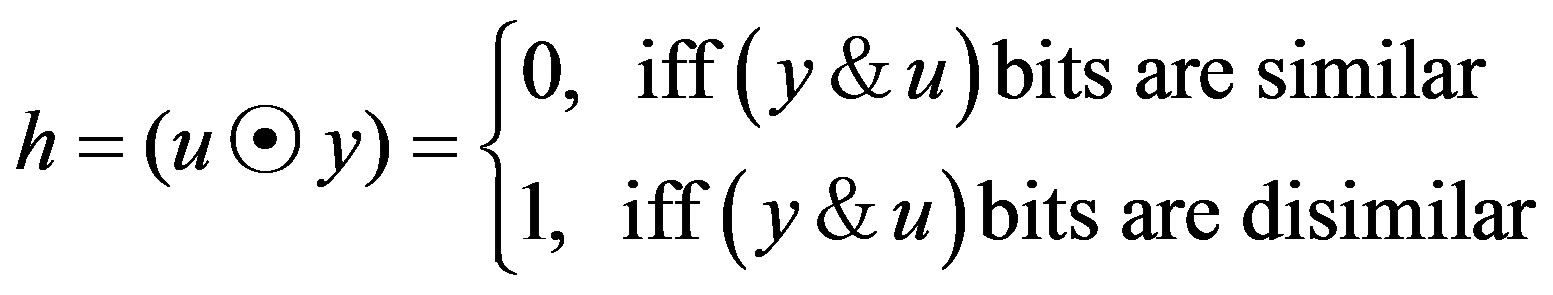 (2)
(2)
where:
 : represents a non-binary operation defined above;
: represents a non-binary operation defined above;
y: represents noisy received symbols with K, word length and;
u: represents a vector of non-binary output data bits for all states at the current time instant associated with y symbol, and the length of this vector is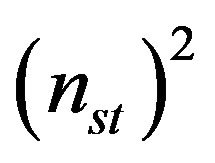 , where
, where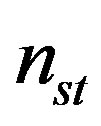 , is the number of non-binary states of the convolutional encoder. Thus the vector h would contain a set of ones and zeros (i.e., binary vector).
, is the number of non-binary states of the convolutional encoder. Thus the vector h would contain a set of ones and zeros (i.e., binary vector).
2) Begin at time t = K, at state 0.
3) Search about the zero logic state in h vector at this current time instant (i.e., t = K), and then store both number of state node and the order of the determined zero logic state to detect the transmitted bit at this time instant (i.e., x at t = K) from the input vector in the state table.
4) Decrement time t (i.e., t = K − 1) and return to Step 3, but search about the zero logic state in the h vector locations only, that have order the same as the state node number that stored in Step 3. Then the transmitted bit at this time instant (i.e., x at t = K − 1) can be detected from the input vector in the state table. In this case the searching about zero locations would be decreased.
5) Continue this process until all the symbols in the code word have been detected at the final time instant (t = 0).
An example of applying the Yaletharatalhussein decoding algorithm for the non-binary 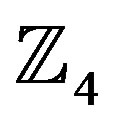 -ring-TCM encoder shown in Figure 2, the encoder takes an input sequence bits x of length K bits and for each bit produces two coded bits denoted as
-ring-TCM encoder shown in Figure 2, the encoder takes an input sequence bits x of length K bits and for each bit produces two coded bits denoted as 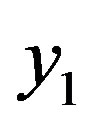 and
and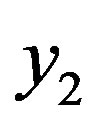 .
.
For simplicity, assuming K = 5 bits, and noiseless data vector 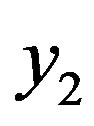 is received at the non-binary decoder input. If the input message to the non-binary
is received at the non-binary decoder input. If the input message to the non-binary 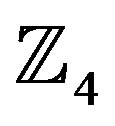 -ring-TCM encoder is:
-ring-TCM encoder is:
x = [1 2 3 3 3], then the coded bits 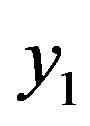 and
and 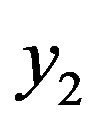 are described below:
are described below:
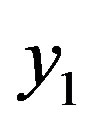 = [1 2 3 3 3], and
= [1 2 3 3 3], and 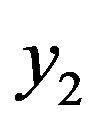 = [2 1 1 0 3].
= [2 1 1 0 3].
Now, from the state table [16], the initial input vectors w’s and output data vectors u’s are shown below, where each script number indicates time instant k:
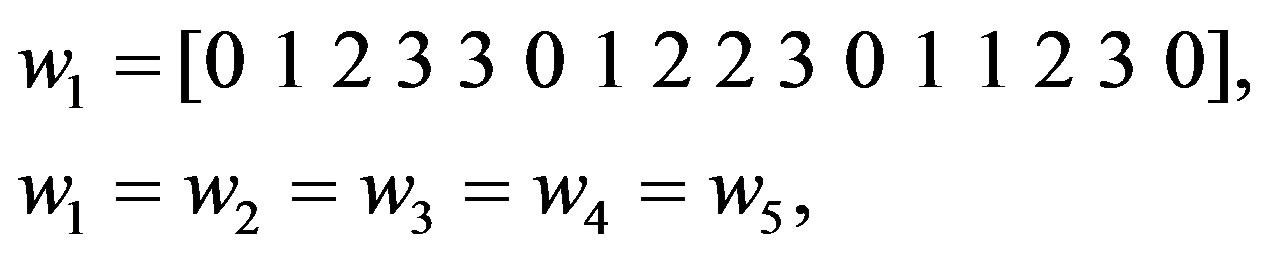
and
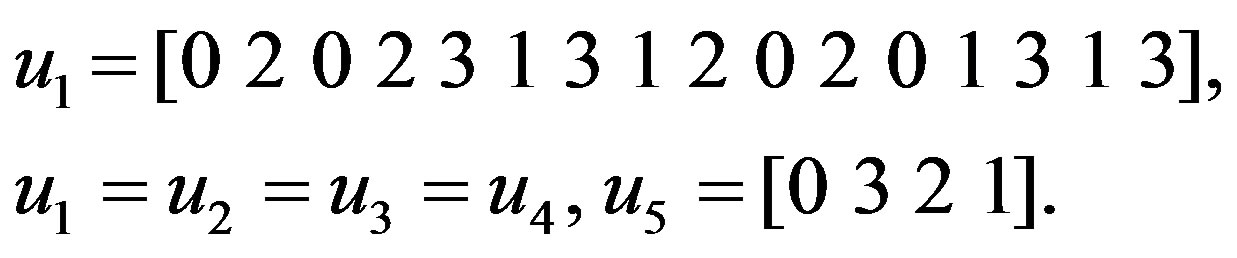
The steps of applying the Yaletharatalhussein decoding algorithm are described below:
1) To find h vectors, using the relation (4.15) then:
h1 = [1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1]h2 = [1 1 1 1 1 0 1 0 1 1 1 1 0 1 0 1]h3 = [1 1 1 1 1 0 1 0 1 1 1 1 0 1 0 1]h4 = [0 1 0 1 1 1 1 1 1 0 1 0 1 1 1 1]h5 = [1 0 1 1]2) Search in h5 = [1 0 1 1], about zero element, this leads to [1; 0; 1; 1], this assigned in state node number = 2, and bit order = 1. Thus the transmitted bit in w5 = [0 1 2 3; 3 0 1 2; 2 3 0 1; 1 2 3 0], is x5 = 3.
3) Search in h4 = [0 1 0 1 1 1 1 1 1 0 1 0 1 1 1 1], about zero element in the 2nd location of each state of h4, this leads to [0 1 0 1; 1 1 1 1; 1 0 1 0; 1 1 1 1], and assigned in state node number = 3, and bit order = 10. Thus the transmitted bit in w4 = [0 1 2 3 3 0 1 2 2 3 0 1 1 2 3 0], is x4 = 3.
4) Search in h3 = [1 1 1 1 1 0 1 0 1 1 1 1 0 1 0 1], about zero element in the 3rd location of each state of h3, this leads to [1 1 1 1; 1 0 1 0; 1 1 1 1; 0 1 0 1], and assigned in state node number = 4, and bit order = 15. Thus the transmitted bit in w3 = [0 1 2 3 3 0 1 2 2 3 0 1 1 2 3 0], is x3 = 3.
5) Search in h2 = [1 1 1 1 1 0 1 0 1 1 1 1 0 1 0 1], about zero element in the 4th location of each state of h2, this leads to [1 1 1 1; 1 0 1 0; 1 1 1 1; 0 1 0 1], and assigned in state node number = 2, and bit order = 8. Thus the transmitted bit in w2 = [0 1 2 3 3 0 1 2 2 3 0 1 1 2 3 0], is x2 = 2.
6) Search in h1 = [1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1], about zero element in the 2nd location of each state of h1, this leads to [1 0 1 0; 1 1 1 1; 0 1 0 1; 1 1 1 1], and assigned in state node number = 2, and bit order = 2. Thus the transmitted bit in w1 = [0 1 2 3 3 0 1 2 2 3 0 1 1 2 3 0], is x1 = 1.
7) The transmitted bits sequence form the non-binary  -ring-TCM encoder is, x = [1 2 3 3 3], which is similar to the given input message.
-ring-TCM encoder is, x = [1 2 3 3 3], which is similar to the given input message.
To enhance the Yaletharatalhussein decoding method, a schematic design of the  -ring-TCM-based Yaletharatalhussein algorithm is shown in Figure 3. The source information bits are first encoded and modulated by the
-ring-TCM-based Yaletharatalhussein algorithm is shown in Figure 3. The source information bits are first encoded and modulated by the  -ring-TCM encoder and modulater.
-ring-TCM encoder and modulater.
The symbols are then transmitted via the channel, and the received noise-contaminated symbols are forwarded to the demodulator.
The recovered signal is then demodulated and the outputs are fed to the  -ring-TCM-decoder which used the Yaletharatalhussein algorithm for recovering the most likely transmitted information bits.
-ring-TCM-decoder which used the Yaletharatalhussein algorithm for recovering the most likely transmitted information bits.
The  -ring-TCM demodulator and decoder-based Yaletharatalhussein decoding algorithm can be represented by a flowchart as shown in Figure 4. The flow chart inside the dashed lines represents the Yaletharatalhussein decoding algorithm.
-ring-TCM demodulator and decoder-based Yaletharatalhussein decoding algorithm can be represented by a flowchart as shown in Figure 4. The flow chart inside the dashed lines represents the Yaletharatalhussein decoding algorithm.
6. Simulation Results
The performances of the  -Ring-TCM-PAM schemebased Yaletharatalhussein algorithm communicating over
-Ring-TCM-PAM schemebased Yaletharatalhussein algorithm communicating over
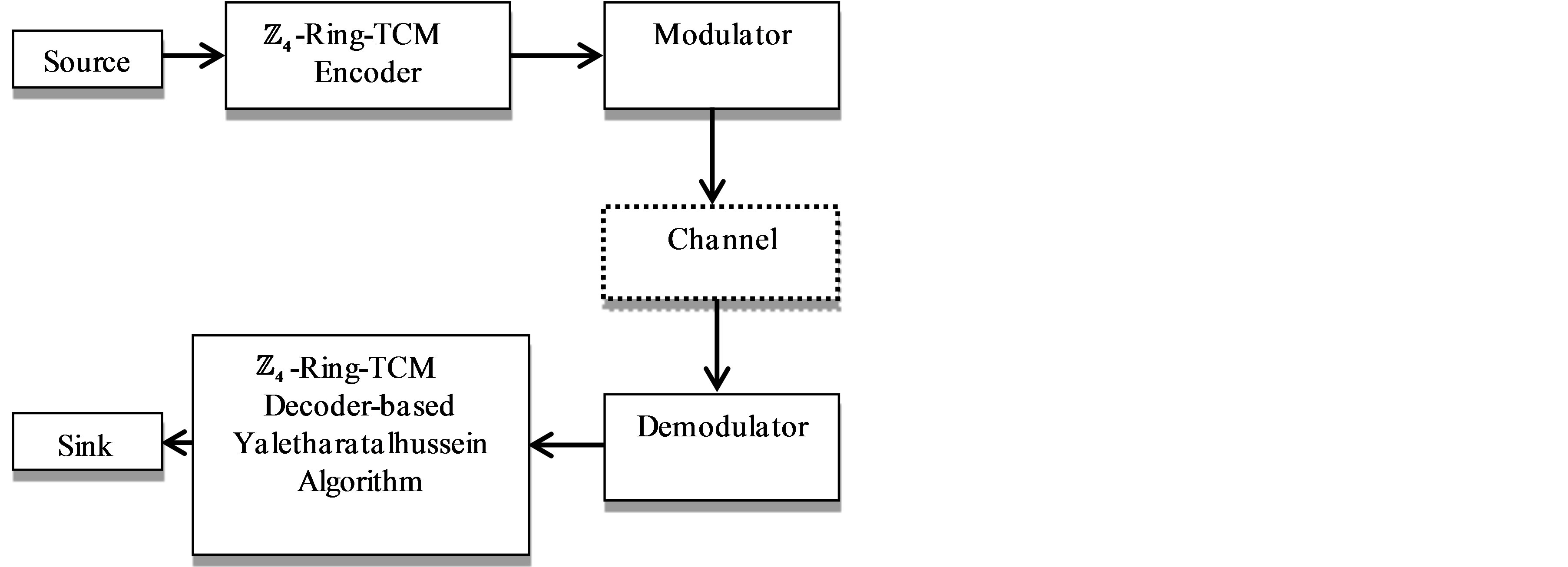
Figure 3. Schematic diagram of the proposed  -ringTCM-based Yaletharatalhussein algorithm.
-ringTCM-based Yaletharatalhussein algorithm.
the AWGN channel are shown in Figure 5.
The performances of the 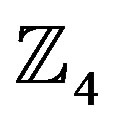 -Ring-TCM-PAM schemebased Yaletharatalhussein decoding algorithm and the schemes of work [16] can be summarized in Table 3, where the coding gains are defined as the
-Ring-TCM-PAM schemebased Yaletharatalhussein decoding algorithm and the schemes of work [16] can be summarized in Table 3, where the coding gains are defined as the 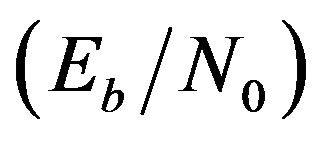 difference, expressed in decibels, at BERs of 10−5 and 10−3. The performance of the best scheme in Table 3 is (printed in bold), since the performance comparison shows that the
difference, expressed in decibels, at BERs of 10−5 and 10−3. The performance of the best scheme in Table 3 is (printed in bold), since the performance comparison shows that the 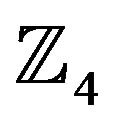 -ring-TCM-PAM scheme-based Yaletharatalhussein algorithm outperforms the 4-state ring-TCMbased Viterbi algorithm by the gains (5.5 dB and 8.7 dB) at the BERs (10−3 and 10−5) respectively.
-ring-TCM-PAM scheme-based Yaletharatalhussein algorithm outperforms the 4-state ring-TCMbased Viterbi algorithm by the gains (5.5 dB and 8.7 dB) at the BERs (10−3 and 10−5) respectively.
7. Conclusions and Future Works
A novel non-binary decoding method, which is called Yaletharatalhussein decoding algorithm, is proposed for decoding non-binary convolutional and TCM codes, which independent on the trellis diagram representing the nonbinary convolutional encoder, as in Viterbi algorithm.
The Yaletharatalhussein algorithm employed a harddecision decoding, which needed less computational complexity over the soft-decision MLD of Viterbi algorithm.
In Yaletharatalhussein algorithm, the code words are detected instantaneously through searching in the developed state vectors, while in Viterbi algorithm, the hamming distances between numbers and transition metrics are calculated and a comparison between competitive accumulated metrics is done for every state of the trellis diagram.
Computational complexity of the Yaletharatalhussein algorithm is much smaller than complexity of the Viterbi algorithm, since in Viterbi algorithm, a survivor path of the lowest accumulated metrics is calculated and repeated for every state of the trellis diagram.
In Yaletharatalhussein algorithm, the massages are decoded in blocks reached to 1,000,000 symbols as seen in simulation results, while in a typical Viterbi code,
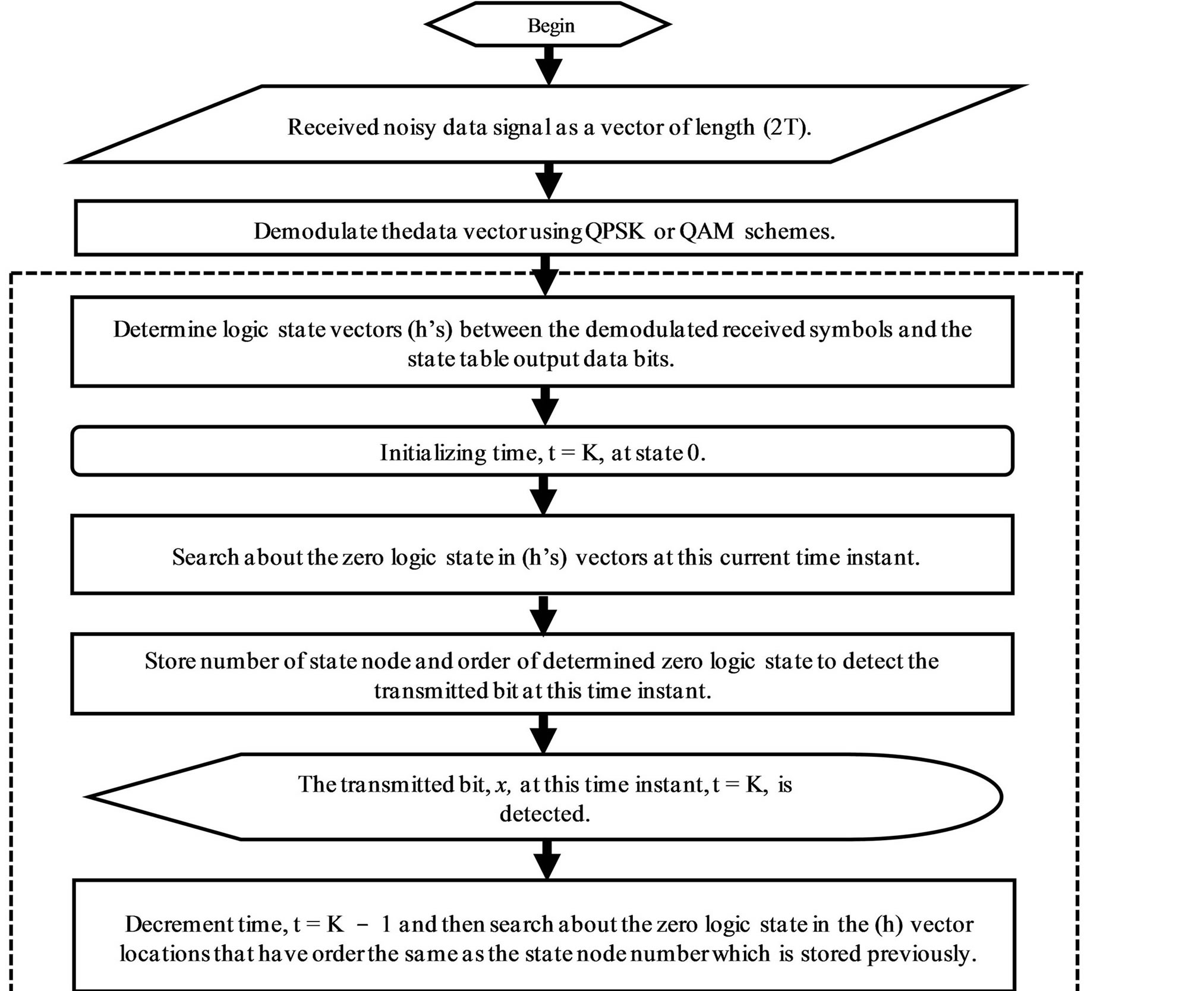
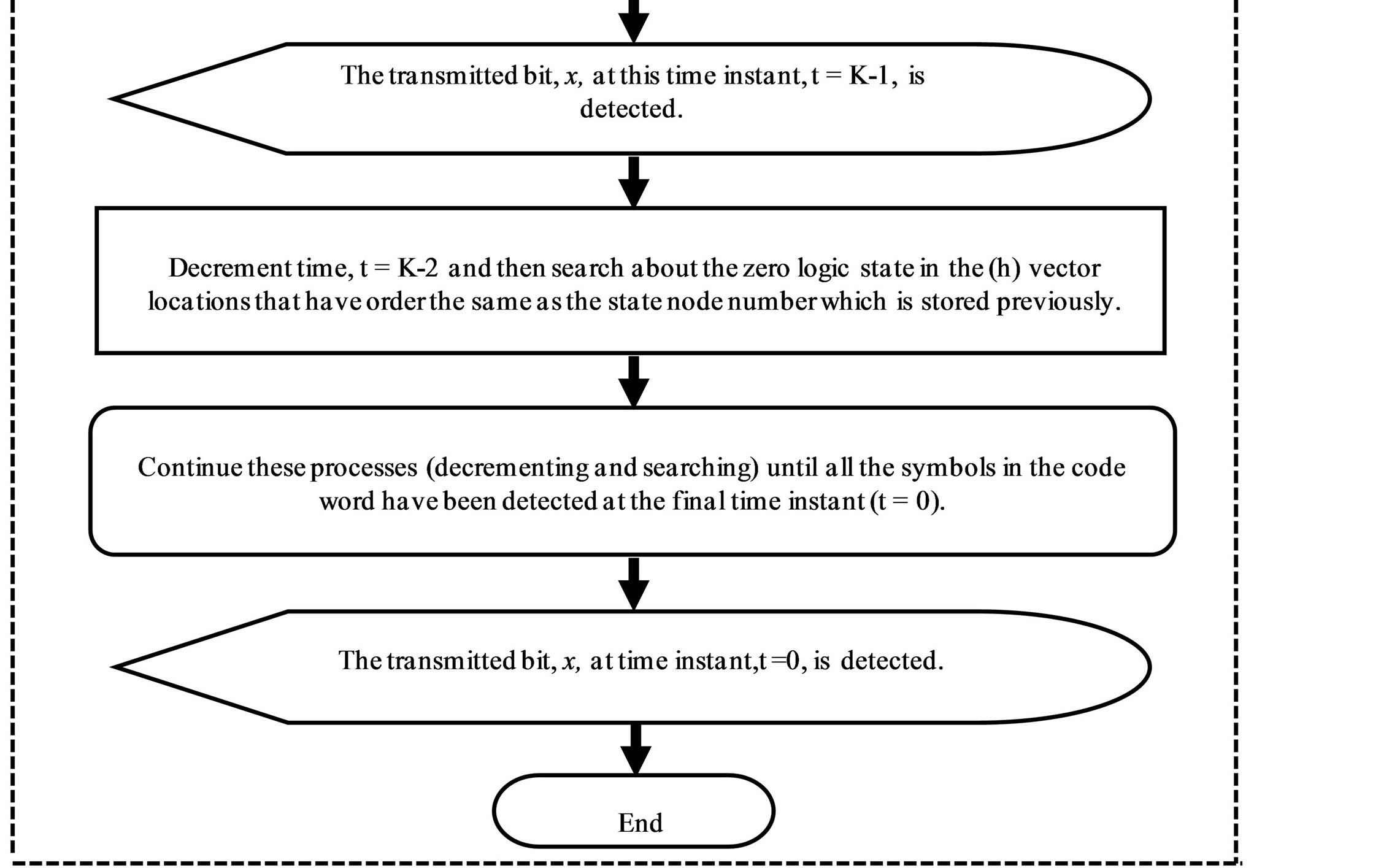
Figure 4. Flow chart of the  -ring-TCM demodulator-decoder-based Yaletharatalhussein decoding algorithm.
-ring-TCM demodulator-decoder-based Yaletharatalhussein decoding algorithm.
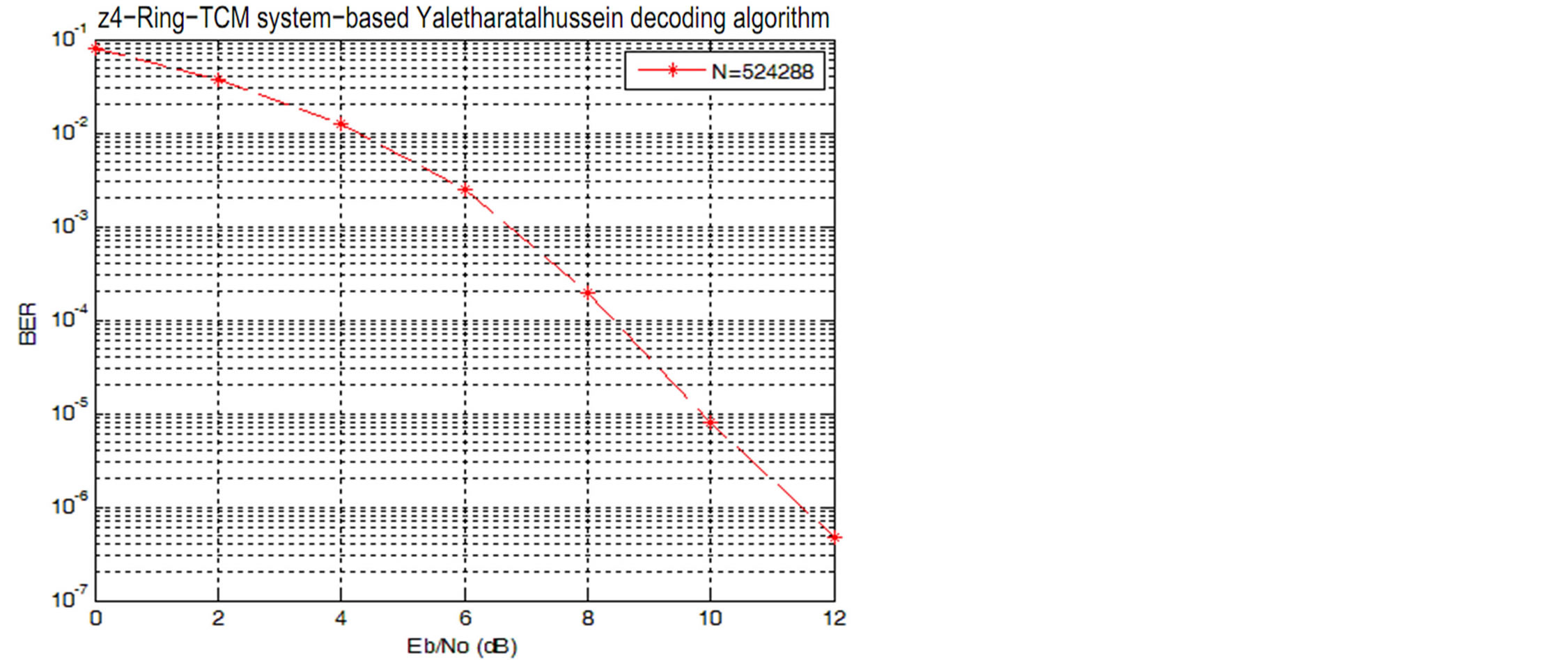
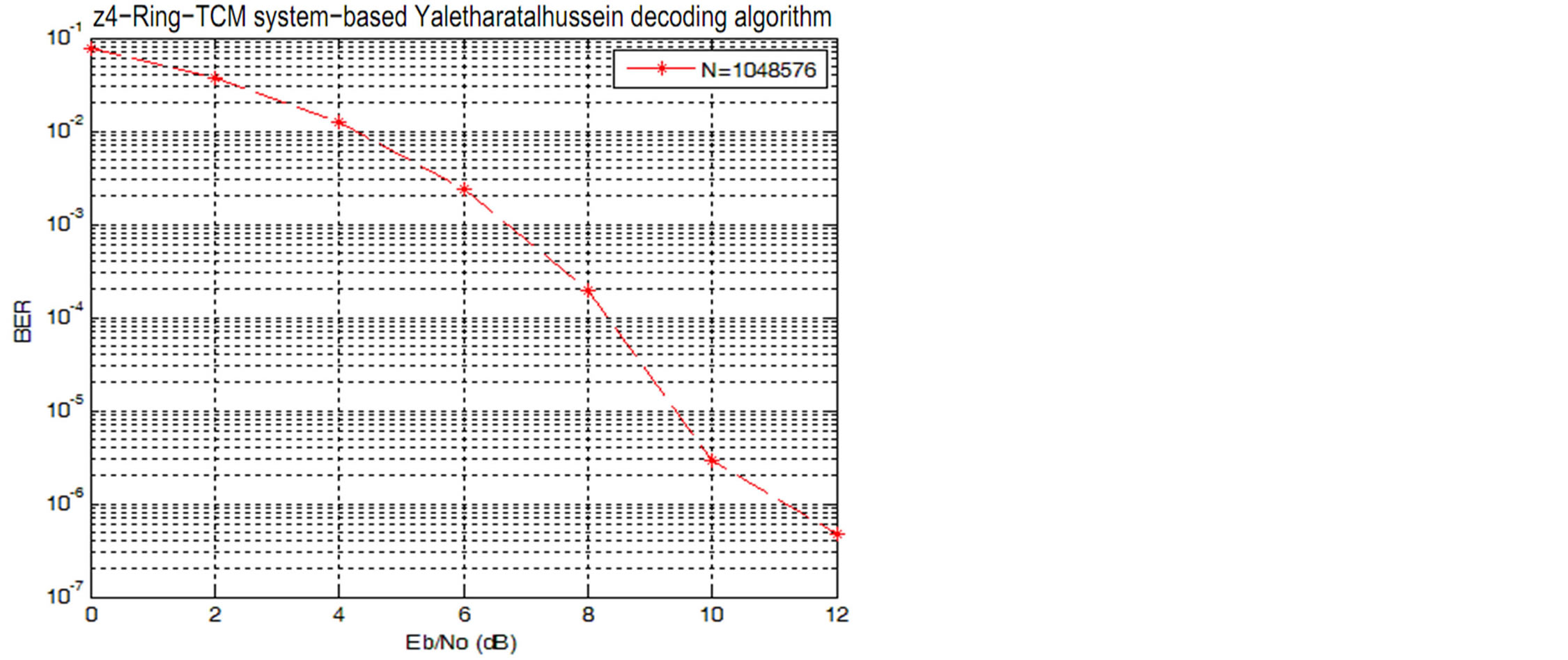
Figure 5. The (BER) versus 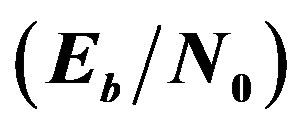 performance of the
performance of the  -Ring-TCM-PAM scheme-based Yaletharatalhussein algorithm.
-Ring-TCM-PAM scheme-based Yaletharatalhussein algorithm.

Table 3. Performance of the ring-TCM schemes.
messages are decoded in blocks of only about 200 bits or so, whereas in turbo coding the blocks are on the order of 16K bits long. Non-binary TCM codes outperform binary TCM codes with a small increase in decoding complexity. The use of non-binary TCM codes led to reduction in the effective input block length, since each m bits of binary information correspond to one non-binary symbol for q = 2m, and thus non-binary system can be used with high number of symbols.
A future work can be done by applying the Yaletharatalhussein decoding algorithm to higher order rings of integers such as, 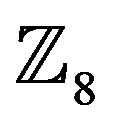 ,
, 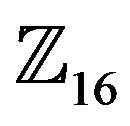 ,
, 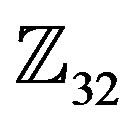 , and
, and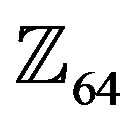 , and then study the error performance and bandwidth efficiency of the system for different types of modulation schemes and orders: 8, 16, 32, and 64.
, and then study the error performance and bandwidth efficiency of the system for different types of modulation schemes and orders: 8, 16, 32, and 64.
REFERENCES
- S. Ortiz, “4G Wireless Begins to Take Shape,” Computer, Vol. 40, No. 11, 2007, pp. 18-21. http://dx.doi.org/10.1109/MC.2007.369
- C. Berrou and A. Glavieux, “Near Optimum Error Correcting Coding and Decoding: Turbo Codes,” IEEE Transactions on Communications, Vol. 44, No. 10, 1996, pp. 1261-1271. http://dx.doi.org/10.1109/26.539767
- R. Gallager, “Low Density Parity Check Codes,” IEEE Transactions on Information Theory, Vol. 8, No. 1, 1962, pp. 21-28. http://dx.doi.org/10.1109/TIT.1962.1057683
- D. J. C. Mackay and R. M. Neal, “Near Shannon Limit Performance of Low Density Parity Check Codes,” Electronics Letters, Vol. 33, No. 6, 1997, pp. 457-458. http://dx.doi.org/10.1049/el:19970362
- B. Lu, X. Wang and K. R. Narayanan, “LDPC-Based Space-Time Coded OFDM Systems over Correlated Fading Channels: Performance Analysis and Receiver Design,” Proceedings of the 2001 IEEE International Symposium on Information Theory, Washington DC, Vol. 1, 24-29 June 2001, p. 313.
- “Using MIMO-OFDM Technology to Boost Wireless LAN Performance Today,” White Paper, Datacomm Research Company, St Louis, 2005.
- H. Sampath, S. Talwar, J. Tellado, V. Erceg and A. J. Paulraj, “A Fourth-Generation MIMO-OFDM Broadband Wireless System: Design, Performance, and Field Trial Results,” IEEE Communications Magazine, Vol. 40, No. 9, 2002, pp. 143-149. http://dx.doi.org/10.1109/MCOM.2002.1031841
- L. R. Bahl, J. Cocke, F. Jelinek and J. Raviv, “Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate,” IEEE Transactions on Information Theory, Vol. 20, No. 2, 1974, pp. 284-287. http://dx.doi.org/10.1109/TIT.1974.1055186
- L. Hanzo, T. H. Liew and B. L. Yeap, “Turbo Coding, Turbo Equalisation and Space-Time Coding,” IEEE Press and John Wiley & Sons, Ltd, Chichester, 2002. http://www-mobile.ecs.soton.ac.uk
- M. O. Damen, A. Chkeif and J.-C. Belfiore, “Lattice Code Decoder for Space-Time Codes,” IEEE Communications Letters, Vol. 4, No. 5, 2000, pp. 161-163. http://dx.doi.org/10.1109/4234.846498
- M. O. Damen, H. E. Gamal and G. Caier, “On MaximumLikelihood Detection and the Search for Closest Lattice Point,” IEEE Transactions on Information Theory, Vol. 49, No. 10, 2003, pp. 2389-2402. http://dx.doi.org/10.1109/TIT.2003.817444
- B. Hochwald and S. ten Brink, “Achieving Near-Capacity on a Multiple-Antenna Channel,” IEEE Transactions on Communications, Vol. 51, No. 3, 2003, pp. 389-399. http://dx.doi.org/10.1109/TCOMM.2003.809789
- D. Pham, K. R. Pattipati, P. K. Willett and J. Luo, “An Improved Complex Sphere Decoder for V-BLAST Systems,” IEEE Signal Processing Letters, Vol. 11, No. 9, 2004, pp. 748-751. http://dx.doi.org/10.1109/LSP.2004.833522
- R. Carrasco, F. Lopez and P. Farrell, “Ring-TCM for M-PSK Modulation: AWGN Channels and DSP Implementation,” IEE Proceedings of Communications, Vol. 143, No. 5, 1996, pp. 273-280. http://dx.doi.org/10.1049/ip-com:19960738
- E. H. Connel, “Elements of Abstract and Linear Algebra,” Coral Gables, Florida, 2004.
- R. A. Carrasco and M. Johnston, “Non-Binary Error Control Coding for Wireless Communications and Data Storage,” John Wiley & Sons, Ltd., UK, 2009.

