Communications and Network
Vol.5 No.3(2013), Article ID:35438,7 pages DOI:10.4236/cn.2013.53024
Throughput Maximization Based on Optimal Access Probabilities in Cognitive Radio System
Electrical and Computer Engineering Department Ryerson University, Toronto, Canada
Email: melalem@ryerson.ca, lzhao@ee.ryerson.ca
Copyright © 2013 Mohamed Elalem, Lian Zhao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 11, 2013; revised March 15, 2013; accepted April 15, 2013
Keywords: Cognitive Radio; Access Probability; Underlay/Overlay Schemes; Marckov Model
ABSTRACT
Well-established fact shows that the fixed spectrum allocation policy conveys to the low spectrum utilization. The cognitive radio technique promises to improve the low efficiency. This paper proposes an optimized access strategy combining overlay scheme and underlay scheme for the cognitive radio. We model the service state of the system as a continuous-time Markov model. Based on the service state, the overlay manner or/and the underlay manner is/are used by the secondary users. When the primary user is not transmitting and only one secondary user has the requirement to transmit, the secondary system adopts the overlay scheme. When the primary user is transmitting and the secondary users want to transmit simultaneously, an underlay scheme with an access probability is adopted. We obtain the optimal access probability in a closed form which maximizes the overall system throughput.
1. Introduction
The wireless spectrum resource has become the major bottleneck for the development of the future wireless communications. Recent researches in spectrum-sharing techniques have enabled different wireless communication technologies to coexist and cooperate towards achieving a better gain from the limited spectrum resources. This started when spectrum utilization measurements showed that most of the allocated spectrum experiences low utilization [1]. Certain authorities, as Federal Communications Commission (FCC) for radio spectrum regulation, divide the radio spectrum into many frequency bands, and licenses for the often exclusive usage of these bands are provided to operators, typically for a long time. Depending on the type of radio service that is then provided by the licensees, frequency bands are often idle in many areas, and inefficiently used. The concept of spectrum sharing (the coexisting of different radio systems in the same spectrum) then occurred [2], as one device may transmit, while others in the area are idle. Moreover, radio systems can dynamically use and release spectrum wherever and whenever they are available. This dynamic spectrum access helps to minimize unused spectral bands.
In spectrum sharing systems, the secondary user can adopt two types of access schemes: overlay scheme and underlay scheme. In underlay scheme, the licensed spectrum band can be accessed without considering the primary user’s activities, but with strict power constraint. In overlay scheme, the secondary user senses the spectrum bands and accesses the unused spectrum spots. The secondary users must be ceased when the primary user appears in the band and resumed when the primary user finishes its service.
The different features of these two schemes enable them to make up with each other. In [3,4], the papers give a mixed access strategy: When the channel is being used by the primary user, the secondary users access the channel with a probability in underlay manner. When the channel is idle, they choose to access in overlay manner.
There have been several previous efforts addressing these two schemes from different points of view. In [3], the authors study the capacity of the secondary users and the impact of the primary user’s activities for both schemes. The authors in [5] conclude that the overlay spectrum sharing strategy offers higher network capacity and the interference threshold limits the capacity in the overlay strategy more than its underlay capacity.
In [6], analytical formulation of DSA with imperfect spectrum sensing has been presented, only the case of same priority for all subscribers has been considered. In [7], the authors assume that primary users and secondary users cannot operate simultaneously on the same spectrum band, then a Continuous Time Markov Chain (CTMC) is proposed to model the interactions between these different users. They derive a tradeoff between spectrum efficiency and fairness. However, the optimal access probability is not a precise value. An optimal access probability with different criteria is given in [8] for pure underlay scheme.
Based on [8], this paper proposes a mixed overlay and underlay access scheme. The secondary users access the channel with an optimal probability in an underlay scheme when the spectrum is occupied by the primary user. Meanwhile, when the spectrum is idle, the secondary users access the channel in an overlay manner. This approach can maximize the total average throughput for the secondary users and limit the interference on the primary user.
The optimized access strategy proposed in this paper is similar in spirit to the work done in [8]. We further introduce a new optimized parameter (r) to determine the best access probability to achieve the highest throughput. Closed forms for the achieved capacity are provided as well as the optimized access parameters.
The rest of this paper is organized as follows. Section 2 introduces the system model and assumptions. In Section 3, the maximal throughput expressions for the two schemes are given. The optimal access strategy for equiprobability case is introduced in Section 4. While Section 5 introduces the case of unlike access probability. Performance analysis and simulation results are given in Section 6. Finally, the paper is summarized in Section 7.
2. System Model and Assumptions
Figure 1 illustrates the system model which consists of a primary user (P) and two cognitive users  sharing a W Hz wireless channel. It is assumed that both cognitive users can sense the primary user perfectly. A cognitive base station is assumed to make the cognitive users exchange their information among them. An example of these information is the real-time service state. The ser-
sharing a W Hz wireless channel. It is assumed that both cognitive users can sense the primary user perfectly. A cognitive base station is assumed to make the cognitive users exchange their information among them. An example of these information is the real-time service state. The ser-
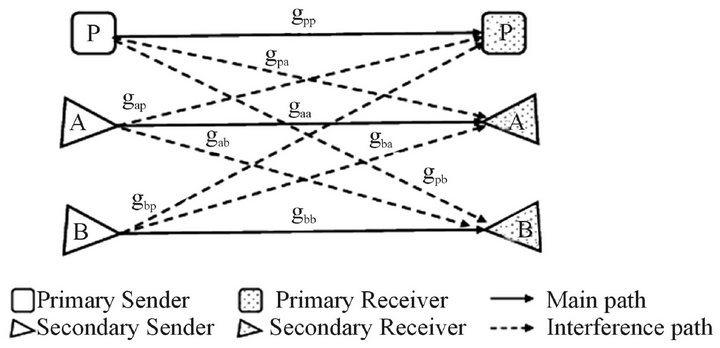
Figure 1. The additive interference channel for a pair of primary and cognitive links with channel gain coefficients: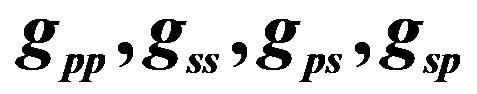 .
.
vice state indicates a user’s requirement for transmitting at specific time. The primary user can employ the channel without considering secondary users’ service state.
The traffic pattern of the primary and the two secondary users is modeled as independent Poisson processes with arrival rates ,
, 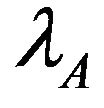 and
and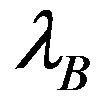 , respectively.
, respectively.
The service times are assumed to be exponentially distributed with rates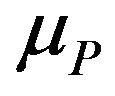 ,
,  and
and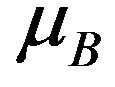 , respectively. We define service state of the system as the sum service state of all the users in the system at a moment. Based on the individual’s service state, we get the service state set for the system as
, respectively. We define service state of the system as the sum service state of all the users in the system at a moment. Based on the individual’s service state, we get the service state set for the system as . State
. State
“0” represents there is no user tends to transmit on the channel; State “P” represents only the primary user is transmitting on the channel; State “A” represents only user A wants to transmit on the channel; State “B” represents only user B wants to transmit on the channel; State “AB” represents both cognitive users want to transmit on the channel at the same time; State “PA” represents user A wants to transmit on the channel while the primary is transmitting; State “PB” represents user B wants to transmit on the channel while the primary user is transmitting; State “PAB” represents both A and B want to transmit on the channel while the primary user is transmitting. These states in the cognitive radio system can be modeled as an eight-state continuous time Markov model, as shown in Figure 2 [8].
The rate at which transitions take place out of state si equals to the rate at which transitions take place into state sj. The normalization equations governing this flow balance can be written as
 (1)
(1)
where  represents the steady-state probability of being in state
represents the steady-state probability of being in state 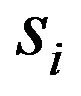 and
and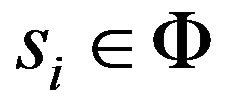 . Also we have
. Also we have
 (2)
(2)
The steady state probabilities for all the states can be found by solving the set of the linear Equations (1) and (2).
3. Secondary User’s Maximal Throughput
3.1. Maximal Throughput for Overlay Scheme
In the overlay scheme, the secondary users can only ac-

Figure 2. The continuous time Markov model of the service state and the flow balance.
cess the spectrum hole which is currently not used by the primary user. They can not co-exist on the same spectrum band. If one secondary user is transmitting, the only interference is the background noise. The user A or B accesses the channel with power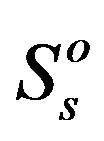 . Since in the overlay manner, only one user can transmit, the maximal data rate for each of them individually is
. Since in the overlay manner, only one user can transmit, the maximal data rate for each of them individually is
 (3)
(3)
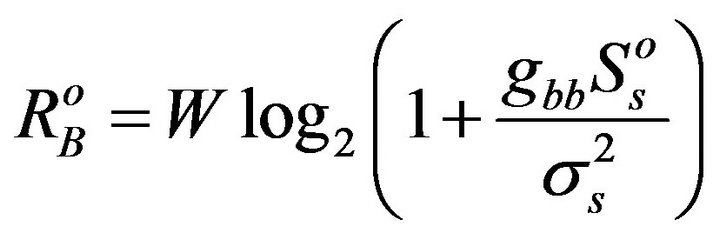 (4)
(4)
where 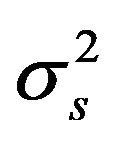 is noise power. These rates can be achievable with the following corresponding probabilities:
is noise power. These rates can be achievable with the following corresponding probabilities:
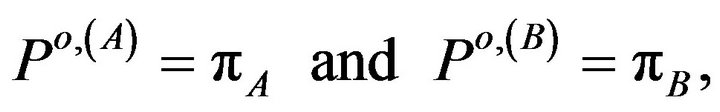
respectively.
3.2. Maximal Throughput for Underlay Scheme
Unlike the overlay scheme, in the underlay system, secondary users are allowed to share the channel simultaneously with the primary user pledging not to violate the limit of interference which is assumed as .
.
Since the secondary users A and B can get the service state of the system with the help of their base station, A and B make access decision based on the service state of the system. Here, there are two possible service state sets. When the service state is , which indicates the primary user P is not transmitting and only one secondary user has the requirement to transmit. The other case is when the service state
, which indicates the primary user P is not transmitting and only one secondary user has the requirement to transmit. The other case is when the service state
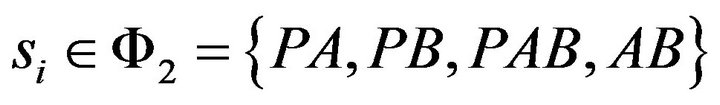 , which indicates that the primary user is transmitting or both secondary users want to transmit at the same time. User A and B have to adopt their powers
, which indicates that the primary user is transmitting or both secondary users want to transmit at the same time. User A and B have to adopt their powers  to access the channel with probabilities
to access the channel with probabilities 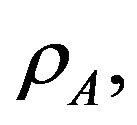 and
and , respectively in the underlay scheme. In order to protect the primary user and decrease the mutual interference between secondary users, we assume that
, respectively in the underlay scheme. In order to protect the primary user and decrease the mutual interference between secondary users, we assume that
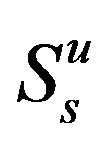 satisfies the minimum SINR requirement.
satisfies the minimum SINR requirement.
These probabilities  and
and  determine the sum throughput of the secondary users and the interference on the primary user. When
determine the sum throughput of the secondary users and the interference on the primary user. When 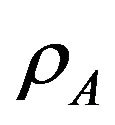 and/or
and/or  are large, the sum throughput may be large and the chance to coexist with primary user is large, too. Our goal is to obtain optimal access probabilities to maximize the total secondary throughput, while limit the interference on the primary user. The service state set of the system in the underlay manner is
are large, the sum throughput may be large and the chance to coexist with primary user is large, too. Our goal is to obtain optimal access probabilities to maximize the total secondary throughput, while limit the interference on the primary user. The service state set of the system in the underlay manner is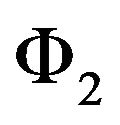 . Hence the actual access state set is
. Hence the actual access state set is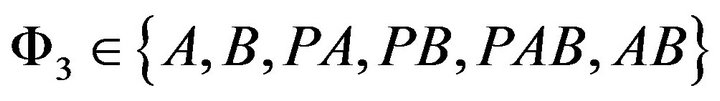 . The users’ maximal data rates under each state in the underlay manner is given in as
. The users’ maximal data rates under each state in the underlay manner is given in as
 (5)
(5)
where 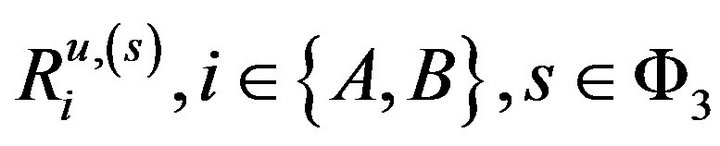 denotes the i’s maximal data rate for the underlay case. The term
denotes the i’s maximal data rate for the underlay case. The term
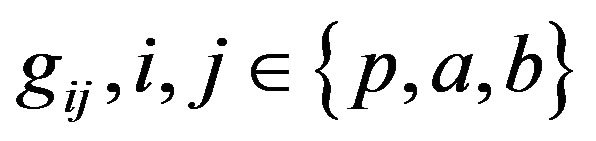 is the channel power gain between the transmitter of the user i and the receiver j as shown in
is the channel power gain between the transmitter of the user i and the receiver j as shown in
Figure 1.  is the transmit power of the primary user.
is the transmit power of the primary user.
The corresponding probabilities of these rates are:
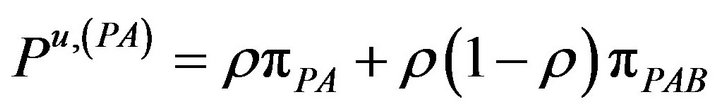 (6.a)
(6.a)
 (6.b)
(6.b)
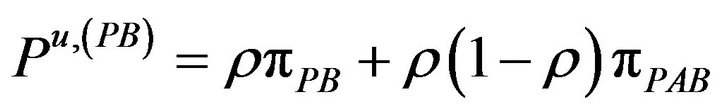 (6.c)
(6.c)
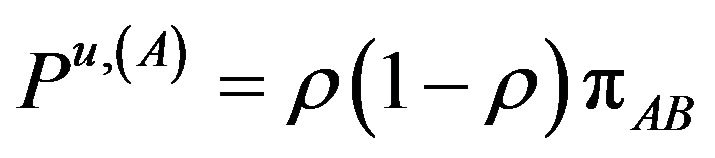 (6.d)
(6.d)
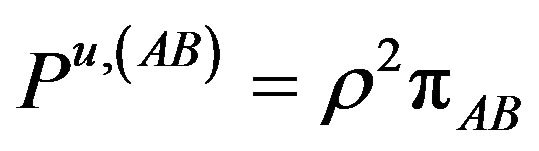 (6.e)
(6.e)
 (6.f)
(6.f)
4. Equiprobability Optimal Access Strategy
In this section we introduce an optimal access strategy which makes the cognitive network to operate in both schemes. During primary user’s idle periods, the network employs the overlay scheme; while in primary user’s busy periods, the network permits the secondary users to use the channel with probability  subject to satisfying the interference threshold constraint. The parameter
subject to satisfying the interference threshold constraint. The parameter  is a secondary service parameter which has to be adjusted based on the spectrum status to achieve maximum throughput.
is a secondary service parameter which has to be adjusted based on the spectrum status to achieve maximum throughput.
Based on Equations (3) to (5), we can get the average throughput for the secondary users as
 (7)
(7)
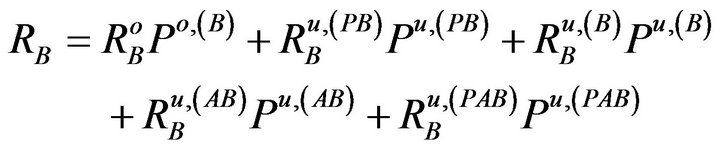 (8)
(8)
The total throughput of the cognitive network is
 (9)
(9)
Using Equaions (6)-(8),  can be written in the quadrature form as
can be written in the quadrature form as
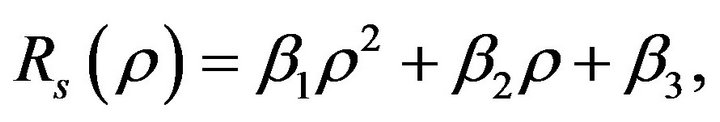 (10)
(10)
where  and
and 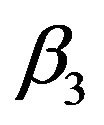 are given as follows
are given as follows
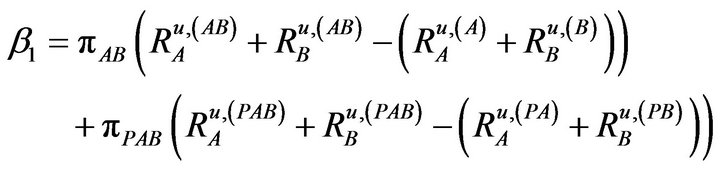
 (11)
(11)
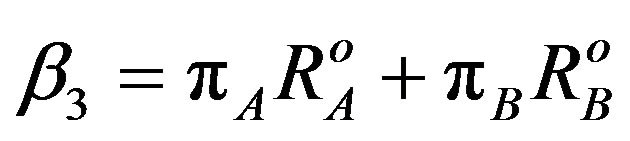
To maximize the secondary throughput, we take the first derivative of  with respect to
with respect to  and equate it to zero.
and equate it to zero.
Solving for  leads to the optimal access probability.
leads to the optimal access probability.
 (12)
(12)
We can note from Equation (12) that  is always positive. Since
is always positive. Since  is a probability value (i.e.,
is a probability value (i.e.,
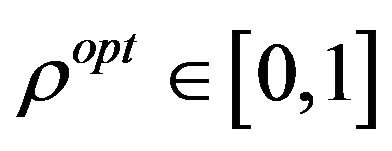 ), the value of
), the value of  is always negative. The throughput function of the secondary network in Equation (9) is concave down. Thus it must have a unique maximum value, it can be expressed as
is always negative. The throughput function of the secondary network in Equation (9) is concave down. Thus it must have a unique maximum value, it can be expressed as
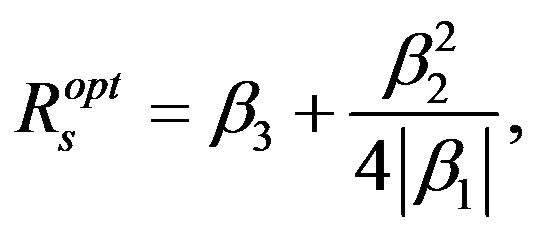 (13)
(13)
where  denotes the absolute value.
denotes the absolute value.
5. Diverse Access Probabilities Strategy
In this section, a similar approach will be followed as in the previous section expect that it is assumed that each user A and B has its own access probability (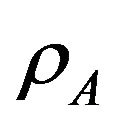 and
and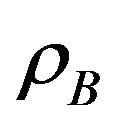 ) respectively. The goal here is to optimize these parameters. So the best access probability for each secondary user is found to achieve the highest possible throughput.
) respectively. The goal here is to optimize these parameters. So the best access probability for each secondary user is found to achieve the highest possible throughput.
User A and B have to adopt their powers 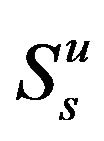 to access the channel with probabilities
to access the channel with probabilities  and
and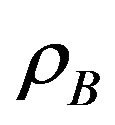 , respectively in the underlay scheme. In order to protect the primary user and decrease the mutual interference between secondary users, we assume again that
, respectively in the underlay scheme. In order to protect the primary user and decrease the mutual interference between secondary users, we assume again that  satisfies the minimum SINR requirement.
satisfies the minimum SINR requirement.
These probabilities  and
and 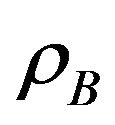 determine the sum throughput of the secondary users and the interference on the primary user. When
determine the sum throughput of the secondary users and the interference on the primary user. When  and/or
and/or 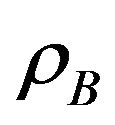 are large, the sum throughput may be large and the chance to coexist with primary user is large, too. Our goal is to obtain optimal access probabilities to maximize the total secondary throughput, while limit the interference on the primary user.
are large, the sum throughput may be large and the chance to coexist with primary user is large, too. Our goal is to obtain optimal access probabilities to maximize the total secondary throughput, while limit the interference on the primary user.
Same service state set 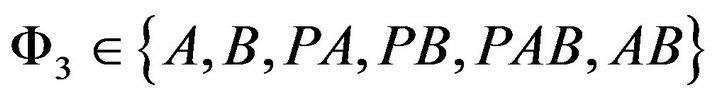
exists. The users’ maximal date rate under each state in the underlay manner is given in Equation (5).
The corresponding probabilities of these rates given in Equation (6) can be written now as
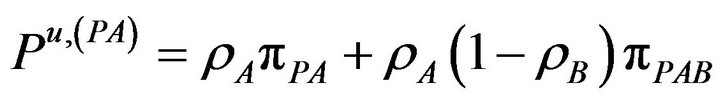 (14.a)
(14.a)
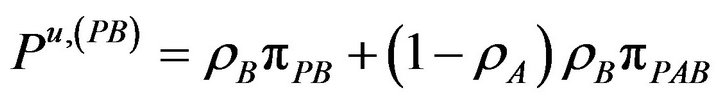 (14.b)
(14.b)
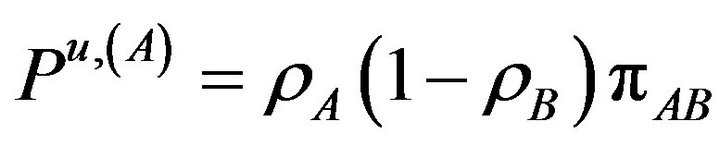 (14.c)
(14.c)
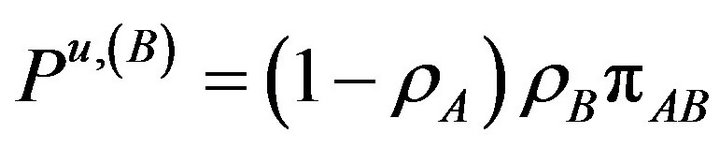 (14.d)
(14.d)
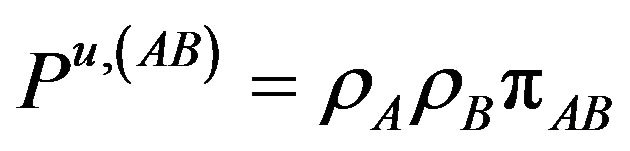 (14.e)
(14.e)
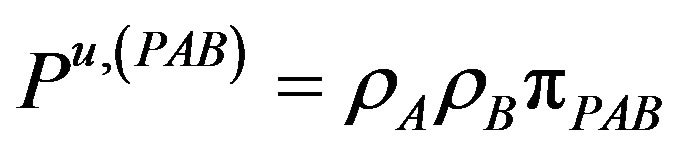 (14.f)
(14.f)
Using Equations (7), (8) and (14),  can be written in a nonlinear equation form as
can be written in a nonlinear equation form as
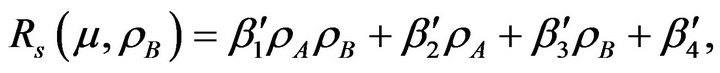 (15)
(15)
where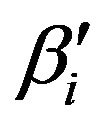 ,
,  is given as follows
is given as follows
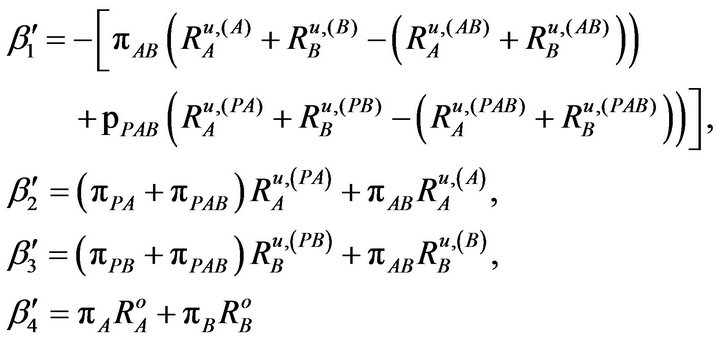 (16)
(16)
To find an optimization solution for Equation (15), we bring up the following theorem:
Theorem 1 Let f be a function with two variables with continuous second order partial derivatives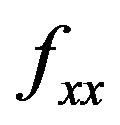 ,
,  and
and  at a critical point
at a critical point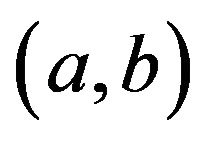 . Let D is the determinant of the Hessian matrix of the function f, i.e.,
. Let D is the determinant of the Hessian matrix of the function f, i.e.,  , thus
, thus
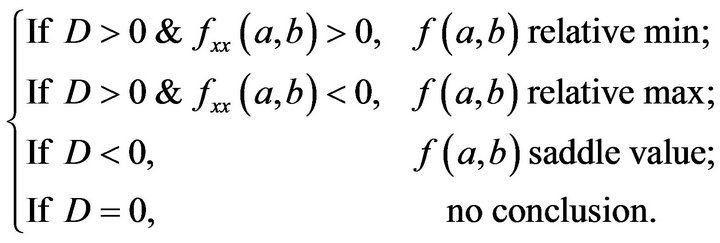
Using Theorem 1, it is forward to conclude that the possible maximum of the utility function  (i.e., Equation (15) occurs at the saddle point of this function which appears at
(i.e., Equation (15) occurs at the saddle point of this function which appears at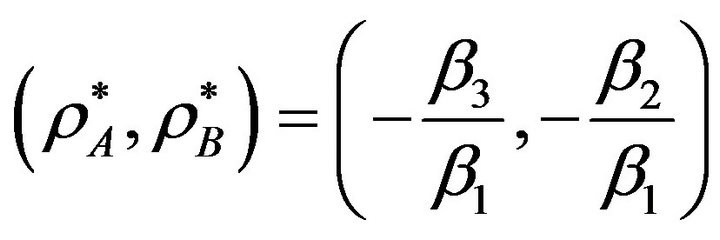 . Then the maximum secondary throughput can be found by substituting this point into Equation (15), this yields
. Then the maximum secondary throughput can be found by substituting this point into Equation (15), this yields
 (17)
(17)
6. Simulation Results
In this section, a simulation example will be carried to illustrate the proposed algorithm. The following powers are set: 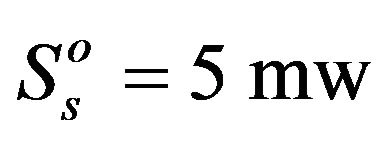 and
and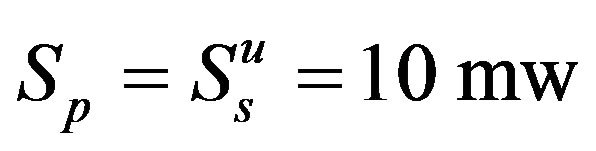 . The arrival rates are set as
. The arrival rates are set as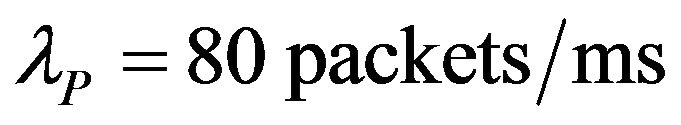 ,
,
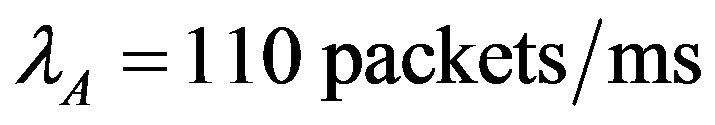 and
and  with equal average times
with equal average times ,
,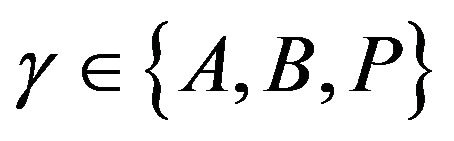 . The wireless channel bandwidth
. The wireless channel bandwidth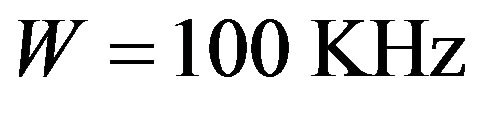 . It is assumed that the loss of power in propagation follows the exponential propagation law with exponent loss 3.5. The position of the primary user’s transmitter and receiver are
. It is assumed that the loss of power in propagation follows the exponential propagation law with exponent loss 3.5. The position of the primary user’s transmitter and receiver are 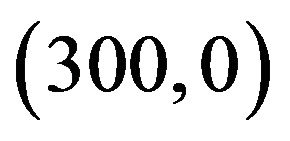 and
and 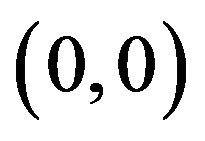 respectively. The user A’s transmitter and receiver location are at
respectively. The user A’s transmitter and receiver location are at  and
and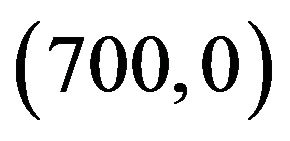 , and for User B’s transmitter and receiver are located at
, and for User B’s transmitter and receiver are located at  and
and 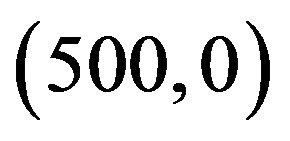 respectively. The interference constraint is assumed double the background noise;
respectively. The interference constraint is assumed double the background noise;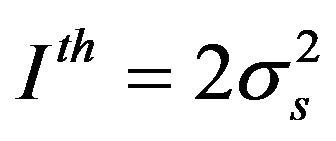 .
.
In Figure 3, the normalized throughput (normalizes to W) for user A, B are shown. Clearly, user B’s throughput is larger than that of A.
This is because B’s transmitter and receiver are located closer than those of A. As the arrival rate of B increases, the throughput of B gets better, which can be understood intuitively. The throughput of A decreases because the user B transmitting creates more interference to it.
In Figure 4, the performance of the optimized access strategy, the pure overlay strategy, the pure underlay strategy and the overall throughput of the secondary network with and without optimization are compared. The underlay strategy can obtain more throughput than the overlay strategy because we have assigned more power for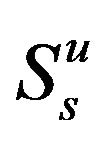 . It should be remembered that the overlay strategy avoids the coexisting time with the primary user, which has the least influence on the primary user. The proposed optimized access strategy maximizes the total throughput and has limited interference on the primary
. It should be remembered that the overlay strategy avoids the coexisting time with the primary user, which has the least influence on the primary user. The proposed optimized access strategy maximizes the total throughput and has limited interference on the primary

Figure 3. Normalized throughput of the secondary system users, A and B.
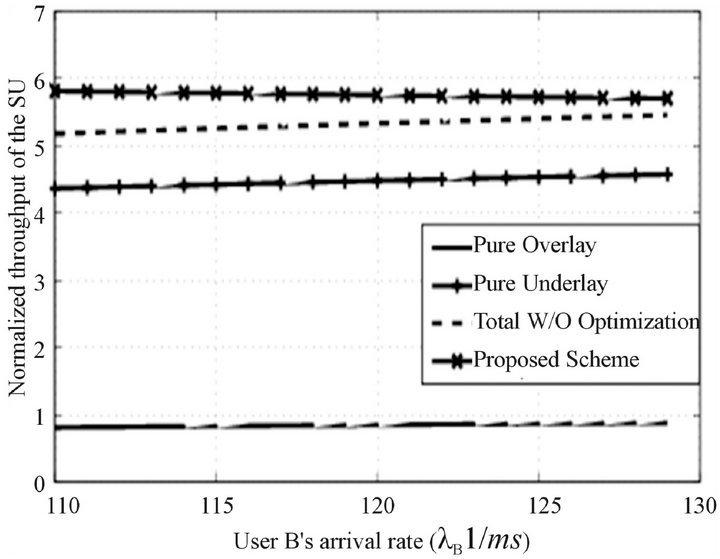
Figure 4. Normalized throughput of the secondary system comparison with with different access schemes.
user, since the condition 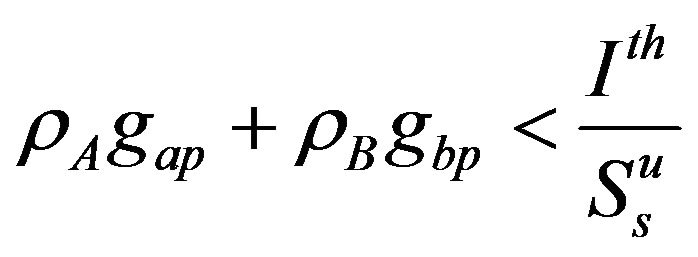 is always guaranteed.
is always guaranteed.
In Figure 5, the normalized throughput for the pure underlay and the proposed underlay strategies versus the access probability is shown. The value of the arrival rate of the user B, 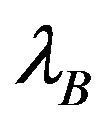 is fixed at 115 ms. As mentioned in Section 4, there is an unique optimal access probability that maximize the throughput.
is fixed at 115 ms. As mentioned in Section 4, there is an unique optimal access probability that maximize the throughput.
In Figure 6, the throughput is plotted versus the two access probabilities. When 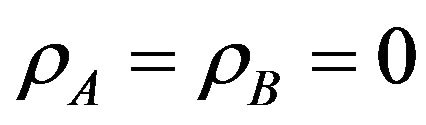 the throughput is at the worst case which equivalent to the overlay throughput. Accessibility of user A enhances the throughput more than that of user B. This is because user A creats less interference on the primary user. The small circle on the graph shows the optimized value of
the throughput is at the worst case which equivalent to the overlay throughput. Accessibility of user A enhances the throughput more than that of user B. This is because user A creats less interference on the primary user. The small circle on the graph shows the optimized value of
 , note that
, note that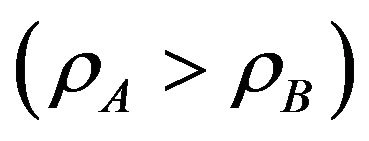 .
.
To study the effect of changing the arrival rate of the far user A, 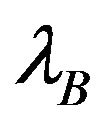 is fixed at 110 ms, while
is fixed at 110 ms, while 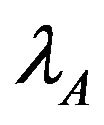 is varied in
is varied in
Figure 7. Because of the nearness of user B where the probability to introduce interference on the primary is hight,  is always less than
is always less than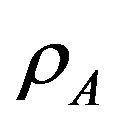 . As
. As  increasesboth access probabilities decrease to mitigate the interference on the primary user. This degradation is more for the near user B.
increasesboth access probabilities decrease to mitigate the interference on the primary user. This degradation is more for the near user B.
7. Conclusion
The two dominant access schemes in the cognitive radio architecture, underlay and overlay, are studied. It is found by some literatures that these two schemes can make up with each other to enhance the system’s performance. This paper proposes a mixed access strategy combining these two schemes. It is assumed that secondary users
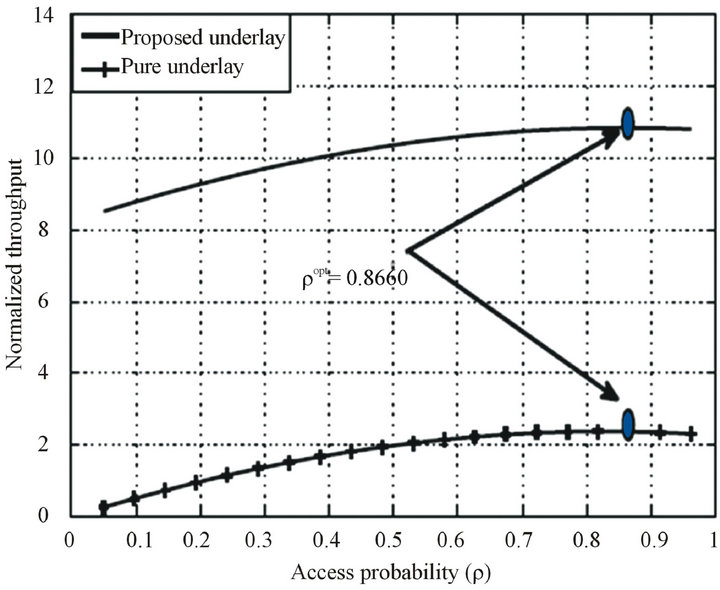
Figure 5. Normalized throughput of the secondary system comparison with with different access schemes.
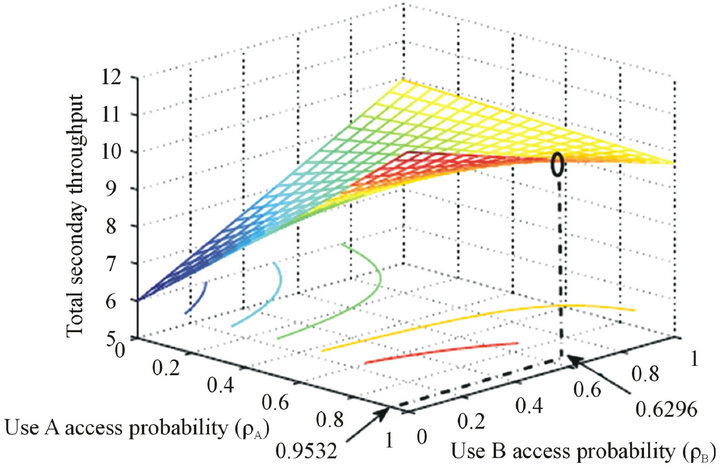
Figure 6. Normalized throughput of the secondary system versus the access probabilities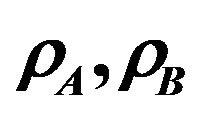 .
.
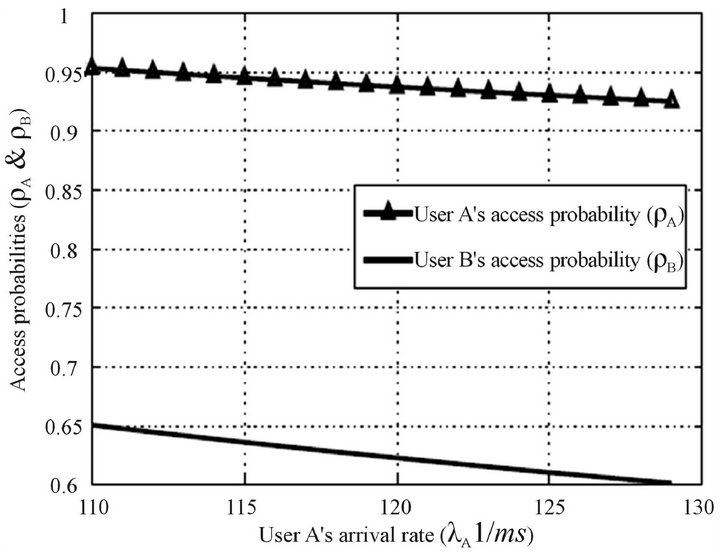
Figure 7. The influence of far user’s arrival rate on the access probabilities.
access the spectrum with certain access probabilities. It is focused on the service state and model the service state of the system as a continuous-time Markov chain. Finally, optimal access probabilities and optimal throughput for this mixed strategy are introduced in closed forms to maximize the overall capacity of the cognitive network. The simulation results show that the proposed access strategy can achieve much better performance for the secondary uses, compared with the single scheme strategies.
REFERENCES
- C. Cordeiro, K. Challapali, D. Birru and N. Shankar, “IEEE 802.22: The First Worldwide Wireless Standard Based on Cognitive Radio,” The First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, 8-11 November 2005, pp. 328- 337. doi:10.1109/DYSPAN.2005.1542649
- M. Marcus, “Unlicensed Cognitive Sharing of TV Spectrum: The Controversy at the Federal Communications Commission,” IEEE Communication Magazine, Vol. 43, No. 5, 2005, pp. 24-25. doi:10.1109/MCOM.2005.1453413
- M. Khoshkholgh, K. Navaie and H. Yanikomeroglu, “Access Strategies for Spectrum Sharing in Fading Environment: Overlay, Underlay, and Mixed,” IEEE Journal on Mobile Computing, Vol. 9, No. 12, 2010, pp. 1780- 1793. doi:10.1109/TMC.2010.57
- X. Kang, Y. Liang, H. Garg and L. Zhang, “SensingBased Spectrum Sharing in Cognitive Radio Networks,” IEEE Transactions on Vehicular Technology, Vol. 58, No. 8, 2009, pp. 4649-4654. doi:10.1109/TVT.2009.2018258
- D. Zhang, Z. Tian and G. Wei, “Spatial Capacity of Narrowband vs. Ultra-Wideband Cognitive Radio Systems,” IEEE Transactions on Wireless Communications, Vol. 7, No. 11, 2008, pp. 4670-4680. doi:10.1109/T-WC.2008.070746
- D. Wong, A. Hoang and F. Chin, “Dynamic Spectrum Access with Imperfect Sensing in Open Spectrum Wireless Networks,” Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), Las Vegas, 31 March 2008-3 April 2008, pp. 2765-2770.
- B. Wang, Z. Ji, K. Liu and T. Clancy, “Primary-Prioritized Markov Approach for Dynamic Spectrum Allocation,” IEEE Transactions on Wireless Communications, Vol. 8, No. 4, 2009, pp. 1854-1865. doi:10.1109/T-WC.2008.080031
- H. Hu and Q. Zhu, “Dynamic Spectrum Access in Underlay Cognitive Radio System with SINR Constraints,” Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Beijing, 24-26 September 2009, pp. 1-4.

