Communications and Network
Vol.4 No.4(2012), Article ID:25004,6 pages DOI:10.4236/cn.2012.44034
Capacity Calculation and Sub-Optimal Power Allocation Scheme for OFDM-Based Systems
Birla Institute of Technology, Mesra, India
Email: infosomu1989@gmail.com, abhishek2003cemk@yahoo.co.in, skumar@bitmesra.in
Received July 19, 2012; revised August 18, 2012; accepted September 21, 2012
Keywords: Interference Reduction; LTE-A; OFDMA; Power Loading; System Capacity
ABSTRACT
For emerging cellular wireless systems, the mitigation of inter-cell interference is the key to achieve a high capacity and good user experience. This paper is devoted to the performance analysis of interference mitigation techniques for the downlink in an orthogonal frequency division multiple access (OFDMA) network, with a focus on the Long Term Evolution-Advanced (LTE-A) standard. Here we have derived a general closed-form equation of system capacity taking multiple cells into consideration and then we have investigated a coordination technique for interference mitigation. For the given interference constraint, how power should be transmitted into each OFDM sub-carrier for prevailing channel condition such that the total transmission rate of the base station can be maximized.
1. Introduction
Radio spectrum is one of the most scarce and valuable resources for wireless communications. Given this fact, new insights into the use of spectrum have challenged the traditional approaches to spectrum management. LTE-A system with OFDMA as downlink multiple access technique will have no intra-cell interference but will have a larger Inter-Cell Interference (ICI). Specifically, in [1] the authors have shown that OFDMA causes inter-cell interference among the users. The amount of interference introduced to the users by adjacent base station depends on the power allocated to the subcarrier as well as the spectral distance between particular subcarrier .The cell edge users are adversely affected due this ICI [2]. 3 GPP has proposed three different solutions to combat ICI i.e. randomization, cancellation and co-ordination, to counter this ICI problem [3]. An intelligent radio resource management is needed for the dynamic allocation of radio resource to its users so as to maintain the QoS and also to best utilize the available spectrum while considering maximization of system throughput and capacity. Transmitter power control is an efficient technique to mitigate the effect of interference specially co-channels interference. Thus, an effective power control algorithms can offer a significant improvement in the system throughput. As we know that OFDM sub-carriers have time-varying fading gains, various power loading schemes have been proposed in the literature [4]. These algorithms maximize the transmission capacity of a single cell scenario. But the use of classical loading algorithms e.g., uniform power and water-filling algorithms, for multi-cellular scenario may result in higher interference since, there exists no coordination. In this paper a downlink transmission has been considered in a multi-cell scenario. Hence, the design problem is as follows. Under interference constraint, how much power should be transmitted into each OFDM sub-carrier for prevailing channels condition such that the total transmission rate of the base station can be maximized?
The organization of this paper is as follows. Section 2 gives a closed-form expression of system capacity for multi-cellular scenario. In Section 3, the system model is described. In Section 4, a suboptimal scheme has been proposed. In Section 5, numerical results are presented. Finally, Section 6 concludes the paper.
2. Closed-Form Expression of System Capacity
From the context of information theory, for M number of adjacent cells closely spaced and N number of nodes in the target cell—the normalized (with respect to bandwidth) system capacity or spectral efficiency can be expressed as
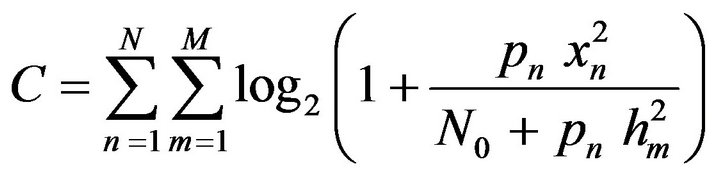 (1)
(1)
where 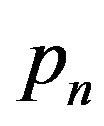 is the delivered power to each sub-channel, N0 is the noise spectral density,
is the delivered power to each sub-channel, N0 is the noise spectral density, 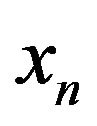 is the sub-channel gain of the cell under consideration, and hm is the subchannel gain associated with the adjacent sub-channels and thus the term
is the sub-channel gain of the cell under consideration, and hm is the subchannel gain associated with the adjacent sub-channels and thus the term 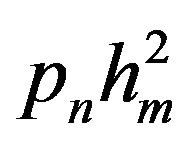 act as inter-cell interference to the system. To maximize the system capacity, we have to maximize the above expression. So, in order to calculate the maximized system capacity, along with the Karush-Kuhn-Tucker (KKT) conditions, the problem is described as follows
act as inter-cell interference to the system. To maximize the system capacity, we have to maximize the above expression. So, in order to calculate the maximized system capacity, along with the Karush-Kuhn-Tucker (KKT) conditions, the problem is described as follows
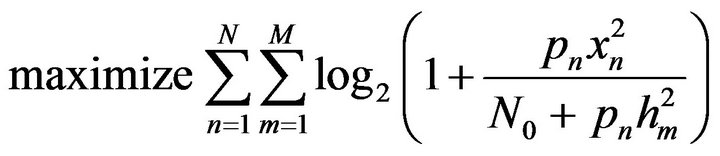 (2)
(2)
or,
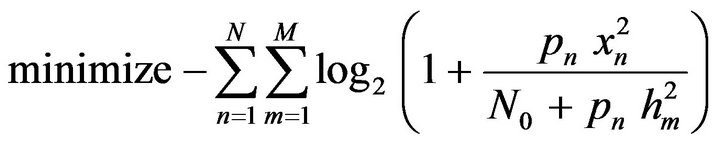 (3)
(3)
subjects to constraints,
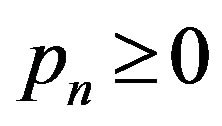


for

The above constraints are self explaining. Here δ is the dual variable and μ is the slack variable. KKT holds for strong duality, which can be solved for two different ways but having equivalent solutions. Here 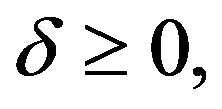
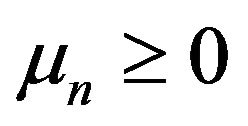 are called Lagrange’s multipliers or dual variables. These KKT conditions are necessary and sufficient conditions for duality.
are called Lagrange’s multipliers or dual variables. These KKT conditions are necessary and sufficient conditions for duality.
Now, taking the problem equation together with the KKT conditions, the partial Lagrangian equation is formulated as,
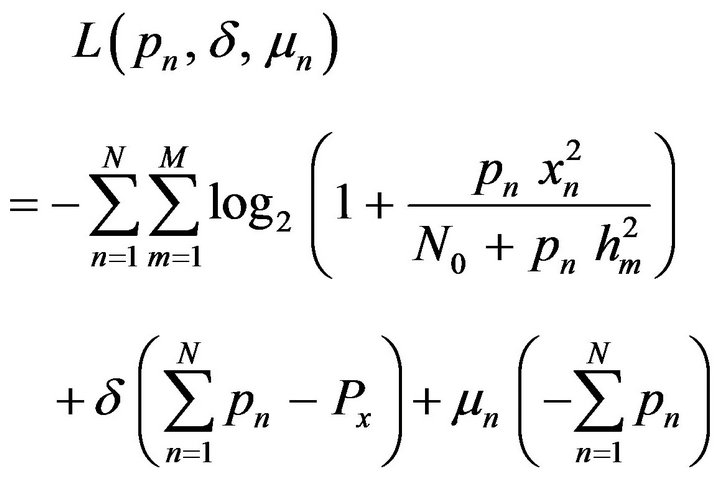 (4)
(4)
To calculate the maximum capacity based on the above expression, partial derivatives of the Lagrangian function with respect to Pn has to be taken and by applying KKT condition, the resulting equation becomes
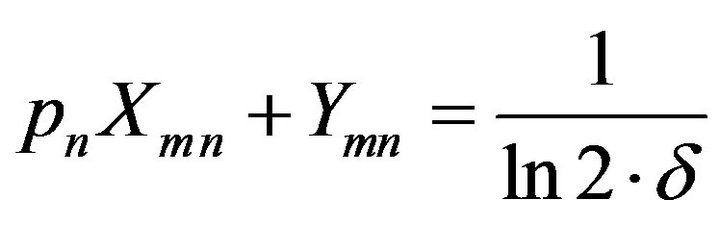 (5)
(5)
where,
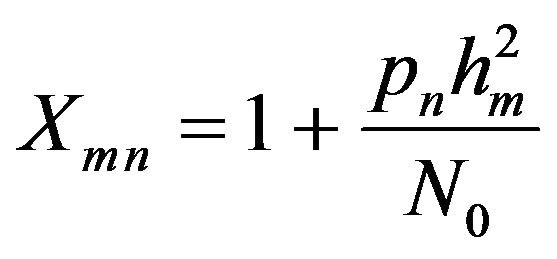

From the above equation, the optimal power has to be calculated and thus the derived closed-form expression of optimized system capacity is given by
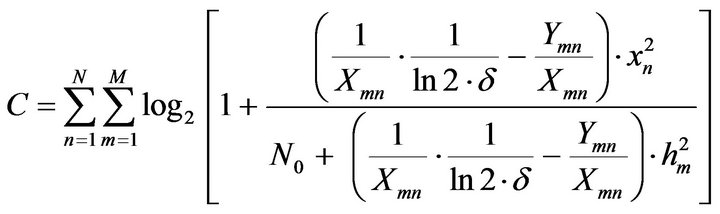 (6)
(6)
This is a generalized closed-form expression of system capacity for multiple cells scenario.
3. System Model
Here we have considered a two-cell scenario. Each cell uses OFDMA and hence, uses frequency reuse factor 1. The available bandwidth is divided into k subcarriers, where k ranges from . It is assumed that the bandwidth for each sub-carrier is Hz and each user uses only one sub-carrier. The numbers of users under BS1 are j, where j ranges from
. It is assumed that the bandwidth for each sub-carrier is Hz and each user uses only one sub-carrier. The numbers of users under BS1 are j, where j ranges from  and users under BS2 are i, where i range from
and users under BS2 are i, where i range from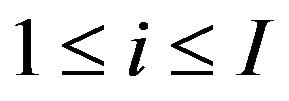 .
. 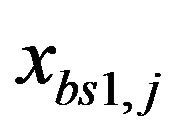 and
and 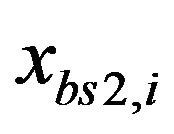 is the transmitted power of BS1 and BS2 respectively.
is the transmitted power of BS1 and BS2 respectively.
In downlink transmission scenario shown in Figure 1, there are four channel gains: i) between the BS2 and its ith user for the sub-carrier denoted as 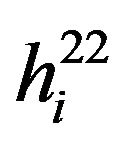 ii) between the BS2 and jth BS1 user, denoted as
ii) between the BS2 and jth BS1 user, denoted as 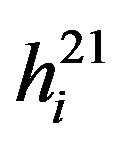 iii) between the BS1 and the ith BS2 user, denoted as
iii) between the BS1 and the ith BS2 user, denoted as 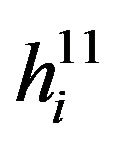 iv) between the BS1 and
iv) between the BS1 and  its jth user for sub-carrier denoted as
its jth user for sub-carrier denoted as 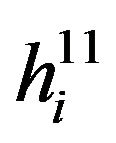 The received signal at the receiver of jth user of BS1 and ith user of BS2 are
The received signal at the receiver of jth user of BS1 and ith user of BS2 are 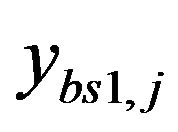 and
and 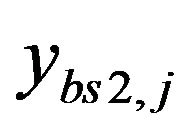 respectively
respectively
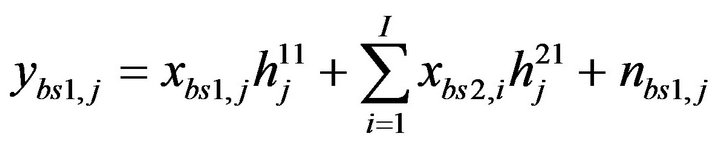 (7)
(7)
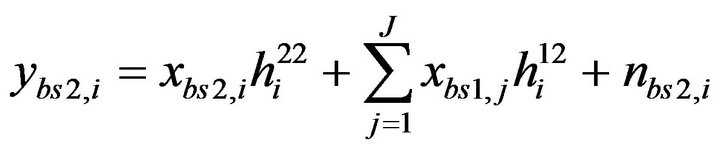 (8)
(8)
where 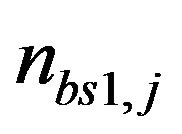 and
and 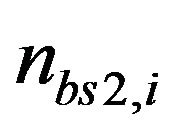 are the received noise at BS1
are the received noise at BS1
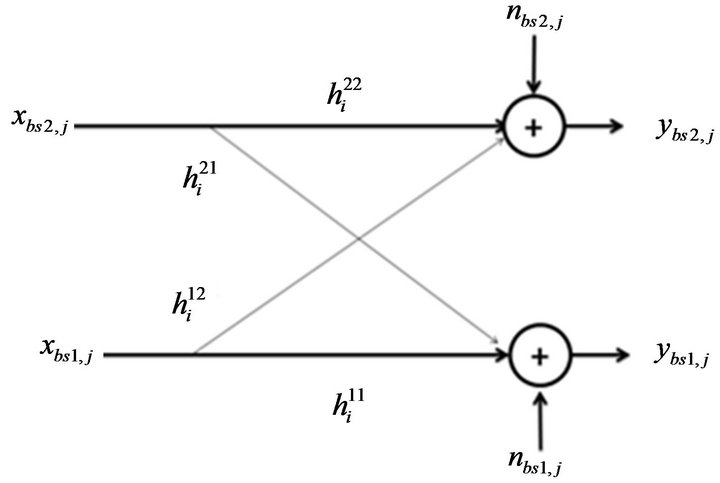
Figure 1. System model.
and BS2 respectively. For protection of BS1 users, we consider constrains on the interference introduced by BS2. The total interference introduced to BS1 can be written as
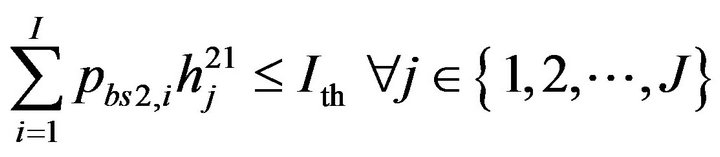 (9)
(9)
4. Proposed Sub-Optimal Scheme
Considering this fact that most of the interference introduced to the BS1 users is induced by BS2 transmission over same sub-carriers. The problem can be formulated as follows
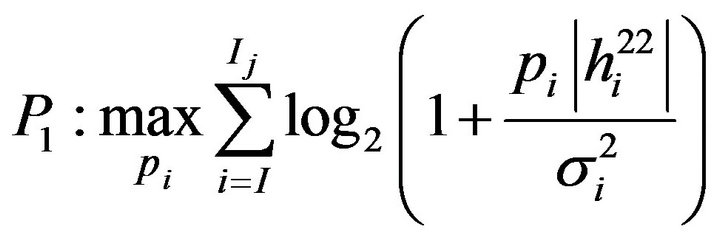 (10)
(10)
subject to
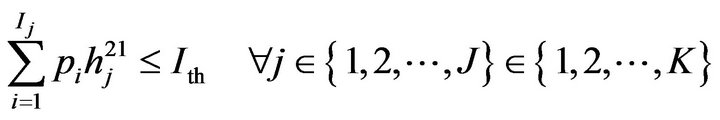 (11)
(11)
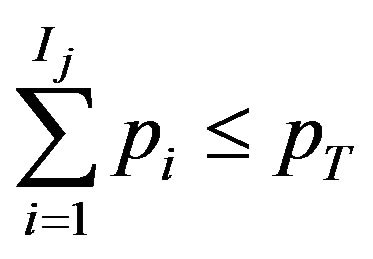 (12)
(12)
 (13)
(13)
where 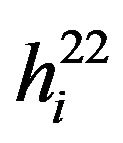 is the channel gain from BS1 to its user and
is the channel gain from BS1 to its user and
 (14)
(14)
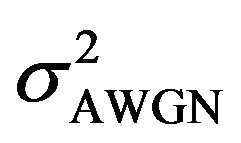 is the mean variance of the additive white Gaussian noise (AWGN). The interference is assumed to be the superposition of large number of independent components; hence, we can model the interference as Gaussian. Assuming that each sub-carrier band is narrow, subcarriers can be approximated as channel having flat and constant gains during transmission. K denotes the total no of sub-carriers, I is the no users of BS2 users and J is the no users of BS1 users. Ith denotes the interference threshold prescribed by the BS1 users. Interference threshold is the maximum tolerable interference on the spectrum being utilized. It is highly variable depending on the allocation of channels to the users within the cell. However for simplicity we can assume a common threshold for all the channels. PT is the fixed total power budget of the system. Ij denotes the set of the same sub-carriers belonging to the BS1. Using the same derivation in [5], we get
is the mean variance of the additive white Gaussian noise (AWGN). The interference is assumed to be the superposition of large number of independent components; hence, we can model the interference as Gaussian. Assuming that each sub-carrier band is narrow, subcarriers can be approximated as channel having flat and constant gains during transmission. K denotes the total no of sub-carriers, I is the no users of BS2 users and J is the no users of BS1 users. Ith denotes the interference threshold prescribed by the BS1 users. Interference threshold is the maximum tolerable interference on the spectrum being utilized. It is highly variable depending on the allocation of channels to the users within the cell. However for simplicity we can assume a common threshold for all the channels. PT is the fixed total power budget of the system. Ij denotes the set of the same sub-carriers belonging to the BS1. Using the same derivation in [5], we get
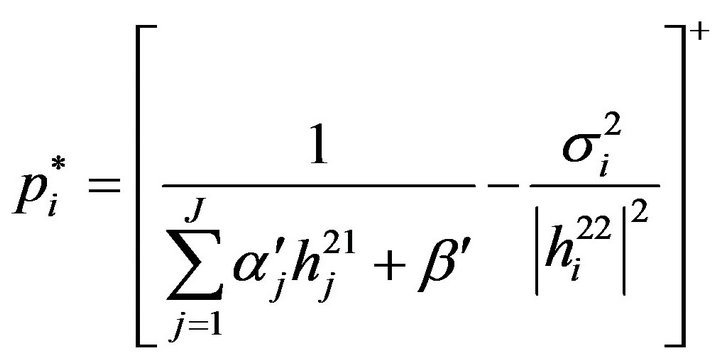 (15)
(15)
where α and β are the non-negative dual variables corresponding to the interference and power constraints respectively. The solution of the problem still has high computational complexity which encourages us to find a simpler, faster and efficient power allocation algorithm. The scheme proposed in this section is based on the fact that if the interference constraints are ignored in P1, the solution of the problem will follow the well-known Waterfilling interpretation [6].
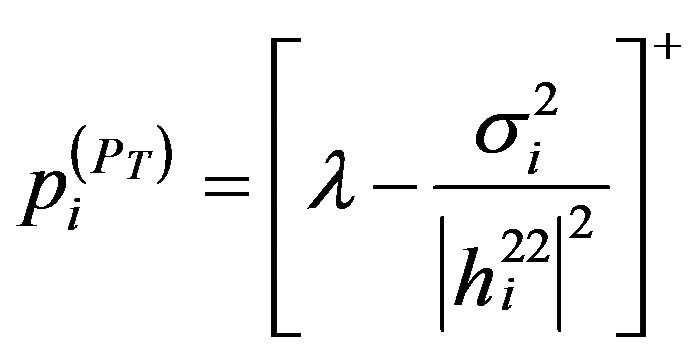 (16)
(16)
where λ is the waterfilling level and is given by
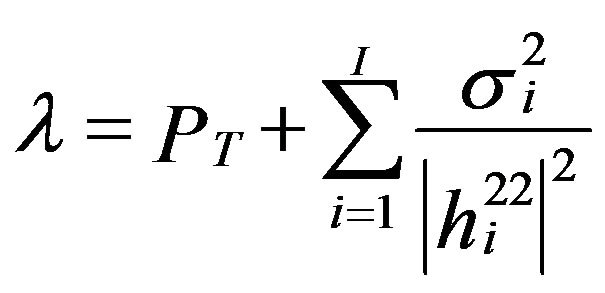 (17)
(17)
On the other side, if the total power constraint is ignored, the Lagrangian of the problem can be written as [7]
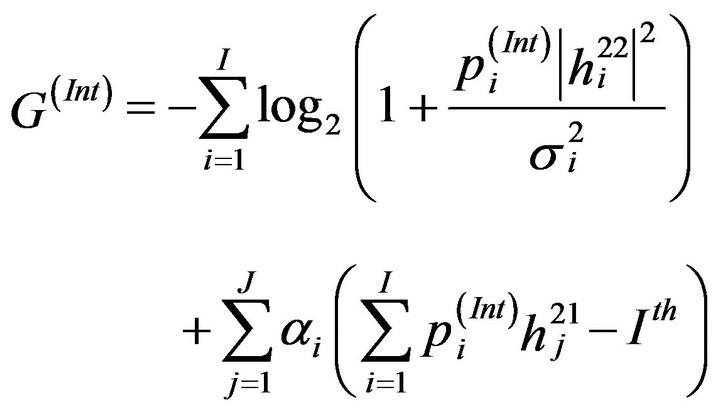 (18)
(18)
where is 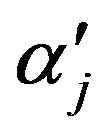 the Lagrange multiplier. Equating
the Lagrange multiplier. Equating

to zero, we get
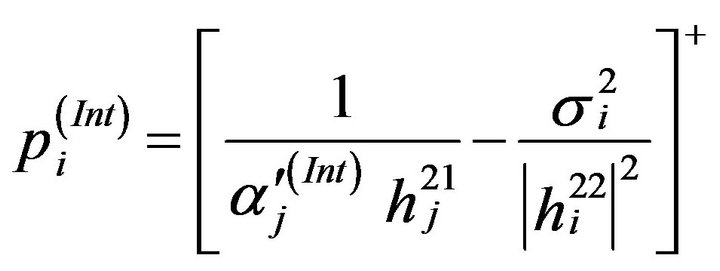 (19)
(19)
where value of 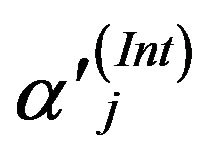 can be calculated by substituting Equation (19) into
can be calculated by substituting Equation (19) into

to get
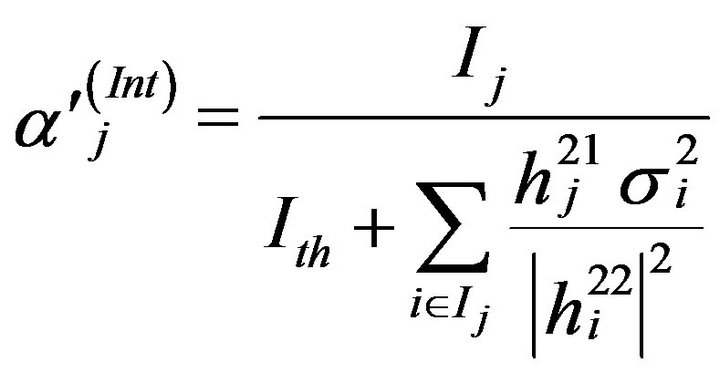 (20)
(20)
In order to solve the optimization problem P1, we can start by assuming that the maximum power that can be allocated for a given subcarrier  is determined according to the interference constraints only by using Equations (11) and (12) for every set of sub-carriers. By such an assumption, we can guarantee that the interference introduced to BS1 users will be under the prespecified threshold. Once the maximum power
is determined according to the interference constraints only by using Equations (11) and (12) for every set of sub-carriers. By such an assumption, we can guarantee that the interference introduced to BS1 users will be under the prespecified threshold. Once the maximum power 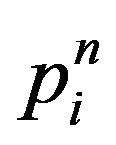 is determined the total power constrain is tested. If the total power constrain is satisfied, then the solution has been found and is equal to maximum power that can be allocated to each subcarrier, i.e.
is determined the total power constrain is tested. If the total power constrain is satisfied, then the solution has been found and is equal to maximum power that can be allocated to each subcarrier, i.e.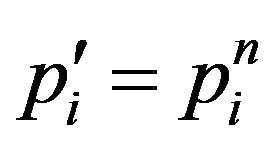 . Otherwise, the available power budget should be distributed among the subcarriers giving that the power allocated to each subcarrier is lower than or equal to the maximum power that can be allocated to each subcarrier
. Otherwise, the available power budget should be distributed among the subcarriers giving that the power allocated to each subcarrier is lower than or equal to the maximum power that can be allocated to each subcarrier , and hence the following problem should be solved:
, and hence the following problem should be solved:
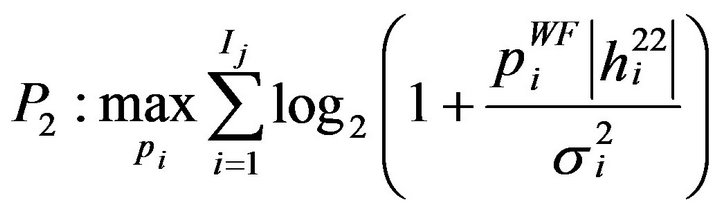 (21)
(21)
subject to
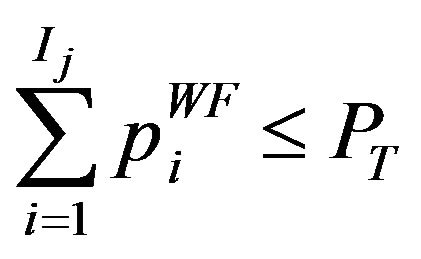 (22)
(22)
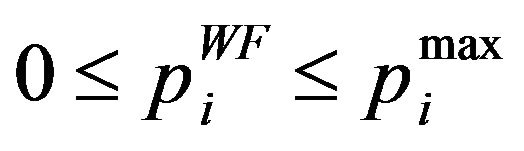 (23)
(23)
The problem can be solved efficiently using the concept of the conventional waterfilling. Given the initial waterfilling solution, the channels that violate the maximum power  are determined and upper bounded with
are determined and upper bounded with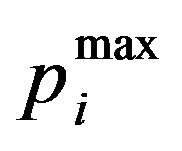 . The total power budget is reduced by subtracting the power assigned so far. At the next step, the algorithm proceeds to successive water-filling over the sub-carriers that did not violate the maximum power
. The total power budget is reduced by subtracting the power assigned so far. At the next step, the algorithm proceeds to successive water-filling over the sub-carriers that did not violate the maximum power  in the last step.
in the last step.
This procedure is repeated until the allocated power  does not violate the maximum power
does not violate the maximum power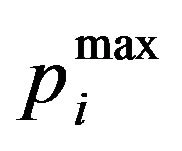 in any of the sub-carriers in the new iteration. The solution
in any of the sub-carriers in the new iteration. The solution 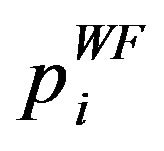 of the problem P2 is satisfying the total power constraint of the problem P2 with equality and also satisfies interference constraints. The suboptimal power allocation implementation algorithm is described in Figure 2. Since it is assumed that
of the problem P2 is satisfying the total power constraint of the problem P2 with equality and also satisfies interference constraints. The suboptimal power allocation implementation algorithm is described in Figure 2. Since it is assumed that 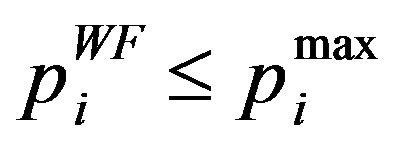 some of the powers allocated to sub-carriers will not reach the maximum allowable values. This will make the interference introduced to
some of the powers allocated to sub-carriers will not reach the maximum allowable values. This will make the interference introduced to

Figure 2. Algorithm flow.
the BS1 user below the threshold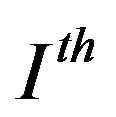 . It is important to mention that the power allocation policy is indeed a waterfilling policy. However, the cut-off value for the channel gain or the threshold for this waterfilling policy is weighted by the inverse of the interference term
. It is important to mention that the power allocation policy is indeed a waterfilling policy. However, the cut-off value for the channel gain or the threshold for this waterfilling policy is weighted by the inverse of the interference term . Specifically, the policy suggests that more power should be allocated to the sub-carrier which has relatively better channel quality.
. Specifically, the policy suggests that more power should be allocated to the sub-carrier which has relatively better channel quality.
5. Results
In the results presented in this section, we assume the values of I and J to be 20 and 4, respectively. We assume the value of total available bandwidth as 1MHz and no of subcarriers to be 33. The value of  is assumed to be 10–11 watts. The total power is assumed to be 10–3 watts. In Figure 3, we plot the achievable transmission rate of the BS2 versus interference threshold prescribed by BS1. The scheme tries to maximize the total throughput of the system under the constraint that each base station cannot transmit more than a specific value PT and the introduced interference to the neighbouring cell is within the interference threshold Ith.
is assumed to be 10–11 watts. The total power is assumed to be 10–3 watts. In Figure 3, we plot the achievable transmission rate of the BS2 versus interference threshold prescribed by BS1. The scheme tries to maximize the total throughput of the system under the constraint that each base station cannot transmit more than a specific value PT and the introduced interference to the neighbouring cell is within the interference threshold Ith.
In Figure 4, we have plotted the interference introduced to BS1 versus the transmit power of BS2. From this figure, we observe that for the same introduced interference level the proposed suboptimal scheme allows transmission of more power than the classical method like uniform power loading. This is possible because the suboptimal scheme considers the interference introduced to BS1 as one of its constraint. So there exists a harmony in power allocation over the sub-carriers which minimize the intercellular interference.
In Figure 5, we have plotted the transmit power and 1/SINR for individual sub-carriers of BS2. 1/SINR basically, represents the amount of interference present in the channel. The suboptimal scheme allows transmission of higher power over sub-carriers where the channel conditions are good and restricts power over sub-carriers where the channel conditions are bad.
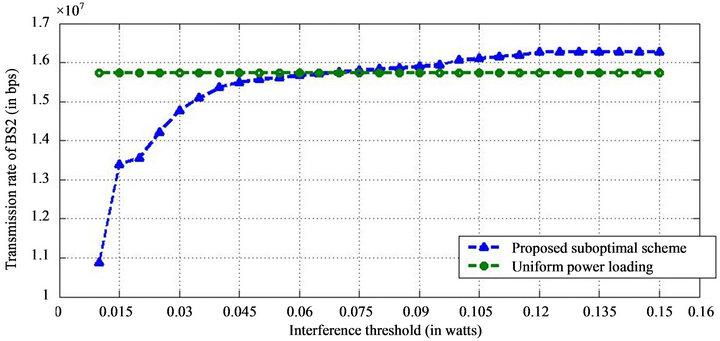
Figure 3. Interference introduced to BS1 vs. transmit power of BS2.
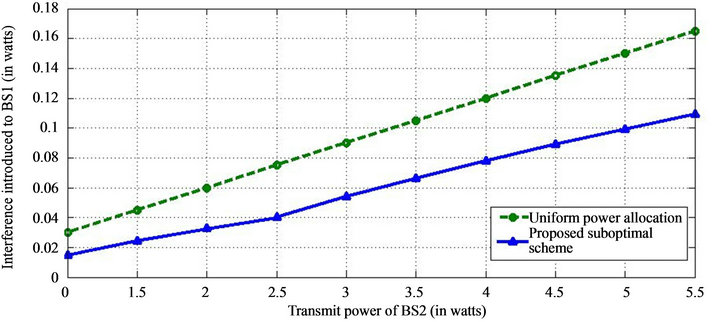
Figure 4. Transmission rate of BS2 vs. interference introduced to BS1.
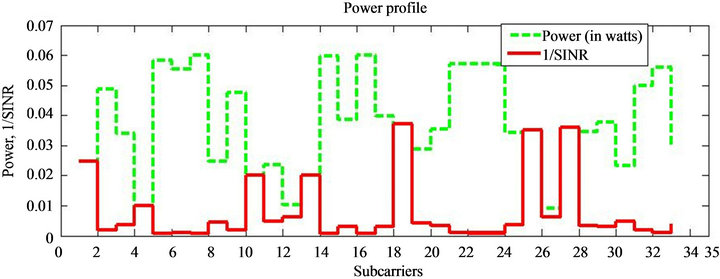
Figure 5. Power profile.
6. Conclusion
In this paper, we have developed a suboptimal power loading algorithm that maximizes the downlink transmission data rate of the BS2 while the interference introduced to the BS1 user remains within a given limit. The proposed algorithm is simpler and more efficient in terms of throughput performance.
7. Acknowledgements
Authors acknowledge the insightful comments of Md. Irfanul Hasan, Research scholar, B. I. T., Mesra, Ranchi, India.
REFERENCES
- T. Weiss, J. Hillenbrand, A. Krohn and F. K. Jondral, “Mutual Interference in OFDM-Based Spectrum Pooling Systems,” Proceeding of IEEE Vehicular Technology Conference (VTC’04), Milan, 17-19 May 2004, pp. 1873-1877.
- Ericsson, “Long Term Evolution (LTE): An Introduction—White Paper,” 2008. http://www.ericsson.com/technology/whitepapers/lte_overview.pdf
- G. Boudreau, J. Panicker, N. Guo, R. Chang, N. Wang and S. V. Nortel, “Interference Coordination and Cancellation for 4G Networks,” IEEE Communications Magazine, Vol. 47, No. 4, 2009, pp. 74-81. doi:10.1109/MCOM.2009.4907410
- A. Leke and J. Cioffi, “A Maximum Rate Loading Algorithm for Discrete Multi-Tone Modulation Systems,” Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM’97), Phoenix, 3-8 November 1997, pp. 1514-1518.
- G. Bansal, M. J. Hossain and V. K. Bhargava, “Adaptive Power Loading for OFDM-Based Cognitive Radio Systems,” IEEE Communications Magazine, Vol. 46, No. 9, 2008, pp. 59-67.
- Y. Zhang, “Resource Allocation for OFDM-Based Cognitive Radio Systems,” Ph.D. Dissertation, University of British Columbia, Vancouver, 2008.
- S. Boyd and L. Vandenberg, “Convex Optimization,” Cambridge University Press, Cambridge, 2004.

