Communications and Network
Vol.3 No.4(2011), Article ID:8469,4 pages DOI:10.4236/cn.2011.34025
Conditional Diagnosability of the Locally Twisted Cubes under the PMC Model*
1School of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an, China
2Department of Mathematics, Xidian University, Xi’an, China
E-mail: {qinshiyue2003, bgq_00}@163.com, wxk1383@126.com
Received August 11, 2011; revised September 20, 2011; accepted September 30, 2011
Keywords: Locally Twisted Cubes, Diagnosability, Conditional Diagnosability, PMC Mode
Abstract
In a multiprocessor systems, it is important to local and to replace the faulty processors to maintain systempsilas high reliability. The fault diagnosis, which is the process of identifying fault processors in a multiprocessor system through testing. The conditional diagnosis requires that for each processor u in a system, all the processors that are directly connected to u do not fail at the same time. In this paper, we study the conditional diagnosability of the n-dimensional locally twisted cubes. After showing some properties of the locally twisted cubes, we prove that it under the PMC model is 4n – 7 for n ≥ 5.
1. Introduction
In recent years, the number of the processors in a multiprocessor system increases as fast as the technology development. Thus some processors may fail in such a multiprocessor operating system. So locating the faulty processors is important for system maintenance and dependable computing. System level diagnosis is an important approach for fault diagnosis in a multiprocessor system. Many different models for system level diagnosis in multiprocessor systems have been proposed, e.g., the PMC (the Perfect Minicomputer Corporation) model [1], the comparison model [2] and the BGM model [3]. So far, the well-studied mode is the PMC model introduced by Preparata, Metze, and Chien [1].
A multiprocessor system is an interconnected collection of processors and can be represented by an undirected graph G = (V, E), where each vertex of the vertex set V represents a processor and each edge of the edge set E represents a communication link between a pair of processors. Two processors interact with each other by sending messages over the communication link. Under the PMC model, two processors can test each other if and only if there is a link between them. The processor which tests the status of the other is called a tester. It is assumed that the test result is reliable if and only if the tester is fault free; otherwise, the test result is unreliable. The collection of all test results is called a syndrome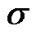 ·r(u, v) denotes the test result of processor u testing processor v. If v pass the test executed by u, r(u, v) = 0; otherwise, r(u, v) = 1. Table 1 shows all possible test results of the test r(u, v).
·r(u, v) denotes the test result of processor u testing processor v. If v pass the test executed by u, r(u, v) = 0; otherwise, r(u, v) = 1. Table 1 shows all possible test results of the test r(u, v).
For a given syndrome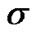 , a subset of vertices
, a subset of vertices  is said to be consistent with
is said to be consistent with  if
if 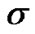 can arise from the circumstance that all nodes in F are faulty and all nodes in V-F are fault free. It is worth pointing out that a given set F of faulty vertices may be consistent with different syndromes. Let
can arise from the circumstance that all nodes in F are faulty and all nodes in V-F are fault free. It is worth pointing out that a given set F of faulty vertices may be consistent with different syndromes. Let 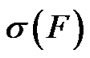 be the set containing all syndromes which can be produced by F. Two distinct sets F1,
be the set containing all syndromes which can be produced by F. Two distinct sets F1, 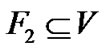 are said to be distinguishable if
are said to be distinguishable if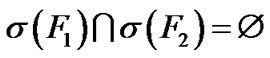 otherwise, F1, F2 are said to be indistinguishable.
otherwise, F1, F2 are said to be indistinguishable.

Table 1. Test results.
A system is said to be t-diagnosable if given a syndrome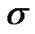 , all processors can correctly be identified faulty or faulty free, provided that the number of faulty processors present in the system does not exceed t. The diagnosability of a system is the maximal number of faulty processors that the system can guarantee to diagnose. The diagnosability of some interconnection networks have been discussed under the PMC model, see [4-6].
, all processors can correctly be identified faulty or faulty free, provided that the number of faulty processors present in the system does not exceed t. The diagnosability of a system is the maximal number of faulty processors that the system can guarantee to diagnose. The diagnosability of some interconnection networks have been discussed under the PMC model, see [4-6].
Lai et al. in [7] introduced conditional diagnosability by restricting that for each processor u in a system, all processors adjacent to u are not faulty at the same time, and showed that conditional diagnosability of the n-dimensional hypercube (Qn) is 4n – 7 for n ≥ 5, which is about four times as large as its classical diagnosability [8]. Zhu et al. in [9] presented that under PMC-model the conditional diagnosability of FQn (tc(FQn)) was 4n – 3 when n ≥ 5 or n > 8; tc(FQ3) = 3, tc(FQ4) = 7.
In recent years, conditional diagnosability of several interconnection networks has also been explored under the PMC model [7,9-12].
In the paper, we prove that conditional diagnosability of locally twisted cubes under the PMC model is 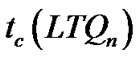
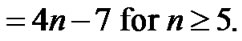
The rest of paper is organized as follows: Preliminary knowledge is provided in Section 2; The main results of this paper are presented and proven in Section 3; The conclusions are made in Section 4.
2. Preliminaries
For all the terminologies and notations not defined here, we follow [13]. For a graph G = (V, E) and S Ì V(G) or S Ì G, we use NG(S) to denote the set of neighboring vertices of S in G-S, when it is easy to know from the context what G denotes, it is usually simplified with N(S). We use AG(S) to denote the union of S and NG(S). And similarly AG(S) can be simplified with A(S).
That is, NG(S) = {vÎ V (G)-S|$ u ÎS such that (u, v) Î E(G)}, AG(S) = NG(S) 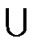 S.
S.
We use dG(u) to denote the degree of u in G and dG(u) can be simplified with d(u).
Definition 1. [14] For n ≥ 2, an n-dimensional locally twisted cube, denoted by LTQn, is defined recursively as follows:
1) LTQ2 is a graph consisting of four nodes labeled with 00, 01, 10 and 11, respectively, connected by four edges {00, 01}, {01, 11},{11, 10} and {10, 00}.
2) For n ≥ 3, LTQn is built from two disjoint copies of LTQn–1 according to the following steps: Let 0LTQn–1 denote the graph obtained from one copy of LTQn–1 by prefixing the label of each node with 0. Let 1LTQn–1 denote the graph obtained from the other copy of LTQn–1 by prefixing the label of each node with 1. Connect each node 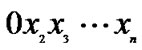 of 0LTQn 1 to the node
of 0LTQn 1 to the node  of 1LTQn 1 with an edge, where “+” represents the modulo 2 addition.
of 1LTQn 1 with an edge, where “+” represents the modulo 2 addition.
Figure 1 shows two examples of locally twisted cubes. The locally twisted cubes can also be equivalently defined in the following non-recursive fashion.
Definition 2. [14] For n ≥ 2, the n-dimensional locally twisted cube, LTQn, is a graph with {0, 1}n as the node set. Two nodes 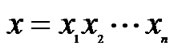 and
and 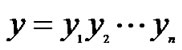 of LTQn are adjacent if and only if either one of the following conditions are satisfied.
of LTQn are adjacent if and only if either one of the following conditions are satisfied.
1) 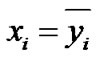 and xi+1 = yi+1 + yn for some 1 £ i £ n – 2, and xj = yj for all the remaining bits;
and xi+1 = yi+1 + yn for some 1 £ i £ n – 2, and xj = yj for all the remaining bits;
2) 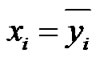 for i Î {n – 1, n}, and xj = yj for all the remaining bits.
for i Î {n – 1, n}, and xj = yj for all the remaining bits.
The definition of the conditional diagnosability is as follows.
Definition 3. [7] A faulty set F Í V is called a conditional faulty set if N(v) Ë F for any vertex v Î V. A system G(V, E) is conditionally t-diagnosable if F1 and F2 are distinguishable, for each pair of conditional faulty sets F1, F2 Í V , and F1 ¹ F2 with |F1|; |F2| £ t. Conditional diagnosability of a system G, written as tc(G) is defined to be the maximum value of t such that G is conditionally t-diagnosable.
Let F1, F2 be two distinct sets, the symmetric difference of F1 and F2 is denoted by F1DF2, that is, F1DF2 = (F1 – F2) È (F2 – F1). The following lemma proposed by Dahbura and Masson [15] gives a necessary and sufficient condition for a system to be t-diagnosable.
Lemma 1. [16] A system G(V, E) is t-diagnosable if and only if, for each pair F, F2 Ì V with|F1|, |F2| £ t and F1 ¹ F2, there is at least one test from V – F1 È F2 to F1DF2.
Lemma 2. [14] k(LTQn) = n for n ≥ 2.
Lemma 3. [17] k (LTQn) = 2n – 2 for n ≥ 3.
Lemma 4. [17] Let S be a set of vertices S Ì V(LTQn) with |S| = n, if LTQn-S is disconnected, there exists a vertex u Î V(V(LTQn)) such that N(u) = S for n ≥ 2.
The following lemma is derived based on [18,19].
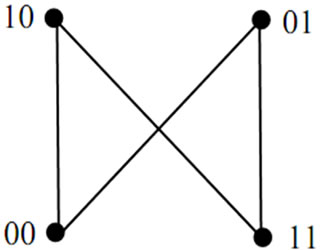
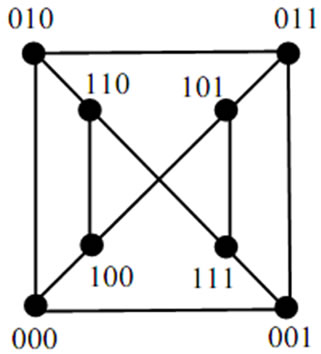
Figure 1. Example of LTQn: LTQ2 and LTQ3.
Lemma 5. Let F be a subgraph of LTQn with
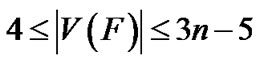 , we have
, we have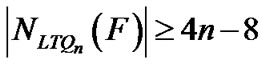 .
.
3. Conditionally Diagnosability
Lemma 6. Let S be a set of vertices S Ì V(LTQn) and n ≥ 3. Suppose that LTQn – S is disconnected. The following two conditions hold:
(1) |S| ≥ n;
(2) If n £ |S| £ 2n – 3, then LTQn-S has exactly two components, one is trivial and the other is nontrivial. The nontrivial component of LTQn-S contains 2n– |S| – 1 vertices.
Proof: By lemma 2 k(LTQn) = n, so condition (1) holds. We need to prove that condition (2) is true. Since 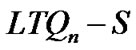 is disconnected, there are at least two components in
is disconnected, there are at least two components in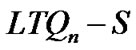 . We will prove that |S| ≥ 2n – 2 when
. We will prove that |S| ≥ 2n – 2 when  contains at least two trivial components or two nontrivial components. It implies that n £ |S| £ 2n – 3 when
contains at least two trivial components or two nontrivial components. It implies that n £ |S| £ 2n – 3 when 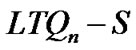 contains a trivial components and nontrivial components.
contains a trivial components and nontrivial components.
Case 1. 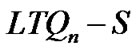 contains at least two trivial components. Let u1, u2 Î V(LTQn) and {u1}, {u2} be two trivial components. Then N(u1) Ì S and N(u2) Ì S. Since any two distinct vertices of a LTQn have at most two common neighbors, we have |N(V1)
contains at least two trivial components. Let u1, u2 Î V(LTQn) and {u1}, {u2} be two trivial components. Then N(u1) Ì S and N(u2) Ì S. Since any two distinct vertices of a LTQn have at most two common neighbors, we have |N(V1)  |N(V2)| £ 2.
|N(V2)| £ 2.
Hence, |S | ≥ |N(V1)| + |N(V2)| – |N(V1)  N(V2)| ≥ 2n + 2n – 2 = 2(2n – 1).
N(V2)| ≥ 2n + 2n – 2 = 2(2n – 1).
Case 2. LTQn-S contains at least two nontrivial components. We prove condition (2) by induction on n. Suppose n £ |S| £ 2n – 3, it is easy to see that |S| = 3 for n = 3. The connectivity of LTQ3 is 3. By Lemma 4, there exist a vertex u Î V (LTQ3) such that S = N(u) Thus LTQ3-S has exactly two components: one is trivial and the other is nontrivial. Therefore, if LTQ3-S has at least two nontrivial components, |S| ≥ 2n – 2, where n = 3. Assume that the result holds for all n – 1, n – 1 ≥ 3. In the following we show that it holds for n.
Let S0 = S 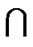 V(0LTQn–1) and S1 = S
V(0LTQn–1) and S1 = S 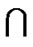 V (1LTQn–1), F and F' be two nontrivial component of LTQn-S. So |V(F)| ≥ 2 and |V(F′)| ≥ 2.
V (1LTQn–1), F and F' be two nontrivial component of LTQn-S. So |V(F)| ≥ 2 and |V(F′)| ≥ 2.
We consider the following three cases:
Case 2.1. F, F′ Í 0LTQn–1 or F, F′ Í 1LTQn–1. Without loss of generality, let F, F′ Í 0LTQn–1 , then 0LTQn-1 -S0 is disconnected and|S1| ≥ |F| +|F′| ≥ 4. So |S0| ≥ k2 = 2n – 4 by lemma 3. Thus |S| = |S0| + |S1| ≥ 2n – 2.
Case 2.2. F Í 0LTQn–1 and F′ Í 1LTQn–1, or F′ Í 1LTQn–1 and F Í 1LTQn–1. Without loss of generality, let F Í 0LTQn–1 and F′ Í 1LTQn–1. If both 0LTQn–1 – S0 and 1LTQn–1 – S1 are connected, then |S0| ≥ 2n – 4 and S1| ≥ 2n – 4. So |S| = |S0| + |S1| ≥ 2n – 4 + 2n– 4 ≥ 2n – 2 for n ≥ 3. If exactly one of 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected, let 0LTQn–1 – S0 be disconnected, then  Í S0. So
Í S0. So
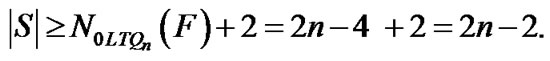
Case2.3. 0LTQn–1 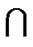
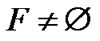 and 1LTQn–1
and 1LTQn–1 
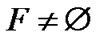 , or 0LTQn–1
, or 0LTQn–1 
 and 1LTQn–1
and 1LTQn–1 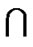
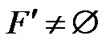 . Without loss of generality, let 0LTQn–1
. Without loss of generality, let 0LTQn–1 
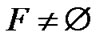 and 1LTQn-1
and 1LTQn-1 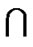
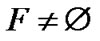 . Since there is another component F′ of LTQn – S, at least one of the two graphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected. So we drive the result by consider two Subcase.
. Since there is another component F′ of LTQn – S, at least one of the two graphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected. So we drive the result by consider two Subcase.
Case 2.3.1. Both 0LTQn–1 – S0 and 1LTQn–1 – S1 are disconnected. Since k(LTQn–1) = n – 1, |S0| ≥ n – 1 and|S1| ≥ n – 1. Then |S| = |S0| + |S1|≥ 2n – 2.
Case 2.3.2. Exactly one of the two subgraphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected. Without loss of generality, assume that 0LTQn–1 – S0 is connected and 1LTQn–1 – S1 is disconnected. Then |S1| ≥ n – 1 and N0LTQn(F) Í S0. Hence, |S0| ≥ |V(F′)| ≥ 2. If |S1| ≥ 2n – 4, then |S| = |S0| + |S1| ≥ 2 + (2n – 4) = 2n – 2. Otherwise, n – 2 £ |S1| £ 2n – 5. By induction hypothesis, 1LTQn–1 – S1 has exactly two components: one is trivial and the other is nontrivial. We know that 1LTQn–1 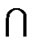 F and F′ are two components of 1LTQn–1 – S1, and F′ is a nontrivial component. Thus 1LTQn–1
F and F′ are two components of 1LTQn–1 – S1, and F′ is a nontrivial component. Thus 1LTQn–1 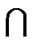 F must be a trivial component of 11LTQn–1 – S1, and |V(F′)| = 2n–1 – |S1| – 1. Note that N0LTQn(F′) Í S0. Hence, |S| = |S0| + |S1| ≥ |V(F′)| + |S1| = 2n–1 – |S1| – 1 + |S1| ≥ 2n – 2 for n ≥ 4.
F must be a trivial component of 11LTQn–1 – S1, and |V(F′)| = 2n–1 – |S1| – 1. Note that N0LTQn(F′) Í S0. Hence, |S| = |S0| + |S1| ≥ |V(F′)| + |S1| = 2n–1 – |S1| – 1 + |S1| ≥ 2n – 2 for n ≥ 4.
Consequently, condition (2) holds.■
Lemma 7: Let S be a set of vertices S Ì V(LTQn) and n ≥ 5. Suppose that LTQn-S is disconnected and every component of LTQn-S is nontrivial, and there exists one component F of LTQn-S such that dF (v) ≥ 2 for any vertex v Î F. Then one of the following two conditions must hold:
(1) |S| ≥ 4n – 8;
(2) |V(F)| ≥ 4n – 9.
Proof: Let F0 = 0LTQn–1 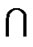 F, F1 = 1LTQn–1
F, F1 = 1LTQn–1 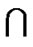 F, S0. = S
F, S0. = S 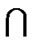 V(0LTQn–1) and S1 = S
V(0LTQn–1) and S1 = S  V(1LTQn–1). We consider two cases: (a) F Ì 0LTQn–1 or F Ì 1LTQn–1. (b) 0LTQn–1
V(1LTQn–1). We consider two cases: (a) F Ì 0LTQn–1 or F Ì 1LTQn–1. (b) 0LTQn–1 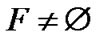
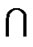 and 1LTQn–1
and 1LTQn–1 
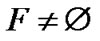 .
.
Case 1. F Ì 0LTQn–1 or F Ì 1LTQn–1. Without loss of generality, let F Ì 0LTQn–1. Then F Ì S1. In the following we consider two cases.
Case 1.1. 0LTQn–1-F is connected. Then |S| = |S0| + |S1| ≥ |S0| + |V(F)| = 2n–1 ≥ 2n – 2 for n ≥ 4 and conditional (a) holds.
Case 1.2. 0LTQn–1 – F is disconnected. If 4 £ |V(F)| £ 3n – 5, by Lemma 5, we have |S0| ≥ |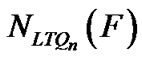 | ≥ 4n – 8.Therefore, |S| ≥ 4n – 8 and conditional (a) holds. If 3n – 4 £ |V(F)| £ 4n – 10, then |S0| ≥ n – 1 since 0LTQn–1 – F is disconnected and |S1| ≥ |V(F)| ≥ 3n – 4. Thus |S| = |S0| + |S1| ≥ n – 1 + 3n – 4 = 4n – 5 and conditional (a) holds. Otherwise, |V(F)| ≥ 4n – 9 and conditional (b) holds.
| ≥ 4n – 8.Therefore, |S| ≥ 4n – 8 and conditional (a) holds. If 3n – 4 £ |V(F)| £ 4n – 10, then |S0| ≥ n – 1 since 0LTQn–1 – F is disconnected and |S1| ≥ |V(F)| ≥ 3n – 4. Thus |S| = |S0| + |S1| ≥ n – 1 + 3n – 4 = 4n – 5 and conditional (a) holds. Otherwise, |V(F)| ≥ 4n – 9 and conditional (b) holds.
Case 2. 0LTQn–1 
 and 1LTQn–1
and 1LTQn–1
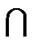 . Since every vertex x in F0 (resp. y in F1) has at most one neighbor in F1(resp. F0), we have
. Since every vertex x in F0 (resp. y in F1) has at most one neighbor in F1(resp. F0), we have 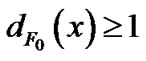 and
and . Since LTQn – S is disconnected, there are at least two components in LTQn – S. At least one of the two graphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected since both LTQn and LTQn–1 contain some non-empty part of the component F.
. Since LTQn – S is disconnected, there are at least two components in LTQn – S. At least one of the two graphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected since both LTQn and LTQn–1 contain some non-empty part of the component F.
In the following we drive the result by consider two cases.
Case 2.1. Exactly one of the two graphs 0LTQn–1 – S0 and 1LTQn–1 – S1 is disconnected. Without loss of generality, assume that 0LTQn–1 – S0 is connected and 1LTQn–1 – S1 is disconnected. Let F′ be another non-trivial component of LTQn – S other than F. Then 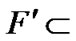
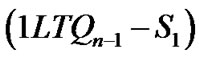 and
and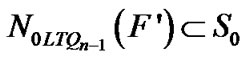 . Note that both
. Note that both 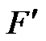 and
and 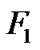 are nontrivial component. By Lemma 6, |S1| ≥ 2n – 4. If j|S0| ≥ 2n – 4, then |S| = |S0| + |S1| ≥ 4n – 8 and condition (1) holds. Otherwise, |S0| £ 2n – 5. Then
are nontrivial component. By Lemma 6, |S1| ≥ 2n – 4. If j|S0| ≥ 2n – 4, then |S| = |S0| + |S1| ≥ 4n – 8 and condition (1) holds. Otherwise, |S0| £ 2n – 5. Then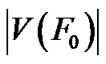 =
=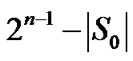 since
since 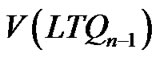 = S0
= S0 V (F0).
V (F0).
Thereby, |V(F)| = |V(F0)|+|V(F1)| ≥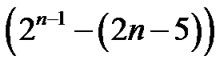 + 2 ≥ 4n – 9 for n ≥ 4 and condition (2) holds.
+ 2 ≥ 4n – 9 for n ≥ 4 and condition (2) holds.
0LTQn–1 – S0 and 1LTQn–1 – S1 are disconnected. We consider the following three subcases.
Case 2.1.1. |S0| ≥ 2n – 4 and |S1| ≥ 2n – 4.Clearly, S| = |S0| + |S1| ≥ 8n – 8. Therefore, condition (1) holds.
Case 2.2.2. Either n – 1 £ |S0| £ 2n – 5, |S1| ≥ 2n – 4 or |S0| ≥ 2n – 4, n – 1 £ | S1| £ 2n – 5. Without loss of generality, assume that S0| ≥ 2n – 4, n – 1 £ | S1| £ 2n – 5. Then we have | V(F1)| = 2n–1 – |S1| – 1 by the lemma 6. Since  for any vertex u
for any vertex u  V (F0),|V(F0)| ≥ 2. Thus, |V(F)| = |V(F0)| + |V(F1)| ≥ 2 +
V (F0),|V(F0)| ≥ 2. Thus, |V(F)| = |V(F0)| + |V(F1)| ≥ 2 + 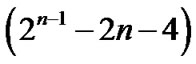 ≥ 4n – 9 for n ≥ 5. Hence, condition (2) holds.
≥ 4n – 9 for n ≥ 5. Hence, condition (2) holds.
Case 2.2.3. n – 1 £ | S0| £ 2n – 5 and n – 1 £ | S1| £ 2n – 5. By the lemma 6, we have |V(F0)| = 2n–1 – |S0| – 1 and |V (F1)| = 2n–1 – |S1| – 1. So |V(F)| = |V(F0)| + |V (F1)| = 2n – |S| – 2. If |S| ≥ 4n – 8, then condition (1) holds. Otherwise, |S| £ 4n – 9, then |V (F)| = 2n – (4n – 9) – 2 ≥ 4n – 9 for n ≥ 4. Hence, condition (2) holds.
Consequently, the lemma holds. ■
Theorem 1. Let F1, F2 Ì  be two indistinguishable conditional faulty sets, then either |F1| ≥ 4n – 6 or |F2| ≥ 4n – 6 for n ≥ 5.
be two indistinguishable conditional faulty sets, then either |F1| ≥ 4n – 6 or |F2| ≥ 4n – 6 for n ≥ 5.
Proof: Let S = F1 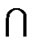 F2, according to LTQn – S is connected or not, we consider the following two cases.
F2, according to LTQn – S is connected or not, we consider the following two cases.
Case 1. LTQn – S is connected. We assert that F0DF1 = V (LTQn) – S. Otherwise, suppose u ÎV(LTQn – S) – F1DF2 = V (LTQn) – F1 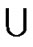 F2.Then u is connected to F1DF2 since LTQn – S is connected. That is, there is an edge between F1DF2 and V – F1
F2.Then u is connected to F1DF2 since LTQn – S is connected. That is, there is an edge between F1DF2 and V – F1 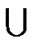 F2. This is a contradiction to the fact F1 and F2 are an indistinguishable. Since |F1| + |F2| = |F1|D|F2| = |V(LTQn)| = 2n ≥ 8n – 13 for n ≥ 5, either |F1| ≥ 4n – 6 or |F2| ≥ 4n – 6. Then the result follows.
F2. This is a contradiction to the fact F1 and F2 are an indistinguishable. Since |F1| + |F2| = |F1|D|F2| = |V(LTQn)| = 2n ≥ 8n – 13 for n ≥ 5, either |F1| ≥ 4n – 6 or |F2| ≥ 4n – 6. Then the result follows.
Case 2. LTQn – S is disconnected. Since F1 and F2 is indistinguishable, there is no edge between F1DF2 and V (LTQn) – F1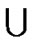 F2 by Lemma 1.That is, for any vertex u
F2 by Lemma 1.That is, for any vertex u  F1 D F2,
F1 D F2, 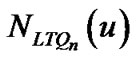 Ì F1
Ì F1  F2. Since both F1and F2 are conditional faulty set,
F2. Since both F1and F2 are conditional faulty set, 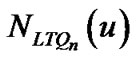 Ë F1and
Ë F1and 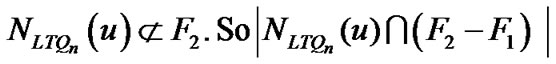
and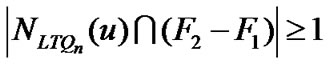 .
.
Thus for any vertex u 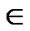 F1 D F2 , |
F1 D F2 , |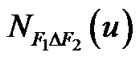 | ≥ 2. So LTQn – S has a component P with V (P) Ì F1 D F2 such that dP(u) ≥ 2 for any vertex u
| ≥ 2. So LTQn – S has a component P with V (P) Ì F1 D F2 such that dP(u) ≥ 2 for any vertex u 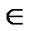 V(P). By Lemma 7, we have |S| ≥ 4n – 8 or |V(P)| ≥ 4n – 9 for n ≥ 5. So we consider the following two subcases.
V(P). By Lemma 7, we have |S| ≥ 4n – 8 or |V(P)| ≥ 4n – 9 for n ≥ 5. So we consider the following two subcases.
Case 2.1. |S| ≥ 4n – 8. Let C be a cycle in P. Since 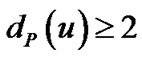 for each vertex u
for each vertex u  V(F), and V (LTQn) ≥ 4, the cycle C of length is not less than 4. Because V(C) Ì V(P) Ì F1 D F2, either |F1 – F2| ≥ 2 or |F2 – F1| ≥ 2. Thereby, either |F1| = |S| + |F1 – F2| ≥ 4n – 6 or |F2| = |S| + |F1 – F2| ≥ 4n – 6.
V(F), and V (LTQn) ≥ 4, the cycle C of length is not less than 4. Because V(C) Ì V(P) Ì F1 D F2, either |F1 – F2| ≥ 2 or |F2 – F1| ≥ 2. Thereby, either |F1| = |S| + |F1 – F2| ≥ 4n – 6 or |F2| = |S| + |F1 – F2| ≥ 4n – 6.
Case 2.2. |V(P)| ≥ 4n – 9. Since |V(P)| ≥ 4n – 9 and V (P) Ì F1 D F2, either |F1 – F2| ≥ 2n – 4 or |F2 – F1| ≥ 2n – 4. And since there is no isolated vertex in LTQn (both F1 and F2 are conditional faulty set) and LTQn – S is disconnected, |S| ≥ 2n – 2 by lemma 3. Thereby, either|F1| = |S| + | F1 – F2| ≥ 4n – 6 or |F2| = |S| + |F2 – F1| ≥ 4n – 6.
Consequently, the theorem holds. ■
The theorem 1 shows that the conditional diagnosability of LTQn is not less than 4n – 7 for n ≥ 5. In the following we will show that the conditional diagnosability of LTQn is not more than 4n – 7 for n ≥ 5.
Theorem 2. 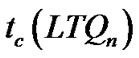 £ 4n – 7 for n ≥ 3.
£ 4n – 7 for n ≥ 3.
Proof: (See Figure 2) Let C = (u1, u2, u3, u4) be a cycle of length 4 in LTQn. u1, u2, u3, u4 are the four consecutively vertices in the cycle C. Let F1 = 
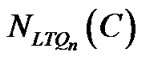 {u1, u2} and F2 =
{u1, u2} and F2 =
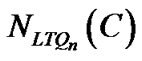 {u3, u4}. It is easy to verify that F1and F2 are two indistinguishable conditional faulty
{u3, u4}. It is easy to verify that F1and F2 are two indistinguishable conditional faulty
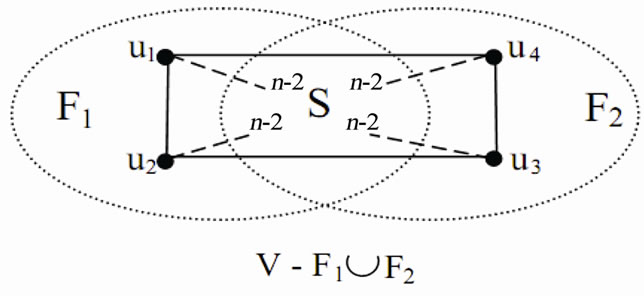
Figure 2. An illustration of the proof of Theorem 2.
set. It is easy to see that there exists no triangle in LTQn and any two distinct vertices in LTQn have at most two common neighbors. Thus we have |F1 F2| =
F2| = 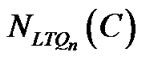 = 4n – 8 and | F1 – F2| = |F2 – F1|. So |F1| = |F2| = 4n – 6. Hence, LTQn is not conditionally (4n – 6) diagnosable. We are done. ■
= 4n – 8 and | F1 – F2| = |F2 – F1|. So |F1| = |F2| = 4n – 6. Hence, LTQn is not conditionally (4n – 6) diagnosable. We are done. ■
By Theorems 1 and 2, the following corollary holds.
Corollary 1. 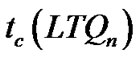 = 4n – 7 for n ≥ 5.
= 4n – 7 for n ≥ 5.
4. Conclusions
Since the probability that any faulty set contains all the neighbors of some processor is very small, conditional diagnosability, requiring that each processor of a system is incident with at least one fault-free processor, can better measure the diagnosability of interconnection. In this paper, the main contribution is the determination of the conditional diagnosability of the locally twisted cubes. We obtain that the conditional diagnosability of a locally twisted cube under the PMC model is 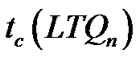 = 4n – 7 for n ≥ 5.
= 4n – 7 for n ≥ 5.
5. References
[1] G. M. F. P. Preparata and R. T. Chien, “On the Connection Assignment Problem of Diagnosable Systems,” IEEE Transactions on Electronic Computers, vol. EC-16, No. 6, December 1967, pp. 848-854. doi:10.1109/PGEC.1967.264748
[2] M. M. J. Maeng, “A Comparison Connection Assignment for Self-Diagnosis of Multiprocessors Systems,” Proceedings of the 11th International Symposium on FaultTolerant Computing, Portland, 1981, pp. 173-175.
[3] F. G. F. Barsi and P. Maestrini, “A Theory of Diagnosability of Digital Systems,” IEEE Transactions on Computers, Vol. C-25, No. 6, June 1976, pp. 585-593. doi:10.1109/TC.1976.1674658
[4] R. Ahlswede and H. Aydinian, “On Diagnosability of Large Multiprocessor Networks,” Discrete Applied Mathematics, Vol. 156, No. 18, 2008, pp. 3464-3474. doi:10.1016/j.dam.2008.02.001
[5] D. Wang, “Diagnosability of Enhanced Hypercubes,” IEEE Transactions on Computers, vol. 43, no. 9, 1994, pp. 1054- 1061. doi:10.1109/12.312114
[6] J. Fan, “Diagnosability of the Mobius Cubes,” IEEE Transactions on Parallel and Distributed Systems, vol. 9, no. 9, 1998, pp. 923-928. doi:10.1109/71.722224
[7] P.-L. Lai, J. Tan, C.-P. Chang and L.-H. Hsu, “Conditional Diagnosability Measures for Large Multiprocessor Systems,” IEEE Transactions on Computers, Vol. 54, No. 2, 2005, pp. 165-175. doi:10.1109/TC.2005.19
[8] S. Hsieh and C. Lee, “Diagnosability of Two-Matching Composition Networks under the MM* Model,” IEEE Transactions on Dependable and Secure Computing, Vol. 8, No. 2, 2009, pp. 246-255.
[9] Q. Zhu, S.-Y. Liu and M. Xu, “On Conditional Diagnosability of the Folded Hypercubes,” Information Sciences, Vol. 178, No. 4, 2008, pp. 1069-1077. doi:10.1016/j.ins.2007.09.005
[10] M. Xu, K. Thulasiraman and X.-D. Hu, “Conditional Diagnosability of Matching Composition Networks under the Pmc Model,” IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 56, No. 11, 2009, pp. 875- 879. doi:10.1109/TCSII.2009.2030361
[11] Q. Zhu, “On Conditional Diagnosability and Reliability of the bc Networks,” The Journal of Supercomputing, Vol. 45, No. 2, 2008, pp. 173-184. doi:10.1007/s11227-007-0167-8
[12] S.-M. Zhou, “The Conditional Diagnosability of Locally Twisted Cubes,” Proceedings of the 4th International Conference on Computer Science and Education, 2009, pp. 221-226.
[13] J. A. Bondy and U. S. R. Murty, “Graph Theory with Applications,” North Holland, New York, 1976.
[14] X.-F. Yang, D. J. Evans and G. M. Megson, “The Locally Twisted Cubes,” International Journal of Computer Mathematics, Vol. 82, No. 4, April 2005, pp. 401-413. doi:10.1080/0020716042000301752
[15] G. M. A. T. Dahbura, “An O(n2.5) Fault Identification Algorithm for Diagnosable Systems,” IEEE Transactions on Computers, Vol. C-33, No. 6, 1984, pp. 486-492. doi:10.1109/TC.1984.1676472
[16] A. T. Dahbura and G. M. Masson, “An O(n2.5) Fault Identification Algorithm for Diagnosable Systems,” IEEE Transactions on Computers, Vol. 33, No. 6, 1984, pp. 486-492. doi:10.1109/TC.1984.1676472
[17] J.-X. Fan, S.-K. Zhang, et al., “The Restricted Connectivity of Locally Twisted Cubes,” 2009 10th International Symposium on Pervasive Systems, Algorithms, and Networks (ISPAN), Kaohsiung, 14-16 December 2009, pp. 574-578. doi:10.1109/I-SPAN.2009.48
[18] J. Fan and X. Lin, “The t/k-Diagnosability of the BC Graphs,” IEEE Transactions on Computers, Vol. 54, No. 2, 2005, pp. 176-184. doi:10.1109/TC.2005.33
[19] X.-F. Yang, J.-Q. Cao, G. M. Megson and J. Luo, “Minimum Neighborhood in a Generalized Cube,” Information Processing Letters, Vol. 97, 2006, pp. 88-93.
NOTES
*The paper supported by the National Natural Science Foundation of China (No.61073196 )and Natural Science Research Foundation of Shanxi Province, China (No. 2011JM8026).

