Communications and Network
Vol.3 No.1(2011), Article ID:3991,8 pages DOI:10.4236/cn.2011.31004
Multi-Branch Fractional Multi-Bit Differential Detection of Continuous Phase Modulation with Decision Feedback
1State Key Lab. of Integrated Service Networks, Xidian University, Xi’an, China
2School of Information Engineering, Chang’an University, Xi’an, China
E-mail: jhsun@xidian.edu.cn, xjwu@chd.edu.cn
Received October 14, 2010; revised January 7, 2011; accepted January 10, 2011
Keywords: continuous phase modulation, differential detection, fractional multi-bit differential detection, decision feedback
Abstract
Differential detection of continuous phase modulation suffers from significant intersymbol interference. To reduce bit error rate, multi-branch fractional multi-bit differential detection (MFMDD) with decision feedback is proposed. By introducing decision feedback in multi-bit differential detected signals, severe intersymbol interference can be removed. Simulation results show that the proposed structure can greatly improves the performance compared with MFMDD without decision feedback, and the performance of 9 FMDD is very near to the performance of the coherent detection.
1. Introduction
Continuous phase modulations make signal phase continuous by filtering the data sequence with smooth phase functions, such as Gaussian pulse (for Gaussian minimum shift keying and Gaussian frequency shift keying), raised cosine pulse, leading to improved bandwidth efficiency. However, the trade-off of having a more compact power spectrum is the decrease of Euclidean distance in the transmitter signal space. For the detection of GMSK, a coherent detector, a differential detector, or a limit discriminator detector can be employed.
For the coherent detection, the required carrier recovery increases the acquisition time and is also relative complex. Furthermore, in a fading channel the coherent detection exhibits high error floors. Hence, for some burst mode applications requiring fast demodulation, incoherent detection is preferred. The conventional incoherent detection are one-bit differential (1DD) and two-bit differential (2DD). The main disadvantage of the incoherent detection compared with coherent detection is the large loss in signal to noise ratio (SNR). When the normalized 3dB bandwidth of Gaussian filter  is small or the pulse expand length is long, the performance of conventional one-bit differential detection and two-bit differential detection degrade greatly. The smallest
is small or the pulse expand length is long, the performance of conventional one-bit differential detection and two-bit differential detection degrade greatly. The smallest  for one-bit differential detection to operate properly is about 0.22. In terms of power efficiency, the two-bit differential detection is about 7dB inferior to the coherent detection [1]. Hence, there is ample room for improvements by introducing additional processing at the receiver. Therefore, Incoherent viterbi demodulation based Laurent decomposition is proposed in [2-4], its performance is about 1.5dB inferior to the optimum coherent detection. However, Laurent representation of CPM signals with small modulation index, long frequency pulse and large cardinality is unfortunately still complex. Multi-symbol differential detection is proposed to greatly improve the system performance by using the memory in CPM [5-7]. Additional, Kee-Hoon Lee [8-9] presents a Fractional Multi-bit Differential Detection (FMDD) technique. The technique improves the performance with a minimum increase in the implementation complexity. When FMDD is applied to GFSK used in Bluetooth systems, a SNR advantage up to 1.8 dB can be achieved compared with the conventional one-bit differential detection (1DD). Reference [10] generalized FMDD to a Multi-branch Fractional Multi-bit Differential Detection (MFMDD), the principle of MFMDD is presented from the physical meaning of phase forming, and theoretical analysis to the upper bound of the fractional bit duration for the maximum performance improvement is given. MFMDD can obtain above 4 dB gain compared with 1DD. Abbas. Y. demonstrates that decision feedback can significantly reduce the effect of destructive intersymbol interference (ISI) in the conventional differential detectors [11]. The bit error rate (BER) performance is nearer to that of coherent detector while carrier recovery is avoided. This paper considers introducing decision feedback to further improve the performance of MFMDD. Firstly, the structure of MFMDD is given. Then, we determine how to apply decision feedback to the detector. Finally, computer simulation results for evaluating the BER performance are presented.
for one-bit differential detection to operate properly is about 0.22. In terms of power efficiency, the two-bit differential detection is about 7dB inferior to the coherent detection [1]. Hence, there is ample room for improvements by introducing additional processing at the receiver. Therefore, Incoherent viterbi demodulation based Laurent decomposition is proposed in [2-4], its performance is about 1.5dB inferior to the optimum coherent detection. However, Laurent representation of CPM signals with small modulation index, long frequency pulse and large cardinality is unfortunately still complex. Multi-symbol differential detection is proposed to greatly improve the system performance by using the memory in CPM [5-7]. Additional, Kee-Hoon Lee [8-9] presents a Fractional Multi-bit Differential Detection (FMDD) technique. The technique improves the performance with a minimum increase in the implementation complexity. When FMDD is applied to GFSK used in Bluetooth systems, a SNR advantage up to 1.8 dB can be achieved compared with the conventional one-bit differential detection (1DD). Reference [10] generalized FMDD to a Multi-branch Fractional Multi-bit Differential Detection (MFMDD), the principle of MFMDD is presented from the physical meaning of phase forming, and theoretical analysis to the upper bound of the fractional bit duration for the maximum performance improvement is given. MFMDD can obtain above 4 dB gain compared with 1DD. Abbas. Y. demonstrates that decision feedback can significantly reduce the effect of destructive intersymbol interference (ISI) in the conventional differential detectors [11]. The bit error rate (BER) performance is nearer to that of coherent detector while carrier recovery is avoided. This paper considers introducing decision feedback to further improve the performance of MFMDD. Firstly, the structure of MFMDD is given. Then, we determine how to apply decision feedback to the detector. Finally, computer simulation results for evaluating the BER performance are presented.
2. The Structure of MFMDD
Assuming a Gaussian additive white noise channel, the signal at the receiver can be represented as follows
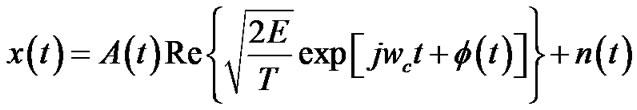 (1)
(1)
where 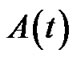 is the time-varying envelope,
is the time-varying envelope, 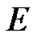 is the symbol energy,
is the symbol energy, is the symbol duration,
is the symbol duration, 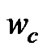 is the carrier frequency,
is the carrier frequency,  is the signal phase forming from the filtering of transmitted data sequence
is the signal phase forming from the filtering of transmitted data sequence
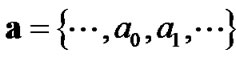 ,
, 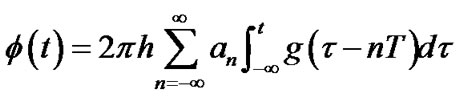 (h is the modulation index,
(h is the modulation index, 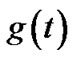 is the frequency pulse),
is the frequency pulse), 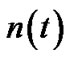 is white additive Gaussian noise.
is white additive Gaussian noise.
A block diagram of a 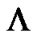 -fold MFMDD receiver is given as Figure 1. Assume
-fold MFMDD receiver is given as Figure 1. Assume  is the branch number, and the total branch number is
is the branch number, and the total branch number is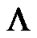 ,
,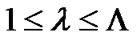 . The oversampling rate of the received signal is
. The oversampling rate of the received signal is 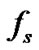 (
(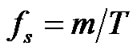 ) and the number of delayed samples is
) and the number of delayed samples is 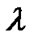 for the
for the  th branch, the delay of fractional-bit differential detector can be expressed as
th branch, the delay of fractional-bit differential detector can be expressed as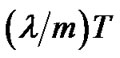 . Use
. Use  as a notation of the unit fractional number. The
as a notation of the unit fractional number. The  th branch input signal delayed by
th branch input signal delayed by 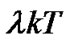 and phase shifted by 90˚ can be represented by
and phase shifted by 90˚ can be represented by
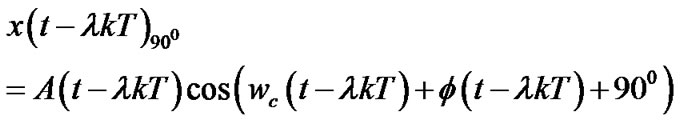 (2)
(2)
The received signal  is multiplied by
is multiplied by  . Ignoring the second harmonic item, the output of the multiplier (the
. Ignoring the second harmonic item, the output of the multiplier (the 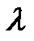 th branch) is
th branch) is
 (3)
(3)
where 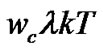 is a phase offset contributed by the
is a phase offset contributed by the th branch,
th branch, 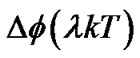 is
is
 (4)
(4)
which represents the change of signal phase over a fractional bit duration . A phase shift and timing delay adjusting block is introduced in FMDD to compensate the influence of phase offset
. A phase shift and timing delay adjusting block is introduced in FMDD to compensate the influence of phase offset 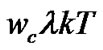 and delay offset of different fractional differential detection branches. Define the complementary phase shift
and delay offset of different fractional differential detection branches. Define the complementary phase shift  such that
such that  and the complementary timing delay
and the complementary timing delay  such that different branches are synchronized. All branch outputs are summarized as,
such that different branches are synchronized. All branch outputs are summarized as,
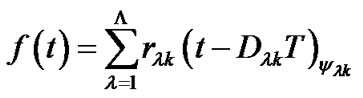 (5)
(5)
where 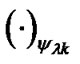 represents
represents  phase shift. After the low pass filtering, we have
phase shift. After the low pass filtering, we have
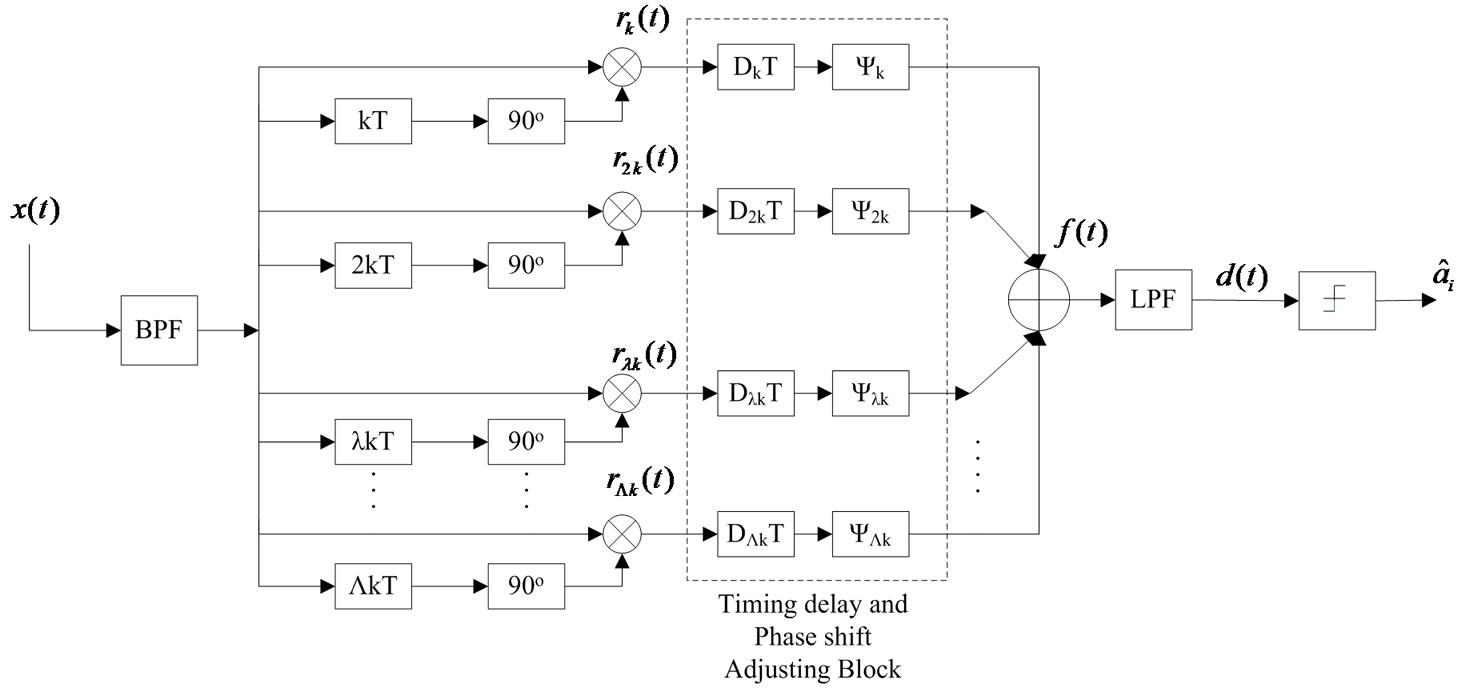
Figure 1. The block diagram of  -fold MFMDD.
-fold MFMDD.
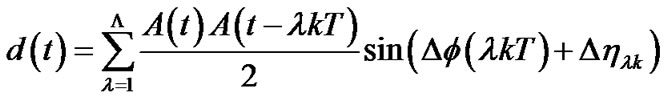 (6)
(6)
where  represents the phase shift introduced by AWGN, which can be assumed to be uniformly distributed in
represents the phase shift introduced by AWGN, which can be assumed to be uniformly distributed in . Therefore the combining of different branches can minimize noise and improve BER performance. The decision is made based on the polarity of
. Therefore the combining of different branches can minimize noise and improve BER performance. The decision is made based on the polarity of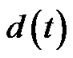 .
.
In fact, (3) is based on the processing of bandpass signal. If the processing is made in baseband, 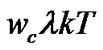 is non-existent, and the phase shift adjustment block is unnecessary. The following section presents a further explanation to MFMDD from the physical meaning of the phase forming. The phase of CPM is the integral of the output of the premodulation filter, that is, the phase at instant
is non-existent, and the phase shift adjustment block is unnecessary. The following section presents a further explanation to MFMDD from the physical meaning of the phase forming. The phase of CPM is the integral of the output of the premodulation filter, that is, the phase at instant 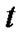 corresponds to the area of the region enclosed by the output waveform of the filter from
corresponds to the area of the region enclosed by the output waveform of the filter from  to
to 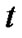 and the abscissa axis. Figure 2 shows the output pulses of the premodulation filter, which corresponds to three symbols
and the abscissa axis. Figure 2 shows the output pulses of the premodulation filter, which corresponds to three symbols  (+1),
(+1), 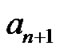 (+1),
(+1), 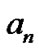 (+1) respectively (Note that the three curves are not superposed).
(+1) respectively (Note that the three curves are not superposed).
In Figure 2, the phase variation over  corresponds to the sum of the areas enclosed by all the curves in this period and the abscissa axis. Taking 5FMDD as example,
corresponds to the sum of the areas enclosed by all the curves in this period and the abscissa axis. Taking 5FMDD as example, 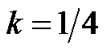 ,
,  are
are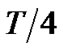 ,
, 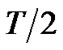 ,
, 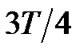 ,
,  and
and  respectively,
respectively,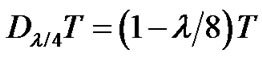 .
.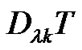 makes different branches be synchronized such that the maximum open points of the baseband eyedigram under different fractional bit durations occur all at the same time. The output of different branches corresponds to the area under the intersecting output pulse during
makes different branches be synchronized such that the maximum open points of the baseband eyedigram under different fractional bit durations occur all at the same time. The output of different branches corresponds to the area under the intersecting output pulse during , which is
, which is 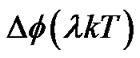 after multiplied by
after multiplied by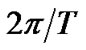 .
.
Figure 3 and Figure 4 present the output waveforms of 1 DD and 5 FMDD under the ideal noiseless channel and additive white Gaussian noise channel respectively. It can be seen that the combination of multi-branch FMDD outputs increases the distance between different phase states, i.e. the detected area is enlarged. So the redundancy between different phase states is increased when the decision is made with zero as the decision threshold.
3. Upper Bound of the Fractional Bit Duration to Achieve the Maximum Performance Gain
From the above analysis, it can be seen that different branch combining is similar to time diversity combining. Each branch signal comes from samples of different duration of one received signal. Since MFMDD has good performance, can we obtain an increase performance gain continually by increasing the number of branches?
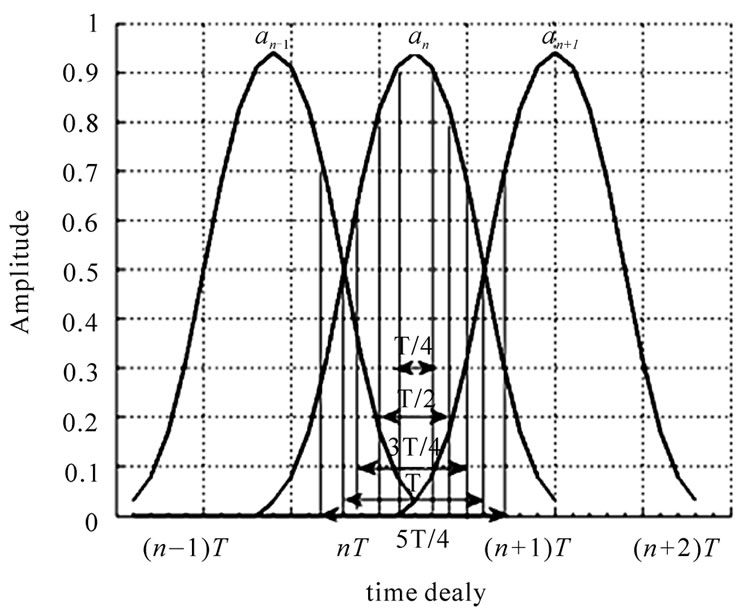
Figure 2. The output of the premodulation filter.

Figure 3. The ideal differential output of 1 DD and 5 FMDD.

Figure 4. The differential output of 1 DD and 5 FMDD (SNR = 12 dB).
Is there a maximum duration 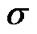 such that no performance gain can be obtained when the fractional bit duration exceeds
such that no performance gain can be obtained when the fractional bit duration exceeds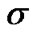 ?
?
Partial response continuous phase modulation introduces intersymbol interference (ISI) in the signal. For the example that Gaussian pulse lasts two symbol durations, when  and
and 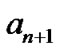 have the same polarity with the current symbol
have the same polarity with the current symbol ,
,  and
and  play a positive role in phase increase from the instant
play a positive role in phase increase from the instant 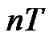 to
to 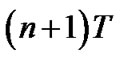 (as shown in Figure 2), otherwise, they play a negative role (as shown in Figure 5). Therefore, the fractional bit duration
(as shown in Figure 2), otherwise, they play a negative role (as shown in Figure 5). Therefore, the fractional bit duration 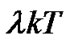 must guarantee that the polarity of
must guarantee that the polarity of  is consistent with that of
is consistent with that of . That is to say, the area under the output of premodulation filter during
. That is to say, the area under the output of premodulation filter during 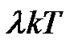 should be large than zero, which can be represented as
should be large than zero, which can be represented as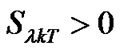 . Assume
. Assume 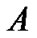 is the set of all possible input data combinations, and
is the set of all possible input data combinations, and  denotes one possible value of
denotes one possible value of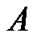 . Search the maximum value of
. Search the maximum value of  for each input data combination,
for each input data combination, 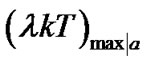 , then find the minimum one among those
, then find the minimum one among those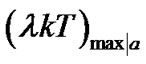 ,
,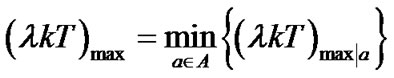 . When the polarities of the interacting data bits in
. When the polarities of the interacting data bits in 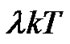 are the same,
are the same,  is larger, the differential output is larger; when the polarities of the interacting data bits in
is larger, the differential output is larger; when the polarities of the interacting data bits in 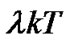 is not the same,
is not the same, 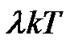 is larger, the output may be smaller. So the minimum
is larger, the output may be smaller. So the minimum 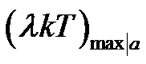 should be the one found when the polarities of
should be the one found when the polarities of 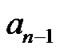 and
and 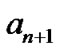 are different from that of
are different from that of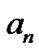 . When
. When 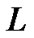 is increased, the number of interacting symbols is also increased. Therefore,
is increased, the number of interacting symbols is also increased. Therefore,
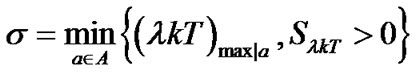 (7)
(7)
Figure 5 shows the premodulation filter output phase pulses where the adjacent symbols play a negative role to the phase increase. It can be seen that the integral of the filter output (the part shown in shadow) is zero when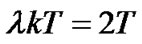 . This means that the branch of
. This means that the branch of  will stop making positive contribution to FMDD. When
will stop making positive contribution to FMDD. When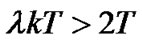 , the output of fractional differential detection is less than zero, the branch will make negative contribu-
, the output of fractional differential detection is less than zero, the branch will make negative contribu-

Figure 5.  to achieve the maximum performance gain.
to achieve the maximum performance gain.
tion. Therefore, for Gaussian pulse lasts two symbol durations,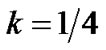 , the value of
, the value of 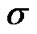 which achieves the maximum performance gain is
which achieves the maximum performance gain is . In summary, the maximum performance gain can be obtained when the fractional bit duration is the maximal duration in which the symbol decision will not be influenced.
. In summary, the maximum performance gain can be obtained when the fractional bit duration is the maximal duration in which the symbol decision will not be influenced.
4. Using Decision Feedback in MFMDD
In 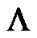 -fold MFMDD, the phase change in
-fold MFMDD, the phase change in  for each branch is
for each branch is
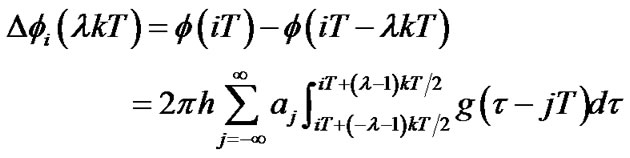 (8)
(8)
The integral in the expression can be understood as the area of  in the duration of
in the duration of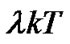 , and the summation is the contribution of the adjacent symbols to the signal phase. Let
, and the summation is the contribution of the adjacent symbols to the signal phase. Let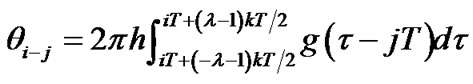 , the received signal after low pass filter at
, the received signal after low pass filter at  can be expressed as
can be expressed as
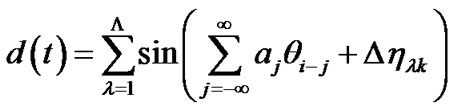 (9)
(9)
That is to say the phase change in 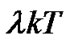 is
is
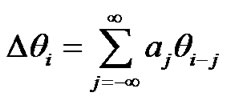 , where
, where  represents the signal and
represents the signal and
 ,
,  ,
, 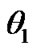 ,
, 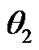 and etc. are the ISI terms. For
and etc. are the ISI terms. For , the values of
, the values of  for different
for different 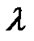 are listed in Table 1,
are listed in Table 1, . Where the minimum differential phase angle
. Where the minimum differential phase angle 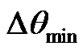 is the phase separation between the
is the phase separation between the
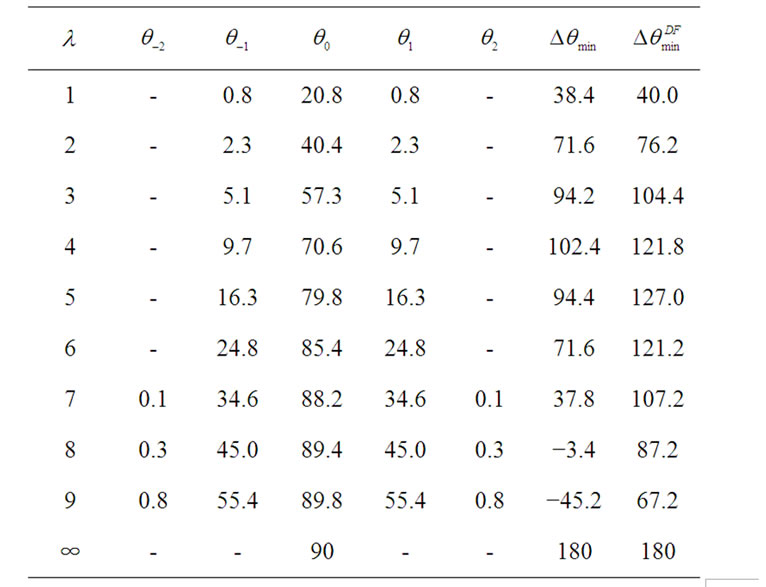
Table 1. phase shifts (in degrees) corresponding to signal 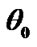 and ISI term as a function of
and ISI term as a function of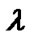 .
.
closest states and is also tabulated in Table 1,
 (10)
(10)
Since the adjacent symbols are intersymbol interference terms to the current symbol, and the past symbols are known when deciding the current symbol, we can reduce the intersymbol interference using decision feedback. The block diagram of  -fold MFMDD using decision feedback is shown in Figure 6.
-fold MFMDD using decision feedback is shown in Figure 6.
From the above analysis, we can see that 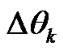 is not only related to
is not only related to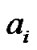 , but also influenced by
, but also influenced by ,
, 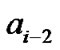 ,
, 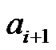 , and
, and 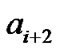 at instant
at instant . When
. When 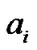 is to be decided,
is to be decided,  (the estimate of
(the estimate of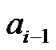 ) and
) and  (the estimate of
(the estimate of ) are already known. Since the influence of
) are already known. Since the influence of  is very small, we only consider
is very small, we only consider 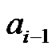 here. Therefore, we can reduce the influence of
here. Therefore, we can reduce the influence of 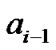 to the received signal by introducing a phase shift of
to the received signal by introducing a phase shift of 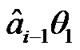 in the
in the  delay arm. If we do not ignore
delay arm. If we do not ignore , the minimum differential phase using decision feedback is:
, the minimum differential phase using decision feedback is:
 (11)
(11)
The value of  is also given in Table 1.
is also given in Table 1.
Table 2 shows the differential phase angles corresponding to different input data combinations for different branches when .
. 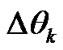 is the differential phase without decision feedback,
is the differential phase without decision feedback,  is the differential phase with decision feedback. From the data in Table 2, we can make the following observations:
is the differential phase with decision feedback. From the data in Table 2, we can make the following observations:
1) For state 3 and state 4, since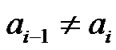 , after introducing phase shift
, after introducing phase shift , the ISI introduced by the previous symbol is cancelled. The differential phase is increased at the sampling instant, the new differential phase is
, the ISI introduced by the previous symbol is cancelled. The differential phase is increased at the sampling instant, the new differential phase is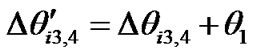 , and the distance from the decision threshold is also increased.
, and the distance from the decision threshold is also increased.
For state 2 and state 5, the effect of the previous symbol may be either constructive or destructive. A phase shift of  may either increase or decrease the distance from the decision threshold. When
may either increase or decrease the distance from the decision threshold. When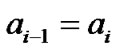 , the new differential phase is
, the new differential phase is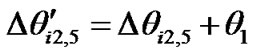 , and the distance from decision threshold is also increased. When
, and the distance from decision threshold is also increased. When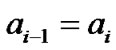 , the new differential phase is
, the new differential phase is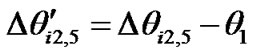 , and the distance from decision threshold is also decreased.
, and the distance from decision threshold is also decreased.
State 1 and state 6 have the widest separation. For these two states,  , the distance from the decision threshold will be decreased by introducing phase shift
, the distance from the decision threshold will be decreased by introducing phase shift , and the new differential phases are
, and the new differential phases are 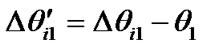 and
and .
.
State 3 and state 4 are very critical to the overall system performance. They are very vulnerable to be falsely decided. Although the  of state 1, 2, 5, and 6 are decreased, the
of state 1, 2, 5, and 6 are decreased, the  of state 3 and 4 are increased more significantly, leading to improved overall system performance.
of state 3 and 4 are increased more significantly, leading to improved overall system performance.
2) By adding the differential output for different branches using decision feedback, the overall differential output is increased, and the bit error rate can be decreased. But this does not mean that we should increase the number of branches infinitely. The differential phase without decision feedback in Table 2 shows that for state 3 and 4, when 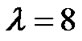 and
and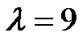 , since the polarity of the current symbol is opposite to
, since the polarity of the current symbol is opposite to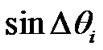 , the differential output of the system will be decreased. For state 1
, the differential output of the system will be decreased. For state 1
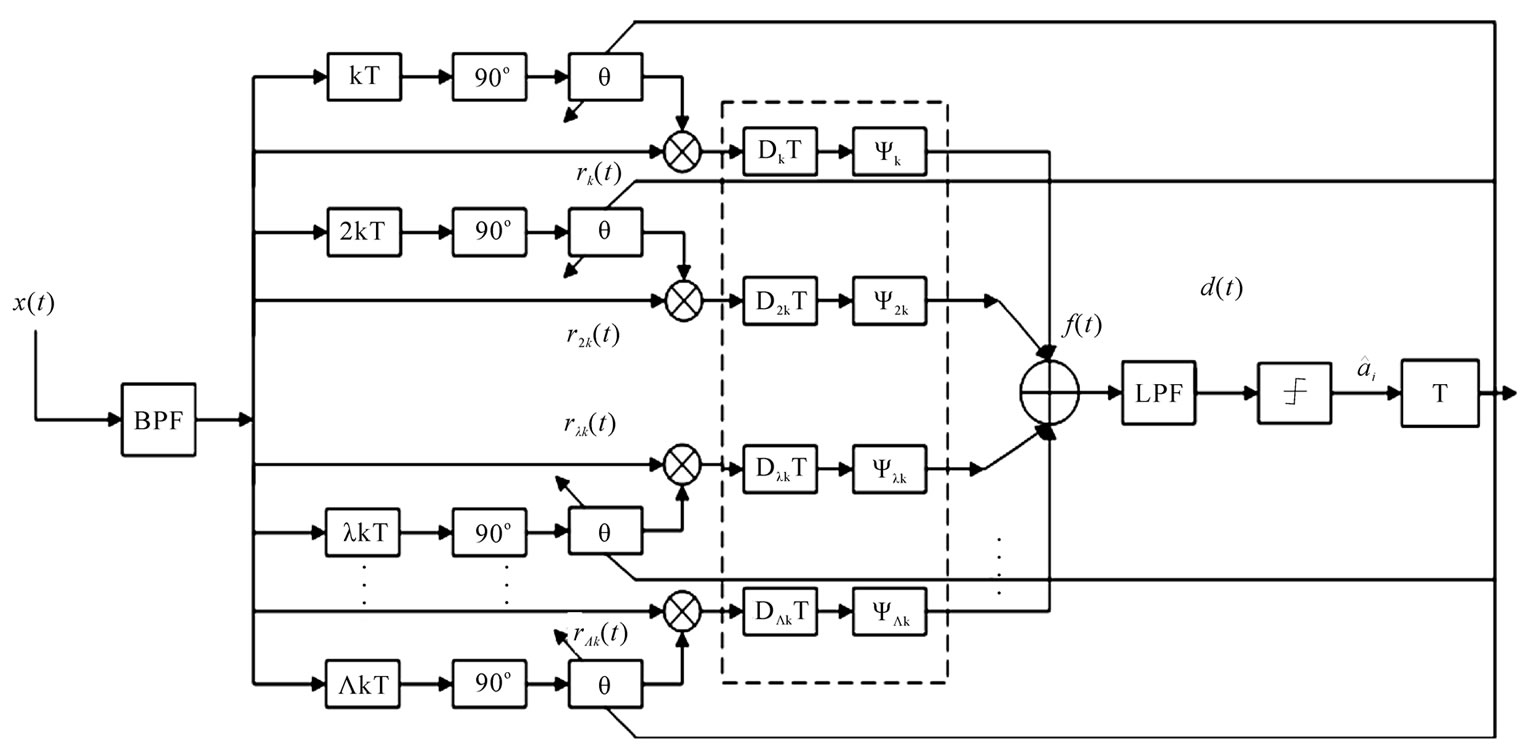
Figure 6. The block diagram of 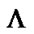 -fold MFMDD using decision feedback.
-fold MFMDD using decision feedback.
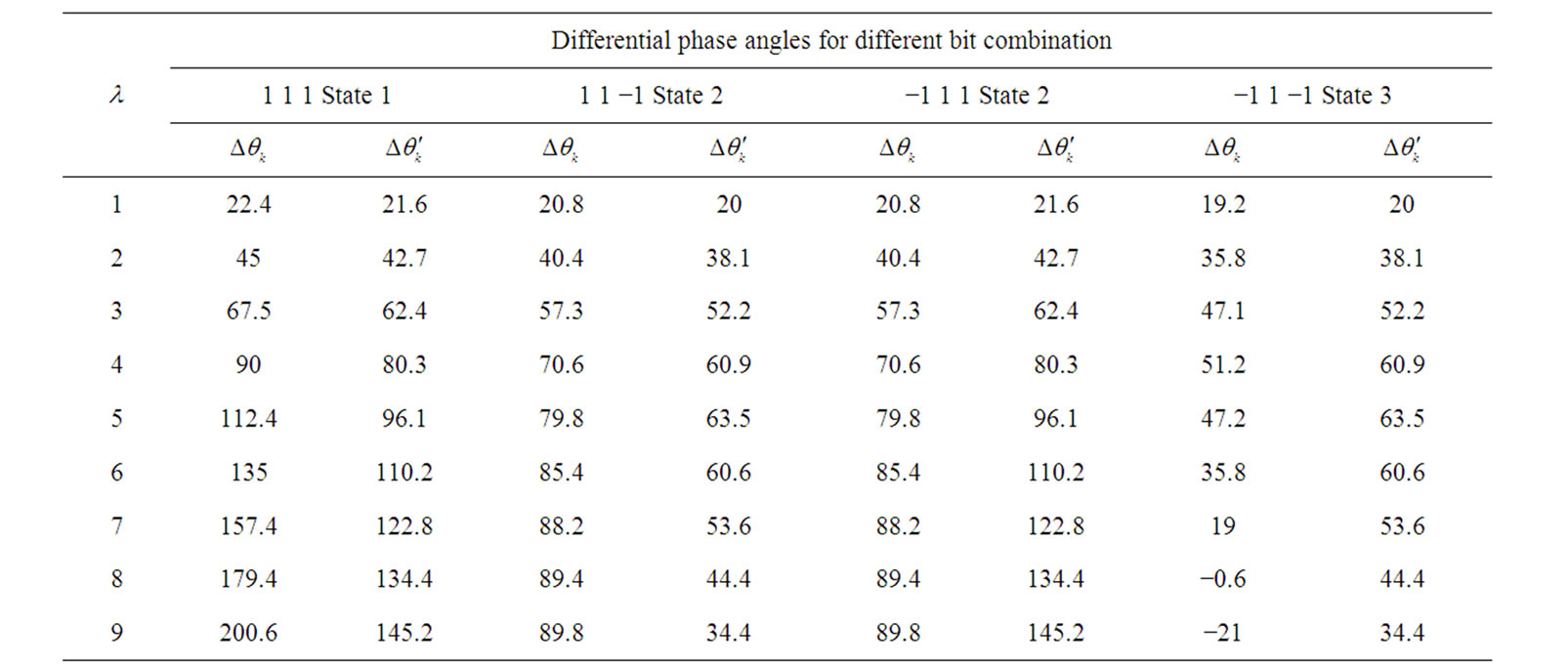

Table 2. differential phase angles (in degrees) before and after using decision feedback corresponding to different bit combinations as a function of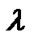 .
.
and 6,  will also decrease the system differential output. Thus, when
will also decrease the system differential output. Thus, when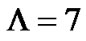 , the system has the maximum distance from the decision threshold and best performance. After introducing decision feedback, for state 3 and 4, when
, the system has the maximum distance from the decision threshold and best performance. After introducing decision feedback, for state 3 and 4, when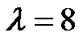 , and for state 1, 3, 4, and 6, when
, and for state 1, 3, 4, and 6, when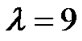 , the polarity of the current symbol is the same as
, the polarity of the current symbol is the same as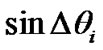 . After introducing decision feedback, these two branches will improve the system performance. When
. After introducing decision feedback, these two branches will improve the system performance. When , the system will have best performance.
, the system will have best performance.
5. Simulation Results
The BER performance and the maximum performance gain of MFMDD using decision feedback have been evaluated through computer simulation. In our simulation, the pulse expand length is 3 symbols, the normalized 3 dB bandwidth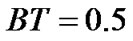 . The BER performance of
. The BER performance of 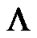 -fold MFMDD without decision feedback is shown in Figure 7, from which we can see that the larger the fractional bit duration the higher the performance gain. The optimal performance gain is reached when
-fold MFMDD without decision feedback is shown in Figure 7, from which we can see that the larger the fractional bit duration the higher the performance gain. The optimal performance gain is reached when . We can see that for
. We can see that for , the performance of 7FMDD is close to the performance of 6 FMDD; the performance of 5FMDD is close to the performance of 8FMDD under high SNR; 7 FMDD outperforms 1 DD by above 4 dB at BER =
, the performance of 7FMDD is close to the performance of 6 FMDD; the performance of 5FMDD is close to the performance of 8FMDD under high SNR; 7 FMDD outperforms 1 DD by above 4 dB at BER = 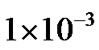 in an AWGN channel.
in an AWGN channel.
We find that after introducing decision feedback, the performance of MFMDD is improved. From Figure 8 we can see that after introducing decision feedback, better BER performance is acquired when we increase the number of branches, reaching the optimum BER in 9 FMDD. When the BER is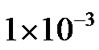 , after introducing
, after introducing
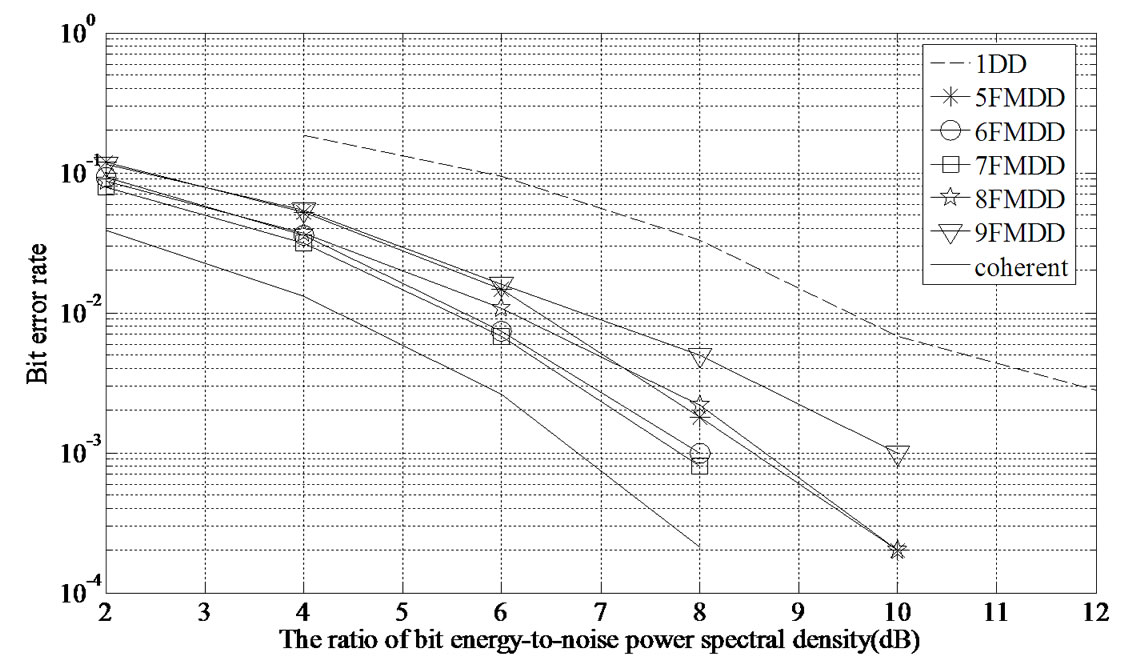
Figure 7. BER of  -fold MFMDD.
-fold MFMDD.
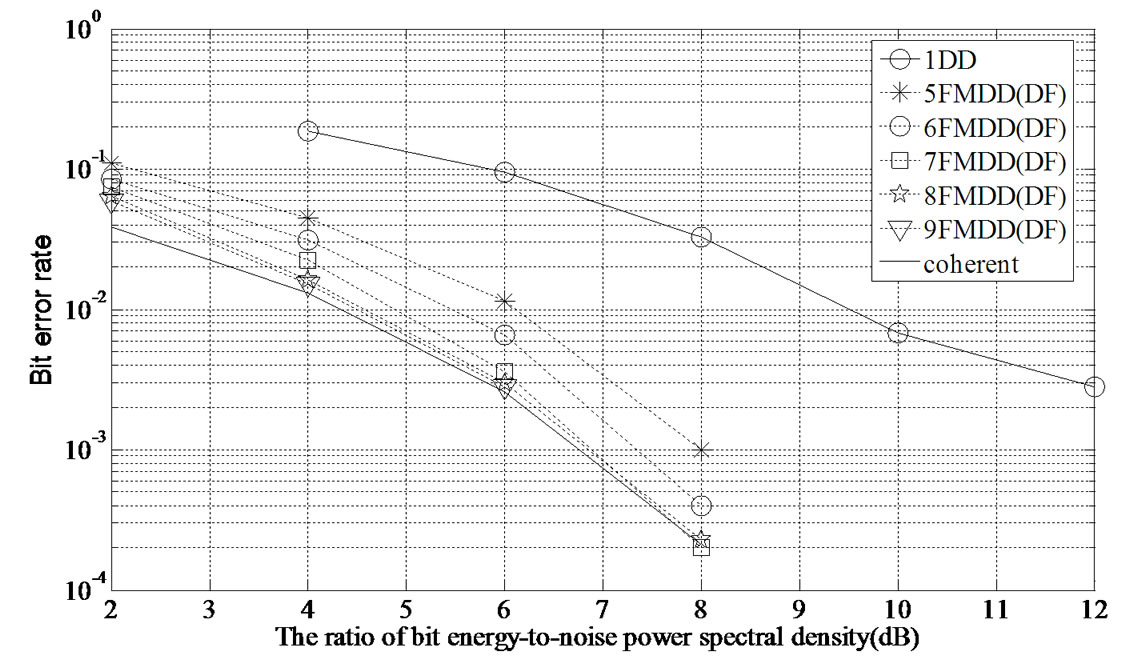
Figure 8. BER of  -fold MFMDD using decision feedback.
-fold MFMDD using decision feedback.
decision feedback, 5 FMDD has a performance gain of 0.5 dB, 6 FMDD has a performance gain of near 0.6 dB, 7 FMDD has a performance gain of about 1 dB, 8 FMDD has a performance gain of 2.2 dB, 9 FMDD has a performance gain of near 4.2 dB than before decision feedback. The performance of 9 FMDD is very near to the coherent detection. We can see that the receiver performance is greatly improved after introducing decision feedback.
6. Conclusions
This paper presents multi-branch fractional multi-bit differential detection technique using decision feedback suitable for continuous phase modulation. By introducing decision feedback in multi-bit differential detected signals, severe intersymbol interference can be removed. For the , the proposed structure can provide different SNR improvement for different branches compared with MFMDD without decision feedback, and the best performance is achieved for 9FMDD which is very near to the performance of the coherent detection .
, the proposed structure can provide different SNR improvement for different branches compared with MFMDD without decision feedback, and the best performance is achieved for 9FMDD which is very near to the performance of the coherent detection .
7. References
[1] M .K. Simon and C. C. Wang, “Differential Detection of Gaussian MSK in a Mobile Radio Environment,” IEEE Transactions on Vehicle Technology, vol. VT-33, no. 4, 1984, pp. 307-320. doi:10.1109/T-VT.1984.24023
[2] G. Colavolpe and R. Raheli, “Noncoherent Sequence Detection of CPM,” Electronics Letters, vol. 34, no. 3, 1998, pp. 259-261. doi:10.1049/el:19980225
[3] M. Wardle and M. Rice, “PAM Approach to Weak CPM and Its Application to Flight Termination Receivers,” IEEE Transactions on Aerospace and Electronic Systems, vol. 44, no. 2, 2008, pp. 468-480. doi:10.1109/TAES. 2008.4560200
[4] E. Perrins and M. Rice, “PAM Representation of Ternary CPM,” IEEE Transactions on Communications, vol. 56, no. 12, 2008, pp. 2020-2024. doi:10.1109/TCOMM. 2008.041108
[5] G. Colavolpe and R. Raheli, “Noncoherent Sequence Detection of Continuous Phase Modulations,” IEEE Transactions on Communications, vol. 47, no. 9, 1999, pp. 1303-1307. doi:10.1109/26.789664
[6] E. Perrins, R. Schober, M. Rice and M. K. Simon, “Multiple-Bit Differential Detection of Shaped-Offset QPSK,” IEEE Transactions on Communications, vol. 55, no. 12, 2007, pp. 2328-2340. doi:10.1109/TCOMM.2007.910972
[7] Q. Zhi, C. H. Zhou and L. M. Xiao, “Non-Coherent Demodulation of Continuous Phase Modulation Signals Based on Multi-Symbol Differential Correlation,” Journal of Tsinghua University, vol. 47, no. 4, 2007, pp. 507- 510.
[8] K. H. Lee and J. S. Seo, “Fractional Multi-Bit Differential Detection of Continuous Phase Modulation,” ETRI Journal, vol. 26, no. 6, 2004, pp. 635-640. doi:10.4218/ etrij.04.0103.0065
[9] K. H. Lee and J. K. Kim, “Correlative Encoded (CE) FSK for Use in RF Home Networking,” Proceedings of IEEE VTC 2002-Fall, Vancouver, IEEE Press, 2002, pp. 2400- 2404.
[10] J. H. Sun and X. J. Wu, “Multi-Branch Fractional MultiBit Differential Detection of Continuous Phase Modulation,” Journal of Xidian University, vol. 37, no. 3, 2010, pp. 423-428.
[11] Y. Abbas, M. Dimitrios and F. Kamilo, “Differential Detection of GMSK Using Decision Feedback,” IEEE Transactions on Communications, vol. 36, no. 6, 1988, pp. 641-649. doi:10.1109/26.2784
NOTES
This work was supported by the National Natural Science Foundation of China (60902039), and the China 111 Project (B08038).

