Advances in Pure Mathematics
Vol.06 No.13(2016), Article ID:72855,50 pages
10.4236/apm.2016.613074
Approach to a Proof of the Riemann Hypothesis by the Second Mean-Value Theorem of Calculus
Alfred Wünsche
Humboldt-Universität Berlin, Institut für Physik, Nichtklassische Strahlung (MPG), Berlin, Germany

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 9, 2016; Accepted: December 17, 2016; Published: December 20, 2016
ABSTRACT
By the second mean-value theorem of calculus (Gauss-Bonnet theorem) we prove that the class of functions 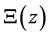 with an integral representation of the form
with an integral representation of the form 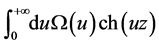 with a real-valued function
with a real-valued function 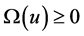 which is non-increasing and decreases in infinity more rapidly than any exponential functions
which is non-increasing and decreases in infinity more rapidly than any exponential functions 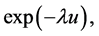
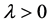 possesses zeros only on the imaginary axis. The Riemann zeta function
possesses zeros only on the imaginary axis. The Riemann zeta function 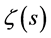 as it is known can be related to an entire function
as it is known can be related to an entire function 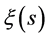 with the same non-trivial zeros as
with the same non-trivial zeros as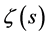 . Then after a trivial argument displacement
. Then after a trivial argument displacement 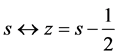 we relate it to a function
we relate it to a function 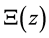 with a representation of the form
with a representation of the form 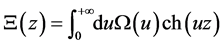 where
where 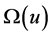 is rapidly decreasing in infinity and satisfies all requirements necessary for the given proof of the position of its zeros on the imaginary axis
is rapidly decreasing in infinity and satisfies all requirements necessary for the given proof of the position of its zeros on the imaginary axis 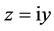 by the second mean-value theorem. Besides this theorem we apply the Cauchy- Riemann differential equation in an integrated operator form derived in the Appendix B. All this means that we prove a theorem for zeros of
by the second mean-value theorem. Besides this theorem we apply the Cauchy- Riemann differential equation in an integrated operator form derived in the Appendix B. All this means that we prove a theorem for zeros of 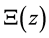 on the imaginary axis
on the imaginary axis 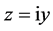 for a whole class of function
for a whole class of function 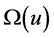 which includes in this way the proof of the Riemann hypothesis. This whole class includes, in particular, also the modified Bessel functions
which includes in this way the proof of the Riemann hypothesis. This whole class includes, in particular, also the modified Bessel functions 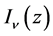 for which it is known that their zeros lie on the imaginary axis and which affirms our conclusions that we intend to publish at another place. In the same way a class of almost-periodic functions to piece-wise constant non-increasing functions
for which it is known that their zeros lie on the imaginary axis and which affirms our conclusions that we intend to publish at another place. In the same way a class of almost-periodic functions to piece-wise constant non-increasing functions 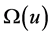 belong also to this case. At the end we give shortly an equivalent way of a more formal description of the obtained results using the Mellin transform of functions with its variable substituted by an operator.
belong also to this case. At the end we give shortly an equivalent way of a more formal description of the obtained results using the Mellin transform of functions with its variable substituted by an operator.
Keywords:
Riemann Hypothesis, Riemann Zeta Function, Xi Function, Gauss-Bonnet
Theorem, Mellin Transformation

1. Introduction
The Riemann zeta function ![]() which basically was known already to Euler establishes the most important link between number theory and analysis. The proof of the Riemann hypothesis is a longstanding problem since it was formulated by Riemann [1] in 1859. The Riemann hypothesis is the conjecture that all nontrivial zeros of the Riemann zeta function
which basically was known already to Euler establishes the most important link between number theory and analysis. The proof of the Riemann hypothesis is a longstanding problem since it was formulated by Riemann [1] in 1859. The Riemann hypothesis is the conjecture that all nontrivial zeros of the Riemann zeta function ![]() for complex
for complex ![]() are positioned on the line
are positioned on the line
![]() that means on the line parallel to the imaginary axis through real value
that means on the line parallel to the imaginary axis through real value
![]() in the complex plane and in extension that all zeros are simple zeros [2] - [17]
in the complex plane and in extension that all zeros are simple zeros [2] - [17]
(with extensive lists of references in some of the cited sources, e.g., ( [4] [5] [9] [12] [14] ). The book of Edwards [5] is one of the best older sources concerning most problems connected with the Riemann zeta function. There are also mathematical tables and chapters in works about Special functions which contain information about the Riemann zeta function and about number analysis, e.g., Whittaker and Watson [2] (chap. 13), Bateman and Erdélyi [18] (chap. 1) about zeta functions and [19] (chap. 17) about number analysis, and Apostol [20] [21] (chaps. 25 and 27). The book of Borwein, Choi, Rooney and Weirathmueller [12] gives on the first 90 pages a short account about achievements concerning the Riemann hypothesis and its consequences for number theory and on the following about 400 pages it reprints important original papers and expert witnesses in the field. Riemann has put aside the search for a proof of his hypothesis “after some fleeting vain attempts” and emphasizes that “it is not necessary for the immediate objections of his investigations” [1] (see [5] ). The Riemann hypothesis was taken by Hilbert as the 8-th problem in his representation of 23 fundamental unsolved problems in pure mathematics and axiomatic physics in a lecture hold on 8 August in 1900 at the Second Congress of Mathematicians in Paris [22] [23] . The vast experience with the Riemann zeta function in the past and the progress in numerical calculations of the zeros (see, e.g., [5] [10] [11] [16] [17] [24] [25] ) which all confirmed the Riemann hypothesis suggest that it should be true corresponding to the opinion of most of the specialists in this field but not of all specialists (arguments for doubt are discussed in [26] ).
The Riemann hypothesis is very important for prime number theory and a number of consequences is derived under the unproven assumption that it is true. As already said a main role plays a function ![]() which was known already to Euler for real variables
which was known already to Euler for real variables ![]() in its product representation (Euler product) and in its series re- presentation (now a Dirichlet series) and was continued to the whole complex
in its product representation (Euler product) and in its series re- presentation (now a Dirichlet series) and was continued to the whole complex ![]() -plane by Riemann and is now called Riemann zeta function. The Riemann hypothesis as said is the conjecture that all nontrivial zeros of the zeta function
-plane by Riemann and is now called Riemann zeta function. The Riemann hypothesis as said is the conjecture that all nontrivial zeros of the zeta function ![]() lie on the axis
lie on the axis
parallel to the imaginary axis and intersecting the real axis at![]() . For the true
. For the true
hypothesis the representation of the Riemann zeta function after exclusion of its only singularity at ![]() and of the trivial zeros at
and of the trivial zeros at ![]() on the negative real axis is possible by a Weierstrass product with factors which only vanish on the
on the negative real axis is possible by a Weierstrass product with factors which only vanish on the
critical line![]() . The function which is best suited for this purpose is the so-called xi
. The function which is best suited for this purpose is the so-called xi
function ![]() which is closely related to the zeta function
which is closely related to the zeta function ![]() and which was also introduced by Riemann [1] . It contains all information about the nontrivial zeros and only the exact positions of the zeros on this line are not yet given then by a closed formula which, likely, is hardly to find explicitly but an approximation for its density was conjectured already by Riemann [1] and proved by von Mangoldt [27] . The “(pseudo)-random” character of this distribution of zeros on the critical line remembers somehow the “(pseudo)-random” character of the distribution of primes where one of the differences is that the distribution of primes within the natural numbers becomes less dense with increasing integers whereas the distributions of zeros of the zeta function on the critical line becomes more dense with higher absolute values with slow increase and approaches to a logarithmic function in infinity.
and which was also introduced by Riemann [1] . It contains all information about the nontrivial zeros and only the exact positions of the zeros on this line are not yet given then by a closed formula which, likely, is hardly to find explicitly but an approximation for its density was conjectured already by Riemann [1] and proved by von Mangoldt [27] . The “(pseudo)-random” character of this distribution of zeros on the critical line remembers somehow the “(pseudo)-random” character of the distribution of primes where one of the differences is that the distribution of primes within the natural numbers becomes less dense with increasing integers whereas the distributions of zeros of the zeta function on the critical line becomes more dense with higher absolute values with slow increase and approaches to a logarithmic function in infinity.
There are new ideas for analogies to and application of the Riemann zeta function in other regions of mathematics and physics. One direction is the theory of random matrices [16] [24] which shows analogies in their eigenvalues to the distribution of the nontrivial zeros of the Riemann zeta function. Another interesting idea founded by Voronin [28] (see also [16] [29] ) is the universality of this function in the sense that each holomorphic function without zeros and poles in a certain circle with radius less
![]() can be approximated with arbitrary required accurateness in a small domain of the zeta function to the right of the critical line within
can be approximated with arbitrary required accurateness in a small domain of the zeta function to the right of the critical line within![]() . An interesting idea is
. An interesting idea is
elaborated in articles of Neuberger, Feiler, Maier and Schleich [30] [31] . They consider a simple first-order ordinary differential equation with a real variable ![]() (say the time) for given arbitrary analytic functions
(say the time) for given arbitrary analytic functions ![]() where the time evolution of the function for every point
where the time evolution of the function for every point ![]() finally transforms the function in one of the zeros
finally transforms the function in one of the zeros ![]() of this function in the complex
of this function in the complex ![]() -plane and illustrate this process graphically by flow curves which they call Newton flow and which show in addition to the zeros the separatrices of the regions of attraction to the zeros. Among many other functions they apply this to the Riemann zeta function
-plane and illustrate this process graphically by flow curves which they call Newton flow and which show in addition to the zeros the separatrices of the regions of attraction to the zeros. Among many other functions they apply this to the Riemann zeta function ![]() in different domains of the complex plane. Whether, however, this may lead also to a proof of the Riemann hypothesis is more than questionable.
in different domains of the complex plane. Whether, however, this may lead also to a proof of the Riemann hypothesis is more than questionable.
Number analysis defines some functions of a continuous variable, for example, the number of primes ![]() less a given real number
less a given real number ![]() which last is connected with the discrete prime number distribution (e.g., [3] [4] [5] [7] [9] [11] ) and establishes the connection to the Riemann zeta function
which last is connected with the discrete prime number distribution (e.g., [3] [4] [5] [7] [9] [11] ) and establishes the connection to the Riemann zeta function![]() . Apart from the product repre- sentation of the Riemann zeta function the representation by a type of series which is now called Dirichlet series was already known to Euler. With these Dirichlet series in number theory are connected some discrete functions over the positive integers
. Apart from the product repre- sentation of the Riemann zeta function the representation by a type of series which is now called Dirichlet series was already known to Euler. With these Dirichlet series in number theory are connected some discrete functions over the positive integers ![]() which play a role as coefficients in these series and are called arithmetic functions (see, e.g., Chandrasekharan [4] and Apostol [13] ). Such functions are the Möbius function
which play a role as coefficients in these series and are called arithmetic functions (see, e.g., Chandrasekharan [4] and Apostol [13] ). Such functions are the Möbius function ![]() and the Mangoldt function
and the Mangoldt function ![]() as the best known ones. A short representation of the connection of the Riemann zeta function to number analysis and of some of the functions defined there became now standard in many monographs about complex analysis (e.g., [15] ).
as the best known ones. A short representation of the connection of the Riemann zeta function to number analysis and of some of the functions defined there became now standard in many monographs about complex analysis (e.g., [15] ).
Our means for the proof of the Riemann hypothesis in present article are more conventional and “old-fashioned” ones, i.e. the Real Analysis and the Theory of Com- plex Functions which were developed already for a long time. The most promising way for a proof of the Riemann hypothesis as it seemed to us in past is via the already mentioned entire function ![]() which is closely related to the Riemann zeta function
which is closely related to the Riemann zeta function![]() . It contains all important elements and information of the last but excludes its trivial zeros and its only singularity and, moreover, possesses remarkable symmetries which facilitate the work with it compared with the Riemann zeta function. This function
. It contains all important elements and information of the last but excludes its trivial zeros and its only singularity and, moreover, possesses remarkable symmetries which facilitate the work with it compared with the Riemann zeta function. This function ![]() was already introduced by Riemann [1] and dealt with, for example, in the classical books of Titchmarsh [3] , Edwards [5] and in almost all of the sources cited at the beginning. Present article is mainly concerned with this xi function
was already introduced by Riemann [1] and dealt with, for example, in the classical books of Titchmarsh [3] , Edwards [5] and in almost all of the sources cited at the beginning. Present article is mainly concerned with this xi function ![]() and
and
its investigation in which, for convenience, we displace the imaginary axis by ![]() to the
to the
right that means to the critical line and call this Xi function ![]() with
with![]() . We derive some representations for it among them novel ones and discuss its properties, including its derivatives, its specialization to the critical line and some other features. We make an approach to this function via the second mean value theorem of analysis (Gauss-Bonnet theorem, e.g., [37] [38] ) and then we apply an operator identity for analytic functions which is derived in Appendix B and which is equivalent to a somehow integrated form of the Cauchy-Riemann equations. This among other not so successful trials (e.g., via moments of function
. We derive some representations for it among them novel ones and discuss its properties, including its derivatives, its specialization to the critical line and some other features. We make an approach to this function via the second mean value theorem of analysis (Gauss-Bonnet theorem, e.g., [37] [38] ) and then we apply an operator identity for analytic functions which is derived in Appendix B and which is equivalent to a somehow integrated form of the Cauchy-Riemann equations. This among other not so successful trials (e.g., via moments of function![]() ) led us finally to a proof of the Riemann hypothesis embedded into a proof for a more general class of functions.
) led us finally to a proof of the Riemann hypothesis embedded into a proof for a more general class of functions.
Our approach to a proof of the Riemann hypothesis in this article in rough steps is as follows:
First we shortly represent the transition from the Riemann zeta function ![]() of complex variable
of complex variable ![]() to the xi function
to the xi function ![]() introduced already by Riemann and derive for it by means of the Poisson summation formula a representation which is convergent in the whole complex plane (Section 2 with main formal part in Appendix
introduced already by Riemann and derive for it by means of the Poisson summation formula a representation which is convergent in the whole complex plane (Section 2 with main formal part in Appendix
A). Then we displace the imaginary axis of variable ![]() to the critical line at
to the critical line at ![]() by
by ![]() that is purely for convenience of further working with the formulae.
that is purely for convenience of further working with the formulae.
However, this has also the desired subsidiary effect that it brings us into the fairway of the complex analysis usually represented with the complex variable![]() . The transformed
. The transformed ![]() function is called
function is called ![]() function.
function.
The function ![]() is represented as an integral transform of a real-valued function
is represented as an integral transform of a real-valued function
![]() of the real variable
of the real variable ![]() in the form
in the form ![]() which is related
which is related
to a Fourier transform (more exactly to Cosine Fourier transform). If the Riemann hypothesis is true then we have to prove that all zeros of the function ![]() occur for
occur for![]() .
.
To the Xi function in mentioned integral transform we apply the second mean-value theorem of real analysis first on the imaginary axes and discuss then its extension from the imaginary axis to the whole complex plane. For this purpose we derive in Appendix B in operator form general relations which allow to extend a holomorphic function from the values on the imaginary axis (or also real axis) to the whole complex plane which are equivalents in integral form to the Cauchy-Riemann equations in differential form and apply this in specific form to the Xi function and, more precisely, to the mean-value function on the imaginary axis (Sections 3 and 4).
Then in Section 5 we accomplish the proof with the discussion and solution of the two most important equations (10) and (11) for the last as decisive stage of the proof. These two equations are derived in preparation before this last stage of the proof. From these equations it is seen that the obtained two real equations admit zeros of the Xi function only on the imaginary axis. This proves the Riemann hypothesis by the equivalence of the Riemann zeta function ![]() to the Xi function
to the Xi function ![]() and embeds it into a whole class of functions with similar properties and positions of their zeros.
and embeds it into a whole class of functions with similar properties and positions of their zeros.
The Sections 6-7 serve for illustrations and graphical representations of the specific parameters (e.g., mean-value parameters) for the Xi function to the Riemann hy- pothesis and for other functions which in our proof by the second mean-value problem are included for the existence of zeros only on the imaginary axis. This is, in particular,
also the whole class of modified Bessel functions ![]() with real
with real
indices ![]() which possess zeros only on the imaginary axis
which possess zeros only on the imaginary axis ![]() and where a proof by means of the differential equations exists and certain classes of almost-periodic functions. We intend to present this last topics in detail in future.
and where a proof by means of the differential equations exists and certain classes of almost-periodic functions. We intend to present this last topics in detail in future.
2. From Riemann Zeta Function ![]() to Related Xi Function
to Related Xi Function ![]() and Its Argument Displacement to Function
and Its Argument Displacement to Function ![]()
In this Section we represent the known transition from the Riemann zeta function ![]() to a function
to a function ![]() and finally to a function
and finally to a function ![]() with displaced complex
with displaced complex
variable ![]() for rational effective work and establish some of the basic
for rational effective work and establish some of the basic
representations of these functions, in particular, a kind of modified Cosine Fourier transformations of a function ![]() to the function
to the function![]() .
.
As already expressed in the Introduction, the most promising way for a proof of the Riemann hypothesis as it seems to us is the way via a certain integral representation of the related xi function![]() . We sketch here the transition from the Riemann zeta function
. We sketch here the transition from the Riemann zeta function ![]() to the related xi function
to the related xi function ![]() in a short way because, in principle, it is known and we delegate some aspects of the derivations to Appendix A.
in a short way because, in principle, it is known and we delegate some aspects of the derivations to Appendix A.
Usually, the starting point for the introduction of the Riemann zeta function ![]() is the following relation between the Euler product and an infinite series continued to the whole complex
is the following relation between the Euler product and an infinite series continued to the whole complex ![]() -plane
-plane
![]() (2.1)
(2.1)
where ![]() denotes the ordered sequence of primes (
denotes the ordered sequence of primes (![]() ). The transition from the product formula to the sum representation in (2.1) via transition to
). The transition from the product formula to the sum representation in (2.1) via transition to
the Logarithm of ![]() and Taylor series expansion of the factors
and Taylor series expansion of the factors ![]() in
in
powers of ![]() using the uniqueness of the prime-number decomposition is well
using the uniqueness of the prime-number decomposition is well
known and due to Euler in 1737. It leads to a special case of a kind of series later introduced and investigated in more general form and called Dirichlet series. The Riemann zeta function ![]() can be analytically continued into the whole complex plane to a meromorphic function that was made and used by Riemann. The sum in (2.1) converges uniformly for complex variable
can be analytically continued into the whole complex plane to a meromorphic function that was made and used by Riemann. The sum in (2.1) converges uniformly for complex variable ![]() in the open semi-planes with arbitrary
in the open semi-planes with arbitrary ![]() and arbitrary
and arbitrary![]() . The only singularity of the function
. The only singularity of the function ![]() is a simple pole at
is a simple pole at ![]() with residue 1 that we discuss below.
with residue 1 that we discuss below.
The product form (2.1) of the zeta function ![]() shows that it involves all prime numbers
shows that it involves all prime numbers ![]() exactly one times and therefore it contains information about them in a coded form. It proves to be possible to regain information about the prime number distribution from this function. For many purposes it is easier to work with mero- morphic and, moreover, entire functions than with infinite sequences of numbers but in first case one has to know the properties of these functions which are determined by their zeros and their singularities together with their multiplicity.
exactly one times and therefore it contains information about them in a coded form. It proves to be possible to regain information about the prime number distribution from this function. For many purposes it is easier to work with mero- morphic and, moreover, entire functions than with infinite sequences of numbers but in first case one has to know the properties of these functions which are determined by their zeros and their singularities together with their multiplicity.
From the well-known integral representation of the Gamma function
![]() (2.2)
(2.2)
follows by the substitutions ![]() with an appropriately fixed parameter
with an appropriately fixed parameter ![]() for arbitrary natural numbers
for arbitrary natural numbers ![]()
![]() (2.3)
(2.3)
Inserting this into the sum representation (2.1) and changing the order of summation and integration, we obtain for choice ![]() of the parameter using the sum evaluation of the geometric series
of the parameter using the sum evaluation of the geometric series
![]() (2.4)
(2.4)
and for choice ![]() with substitution
with substitution ![]() of the integration variable (see [1] and, e.g., [3] [4] [5] [7] [9] )
of the integration variable (see [1] and, e.g., [3] [4] [5] [7] [9] )
![]() (2.5)
(2.5)
Other choice of ![]() seems to be of lesser importance. Both representations (2.4) and (2.5) are closely related to a Mellin transform
seems to be of lesser importance. Both representations (2.4) and (2.5) are closely related to a Mellin transform ![]() of a function
of a function ![]() which together with its inversion is generally defined by (e.g., [15] [32] [33] [34] [35] )
which together with its inversion is generally defined by (e.g., [15] [32] [33] [34] [35] )
![]() (2.6)
(2.6)
where ![]() is an arbitrary real value within the convergence strip of
is an arbitrary real value within the convergence strip of ![]() in complex
in complex ![]() -plane. The Mellin transform
-plane. The Mellin transform ![]() of a function
of a function ![]() is closely related to the Fourier transform
is closely related to the Fourier transform ![]() of the function
of the function ![]() by variable substitution
by variable substitution ![]() and
and![]() . Thus the Riemann zeta function
. Thus the Riemann zeta function ![]() can be represented, substantially (i.e., up to factors depending on
can be represented, substantially (i.e., up to factors depending on![]() ), as the Mellin transforms of the
), as the Mellin transforms of the
functions ![]() or of
or of![]() , respectively. The
, respectively. The
kernels of the Mellin transform are the eigenfunctions of the differential operator
![]() to eigenvalue
to eigenvalue ![]() or, correspondingly, of the integral operator
or, correspondingly, of the integral operator ![]()
of the multiplication of the argument of a function by a factor ![]() (scaling of argument). Both representations (2.4) and (2.5) can be used for the derivation of further representations of the Riemann zeta function and for the analytic continuation. The analytic continuation of the Riemann zeta function can also be obtained using the Euler-Maclaurin summation formula for the series in (2.1) (e.g., [5] [11] [15] ).
(scaling of argument). Both representations (2.4) and (2.5) can be used for the derivation of further representations of the Riemann zeta function and for the analytic continuation. The analytic continuation of the Riemann zeta function can also be obtained using the Euler-Maclaurin summation formula for the series in (2.1) (e.g., [5] [11] [15] ).
Using the Poisson summation formula, one can transform the representation (2.5) of the Riemann zeta function to the following form
![]() (2.7)
(2.7)
This is known [1] [3] [5] [7] [9] but for convenience and due to the importance of this representation for our purpose we give a derivation in Appendix A. From (2.7) which is now already true for arbitrary complex ![]() and, therefore, is an analytic continuation of the representations (2.1) or (2.5) we see that the Riemann zeta function satisfies a functional equation for the transformation of the argument
and, therefore, is an analytic continuation of the representations (2.1) or (2.5) we see that the Riemann zeta function satisfies a functional equation for the transformation of the argument![]() . In simplest form it appears by “renormalizing” this function via introduction of the xi function
. In simplest form it appears by “renormalizing” this function via introduction of the xi function ![]() defined by Riemann according to [1] and to [5] [20] 1
defined by Riemann according to [1] and to [5] [20] 1
![]() (2.8)
(2.8)
and we obtain for it the following representation converging in the whole complex plane of ![]() (e.g., [1] [4] [5] [7] [9] )
(e.g., [1] [4] [5] [7] [9] )
![]() (2.9)
(2.9)
with the “normalization”
![]() (2.10)
(2.10)
For ![]() the xi function and the zeta function possess the (likely transcendental)
the xi function and the zeta function possess the (likely transcendental)
values
![]() (2.11)
(2.11)
Contrary to the Riemann zeta function ![]() the function
the function ![]() is an entire function. The only singularity of
is an entire function. The only singularity of ![]() which is the simple pole at
which is the simple pole at![]() , is removed by multiplication of
, is removed by multiplication of ![]() with
with ![]() in the definition (2.8) and the trivial zeros of
in the definition (2.8) and the trivial zeros of ![]() at
at ![]() are also removed by its multiplication with
are also removed by its multiplication with
![]() which possesses simple poles there.
which possesses simple poles there.
The functional equation
![]() (2.12)
(2.12)
from which follows for the ![]() -th derivatives
-th derivatives
![]() (2.13)
(2.13)
and which expresses that ![]() is a symmetric function with respect to
is a symmetric function with respect to ![]() as it is
as it is
immediately seen from (2.9) and as it was first derived by Riemann [1] . It can be easily converted into the following functional equation for the Riemann zeta function ![]() 2
2
![]() (2.14)
(2.14)
Together with ![]() we find by combination with (2.12)
we find by combination with (2.12)
![]() (2.15)
(2.15)
that combine in simple way, function values for 4 points ![]() of the complex plane. Relation (15) means that in contrast to the function
of the complex plane. Relation (15) means that in contrast to the function ![]() which is only real-valued on the real axis the function
which is only real-valued on the real axis the function ![]() becomes real-valued on the real
becomes real-valued on the real
axis (![]() ) and on the imaginary axis (
) and on the imaginary axis (![]() ).
).
As a consequence of absent zeros of the Riemann zeta function ![]() for
for ![]() together with the functional relation (14) follows that all nontrivial zeros of this function have to be within the strip
together with the functional relation (14) follows that all nontrivial zeros of this function have to be within the strip ![]() and the Riemann hypothesis asserts that all zeros of the related xi function
and the Riemann hypothesis asserts that all zeros of the related xi function ![]() are positioned on the
are positioned on the
so-called critical line![]() . This is, in principle, well known.
. This is, in principle, well known.
We use the functional Equation (2.12) for a simplification of the notations in the following considerations and displace the imaginary axis of the complex variable
![]() from
from ![]() to the value
to the value ![]() by introducing the entire function
by introducing the entire function ![]()
of the complex variable ![]() as follows
as follows
![]() (2.16)
(2.16)
with the “normalization” (see (2.10) and (2.11))
![]() (2.17)
(2.17)
following from (2.10). Thus the full relation of the Xi function ![]() to the Riemann zeta function
to the Riemann zeta function ![]() using definition (2.8) is
using definition (2.8) is
![]() (2.18)
(2.18)
We emphasize again that the argument displacement (2.16) is made in the following only for convenience of notations and not for some more principal reason.
The functional equation (2.12) together with (2.13) becomes
![]() (2.19)
(2.19)
and taken together with the symmetry for the transition to complex conjugated variable
![]() (2.20)
(2.20)
This means that the Xi function ![]() becomes real-valued on the imaginary axis
becomes real-valued on the imaginary axis ![]() which becomes the critical line in the new variable
which becomes the critical line in the new variable ![]()
![]() (2.21)
(2.21)
Furthermore, the function ![]() becomes a symmetrical function and a real-valued one on the real axis
becomes a symmetrical function and a real-valued one on the real axis ![]()
![]() (2.22)
(2.22)
In contrast to this the Riemann zeta function ![]() the function is not a real-valued
the function is not a real-valued
function on the critical line ![]() and is real-valued but not symmetric on the real
and is real-valued but not symmetric on the real
axis. This is represented in Figure 1. (calculated with “Mathematica 6” such as the
further figures too). We see that not all of the zeros of the real part ![]() are also zeros of the imaginary part
are also zeros of the imaginary part ![]() and, vice versa, that not all of the
and, vice versa, that not all of the
zeros of the imaginary part are also zeros of the real part and thus genuine zeros of the
function ![]() which are signified by grid lines. Between two zeros of the real part which are genuine zeros of
which are signified by grid lines. Between two zeros of the real part which are genuine zeros of ![]() lies in each case (exception first interval)
lies in each case (exception first interval)
an additional zero of the imaginary part, which almost coincides with a maximum of the real part.
![]()
Figure 1. Real and imaginary part and absolute value of Riemann zeta function on critical line. The position of the zeros of the whole function ![]() on the critical line are shown by grid lines. One can see that not all zeros of the real part are also zeros of the imaginary part and vice versa. The figures are easily to generate by program “Mathematica” and are published in similar forms already in literature.
on the critical line are shown by grid lines. One can see that not all zeros of the real part are also zeros of the imaginary part and vice versa. The figures are easily to generate by program “Mathematica” and are published in similar forms already in literature.
Using (2.9) and definition (2.16) we find the following representation of ![]()
![]() (2.23)
(2.23)
With the substitution of the integration variable ![]() (see also (2.10) in Appendix A) representation (2.23) is transformed to
(see also (2.10) in Appendix A) representation (2.23) is transformed to
![]() (2.24)
(2.24)
In Appendix A we show that (2.24) can be represented as follows (see also Equation (2.2) on p. 17 in [5] which possesses a similar principal form)
![]() (2.25)
(2.25)
with the following explicit form of the function ![]() of the real variable
of the real variable ![]()
![]() (2.26)
(2.26)
The function ![]() is symmetric
is symmetric
![]() (2.27)
(2.27)
that means it is an even function although this is not immediately seen from representation (2.26)3. We prove this in Appendix A. Due to this symmetry, formula (2.25) can be also represented by
![]() (2.28)
(2.28)
In the formulation of the right-hand side the function ![]() appears as analytic continuation of the Fourier transform of the function
appears as analytic continuation of the Fourier transform of the function ![]() written with imaginary argument
written with imaginary argument ![]() or, more generally, with substitution
or, more generally, with substitution ![]() and complex
and complex![]() . From this follows as inversion of the integral transformation (2.28) using (2.27)
. From this follows as inversion of the integral transformation (2.28) using (2.27)
![]() (2.29)
(2.29)
or due to symmetry of the integrand in analogy to (2.25)
![]() (2.30)
(2.30)
where ![]() is a real-valued function of the variable
is a real-valued function of the variable ![]() on the imaginary axis
on the imaginary axis
![]() (2.31)
(2.31)
due to (2.25).
A graphical representation of the function ![]() and of its first derivatives
and of its first derivatives ![]() is given in Figure 2. The function
is given in Figure 2. The function ![]() is monotonically de-
is monotonically de-
creasing for ![]() due to the non-positivity of its first derivative
due to the non-positivity of its first derivative ![]()
which explicitly is (see also Appendix A)
![]() (2.32)
(2.32)
with one relative minimum at ![]() of depth
of depth![]() . Moreover, it is very important for the following that due to presence of factors
. Moreover, it is very important for the following that due to presence of factors ![]() in the sum terms in (2.26) or in (2.32) the functions
in the sum terms in (2.26) or in (2.32) the functions ![]() and
and ![]() and all their higher derivatives are very rapidly decreasing for
and all their higher derivatives are very rapidly decreasing for![]() , more rapidly than any exponential function with a polynomial of
, more rapidly than any exponential function with a polynomial of ![]() in the argument. In this sense the function
in the argument. In this sense the function ![]() is more comparable with functions of finite support which vanish from a certain
is more comparable with functions of finite support which vanish from a certain ![]() on than with any exponentially decreasing function. From (2.27) follows immediately that the function
on than with any exponentially decreasing function. From (2.27) follows immediately that the function ![]() is antisymmetric
is antisymmetric
![]() (2.33)
(2.33)
that means it is an odd function.
It is known that smoothness and rapidness of decreasing in infinity of a function change their role in Fourier transformations. As the Fourier transform of the smooth (infinitely continuously differentiable) function ![]() the Xi function on the critical line
the Xi function on the critical line ![]() is rapidly decreasing in infinity. Therefore it is not easy to represent the real-valued function
is rapidly decreasing in infinity. Therefore it is not easy to represent the real-valued function ![]() with its rapid oscillations under the envelope of rapid decrease for increasing variable
with its rapid oscillations under the envelope of rapid decrease for increasing variable ![]() graphically in a large region of this variable
graphically in a large region of this variable![]() . An appropriate real amplification envelope is seen from (2.18) to be
. An appropriate real amplification envelope is seen from (2.18) to be
![]() which rises
which rises ![]() to the level of the Riemann zeta function
to the level of the Riemann zeta function ![]() on the critical line
on the critical line![]() . This is shown in Figure 3. The partial
. This is shown in Figure 3. The partial
picture for ![]() in Figure 3. with negative part folded up is identical with the
in Figure 3. with negative part folded up is identical with the
absolute value ![]() of the Riemann zeta function
of the Riemann zeta function ![]() on the imaginary axis
on the imaginary axis ![]() (fourth partial picture in Figure 1).
(fourth partial picture in Figure 1).
We now give a representation of the Xi function by the derivative of the Omega
function. Using ![]() one obtains from (2.25) by partial integration
one obtains from (2.25) by partial integration
the following alternative representation of the function ![]()
![]() (2.34)
(2.34)
that due to antisymmetry of ![]() and
and ![]() with respect to
with respect to ![]() can also be written
can also be written
![]() (2.35)
(2.35)
Figure 2 gives a graphical representation of the function ![]() and of its first
and of its first
derivative ![]() which due to rapid convergence of the sums is easily to
which due to rapid convergence of the sums is easily to
generate by computer. One can express ![]() also by higher derivatives
also by higher derivatives
![]() of the Omega function
of the Omega function ![]() according to
according to
![]() (2.36)
(2.36)
with the symmetries of the derivatives of the function ![]() for
for ![]()
![]() (2.37)
(2.37)
This can be seen by successive partial integrations in (2.25) together with complete induction. The functions ![]() in these integral transformations are for
in these integral transformations are for ![]() not monotonic functions.
not monotonic functions.
We mention yet another representation of the function![]() . Using the trans- formations
. Using the trans- formations
![]() (2.38)
(2.38)
the function ![]() according to (2.28) with the explicit representation of the function
according to (2.28) with the explicit representation of the function ![]() in (2.26) can now be represented in the form
in (2.26) can now be represented in the form
![]() (2.39)
(2.39)
where ![]() denotes the incomplete Gamma function defined by (e.g., [18] [21] [36] )
denotes the incomplete Gamma function defined by (e.g., [18] [21] [36] )
![]() (2.40)
(2.40)
However, we did not see a way to prove the Riemann hypothesis via the repre- sentation (2.39).
The Riemann hypothesis for the zeta function ![]() is now equivalent to the hypothesis that all zeros of the related entire function
is now equivalent to the hypothesis that all zeros of the related entire function ![]() lie on the imaginary axis
lie on the imaginary axis ![]() that means on the line to real part
that means on the line to real part ![]() of
of ![]() which becomes now the critical line. Since the zeta function
which becomes now the critical line. Since the zeta function ![]() does not possess zeros in the convergence region
does not possess zeros in the convergence region ![]() of the Euler product (2.1) and due to symmetries (2.27) and (2.31) it is only necessary to prove that
of the Euler product (2.1) and due to symmetries (2.27) and (2.31) it is only necessary to prove that ![]() does not possess zeros within the
does not possess zeros within the
strips ![]() and
and ![]() to both sides of the imaginary axis
to both sides of the imaginary axis ![]() where
where
for symmetry the proof for one of these strips would be already sufficient. However, we will go another way where the restriction to these strips does not play a role for the proof.
3. Application of Second Mean-Value Theorem of Calculus to Xi Function
After having accepted the basic integral representation (2.25) of the entire function ![]() according to
according to
![]() (3.1)
(3.1)
with the function ![]() explicitly given in (2.26) we concentrate us on its further treatment. However, we do this not with this specialization for the real-valued function
explicitly given in (2.26) we concentrate us on its further treatment. However, we do this not with this specialization for the real-valued function ![]() but with more general suppositions for it. Expressed by real part
but with more general suppositions for it. Expressed by real part ![]() and imaginary part
and imaginary part ![]() of
of ![]()
![]() (3.2)
(3.2)
we find from (3.1)
![]() (3.3)
(3.3)
We suppose now as necessary requirement for ![]() and satisfied in the special case (2.26)
and satisfied in the special case (2.26)
![]() (3.4)
(3.4)
Furthermore, ![]() should be an entire function that requires that the integral (3.1) is finite for arbitrary complex
should be an entire function that requires that the integral (3.1) is finite for arbitrary complex ![]() and therefore that
and therefore that ![]() is rapidly decreasing in infinity, more precisely
is rapidly decreasing in infinity, more precisely
![]() (3.5)
(3.5)
for arbitrary![]() . This means that the function
. This means that the function ![]() should be a nonsingular function which is rapidly decreasing in infinity, more rapidly than any exponential function
should be a nonsingular function which is rapidly decreasing in infinity, more rapidly than any exponential function ![]() with arbitrary
with arbitrary![]() . Clearly, this is satisfied for the special function
. Clearly, this is satisfied for the special function ![]() in (2.26).
in (2.26).
Our conjecture for a longer time was that all zeros of ![]() lie on the imaginary axis
lie on the imaginary axis ![]() for a large class of functions
for a large class of functions ![]() and that this is not very specific for the special function
and that this is not very specific for the special function ![]() given in (2.26) but is true for a much larger class. It seems that to this class belong all non-increasing functions
given in (2.26) but is true for a much larger class. It seems that to this class belong all non-increasing functions![]() , i.e such functions for which holds
, i.e such functions for which holds ![]() for its first derivative and which rapidly decrease in infinity. This means that they vanish more rapidly in infinity than any power functions
for its first derivative and which rapidly decrease in infinity. This means that they vanish more rapidly in infinity than any power functions ![]() (practically they vanish exponentially). However, for the conver- gence of the integral (3.1) in the whole complex
(practically they vanish exponentially). However, for the conver- gence of the integral (3.1) in the whole complex ![]() -plane it is necessary that the functions have to decrease in infinity also more rapidly than any exponential function
-plane it is necessary that the functions have to decrease in infinity also more rapidly than any exponential function ![]() with arbitrary
with arbitrary ![]() expressed in (3.5). In particular, to this class belong all rapidly decreasing functions
expressed in (3.5). In particular, to this class belong all rapidly decreasing functions ![]() which vanish from a certain
which vanish from a certain ![]() on and which may be called non-increasing finite functions (or functions with compact support). On the other side, continuity of its derivatives
on and which may be called non-increasing finite functions (or functions with compact support). On the other side, continuity of its derivatives ![]() is not required. The modified Bessel functions
is not required. The modified Bessel functions ![]() “normalized” to the form of entire
“normalized” to the form of entire
functions ![]() for
for ![]() possess a representation of the form (3.1) with
possess a representation of the form (3.1) with
functions ![]() which vanish from
which vanish from ![]() on but a number of derivatives of
on but a number of derivatives of ![]() for the functions is not continuous at
for the functions is not continuous at ![]() depending on the index
depending on the index![]() . It is valuable that here an independent proof of the property that all zeros of the modified Bessel functions
. It is valuable that here an independent proof of the property that all zeros of the modified Bessel functions ![]() lie on the imaginary axis can be made using their differential eq- uations via duality relations. We intend to present this in detail in a later work.
lie on the imaginary axis can be made using their differential eq- uations via duality relations. We intend to present this in detail in a later work.
Furthermore, to the considered class belong all monotonically decreasing functions with the described rapid decrease in infinity. The fine difference of the decreasing functions to the non-increasing functions ![]() is that in first case the function
is that in first case the function ![]() cannot stay on the same level in a certain interval that means we have
cannot stay on the same level in a certain interval that means we have ![]() for all points
for all points ![]() instead of
instead of ![]() only. A function which de- creases not faster than
only. A function which de- creases not faster than ![]() in infinity does not fall into this category as, for example,
in infinity does not fall into this category as, for example,
the function ![]() shows.
shows.
To apply the second mean-value theorem it is necessary to restrict us to a class of functions ![]() which are non-increasing that means for which for all
which are non-increasing that means for which for all ![]() in considered interval holds
in considered interval holds
![]() (3.6)
(3.6)
or equivalently in more compact form
![]() (3.7)
(3.7)
The monotonically decreasing functions in the interval![]() , in particular, belong to the class of non-increasing functions with the fine difference that here
, in particular, belong to the class of non-increasing functions with the fine difference that here
![]() (3.8)
(3.8)
is satisfied. Thus smoothness of ![]() for
for ![]() is not required. If furthermore
is not required. If furthermore ![]() is a continuous function in the interval
is a continuous function in the interval ![]() the second mean-value theorem (often called theorem of Bonnet (1867) or Gauss-Bonnet theorem) states an equivalence for the following integral on the left-hand side to the expression on the right-hand side according to (see some monographs about Calculus or Real Analysis; we recommend the monographs of Courant [37] (Appendix to chap IV) and of Widder [38] who called it Weierstrass form of Bonnet’s theorem (chap. 5,
the second mean-value theorem (often called theorem of Bonnet (1867) or Gauss-Bonnet theorem) states an equivalence for the following integral on the left-hand side to the expression on the right-hand side according to (see some monographs about Calculus or Real Analysis; we recommend the monographs of Courant [37] (Appendix to chap IV) and of Widder [38] who called it Weierstrass form of Bonnet’s theorem (chap. 5, ![]() 4))
4))
![]() (3.9)
(3.9)
where ![]() is a certain value within the interval boundaries
is a certain value within the interval boundaries ![]() which as a rule we do not exactly know. It holds also for non-decreasing functions which include the monotonically increasing functions as special class in analogous way. The proof of the second mean-value theorem is comparatively simple by applying a substitution in the (first) mean-value theorem of integral calculus [37] [38] .
which as a rule we do not exactly know. It holds also for non-decreasing functions which include the monotonically increasing functions as special class in analogous way. The proof of the second mean-value theorem is comparatively simple by applying a substitution in the (first) mean-value theorem of integral calculus [37] [38] .
Applied to our function ![]() which in addition should rapidly decrease in infinity according to (3.5) this means in connection with monotonic decrease that it has to be positively semi-definite if
which in addition should rapidly decrease in infinity according to (3.5) this means in connection with monotonic decrease that it has to be positively semi-definite if ![]() and therefore
and therefore
![]() (3.10)
(3.10)
and the theorem (3.9) takes on the form
![]() (3.11)
(3.11)
where the extension to an upper boundary ![]() in (3.9) for
in (3.9) for ![]() and in case of existence of the integral is unproblematic.
and in case of existence of the integral is unproblematic.
If we insert in (3.9) for ![]() the function
the function ![]() which apart from the real variable
which apart from the real variable ![]() depends in parametrical way on the complex variable
depends in parametrical way on the complex variable ![]() and is an analytic function of
and is an analytic function of ![]() we find that
we find that ![]() depends on this complex parameter also in an analytic way as follows
depends on this complex parameter also in an analytic way as follows
![]() (3.12)
(3.12)
where ![]() is an entire function with
is an entire function with ![]() its real and
its real and ![]() its imaginary part. The condition for zeros
its imaginary part. The condition for zeros ![]() is that
is that ![]() vanishes that leads to
vanishes that leads to
![]() (3.13)
(3.13)
or split in real and imaginary part
![]() (3.14)
(3.14)
for the real part and
![]() (3.15)
(3.15)
for the imaginary part.
The multi-valuedness of the mean-value functions in the conditions (3.13) or (3.15) is an interesting phenomenon which is connected with the periodicity of the function ![]() on the imaginary axis
on the imaginary axis ![]() in our application (3.12) of the second mean-value theorem (3.11). To our knowledge this is up to now not well studied. We come back to this in the next Sections 4 and, in particular, Section 7 brings some illustrative clarity when we represent the mean-value functions graphically. At present we will say only that we can choose an arbitrary
in our application (3.12) of the second mean-value theorem (3.11). To our knowledge this is up to now not well studied. We come back to this in the next Sections 4 and, in particular, Section 7 brings some illustrative clarity when we represent the mean-value functions graphically. At present we will say only that we can choose an arbitrary ![]() in (3.15) which provides us the whole spectrum of zeros
in (3.15) which provides us the whole spectrum of zeros ![]() on the upper half-plane and the corresponding spectrum of zeros
on the upper half-plane and the corresponding spectrum of zeros ![]() on the lower half-plane of
on the lower half-plane of ![]() which as will be later seen lie all on the imaginary axis. Since in computer calculations the values of
which as will be later seen lie all on the imaginary axis. Since in computer calculations the values of
the Arcus Sine function are provided in the region from ![]() to
to ![]() it is convenient
it is convenient
to choose ![]() but all other values of
but all other values of ![]() in (3.15) lead to equivalent results.
in (3.15) lead to equivalent results.
One may represent the conditions (3.14) and (3.15) also in the following equivalent form
![]() (3.16)
(3.16)
from which follows
![]() (3.17)
(3.17)
All these forms (3.14)-(3.17) are implicit equations with two variables ![]() which cannot be resolved with respect to one variable (e.g., in forms
which cannot be resolved with respect to one variable (e.g., in forms ![]() for each fixed
for each fixed ![]() and branches
and branches![]() ) and do not provide immediately the necessary conditions for zeros in explicit form but we can check that (3.16) satisfies the Cauchy-Riemann equations as a minimum requirement
) and do not provide immediately the necessary conditions for zeros in explicit form but we can check that (3.16) satisfies the Cauchy-Riemann equations as a minimum requirement
![]() (3.18)
(3.18)
We have to establish now closer relations between real and imaginary part ![]() and
and ![]() of the complex mean-value parameter
of the complex mean-value parameter![]() . The first step in preparation to this aim is the consideration of the derived conditions on the imaginary axis.
. The first step in preparation to this aim is the consideration of the derived conditions on the imaginary axis.
4. Specialization of Second Mean-Value Theorem to Xi Function on Imaginary Axis
By restriction to the real axis ![]() we find from (3.3) for the function
we find from (3.3) for the function ![]()
![]() (4.1)
(4.1)
with the following two possible representations of ![]() related by partial in- tegration
related by partial in- tegration
![]() (4.2)
(4.2)
The inequality ![]() follows according to the supposition
follows according to the supposition ![]() from the non-negativity of the integrand that means from
from the non-negativity of the integrand that means from![]() . Therefore, the case
. Therefore, the case ![]() can be excluded from the beginning in the further considerations for zeros of
can be excluded from the beginning in the further considerations for zeros of ![]() and
and![]() .
.
We now restrict us to the imaginary axis ![]() and find from (3.3) for the function
and find from (3.3) for the function ![]()
![]() (4.3)
(4.3)
with the following two possible representations of ![]() related by partial in- tegration
related by partial in- tegration
![]() (4.4)
(4.4)
From the obvious inequality
![]() (4.5)
(4.5)
together with the supposed positivity of ![]() one derives from the first repre- sentation of
one derives from the first repre- sentation of ![]() in (4) the inequality
in (4) the inequality
![]() (4.6)
(4.6)
In the same way by the inequality
![]() (4.7)
(4.7)
one derives using the non-positivity of ![]() (see (3.10)) together with the second representation of
(see (3.10)) together with the second representation of ![]() in (4.4) the inequality
in (4.4) the inequality
![]() (4.8)
(4.8)
which as it is easily seen does not depend on the sign of![]() . Therefore we have two non-negative parameters, the zeroth moment
. Therefore we have two non-negative parameters, the zeroth moment ![]() and the value
and the value![]() , which according to (4.6) and (4.8) restrict the range of values of
, which according to (4.6) and (4.8) restrict the range of values of ![]() to an interior range both to (4.6) and to (4.8) at once.
to an interior range both to (4.6) and to (4.8) at once.
For mentioned purpose we now consider the restriction of the mean-value parameter ![]() to the imaginary axis
to the imaginary axis ![]() for which
for which ![]() is a real- valued function of
is a real- valued function of![]() . For arbitrary fixed
. For arbitrary fixed ![]() we find by the second mean-value theorem a parameter
we find by the second mean-value theorem a parameter ![]() in the interval
in the interval ![]() which naturally depends on the chosen value
which naturally depends on the chosen value ![]() that means
that means![]() . The extension from the imaginary axis
. The extension from the imaginary axis ![]() to the whole complex plane
to the whole complex plane ![]() can be made then using methods of complex analysis. We discuss some formal approaches to this in Appendix B. Now we apply (3.12) to the imaginary axis
can be made then using methods of complex analysis. We discuss some formal approaches to this in Appendix B. Now we apply (3.12) to the imaginary axis![]() .
.
The second mean-value theorem (3.12) on the imaginary axis ![]() (or
(or![]() ) takes on the form
) takes on the form
![]() (4.9)
(4.9)
As already said since the left-hand side is a real-valued function the right-hand side has also to be real-valued and the parameter function ![]() is real-valued and there- fore it can only be the real part
is real-valued and there- fore it can only be the real part ![]() of the complex function
of the complex function ![]() for
for![]() .
.
The second mean-value theorem states that ![]() lies between the minimal and maximal values of the integration borders that is here between 0 and
lies between the minimal and maximal values of the integration borders that is here between 0 and ![]() and this means that
and this means that ![]() should be positive. Here arises a problem which is connected with the periodicity of the function
should be positive. Here arises a problem which is connected with the periodicity of the function ![]() as function of the variable
as function of the variable ![]() for fixed variable
for fixed variable ![]() in the application of the mean-value theorem. Let us first consider the special case
in the application of the mean-value theorem. Let us first consider the special case ![]() in (4.9) which leads to
in (4.9) which leads to
![]() (4.10)
(4.10)
From this relation follows ![]() and it seems that all is correct also with the continuation to
and it seems that all is correct also with the continuation to ![]() for arbitrary
for arbitrary![]() . One may even give the approximate values
. One may even give the approximate values ![]() and
and ![]() and therefore
and therefore ![]() which, however, are not of importance for the later proofs. If we now start from
which, however, are not of importance for the later proofs. If we now start from ![]() and continue it continuously to
and continue it continuously to ![]() then we see that
then we see that ![]() goes monotonically to zero and approaches zero approximately at
goes monotonically to zero and approaches zero approximately at ![]() that is at the first zero of the function
that is at the first zero of the function ![]() on the positive imaginary axis and goes then first beyond zero and oscillates then with decreasing amplitude for increasing
on the positive imaginary axis and goes then first beyond zero and oscillates then with decreasing amplitude for increasing ![]() around the value zero with intersecting it exactly at the zeros of
around the value zero with intersecting it exactly at the zeros of![]() . We try to illustrate this graphically in Section 7. All zeros lie then on the branch
. We try to illustrate this graphically in Section 7. All zeros lie then on the branch ![]() with
with![]() . That
. That ![]() goes beyond zero seems to contradict the content of the second mean-value theorem according which
goes beyond zero seems to contradict the content of the second mean-value theorem according which ![]() has to be positive in our application. Here comes into play the multi-valuedness of the mean-value function
has to be positive in our application. Here comes into play the multi-valuedness of the mean-value function![]() . For the zeros of
. For the zeros of ![]() in (4.9) the relations
in (4.9) the relations ![]() with different integers
with different integers ![]() are equivalent and one may find to values
are equivalent and one may find to values ![]() equivalent curves
equivalent curves ![]() with
with ![]() and all these curves begin with
and all these curves begin with ![]() for
for![]() . However, we cannot continue
. However, we cannot continue ![]() in continuous way to only positive values for
in continuous way to only positive values for![]() .
.
For ![]() the inequality (4.8) is stronger than (4.6) and characterizes the restric- tions of
the inequality (4.8) is stronger than (4.6) and characterizes the restric- tions of ![]() and via the equivalence
and via the equivalence ![]() follows from (4.8)
follows from (4.8)
![]() (4.11)
(4.11)
where the choice of ![]() determines a basis interval of the involved multi-valued function
determines a basis interval of the involved multi-valued function ![]() and the inequality says that it is in every case possible to choose it from the same interval of length
and the inequality says that it is in every case possible to choose it from the same interval of length![]() . The zeros
. The zeros ![]() of the Xi function
of the Xi function ![]() on the imaginary axis
on the imaginary axis ![]() (critical line) are determined alone by the (multi-valued) function
(critical line) are determined alone by the (multi-valued) function ![]() whereas
whereas ![]() vanishes automatically on the imaginary axis in considered special case and does not add a second condition. Therefore, the zeros are the solutions of the conditions
vanishes automatically on the imaginary axis in considered special case and does not add a second condition. Therefore, the zeros are the solutions of the conditions
![]() (4.12)
(4.12)
It is, in general, not possible to obtain the zeros ![]() on the critical line exactly from the mean-value function
on the critical line exactly from the mean-value function ![]() in (4.9) since generally we do not possess it ex- plicitly.
in (4.9) since generally we do not possess it ex- plicitly.
In special cases the function ![]() can be calculated explicitly that is the case, for
can be calculated explicitly that is the case, for
example, for all (modified) Bessel functions![]() . The most simple case among these is the case
. The most simple case among these is the case ![]() when the corresponding function
when the corresponding function ![]() is a step function
is a step function
![]() (4.13)
(4.13)
where ![]() is the Heaviside step function. In this case follows
is the Heaviside step function. In this case follows
![]() (4.14)
(4.14)
where ![]() is the area under the function
is the area under the function ![]()
(or the zeroth-order moment of this function. For the squared modulus of the function ![]() we find
we find
![]() (4.15)
(4.15)
from which, in particular, it is easy to see that this special function ![]() possesses zeros only on the imaginary axis
possesses zeros only on the imaginary axis ![]() or
or ![]() and that they are determined by
and that they are determined by
![]() (4.16)
(4.16)
The zeros on the imaginary axis are here equidistant but the solution ![]() is absent since then also the denominators in (4.15) are vanishing. The parameter
is absent since then also the denominators in (4.15) are vanishing. The parameter ![]() in the second mean-value theorem is here a real constant
in the second mean-value theorem is here a real constant ![]() in the whole complex plane
in the whole complex plane
![]() (4.17)
(4.17)
Practically, the second mean-value theorem compares the result for an arbitrary function ![]() under the given restrictions with that for a step function
under the given restrictions with that for a step function ![]() by preserving the value
by preserving the value ![]() and making the parameter
and making the parameter ![]() depending on
depending on ![]() in the whole complex plane. Without discussing now quantitative relations the formulae (4.17) suggest that
in the whole complex plane. Without discussing now quantitative relations the formulae (4.17) suggest that ![]() will stay a “small” function compared with
will stay a “small” function compared with ![]() in the neighborhood of the imaginary axis (i.e. for
in the neighborhood of the imaginary axis (i.e. for![]() ) in a certain sense.
) in a certain sense.
We will see in next Section that the function ![]() taking into account
taking into account ![]() determines the functions
determines the functions ![]() and
and ![]() and thus
and thus ![]() in the whole complex plane via the Cauchy-Riemann equations in an operational ap- proach that means in an integrated form which we did not found up to now in literature. The general formal part is again delegated to an Appendix B.
in the whole complex plane via the Cauchy-Riemann equations in an operational ap- proach that means in an integrated form which we did not found up to now in literature. The general formal part is again delegated to an Appendix B.
5. Accomplishment of Proof for Zeros of Xi Functions on Imaginary Axis Alone
In last Section we discussed the application of the second mean-value theorem to the function ![]() on the imaginary axis
on the imaginary axis![]() . Equations (3.14) and (3.15) or their equivalent forms (3.16) or (3.17) are not yet sufficient to derive conclusions about the position of the zeros on the imaginary axis in dependence on
. Equations (3.14) and (3.15) or their equivalent forms (3.16) or (3.17) are not yet sufficient to derive conclusions about the position of the zeros on the imaginary axis in dependence on![]() . We have yet to derive more information about the mean-value functions
. We have yet to derive more information about the mean-value functions ![]() which we obtain by relating the real-valued function
which we obtain by relating the real-valued function ![]() and
and ![]() to the function
to the function ![]() on the imaginary axis taking into account
on the imaginary axis taking into account![]() .
.
The general case of complex ![]() can be obtained from the special case
can be obtained from the special case ![]() in
in
(4.9) by application of the displacement operator ![]() to the function
to the function ![]()
according to
![]() (5.1)
(5.1)
The function ![]() is related to
is related to ![]() as follows
as follows
![]() (5.2)
(5.2)
or in more compact form
![]() (5.3)
(5.3)
This is presented in Appendix B in more general form for additionally non- vanishing ![]() and arbitrary holomorphic functions. It means that we may obtain
and arbitrary holomorphic functions. It means that we may obtain ![]()
and ![]() by applying the operators
by applying the operators ![]() and
and![]() , respectively, to
, respectively, to
the function ![]() on the imaginary axis (remind
on the imaginary axis (remind ![]() vanishes there in our case). Clearly, Equations (5.2) are in agreement with the Cauchy-Riemann eq-
vanishes there in our case). Clearly, Equations (5.2) are in agreement with the Cauchy-Riemann eq-
uations ![]() and
and ![]() as a minimal requirement.
as a minimal requirement.
We now write ![]() in the form equivalent to (5.1)
in the form equivalent to (5.1)
![]() (5.4)
(5.4)
The denominator ![]() does not contribute to zeros. Since the Hyperbolic Sine possesses zeros only on the imaginary axis we see from (5.4) that we may expect zeros only for such related variables
does not contribute to zeros. Since the Hyperbolic Sine possesses zeros only on the imaginary axis we see from (5.4) that we may expect zeros only for such related variables ![]() which satisfy the necessary condition of vanishing of its real part of the argument that leads as we already know to (see (3.14))
which satisfy the necessary condition of vanishing of its real part of the argument that leads as we already know to (see (3.14))
![]() (5.5)
(5.5)
The zeros with coordinates ![]() themselves can be found then as the (in general non-degenerate) solutions of the following equation (see (3.15))
themselves can be found then as the (in general non-degenerate) solutions of the following equation (see (3.15))
![]() (5.6)
(5.6)
if these pairs ![]() satisfy the necessary condition (5.5). Later we will see that it provides the whole spectrum of solutions for the zeros but we can also obtain each
satisfy the necessary condition (5.5). Later we will see that it provides the whole spectrum of solutions for the zeros but we can also obtain each ![]() separately from one branch
separately from one branch ![]() and would they then denote by
and would they then denote by![]() . Thus we have first of all to look for such pairs
. Thus we have first of all to look for such pairs ![]() which satisfy the condition (5.5) off the imaginary axis that is for
which satisfy the condition (5.5) off the imaginary axis that is for ![]() since we know already that these functions may possess zeros on the imaginary axis
since we know already that these functions may possess zeros on the imaginary axis![]() .
.
Using (5.2) we may represent the necessary condition (5.5) for the proof by the second mean-value theorem in the form
![]() (5.7)
(5.7)
and Equation (5.6) which determines then the position of the zeros can be written with equivalent values ![]()
![]() (5.8)
(5.8)
We may represent Equations (5.7) and (5.8) in a simpler form using the following operational identities
![]() (5.9)
(5.9)
which are a specialization of the operational identities (B.11) in Appendix B with ![]() and therefore
and therefore![]() . If we multiply (5.7) and (5.8) both by the function
. If we multiply (5.7) and (5.8) both by the function ![]() then we may write (5.7) in the form (changing order
then we may write (5.7) in the form (changing order![]() )
)
![]() (5.10)
(5.10)
and (5.8) in the form
![]() (5.11)
(5.11)
The left-hand side of these conditions possess the general form for the extension of a holomorphic function ![]() from the functions
from the functions ![]() and
and ![]() on the imaginary axis to the whole complex plane in case of
on the imaginary axis to the whole complex plane in case of ![]() and if we apply this to the function
and if we apply this to the function![]() . Equations (5.10) and (5.11) possess now the most simple form, we found, to accomplish the proof for the exclusive position of zeros on the imaginary axis. All information about the zeros of the Xi function
. Equations (5.10) and (5.11) possess now the most simple form, we found, to accomplish the proof for the exclusive position of zeros on the imaginary axis. All information about the zeros of the Xi function ![]() for arbitrary
for arbitrary ![]() is now contained in the conditions (5.10) and (5.11) which we now discuss.
is now contained in the conditions (5.10) and (5.11) which we now discuss.
Since ![]() is a nonsingular operator we can multiply both sides of equation (5.11) by the inverse operator
is a nonsingular operator we can multiply both sides of equation (5.11) by the inverse operator ![]() and obtain
and obtain
![]() (5.12)
(5.12)
This equation is yet fully equivalent to (5.11) for arbitrary ![]() but it provides only the same possible solutions for the values
but it provides only the same possible solutions for the values ![]() of zeros as for zeros on the imaginary axis. This alone already suggests that it cannot be that zeros with
of zeros as for zeros on the imaginary axis. This alone already suggests that it cannot be that zeros with ![]() if they exist possess the same values of
if they exist possess the same values of ![]() as the zeros on the imaginary axis. But in such form the proof of the impossibility of zeros off the imaginary axis seemed to be not satisfactory and we present in the following some slightly different variants which go deeper into the details of the proof.
as the zeros on the imaginary axis. But in such form the proof of the impossibility of zeros off the imaginary axis seemed to be not satisfactory and we present in the following some slightly different variants which go deeper into the details of the proof.
In analogous way by multiplication of (5.10) with the operator ![]() and (5.11) with the operator
and (5.11) with the operator ![]() and addition of both equations we also obtain
and addition of both equations we also obtain
condition (5.12) that means
![]() (5.13)
(5.13)
The equal conditions (5.12) and (5.13) which are identical with the condition for zeros on the imaginary axis are a necessary condition for all zeros. For each chosen equivalent ![]() (remind
(remind ![]() depends then on
depends then on ![]() which we do not mention by the notation) one obtains an infinite series of solutions
which we do not mention by the notation) one obtains an infinite series of solutions ![]() for the zeros of the function
for the zeros of the function ![]()
![]() (5.14)
(5.14)
whereas for ![]() Equation (5.12), by definition of
Equation (5.12), by definition of![]() , is not satisfied. Supposing that we know
, is not satisfied. Supposing that we know ![]() that is as a rule not the case, we could solve for each
that is as a rule not the case, we could solve for each ![]() the usually transcendental Equation (5.13) graphically, for example, by drawing the equivalent functions
the usually transcendental Equation (5.13) graphically, for example, by drawing the equivalent functions ![]() over variable
over variable ![]() as abscissa and looking for the intersections points with the lines
as abscissa and looking for the intersections points with the lines ![]() over
over ![]() (Section 7). These intersection points
(Section 7). These intersection points ![]() are the solutions for zeros
are the solutions for zeros ![]() on the imaginary axis. Choosing
on the imaginary axis. Choosing ![]() the condition (5.10) is identically satisfied that, however, is not the case for
the condition (5.10) is identically satisfied that, however, is not the case for ![]() in general.
in general.
Now we have to look for zeros ![]() in case
in case ![]() by an additional independent condition in comparison to (5.13). Whereas for zeros with
by an additional independent condition in comparison to (5.13). Whereas for zeros with ![]() the condition (5.10) is identically satisfied we have to examine this condition for zeros with
the condition (5.10) is identically satisfied we have to examine this condition for zeros with![]() . In the case of
. In the case of ![]() we may divide both sides of the condition (5.10) by
we may divide both sides of the condition (5.10) by ![]() and obtain
and obtain
![]() (5.15)
(5.15)
Since ![]() is a nonsingular operator (in contrast to
is a nonsingular operator (in contrast to ![]() which pos-
which pos-
sesses 0 as eigenvalue to eigenfunction
![]()
![]() arbitrary) we may multiply
arbitrary) we may multiply
Equation (5.15) by the inverse operator ![]() and obtain
and obtain
![]() (5.16)
(5.16)
This condition has also to be satisfied for the solution ![]() of (5.12) in case of
of (5.12) in case of ![]() that means
that means
![]() (5.17)
(5.17)
Both conditions (5.13) and (5.16) taken together mean that a corresponding zero ![]() must possess a twofold degeneration.
must possess a twofold degeneration.
From condition (5.11) combined with (5.10) follows by Taylor series expansion with
respect to ![]() for arbitrary complex
for arbitrary complex ![]()
![]() (5.18)
(5.18)
and the independence of the left-hand side of ![]() for arbitrary complex
for arbitrary complex ![]() requires
requires
vanishing of the coefficients ![]() for
for ![]() for solutions
for solutions![]() . Let us
. Let us
assume
![]() (5.19)
(5.19)
From the Taylor series expansion of the function ![]() in the neighborhood of a solution
in the neighborhood of a solution ![]() follows then
follows then
![]() (5.20)
(5.20)
Thus using (5.19) we can find zeros for ![]() that means off the imaginary axis if the mean-value function
that means off the imaginary axis if the mean-value function ![]() possesses the form
possesses the form
![]() (5.21)
(5.21)
for a certain integer![]() . According to (5.2) the whole mean-value functions
. According to (5.2) the whole mean-value functions ![]() and
and ![]() are then
are then
![]() (5.22)
(5.22)
![]()
or in compact form
![]() (5.23)
(5.23)
If we insert ![]() into Equation (3.12) then we get
into Equation (3.12) then we get ![]() for all
for all ![]() and
and![]() . This means that all conditions for zeros with
. This means that all conditions for zeros with ![]() together do not lead to a solution for certain
together do not lead to a solution for certain![]() . Under the assumption (5.19) we have proved that all zeros of Xi functions
. Under the assumption (5.19) we have proved that all zeros of Xi functions ![]() lie on the imaginary axis
lie on the imaginary axis![]() .
.
For an alternative proof let us now solve the two Equations (5.15) and (5.11) directly and to show in this way the impossibility of zeros for![]() . To solve these equations we make a Fourier decomposition of the function
. To solve these equations we make a Fourier decomposition of the function ![]() as follows
as follows
![]() (5.24)
(5.24)
Then (5.15) takes on the form
![]() (5.25)
(5.25)
that due to the uniqueness of the Fourier decomposition of a function in a Fourier integral is only possible if
![]() (5.26)
(5.26)
as a necessary condition. Nontrivial solutions of this equation for ![]() are only
are only
possible for such ![]() for which
for which ![]() vanishes that means for
vanishes that means for
![]() and where
and where ![]() is then proportional to a delta function. Thus the general solution of (5.26) possesses the following form of a generalized function (the prime at the sum means that the term to
is then proportional to a delta function. Thus the general solution of (5.26) possesses the following form of a generalized function (the prime at the sum means that the term to ![]() is absent)
is absent)
![]() (5.27)
(5.27)
with complex numbers ![]() as amplitudes. As remark we mention that de- rivatives of delta functions we do not have to include in this solution since all zeros of
as amplitudes. As remark we mention that de- rivatives of delta functions we do not have to include in this solution since all zeros of ![]() are simple zeros and, furthermore, that
are simple zeros and, furthermore, that ![]() is a generalized analytic function (also called analytical functional) with the possible extension of the variable
is a generalized analytic function (also called analytical functional) with the possible extension of the variable ![]() to the whole complex plane.
to the whole complex plane.
The inverse Fourier transformation of ![]() according to (5.27) provides
according to (5.27) provides
![]() (5.28)
(5.28)
Already this form excludes (5.28) as a possible solution for ![]() which does not have to depend on variable
which does not have to depend on variable ![]() with exception of the case
with exception of the case ![]() which we already could exclude as possible case for zeros (see beginning of Section 4). In addition, we will show that it is not compatible with the general solution of (5.11) which determines the position of the zeros and which with the Fourier decomposition (5.24) takes on the form
which we already could exclude as possible case for zeros (see beginning of Section 4). In addition, we will show that it is not compatible with the general solution of (5.11) which determines the position of the zeros and which with the Fourier decomposition (5.24) takes on the form
![]() (5.29)
(5.29)
It leads to the following equation for the Fourier coefficients ![]()
![]() (5.30)
(5.30)
with the general solution (analogously to (5.27))
![]() (5.31)
(5.31)
with arbitrary coefficients![]() . The inversion of this solution is
. The inversion of this solution is
![]() (5.32)
(5.32)
which for ![]() is only possible if all coefficients
is only possible if all coefficients ![]() and
and ![]() are vanishing.
are vanishing.
The two general solutions (5.28) and (5.32) of the two Equations (5.15) and (5.11) for![]() , the first for the case
, the first for the case ![]() only, are incompatible for any choice of the coefficients
only, are incompatible for any choice of the coefficients ![]() and
and ![]() with the only exception of
with the only exception of ![]() that means on the real axis where the exponential functions in (5.28) and (5.32) become constant functions. How- ever, the case
that means on the real axis where the exponential functions in (5.28) and (5.32) become constant functions. How- ever, the case ![]() for arbitrary
for arbitrary ![]() could be excluded from the beginning according to (4.2) as a consequence of the positive (semi-)definiteness of the function
could be excluded from the beginning according to (4.2) as a consequence of the positive (semi-)definiteness of the function ![]() by supposition.
by supposition.
We have now finally proved that all Xi functions ![]() of the form (3.1) for which the second mean-value theorem is applicable (function
of the form (3.1) for which the second mean-value theorem is applicable (function ![]() positively semi-definite and non-increasing) may possess zeros only on the imaginary axis. The decisive dif- ference for possible zeros on and off the imaginary axis in the approach by the second mean-value theorem was that we have to satisfy in general case two independent real-valued conditions from which one in case of the imaginary axis and only there is automatically satisfied for the whole imaginary axis and not only for the zeros on it.
positively semi-definite and non-increasing) may possess zeros only on the imaginary axis. The decisive dif- ference for possible zeros on and off the imaginary axis in the approach by the second mean-value theorem was that we have to satisfy in general case two independent real-valued conditions from which one in case of the imaginary axis and only there is automatically satisfied for the whole imaginary axis and not only for the zeros on it.
6. Some Consequences from Proof of the Riemann Hypothesis
The given proof for zeros only on the imaginary axis ![]() for the considered Xi function
for the considered Xi function ![]() includes as special case the function
includes as special case the function ![]() to the Rie- mann hypothesis which is given in (2.26). However, it includes also the whole class of modified Bessel functions of imaginary argument
to the Rie- mann hypothesis which is given in (2.26). However, it includes also the whole class of modified Bessel functions of imaginary argument ![]() which possess zeros only on the imaginary axis and if we make the substitution
which possess zeros only on the imaginary axis and if we make the substitution ![]() also the usual Bessel function
also the usual Bessel function ![]() which possess zeros only on the real axis.
which possess zeros only on the real axis.
We may ask about possible degeneracies of the zeros of the Xi functions ![]() on the imaginary axis
on the imaginary axis![]() . Our proof does not give a recipe to see whether such degeneracies are possible or not. In case of the Riemann zeta function
. Our proof does not give a recipe to see whether such degeneracies are possible or not. In case of the Riemann zeta function ![]() one cannot expect a degeneracy because the countable number of all nontrivial zeros are (likely) irrational (transcendental?, proof?) numbers but we do not know a proof for this.
one cannot expect a degeneracy because the countable number of all nontrivial zeros are (likely) irrational (transcendental?, proof?) numbers but we do not know a proof for this.
For ![]() as an entire function one may pose the question of its factorization with
as an entire function one may pose the question of its factorization with
factors of the form ![]() where
where ![]() goes through all roots where in case of de-
goes through all roots where in case of de-
generacy the same factors are taken multiple times according to the degeneracy. It is well known that an entire function using its ordered zeros ![]() can be represented in Weierstrass product form multiplied by an exponential function
can be represented in Weierstrass product form multiplied by an exponential function ![]() with an entire function function
with an entire function function ![]() in the exponent with the result that
in the exponent with the result that ![]() is an entire function without zeros. This possesses the form (e.g., [15] )
is an entire function without zeros. This possesses the form (e.g., [15] )
![]() (6.1)
(6.1)
with a polynomial ![]() of degree
of degree ![]() which depending on the roots
which depending on the roots ![]() must be appropriately chosen to guarantee the convergence of the product. This polynomial is defined by first
must be appropriately chosen to guarantee the convergence of the product. This polynomial is defined by first ![]() sum terms in the Taylor series for
sum terms in the Taylor series for ![]() 4
4
![]() (6.2)
(6.2)
By means of these polynomials the Weierstrass factors are defined as the functions
![]() (6.3)
(6.3)
from which follows
![]() (6.4)
(6.4)
From this form it is seen that ![]() possesses the following initial terms of the Taylor series
possesses the following initial terms of the Taylor series
![]() (6.5)
(6.5)
and is a function with a zero at ![]() but with a Taylor series expansion which begins
but with a Taylor series expansion which begins
with the terms![]() .
.
Hadamard made a precision of the Weierstrass product form by connecting the degree ![]() of the polynomials in (6.1) with the order
of the polynomials in (6.1) with the order ![]() of growth of the entire function and showed that
of growth of the entire function and showed that ![]() can be chosen independently of the
can be chosen independently of the ![]() -th root
-th root ![]() by
by![]() . The order of
. The order of ![]() which is equal to 1 is not a strict order
which is equal to 1 is not a strict order ![]() (for this last notion see [15] ). However, this does not play a role in the Hadamard product representation of
(for this last notion see [15] ). However, this does not play a role in the Hadamard product representation of ![]() and the polynomials
and the polynomials ![]() in (6.1) can be chosen as
in (6.1) can be chosen as ![]() that means equal to 0 according to
that means equal to 0 according to![]() . The entire function
. The entire function ![]() in the exponent in (6.1) can be only a constant since in other case it would introduce a higher growth of
in the exponent in (6.1) can be only a constant since in other case it would introduce a higher growth of![]() . Thus the product representation of
. Thus the product representation of ![]() possesses the form
possesses the form
![]() (6.6)
(6.6)
where we took into account the symmetry ![]() of the zeros and the proof
of the zeros and the proof ![]() that all zeros lie on the imaginary axis and a zero
that all zeros lie on the imaginary axis and a zero ![]() is absent. With
is absent. With ![]() we denoted the first moment of the function
we denoted the first moment of the function![]() .
.
Formula (6.6) in connection with his hypothesis was already used by Riemann in [1] and later proved by von Mangoldt where the product representation of entire functions by Weierstrass which was later stated more precisely by Hadamard plays a role. There is another formula for an approximation to the number of nontrivial zeros of ![]() or
or ![]() which in application to the number of zeros
which in application to the number of zeros ![]() of
of ![]() on the imaginary axis
on the imaginary axis ![]() in the interval between
in the interval between ![]() and
and![]() . It takes on the form (
. It takes on the form (![]() for
for ![]() is equivalent to usual
is equivalent to usual ![]() for
for![]() )
)
![]() (6.7)
(6.7)
with the logarithmically growing density
![]() (6.8)
(6.8)
As long as the Riemann hypothesis was not proved it was formulated for the critical strip ![]() of the complex coordinate
of the complex coordinate ![]() in
in ![]() parallel to the imaginary axis and with
parallel to the imaginary axis and with ![]() between
between ![]() and
and ![]() (with
(with ![]() equal to our
equal to our ![]() in (6.7)). It was already suggested by Riemann [1] but not proved in detail there and was later proved by von Mangoldt in 1905. A detailed proof by means of the argument principle can be found in [12] . It seems that from our approach also follows a simple proof. The result of Hardy (1914) (cited in [5] ) that there exist an infinite number of zeros on the critical line is a step to the full proof of the Riemann hypothesis. Section 4 of present article may be considered as involving such proof of this last statement.
in (6.7)). It was already suggested by Riemann [1] but not proved in detail there and was later proved by von Mangoldt in 1905. A detailed proof by means of the argument principle can be found in [12] . It seems that from our approach also follows a simple proof. The result of Hardy (1914) (cited in [5] ) that there exist an infinite number of zeros on the critical line is a step to the full proof of the Riemann hypothesis. Section 4 of present article may be considered as involving such proof of this last statement.
We have now proved that functions ![]() defined by integrals of the form (3.1) with non-increasing functions
defined by integrals of the form (3.1) with non-increasing functions ![]() which decrease in infinity sufficiently rapidly in a way that
which decrease in infinity sufficiently rapidly in a way that ![]() becomes an entire function of
becomes an entire function of ![]() possess zeros only on the im- aginary axis
possess zeros only on the im- aginary axis![]() . As already said this did not provide a recipe to see in which cases all zeros on the imaginary axis are simple zeros but it is unlikely that within a countable sequence of (pseudo-) randomly chosen real numbers (the zeros) two of them are coincident (it seems to be difficult to formulate last statement in a more rigorous way). It also did not provide a direct formula for the number of zeros in an interval
. As already said this did not provide a recipe to see in which cases all zeros on the imaginary axis are simple zeros but it is unlikely that within a countable sequence of (pseudo-) randomly chosen real numbers (the zeros) two of them are coincident (it seems to be difficult to formulate last statement in a more rigorous way). It also did not provide a direct formula for the number of zeros in an interval ![]() from zero to
from zero to ![]() on the imaginary axis or of its density there but, as mentioned, Riemann [1] suggested for this an approximate formula and von Mangoldt proved it
on the imaginary axis or of its density there but, as mentioned, Riemann [1] suggested for this an approximate formula and von Mangoldt proved it
The proof of the Riemann hypothesis is included as the special case (2.26) of the function ![]() into a wider class of functions with an integral representation of the form (3.1) which under the discussed necessary conditions allowing the application of the second mean-value theorem of calculus possess zeros only on the imaginary axis. The equivalent forms (2.35) and (2.36) of the integral (3.1) where the functions, for example
into a wider class of functions with an integral representation of the form (3.1) which under the discussed necessary conditions allowing the application of the second mean-value theorem of calculus possess zeros only on the imaginary axis. The equivalent forms (2.35) and (2.36) of the integral (3.1) where the functions, for example![]() , are no more generally non-increasing suggest that conditions for zeros only on the imaginary axis are existent for more general cases than such prescribed here by the second mean-value theorem. A certain difference may happen then, for example, for
, are no more generally non-increasing suggest that conditions for zeros only on the imaginary axis are existent for more general cases than such prescribed here by the second mean-value theorem. A certain difference may happen then, for example, for ![]() because powers of it are in the denominators in the representations in (2.36).
because powers of it are in the denominators in the representations in (2.36).
7. Graphical Illustration of Mean-Value Parameters to Xi Function for the Riemann Hypothesis
To get an imagination how the mean-value function ![]() looks like we calculate it for the imaginary axis and for the real axis for the case of the function
looks like we calculate it for the imaginary axis and for the real axis for the case of the function ![]() in (2.26) that is possible numerically. From the two equations for general
in (2.26) that is possible numerically. From the two equations for general ![]() and for
and for ![]()
![]() (7.1)
(7.1)
follows
![]() (7.2)
(7.2)
with the two initial terms of the Taylor series
![]() (7.3)
(7.3)
and with the two initial terms of the asymptotic series
![]() (7.4)
(7.4)
From (7.2) follows
![]() (7.5)
(7.5)
This can be numerically calculated from the explicit form (2.26) of![]() . For
. For
![]() and for
and for ![]() (and only for these cases) the function
(and only for these cases) the function ![]() is real-valued, in
is real-valued, in
particular, for ![]()
![]() (7.6)
(7.6)
and for ![]()
![]() (7.7)
(7.7)
where we applied the first two terms of the Taylor series expansion of ![]() in powers of
in powers of![]() . A small problem is here that we get the value for this multi-valued
. A small problem is here that we get the value for this multi-valued
function in the range![]() . Since
. Since ![]() is an even function
is an even function
with only positive coefficients in its Taylor series the term in braces is in every case positive that becomes important below.
The two curves which we get for ![]() and for
and for ![]() are shown in Figure 4.
are shown in Figure 4.
The function for ![]() on the real axis
on the real axis ![]() (second partial picture) is not very exciting. The necessary condition
(second partial picture) is not very exciting. The necessary condition ![]() (see (5.5)) can be satisfied only for
(see (5.5)) can be satisfied only for
![]() but it is easily to see from
but it is easily to see from ![]() that there is no zero.
that there is no zero.
For the function ![]() on the imaginary axis
on the imaginary axis ![]() the necessary condition
the necessary condition ![]() (see (5.5)) is trivially satisfied since
(see (5.5)) is trivially satisfied since ![]() and does not restrict the solutions for zeros. In this case only the sufficient condition
and does not restrict the solutions for zeros. In this case only the sufficient condition ![]() determines the position of the zeros on the im- aginary axis. The first two pairs of zeros are at
determines the position of the zeros on the im- aginary axis. The first two pairs of zeros are at ![]() and the reason that we do not see them in Figure 4 is the rapid decrease of the function
and the reason that we do not see them in Figure 4 is the rapid decrease of the function ![]() with increasing
with increasing![]() . If we enlarge this range we see that the curve goes beyond the
. If we enlarge this range we see that the curve goes beyond the ![]() -axis after the first root at 14.135 of the Xi function. As a surprise for the second mean-value method we see that the parameter
-axis after the first root at 14.135 of the Xi function. As a surprise for the second mean-value method we see that the parameter ![]() becomes oscillating around this axis. This means that the roots which are generally determined by the equation
becomes oscillating around this axis. This means that the roots which are generally determined by the equation ![]() (see (5.6)) are determined here by the value
(see (5.6)) are determined here by the value ![]() alone. The reason for this is the multi-valuedness of the ArcSine function according to
alone. The reason for this is the multi-valuedness of the ArcSine function according to
![]() (7.8)
(7.8)
If we choose the values for the ![]() -function not in the basic interval
-function not in the basic interval
![]() for which the Taylor series provides the values but from other equivalent
for which the Taylor series provides the values but from other equivalent
intervals according to (7.8) we get other curves for ![]() and
and ![]() from which we also may determine the zeros (see Figure 5), however, with other values
from which we also may determine the zeros (see Figure 5), however, with other values ![]()
in the relation ![]() and the results are invariant with respect to the multi-valuedness. This is better to see in case of the modified Bessel functions for which the curves vanish less rapidly with increasing
and the results are invariant with respect to the multi-valuedness. This is better to see in case of the modified Bessel functions for which the curves vanish less rapidly with increasing ![]() as we intend to show at another place. All these considerations do not touch the proof of the non- existence of roots off the imaginary axis but should serve only for better understanding of the involved functions. It seems that the specific phenomenons of the second mean-value theorem (3.9) if the functions
as we intend to show at another place. All these considerations do not touch the proof of the non- existence of roots off the imaginary axis but should serve only for better understanding of the involved functions. It seems that the specific phenomenons of the second mean-value theorem (3.9) if the functions ![]() there are oscillating functions (re- mind, only continuity is required) are not yet well illustrated in detail.
there are oscillating functions (re- mind, only continuity is required) are not yet well illustrated in detail.
We now derive a few general properties of the function ![]() which can be seen in the Figures. From (4.9) written in the form and by Taylor series expansion according to
which can be seen in the Figures. From (4.9) written in the form and by Taylor series expansion according to
![]() (7.9)
(7.9)
follows from the even symmetry of the left-hand side that ![]() also has to be a
also has to be a
function of the variable ![]() with even symmetry (notation
with even symmetry (notation![]() )
)
![]() (7.10)
(7.10)
with the consequence
![]() (7.11)
(7.11)
Concretely, we obtain by ![]() -fold differentiation of both sides of (7.9) at
-fold differentiation of both sides of (7.9) at ![]() for the first coefficients of the Taylor series
for the first coefficients of the Taylor series
![]() (7.12)
(7.12)
from which follows
![]() (7.13)
(7.13)
Since the first sum term on the right-hand side is negative and the second is positive it depends from their values whether or not ![]() possesses a positive or negative value. For the special function
possesses a positive or negative value. For the special function ![]() in (2.26) which plays a role in the Riemann hypothesis we find approximately
in (2.26) which plays a role in the Riemann hypothesis we find approximately
![]() (7.14)
(7.14)
meaning that the second coefficient in the expansion of ![]() in a Taylor series in powers of
in a Taylor series in powers of ![]() is negative that can be seen in the first part of Figure 4. However, as we have seen the proof of the Riemann hypothesis is by no means critically connected with some numerical values.
is negative that can be seen in the first part of Figure 4. However, as we have seen the proof of the Riemann hypothesis is by no means critically connected with some numerical values.
In principle, the proof of the Riemann hypothesis is accomplished now and illustrated and we will stop here. However, for a deeper understanding of the proof it would be favorable to consider some aspects of the proof such as, for example, analogues to other functions with a representation of the form (3.1) and with zeros only on the imaginary axis and some other approaches although they did not lead to the full proof that, however, we cannot make here.
8. Equivalent Formulations of the Main Theorems in a Summary
In present article we proved the following main result
Theorem 1:
Let ![]() be a real-valued function of variable
be a real-valued function of variable ![]() in the interval
in the interval ![]() which is positive semi-definite in this interval and non-increasing and is rapidly vanishing in infinity, more rapidly than any exponential function
which is positive semi-definite in this interval and non-increasing and is rapidly vanishing in infinity, more rapidly than any exponential function![]() , that means
, that means
![]() (8.1)
(8.1)
Then the following integral with arbitrary complex parameter ![]()
![]() (8.2)
(8.2)
is an entire function of ![]() with possible zeros
with possible zeros ![]() only on the imaginary axis
only on the imaginary axis ![]() that means
that means
![]() (8.3)
(8.3)
Proof:
The proof of this theorem for non-increasing functions ![]() takes on Sections 3-5 of this article. The function
takes on Sections 3-5 of this article. The function ![]() in (2.26) satisfies these conditions and thus provides a proof of the Riemann hypothesis.
in (2.26) satisfies these conditions and thus provides a proof of the Riemann hypothesis.
Remark:
An analogous theorem is obviously true by substituting in (8.2) ![]() and by interchanging the role of the imaginary and of the real axis
and by interchanging the role of the imaginary and of the real axis![]() . Furthermore, a similar theorem with a few peculiarities (e.g., degeneracy) is true for substituting
. Furthermore, a similar theorem with a few peculiarities (e.g., degeneracy) is true for substituting ![]() in (8.2) by
in (8.2) by![]() .
.
Theorem 1 can be formulated in some equivalent ways which lead to interesting consequences5. The Mellin transformation ![]() of an arbitrary function
of an arbitrary function ![]() together with its inversion is defined by [32] [33] [34]
together with its inversion is defined by [32] [33] [34]
![]() (8.4)
(8.4)
where the real value ![]() has only to lie in the convergence strip for the definition of
has only to lie in the convergence strip for the definition of ![]() by the integral. Formula (8.2) is an integral transform of the function
by the integral. Formula (8.2) is an integral transform of the function ![]() and can be considered as the application of an integral operator to the function
and can be considered as the application of an integral operator to the function ![]() which using the Mellin transform
which using the Mellin transform ![]() of the function
of the function ![]() can be written in the following convenient form
can be written in the following convenient form
![]() (8.5)
(8.5)
This is due to
![]() (8.6)
(8.6)
where ![]() is the operator of multiplication of the argument of an arbitrary function
is the operator of multiplication of the argument of an arbitrary function
![]() by the number
by the number![]() , i.e. it transforms as follows
, i.e. it transforms as follows
![]() (8.7)
(8.7)
according to the following chain of conclusions starting from the property that all
functions ![]() are eigenfunctions of
are eigenfunctions of ![]() to eigenvalue
to eigenvalue ![]()
![]() (8.8)
(8.8)
This chain is almost obvious and does not need more explanations. The operators
![]() are linear operators in linear spaces depending on the considered set of numbers
are linear operators in linear spaces depending on the considered set of numbers
![]() .
.
Expressed by real variables ![]() and by
and by
![]() we find from (8.5)
we find from (8.5)
![]() (8.9)
(8.9)
From this formula follows that ![]() may be obtained by transformation of
may be obtained by transformation of ![]() alone via
alone via
![]() (8.10)
(8.10)
On the right-hand side we have a certain redundance since in analytic functions the information which is contained in the values of the function on the imaginary axis is fully contained also in other parts of the function (here of![]() ).
).
The most simple transformation of ![]() is by a delta function
is by a delta function ![]() as function
as function ![]() which stretches only the argument of the Hyperbolic Cosine function
which stretches only the argument of the Hyperbolic Cosine function![]() . The next simple transformation is with a function function
. The next simple transformation is with a function function ![]() in form of a step function
in form of a step function ![]() which leads to the transformation
which leads to the transformation
![]() . Our application of the second mean-value theorem reduced other
. Our application of the second mean-value theorem reduced other
cases under the suppositions of the theorem to this case, however, with parameter ![]() depending on complex variable
depending on complex variable![]() .
.
The great analogy between displacement operators (infinitesimal![]() ) of the argument of a function and multiplication operator (infinitesimal
) of the argument of a function and multiplication operator (infinitesimal![]() ) of the argu-
) of the argu-
ment of a function with respect to the role of Fourier transformation and of Mellin transformation can be best seen from the following two relations
![]() (8.11)
(8.11)
We remind that Mellin and Fourier transform are related by substituting the in- tegration variables ![]() and the independent variables
and the independent variables ![]() and by the sub- stitutions
and by the sub- stitutions ![]() and
and ![]() in (8.11).
in (8.11).
Using the discussed Mellin transformation Theorem 1 can be reformulated as follows
Theorem![]() :
:
The mapping of the function ![]() of the complex variable
of the complex variable ![]() into the function
into the function
![]() by an operator
by an operator ![]() according to
according to
![]() (8.12)
(8.12)
where ![]() is the Mellin transformation of the function
is the Mellin transformation of the function ![]() which last possesses the properties given in Theorem 1 maps the function
which last possesses the properties given in Theorem 1 maps the function ![]() with zeros only on the imaginary axis again into a function
with zeros only on the imaginary axis again into a function ![]() with zeros only on the imaginary axis.
with zeros only on the imaginary axis.
Proof:
It is proved as a reformulation of the Theorem 1 which is supposed here to be correctly proved.
It was almost evident that the theorem may be formulated for more general functions ![]() as supposed for the application of the second mean-value theorem as was already mentioned. Under the suppositions of the theorem the integral on the left-hand side of (8.5) can be transformed by partial integration to (notation:
as supposed for the application of the second mean-value theorem as was already mentioned. Under the suppositions of the theorem the integral on the left-hand side of (8.5) can be transformed by partial integration to (notation:
![]() )
)
![]() (8.13)
(8.13)
The derivative ![]() of the function
of the function ![]() to the Riemann hypothesis although semi-definite (here negatively) and rapidly vanishing in infinity is not monotonic and possesses a minimum (see (2.26) and Figure 2). In case of the (modified) Bessel functions we find by partial integration (e.g., [32] )
to the Riemann hypothesis although semi-definite (here negatively) and rapidly vanishing in infinity is not monotonic and possesses a minimum (see (2.26) and Figure 2). In case of the (modified) Bessel functions we find by partial integration (e.g., [32] )
![]() (8.14)
(8.14)
where the functions in the second transform ![]() for
for ![]() are non-negative
are non-negative
but not monotonic and possess a maximum for a certain value ![]() within the interval
within the interval![]() . The forms (8.13) for
. The forms (8.13) for ![]() and (8.14) suggest that there should be true a similar theorem to the integral in (8.2) with substitution
and (8.14) suggest that there should be true a similar theorem to the integral in (8.2) with substitution ![]() and that monotonicity of the corresponding functions should not be the ultimate requirement for the zeros in such transforms on the imaginary axis.
and that monotonicity of the corresponding functions should not be the ultimate requirement for the zeros in such transforms on the imaginary axis.
Another consequence of the Theorem 1 follows from the non-negativity of the squared modulus of the function ![]() resulting in the obvious inequality (here
resulting in the obvious inequality (here![]() )
)
![]() (8.15)
(8.15)
which can be satisfied with the equality sign only on the imaginary axis ![]() for discrete values
for discrete values ![]() (the zeros of
(the zeros of![]() ). By transition from Cartesian coordinates
). By transition from Cartesian coordinates ![]() to inertial-point coordinates
to inertial-point coordinates ![]() according to
according to
![]() (8.16)
(8.16)
Equation (8.15) can be also written
![]() (8.17)
(8.17)
As already said the case of the equality sign in (8.15) or (8.17) can only be obtained for ![]() and then only for discrete values of
and then only for discrete values of ![]() by solution of this inequality with the specialization for
by solution of this inequality with the specialization for ![]()
![]() (8.18)
(8.18)
A short equivalent formulation of the inequality (8.15) and (8.17) together with (8.18) is the following
Theorem 2:
If the function ![]() satisfies the suppositions in Theorem 1 then with
satisfies the suppositions in Theorem 1 then with ![]()
![]() (8.19)
(8.19)
Proof:
As a consequence of proved Theorem 1 it is also true.
The sufficient condition that this inequality is satisfied with the equality sign is that we first set ![]() in the expressions on the right-hand side of (8.15) and that we then determine the zeros
in the expressions on the right-hand side of (8.15) and that we then determine the zeros ![]() of the obtained equation for
of the obtained equation for![]() . In case of indefinite
. In case of indefinite ![]() there are possible in addition zeros on the
there are possible in addition zeros on the ![]() -axis.
-axis.
Remark:
Practically, (8.15) is an inequality for which it is difficult to prove in another way that it can be satisfied with the equality sign only for![]() . Proved in another way with specialization (2.26) for
. Proved in another way with specialization (2.26) for ![]() it would be an independent proof of the Riemann hypothesis.
it would be an independent proof of the Riemann hypothesis.
9. Conclusion
We proved in this article the Riemann hypothesis embedded into a more general theorem for a class of functions ![]() with a representation of the form (3.1) for real- valued functions
with a representation of the form (3.1) for real- valued functions ![]() which are positive semi-definite and non-increasing in the interval
which are positive semi-definite and non-increasing in the interval ![]() and which are vanishing in infinity more rapidly than any exponential function
and which are vanishing in infinity more rapidly than any exponential function ![]() with
with![]() . The special Xi function
. The special Xi function ![]() to the function
to the function ![]() given in (26) which is essentially the xi function
given in (26) which is essentially the xi function ![]() equivalent to the Riemann zeta function
equivalent to the Riemann zeta function ![]() concerning the hypothesis belongs to the described class of functions.
concerning the hypothesis belongs to the described class of functions.
Modified Bessel functions of imaginary argument “normalized” to entire functions
![]() for
for ![]() belong also to this class of functions with a re-
belong also to this class of functions with a re-
presentation of the form (3.1) with ![]() which satisfy the mentioned conditions and in this last case it is well known and proved in independent way that their zeros lie only on the imaginary axis corresponding to the critical line in the Riemann hypothesis. Knowing this property of the modified Bessel functions we looked from beginning for whole classes of functions including the Riemann zeta function which satisfy analogous conditions as expressed in the Riemann hypothesis. The details of the approach to Bessel functions and also to certain classes of almost-periodic functions we prepare for another work.
which satisfy the mentioned conditions and in this last case it is well known and proved in independent way that their zeros lie only on the imaginary axis corresponding to the critical line in the Riemann hypothesis. Knowing this property of the modified Bessel functions we looked from beginning for whole classes of functions including the Riemann zeta function which satisfy analogous conditions as expressed in the Riemann hypothesis. The details of the approach to Bessel functions and also to certain classes of almost-periodic functions we prepare for another work.
The numerical search for zeros of the Riemann zeta function ![]() in the critical strip, in particular, off the critical line may come now to an end by the proof of the Riemann hypothesis since its main purpose was, in our opinion, to find a counter- example to the Riemann hypothesis and thus to disprove it. We did not pay attention in this article to methods of numerical calculation of the zeros with (ultra-)high precision and for very high values of the imaginary part. However, the proof if correct may deliver some calculators now from their pain to have to calculate more and more zeros of the Riemann zeta function.
in the critical strip, in particular, off the critical line may come now to an end by the proof of the Riemann hypothesis since its main purpose was, in our opinion, to find a counter- example to the Riemann hypothesis and thus to disprove it. We did not pay attention in this article to methods of numerical calculation of the zeros with (ultra-)high precision and for very high values of the imaginary part. However, the proof if correct may deliver some calculators now from their pain to have to calculate more and more zeros of the Riemann zeta function.
We think that some approaches in this article may possess importance also for other problems. First of all this is the operational approach of the transition from real and imaginary part of a function on the real or imaginary axis to an analytic function in the whole complex plane. In principle, this is possible using the Cauchy-Riemann eq- uations but the operational approach integrates this to two integer instead of dif- ferential equations. We think that this is possible also in curved coordinates and is in particular effective starting from curves of constant real or imaginary part of one of these functions on a curve.
One of the fascinations of prime number theory is the relation of the apparently chaotic distribution function of prime numbers ![]() on the real axis
on the real axis ![]() to a fully well-ordered analytic function, the Riemann zeta function
to a fully well-ordered analytic function, the Riemann zeta function![]() , at least, in its representation in sum form as a special Dirichlet series and thus providing the relations between multiplicative and additive representations of arithmetic functions.
, at least, in its representation in sum form as a special Dirichlet series and thus providing the relations between multiplicative and additive representations of arithmetic functions.
Cite this paper
Wünsche, A. (2016) Approach to a Proof of the Riemann Hypothesis by the Second Mean-Value The- orem of Calculus. Advances in Pure Mathematics, 6, 972-1021. http://dx.doi.org/10.4236/apm.2016.613074
References
- 1. Riemann, B. (1859) über die Anzahl der Primzahlen unter einer gegebenen Grösse. Monatsber. Akad. Berlin, 671-680; also in: Riemann, B. Gesammelte Werke, Teubner, Leipzig 1. Aufl. 1876, S. 136, 2. Aufl. 1892, S. 145; in different English tranlations as Appendix in and as reprint under Original papers 12.2 in .
- 2. Whittaker, E.T. and Watson, G.N. (1927) A Course of Modern Analysis. Cambridge University Press, Cambridge.
- 3. Titchmarsh, E.C. (1951) The Theory of the Riemann Zeta-Function. Oxford University Press, Oxford.
- 4. Chandrasekharan, K. (1970) Arithmetical Functions. Springer-Verlag, Berlin.
https://doi.org/10.1007/978-3-642-50026-8
- 5. Edwards, H.M. (1974) Riemann’s Zeta Function. Dover, New York.
- 6. Parshin, A.N. (1979) Dzeta funkziya. In: Vinogradov, I.M., Ed., Matematicheskaya Enzyklopediya, Sovyetskaya Enzyklopedia, Moskva, Vol. 2, 112-122. (In Russian)
- 7. Patterson, S.J. (1985) An Introduction to the Theory of the Riemann Zeta-Function. Cambridge University Press, Cambridge.
- 8. Cartier, P. (1989) An Introduction to Zeta Functions. In: Waldschmidt, M., Moussa, P., Luck, J.-M. and Itzykson, C., Eds., From Number Theory to Physics, Springer-Verlag, Berlin, 1-63.
- 9. Ivić, A. (1985) The Riemann Zeta-Function, Theory and Applications. John Wiley & Sons, New York. (Dover Publications, Mineola, New York, 2003)
- 10. Havil, J. (2003) Gamma Exploring Euler’s Constant. Princeton University Press, Princeton.
- 11. Ribenboim, P. (2004) The Little Book of Bigger Primes. Springer, New York. (German transl., Die Welt der Primzahlen. Springer, Berlin, 2006)
- 12. Borwein, P., Choi, S., Rooney, B. and Weirathmueller, A. (2008) The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike. Springer, New York.
- 13. Apostol, T.M. (2010) Introduction to Analytic Number Theory. Springer, New York.
- 14. Weisstein (2009) Riemann Zeta Function and R.Z.F. Zeros. In: CRC Encyclopedia of Mathematics, 3rd Edition, CRC Pr Inc. and Web: WolframMathWorld (We used the last).
- 15. Lang, S. (1993) Complex Analysis. 3rd Edition, Springer-Verlag, New York.
https://doi.org/10.1007/978-3-642-59273-7
- 16. Meier, P. and Steuding, J. (2009) Wer die Zetafunktion kennt, kennt die Welt. In: Spektrum der Wissenschaft, Dossier 6/09, 12-19, Spekt. d. Wiss. Verlagsgesellschaft, Heidelberg.
- 17. Stewart, I. (2013) The Great Mathematical Problems. Profile Books, London.
- 18. Erdélyi, A. (1953) Higher Transcendental Functions, Vol. 1. McGraw Hill, New York.
- 19. Erdélyi, A. (1953) Higher Transcendental Functions, Vol. 3. McGraw Hill, New York.
- 20. Apostol, T.M. (2010) Zeta and Related Functions and Functions of Number Theorie, chaps. 25 and 27. In: Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, Ch.W., Eds., NIST Handbook of Mathematical Functions, Cambridge University Press, Cambridge.
- 21. Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, Ch.W., Eds. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
- 22. Hilbert, D. (1902) Problèmes futures des mathématiques. C.R. 2nd Congr. Int. Math., p. 85, Paris; (Russian transl. with remarks on the state of the solution of each problem in ).
- 23. Linnik, Yu.V. (1969) Problemy Gilberta (in Russian). In: Aleksandrov, P.S. Ed., The Hilbert problems (in English), Nauka Moskva, 128-130.
- 24. Conrey, J.B. (2008) The Riemann Hypothesis. In: Borwein, P., Choi, S., Rooney, B. and Weirathmueller, A., Eds., The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, Springer, New York, 117-129.
- 25. Bombieri, E. (2008) Problems of the Millenium: The Riemann Hypothesis. In: Borwein, P., Choi, S., Rooney, B. and Weirathmueller, A., Eds., The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, Springer, New York, 94.
- 26. Ivić, A. (2008) On Some Reasons for Doubting the Riemann Hypothesis. In: Borwein, P., Choi, S., Rooney, B. and Weirathmueller, A., Eds., The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, Springer, New York, 130.
- 27. von Mangoldt, H. (1905) Zur Verteilung der Nullstellen der Riemannschen Funktion . Mathematische Annalen, 60, 1-19.
https://doi.org/10.1007/BF01447494
- 28. Voronin, S.M. (1975) Theorem on the Universality of the Riemann Zeta Function. Izv. Akad. Nauk SSSR, Ser. Matem., 39, 475-486, reprinted in Mathematics of the USSR-Izvestiya, 9, 443-445.
https://doi.org/10.1070/IM1975v009n03ABEH001485
- 29. Steuding, J. (2004) Voronin Universality Theorem. From MathWorld—A Wolfram Web Resource, created by Eric W. Weisstein.
http://mathworld.wolfram.com/VoroninUniversalityTheorem.html
- 30. Neuberger, J.W., Feiler, C., Maier, H. and Schleich, W.P. (2014) Newton Flow of the Riemann Zeta Function: Separatrices Control the Appearance of Zeros. New Journal of Physics, 16, 103023.
https://doi.org/10.1088/1367-2630/16/10/103023
- 31. Neuberger, J.W., Feiler, C., Maier, H. and Schleich, W.P. (2015) The Riemann hypothesis illuminated by the Newton flow of . Physica Scripta, 90, 108015.
https://doi.org/10.1088/0031-8949/90/10/108015
- 32. Bateman, H. and Erdélyi, A. (1954) Tables of Integral Transforms, Vol. 1 and Vol. 2. McGraw-Hill, New York.
- 33. Zemanian, A.H. (1987) Generalized Integral Transformations. Dover, New York.
- 34. Brychkov, J.A. and Prudnikov, A.P. (1977) Integral Transformations of Generalized Functions. Nauka, Moskva. (In Russian)
- 35. Bertrand, J., Bertrand, P. and Ovarlez, J. (2000) The Mellin Transform, chap. 11. In: Poularikas, A.D., Ed., The Transforms and Application Handbook, 2nd Edition, CRC Press LLC, Boca Raton.
https://doi.org/10.1201/9781420036756.ch11
- 36. Paris, R.B. (2010) Incomplete Gamma and Related Functions, chap. 8. In: Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, Ch.W., Eds., NIST Handbook of Mathematical Functions, Cambridge University Press, Cambridge, 173-192.
- 37. Courant, R. (1992) Differential and Integral Calculus, Vol. 1. John Wiley & Sons, New York.
- 38. Widder, D.V. (1947) Advanced Calculus. 2nd Edition, Prentice-Hall, Englewood Cliffs, New York. (Dover Publications, New York, 1989)
- 39. Erdélyi, A. (1953) Higher Transcendental Functions, Vol. 2. McGraw Hill, New York.
Appendix A
Transformation of the Xi Function
In this Appendix we transform the function ![]() defined in (2.8) by means of the zeta function
defined in (2.8) by means of the zeta function ![]() from the form taken from (2.5) to the form (2.9) using the Poisson summation formula. The Poisson summation formula is the transformation of a sum over a lattice into a sum over the reciprocal lattice. More generally, in one- dimensional case the decomposition of a special periodic function
from the form taken from (2.5) to the form (2.9) using the Poisson summation formula. The Poisson summation formula is the transformation of a sum over a lattice into a sum over the reciprocal lattice. More generally, in one- dimensional case the decomposition of a special periodic function ![]() with period
with period ![]() defined by the following series over functions
defined by the following series over functions ![]()
![]() (A.1)
(A.1)
can be transformed into the reciprocal lattice providing a Fourier series as follows. For this purpose we expand ![]() in a Fourier series with Fourier coefficients
in a Fourier series with Fourier coefficients ![]() and
and
make then obvious transformations (![]() and ch-
and ch-
anging the order of summation and integration) according to
![]() (A.2)
(A.2)
where the coefficients ![]() of the decomposition of
of the decomposition of ![]() are given by the Fourier transform
are given by the Fourier transform ![]() of the function
of the function ![]() defined in the following way
defined in the following way
![]() (A.3)
(A.3)
Using the period ![]() of the reciprocal lattice relation on the right-hand side of
of the reciprocal lattice relation on the right-hand side of
(A.2) it may be written in the forms
![]() (A.4)
(A.4)
In the special case ![]() one obtains from (A.4) the well-known basic form of the Poisson summation formula
one obtains from (A.4) the well-known basic form of the Poisson summation formula
![]() (A.5)
(A.5)
Formula (A.5) applied to the sum ![]() corresponding to
corresponding to
![]() with Fourier transform
with Fourier transform ![]() provides a relation
provides a relation
which can be written in the following symmetric form (we need it in the following only for![]() )
)
![]() (A.6)
(A.6)
This is essentially a transformation of the Theta function ![]() in special case
in special case
![]() . We now apply this to a transformation of the function
. We now apply this to a transformation of the function![]() .
.
From (2.9) and (2.5) follows
![]() (A.7)
(A.7)
The second term in braces is convergent for arbitrary ![]() due to the rapid vanishing of the summands of the sum for
due to the rapid vanishing of the summands of the sum for![]() . To the first term in braces we apply the Poisson summation formula (A.5) and obtain from the special result (A.6)
. To the first term in braces we apply the Poisson summation formula (A.5) and obtain from the special result (A.6)
![]() (A.8)
(A.8)
with the substitution ![]() of the integration variable made in last line. Thus from
of the integration variable made in last line. Thus from
(A.7) we find
![]() (A.9)
(A.9)
With the substitution of the integration variable
![]() (A.10)
(A.10)
and with displacement of the complex variable ![]() to
to ![]() and introduction of
and introduction of
![]() instead of
instead of ![]() this leads to the representation
this leads to the representation
![]() (A.11)
(A.11)
given in (2.24). In the following we transform this representation by means of partial integration to a form which due to symmetries is particularly appropriate for the further considerations about the Riemann zeta function.
Using the substitution (A.10) we define a function ![]() by means of the function
by means of the function ![]() in (A.6) as follows
in (A.6) as follows
![]() (A.12)
(A.12)
and explicitly due to Poisson summation formula
![]() (A.13)
(A.13)
From ![]() according to (A.6) follows that
according to (A.6) follows that ![]() is a symmetric function
is a symmetric function
![]() (A.14)
(A.14)
Therefore, all even derivatives of ![]() are also symmetric functions, whereas all odd derivatives of
are also symmetric functions, whereas all odd derivatives of ![]() are antisymmetric functions (we denote these derivatives by
are antisymmetric functions (we denote these derivatives by
![]() )
)
![]() (A.15)
(A.15)
Explicitly, one obtains for the first two derivatives
![]() (A.16)
(A.16)
As a subsidiary result we obtain from vanishing of the odd derivatives of ![]() at
at ![]() that means from
that means from ![]() an infinite sequence of special sum evaluations from which the first two are
an infinite sequence of special sum evaluations from which the first two are
![]() (A.17)
(A.17)
We checked relations (A.17) numerically by computer up to a sufficiently high precision. We also could not find (A.17) among the known transformations of theta functions. The interesting feature of these sum evaluations is that herein power functions as well as exponential functions containing the transcendental number ![]() in the exponent are involved in a way which finally leads to a rational number that should also be attractive for recreation mathematics. In contrast, in the well-known series for the trigonometric functions one obtains for certain rational multiples of
in the exponent are involved in a way which finally leads to a rational number that should also be attractive for recreation mathematics. In contrast, in the well-known series for the trigonometric functions one obtains for certain rational multiples of ![]() as argu- ment also rational numbers but one has involved there only power functions with rational coefficients that means rational functions although an infinite number of them.
as argu- ment also rational numbers but one has involved there only power functions with rational coefficients that means rational functions although an infinite number of them.
Using the function ![]() the function
the function ![]() in (A.11) can be represented as
in (A.11) can be represented as
![]() (A.18)
(A.18)
From this we obtain by partial integration
![]() (A.19)
(A.19)
where the contribution from the lower integration limit at ![]() has exactly canceled
has exactly canceled
the constant term ![]() on the right-hand side of (A.18) and the contributions from the
on the right-hand side of (A.18) and the contributions from the
upper limit ![]() is vanishing. Using (A.16) we find with abbreviation
is vanishing. Using (A.16) we find with abbreviation ![]() according to
according to
![]() (A.20)
(A.20)
the following basic structural form of the Xi function
![]() (A.21)
(A.21)
with the following explicit representation of ![]()
![]() (A.22)
(A.22)
Since according to (A.15) the even derivatives of ![]() are symmetric functions it follows from relation (A.22) that
are symmetric functions it follows from relation (A.22) that ![]() is also a symmetric function and (A.27) holds. This is not immediately seen from the explicit representation (A.22). Furthermore,
is also a symmetric function and (A.27) holds. This is not immediately seen from the explicit representation (A.22). Furthermore, ![]() is positively definite for
is positively definite for ![]() since the factor
since the factor ![]() in (A.22) is positive for
in (A.22) is positive for ![]() and
and ![]() and all other factors too. It goes rapidly to zero for
and all other factors too. It goes rapidly to zero for![]() , more rapidly than any exponential function
, more rapidly than any exponential function ![]() with arbitrary
with arbitrary ![]() and arbitrary
and arbitrary ![]() due to factors
due to factors ![]() in the sum terms in (A.22). For the first derivative of
in the sum terms in (A.22). For the first derivative of ![]() we find
we find
![]() (A.23)
(A.23)
It is vanishing for ![]() due to its antisymmetry and negatively definite for
due to its antisymmetry and negatively definite for ![]() as the negative sign of
as the negative sign of ![]() together with considerations of the sum for
together with considerations of the sum for ![]() show (i.e., the polynomial
show (i.e., the polynomial ![]() for
for
![]() and negativity is already obtained taking the first two sum
and negativity is already obtained taking the first two sum
terms to ![]() and
and ![]() alone). Thus
alone). Thus ![]() is monotonically decreasing for
is monotonically decreasing for![]() . A few approximate numerical values of parameters for the function
. A few approximate numerical values of parameters for the function ![]() are
are
![]() (A.24)
(A.24)
In next Appendix we consider the transition from analytic functions given on the real or imaginary axis to the whole complex plane.
Appendix B
Transition from Analytic Functions on Real or Imaginary Axis to Whole Complex Plane
The operator ![]() is the infinitesimal displacement operator and
is the infinitesimal displacement operator and ![]() the
the
finite displacement operator for the displacement of the argument of a function![]() . In complex analysis the real variable
. In complex analysis the real variable ![]() can be displaced with view to an analytic function to the complex variable
can be displaced with view to an analytic function to the complex variable ![]() in the whole complex plane by
in the whole complex plane by
![]() (B.1)
(B.1)
where ![]() denotes the commutator of two operators A and B, in particular
denotes the commutator of two operators A and B, in particular ![]() and (B.1) may be written in the form
and (B.1) may be written in the form
![]() (B.2)
(B.2)
Analogously, the transition from the variable ![]() on the imaginary axis
on the imaginary axis ![]() to the variable
to the variable ![]() in the whole complex plane may be written as
in the whole complex plane may be written as
![]() (B.3)
(B.3)
In the following we consider only the case (B.2) since the case (B.3) is completely analogous with simple substitutions.
We wrote the Equations (B.1), (B.2) and (B.3) in a form which we call operational form and meaning that they may be applied to further functions on the left-hand and correspondingly right-hand side6. It is now easy to see that an analytic function
![]() can be generated from
can be generated from ![]() on the
on the ![]() -axis in ope-
-axis in ope-
rational form by
![]() (B.4)
(B.4)
and analogously from ![]() on the imaginary axis by
on the imaginary axis by
![]() (B.5)
(B.5)
Writing the function ![]() with real part
with real part ![]() and imaginary part
and imaginary part ![]() in the form
in the form
![]() (B.6)
(B.6)
we find from (B.4)
![]() (B.7)
(B.7)
and correspondingly
![]() (B.8)
(B.8)
From (B.7) and (B.8) follows forming the sum and the difference
![]()
![]() (B.9)
(B.9)
These are yet operational identities which can be applied to arbitrary functions![]() . Applied to the function
. Applied to the function ![]() follows
follows
![]() (B.10)
(B.10)
In full analogy we may derive the continuation of an analytic function from the imaginary axes ![]() to the whole complex plane
to the whole complex plane ![]() in operational form
in operational form
![]() (B.11)
(B.11)
and this applied to the function ![]()
![]() (B.12)
(B.12)
It is easy to check that both (B.10) and (B.12) satisfy the Cauchy-Riemann equations
![]() (B.13)
(B.13)
and it is even possible to derive these relations from these equations by Taylor series expansions of ![]() and
and ![]() in powers of
in powers of ![]() or
or ![]() in dependence from which axis we make the continuation to the whole complex plane. For example, in expansion in powers of
in dependence from which axis we make the continuation to the whole complex plane. For example, in expansion in powers of ![]() we obtain using (B.13) (and the resulting equations
we obtain using (B.13) (and the resulting equations
![]() from them)
from them)
![]() (B.14)
(B.14)
that can be written in compact form
![]() (B.15)
(B.15)
and is equivalent to (B.10). Analogously by expansion in powers of ![]() as intermediate step we obtain
as intermediate step we obtain
![]() (B.16)
(B.16)
that is equivalent to (B.12). Therefore, relations (B.15) and (B.16) represent some integral forms of the Cauchy-Riemann equations.
In cases if one of the functions ![]() or
or ![]() in (B.10) or
in (B.10) or ![]() or
or ![]() in (B.12) is vanishing these formulae simplify and the case
in (B.12) is vanishing these formulae simplify and the case ![]() is applied in Section 5. We did not find up to now such representations in textbooks to complex analysis but it seems to be possible that they are somewhere.
is applied in Section 5. We did not find up to now such representations in textbooks to complex analysis but it seems to be possible that they are somewhere.
NOTES
1Riemann [1] defines it more specially for argument ![]() and writes it
and writes it ![]() with real
with real ![]() corresponding to our
corresponding to our![]() . Our definition agrees, e.g., with Equation (1) in Section 1.8 on p. 16 of Edwards [5] and with [20] and many others.
. Our definition agrees, e.g., with Equation (1) in Section 1.8 on p. 16 of Edwards [5] and with [20] and many others.
2According to Havil [10] , (p. 193), already Euler correctly conjectured this relation for the zeta function ![]() which is equivalent to relation (2.12) for the function
which is equivalent to relation (2.12) for the function ![]() but could not prove it. Only Riemann proved it first.
but could not prove it. Only Riemann proved it first.
3It was for us for the first time and was very surprising to meet a function where its symmetry was not easily seen from its explicit representation. However, if we substitute in (2.26) ![]() and calculate and plot the part of
and calculate and plot the part of ![]() for
for ![]() with the obtained formula then we need much more sum terms for the same accurateness than in case of calculation with (2.26).
with the obtained formula then we need much more sum terms for the same accurateness than in case of calculation with (2.26).
4Sometimes our ![]() is denoted by
is denoted by![]() .
.
![]()
5Some of these equivalences now formulated as consequences originate from trials to prove the Riemann hypothesis in other way.
6Non-operational form would be if we write, for example, ![]() instead of (B.2) which is correct but cannot be applied to further functions
instead of (B.2) which is correct but cannot be applied to further functions![]() , for example to
, for example to![]() .
.




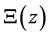 with an integral representation of the form
with an integral representation of the form 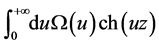 with a real-valued function
with a real-valued function 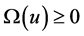 which is non-increasing and decreases in infinity more rapidly than any exponential functions
which is non-increasing and decreases in infinity more rapidly than any exponential functions 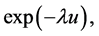
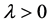 possesses zeros only on the imaginary axis. The Riemann zeta function
possesses zeros only on the imaginary axis. The Riemann zeta function 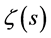 as it is known can be related to an entire function
as it is known can be related to an entire function 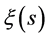 with the same non-trivial zeros as
with the same non-trivial zeros as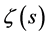 . Then after a trivial argument displacement
. Then after a trivial argument displacement 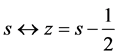 we relate it to a function
we relate it to a function 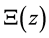 with a representation of the form
with a representation of the form 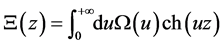 where
where 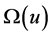 is rapidly decreasing in infinity and satisfies all requirements necessary for the given proof of the position of its zeros on the imaginary axis
is rapidly decreasing in infinity and satisfies all requirements necessary for the given proof of the position of its zeros on the imaginary axis  by the second mean-value theorem. Besides this theorem we apply the Cauchy- Riemann differential equation in an integrated operator form derived in the Appendix B. All this means that we prove a theorem for zeros of
by the second mean-value theorem. Besides this theorem we apply the Cauchy- Riemann differential equation in an integrated operator form derived in the Appendix B. All this means that we prove a theorem for zeros of 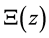 on the imaginary axis
on the imaginary axis 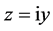 for a whole class of function
for a whole class of function 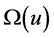 which includes in this way the proof of the Riemann hypothesis. This whole class includes, in particular, also the modified Bessel functions
which includes in this way the proof of the Riemann hypothesis. This whole class includes, in particular, also the modified Bessel functions 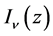 for which it is known that their zeros lie on the imaginary axis and which affirms our conclusions that we intend to publish at another place. In the same way a class of almost-periodic functions to piece-wise constant non-increasing functions
for which it is known that their zeros lie on the imaginary axis and which affirms our conclusions that we intend to publish at another place. In the same way a class of almost-periodic functions to piece-wise constant non-increasing functions  belong also to this case. At the end we give shortly an equivalent way of a more formal description of the obtained results using the Mellin transform of functions with its variable substituted by an operator.
belong also to this case. At the end we give shortly an equivalent way of a more formal description of the obtained results using the Mellin transform of functions with its variable substituted by an operator.



































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































