Received 1 June 2016; accepted 24 June 2016; published 27 June 2016

ABSTRACT

In this paper, we consider 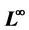estimates of eigenfunction, or more generally, the 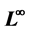estimates of equation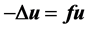. We use heat flow to give a new proof of the estimates for such type equations.

Keywords:

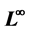Estimates, Eigenfunction, Heat Flow

1. Introduction

Let 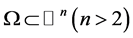be a bounded domain. Assume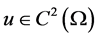, we consider the Laplacian equation

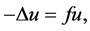
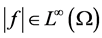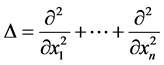where and with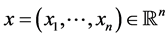. This is a second order differential

equation. If 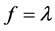is a constant, then u is an eigenfunction with eigenvalue. By a standard Moser’s iteration in [1] - [5] , we have 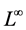interior estimates of u controlled by the 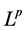norm of u for. In this paper, we use heat flow to consider the estimate and give a new proof of the estimates without using iteration. First, we recall the definition of the heat kernel. For any and, let

be the heat kernel in. For fixed, we know that

where is the standard Laplacian in with respect to x. Our main result is the following

Theorem 1. Let be a bounded domain with. Assume and

on with. Then for any and any compact sub-domain, we have the interior estimate

(1)

where is the distance of and the boundary of.

Remark 2. Following from the proof, one can consider equation or by choosing appropriate kernel function.

2. Proving the Theorem

To estimates on, by the translation invariant and scaling invariant of the estimates, we only need to consider and. By using heat flow, we have the following lemma.

Lemma 1. Let be a unite ball. Assume and

on with. Then for any, we have the interior estimate

(2)

Proof. Let be a standard smooth cutoff function with support in and on, moreover,. For any, let

By the heat equation, integrating by parts, we have

(3)

(4)

(5)

(6)

(7)

(8)

where we use integrating by parts for term to get (7) from (6). By direct estimate, since for and, then. Therefore, for, we have

Hence, for and noting that, we have

Since, then we have

By the property of heat kernel, we have. Then we have

On the other hand, as, we have

(9)

Combining with, we have

Hence we finish the proof.

The following lemma is fundamental.

Lemma 2. For any and any, we have

Proof. Let and. Then

(10)

(11)

Now we are ready to prove Theorem 1.

Proof of Theorem 1. Refmaintheorem. For any compact subset, let. For any, we have. Consider equation

on. By Lemma 1, since the estimates are scaling invariant, we have

If, then. By Lemma 2, we have

Hence we finish the proof.

Acknowledgements

The research is supported by National Natural Science Foundation of China under grant No.11501027. The first author would like to thank Dr. Wenshuai Jiang, Xu Xu for many helpful conversations.

Cite this paper

Huabin Ge,Yipeng Shi, (2016) A Remark on Eigenfunction Estimates by Heat Flow. Advances in Pure Mathematics,06,512-515. doi: 10.4236/apm.2016.67038

References