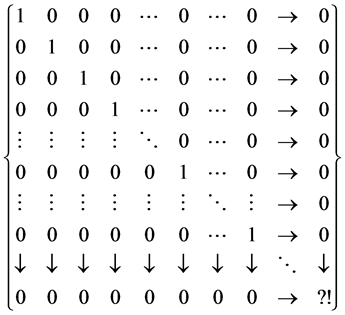Received 3 April 2016; accepted 21 May 2016; published 24 May 2016

ABSTRACT

Double sequences have some unexpected properties which derive from the possibility of commuting limit operations. For example, 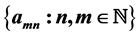may be defined so that the iterated limits 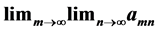and 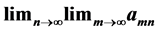exist and are equal for all x, and yet the Pringsheim limit 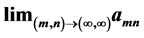does not exist. The sequence 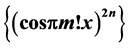is a classic example used to show that the iterated limit of a double sequence of continuous functions may exist, but result in an everywhere discontinuous limit. We explore whether the limit of this sequence in the Pringsheim sense equals the iterated result and derive an interesting property of cosines as a byproduct.

Keywords:

Convergence, Pointwise Limit, Double Sequence, Pringsheim, Dirichlet Function, Baire Category Theorem, Cosine

1. Introduction

The problem of convergence of a doubly indexed sequence presents some interesting phenomena related to the order of taking iterated limits as well as subsequences where one index is a function of the other. Convergence of a double sequence in the sense of Pringsheim is a strong enough condition to allow us to characterize the behavior of the iterated limits as well as the limits of ordinary sequences induced by collapsing the two indices into one according to a suitable functional dependence (e.g. re-index 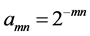by setting 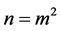to obtain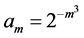). We will show that an unconditional converse establishing convergence in the Pringsheim sense from properties of the iterated limits is not obtainable.

We can easily extend the notion of Pringsheim convergence of numerical sequences to pointwise convergence in the Pringsheim sense for functions. Our main goal is to investigate the doubly indexed sequence of real functions of the form 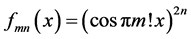in this context. One iterated limit of this sequence, namely

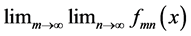, is a well-known example of the construction of the Dirichlet “salt-and-pepper” function

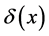. Recall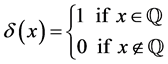. In addition to establishing a theorem on Pringsheim convergence which is

useful in its own right, we will be able to conclude that 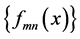does not converge pointwise in this sense. Moreover, it will be shown that there are irrational numbers for which the ordinary sequence does not converge to zero.

2. Background

The German mathematician Alfred Pringsheim formulated the following definition of convergence for double sequences in 1897 [1] .

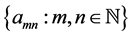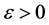
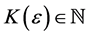
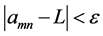
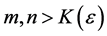
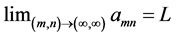
Definition 1: Given the doubly indexed sequence, we say it converges to the limit L if for every preassigned there exists a such that whenever. This situation will be denoted by.

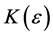
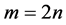
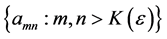
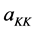
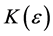
In this definition, it is understood that m and n are to exceed independently. Specifically, there should be no functional relationship between m and n, such as, for example. The definition lends itself to an intuitively appealing visual. We will call the semi-infinite set of grid points below and to the right of a Pringsheim square:

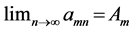
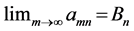
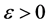
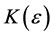
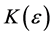
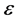
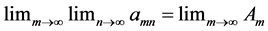
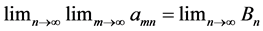
In this array the rows represent fixed m with n increasing, and the columns represent fixed n with m increasing. The column to the extreme right records and the row at the bottom records, whenever these limits exist. For arbitrary the double limit L exists if there is a such that the absolute difference between L and any term in the Pringsheim square is strictly less than. The iterated limits and may or may not be equal. A trivial

but illustrative case is given by the double sequence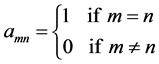. The array with iterated limits is:

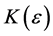
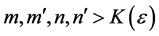
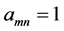
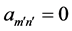
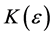
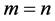
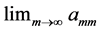
Observing that the iterated limits exist and are equal to zero, but the double limit in the Pringsheim sense does not even exist, since for any there are terms with such that and. Note also that if we violate the condition that m and n exceed independently by setting, exists and equals 1. This example immediately dashes any hope of establishing a Fubini-like result where if the two iterated limits exist and are equal then the double limit in the Pringsheim sense exists and is the same.

A more optimistic case is this:

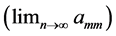
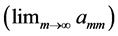
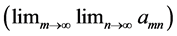
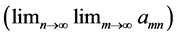
This array shows that a double sequence can be Pringsheim convergent, and although none of the row or column partial limits equal the Pringsheim limit (1), the respective row-first and column-first iterated limits can equal the Pringsheim limit. Motivated by this example we formulate a theorem that connects Pringsheim convergence to the existence and equality of the associated iterated limits.

3. Main Theorem

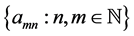
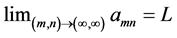
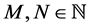
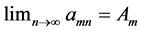
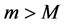
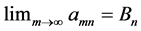
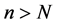
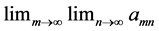
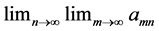
Theorem 1: Let be a double sequence of real numbers with Pringsheim limit . If for some both the partial limit exists for and the partial limit exists for, then the iterated limits and exist and are equal to L.

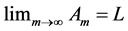
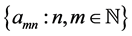
Proof: Without restriction of generality, consider the column sequence formed by the partial limits A_m for m > M. Fix ε > 0. We claim that. Since converges to L in the sense of Pring-

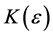
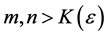
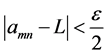
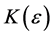
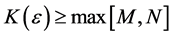
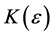
sheim, there exists such that implies. Increase, if warranted, so that

. This defines a Pringsheim square for which all of the row and column partial lim-

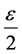
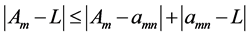
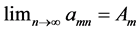
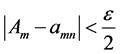
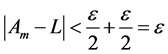
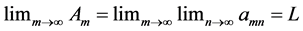
its exist and every a_mn within the square differs absolutely from L by less than. Now

, and since, we may stipulate that. It is clear that, and our claim that is established. The same argu-

ment mutatis mutandi shows that. +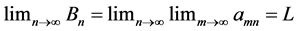

In view of the array we have used to visualize the Pringsheim definition, let us call a double subsequence southeastern if, where is strictly monotone increasing. The terminology is suggested by the fact that for any Pringsheim square the double subsequence will eventually enter and stay inside the part of the square below (south) and to the right (east) of a_KK. The ordinary subsequences where either m or n are held constant (the horizontal or vertical subsequences in the array) do not have this property. Clearly, every southeastern subsequence can be converted to an ordinary subsequence.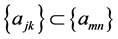

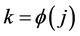
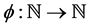
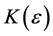
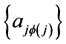
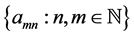
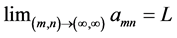
Corollary 1a: If is a double sequence of real numbers, then if and only if every southeastern subsequence of a_mn converges to L.

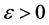
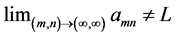
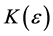
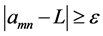
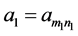
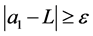
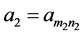
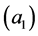
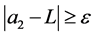
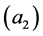
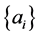
Proof: (Necessity) Suppose every southeastern subsequence of a_mn converges to L. Fix and assume for the sake of contradiction that. Then every Pringsheim square contains an a_mn such that. Construct a southeastern subsequence of “bad” terms as follows: Let K = 1. Choose a term in the (1)-Pringsheim square (the entire array) such that. Now select in the -Pringsheim square so that. Likewise select a₃ from the -Pringsheim square and so forth recursively. By the manner of construction, i > j requires m_i > m_j and n_i > n_j, so the resulting subsequence is certainly southeastern. Moreover, cannot converge to L. The contradiction establishes necessity.

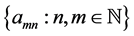
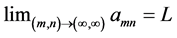
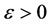
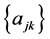
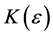
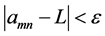
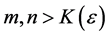
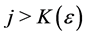
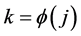
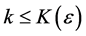
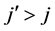
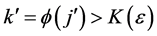
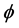
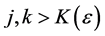
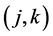
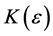
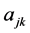
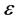
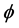
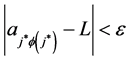
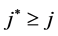
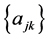
(Sufficiency) Suppose is a double sequence of real numbers with. Fix and consider the southeastern subsequence. By Pringsheim convergence, there exists a Pringsheim square such that for all. Choose and determine. If, we may choose such that by the isotonicity of. In any case, by relabelling, if necessary, we may arrange that. Thus belongs to the Pringsheim square that constrains the absolute difference between and L to be less than. Again by the isotonicity of

, for. Hence the southeastern sequence converges to L. +

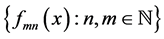
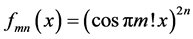
Let us formulate a definition of pointwise Pringsheim convergence of functions so that we have a basis for studying. In particular, we will consider.

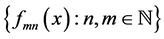
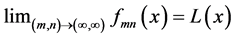
Definition 2: The doubly indexed sequence of real functions converges pointwise in the Pringsheim sense if whenever x is fixed, the resulting numerical sequence converges in the regular Pringsheim sense (definition 1). This situation will be denoted by.

If a doubly indexed sequence of functions were simply pointwise convergent and the iterated limits did not commute, the limit function would be ill-defined. Our definition along with Theorem 1 resolves this issue.

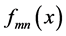
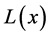
Corollary 1b: Theorem 1 applies to the pointwise limits of doubly indexed sequences of functions with a_mn replaced by and L replaced by.

Proof: Fix x and use definition 2. +

4. Dirichlet Function

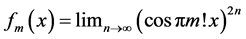
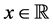
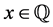
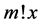
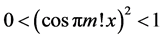
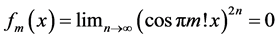
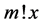
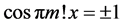
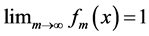
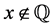
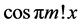
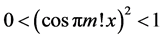
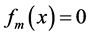
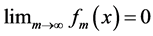
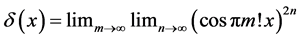
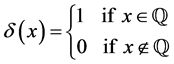
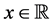
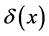
Consider [2] [3] for. If, and is not an integer, then

, and consequently. However, once m is sufficiently large, becomes and remains an integer, hence for those cases. It follows that for rational x. On the other hand, if, the quantity is never an integer for any m, hence, and consequently for all m, so. Defining

, we have for. Dirichlet’s function is

everywhere discontinuous, and a fanciful image of its “graph” has given rise to the name “salt-and-pepper” function. It is often used as an example of a function that is Lebesgue integrable but not Riemann integrable (although integrable in the generalized Riemann sense).

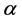
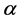
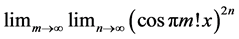
Dirichlet’s function turns out to be an example of a Baire class 2 function. Recall that Baire class 0 consists of functions that are continuous. Baire class 1 functions are pointwise limits of sequences of Baire class 0 functions. In general, a Baire class function is the pointwise limit of a sequence of functions from the union of all Baire classes with indices less than, where the class index is allowed to range over the countable ordinals. The fact that the Dirichlet function cannot be expressed as the limit of a sequence of continuous functions will play a key role in establishing our claim that does not converge in the Pringsheim sense.

5. Baire’s Category Theorem (BCT)

René-Louis Baire proved the seminal theorem that bears his name in 1899 as part of his doctoral dissertation [4] . He introduced the famously bland terminology Category 1 for meager sets and Category 2 for non-meager sets. Recall that a meager set is a countable union of nowhere-dense sets, which in turn are sets whose closures have void interiors. Non-meager sets are all the others. BCT states (in one formulation) that complete metric spaces must be non-meager. We use this fact in the following:

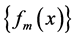
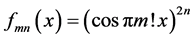
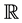
Theorem 2: The southeastern sequence induced from by setting does not converge pointwise to Dirichlet’s function on.

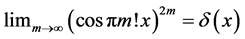
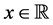
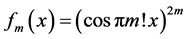
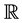
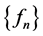
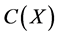
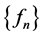
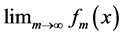
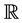
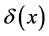
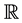
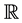
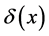
Proof: Suppose to the contrary that for. For fixed m, is continuous on. It can be shown (see [5] , for example) that for any topological space X, if is a sequence in, and f is the pointwise limit of, the set of discontinuities of f cannot be arbitrary, but must in fact be a meager set. Now, is a pointwise limit of continuous functions, and therefore converges to a Baire class 1 function, which by the preceding must have a meager set of discontinuities on. However, the set of discontinuities of is all of. By BCT, since is a complete metric space, it is non-meager. Therefore cannot be a Baire class 1 function and the result follows from the contradiction. +

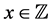
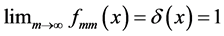
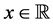
Note that for infinitely many values of x (will do), but the point of the theorem is that it cannot be true for all.

Theorem 3: The double sequence 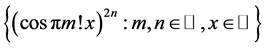is not pointwise convergent in the Pringsheim sense.

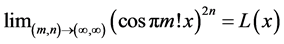
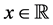
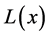
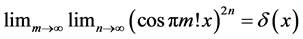
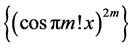
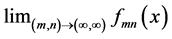
Proof: Suppose to the contrary that for. By Theorem 1 the iterated pointwise limits and the pointwise limits of all induced southeastern sequences should be. However we know from the discussion above regarding Dirichlet’s function that the iterated limit on, but the southeastern sequence does not have this limit function by Theorem 2. The contradiction establishes that the pointwise Pringsheim limit does not exist. +

Theorems 2 and 3 allow us to conclude that “curious cosines” exist. These have the property that they form a numerical sequence where each term is absolutely less than one and the successive terms are raised to arbitrarily high powers, but they nevertheless avoid converging to zero. The apparently intimate coördination between the arguments of the cosines and the powers to which they are raised prevents this.

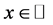
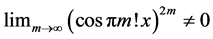
Theorem 4: (Curious Cosines Exist) There exists an irrational such that.

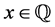
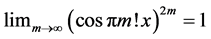
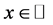
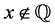
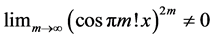
Proof: For, , as eventually the tail of the sequence is constantly 1. If every irrational resulted in 0 as a limit, we would have the Dirichlet function, contradicting Theorem 2. Hence there must exist an such that. +

6. Postscript

The subject of Pringsheim convergence seems to have been neglected over the years. Only recently has the subject of Pringsheim convergence of series been revived [6] , with new results paralleling the single index theory and correcting previous errant results.

Cite this paper

Thomas Beatty,Bradley Hansen, (2016) Pringsheim Convergence and the Dirichlet Function. Advances in Pure Mathematics,06,441-445. doi: 10.4236/apm.2016.66031

References