Advances in Pure Mathematics
Vol.06 No.05(2016), Article ID:65534,10 pages
10.4236/apm.2016.65023
A Two-Step Growth Curve: Approach to the von Bertalanffy and Gompertz Equations
Laura Rogers-Bennett1,2, Donald W. Rogers3,4
1California Department of Fish and Wildlife and Karen C. Drayer, Wildlife Health Center, UC Davis, CA, USA
2Bodega Marine Laboratory, Bodega Bay, CA, USA
3Chemistry Department, Long Island University, Brooklyn, NY, USA
4Friday Harbor Laboratories, Whiteley Center, University of Washington, Friday Harbor, WA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 February 2016; accepted 12 April 2016; published 15 April 2016
ABSTRACT
Many curves have been proposed and debated to model individual growth of marine invertebrates. Broadly, they fall into two classes, first order (e.g. von Bertalanffy) and sigmoidal (e.g. Gompertz). We provide an innovative approach which demonstrates that the growth curves are not mutually exclusive but that either may arise from a simple three-stage growth model 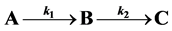 with two steps (k1 and k2) depending on the ratio of the growth parameters
with two steps (k1 and k2) depending on the ratio of the growth parameters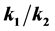 . The new approach predicts sigmoidal growth when
. The new approach predicts sigmoidal growth when 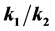 is close to 1, but if either growth from stage A to stage B or B to C is fast relative to the other, the slower of the two steps becomes the growth limiting step and the model reduces to first order growth. The resulting curves indicate that there is a substantial difference in the estimated size at time t during the period of active growth. This novel two-step rate model generates a growth surface that allows for changes in the rate parameters over time as reflected in the new parameter n(t) = k1(t) − k2(t). The added degree of freedom brings about individual growth trajectories across the growth surface that is not easily mapped using conventional growth modeling techniques. This two (or more) stage growth model yields a growth surface that allows for a wide range of growth trajectories, accommodating staged growth, growth lags, as well as indeterminate growth and can help resolve debates as to which growth curves should be used to model animal growth. This flexibility can improve estimates of growth parameters used in population models influencing model outcomes and ultimately management decisions.
is close to 1, but if either growth from stage A to stage B or B to C is fast relative to the other, the slower of the two steps becomes the growth limiting step and the model reduces to first order growth. The resulting curves indicate that there is a substantial difference in the estimated size at time t during the period of active growth. This novel two-step rate model generates a growth surface that allows for changes in the rate parameters over time as reflected in the new parameter n(t) = k1(t) − k2(t). The added degree of freedom brings about individual growth trajectories across the growth surface that is not easily mapped using conventional growth modeling techniques. This two (or more) stage growth model yields a growth surface that allows for a wide range of growth trajectories, accommodating staged growth, growth lags, as well as indeterminate growth and can help resolve debates as to which growth curves should be used to model animal growth. This flexibility can improve estimates of growth parameters used in population models influencing model outcomes and ultimately management decisions.
Keywords:
Growth Model, Growth Surface, Rate Equation, Staged Growth, Population Models

1. Introduction
Selecting a curve to model individual growth for marine invertebrates can be difficult because invertebrates exhibit a suite of complicated growth features [1] . Many invertebrates exhibit staged growth, for example crabs and lobsters molt their hard exoskeleton to permit growth [2] . Some invertebrates are thought to have continuous or indeterminate growth throughout their lives [3] . Growth during the juvenile stage may include a lag until some intermediate size is reached after which growth is maximized [4] . Somatic growth may slow when invertebrates mature and shift energy allocation to reproduction [5] [6] . Invertebrates can also shrink in size, restructuring calcium hard-parts such as sea urchin tests, and rough wave action can wear down mollusk shells out pacing slow growth in large adults. Invertebrates and some fishes do not appear to follow first order growth as suggested by traditional von Bertalanffy growth curves, so that new models have been proposed [7] - [9] . Furthermore, decisions regarding which growth models to use can have major impacts on predicted growth rates. For example, if 75% of adult size is a minimum legal size, the time to fishery estimated by the sigmoidal curve may be double that of the first order curve.
Due to these complications and the importance for modeling invertebrate growth, there has been disagreement in the modeling community as to the appropriateness of selecting a first order growth equation (e.g. von Bertalanffy) or a sigmoidal curve (e.g. Gompertz). Even with the von Bertalanffy model there have been calls for use of the three-parameter von Bertalanffy compared with the two-parameter model due to bias in estimates generated from the two parameter form [10] . It has been suggested that since some invertebrates continue to grow very slowly, models which approach a gradual linear increase may be best, a feature the von Bertalanffy model lacks. The von Bertalanffy function [11] , which is commonly used to model growth in fishes, has been shown to overestimate juvenile growth for invertebrates [4] [7] . Therefore, other models have been used such as the Gompertz model [12] - [15] and the Ricker family of curves [16] . Models such as the Tanaka function [17] and the Gaussian model [18] have also been used as they can accommodate some of the complications observed for invertebrate growth. The inverse logistic has been shown to perform best for some invertebrates [7] [8] and this type of model has the advantage of having low biological prediction error [19] . Growth can also be seasonal and there have been efforts to incorporate seasonality into growth models [15] [20] which require an increase in the number of parameters in the model [21] . Therefore, selecting an appropriate growth model is not a trivial task and selection has been shown to have an impact on fisheries model results impacting management decisions.
Fishery modeling efforts are sensitive to both growth model selection and growth parameters. Optimal fishing mortality rates (F) are heavily influenced by growth parameters. Calculating growth rates directly based on tag recapture or indirectly using size frequency methods can also lead to disparate results [22] . Selecting models or methods which overestimate growth can lead to fishing policies that are too liberal while underestimating growth can lead to conservative fishing policies. Excessive fishing compared to growth capacity can lead to overfishing and population collapse. Overly conservative fishing policies can hurt the economic viability of fisheries. Egg per recruit models, for example, have been shown to be sensitive to growth parameter estimates significantly changing EPR model projections [23] . Therefore, given the critical importance of growth parameter estimation a method that allows for flexibility in mapping a wide range of growth possibilities is needed.
To examine how different types of growth can be accommodated, we explored a novel method of visualizing and modeling growth using a simple two-step, three-stage growth model 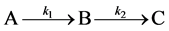 which may ameliorate some of the apparent contradictions reported for both increment data and growth modeling. We examine the rate equations which progress through three (or more) growth stages A, B, and C. These equations yield either a sigmoidal approach to the fully grown state if the growth rates k1 and k2 are similar, or to a first order von Bertalanffy curve if they are not. Finally, we show by allowing the growth rate ratio to vary with time that the result produces a growth surface over which the actual growth of an individual organism can be mapped. We emphasize that we are not proposing a new model to add to the vast collection of growth models being used already, but that we are showing how apparent contradictions in previous studies can be reconciled for organisms that grow by two or more stages since growth can be envisioned across a growth surface that encompasses a suite of growth trajectories (models).
which may ameliorate some of the apparent contradictions reported for both increment data and growth modeling. We examine the rate equations which progress through three (or more) growth stages A, B, and C. These equations yield either a sigmoidal approach to the fully grown state if the growth rates k1 and k2 are similar, or to a first order von Bertalanffy curve if they are not. Finally, we show by allowing the growth rate ratio to vary with time that the result produces a growth surface over which the actual growth of an individual organism can be mapped. We emphasize that we are not proposing a new model to add to the vast collection of growth models being used already, but that we are showing how apparent contradictions in previous studies can be reconciled for organisms that grow by two or more stages since growth can be envisioned across a growth surface that encompasses a suite of growth trajectories (models).
2. Theory
Growth studies often follow a conventional one-step model
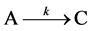
which leads to the first order equation
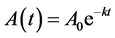 (1)
(1)
which yields
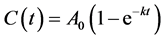 (2)
(2)
A change of notation gives,
 (2a)
(2a)
where  denotes size and
denotes size and 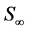 denotes the final size attained at a time substantially greater than the period of active growth (“infinite” time). This equation is commonly called the von Bertalanffy equation or Brody-von Bertalanffy equation [10] .
denotes the final size attained at a time substantially greater than the period of active growth (“infinite” time). This equation is commonly called the von Bertalanffy equation or Brody-von Bertalanffy equation [10] .
We seek to examine results from a sequential growth model which focuses on transitions between distinct stages. These stages may encompass radical metamorphosis (changes in body plan) or more subtle transitions from juvenile to reproductive adult which do not change outward appearance.
A sequential growth mechanism involving first order steps

follows the equations
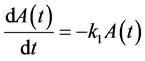 (3a)
(3a)
 (3b)
(3b)
and
 (3c)
(3c)
At time zero,


From Equation 3(a),
where
as in Equation (1). The result for B ® C requires substituting for A(t) into the rate law of B(t)
A (no italic) identifies a stage A and italic 


At any time,
where n = k1 − k2.
3. Methods and Results
We shall maintain the distinction between growth of an animal and growth of a population. Here we consider animal growth and not population growth. We have expressions for transitions from stages A, to B, and B to C as a function of time t, A(t), B(t), and C(t) (Notice that 
One can look at the model from two sides, the two extreme cases, one in which 


In the second extreme case, the rate controlling step is the first transfer, which is slow from A to B followed by a fast transfer from B to C. The growing animal moves through the transition from A to B slowly but the magnitude of the potential growth function B(t) is quickly drawn off to growth stage C. B(t) never becomes very large (see Mathematical Supplement Figure S1). The rate equation is again first order but it has a different rate constant
An interesting point arises when we take the growth surface through the minimum at


Figure 1. Two views of the growth model surface. The views differ in the range of the n = k1 − k2 or n = k2 − k1 axis which varies from 0 to 1000 on the left and 0 to 1.4 on the right. For two-stage growth over a range of n = large, (a) there is only first order growth but when n = small, (b) the same two-stage mechanism predicts sigmoidal growth of size C(t).
Table 1. Parameters in the growth model.
reinstated on the negative side of k1/k2 − k1.
B(t) has a maximum at the inflection point of the function C(t) = f(t). It can be related to the distance between the actual curve at the inflection point and the curve that would be found if von Bertalanffy kinetics had been followed. The ratio of k1/k2 can be estimated from the distance between the actual curve and the experimental curve had the first order function been followed. As the distance between the actual curve and the hypothetical first order curve approaches zero, the ratio approaches 1. Practical use of this relationship would require very accurate experimental data.
4. Discussion
In this paper, we present a multistage growth model which shows the relationship between a suite of linear and non-linear growth curves across a growth surface used to model individual growth. We show that the rates of growth between stages determine the growth trajectory that can be described as a family of curves with the first order curve or the sigmoidal curve as limits. Depending on the difference in the values of the growth rate constants (n = k2 − k1), the growth trajectory follows a first order or sigmoidal portion of the growth surface in Figure 1 with the slower growth rate as the rate limiting step.
When both growth rates k1 and k2 are similar, the final growth trajectory follows a sigmoidal curve and when they differ it follows a first order trajectory (1 − e−kt). Because growth from stage A to growth stage C can be represented as a surface, we envision growth curves that vary across the entire surface such that size is a function of two variables C(t) = f (n, t). With this model, we see that individual growth can be described as a first order curve or as sigmoidal curve depending on the difference in the values of k. This allows for an infinite number of combinations and variations in individual growth across the growth surface as may occur with marine invertebrates.
The three stage model can be expanded to stages beyond C as a simple extension of the present model to stages D, E, and so on. Within a two (or more) stage growth model, it is possible for different research groups to report (correctly) different growth curves for similar populations. Different portions of the growth surface dominate during different life history stages. Likewise, different portions of the curve describe growth under different environmental conditions. For example, growth in red abalone slows during warm water periods such as El Niño events when kelp resources are scarce [27] . In addition, growth is often seasonal such that animals grow more during some parts of the year than others [21] [28] .
There are many factors which may influence growth in addition to environmental factors. Selection, either natural or artificial, may act as a force favoring fast or slow growth. Variation in abalone size plays a role in abalone culture facilities for aquaculture (R. Fields pers. comm.) and conservation. Small size adults may dominate especially in heavily fished populations [29] . Queen conch, for example, is fished in the Caribbean and at some sites there are only small adults with thick shells called “sambas” [30] . Similarly, in the abalone fishery in Australia differences in growth are found in abalone leading to protected reefs with small adults known as “short beds” just under the minimum legal size [31] . Regional growth rates may also differ such as with Geoduck, Panopea globose, in Mexico with important implications for management [32] . Adults that reach a small final size may have different growth rates compared to those which reach larger final sizes [33] .
Invertebrates tend to have high levels of individual variation in both growth rate and final size. Final size, C∞ in the von Bertalanffy or Gompertz model can be thought of as a distribution of maximum lengths since populations are filled with adults of varying sizes [33] . Model final size can also be thought of as the “most probable” value in a distribution of actual final sizes [7] . Differences in the shape of the growth model have been accommodated in the earlier Richards family of curves [34] by the addition of a poorly defined “shape parameter” which when it = 1 gives the logistic curve (sigmoidal) and when it = −1 gives the von Bertalanffy (first order).
Figure 2. Two-stage growth curve for n large (a) and n small 1 (b) (see Mathematical Supplement below). Units of k are reciprocal time, typically years. Numerical labeling of the axes, in Figure 2, is arbitrary because we can choose any unit for size or time but note the change in scale for the time axis. We have chosen the size at “infinite time” to be 1.0 which makes the potential for growth also 1.0 arbitrary units at t0 = 0.
In this work, we show that in a two stage model, shape is controlled by the well defined ratio k1/k2 − k1. This ratio is an improvement over previous methods as it explicitly shows what stage is controlling the growth trajectory.
The trajectory across the surface defines a path of the probability maximum over points on the growth surface. Fast, slow and negative growth can be accommodated by the growth surface in Figure 2.
In a two stage model, the growth rate C(t) = f(n, t), on the surface represents all possible curves. By selecting one growth curve it is possible to specify the curve which represents the most probable growth curve. There are many ways growth may vary because individual trajectories can move along the k1/k2 − k1 surface in any direction. This flexible growth surface allows for visualization of all possible growth trajectories and will be useful in modeling growth in animals with complex life histories, staged growth and even negative growth. The well defined parameters will allow for better estimates of growth for use in fishery and population models.
Acknowledgements
We thank the Whiteley Center at Friday Harbor Laboratories (University of Washington) for creating a space for us to think about growth modeling. We thank K. Rogers for facilitating this work. This work was funded in part by a grant to LRB from the SeaDoc Society, Wildlife Health Center at the University of California, Davis. This research was supported by a NOAA Section 6 grant to the California Department of Fish and Wildlife NA10NMF4720024 and to its partner the University of California, Davis at the Karen C. Dreyer Wildlife Health Center (P1570004). This work benefited from Tully’s coffee cups and fried oysters (Friday’s Crab Shack, Friday Harbor, WA). The first author LRB is supported by the California Department of Fish and Wildlife. This is a contribution of the Bodega Marine Laboratory at the University of California, Davis.
Cite this paper
Laura Rogers-Bennett,Donald W. Rogers,1 1,1 1, (2016) A Two-Step Growth Curve: Approach to the von Bertalanffy and Gompertz Equations. Advances in Pure Mathematics,06,321-330. doi: 10.4236/apm.2016.65023
References
- 1. Ebert, T.A. and Russell, M.P. (1993) Growth and Mortality of Subtidal Red Sea Urchins Strongylocentrotus franciscanus at San Nicolas Island, California, USA: Problems with Models. Marine Biology, 117, 79-89.
http://dx.doi.org/10.1007/bf00346428 - 2. Chang, Y., Sun, C., Chen, Y. and Yeh, S. (2012) Modelling the Growth of Crustacean Species. Reviews in Fish Biology and Fisheries, 22, 157-187.
http://dx.doi.org/10.1007/s11160-011-9228-4 - 3. Sebens, K.P. (1987) The Ecology of Indeterminate Growth in Animals. Annual Review of Ecology, Evolution, and Systematics, 18, 371-407.
http://dx.doi.org/10.1146/annurev.es.18.110187.002103 - 4. Yamaguchi, G. (1975) Estimating Growth Parameters from Growth Rate Data: Problems with Marine Sedentary Invertebrates. Oecologia, 20, 321-332.
http://dx.doi.org/10.1007/BF00345522 - 5. Lester, N.P., Shuter, B.J. and Abrams, P.A. (2004) Interpreting the von Bertalanffy Model of Somatic Growth in Fishes: The Cost of Reproduction. Proceedings of the Royal Society B: Biological Sciences, 271, 1625-1631.
http://dx.doi.org/10.1098/rspb.2004.2778 - 6. Quince, C., Abrams, P.A., Shuter, B.J. and Lester, N.P. (2008) Biphasic Growth in Fish 1: Theoretical Foundations. Journal of Theoretical Biology, 254, 197-206.
http://dx.doi.org/10.1016/j.jtbi.2008.05.029 - 7. Rogers-Bennett, L., Rogers, D.W., Bennett, W.A. and Ebert, T.A. (2003) Modeling Red Sea Urchin Growth Using Six Growth Models. Fishery Bulletin, 101, 614-626.
- 8. Haddon, M.J., Mundy, C. and Tarbath, D. (2008) Using an Inverse-Logistic Model to Describe Growth Increments of Blacklip Abalone (Haliotis rubra) in Tasmania. Fishery Bulletin, 106, 58-71.
- 9. Hernandez-Llamas, A. and Ratkowsky, D. (2004) Growth of Fishes, Crustaceans and Mollusks: Estimation of the von Bertalanffy, Logistic, Gompertz and Richards Curves and a New Growth Model. Marine Ecology Progress Series, 282, 237-244.
http://dx.doi.org/10.3354/meps282237 - 10. Cooper, A.B., Dulvy, N.K., Pardo, S.A. and Hodgson, D.D. (2013) Avoiding Fishy Growth Curves. Methods in Ecology and Evolution, 4, 353-360.
http://dx.doi.org/10.1111/2041-210x.12020 - 11. von Bertalanffy, L. (1938) A Quantitative Theory of Organic Growth (Inquiries on Growth Laws. II). Human Biology, 10, 181-213.
- 12. Day, R.W. and Fleming, A.E. (1992) The Determinants and Measurement of Abalone Growth. In: Shepherd, S.A., Tegner, M.J. and Guzmán del Próo, S.A., Eds., Abalone of the World: Biology, Fisheries and Culture, Blackwell, Oxford, 141-164.
- 13. Nash, W.J. (1992) Growth of Blacklip Abalone (Haliotis rubra) in Tasmania. Proceedings Bureau Rural Research, 12, 137-141.
- 14. Matsuishi, T.K., Saito, S. and Kanno, Y. (1995) Growth Curve of Abalone. Bulletin of the Faculty of Fisheries, Hokkaido University, 46, 53-62.
- 15. Troynikov, V.S., Day, R.W. and Leorke, A. (1998) Estimation of Seasonal Growth Parameters Using a Stochastic Gompertz Model for Tagging Data. Journal of Shellfish Research, 17, 833-838.
- 16. Ebert, T.A. (1999) Plant and Animal Populations. Academic Press, San Diego.
- 17. Tanaka, M. (1982) A New Growth Curve Which Expresses Infinite Increase. Publications of the Amakusa Marine Biological Laboratory, Kyushu University, Vol. 6, 167-177.
- 18. Rogers-Bennett, L., Rogers, D.W. and Schultz, S. (2007) Modeling Growth and Mortality of Red Abalone (Haliotis rufescens) in Northern California. Journal of Shellfish Research, 26, 719-727.
http://dx.doi.org/10.2983/0730-8000(2007)26[719:MGAMOR]2.0.CO;2 - 19. Helidoniotis, F. and Haddon, M. (2013) Growth Models for Fisheries: The Effect of Unbalanced Sampling Error on Model Selection, Parameter Estimation, and Biological Predictions. Journal of Shellfish Research, 32, 223-235.
http://dx.doi.org/10.2983/035.032.0129 - 20. Helidoniotis, F. and Haddon, M. (2011) Growth Model Selection for Juvenile Blacklip Abalone (Haliotis rubra): Assessing Statistical and Biological Validity. Marine & Freshwater Research, 63, 23-33.
http://dx.doi.org/10.1071/MF11103 - 21. Pitcher, T.J. and MacDonald, P.D.M. (1973) Two Models of Seasonal Growth in Fishes. Journal of Applied Ecology, 10, 599-606.
http://dx.doi.org/10.2307/2402304 - 22. Fontoura-da-Silva, V., Cardoso, R., Silvo, C. and Soares, C.H. (2016) Mark-Recapture versus Length-Frequency Based Methods: Evaluation Using a Marine Gastropod as a Model. Journal of Experimental Marine Biology and Ecology, 474, 171-179.
http://dx.doi.org/10.1016/j.jembe.2015.10.013 - 23. Leaf, R.T., Rogers-Bennett, L. and Jiao, Y. (2008) Exploring the Use of a Size Based Egg per Recruit Model for the Red Abalone Fishery in California. North American Journal of Fisheries Management, 28, 1638-1647.
http://dx.doi.org/10.1577/M07-132.1 - 24. Jordan, D.W. and Smith, P. (1997) Mathematical Techniques. 2nd Edition, Oxford University Press, New York.
- 25. Wyle, C.R. and Barrett, L.C. (1982) Advanced Engineering Mathematics. McGraw-Hill Book Co., New York.
- 26. Spiegel, M.R. (1965) Schaum’s Outline of Laplace Transforms. McGraw-Hill Book Co., New York.
- 27. Haaker, P.L., Parker, D.O., Barsky, K.C. and Chun, C. (1998) Growth of Red Abalone, Haliotis rufescens (Swainson), at Johnson’s Lee Santa Rosa Island, California. Journal of Shellfish Research, 17, 747-753.
- 28. Garcia-Berthou, E., Carmona-Catot, G., Merciai, R. and Ogle, D.H. (2012) A Technical Note on Seasonal Growth Models. Reviews in Fish Biology and Fisheries, 22, 635-640.
http://dx.doi.org/10.1007/s11160-012-9262-x - 29. Jennings, S., Greenstreet, S.P.R. and Reynolds, J.D. (1999) Structural Change in an Exploited Fish Community: A Consequence of Differential Fishing Effects on Species with Contrasting Life Histories. Journal of Animal Ecology, 68, 617-627.
http://dx.doi.org/10.1046/j.1365-2656.1999.00312.x - 30. Stoner, A.W. (1994) Significance of Habitat and Stock Pre-Testing for Enhancement of Natural Fisheries: Experimental Analyses with Queen Conch Stombus gigas. Journal of the World Aquaculture Society, 25, 155-165.
http://dx.doi.org/10.1111/j.1749-7345.1994.tb00815.x - 31. Saunders, T., Connell, S. and Mayfield, S. (2009) Differences in Abalone Growth and Morphology between Locations with High and Low Food Availability: Morphologically Fixed or Plastic Traits? Marine Biology, 156, 1255-1263.
http://dx.doi.org/10.1007/s00227-009-1167-4 - 32. Gonzalez-Pelaez, S.S., Morales-Bojorquez, E., Lluch-Cota, D.B., Lluch-Cota, S.E. and Bautista-Romero, J.J. (2015) Modeling Geoduck Growth: Multimodel Inference in Panopea globosa from the Southwestern Baja California Peninsula, Mexico. Journal of Shellfish Research, 34, 101-112.
http://dx.doi.org/10.1007/s00227-009-1167-4 - 33. Sainsbury, K.J. (1980) Effect of Individual Variability on the von Bertalanffy Growth Equation. Canadian Journal of Fisheries and Aquatic Sciences, 37, 241-247.
http://dx.doi.org/10.1139/f80-031 - 34. Richards, F.J. (1959) A Flexible Growth Function for Empirical Use. Journal of Experimental Botany, 10, 290-300.
http://dx.doi.org/10.1093/jxb/10.2.290
Mathematical Supplement
S.1. The Laplace Integral Transform
The Laplace Transform 
Its usefulness is in stepping down from a more difficult problem to an easier one, for example stepping down from 

Integration by parts gives
which is the simplification we sought.
S.2. Application
We wish to solve
Find 
An initial condition was that
Figure S1. Replicates Figure 2(b) text but it shows A(t), B(t), and C(t).
Figure S2. B(t) is just visible (bottom right).
Figure S3. B(t) goes negative but A(t) and C(t) are normal [see text].
Now taking the inverse transforms
There is no reason to believe that the rate parameter governing any stage transition will be constant (deterministic). For this reason we propose a growth surface over which an animal or population growth mean may wander during the growth process (Figure S1-S3).
























