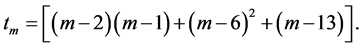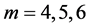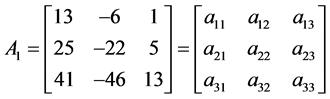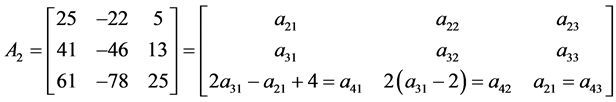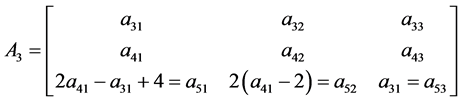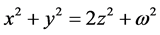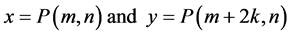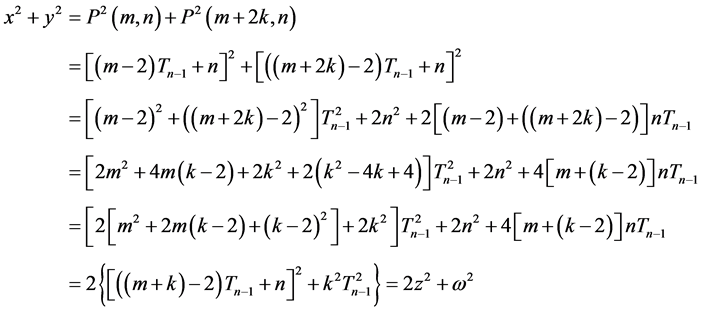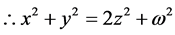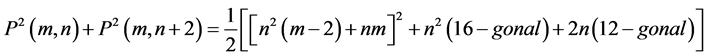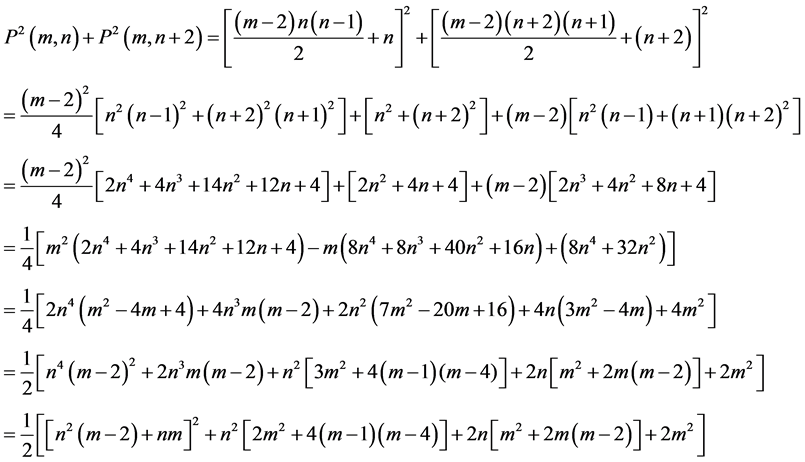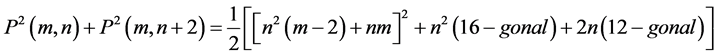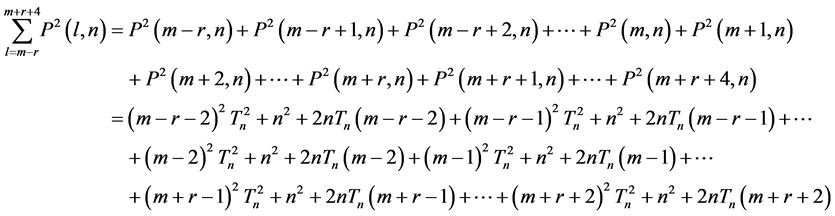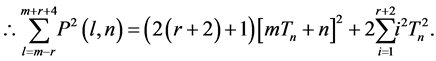Received 6 February 2016; accepted 26 March 2016; published 29 March 2016

ABSTRACT

Polygonal numbers and sums of squares of primes are distinct fields of number theory. Here we consider sums of squares of consecutive (of order and rank) polygonal numbers. We try to express sums of squares of polygonal numbers of consecutive orders in matrix form. We also try to find the solution of a Diophantine equation 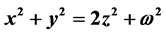in terms of polygonal numbers.

Keywords:

Polygonal Numbers, Sums of Squares, Triangular Numbers

1. Introduction [1]

Polygonal numbers have been meticulously studied since their very beginnings in ancient Greece. Numerous discoveries stemmed from these peculiar numbers can be seen in the basic fundamental group work of number theory today with finding such as pascal’s triangle and Fermat triangular number theorem. It becomes a popular field of research for mathematicians. The concept of polygonal numbers was first defined by the Greek Mathematical hypsicles in the year 170 BC. If the polygonal numbers are divided successively into triangles it will ultimately end up with right triangle. The right triangles immediately remind us of Pythagorean property. This leads to the idea of finding sums of squares of consecutive polygonal numbers. In this paper we calculate sums of squares polygonal numbers of consecutive orders. We also calculate the sums of squares of m-gonal numbers of consecutive ranks. We analyze some properties of the above.

2. Polygonal Number

2.1. Definition

For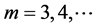

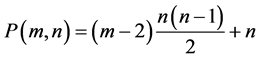with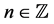

are called generalized m-gonal numbers.

Also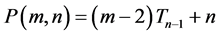

where

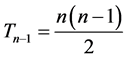with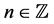, a triangular number of rank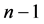

Sums of Squares of Polygonal numbers of Consecutive Orders of Same Rank

2.2. Proposition

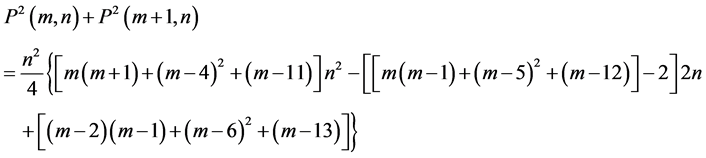
Proof

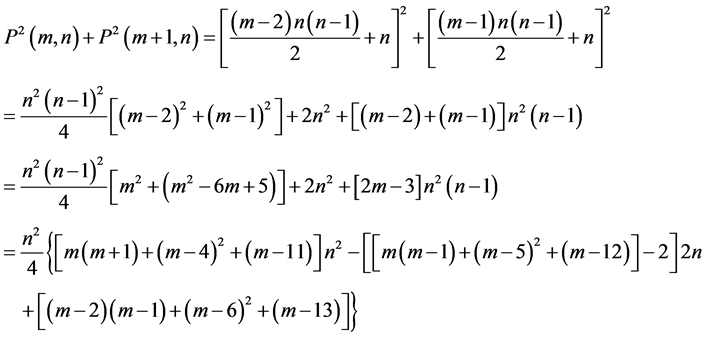
Sums of squares of Polygonal numbers of Consecutive Orders in Matrix Form [2]

Expressing the coefficients of 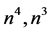and 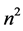for 3 consecutive sums of squares in a 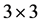matrix the coefficients of sums of squares of any three consecutive terms of higher order can be obtained.

The coefficient matrix 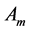of sums of squares polygonal numbers is

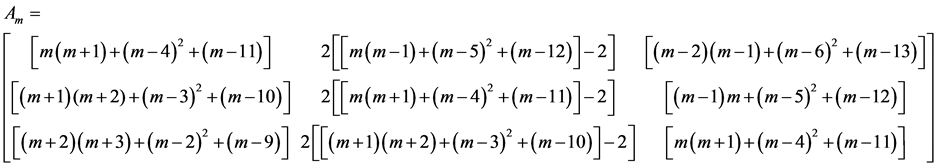
for.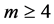

In general,

where

Recursive matrix form

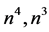
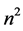
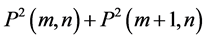
Consider the initial matrix as the coefficients of, and in for

The elements of next order depends on the previous order elements in except the elements of first row.

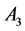
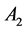
The first two rows elements of are already occurred in and the third row elements are depend on the elements of first two row elements.

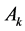
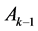
In general, the matrix of order depends on the previous order matrix elements.

Sums of squares of Polygonal Numbers with Consecutive ranks n, n+1.

2.3. Proposition [3]

Proof

.

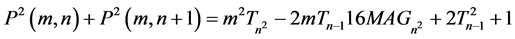
2.4. Proposition

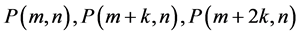
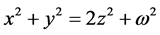
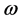
The Triple form the solution of the Diophantine equation , is a constant.

Proof

Consider the Diophantine equation

We try for the solution in polygonal numbers.

Take

Taking 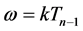it is clear that the triple form the solution of the given equation in the order.

2.5. Proposition

Proof

2.6. Proposition

Proof

3. Conclusion

It is observed that the polygonal numbers of consecutive ranks constitute the solution of the Diophantine equation 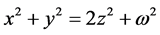in the order. Also we try to find that sums of squares of polygonal numbers are general.

Cite this paper

A. Gnanam,B. Anitha, (2016) Sums of Squares of Polygonal Numbers. Advances in Pure Mathematics,06,297-301. doi: 10.4236/apm.2016.64019

References

Notations

: Polygonal number of order m rank n.

: Triangular Number.

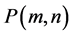
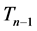
16MAG_n: Magna Number order n.