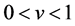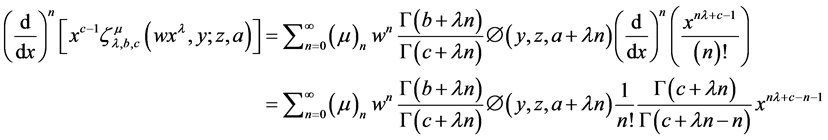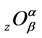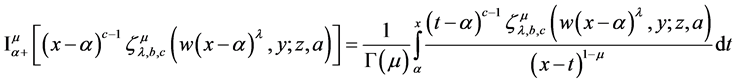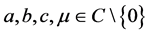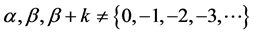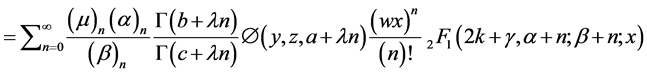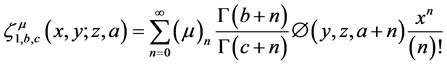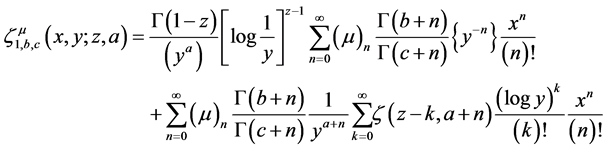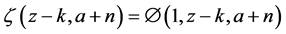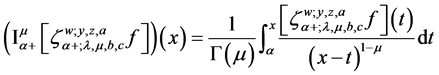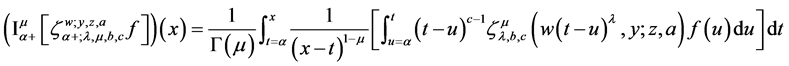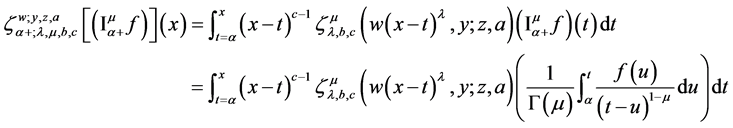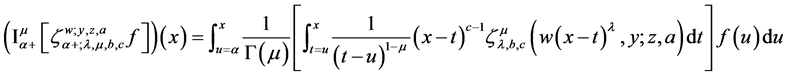Received 4 November 2015; accepted 24 February 2016; published 29 February 2016

ABSTRACT

The present paper aims at introducing and investigating a new class of generalized double zeta function i.e. modified double zeta function which involves the Riemann, Hurwitz, Hurwitz-Lerch, Barnes double zeta function and Bin-Saad generalized double zeta function as particular cases. The results are obtained by suitably applying Riemann-Liouville type and Tremblay fractional integral and differential operators. We derive the expansion formula for the proposed function with some of its properties via fractional operators and discuss the link with known results.

Keywords:

Modified Zeta Function, Riemann-Liouville Operator, Tremblay Fractional Operators, Hypergeometric Function

1. Introduction and Preliminaries

The Hurwitz-Lerch zeta function [1] is defined by

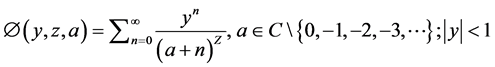(1)

is an analytic function in both variables y and z in suitable region.

The further generalization of Hurwitz-Lerch zeta function 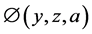is defined by 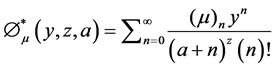[2]

(2)

where 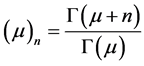denotes the Pochhammer’s symbol, ,

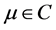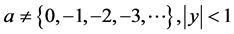
In [3] [4] Bin-Saad and Al-Gonah introduced two hypergeometric type generating functions of generalized zeta function as follows

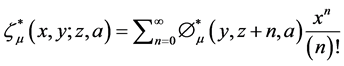(3)

and

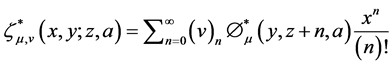(4)

The generalized double zeta function of Bin-Saad [5] is defined by

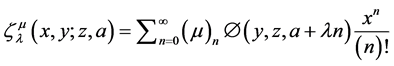(5)

where;,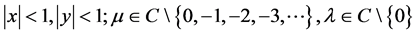

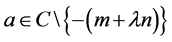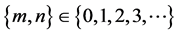
The alternate representation is

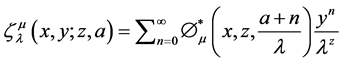(6)

where 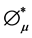is the generalized zeta function defined by (2).

The generalized hypergeometric function in classical form has been defined [6] as

(7)

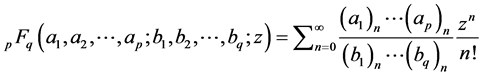
where; denominator parameters are neither zero nor negative integers.

Bin-Saad [5] discussed following relationships.

(8)

(9)

(10)

(11)

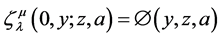
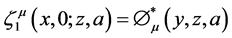
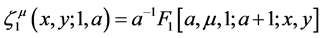
where F₁ is the Appell’s function of two variables [7] defined as

(12)

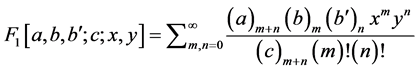
We further recall the following well known expansion formula of Hurwitz-Lerch zeta function [1]

(13)

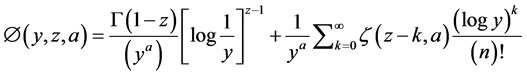
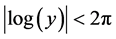
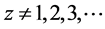
where,; and

(14)

is Hurwitz zeta function which is generalization of the Riemann zeta function given as

(15)

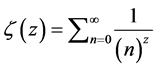
Due to great potential and significant role of special functions especially hypergeometric functions in various problems occurring in mathematical physics, engineering [8] [9] , the author has motivated to further investigate the topic. Several generalizations of hypergeometric functions have been made by many authors [10] [11] . Recently Rao [12] defined Wright type generalized hypergeometric function via fractional calculus. Many authors investigated the fractional calculus approach in study of generalized hypergeometric type function [13] [14] . The subject fractional calculus has gained much attention amongst researchers due to its vast potential of demonstrated mathematical models in various fields of science and engineering such as diffusion, oscillation, dynamical process in porous structures, propagation of waves, diffusive transport, fluid flow, etc. The present paper aims at introducing and investigating a new kind of hypergeometric type function that is modified double zeta function via fractional calculus. The layout of the paper is as follows

In section 2 we introduce and discuss some properties of the modified double zeta function. Section 3 devoted to discuss the Trembley [15] well poised fractional calculus operator together with its properties. In section 4, we establish some interesting results of modified double zeta function through fractional operators and also derive its summation formula. In section 5, we develop some properties of fractional operators. Many Lemmas and particular cases have been discussed to relate known results.

2. Modified Double Zeta Function

In a sequel of result (5) here we introduce a modified double zeta function as follows

(16)

where;

,.

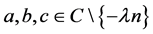
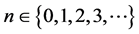
We can readily obtain following relationship

(17)

(18)

(19)

(20)

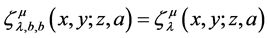
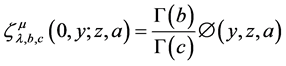
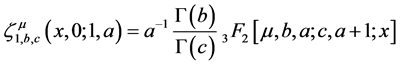
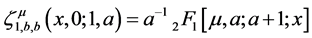
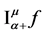
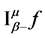
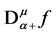
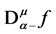
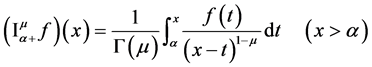
Integration and differentiation of fractional order are traditionally defined by the left side Riemann fractional integral operator and right hand operator and the corresponding R-L fractional derivative operators and [8] , which are given as follows

(21)

(22)

Further for 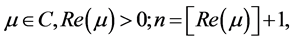the left sided and right sided Riemann fractional differential operators are defined as

(23)

(24)

A generalization of Riemann-Liouville fractional derivatives 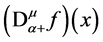[9] is given by

(25)

(throughout this paper we apply all operators with respect to x variable).

is the space of Lebesgue measurable real or complex valued functions such that

(26)

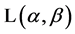
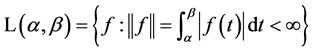
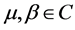
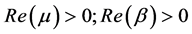
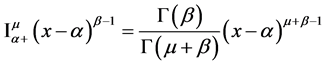
Lemma 2.1. (Mathai and Haubold [16] ) If; then

(27)

Lemma 2.2. (Srivastava and Tomovski [14] ) If, , then

(28)

Lemma 2.3. If, , , w > 0 then

(29)

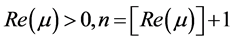
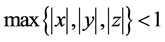
Proof. On using definition (16), we get

Simplify and using definition (16) again, yields the proof of (29).

Now we define the integral operator as follows:

(30)

where;

, (31)

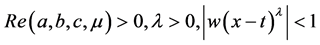
3. The Well Poised Fractional Calculus Operator

The fractional calculus operator that was introduced by Tremblay [15] is given as

(32)

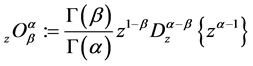
where and due to [17] we have

(33)

We can easily obtain the following result of

(34)

(35)

(36)

(37)

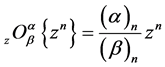
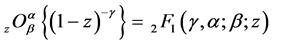
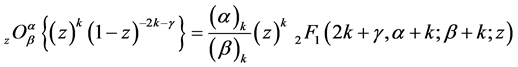
where 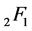is Gauss hypergeometric function.

The operator 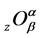has lot more interesting properties and applications. Tremblay introduced this operator to deal with special function more efficiently.

4. The Main Results

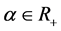
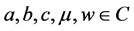
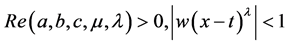
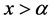
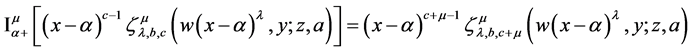
Theorem 4.1 If;;, then for following results holds true

(38)

(39)

If then

(40)

Proof. L.H.S of (38) after using (21) gives

Using definition (16) suitably changing the order of summation and integration, we have

(41)

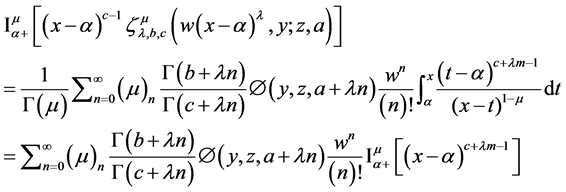
By virtue of (27)

(42)

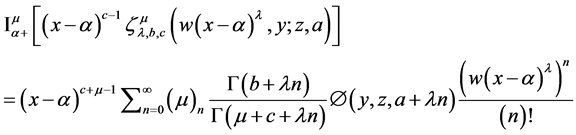
Finally by using definition (16), yields result (38).

Further to prove (39), we use (16) and (23)

(43)

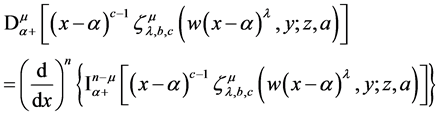
Using (38) we get

(44)

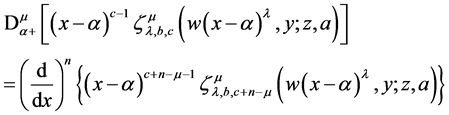
Finally using lemma 2.3 yields R.H.S of (39).

To prove (40), we have

(45)

Using Equation (28), yields proof of (40).

Theorem 4.2 If, , then

(46)

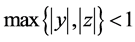
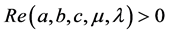
Proof. We have

(47)

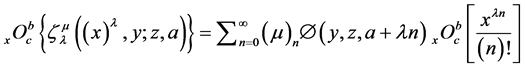
On using (35) we get

(48)

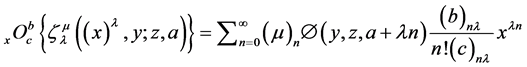
After little simplification and using definition (16), yields the results (46).

Remark 4.1. For, z = 1 Equation (46) yields.

(49)

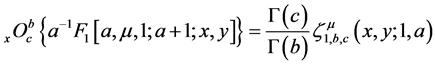
Remark 4.2. On putting y = 0 in Equation (49), we get

(50)

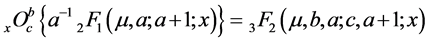
Remark 4.3. Further if we set b = c in Equation (46), it reduces to known identity due to Trembley [15]

(51)

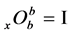
Theorem 4.3. If;, ,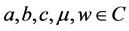

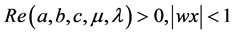
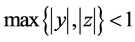
then

(52)

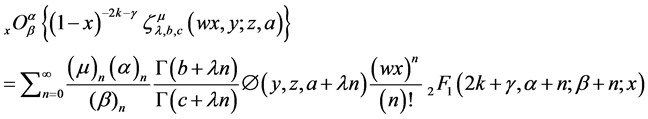
Proof. Expressing modified zeta function in L.H.S as series and changing the order of integration and summation, gives

(53)

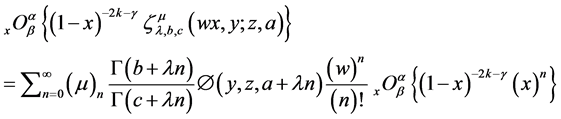
employing (37), yields

which completes the proof.

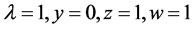
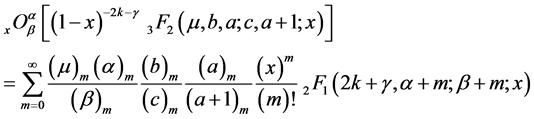
Corollary 4.1. On putting Equation (52) reduces to

(54)

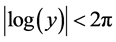
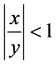
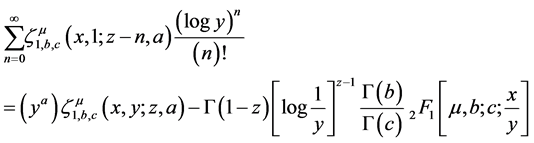
Theorem 4.4. If, and all conditions mentioned in theorem 4.1 holds, then

(55)

where;.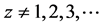

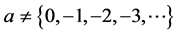
Proof. From (16) we have

Now employing series representation of at R.H.S in above equation by using (13)

(56)

Clearly

After little simplification

(57)

This completes the proof of (55).

Remark 4.4. For b = c equation (55) yields the result [Bin-Saad [5] : p. 273, Equation (2.18), theorem 2.1].

5. Some Properties of the Operator

Theorem 5.1. With all conditions on parameters as stated in Equations (27) and (30), the following properties holds true

(58)

Proof. From (21) and (30), we have

Therefore

Interchanging the order of integration and using Dirichlet formula [17] , we obtain

and substituting, we have

(59)

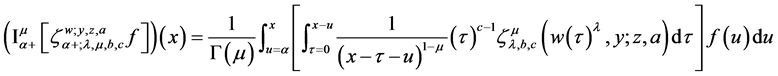
Making use of (21) leads

this leads the proof of L.H.S of (58).

again

Using the Dirichlet formula [17] and interchanging the order of integration we get

Substituting, we get

(60)

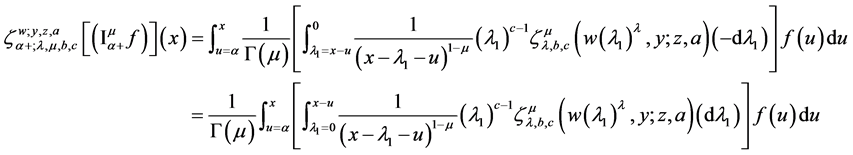
making use of (59) readily leads to the proof of R.H.S of (58).

6. Conclusion

Recently fractional operator’s theory was recognized to be a good tool for modeling complex problems, kinetic equations, fractional reaction, diffusion equations, etc. In this work we introduce and study the new class of generalized zeta function through Riemann Liouville type and Tremblay fractional integral and differential operators. In section 4, interesting images of modified double zeta function have been obtained and useful link between generalized and modified zeta function has been established through Trembley fractional operator. Series expansion of the new class of generalized zeta function is a significant contribution in the direction along that developed in [5] . In section 5, interesting properties of operator 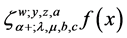have been derived. Many lemmas, corollaries and remarks are obtained to link results with earlier known work. Composition results of Trembley fractional operators and modified zeta function are very useful due to general nature proposed function which may lead several functions and open vast scope of further research in the operator’s field.

Cite this paper

Arif M.Khan, (2016) Modified Double Zeta Function and Its Properties. Advances in Pure Mathematics,06,159-167. doi: 10.4236/apm.2016.63013

References