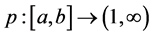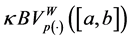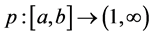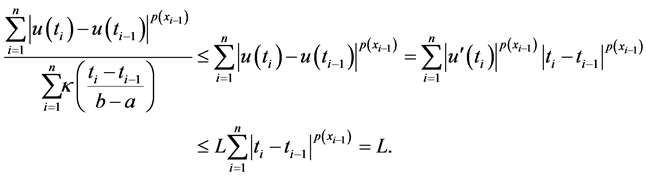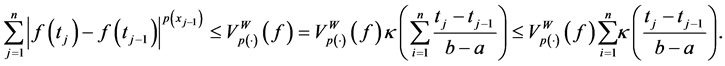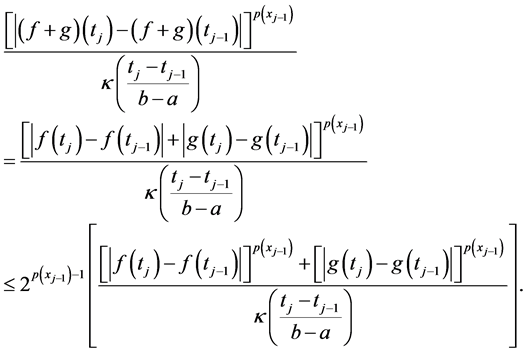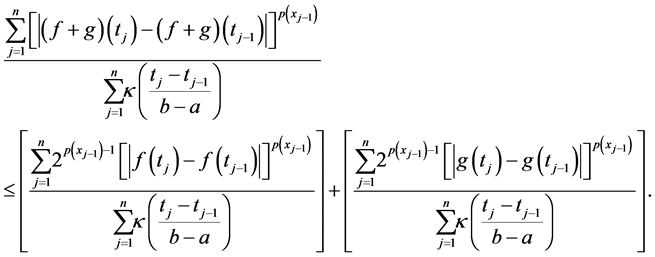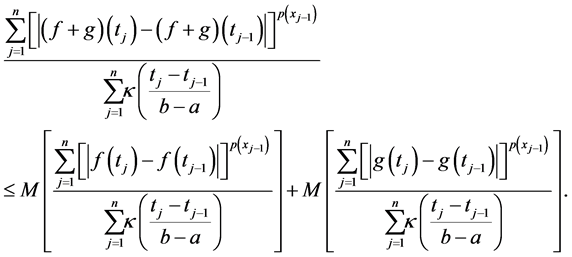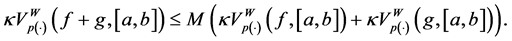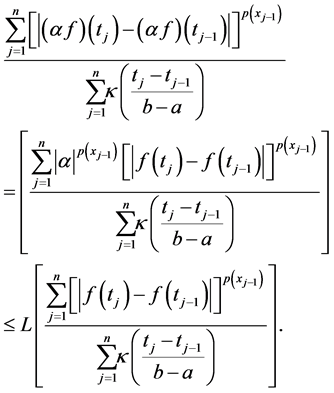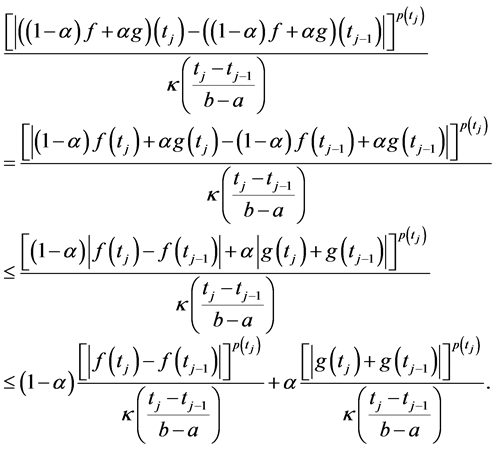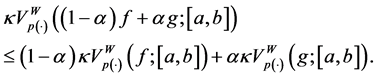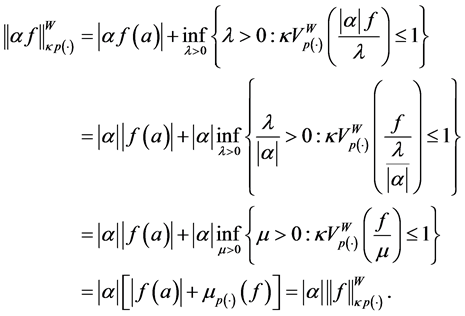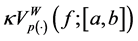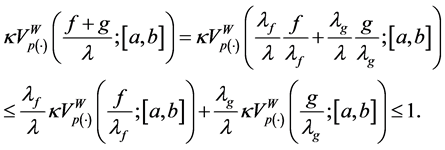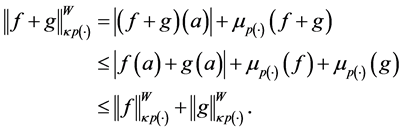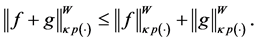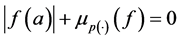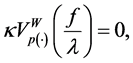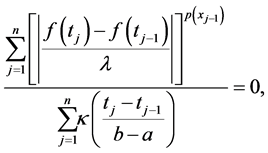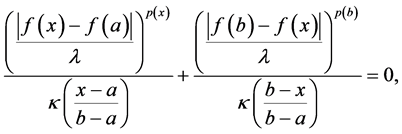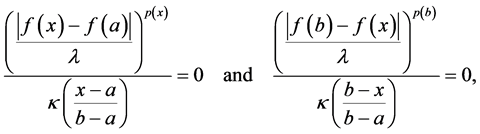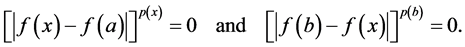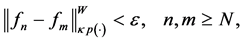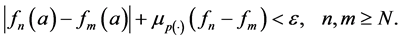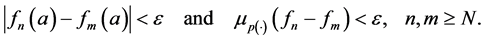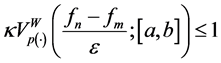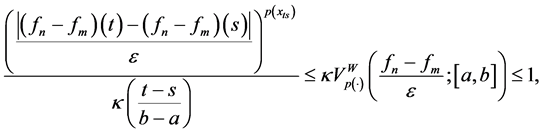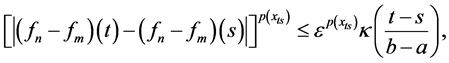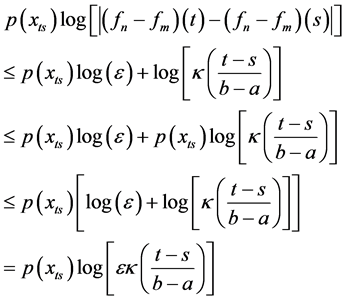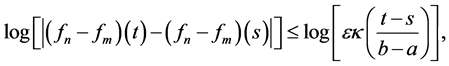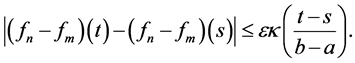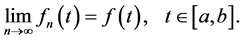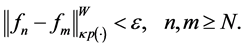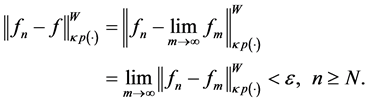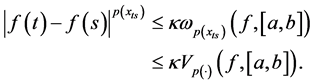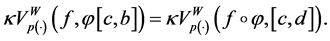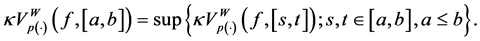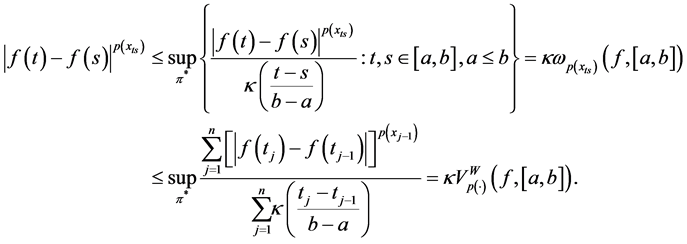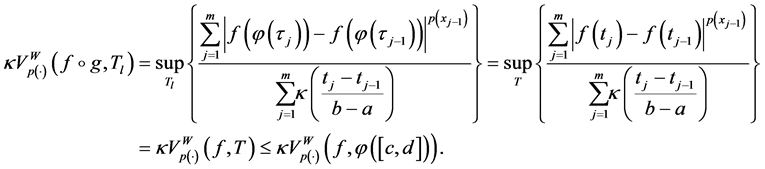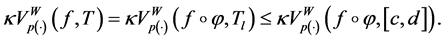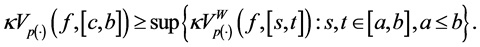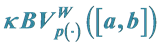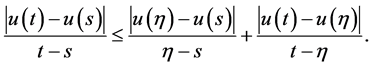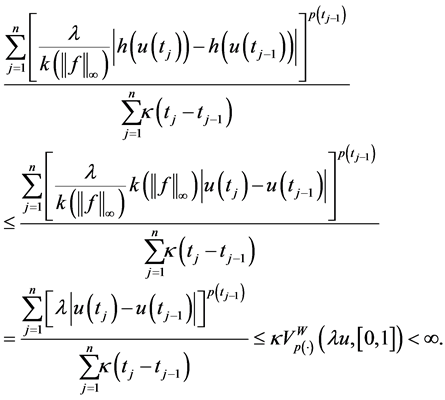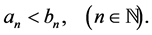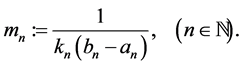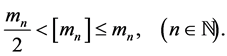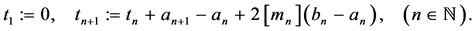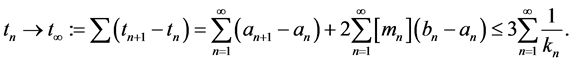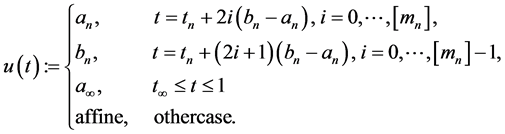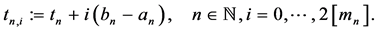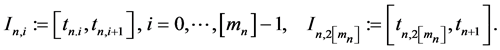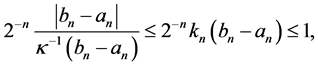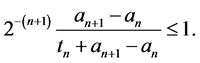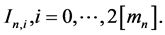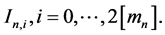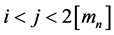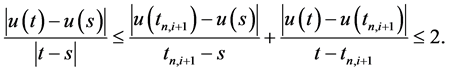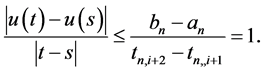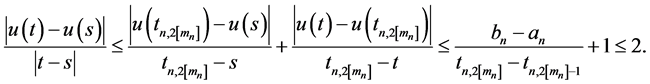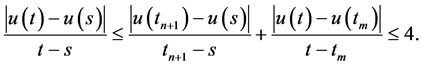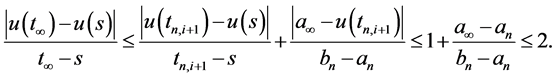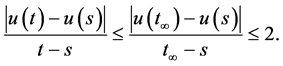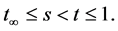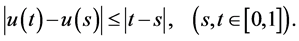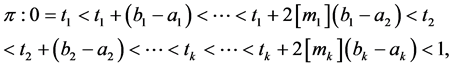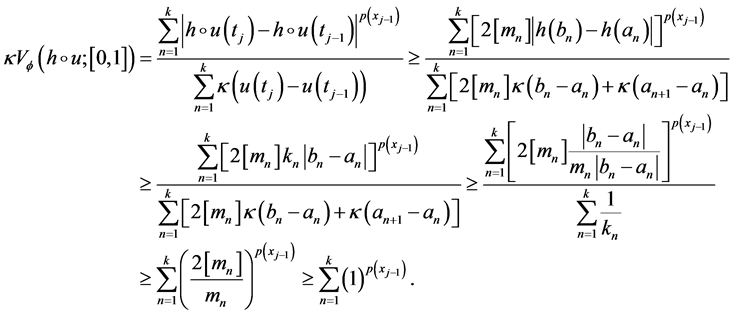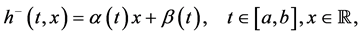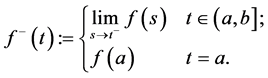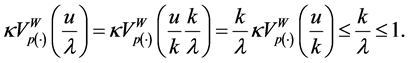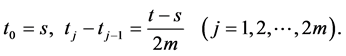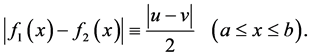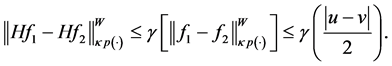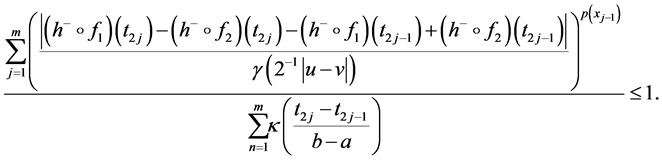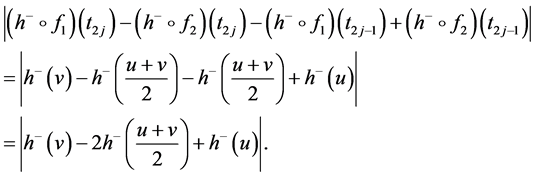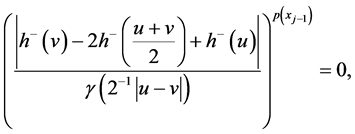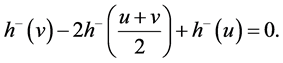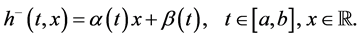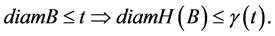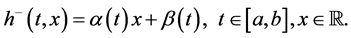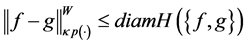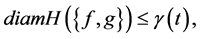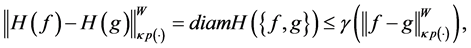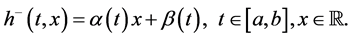Advances in Pure Mathematics
Vol.06 No.01(2016), Article ID:62842,20 pages
10.4236/apm.2016.61004
The Space of Bounded p(×)-Variation in the Sense Wiener-Korenblum with Variable Exponent
O. Mejía, N. Merentes, J. L. Sánchez, M. Valera-López
Departamento de Matemática, Universidad Central de Venezuela, Caracas, Venezuela
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 October 2015; accepted 16 January 2016; published 19 January 2016
ABSTRACT
In this paper we present the notion of the space of bounded p(×)-variation in the sense of Wiener-Korenblum with variable exponent. We prove some properties of this space and we show that the composition operator H, associated with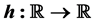 , maps the
, maps the 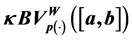 into itself, if and only if h is locally Lipschitz. Also, we prove that if the composition operator generated by
into itself, if and only if h is locally Lipschitz. Also, we prove that if the composition operator generated by 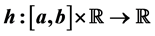 maps this space into itself and is uniformly bounded, then the regularization of h is affine in the second variable, i.e. satisfies the Matkowski’s weak condition.
maps this space into itself and is uniformly bounded, then the regularization of h is affine in the second variable, i.e. satisfies the Matkowski’s weak condition.
Keywords:
Generalized Variation, p(×)-Variation in the Sense of Wiener-Korenblum, Exponent Variable, Composition Operator, Matkowski’s Condition

1. Introduction
A number of generalizations and extensions of variation of a function have been given in many directions since Camile Jordan in 1881 gave a first notion of bounded variation in the paper [1] devoted to the convergence of Fourier series. Consequently, the study of notions of generalized bounded variation forms an important direction in the field of mathematical analysis. Two well-known generalizations are the functions of bounded p-variation and the functions of bounded j-variation, due to N. Wiener [2] and L. C. Young [3] respectively. In 1924 N. Wiener [2] generalized the Jordan notion and introduced the notion of p-variation (variation in the sense of Wiener). Later, in 1937, L. Young [3] introduced the notion of j-variation of a function. The p-variation of a function f is the supremum of the sums of the pth powers of absolute increments of f over no overlapping intervals. Wiener mainly focused on the case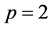 , the 2-variation. For p-variations with
, the 2-variation. For p-variations with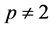 , the first major work was done by Young [3] , partly with Love [4] . After a long hiatus following Young’s work, pth-variations were reconsidered in a probabilistic context by R. Dudley [5] [6] , in 1994 and 1997, respectively. Many basic properties of the variation in the sense of Wiener and a number of important applications of the concept can be found in [7] [8] . Also, the paper by V. V. Chistyakov and O. E. Galkin [9] , in 1998, is very important in the context of p-variation. They study properties of maps of bounded p-variation
, the first major work was done by Young [3] , partly with Love [4] . After a long hiatus following Young’s work, pth-variations were reconsidered in a probabilistic context by R. Dudley [5] [6] , in 1994 and 1997, respectively. Many basic properties of the variation in the sense of Wiener and a number of important applications of the concept can be found in [7] [8] . Also, the paper by V. V. Chistyakov and O. E. Galkin [9] , in 1998, is very important in the context of p-variation. They study properties of maps of bounded p-variation 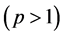 in the sense of Wiener, which are defined on a subset of the real line and take values in metric or normed spaces.
in the sense of Wiener, which are defined on a subset of the real line and take values in metric or normed spaces.
In 1997 while studying Poisson integral representations of certain class of harmonic functions in the unit disc of the complex plan B. Korenblum [10] introduced the notion of bounded k-variation and proved that a function f is of bounded k-variation if ot can be written as the difference of two k-decreasing functions. This concept differs from others due to the fact that it introduces a distortion function k that measures intervals in the domain of the function and not in the range. In 1986, S. Ki Kim and J. Kim [11] , gave the notion of the space of functions of kf-bounded variation on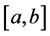 , which is a combination of the notion of bounded f-variation in the sense of Schramm and bounded k-variation in the sense of Korenblum, and J. Park et al. [12] [13] proved some properties in this space. Considering
, which is a combination of the notion of bounded f-variation in the sense of Schramm and bounded k-variation in the sense of Korenblum, and J. Park et al. [12] [13] proved some properties in this space. Considering 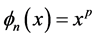 for
for 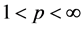 and
and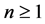 , then it follows that this space generalized the space of functions of kp-bounded variation in the sense of Wiener-Korenblum. In 1990 S. Ki Kim and J. Yoon [14] showed the existence of the Riemann-Stieltjes integral of functions of bounded k-variation and in 2011 W. Aziz, J. Guerrero, J. L. Sánchez and M. Sanoja, in [15] , showed that the space of bounded k-variation satisfies the Matkowski’s weak condition. Also, in 2012, M. Castillo, M. Sanoja and I. Zea [16] presented the space of functions of bounded k-variation in the sense of Riez-Korenblum, denoted by
, then it follows that this space generalized the space of functions of kp-bounded variation in the sense of Wiener-Korenblum. In 1990 S. Ki Kim and J. Yoon [14] showed the existence of the Riemann-Stieltjes integral of functions of bounded k-variation and in 2011 W. Aziz, J. Guerrero, J. L. Sánchez and M. Sanoja, in [15] , showed that the space of bounded k-variation satisfies the Matkowski’s weak condition. Also, in 2012, M. Castillo, M. Sanoja and I. Zea [16] presented the space of functions of bounded k-variation in the sense of Riez-Korenblum, denoted by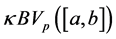 , which is a combination of the notions of bounded p-variation in the sense of Riesz
, which is a combination of the notions of bounded p-variation in the sense of Riesz 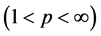 and bounded k-variation in the sense of Korenblum.
and bounded k-variation in the sense of Korenblum.
Recently, there has been an increasing interest in the study of various mathematical problems with variable exponents. With the emergency of nonlinear problems in applied sciences, standard Lebesgue and Sobolev spaces demonstrated their limitations in applications. The class of nonlinear problems with exponent growth is a new research field and it reflects a new kind of physical phenomena. In 2000 the field began to expand even further. Motivated by problems in the study of electrorheological fluids, L. Diening [17] raised the question of when the Hardy-Littlewood maximal operator and other classical operators in harmonic analysis are bounded on the variable Lebesgue spaces. These and related problems are the subject of active research nowadays. These problems are interesting in applications (see [18] -[21] ) and give rise to a revival of the interest in Lebesgue and Sobolev spaces with variable exponent, the origins of which can be traced back to the work of W. Orlicz in the 1930’s [22] . In the 1950’s, this study was carried on by H. Nakano [23] [24] who made the first systematic study of spaces with variable exponent. Later, Polish and Czechoslovak mathematicians investigated the modular function spaces (see for example J. Musielak [25] [26] , O. Kovacik and J. Rakosnik [27] ). We refer to books [21] for the detailed information on the theoretical approach to the Lebesgue and Sobolev spaces with variable exponents. In 2015, R. Castillo, N. Merentes and H. Rafeiro [28] studied a new space of functions of generalized bounded variation. There the authors introduced the notion of bounded variation in the Wiener sense with the exponent p(×)-variable. In the same year, O. Mejia, N. Merentes and J. L. Sánchez in [29] , proved some properties in this space, for the composition operator and showed a structural theorem for mappings of bounded variation in the sense of Wiener with the exponent p(×)-variable.
The main purpose of this paper is threefold: First, we provide extension of the space of generalized bounded variation present in [28] and [29] in the sense Wiener-Korenblum and we give a detailed description of the new class formed by the functions of bounded variation in the sense of Wiener-Korenblum with the exponent p(×)- variable. Second, we prove a necessary and sufficient condition for the acting of composition operator
(Nemystskij) on the space 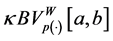 and, third we show that any uniformly bounded composition operator that maps the space
and, third we show that any uniformly bounded composition operator that maps the space 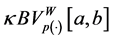 into itself necessarily satisfies the so called Matkowski’s weak condition.
into itself necessarily satisfies the so called Matkowski’s weak condition.
2. Preliminaries
We use throughout this paper the following notation: we will denote by
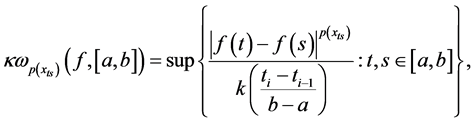
the diameter of the image 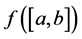
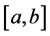
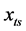
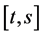
The class of bounded variation functions exhibit many interesting properties that it makes them a suitable class of functions in a variety of contexts with wide applications in pure and applied mathematics (see [8] and [30] ). Since C. Jordan in 1881 (see [1] ) gave the complete characterization of functions of bounded variation as a difference of two increasing functions, the notion of bounded variation functions has been generalized in different ways.
Definition 2.1. Let 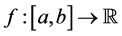
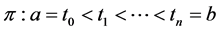
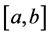
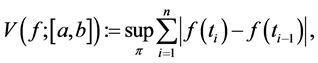
where the supremum is taken over all partitions 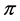
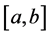
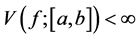
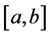
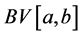
A generalization of this notion was presented by N. Wiener (see [2] ) who introduced the notion of p-variation as follows.
Definition 2.2. Given a real number
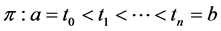
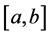
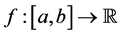
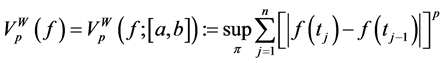
is called the Wiener variation (or p-variation in Wiener’s sense) of f on 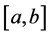
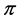
In case that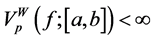
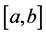
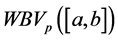
Wiener’s sense on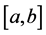
Other generalized version was given by B. Korenblum in 1975 [10] . He considered a new kind of variation, called k-variation, and introduced a function k for distorting the expression 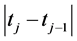
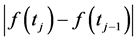
Definition 2.3. A function 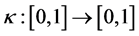
1) k is continuous with 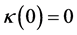
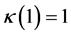
2) k is concave and increasing;
3)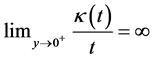
B. Korenblum (see [10] ), introduced the definition of bounded k-variation as follows.
Definition 2.4. Let k be a distortion function, f a real function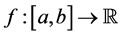
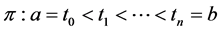
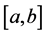

where the supremum is taken over all partitions 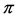
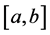
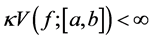
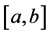
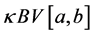
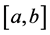
Some properties of k-function cab be found in [12] [14] [16] .
In 2013 R. Castillo, N. Merentes and H. Rafeiro [28] introduce the notation of bounded variation space in the Wiener sense with variable exponent on 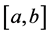
Definition 2.5. Given a function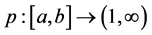
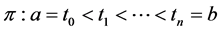
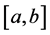
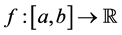
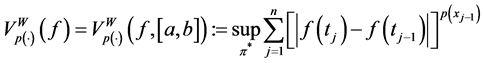
is called Wiener variation with variable exponent (or p(×)-variation in Wiener’s sense) of f on 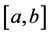
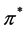
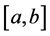
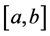
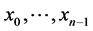
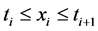
In case that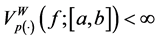
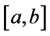
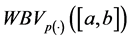
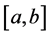
Remark 2.6. Given a function
1) If 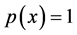
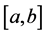
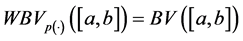
2) If 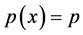
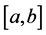
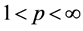
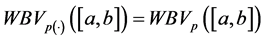
In [29] , O. Mejia, N. Merentes and J. L. Sánchez proved some properties in this space, for the composition operator and show a structural theorem for mappings of bounded variation in the sense of Wiener with the exponent p(×)-variable.
Now, we generalized the notion of bounded variation space in the sense of Wiener-Korenblum with variable exponent on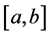
Definition 2.7. Given a function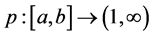
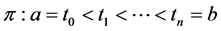
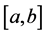
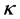
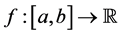
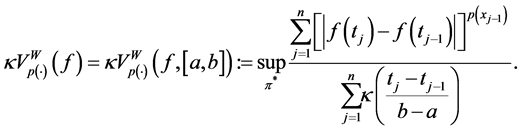
is called Wiener-Korenblum variation with variable exponent (or p(×)-variation in the sense of Wiener-Korenblum) of f on 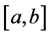
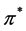
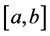
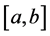
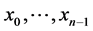
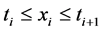
In case that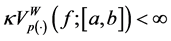
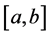
will denote the space of functions of bounded p(×)-variation in the sense Wiener-Korenblum with variable exponent on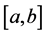
Remark 2.8. Given a function
1) If 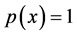
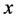
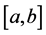
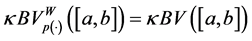
2) If 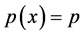
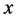
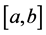
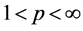
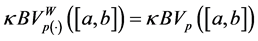
Example 2.9. Let 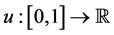
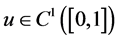
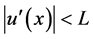
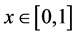
Therefore,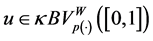
3. Properties of the Space
Theorem 3.1. Let 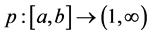
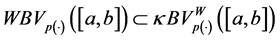
Proof. Let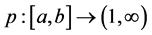
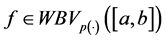
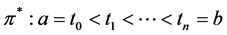
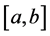
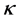
Thus,
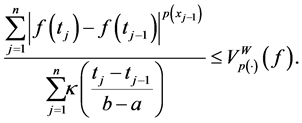
Then considering the supremum of the left side we get
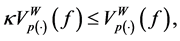
therefore, 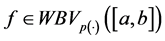
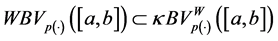
Remark 3.2. From this result we deduce that every function of bounded p(×)-variation in of Wiener’s sense with variable exponent on the interval 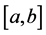
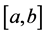
Now we will see that the class of function of bounded p(×)-variation in the sense of Wiener-Korenblum has a structure of vector space.
Theorem 3.3. Let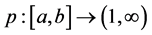
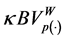
Proof. Let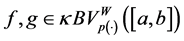
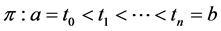
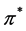
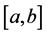
Now adding from 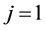
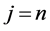
Since p(×) is bounded, then there is a 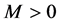
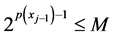
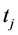
In other word, if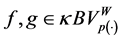
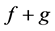
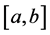
On the other hand, since p(×) is bounded, there exists 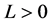
therefore,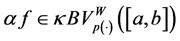
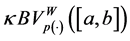
Proposition 3.4. Given a function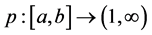
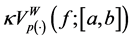
Proof. Let 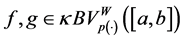
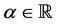
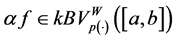
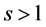
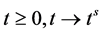
Then,
W
Definition 3.5. (Norm in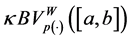
Let 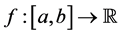
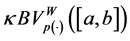
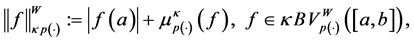
where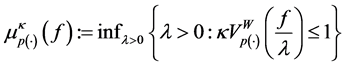
Theorem 3.6. 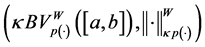
Proof. Let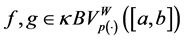
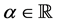
a) 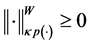
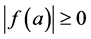
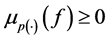
b)
Therefore,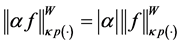
c) Fix 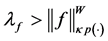
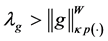
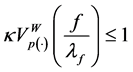
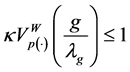
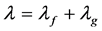
Hence
Thus,
d) Let us now prove that 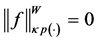
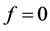
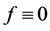
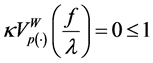
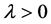
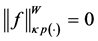
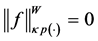
then 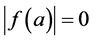
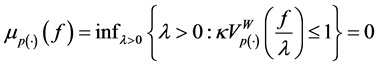
i.e.,
without loss of generality, considering the partition 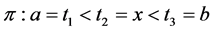
then
we get
Hence, 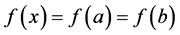
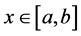
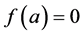
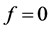
In the following, we show that 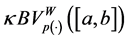
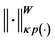
Theorem 3.7. Let 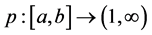
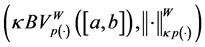
Proof. Let 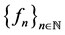
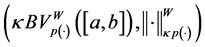
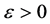
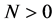
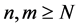
i.e.
Then
Thus, for all 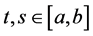
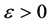
then
therefore
by properties of function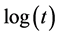
then
hence
In consequence, the sequence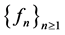
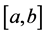
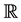
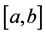
We will show that 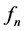
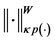
Since the 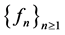
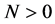
From the fact that 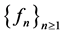
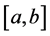
Therefore, the sequence 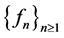
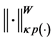
Thus 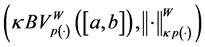
The following properties of elements of 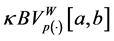
Lemma 3.8. (General properties of the p(×)-variation) Let 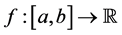
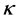
(P1) Minimality: if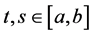
(P2) Change of variable: if 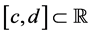
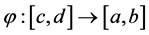
(P3) Regularity:
Proof. (P1) Let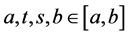
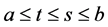
(P2) Let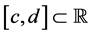
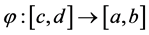
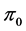
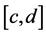
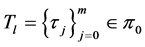
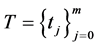
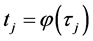
On the other hand, if a partition 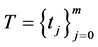
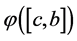
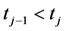
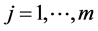
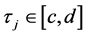
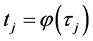
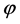
(P3) By monotonocity of 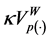
On the other hand, for any number 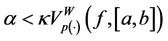
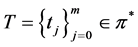
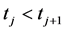
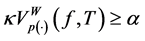
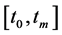
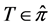
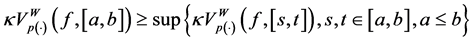
In the next section we will be dealing with the composition operator (Nemitskij).
4. Composition Operator between the Space
In any field of nonlinear analysis composition operators (Nemytskij), the superposition operators generated by appropriate functions, play a crucial role in the theory of differential, integral and functional equations. Their analytic properties depend on the postulated properties of the defining function and on the function space in which they are considered. A rich source of related questions is the monograph by J. Appell and P. P. Zabrejko [31] and J. Appell, J. Banas, N. Merentes [8] .
The composition operator problem refers to determining the conditions on a function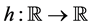
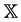
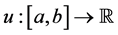
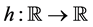
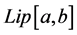
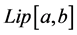
The first work on the composition operator problem in the space of functions of bounded variation 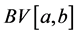
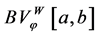
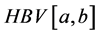
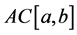
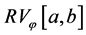
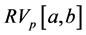
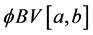
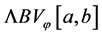
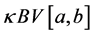
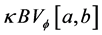
Now, we define the composition operator. Given a function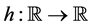
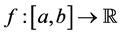
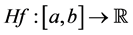
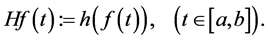
More generally, given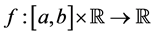
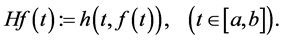
This operator is also called superposition operator or susbtitution operator or Nemytskij operator. In what follows, will refer (9) as the autonomus case and to (10) as the non-autonomus case.
In order to obtain the main result of this section, we will use a function of the zig-zag type such as the employed by J. Appell et al. [8] [37] that the locally Lipschitz condition of the function h is a necessary and suffi-
cient condition such that 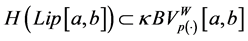
One of our main goals is to prove a result in the case when h is locally Lipschitz if and only if the composition operator maps the space of functions of bounded p(×)-variation into itself.
The following lemma, established in [38] , will be useful in the proof of our main Theorem (Theorem 4.2).
Lemma 4.1. Let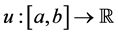
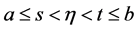
Theorem 4.2. Let H be a composition operator associated to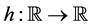
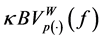
Proof. We may suppose without loss generality that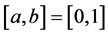
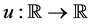
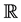
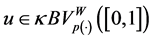
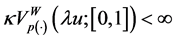
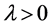
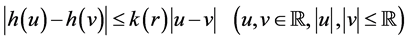
for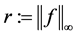
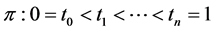
This shows that for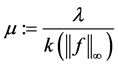
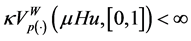
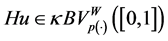
The proof of the only if direction will be by contradiction, that is we assume 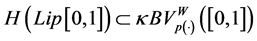
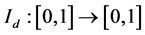
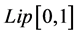
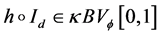
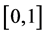
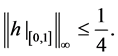
Since h is not locally Lipschitz in 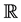
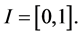
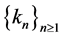
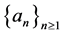
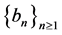
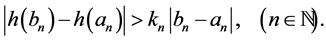
In addition choose 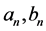
Considering subsequence if it necessary, we can assume without loss of generality that the sequence 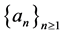
Since 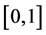
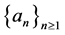
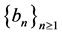
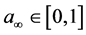
Since the sequence 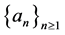
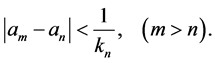
Again considering subsequences if needed and using the properties of the function 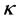
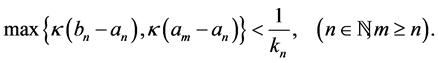
Consider the new sequence 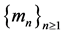
From of inequalities (12) and (13) it follows that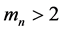
Consider the sequence defined recursively 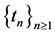
This sequence is strictly increasing and from the relations (14) and (15), we get
Then to ensure that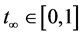
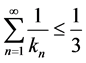
We define the continuous zig-zag function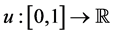
Put
We can write each interval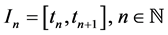
And function u is defined on 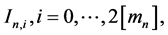
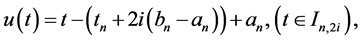
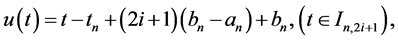
and
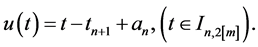
In all these situations the slopes of these segments of lines is 1.
Hence, we have for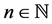
We will show that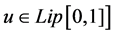
Let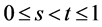
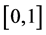
Case 1: If 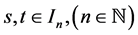
From relations (16), (17) and (18) follows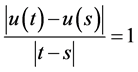
Case 2: If 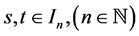
There are several possibilities:
a)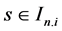
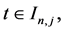
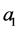
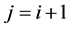
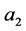
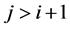
b)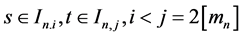
If 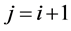
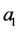
If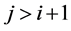
Case 3: If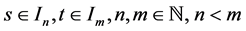
From Lemma 4.1 and the second case, we conclude
Case 4: If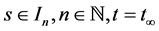
Then from Lemma 4.1
Case 5: If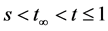
From Lemma 4.1 and Case 4
Case 6: If
In this circumstance 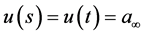
So u is Lipschitz in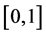
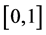
and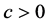
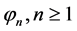
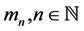
As the serie 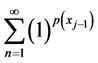
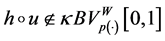
5. Uniformly Continuous Composition Operator
In a seminal article of 1982, J. Matkowski [39] showed that if the composition operator H, associated with the function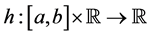
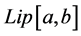
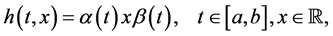
for some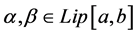
There are a variety of spaces besides 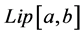
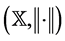
In 1984, J. Matkowski and J. Miś [40] considered the same hypotheses on the operator H for the space 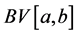
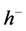
where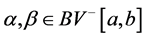
In this section, we give the other main result of this paper, namely, we show that any uniformly bounded composition operator that maps the space 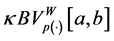
First of all we will give the definition of left regularization of a function.
Definition 5.1. Let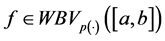
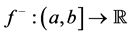
We will denote by 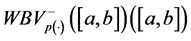
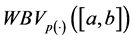
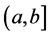
Lemma 5.2. If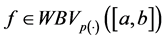
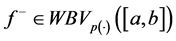
Thus, if a function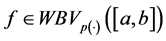
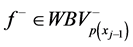
Also, we will denote by 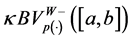
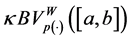
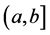
Lemma 5.3. If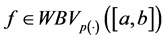
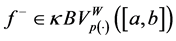
Proof. By Lemma 5.2, we have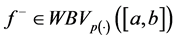
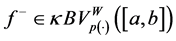
Thus, if a function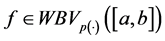
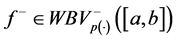
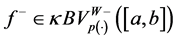
Another lemma useful for the follow theorem is developed below:
Lemma 5.4. Let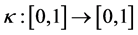
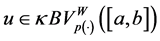
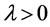
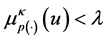
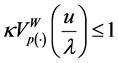
Proof. Let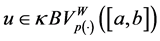
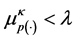
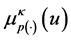
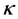
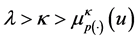
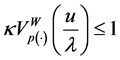
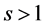
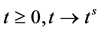
Conversely, assume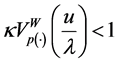
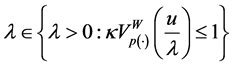
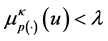
Theorem 5.5. Suppose that the composition operator H generated by 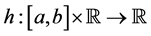
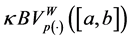
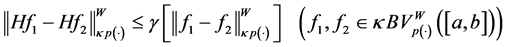
for some function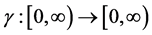
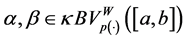
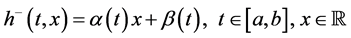
where 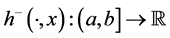
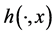
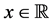
Proof. By hypothesis, for 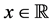
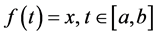
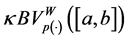
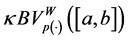
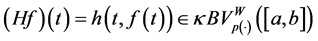
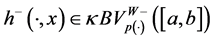
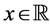
From the inequality (20) and definition of the norm 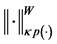
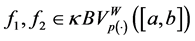
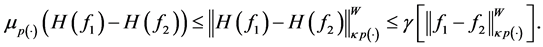
From the inequality (22) and Lemma 5.2, if 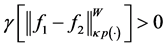
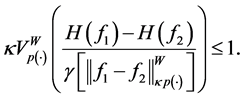
Let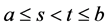
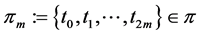
Given 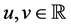
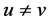
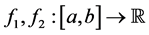
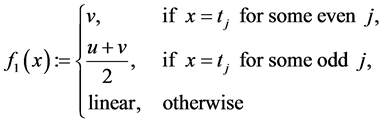
and
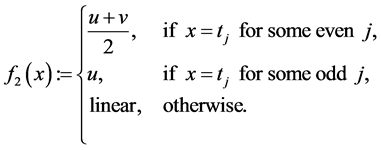
Then the difference 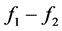
Consequently, by the inequality (20)
From the inequality (23) and the definition of p(×)-variation in the sense of Wiener-Korenblum we have
However, by definition of the functions 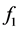
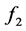
Then
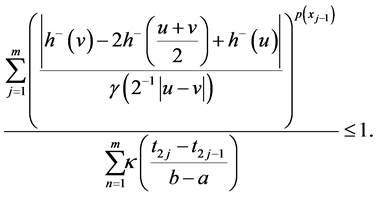
Since 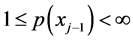
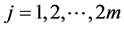
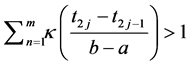
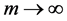
hence,
So, we conclude that 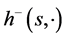
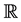
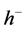
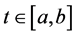
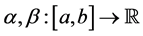
Because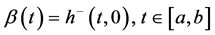
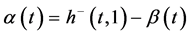
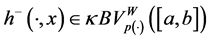
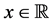
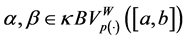
J. Matkowski [42] introduced the notion of a uniformly bounded operator and proved that any uniformly bounded composition operator acting between general Lipschitz function normed spaces must be of the form (21).
Definition 5.6. ([42] , Def. 1) Let 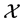
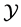
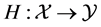
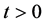
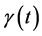
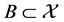
Remark 5.7. Every uniformly continuous operator or Lipschitzian operator is uniformly bounded.
Theorem 5.8. Let 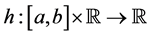
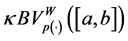
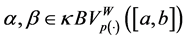
where 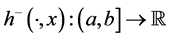
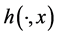
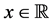
Proof. Take any 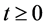
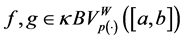
Since 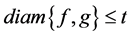
that is,
and therefore, by the Theorem 5.5 we get
Acknowledgements
This research has been partially supported by the Central Bank of Venezuela. We want to give thanks to the library staff of B.C.V for compiling the references.
Cite this paper
O.Mejía,N.Merentes,J. L.Sánchez,M.Valera-López, (2016) The Space of Bounded p(·)-Variation in the Sense Wiener-Korenblum with Variable Exponent. Advances in Pure Mathematics,06,21-40. doi: 10.4236/apm.2016.61004
References
- 1. Jordan, C. (1881) Sur la série de Fourier. Comptes Rendus de l’Académie des Sciences, 228-230.
- 2. Wiener, N. (1924) The Quadratic Variation of a Function and Its Fourier Coefficients. Journal of Mathematical Physics, 3, 73-94.
http://dx.doi.org/10.1002/sapm19243272 - 3. Young, L.C. (1937) Sur une généralisation de la notion de variation de pussance piéme bornée au sens de M. Wiener, et sur la convergence des séries de Fourier. Comptes Rendus de l’Académie des Sciences, 204, 470-472.
- 4. Love, E.R. and Young, L.C. (1937) Sur une classe de fonctionelles linéaires. Fundamenta Mathematicae, 28, 243-257.
- 5. Dudley, R.M. (1994) The Order of the Remainder in Derivatives of Composition and Inverse Operators for p-Variation Norms. Annals of Statistics, 22, 1-20.
http://dx.doi.org/10.1214/aos/1176325354 - 6. Dudley, R.M. (1997) Empirical Processes and p-Variation. In: Pollard, D., Torgersen, E. and Yang, G.L., Eds., Festschrift for Lucien Le Cam, Springer, New York, 219-233.
http://dx.doi.org/10.1007/978-1-4612-1880-7_13 - 7. Dudley, R.M. and Norvaisa, R. (1999) Differentiability of Six Operators on Nonsmooth Functions and p-Variation. Springer, Berlin.
- 8. Appell, J., Banas, J. and Merentes, N. (2014) Bounded Variation and Around. De Gruyter, Boston.
- 9. Chistyakov, V.V. and Galkin, O.E. (1998) On Maps of Bounded p-Variation with p>1. Positivity, 2, 19-45.
http://dx.doi.org/10.1023/A:1009700119505 - 10. Korenblum, B. (1975) An Extension of the Nevalinna Theory. Acta Mathematica, 135, 187-219.
http://dx.doi.org/10.1007/BF02392019 - 11. Kim, S.K. and Kim, J. (1986) Functions of kø-Bounded Variation. Bulletin of the Korean Mathematical Society, 23, 171-175.
- 12. Park, J. (2010) On the Functional of Bounded kø-Variations (I). Journal of Applied Mathematics & Informatics, 28, 171-175.
- 13. Sok, Y.-U. and Park, J.-K. (1989) A Study on the Functions of kø-Bounded Variation. Journal of the Chungcheong Mathematical Society, 2, 55-64.
- 14. Kim, S.K. and Yoon, J. (1990) Riemman-Stieltjes Integral of Functions of k-Bounded Variation. Communications of the Korean Mathematical Society, 5, 65-73.
- 15. Aziz, W., Guerrero, J., Sánchez, J. and Sanoja, M. (2011) Lipschitzian Composition Operator in the Space . Journal of Mathematical Control Science and Applications (JMCSA), 4, 67-73.
- 16. Castillo, M., Sanoja, M. and Zea, I. (2012) The Space Functions of Bounded k-Variation in the Sense of Riesz-Korenblum. Journal of Mathematical Control Science and Applications (JMCSA), 2012, 1-16.
- 17. Diening, L. (2004) Maximal Function on Generalize Lebesgue Spaces . Mathematical Inequalities & Applications, 7, 245-253.
- 18. Azroul, E., Barbara, A. and Redwane, H. (2014) Existence and Nonexistence of a Solution for a Nonlinear p(x)-Elliptic Problem with Right-Hand Side Measure. International Journal of Analysis, 2014, 1-15.
- 19. Fan, X., Zhao, Y. and Zhao, D. (2001) Compact Imbedding Theorems with Symmetry of Strauss-Lions Type for the Space . Journal of Mathematical Analysis and Applications, 255, 333-348.
http://dx.doi.org/10.1006/jmaa.2000.7266 - 20. Yin, L., Liang, Y., Zhang, Q. and Zhao, C. (2015) Existence of Solutions for a Variable Exponent System without PS Conditions. Journal of Differential Equations, 2015, 1-23.
- 21. Radulescu, V.D. and Repovs, D.D. (2015) Partial Differential Equations with Variable Exponent: Variational Methods and Qualitative Analysis. CRC Press, Taylor & Francis Group, Boca Raton.
- 22. Orlicz, W. (1931) über konjugierte exponentenfolgen. Studia Mathematica, 3, 200-211.
- 23. Nakano, H. (1950) Modulared Semi-Ordered Linear Spaces. Maruzen Co., Ltd., Tokyo.
- 24. Nakano, H. (1951) Topology and Topological Linear Spaces. Maruzen Co., Ltd., Tokyo.
- 25. Musielak, J. (1983) Orlicz Spaces and Modular Spaces. Springer-Verlag, Berlin.
- 26. Musielak, J. and Orlicz, W. (1959) On Modular Spaces. Studia Mathematica, 18, 49-65.
- 27. Kovácik, O. and Rákosník, J. (1991) On Spaces and . Czechoslovak Mathematical Journal, 41, 592-618.
- 28. Castillo, R., Merentes, N. and Rafeiro, H. (2014) Bounded Variation Spaces with p-Variable. Mediterranean Journal of Mathematics, 11, 1069-1079.
http://dx.doi.org/10.1007/s00009-013-0342-5 - 29. Mejia, O., Merentes, N. and Sánchez, J. (2015) The Space of Bounded p(·)-Variation in Wiener’s Sense with Variable Exponent. Advances in Pure Mathematics, 5, 703-716.
http://dx.doi.org/10.4236/apm.2015.511064 - 30. Merentes, N. and Rivas, S. (1996) El Operador de Composición en Espacios de Funciones con Algún Tipo de Variación Acotada, IX Escuela Venezolana de Matemáticas, Facultad de Ciencias-ULA, Mérida-Venezuela.
- 31. Appell, J. and Zabreiko, P.P. (1990) Nonlinear Superposition Operators. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511897450 - 32. Appell, J., Guanda, N. and Väth, M. (2011) Function Spaces with the Matkowski Property and Degeneracy Phenomena for Composition Operators. Fixed Point Theory, 12, 265-284.
- 33. Appell, J., Jesús, Z. and Mejía, O. (2011) Some Remarks on Nonlinear Composition Operators in Spaces of Differentiable Functions. Bolletino Della Unione Matematica Italiana, 4, 321-336.
- 34. Babaev, A.A. (1961) On the Structure of a Certain Nonlinear Operator and Its Application. Uchenye Zapiski Azerbajdzh Gos. Univ., 4, 13-16.
- 35. Mukhtarov, K.S. (1967) On the Properties of the Operator in the Space . Sbornik Nauchm. Rabot Mat. Kaf. Dagestan Univ, 83, 145-150.
- 36. Josephy, M. (1981) Composing Functions of Bounded Variation. Proceedings of the American Mathematical Society, 83, 354-356.
http://dx.doi.org/10.1090/S0002-9939-1981-0624930-9 - 37. Appell, J., Guanda, N., Merentes, N. and Sanchez, J.L. (2011) Some Boundedness and Continuity Properties of Nonlinear Composition Operators: A Survey. Communications in Applied Analysis, 15, 153-182.
- 38. Jesús, Z., Mejia, O., Merentes, N. and Rivas, S. (2013) The Composition Operator and the Space of the Functions of Bounded Variation in Schramm-Korenblum’s Sense. Journal of Functional Spaces and Applications, 2013, 1-13.
http://dx.doi.org/10.1155/2013/284389 - 39. Matkowski, J. (1982) Functional Equation and Nemytskiǐ Operators. Fako de l’Funkcialaj Ekvacioj Japana Matematika Societo, 25, 127-132.
- 40. Matkowski, J. and Miǐ, J. (1984) On a Characterization of Lipschitzian Operators of Substitution in the Space . Mathematische Nachrichten, 117, 155-159.
http://dx.doi.org/10.1002/mana.3211170111 - 41. Kuczma, M. (1885) An Introduction to the Theory of Functional Equations and Inequalities. Polish Scientific Editors and Silesian University, Warszawa.
- 42. Matkowski, J. (2011) Uniformly Bounded Composition Operators between General Lipschitz Function Normed Spaces. Topological Methods in Nonlinear Analysis, 38, 395-405.