Received 2 September 2015; accepted 17 October 2015; published 20 October 2015

ABSTRACT

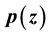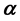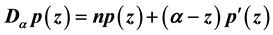Let be a polynomial of degree n and for a complex number, let denote the polar derivative of the polynomial 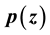with respect to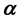. In this paper, first we extend as well as generalize the result proved by Dewan and Mir [Inter. Jour. Math. and Math. Sci., 16 (2005), 2641-2645] to polar derivative. Besides, another result due to Dewan et al. [J. Math. Anal. Appl. 269 (2002), 489-499] is also extended to polar derivative.

Keywords:

Polynomials, Polar Derivative of a Polynomial, Zeros, Extremal Polynomials

1. Introduction and Statements of the Results

Let 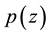be a polynomial of degree n and denote by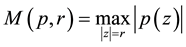. Then we have the following well-known Bernstein’s inequality 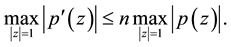[1] .

(1.1)

Equality holds in (1.1) if and only if 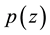has all its zeros at the origin.

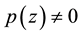Inequality (1.1) can be sharpened if we restrict ourselves to the class of polynomials having no zeros in. In fact, it was conjectured by Erdösand later verified by Lax [2] that if in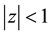, then

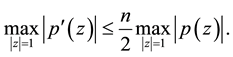(1.2)

Inequality (1.2) is the best possible and equality attains for,.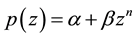

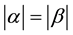Malik [3] extended (1.2) by considering the class of polynomials 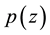of degree n not vanishing in, , and proved

. (1.3)

As a generalization of (1.3), Bidkham and Dewan [4] proved that if was a polynomial of degree n having no zero in, , then for,

(1.4)

Equality holds in (1.4) for.

Further, Dewan and Mir [5] obtained the following result which was a generalization as well as an improvement of (1.4).

Theorem A. If is a polynomial of degree n having no zero in, , then for,

(1.5)

Let be a polynomial of degree n and let denote the polar derivative with respect to a point, then

The polynomial is of degree at most and it generalizes the ordinary derivative in the sense that

Aziz [6] extended (1.3) to the polar derivative of by showing that if had no zero in, , the for every real or complex number with,

(1.6)

Inequality (1.6) is the best possible and equality holds for with a real number, and.

In this paper, we establish the following result, which deduces to a result giving, in turn, a generalization as well as an extension of Theorem A to polar derivative. In fact, we prove:

Theorem 1. If, is a polynomial of degree n having no zero in, , then for, and for every real or complex number with,

(1.7)

The result is the best possible and equality occurs for, with a real number.

Remark 1. For,we have

(1.8)

Also, for, inequality (1.8) holds trivially and hence inequality (1.8) is true for. Using this fact in the above theorem, we have:

Corollary 1. If, is a polynomial of degree n having no zero in, , then for, and for every real or complex number with,

(1.9)

It is seen that Corollary 1 is a generalization as well as an extension of a result due to Dewan and Mir [5] into polar derivative.

Dividing both sides of (1.9) by and making, we obtain the following, which is an extension of the theorem due to Dewan and Mir [5] .

Corollary 2. If is a polynomial of degree n having no zero in, , then for,

(1.10)

The result is the best possible and the extremal polynomial is,.

Remark 2. Both the inequalities (1.7) and (1.9) of Theorem 1 and Corollary 1, respectively reduce to inequality (1.6) for.

Further, it was shown by Turán [7] that if is a polynomial of degree n having all its zeros in, then

. (1.11)

The result is sharp and equality in (1.11) holds if all the zeros lie on.

As an extension of (1.11), Malik [3] showed that if has all its zeros in, , then

(1.12)

whereas, if has all its zeros in, , then Govil [8] proved that

(1.13)

Both the estimates (1.12) and (1.13) are sharp. Equality in (1.12) holds for, whereas equality in (1.13) holds for,.

Although the above result is sharp but still it is easy to see that it has two drawbacks. Firstly, the bound in (1.13) depends only on the zero of largest modulus and not on other zeros even if some of them are very close to the origin. Secondly, since the extremal polynomial in (1.13) is, it should be possible to obtain a better

bound for the polynomials, where not all the co-efficients are zero. It would, therefore, be interesting to obtain a bound which depends on the location of all the zeros of the polynomial and also on the co-efficients. In this connection, Dewan et al. [9] proved.

Theorem B. If, is a polynomial of degree such that, , and, then

(1.14)

and

(1.15)

The result is the best possible and equality in (1.14) and (1.15) holds for.

Aziz and Rather [10] obtained a result which not only extended (1.12) into polar derivative of, but also was a generalization by proving that if all the zeros of the polynomial of degree n lie in where, then for every real or complex number with,

. (1.16)

The result is sharp and equality holds for with.

While, the corresponding extension which was also a generalization of (1.13) for, was done by Rather [11] who proved that if all the zeros of the polynomial of degree n lie, , then for every real or complex number with,

(1.17)

Next, we further prove the following theorem in which inequality (1.18) not only extends inequality (1.14) into polar derivative but is also a generalization, while inequality (1.19) extends inequality (1.15) into polar derivative.

Theorem 2. If, is polynomial of degree, such that, , and if, then for every real or complex number with, and for,

(1.18)

and

(1.19)

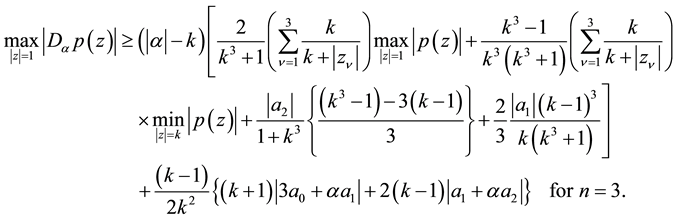
If we divide both sides of (1.18) and (1.19) by and make, we obtain inequalities (1.14) and (1.15) respectively.

Remark 3. For polynomials of degree, Theorem 2 gives a refinement of inequality (1.17) due to Rather [11] .

Since for, Theorem 2 gives, in particular:

Corollary 3. If, , is a polynomial of degree having all its zeros in, , then for every real or complex number with, for,

(1.20)

and

(1.21)

Remark 4. For and, and are both increasing functions of x and so the expressions

and

are always non-negative so that for polynomials of degree, inequalities (1.20) and (1.21) together provide a refinement of inequality (1.17). In fact, excepting the case when has all its zeros on, with, , and, the bound obtained in Theorem 2 is always sharper than the bound obtained from inequality (1.17).

2. Lemmas

We require the following lemmas for the proofs of the theorems.

Lemma 2.1. If is a polynomial of degree n having no zero in, , then

The above result is due to Govil et al. [12] .

Lemma 2.2. If is a polynomial of degree n having no zero in, , then for,

.

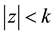
There is equality in (2.2) for.

Lemma 2.2 is due to Jain [13] .

Lemma 2.3. If is a polynomial of degree n having no zero in, , then the function

(2.2)

is a non-decreasing function of t in.

Proof of Lemma 2.3.We prove this by derivative test. Now, we have

,

which is non-negative since (see Remark 1 with m = 1) [14] and the fact that.

Lemma 2.4. If is a polynomial of degree n having no zero in, , then for,

(2.3)

Inequality (2.3) is the best possible for,.

Remark 5. Lemma 2.4 is of independent interest because by employing the simple fact that

of Remark 1, it gives a result which extends the theorem due to Dewan and Kaur [15] .

The proof of Lemma 2.4 follows on the same lines as that of Lemma 2.3 due to Dewan and Mir [5] , but for the sake of completeness we give a brief outline of its proof.

Proof of Lemma 2.4. Since has no zero in, , the polynomial where has no zero in, where. Hence applying Lemma 2.1 to the polynomial, we get

,

which implies

. (2.4)

Now, for and, we have

(using (2.4))

which implies on using (2.2) of Lemma 2.2,

which gives for,

(2.5)

For, by Lemma 2.3, we have

(2.6)

Using (2.6) to (2.5), we have

which completes the proof of Lemma 2.4.

Lemma 2.5. If is a polynomial of degree, then for,

(2.7)

and

(2.8)

Lemma 2.5 is due to Dewan et al. [9] .

Lemma 2.6. If is a polynomial of degree having all its zeros in, then for,

(2.9)

and

(2.10)

The result is sharp and equality in (2.9) and (2.10) holds for, where and.

This result is also due to Dewan et al. [9] .

3. Proof of the Theorems

Proof of Theorem 1. Since the polynomial has no zero in, , it follows that has no zero in, where. Applying inequality (1.6) to the polynomial and noting that, we have

or

,

which is equivalent to

. (3.1)

For and, inequality (3.1) when combined with Lemma 2.4, we get

,

hence the proof of Theorem 1 is completed.

Proof of Theorem 2. We first prove inequality (1.8). Since the zeros of are, , the zeros of the polynomial are, , and because the polynomial has all its zeros in, , the polynomial has all its zeros in. Hence for every real or complex number with, we have by inequality (1.16) with,

or

which is equivalent to

or

. (3.2)

Since the polynomial is of degree, and also by our assumption, the co-efficient of in the polar derivative viz., , it follows that is a polynomial of degree. Thus, applying (2.7) of Lemma 2.5 to with, we get

(3.3)

Combining (3.2) and (3.3), we get

(3.4)

Let be the reciprocal polynomial of. Since has all its zeros in, , , it follows that the polynomial has all its zeros in and is of degree. Applying inequality (2.9) of Lemma 2.6 to for, we get

which is equivalent to

which gives

(3.5)

Combining (3.4) and (3.5), we get

which on simplification yields

which proves inequality (1.18) completely.

The proof of inequality (1.19) follows on the same lines as that of (1.18), but instead of applying (2.7) of Lemma 2.5 and (2.9) of Lemma 2.6, inequalities (2.8) and (2.10) respectively of Lemmas 2.5 and 2.6 are used.

Cite this paper

BarchandChanam, (2015) Polar Derivative Versions of Polynomial Inequalities. Advances in Pure Mathematics,05,745-755. doi: 10.4236/apm.2015.512068

References