Received 29 August 2015; accepted 13 December 2015; published 16 December 2015

ABSTRACT

The main objective of this paper is to provide the tool rather than the classical adjoint representation of Lie algebra; which is essential in the conception of the Chevalley Eilenberg Cohomology. We introduce the notion of representation induced by a 2 - 3 matrix. We construct the corresponding Chevalley Eilenberg differential and we compute all its cohomological groups.

Keywords:

Lie Algebra, Cochain, 2 - 3 Matrix Chevalley Eilenberg, Cohomology

1. Introduction

This work is included in the domain of differential geometry which is the continuation of infinitesimal calculation. It is possible to study it due to the new techniques of differential calculus and the new family of topological spaces applicable as manifold. The study of Lie algebra with classical example puts in place with so many homological materials [1] -[3] (Lie Bracket, Chevalley Eilenberg Cohomology...). The principal objective of this work is to introduce the notions of deformation of Lie algebra in the more general representation rather than the adjoint representation.

This work is base on 2 - 3 matrix Chevally Eilenberg Chohomology representation, in which our objective is to fixed a matrix representation and comes out with a representation which is different from the adjoint repre- sentation. Further, given a Lie algebra V, W respectively of dimension 2 and 3, we construct a linear map that will define a Lie algebra structure from a Lie algebra V into 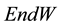by putting the commutator structure in place.

This does lead us to a fundamental condition of our 2 - 3 matrix Chevalley Eilenberg Cohomology. We com- pute explicitly all the associated cohomological groups.

2. 2 - 3 Matrix Representation Theorem

We begin by choosing V to be a 2-dimensional vector space and W a 3-dimensional vector space, then we called our cohomology on a domain vector space V and codomain W a 2 - 3 matrix Chevalley Eilenberg Cohomology. In what follow, we denoted for all 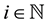by the space of i-multilinear skew symmetric map on V

with valor in W; we also denoted by 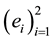and 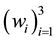respectively the basis of V and W. We also suppose

that 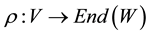is a representation of the Lie algebra 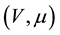where is the associated Lie structure.

2.1. Description of Cochain Spaces

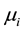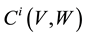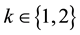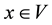Since element of of skew symmetric, then for all, we have [4] . Let and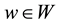, we have and, where.

implies that. iff is a linear map.

Then,

Lemma 1: If the and, then.

Proof. Since then,

.

Thus, we define an isomorphic map from to as follows;

. □

iff is bilinear and antisymmetric map; then

Lemma 2: If and then

Proof. From the expression of an element in from above, can be represented as a

column matrix of the lie constant structures. □

iff is a tri-linear and skew symmetric map,

then

since is a linear anti-symmetric mapping.

Lemma 3: If and then.

Proof. Since for every, we have that from the expression of above. □

2.2. Diagram of a Sequence of Linear Maps

According to the above results, we have the following diagram where we shall identify and define and in order to contruct our 2 - 3 Matrix Chevalley-Eilenberg Cohomology.

Expression of [1] [4] :

Expression of [1] [4] :

Expression of [1] [4] :

since is mapped to the zero space. A direct computation, give us [1]

Definition of:

i.e is the identity mappings from W to W.

Definition of:

which is the matrix of, , and.

Definition of:

which is the matrix of, ,.

2.3. Homological Differential

In this section, we are going to determine expressions of and also prove that for us to obtain our 2 - 3 matrix Chevalley-Eilenberg differential complex. This is possible unless by stating an important hypothesis which we call 2 - 3 matrix Chevalley-Eilenberg hypothesis.

Proposition 1: If for all x, y in V, then.

Proof. We assume that for all x, y in V.

By definition, we have that

(1)

. (2)

Then by substituting equation (1) into (2),we have

by hypothesis.

Expression of:

Let V be a two dimensional Lie-algebra with basis and the Lie’s bracket where

and W a three dimensional vector space with basis. We define

by

, where and is a linear mapping associated to the matrix.

Let defined by

Therefore;

Since

Therefore,

Also, we have

,

where

, where

So,

Therefore,

Now, we compute where and are basis vectors of V.

By replacing the constants and, we obtain which is given as;

Thus,

.

Hence, is defined by

with

, .

Corollary 1: If

then is defined by

.

2.4. Fundametal Condition of 2 - 3 Matrix Chevalley-Eilenberg Cohomology

We now state the main hypothesis for our 2 - 3 matrix Chevalley-Eilenberg Cohomology, which we suppose that

i.e

i.e,

and

.

This is an important tool in the construction of our 2 - 3 matrix cohomology differential complex.

2.5. Expression of

From the diagram,

where

and. Thus, using the basis vectors and in V, we have

Hence, the mapping is defined as;

Corollary 2: If

then the mapping is defined as;

The matrix has been assigned to the matrix to simplify the composition of and.

Proposition 2:.

Proof. Since and We have:

Which gives us our 2 - 3 matrix Chevalley Eilenberg homological hypothesis

. □

Remark 1: By straightforward computation, we have

2.6. Determination of the and

.

iff

iff

(3)

(4)

(5)

Now, we compute the using the standard basis

If then

If then

If then

If then

If then

If then

Thus, we have the image matrix as follows:

Next, we calculate the rank of the matrix which will help us to know the and by using the dimension rank theorem of the vector spaces [5] [6] .

We now reduce the matrix to reduce row echelon form. We then replace the entries of the matrix by the follows constants:

where Let and by dividing each of the

entries of row 1 by and carrying out the following row operation and, we obtain

Let be such that and by carrying the following row operations, and, and setting thus we obtain the following matrix.

Let be such that, and by carry the following row operations

, and. By setting

and. Also, if we let

,

we obtain the following matrix.

.

Hence we obtain the reduce row echelon form of of rank 3 [5] [6] .

We wish to consider now the cases of the matrix of rank 1 and rank 2 since the case of rank Zero is trivial.

Rank 1: By setting each of the entries on row 2 and 3 of matrix A to zero, we obtain the rank of to be 1.

Rank 2: By setting each of the entries on row 3 of matrix B to zero, we obtain the rank of to be 2.

Proposition 3: if

,

,

then and the. Further

and.

Proposition 4: From matrix A, if,

then

and. Further, and.

Proof. Since the, we have that， thus. We now show that

. By the dimension rank theorem, we have that which is

. □

Proposition 5: From matrix B, if,

then

and. Further, and.

Proof. Since the, we have that, thus. We now show that.

By the dimension rank theorem, we have that that is

Proposition 6: if

, ,

then

and the. Further, and.

Proof. Since the, we have that, thus. We now show that

. By the dimension rank theorem, we have that that is

□

Now, we compute our quotient spaces of the 2 - 3 matrix Chevalley Eilenberg cohomology which are

, and.

For, we have the following quotient space:

Case 1: and

.

For, we have the following quotient spaces:

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 4: and

.

Case 5: and

.

Case 6: and

.

Case 7: and

.

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 4: and

.

Case 5: and

.

Case 6: and

.

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 4: and

.

Case 5: and

.

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 4: and

.

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 1: and

.

Case 2: and

.

For, we have the following quotient spaces:

Case 1: and

.

Case 2: and

.

Case 3: and

.

Case 4: and

.

We suggest that further research in this direction is to carry out the deformation on the Cohomological spaces, and which are 32 in number and apply a specific example with. We will also carry out an extensive study on the solution of our system of linear equations on the 2 - 3 matrix Chavelley Eilenberg fundamental condition.

Acknowledgements

We thank the Editor and the referee for their comments.

Cite this paper

JosephDongho,EpizitoneDuebe-Abi,Shuntah RolandYotcha, (2015) On 2 - 3 Matrix Chevalley Eilenberg Cohomology. Advances in Pure Mathematics,05,835-849. doi: 10.4236/apm.2015.514078

References

NOTES

^*Corresponding author.