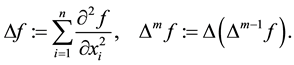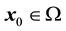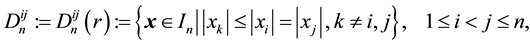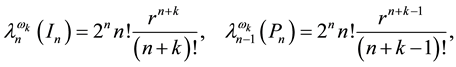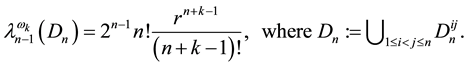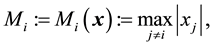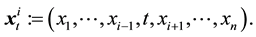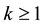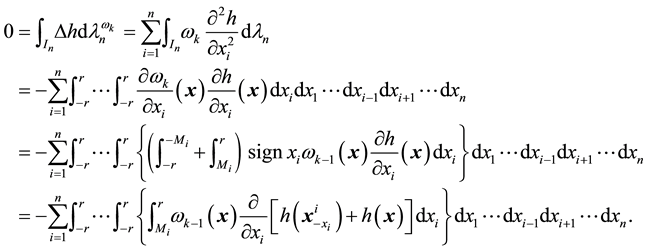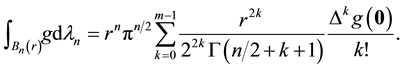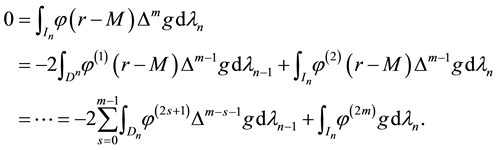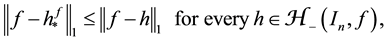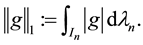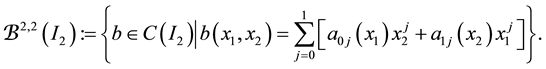Advances in Pure Mathematics
Vol.05 No.11(2015), Article ID:59617,5 pages
10.4236/apm.2015.511062
Mean-Value Theorems for Harmonic Functions on the Cube in

Petar Petrov
Faculty of Mathematics and Informatics, Sofia University, Sofia, Bulgaria
Email: peynov@fmi.uni-sofia.bg
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 4 August 2015; accepted 13 September 2015; published 16 September 2015

ABSTRACT
Let
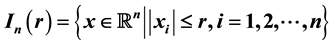 be a hypercube in
be a hypercube in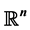 . We prove theorems concerning mean-values of harmonic and polyharmonic functions on
. We prove theorems concerning mean-values of harmonic and polyharmonic functions on , which can be considered as natural analogues of the famous Gauss surface and volume mean-value formulas for harmonic functions on the ball in
, which can be considered as natural analogues of the famous Gauss surface and volume mean-value formulas for harmonic functions on the ball in
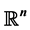 and their extensions for polyharmonic functions. We also discuss an application of these formulas―the problem of best canonical one-sided L1-approximation by harmonic functions on
and their extensions for polyharmonic functions. We also discuss an application of these formulas―the problem of best canonical one-sided L1-approximation by harmonic functions on .
.
Keywords:
Harmonic Functions, Polyharmonic Functions, Hypercube, Quadrature Domain, Best One-Sided Approximation

1. Introduction
This note is devoted to formulas for calculation of integrals over the n-dimensional hypercube centered at
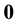
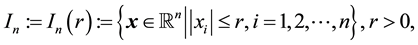
and its boundary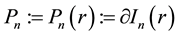 , based on integration over hyperplanar subsets of
, based on integration over hyperplanar subsets of
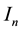 and exact for harmonic or polyharmonic functions. They are presented in Section 2 and can be considered as natural analogues on
and exact for harmonic or polyharmonic functions. They are presented in Section 2 and can be considered as natural analogues on
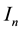 of Gauss surface and volume mean-value formulas for harmonic functions ([1] ) and Pizzetti formula [2] , ( [3] , Part IV, Ch. 3, pp. 287-288) for polyharmonic functions on the ball in Rn. Section 3 deals with the best one-sided L1-approximation by harmonic functions.
of Gauss surface and volume mean-value formulas for harmonic functions ([1] ) and Pizzetti formula [2] , ( [3] , Part IV, Ch. 3, pp. 287-288) for polyharmonic functions on the ball in Rn. Section 3 deals with the best one-sided L1-approximation by harmonic functions.
Let us remind that a real-valued function f is said to be harmonic ( polyharmonic of degree ) in a given domain
) in a given domain
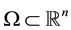 if
if
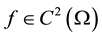
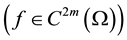 and
and
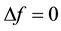
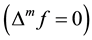
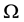
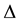
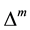
For any set
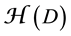
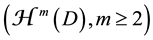
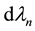
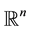
2. Mean-Value Theorems
Let

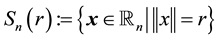
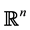
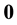
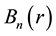
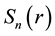


The surface mean-value theorem. If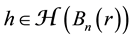
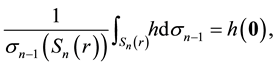
where
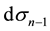

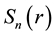
The volume mean-value theorem. If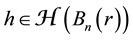
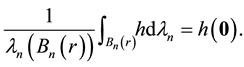
The balls are known to be the only sets in

such that
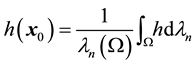
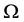
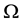
open ball centered at
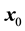
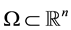
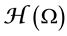

and there is a Borel measure

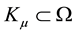
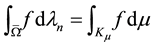

integrable harmonic function f on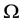
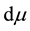
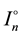
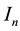
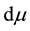
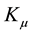
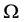
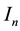
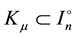
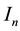
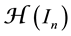
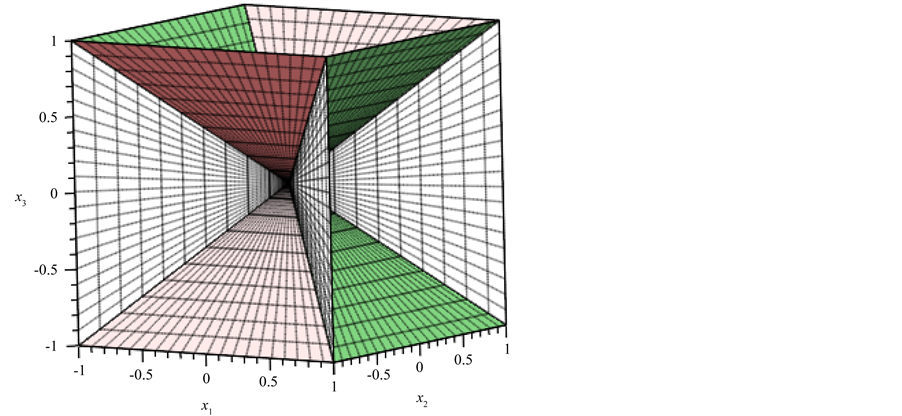
Let us denote by
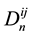

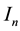
(see Figure 1). Denote also
and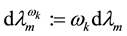
Figure 1. The sets
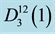
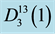
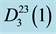
and
The following holds true.
Theorem 1 If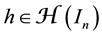
(i) Surface mean-value formula for the hypercube
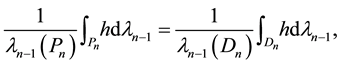
(ii) Volume mean-value formula for the hypercube
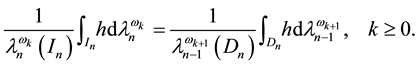
In particular, both surface and volume mean values of h are attained on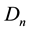
Proof. Set
and
Using the harmonicity of h, we get for
Hence, we have
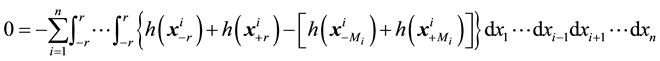
if
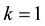
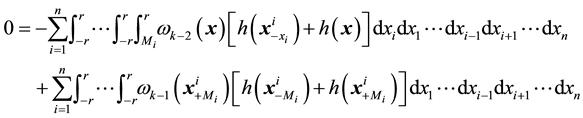
if
Clearly, (5) is equivalent to (3) and from (6) it follows
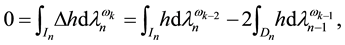
which is equivalent to (4). □
Let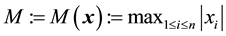
Corollary 1 If
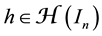
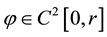
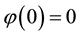
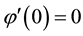
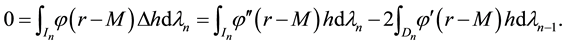
The volume mean-value formula (2) was extended by P. Pizzetti to the following [2] [3] [8] .
The Pizzetti formula. If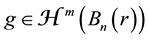
Here, we present a similar formula for polyharmonic functions on the hypercube based on integration over the set
Theorem 2 If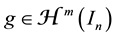
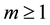

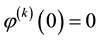
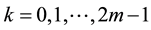
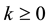
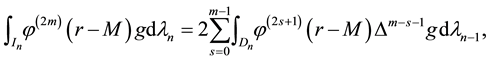
where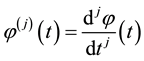
Proof. Equation (9) is a direct consequence from (8):
3. A Relation to Best One-Sided L1-Approximation by Harmonic Functions
Theorem 1 suggests that for a certain positive cone in

For a given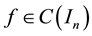
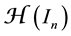
A harmonic function
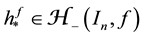
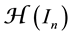
where
Theorem 1 (ii) readily implies the following ([6] [9] ).
Theorem 3 Let
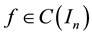
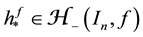
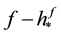
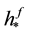
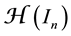
Corollary 2 If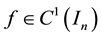
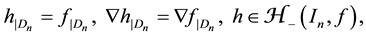
is a best one-sided L1-approximant from below to f with respect to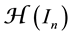
Corollary 3 If
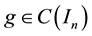


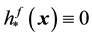
a best one-sided L1-approximant from below to f with respect to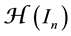
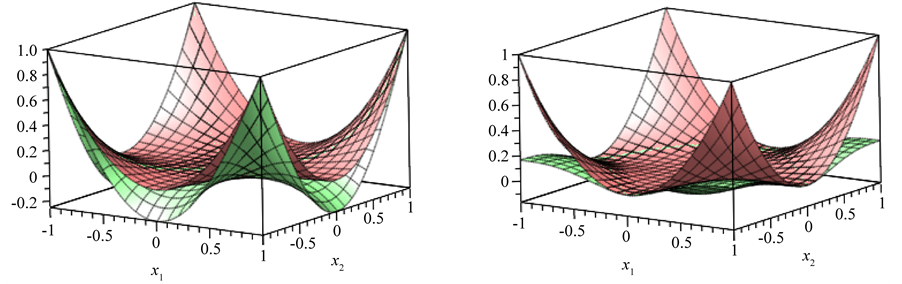
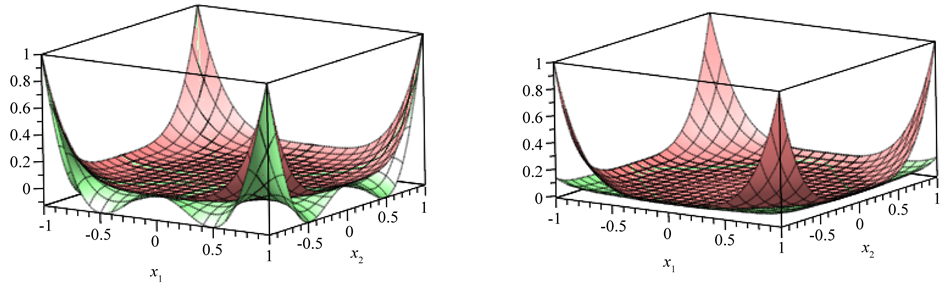
Example 1 Let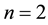
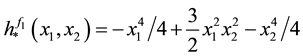
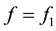
appro-ximant from below to f1 with respect to
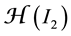
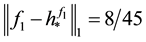
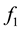
to the positive cone of the partial differential operator
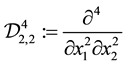

the best harmonic one-sided L1-approximation to f1 with the corresponding approximation from the linear sub- space of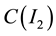
The possibility for explicit constructions of best one-sided L1-approximants from
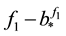
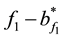
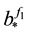
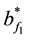
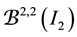
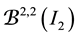
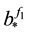
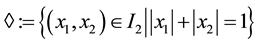

Example 2 Let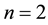
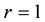
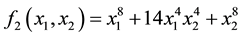

below to
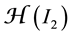
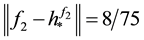
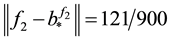
Figure 2. The graphs of the function
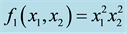
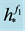
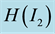
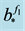
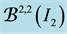
Figure 3. The graphs of the function
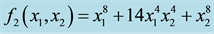
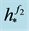
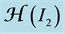
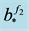
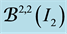
Remark 1 Let

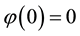
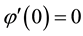
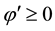
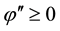
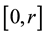
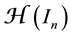

Cite this paper
PetarPetrov, (2015) Mean-Value Theorems for Harmonic Functions on the Cube in Rn. Advances in Pure Mathematics,05,683-688. doi: 10.4236/apm.2015.511062
References
- 1. Helms, L.-L. (2009) Potential Theory. Springer-Verlag, London.
http://dx.doi.org/10.1007/978-1-84882-319-8 - 2. Pizzetti, P. (1909) Sulla media dei valori che una funzione dei punti dello spazio assume sulla superficie della sfera. Rendiconti Linzei—Matematica e Applicazioni, 18, 182-185.
- 3. Courant, R. and Hilbert, D. (1989) Methods of Mathematical Physics Vol. II. Partial Differential Equations Reprint of the 1962 Original. John Wiley & Sons Inc., New York.
- 4. Goldstein, M., Haussmann, W. and Rogge, L. (1988) On the Mean Value Property of Harmonic Functions and Best Harmonic L1-Approximation. Transactions of the American Mathematical Society, 305, 505-515.
- 5. Sakai, M. (1982) Quadrature Domains. Lecture Notes in Mathematics, Springer, Berlin.
- 6. Gustafsson, B., Sakai, M. and Shapiro, H.S. (1977) On Domains in Which Harmonic Functions Satisfy Generalized Mean Value Properties. Potential Analysis, 71, 467-484.
- 7. Gustafsson, B. (1998) On Mother Bodies of Convex Polyhedra. SIAM Journal on Mathematical Analysis, 29, 1106-1117.
http://dx.doi.org/10.1137/S0036141097317918 - 8. Bojanov, B. (2001) An Extension of the Pizzetti Formula for Polyharmonic Functions. Acta Mathematica Hungarica, 91, 99-113.
http://dx.doi.org/10.1023/A:1010687011674 - 9. Armitage, D.H. and Gardiner, S.J. (1999) Best One-Sided L1-Approximation by Harmonic and Subharmonic Functions. In: Haußmann, W., Jetter, K. and Reimer, M., Eds., Advances in Multivariate Approximation, Mathematical Research (Volume 107), Wiley-VCH, Berlin, 43-56.
- 10. Dryanov, D. and Petrov, P. (2002) Best One-Sided L1-Approximation by Blending Functions of Order (2,2). Journal of Approximation Theory, 115, 72-99.
http://dx.doi.org/10.1006/jath.2001.3652