Received 11 May 2015; accepted 13 June 2015; published 16 June 2015

ABSTRACT

Let M be a n-dimensional compact irreducible complex space with a line bundle L. It is shown that if M is completely intersected with respect to L and dimH⁰(M, L) = n + 1, then M is biholomorphic to a complex projective space Pⁿ of dimension n.

Keywords:

Complex Space, Projective Space, Line Bundle, Complete Intersected

1. Introduction

Kobayashi and Ochiai [1] have given Characterizations of the complex projective spaces. Kobayashi-Ochiai Theorem [1] has been applied to obtain many important characterizations of the projective spaces, such as the proof of Frankel conjectures [2] , the proof of Hartshorne conjecture [3] , and many others [4] -[7] . In this note, we want to give a characterization of the complex projective spaces via sections of line bundles.

Results which can be found in [1] [8] and [9] are used freely often without explicit references. Let M be a complex space with a line bundle L. 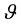is the sheaf of germs of sheaf of holomorphic functions, 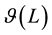is the sheaf of germs of holomorphic sections of a line bundle L. 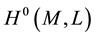means.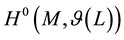

2. Characterization of the Projective Spaces

In this paper, a characterization of the projective space will be given.

Definition. Let M be a compact complex space with a line bundle L. M is said to be completely intersected with respect to a line bundle L, provided that complex subspace 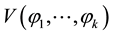is irreducible for any linearly independent elements 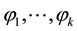of of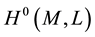, where each 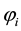is irreducible, and 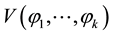is the common zeros of.

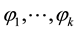From the Lemma 1.1 [1] and the proof of theorem 16.2.1 [8] , we have

Lemma 1. Let V be a compact irreducible complex space. Let F and L be line bundles over V. Let 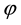be an irreducible section of L and put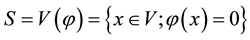. The following sequence of sheaf homomorphisms is exact:

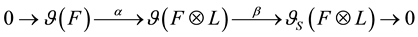
where 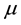is the multiplication by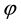, 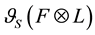is the sheaf defined by and is the restriction map.

Lemma 2. Let M be a n-dimensional compact complex space with a line bundle L. Let be linear independent elements of, such that each is irreducible. If M is completely intersected with respect to L, then there is an exact sequence:

where is the subspace of spanned by the sections and is the restriction map.

Proof. The proof is by induction on k. The case k = 0 is trivial. Since M is completely intersected with respect to L, and are irreducible. Assume the lemma for, we have the exact sequence:

If, then from which it follows that are linearly dependent, a contradiction. Thus, is nontrivial on; it follows that defined as the set of zeros of = on is an irreducible divisor.

We apply Lemma l to, ,. Then,. The exact sequence in Lemma 1 induces the following exact sequence

This means that the kernel of the restriction map is spanned by the restriction of to. Combining this with the lemma for, we obtain the lemma for k.

Now we give the main result of this paper.

Theorem. Let M be a n-dimensional compact irreducible complex space with a line bundle L. If and M is completely intersected with respect to L, then M is biholomorphic to a complex space of dimension n.

Proof. Since, we can choose linearly independent sections from with each irreducible. Put.

Claim 1. Each is an irreducible divisor of M.

First of all, is nonempty. Indeed, if for some i, then for all. Define map by. It is clear that h is isomorphic, that is, L is a trivial line bundle over M. It follows that, which is contradictory to the hypothesis that. Thus, each. Since is irreducible, is irreducible and by [Corollary 14, Ch II, 3] and [Theorem 11, Ch III, 3]. Hence, is an irreducible divisor.

Let be the common zeros of, then. By the hypothesis, M is completely intersected with respect to L; each is irreducible.

Claim 2..

For, is an irreducible divisor by Claim 1, thus. Assume that . If, then by Lemma 2. This induces that are linearly dependent, a contradiction. Thus, is nontrivial on the irreducible complex subspace. It follows by [Theorem 14, Ch. III, 3] that.

Claim 3. is base point free.

By Claim 2, is an irreducible complex subspace of dimension. In particular, is one point. If vanishes at, then are linearly dependent by Lemma 2. Since are defined as linearly independent sections in the beginning of this proof, it is a contradiction. Thus, does not vanish at. This shows that have no common zeros, that is, is base point free.

Since, we may let be the complex projective space of dimension n defined as the set of hyperplanes through the origin in. For any point, put

. Since is base point free, is a hyperplane through the origin in and so. We now obtain a holomorphic mapping.

Claim 4. The mapping is bijective.

Giving a point y of, it is a hyperplane through the origin in. Let be a basis for this hyperplane with each irreducible. Then, y is the complex subspace spanned by, that is,. Let be the set of zeros of for. Since M is completely intersected with respect to L, is irreducible and by Claim 2, that is, is a point. It follows that there exists a point x of M, such that.

Thus,. By Lemma 2, we have the exact sequence

.

For any, we have. Since and the above sequence is exact, it follows that and so. Thus, is surjective.

On the other hand, let u and v be any two points of M. is a hyperplane through the origin in. Let be a basis for with each irreducible. By Claim 2, is a single point and this induces that. If, then. It follows that, that is,. Thus is injective.

Consequently, we have shown that M is biholomorphic to a complex projective space of dimension n.

As an application of the theorem above, we give a proof for the famous Kobayashi-Ochiai Theorem [1] .

Corollary ([Theorem 1.1 [1] ). Let M be a n-dimensional complex irreducible complex space with an ample line bundle F. If and, then M is biholomorphic to a complex projective space of dimension n.

Proof. By the theorem in this paper, it suffices to show that M is completely intersected with respect to F. Let be linearly independent elements of with each irreducible. Let be the common zeros of on M.

Assume that is reducible, then write for some nontrivial and. Because are linearly independent elements of with each irreducible, there are no common zeros of on. And due to the definition of, we have

By the hypothesis, , and so

.

Since F is ample, and are positive integers. Thus, , a contradiction. It follows that is irreducible. By the theorem above, M is biholomorphic to.

References

NOTES

^*Corresponding author.