Advances in Pure Mathematics
Vol.05 No.05(2015), Article ID:55718,10 pages
10.4236/apm.2015.55027
Bell’s Ternary Quadratic Forms and Tunnel’s Congruent Number Criterion Revisited
Werner Hürlimann
Swiss Mathematical Society, Fribourg, Switzerland
Email: whurlimann@bluewin.ch
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 March 2015; accepted 9 April 2015; published 16 April 2015
ABSTRACT
Bell’s theorem determines the number of representations of a positive integer in terms of the ternary quadratic forms 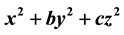 with
with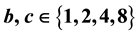 . This number depends only on the number of representations of an integer as a sum of three squares. We present a modern elementary proof of Bell’s theorem that is based on three standard Ramanujan theta function identities and a set of five so-called three-square identities by Hurwitz. We use Bell’s theorem and a slight extension of it to find explicit and finite computable expressions for Tunnel’s congruent number criterion. It is known that this criterion settles the congruent number problem under the weak Birch-Swin- nerton-Dyer conjecture. Moreover, we present for the first time an unconditional proof that a square-free number
. This number depends only on the number of representations of an integer as a sum of three squares. We present a modern elementary proof of Bell’s theorem that is based on three standard Ramanujan theta function identities and a set of five so-called three-square identities by Hurwitz. We use Bell’s theorem and a slight extension of it to find explicit and finite computable expressions for Tunnel’s congruent number criterion. It is known that this criterion settles the congruent number problem under the weak Birch-Swin- nerton-Dyer conjecture. Moreover, we present for the first time an unconditional proof that a square-free number 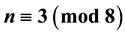 is not congruent.
is not congruent.
Keywords:
Sum of Squares, Ternary Quadratic Form, Theta Function, Hurwitz Three-Squares Formula, Congruent Number, Weak Birch-Swinnerton-Dyer Conjecture

1. Introduction
A seminal breakthrough in the theory of numbers is the determination by Gauss [1] of the number of representations 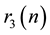 of an integer n as a sum of three squares
of an integer n as a sum of three squares 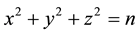 counting zeros, permutations and sign changes (e.g. Dickson [2] , Preface, pp. ix, x). A very explicit modern expression for this counting function is given in Cooper and Hirschhorn [3] , Lemma 4, Equation (3.1), and Theorem 3, Equation (1.27), (1.28). Note that the latter result has only been obtained quite recently by Hirschhorn and Sellers [4] .
counting zeros, permutations and sign changes (e.g. Dickson [2] , Preface, pp. ix, x). A very explicit modern expression for this counting function is given in Cooper and Hirschhorn [3] , Lemma 4, Equation (3.1), and Theorem 3, Equation (1.27), (1.28). Note that the latter result has only been obtained quite recently by Hirschhorn and Sellers [4] .
More generally, given a ternary (diagonal) quadratic form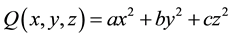 , one is interested in the total number
, one is interested in the total number 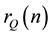 of integer solutions of the Diophantine equation
of integer solutions of the Diophantine equation . This number is also
. This number is also
denoted by . By the time of Dickson’s monumental “History of the Theory of Numbers”, only few
. By the time of Dickson’s monumental “History of the Theory of Numbers”, only few
specific results are known for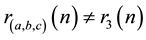 . Bell [5] mentions an unproven result by Liouville and incomplete results by Torelli and Stieltjes (see Dickson [2] , pp. 294, 295, and Dickson [6] , pp. 133, 216).
. Bell [5] mentions an unproven result by Liouville and incomplete results by Torelli and Stieltjes (see Dickson [2] , pp. 294, 295, and Dickson [6] , pp. 133, 216).
Using 13 identities about theta functions, including some important ones by Kronecker and Hermite, Bell [5] determines 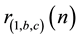 for the 10 possible ternary quadratic forms with
for the 10 possible ternary quadratic forms with ,
,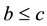 . For these forms, the corresponding counting functions depend only upon
. For these forms, the corresponding counting functions depend only upon . Bell’s theorem is relevant for an important con- temporary problem, namely the theorem of Tunnel [7] , which states, conditionally on the weak Birch-Swinnterton- Dyer (BSD) conjecture for elliptic curves, a necessary and sufficient condition for a number to be congruent.
. Bell’s theorem is relevant for an important con- temporary problem, namely the theorem of Tunnel [7] , which states, conditionally on the weak Birch-Swinnterton- Dyer (BSD) conjecture for elliptic curves, a necessary and sufficient condition for a number to be congruent.
The ancient but still unsolved congruent number problem has already been studied by Diophantus, the Arab scholars of the tenth century and Leonardo of Pisa (Fibonacci) (e.g. Dickson [2] , Chap. XVI, Mordell [8] , p. 71). A positive rational number is a congruent number if it is the area of some right triangle with rational sides. As shown by Koblitz [9] , Section 1.1, one can restrict the analysis to square-free natural numbers, which will be assumed throughout. It is also known that n is a congruent number if, and only if, the elliptic curve  has a non-trivial rational point (for a precise constructive characterization see Hürlimann [10] , criterion (E3)). Up to the weak Birch-Swinnerton-Dyer (BSD) conjecture for the elliptic curve
has a non-trivial rational point (for a precise constructive characterization see Hürlimann [10] , criterion (E3)). Up to the weak Birch-Swinnerton-Dyer (BSD) conjecture for the elliptic curve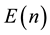 , an elegant characterization of congruent numbers has been obtained by Tunnel [7] (see Koblitz [9] , Theorem, p. 221, or Cohen [11] , Theorem 6.12.4). Nowadays, it is even possible to compute large tables of congruent numbers conditionally on the validity of the weak BSD conjecture (e.g. Cohen [11] , Remark, p. 568) without using Tunnel’s theorem. Nevertheless, this exercise requires advanced mathematics and, for this reason, Tunnel’s theorem remains attractive from the viewpoint of elementary number theory. According to this result, if
, an elegant characterization of congruent numbers has been obtained by Tunnel [7] (see Koblitz [9] , Theorem, p. 221, or Cohen [11] , Theorem 6.12.4). Nowadays, it is even possible to compute large tables of congruent numbers conditionally on the validity of the weak BSD conjecture (e.g. Cohen [11] , Remark, p. 568) without using Tunnel’s theorem. Nevertheless, this exercise requires advanced mathematics and, for this reason, Tunnel’s theorem remains attractive from the viewpoint of elementary number theory. According to this result, if 

Moreover, if a weak form of the BSD conjecture holds (i.e. if the L-function of 




A brief description of the content follows. In Section 2, a modern elementary proof of Bell’s theorem is given. It uses only three standard theta function identities and a set of five three-square identities by Hurwitz [12] that have been revisited in Cooper and Hirschhorn [13] . Henceforth, the proof is more direct and less complex than the original derivation by Bell [5] . In Section 3, explicit expressions for the counting functions involved in (1.1) are determined and applied to the congruent number problem. In particular, an unconditional proof that 
2. Ramanujan’s Theta Functions and Bell’s Theorem
We give a new elementary proof of Bell’s theorem. It uses Ramanujan’s theta functions

the three basic identities



and the following three squares identities of Hurwitz [12] (see Cooper and Hirschhorn [13] , Theorem 1, identities (1.3)-(1.4), (1.6)-(1.8))





Note that (2.2)-(2.4) follow from Berndt [14] , Entry 25, p. 40. Equation (2.2) is entry 25(iv), Equation (2.3) is obtained by adding 25(i) and 25(ii), and Equation (2.4) is obtained by adding 25(v) and 25(vi).
Theorem 2.1. (Theorem of Bell). The nine counting functions



Form (1,1,2)

Form (1,1,4)

Form (1,1,8)

Form (1,2,2)

Form (1,2,4)

Form (1,2,8)

Form (1,4,4)

Form (1,4,8)

Form (1,8,8)

Proof. Recall that the generating function of 


plicity the abbreviation 

Form (1,1,2). With 

Form (1,1,4). One has
and (2.11) is shown through the uniquely defined identifications
Form (1,1,8). A calculation shows that
which implies (2.12) through the identifications
Form (1,2,2). Similarly to the above one obtains
from which one gets (2.13) as follows:
Form (1,2,4). With successive calculation one obtains
and (2.14) follows from the identifications
Form (1,2,8). In the same manner, one gets
which implies (2.15) as follows:
Form (1,4,4). One has
Form (1,4,8). Through calculation one gets
and (2.17) follows from
Form (1,8,8). A successive calculation shows that
from which one gets (2.18) through identification of
The proof of Theorem 2.1 is complete. ◊
3. Tunnel’s Congruent Number Criterion
As seen in Section 1, Tunnel’s theorem depends upon the determination of the counting functions in Equation (1.1). While 



3.1. Even Square-Free Congruent Numbers
The following auxiliary result in the style of Bell is required.
Lemma 3.1. Let




respectively


Proof. We proceed similarly to the proof of Theorem 2.1. One has
from which one obtains (3.1) through the uniquely defined identifications

We are ready for the following result.
Theorem 3.1. (Even square-free congruent numbers) Suppose the weak BSD conjecture holds and let n = 2m be a square-free number. Two cases can occur.
Case 1: If

Case 2:
The number 


Proof. Case 1 is easy. If m = 4j + 3 then by (2.17) and (3.1) one has 


where 


Using that 


Remark 3.1. The first formula in (3.2) implies some identities between squares (respectively triangles) and certain partial sums of Jacobi symbols. Indeed, alternatively to the above one has with Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28), the formulas
3.2. Odd Square-Free Congruent Numbers
Again, one needs an auxiliary result.
Lemma 3.2. Let







Proof. As in the proof of Theorem 2.1 one has
The first product with 


Since there is no contribution to the counting function for odd numbers congruent to 5 and 7 mod 8, the Lemma is shown. ◊
Theorem 3.2. (Odd square-free congruent numbers). Suppose the weak BSD conjecture holds and let m be an odd square-free number. Three cases can occur.
Case 1: If
Case 2: If
Case 3:
The number 


Proof. We begin with Case 2. If 



which implies the first formula in (3.4). According to Lemma 3.2 one can write








which yields the first sum in the second formula of (3.4). Similarly, one has

Making use of the fact that 

On the other hand from Lemma 3.2 one knows that

Clearly, the theta function product 



where


one-to-one correspondence between solutions of 







are non-negative integers that satisfy the equations

hence


which is strictly positive by the Gauss-Legendre theorem on the sum of three squares. Case 1 follows and the proof is complete. ◊
Remark 3.2. Similarly to Remark 3.1, the first formula in (3.4) implies the following identity (see Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28))

4. Notes on Congruent Numbers
To conclude the present work, some comments on the obtained results might be of interest for future research in this area. In the era before Tunnel [7] , some important results were already known. For example, Genocchi proved in 1855 and 1874 that a prime 












References
- Gauss, C.F. (1801) Disquitiones Arithmeticae. Fleischer, Leipzig.
- Dickson, L.E. (1920) History of the Theory of Numbers, Vol. II. Carnegie Institute of Washington, Washington.
- Cooper, S. and Hirschhorn, M.D. (2007) On the Number of Primitive Representations of Integers as Sums of Squares. Ramanujan Journal, 13, 7-25. http://dx.doi.org/10.1007/s11139-006-0240-6
- Hirschhorn, M.D. and Sellers, J.A. (1999) On Representations of a Number as a Sum of Three Squares. Discrete Mathematics, 199, 85-101. http://dx.doi.org/10.1016/S0012-365X(98)00288-X
- Bell, E.T. (1924) The Numbers of Representations of Integers in Certain Forms ax2 + by2 + cz2. American Mathematical Monthly, 31, 126-131. http://dx.doi.org/10.2307/2299890
- Dickson, L.E. (1923) History of the Theory of Numbers, Vol. III. Carnegie Institute of Washington, Washington.
- Tunnel, J. (1983) A Classical Diophantine Problem and Modular Forms of Weight 3/2. Inventiones Mathematicae, 72, 323-334. http://dx.doi.org/10.1007/BF01389327
- Mordell, L.J. (1969) Diophantine Equations. Pure and Applied Mathematics, Vol. 30, London and New York.
- Koblitz, N. (1984) Introduction to Elliptic Curves and Modular Forms. Springer, New York. http://dx.doi.org/10.1007/978-1-4684-0255-1
- Hürlimann, W. (2011) A Congruent Twin Number Problem. Pioneer Journal of Algebra, Number Theory and Its Applications, 1, 53-66.
- Cohen, H. (2007) Number Theory, Volume I: Tools and Diophantine Equations (Graduate Texts in Mathematics). Springer Science + Business Media, LLC, New York.
- Hurwitz, A. (1886) Ueber die Anzahl der Classen Quadratischer Formen von Negativer Diskriminante. Journal für Diereine und Angewandte Mathematik, 99, 165-168.
- Cooper, S. and Hirschhorn, M.D. (2004) Results of Hurwitz Type for Three Squares. Discrete Mathematics, 274, 9-24. http://dx.doi.org/10.1016/S0012-365X(03)00079-7
- Berndt, B.C. (1991) Ramanujan’s Notebooks, Part III. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0965-2
- Bateman, P.T. and Knopp, M.I. (1998) Some New Old-Fashioned Modular Identities. The Ramanujan Journal, 2, 247- 269. http://dx.doi.org/10.1023/A:1009782529605
- Barrucand, P., Cooper, S. and Hirschhorn, M.D. (1998) Relations between Squares and Triangles. Discrete Mathematics, 248, 245-247. http://dx.doi.org/10.1016/S0012-365X(01)00344-2
- Cooper, S. and Hirschhorn, M.D. (2004) A Combinatorial Proof of a Result from Number Theory. Integers, 4, Paper A09.
- Nagell, T. (1929) L’analyse indéterminée de degré supérieur. Gauthier-Villars, Paris.
- Bastien, L. (1915) Nombres Congruents. L’Intermédiaire des Mathématiciens, 22, 231-232.
- Heegner, K. (1952) Diophantische Analysis und Modulfunktionen. Mathematische Zeitschrift, 56, 227-253. http://dx.doi.org/10.1007/BF01174749
- Birch, B.J. (1968) Diophantine Analysis and Modular Functions. Oxford University Press, Oxford, 35-42.
- Stephens, N.M. (1975) Congruence Properties of Congruent Numbers. Bulletin of the London Mathematical Society, 7, 182-184. http://dx.doi.org/10.1112/blms/7.2.182
- Alter, R., Curtz, T.B. and Kubota, K.K. (1972) Remarks and Results on Congruent Numbers. Proceedings of the 3rd Southeastern Conference on Combinatorics, Graph Theory and Computing, Boca Raton, 28 February-2 March 1972, 27-35.
- Conrad, K. (2008) The Congruent Number Problem. Harvard College Mathematical Review, 2, 58-73.
- Ono, T. (1994) Variations on a Theme of Euler. Quadratic Forms, Elliptic Curves, and Hopf Maps. Plenum Press, New York and London. http://dx.doi.org/10.1007/978-1-4757-2326-7






















