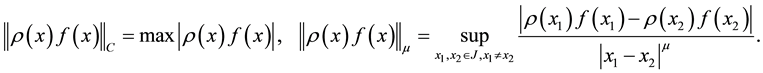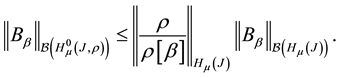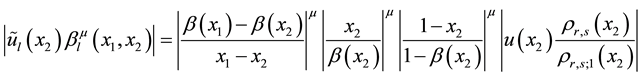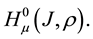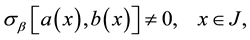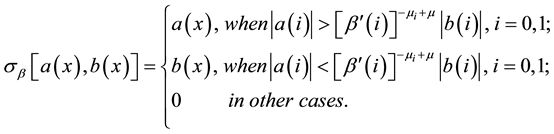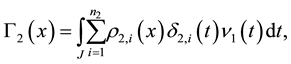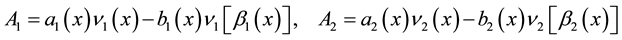Advances in Pure Mathematics
Vol.04 No.11(2014), Article ID:51576,5 pages
10.4236/apm.2014.411068
On Invertibility of Functional Operators with Shift in Weighted Hölder Spaces
Anna Tarasenko1, Oleksandr Karelin2
1Mathematical Research Center, Hidalgo State University, Pachuca, Mexico
2Advanced Research Center on Industrial Engineering, Hidalgo State University, Pachuca, Mexico
Email: anataras@uaeh.edu.mx, karelin@uaeh.edu.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 October 2014; revised 1 November 2014; accepted 7 November 2014
ABSTRACT
In this paper, we consider functional operators with shift in weighted Hölder spaces. We present the main idea and the scheme of proof of the conditions of invertibility for these operators. As an application, we propose to use these results for solution of equations with shift which arise in the study of cyclic models for natural systems with renewable resources.
Keywords:
Functional Operator with Shift, Hölder Space, Conditions of Invertibility, Renewable Resources

1. Introduction
The interest towards the study of functional operators with shift was stipulated by the development of solvability theory and Fredholm theory for some classes of linear operators, in particular, singular integral operators with Carleman and non-Carleman shift [1] -[3] . Conditions of invertibility for functional operators with shift in weighted Lebesgue spaces were obtained [1] .
Our study of functional operators with shift in Hölder spaces with weight has an additional motivation: on modeling systems with renewable resources, equations with shift arise [4] [5] , and the theory of linear functional operators with shift is the adequate mathematical instrument for the investigation of such systems.
In Section 2, some auxiliary lemmas are proposed. These are to be used in the proof of invertibility conditions. In Section 3, conditions of invertibility for functional operators with shift in Hölder spaces with power wight are obtained. We provide the main idea and the scheme of proof of the conditions of invertibility. At the end of the article, an application to modeling systems with renewable resources is specified.
2. Auxiliary Lemmas
We introduce [6] weighted Hölder spaces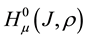 , in which we consider functional operators with shift.
, in which we consider functional operators with shift.
A function 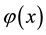 that satisfies the following condition on
that satisfies the following condition on ,
,
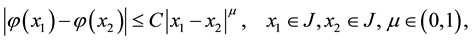
is called Hölder’s function with exponent  and constant
and constant 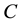 on
on .
.
Let 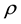 be a power function which has zeros at the endpoints
be a power function which has zeros at the endpoints ,
, :
:
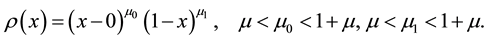
The functions that become Hölder functions and turn into zero at the points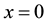 ,
,  , after being multiplied by
, after being multiplied by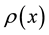 , form a Banach space:
, form a Banach space: 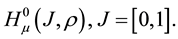 The norm in the space
The norm in the space 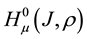 is defined by
is defined by
where
and
We denote by 


Let 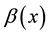
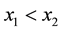


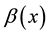

addition, let 

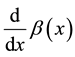

Without loss of generality, we assume that for any fixed
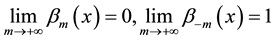


We will use the following notation,
Lemma 1.
An essential point is that 
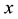
Proof. This lemma follows from the properties of shift
Lemma 2. If the following condition is fulfilled,
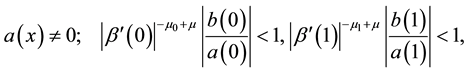
then the following inequalities are correct in some 


Proof. This lemma follows from (1) and from the properties of

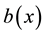
From Lemma 1 and Lemma 2 it follows that for 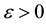
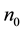




The following lemmas hold.
Lemma 3. Operator 

Operator 
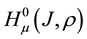
Lemma 4. For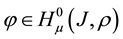
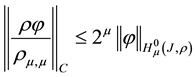
We shall take advantage of these lemmas in the proof of invertibility conditions in Section 3.
3. Conditions of Invertibility for Operator A in Weighted Hölder Spaces
In weighted Hölder space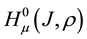
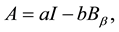


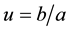
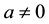

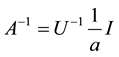
If a certain natural number 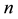


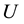
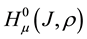
This statement in weighted Lebesgue spaces was proved in [1] . The proof is completely transferred without change to the weighted Hölder space as the applied algebraic operations do not depend on the specific properties of the spaces.
Analogously, if 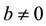
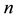
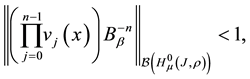


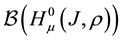
It is obvious that
We will use the following notation
Theorem 1. From conditions (1) it follows that such 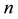
Proof. In order to prove
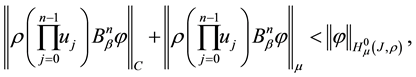
we estimate every summand separately, starting with the first

We took into account 
From (2) of Lemma 2, it follows that the first factor on the right side of inequality (4): 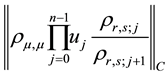
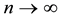
Now, we estimate the second summand of (3). The following estimate holds

From Lemma 1 and (2) of Lemma 2, it follows that only 
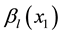

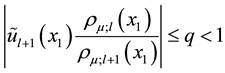
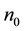
From (2) of Lemma 2 and the identity
it follows that some number 
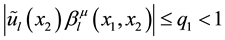

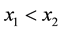
All expressions with 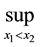
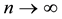
Thus, such 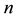
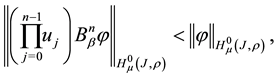
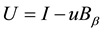
We will now formulate and prove conditions of invertibility for operator 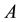
Theorem 2. Operator 

where function 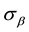
Proof. We consider the following case:
In space

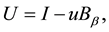
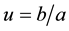
Thus, such 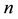
which means that operator 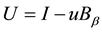
The case 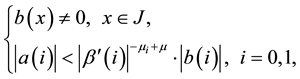
Now, we will focus on the application of these results to the modeling of systems with renewable resources. For the study of such systems, cyclic models were elaborated based on functional operators with shift [4] . The balance relation describing the state of cyclic equilibrium is the equation 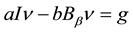


If we model the behavior of a system with two resources, taking into account the interaction between them, by integrals with degenerate kernels and following the principles of modeling from [4] , we shall obtain two equations with two unknowns, 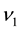

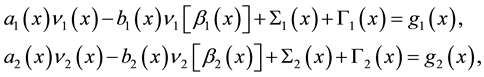
where 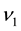

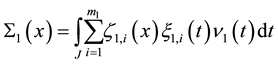
are the terms of reproduction and interaction process respectively.
Let 
in 

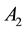
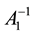
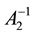

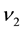
References
- Karlovich, Y.I. and Kravchenko, V.G. (1981) Singular Integral Equations with Non-Carleman Shift on an Open Contour. Differential Equations, 17, 2212-2223.
- Litvinchuk, G.S. (2000) Solvability Theory of Boundary Value Problems and Singular Integral Equations with Shift. Kluwer Academic Publishers, Dordrecht, Boston, London. http://dx.doi.org/10.1007/978-94-011-4363-9
- Kravchenko, V.G. and Litvinchuk, G.S. (1994) Introduction to the Theory of Singular Integral Operators with Shift. Kluwer Academic Publishers, Dordrecht, Boston, London. http://dx.doi.org/10.1007/978-94-011-1180-5
- Tarasenko, A., Karelin, A., Lechuga, G.P. and Hernández, M.G. (2010) Modelling Systems with Renewable Resources Based on Functional Operators with Shift. Applied Mathematics and Computation, 216, 1938-1944. http://dx.doi.org/10.1016/j.amc.2010.03.023
- Karelin, O., Tarasenko, A. and Hernández, M.G. (2013) Application of Functional Operators with Shift to the Study of Renewable Systems When the Reproductive Processed Is Described by Integrals with Degenerate Kernels. Applied Mathematics (AM), 4, 1376-1380. http://dx.doi.org/10.4236/am.2013.410186
- Duduchava, R.V. (1973) Unidimensional Singular Integral Operator Algebras in Spaces of Holder Functions with Weight. Proceedings of A. Razmadze Mathematical Institute, 43, 19-52. (In Russian)