Advances in Pure Mathematics
Vol.4 No.8(2014), Article ID:48976,10 pages
DOI:10.4236/apm.2014.48049
Optimal Separation of Twin Convex Sets under Externalities
Indrajit Mallick
Centre for Studies in Social Sciences, Kolkata, India
Email: imallick5@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 June 2014; revised 15 July 2014; accepted 26 July 2014
ABSTRACT
This paper studies the outcomes of independent and interdependent pair-wise contests between economic agents subject to an optimal external decision problem for each pair. The external decision maker like the government or regulator is faced with the problem of how to devise rules and regulations regarding contests. In this paper, a decision problem is faced under negative and positive externalities. A pair of entities is represented by disjoint convex sets in a small area in a neighborhood. I assume that each entity imposes an equal externality on the other (and the other only) and thus they can be considered to be twins. Among the group of twins in any neighborhood, there is a set of twin pairs such that, for each pair in the set, each twin can impose a strictly negative externality on the other (and the other only), and this is a potential welfare loss which concerns the decision maker. A separating hyper-plane can block the negative externalities between any pair of twins given convexity. However, this can be costly if positive externality from the neighborhood is also blocked by the separation technology. Thus, this paper compares the pair-wise utility from separation to that of non-separation. A simple representation of the decision problem is developed with respect to a single and isolated neighborhood. A complete characterization of the decision problem is obtained with a large number of pair-wise intersecting neighborhoods.
Keywords:Convex Set, Separation, Externality

1. Introduction
Regulation and decentralization of institutional (legal rules and economic organization structure) setup are a primary challenge to improve the performance of an economy and bring about economic growth, financial stability and equitable wealth and income distribution. That an economy does not automatically achieve optimality with respect to these goals is by now well established (see in particular [1] -[4] ). A regulator has to use some contingent intervention mechanisms in order to improve outcomes. All of these involve optimization under some basic assumptions about convexity.
Optimization and rules for decentralization in economic theory of choice and decision making rely heavily on convexity which naturally arises in the underlying preferences, budget sets, production sets and valuation sets. Maximization thus involves separating the set of benefits from the set of costs thus selecting the optimum while decentralization of resources uses the price system to separately allocate net benefits to economic units. However, additional complexity is introduced by a structure of externalities which leads to market failure unless corrected by some regulatory mechanisms. In this paper, I suggest such a mechanism under externalities by characterizing the decision problem of the regulator. It seems intuitively that when an economic entity makes a loss in engaging in games (of conflict, cooperation and coordination activities) with another entity due to negative externality imposed on each other, the loss could be minimized by not allowing the two entities to transact with each other. However, under positive externalities coming from some other source, separation decision might not be always optimal (except in case of outliers in a neighborhood). This is true both for independent and interdependent transactions and for both an isolated and a non-isolated neighborhood.
Consider the world of utility or value maximization by the individual units (like consumers, producers, traders, financial intermediaries, political groups (like political parties or political states) and social groups). Utility or value can be maximized through consumption, power, wealth and attainment of social objectives under economic, social and political interactions. Success is conditional on (besides own actions and resources) competing, cooperating and coordinating actions and resources of others. Thus selection of strategy by an agent is necessarily contingent on the strategies of others and the economic environment. Strategic contests thus characterize all economies, political systems and societies. A basic characteristic of strategic interaction is that utility (or value) maximizing economic agents are matched in a pair-wise fashion. A buyer is matched to a seller and a buyer may be matched to a number of sellers. With some loss of generality, it can be assumed that an economic unit like a buyer (who is a buyer in some matches and a seller in other matches) has multiple identities (with each identity relevant for each match) without some consolidating and general characteristics. The same can be assumed for a seller. Though pair-wise contests are potentially dependent on each other, independent pair-wise contests and the decision problems for regulators are first studied. This simplifies the analysis and the corresponding decision problem. I also discuss the implications of relaxing this restrictive assumption and derive a qualitatively similar result for the decision maker with interdependent pair-wise contests. The decision problem requires separation only when the sum of negative externalities dominates the sum of positive externalities.
Given that a buyer and a seller are matched, they engage in strategies of conflict like bargaining and contracting. Cooperation and coordination results if bargaining and contracting succeed and there is no cooperation and coordination if bargaining or contracting fails. Pair-wise contests are assumed to be driven by potential gains from trade and traditional rivalry with access to each other and where pairs are self-selected given their characteristics and their environments (see the analysis in [5] -[7] ). This paper is based on a combination of economic phenomena which is generally observed in world where allocation of scarce resources is determined by pairwise decentralized competition given non-satiation in demand and the economy does not automatically attain the first best welfare given a structure of exogenously and endogenously determined externalities (see the discussion in [8] -[10] ). Under these circumstances, it is well known that an appropriate system of regulation and an optimal design of a mix of centralization-decentralization of the institutional structure are required to achieve economic efficiency. This paper studies the optimal design of regulation and the required optimal mix of centralization and decentralization of the institutional and corresponding organization structure by an analysis of outcomes of pairwise contests between economic agents subject to an optimal external decision problem for each pair.
I first describe twin convex sets in a neighborhood. A pair of entities is represented by two disjoint convex sets (closed balls of same radius) in an arbitrarily small area of a neighborhood and a set of utility assignments associated with different types of externalities faced. The potential utility from positive externality to each of the twin convex sets is same. The centre of each set is equidistant to the centre of the neighborhood and each can potentially receive the same amount of positive externality from a ray coming from the centre. The potential externality can be interpreted as coming from public goods (see the exposition in [11] [12] ), government programs (see the discussions in [13] -[19] ) and coordination games of private activity with positive spillovers at the heart of the economy as the analysis in [4] [11] [14] [15] demonstrate.
I also assume that each entity can potentially impose an equal amount of externality
on the other (and the other only). Thus they can be called twins. When a buyer and
seller realize gains from trade they are essentially imposing non-negative externality
on each other. This is satisfactory from the viewpoint of the decision maker and
does not need any intervention. On the other hand, strictly negative externality
imposed by a twin on the other and vice versa, is the essential welfare loss problem.
It is assumed that the set of pairs of twins which realize gains from trade in a
neighborhood
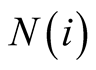 is denoted by the set
is denoted by the set
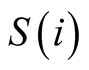 (
(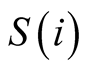 stands for success set) and the complement
set in neighborhood
stands for success set) and the complement
set in neighborhood
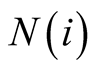 is denoted by
is denoted by
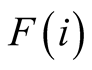 (
(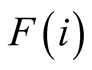 stands for the failure set).
stands for the failure set).
There are pairs of twins which achieve gains from trade or gains from collusion or gains from coordination despite potential destructive competition or costs of coordination but these are not considered to be problems that affect a neighborhood. However, it is instructive to note how gains from trade are realized in pair-wise contests (see the analysis in [4] [10] [11] [15] [20] [21] ). One or more of the following conditions are usually present: there is specific structure of specialization patterns, which through increasing productivity in activities creates a potential for gainful exchange, there is also the comparative advantage phenomena, differences in resource combinations and qualities, and the relative advantages of safe and risky assets. Each requires some degree of heterogeneity among entities. Entities can specialize in high risk but high coordination activities and insure against extreme specialization through risk sharing ex ante (see [15] ). Positive externality is also realized in exchange when one economic entity creates a favorable situation for production or consumption of the counterparty and this increases the region of gains from trade. Of course in any of these situations, valuation to a buyer exceeds that of the seller.
The economics literature also discusses the reasons for negative externalities. One can start by assuming that the advantages in trade discussed above are missing and moreover different kinds of disadvantages manifest. But there is more than that. Preferences, endowments and production sets may be very different and generate negative externalities. The abstract analysis of standard negative externalities like pollution and encroachment are discussed in [8] [10] while [9] [10] discuss the costly contracting problems of moral hazard and adverse selection. The negative externalities of transaction costs like holdup and state verification problem which leads to suboptimal investment and under-provision of liquidity is analyzed in [22] . Incomplete information also results in bargaining inefficiency and is discussed in [7] [10] [15] . Other sources of negative externalities are absence of properly defined property rights (see the discussion in [8] [11] [22] ), lack of incentives to invest and trade due to strategic uncertainty and unforeseen contingencies (see the analysis in [4] [11] [22] , imperfect information (discussed in [9] [10] ) and envy (analyzed in [11] ).
I shall focus on the problem of negative externality imposed by any twin on the
corresponding twin in
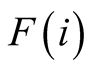 subject to other considerations. I assume that each twin in
subject to other considerations. I assume that each twin in
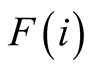 has a potential net loss of −n (n > 0) due to the negative externality that
can be imposed by the other twin without separation. Given that for any twin-pair
in
has a potential net loss of −n (n > 0) due to the negative externality that
can be imposed by the other twin without separation. Given that for any twin-pair
in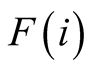 , the twins are disjoint and convex, there
exists a hyper-plane which can separate the twins. I assume that the hyper-plane
is a technology which can completely block the negative externalities between any
pair of twins. Thus it may seem that using the separation technology will be the
right decision by the government regulating pair-wise contests. However, considerations
become complicated because of the presence of the positive externality on each of
the twins within its neighborhood coming from the centre of a neighborhood. Thus,
this paper undertakes to analyze whether there is any need for separation technology
when positive externality is blocked by the hyper-plane. A simple representation
of the decision problem is developed with respect to a single neighborhood. A complete
characterization of the decision problem is obtained with a large number of neighborhoods
and overlapping positive externalities. This paper is more concerned about the desirability
(normative analysis) of separation even if separation is feasible given the assumptions
of convexity and disjoint twin sets (positive analysis). The focus of the paper
is to first highlight the possible tradeoffs in the separation decision. The decision
problem is characterized so that pair-wise utility value of separation is compared
to pair-wise utility value of non-separation. The decision problem of the regulator
is developed for independent as well as interdependent pair-wise contests where
the latter is a generalization of the former with some restriction on separation
decisions. At the same time, it should be noted that the present paper has a special
approach which when generalized, could inform and improvise the decentralized interdependent
bargaining model by introducing potential dynamics. The discussion about interdependent
dynamic bargaining games is made in the conclusion where several suggestions for
optimal regulation and decentralization decisions are developed for analyzing more
complicated problems.
, the twins are disjoint and convex, there
exists a hyper-plane which can separate the twins. I assume that the hyper-plane
is a technology which can completely block the negative externalities between any
pair of twins. Thus it may seem that using the separation technology will be the
right decision by the government regulating pair-wise contests. However, considerations
become complicated because of the presence of the positive externality on each of
the twins within its neighborhood coming from the centre of a neighborhood. Thus,
this paper undertakes to analyze whether there is any need for separation technology
when positive externality is blocked by the hyper-plane. A simple representation
of the decision problem is developed with respect to a single neighborhood. A complete
characterization of the decision problem is obtained with a large number of neighborhoods
and overlapping positive externalities. This paper is more concerned about the desirability
(normative analysis) of separation even if separation is feasible given the assumptions
of convexity and disjoint twin sets (positive analysis). The focus of the paper
is to first highlight the possible tradeoffs in the separation decision. The decision
problem is characterized so that pair-wise utility value of separation is compared
to pair-wise utility value of non-separation. The decision problem of the regulator
is developed for independent as well as interdependent pair-wise contests where
the latter is a generalization of the former with some restriction on separation
decisions. At the same time, it should be noted that the present paper has a special
approach which when generalized, could inform and improvise the decentralized interdependent
bargaining model by introducing potential dynamics. The discussion about interdependent
dynamic bargaining games is made in the conclusion where several suggestions for
optimal regulation and decentralization decisions are developed for analyzing more
complicated problems.
A classification of games is useful for a deeper understanding of economic phenomena and the need for regulation and redesign of economic systems. Economic entities compete for scarce resources that allow utility or value through consumption. As the analysis in [11] [15] [20] [21] suggest, at the basic level, potential competitors enter into costly conflicts with games of entry, predation, market share rivalry, takeover and attrition with exit resulting. In a pair-wise contest, conflict is always primary between two matched contestants. However, cooperation can emerge to a large extent due to self-preservation tendencies that equalizes the value of strategic options of being an aggressor and being timid. The credit for this insight goes to [23] who analyzes pair wise contests in an evolutionary biology context leading to the powerful concept of “Evolutionarily Stable Strategy”.
The literature on dynamic matching and bargaining games is relevant for pair-wise matching contests. Different kinds of matchings (exogenous and endogenous) and assumptions about bargaining can be made. Both gain and loss is possible in these bargaining games and a general dynamic game should accommodate both. I start with a discussion of gains and cooperation. One significant notion of cooperation is potential gains from exchange through bargaining and contracting between a matched pair (though one should note that bargaining and contracting is potentially a game of conflict and cooperation). The result of such a game between a matched pair could have multiple solutions or exhibit indeterminacy as noted by [24] . However, as the number of agents grows sufficiently large and re-contracting possibilities are allowed, [24] shows the outcome to be the perfectly competitive equilibrium outcome with no indeterminacy. In the same spirit, dynamic matching and bargaining games are discussed by [6] [7] where games go over time and at any time, each of the simultaneous bargaining games is a pair-wise contest. Each bargaining depends on the future outcomes like exit if bargaining succeeds and re-matching and prospective value from future bargaining if bargaining fails at present. Bargained prices are shown by [6] to converge to the Walrasian price(s) even with dispersed characteristics provided discount factors approach unity. However, the decentralized pair-wise exchange process has several hazards which prevent its attainability and reduce its utility even if attainable. Costs of different exchange related phenomena like search, matching, learning to bargain, contract drafting and post-contractual unforeseen contingencies that are known as transaction costs are discussed by [25] [26] which are shown to impede trade. In the context of industrial organization, [21] shows that duopoly competition does not attain efficiency. Negative externalities discussed above lead to the pair dissolving and waiting for a favorable match under a dynamic game.
This paper is a brief attempt to characterize optimal regulation and institutional design. It anticipates a more general problem of regulation given the additional complexity introduced by interdependence and interdependence of pair-wise contests and given complexity induced by different possible kinds of dynamics. As such, a brief review of the literature on regulation is necessary. The problems of regulating a (potential) monopoly, inefficiently excessive competition, inefficient collusion and unstable coordination problems require the optimal design of regulation and are discussed in [5] [9] -[11] [15] [19] [21] . Standard devises suggested in the literature on industrial regulation are antitrust regulation, price control and control of entry. Other devices suggested by the literature are discriminating screening contracts devised by the government, vertical and horizontal integration and prudential regulation of banks. In the context of the problem of transaction costs associated with organizing economic activity, [8] has argued that, decentralized market solution is not necessarily optimal and the authority (which reduces transaction costs) based firm must play a relatively more important role. In an insightful analysis by [8] , it is argued that in particular, for the problem of externalities in the presence of transaction costs, the optimal solution should be the efficient allocation of property rights such that the efficient methods of countering the negative externality and allowing the positive externality are actually implemented. In discussing the optimal combination of centralization and decentralization in firms and economic systems, [27] has emphasized management and organization design as the principal coordination devices.
The historical development of relevant mathematical tools provides clues on the appropriate ways to approach the problem, the crucial assumptions needed, and the creative avenues that can be explored using optimization techniques, and the use of convexity. The first systematic study of the general properties of convexity and the separating hyper-plane theorem was due to [28] . A major work with comprehensive coverage on convex analysis is due to [29] which is still the basic text on the subject. The theoretical framework of linear economic models was developed by [30] who also provided analysis of two person games with other notable contemporary game theories and mathematicians and showed equivalence of two person games to appropriately redefined linear programming problems. Optimization by vector space methods was pioneered by [31] and allowed more productive use of linear algebra in optimization. The pioneering work by [32] elegantly analyzes the properties of convex sets and concave functions and provides an economic interpretation of separation through a hyperplane as optimization by decentralizing resources using a price system. A nice treatment of mathematical analysis especially in terms of basic topology, sequence and series convergence and properties of continuity has been provided in [33] .
2. The Decision Problem for a Single Isolated Neighborhood
Given the assumptions about twin sets, the structure of externalities and the convexity assumptions, I discuss the decision problem both for independent and interdependent pair-wise contests. In particular, I discuss the relative merit and demerit of applying the hyper-plane theorem for the disjoint convex twin sets. First I describe the neighborhood and the externalities. I only discuss twins with negative externalities.
Assumption 2.1. Consider the Euclidean Space RK. A neighborhood in RK
is an open set
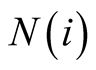 where i is a positive integer and the centre of the set is
where i is a positive integer and the centre of the set is
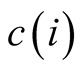 which has radius
which has radius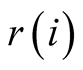 .
.
Assumption 2.2. I assume that each neighborhood
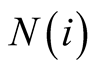 is isolated in the sense that there is no intersection between any of the neighborhoods.
is isolated in the sense that there is no intersection between any of the neighborhoods.
Assumption 2.3. For set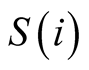 , any twin in a pair can receive
a positive externality (equal to net gain in utility = m > 0) from the other twin
in the pair, if non-separated. For set
, any twin in a pair can receive
a positive externality (equal to net gain in utility = m > 0) from the other twin
in the pair, if non-separated. For set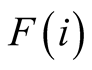 , any twin in a pair
can receive a negative externality (equal to net loss in utility = −n < 0)
from the other twin in the pair, if non-separated. The decision problem is for each
twin-pair in
, any twin in a pair
can receive a negative externality (equal to net loss in utility = −n < 0)
from the other twin in the pair, if non-separated. The decision problem is for each
twin-pair in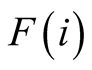 .
.
Assumption 2.4. Let X and Y be two twin disjoint convex sets (closed balls of same
radius belonging to set
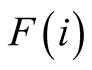 in the neighborhood
in the neighborhood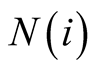 ). The positive externality
comes from the centre of the neighborhood and in order to have the positive utility
effect on each of the twin pairs, it must reach the centre of each set representing
the twins. The centre of each neighborhood emits a ray throughout the neighborhood
with utility value equal to positive externality
). The positive externality
comes from the centre of the neighborhood and in order to have the positive utility
effect on each of the twin pairs, it must reach the centre of each set representing
the twins. The centre of each neighborhood emits a ray throughout the neighborhood
with utility value equal to positive externality
 where
where
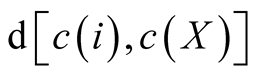 represents distance travelled by the ray from the centre of the neighborhood to
the centre of any set
represents distance travelled by the ray from the centre of the neighborhood to
the centre of any set
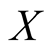 in the neighborhood. The maximum distance travelled by the ray is
in the neighborhood. The maximum distance travelled by the ray is
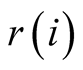 such that
such that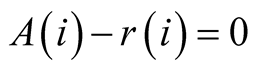 . In other words,
the positive externality is exhausted when maximum distance equivalent to the radius
is attained by a ray. If X and Y are twin sets then
. In other words,
the positive externality is exhausted when maximum distance equivalent to the radius
is attained by a ray. If X and Y are twin sets then
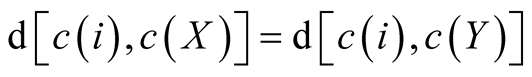 .
.
Assumption 2.5. Separation is a technology. Since any of a pair of twin sets are convex and disjoint, they can be separated using a separating hyper-plane (see [28] [29] [32] ). I assume that a separating hyper-plane has real life separating properties in the sense that it blocks the negative externalities imposed by each set on the twin set and vice versa. This will ensure that as long as separation holds, there is no negative externality effect. I further assume that a separating hyper-plane is confined to the (arbitrarily) small area where any pair of the twin sets lie.
There are two ways of separation:
Case 1. There exists, and is optimally chosen, a separating hyper-plane line which meets the centre of the neighborhood from where the positive externality is coming. This ensures that negative externality can be removed without any effect on the positive externality since the hyper-plane does not block the path of positive externality on each set. In this case, separation is always an optimal decision.
Case 2. No separating hyper-plane line exists which meets the centre of the neighborhood.
This is due to the fact that the twin sets are at an angle such that the separating
line does not meet the centre of the neighborhood. This implies that due to separation,
one set of the twins (let us call it Y) will not be a beneficiary of the positive
externality coming from the centre of the neighborhood since the hyper-plane blocks
the path of the positive externality. It does not matter which twin set will be
denied positive externality, the total value of positive externality for the pair
of sets is the same because the addition to utility from
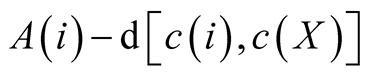 is constant over the two sets.
is constant over the two sets.
Assumption 2.6. Any ray from
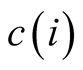 potentially reaches only one convex twin set. This means that no other twin set
(say Z or W) comes in the way of the positive externality on X and Y. Further, each
set in the neighborhood potentially receives a ray from
potentially reaches only one convex twin set. This means that no other twin set
(say Z or W) comes in the way of the positive externality on X and Y. Further, each
set in the neighborhood potentially receives a ray from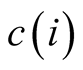 . Positive externality
is generated from the centre of the neighborhood and is received by a set unless
separation involves blocking of the positive externality coming to a twin set.
. Positive externality
is generated from the centre of the neighborhood and is received by a set unless
separation involves blocking of the positive externality coming to a twin set.
Assumption 2.7. In Case 2, if separation is considered to be optimal then
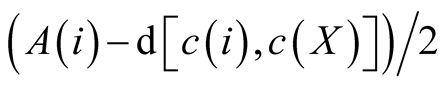 will be allocated to each set.
will be allocated to each set.
2.1. Independent Pair-Wise Contests with Externalities
The decision criterion for Case 1. Separation is optimal.
wang#title3_4:spThe decision criterion for Case 2.
Value from separation:
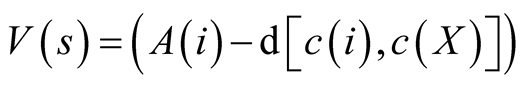 (1)
(1)
Value from non-separation:
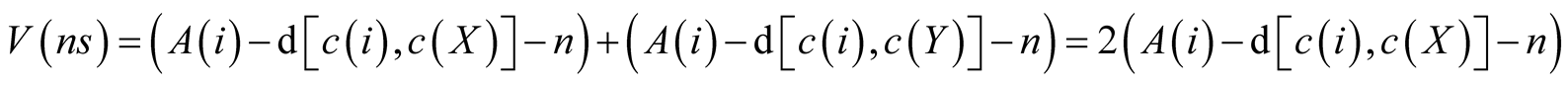 (2)
(2)
Since the centre of each of the twin sets are equidistant from the centre of the neighborhood.
So non-separation is optimal iff: .
.
2.2. Interdependent Pair-Wise Contests with Externalities
I consider only twin (disjoint and convex) sets with negative externalities in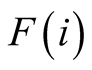 . Positive externalities as in
. Positive externalities as in
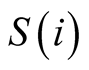 can be ignored without loss of generality. I therefore consider interdependent contests
where each entity is represented in multiple contests with loss in each contest.
Therefore the decision problem is with respect to the consolidated entity or the
basic economic unit.
can be ignored without loss of generality. I therefore consider interdependent contests
where each entity is represented in multiple contests with loss in each contest.
Therefore the decision problem is with respect to the consolidated entity or the
basic economic unit.
Assumption 2.2.1. Each twin set is denoted by
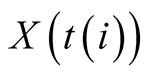 and the corresponding twin
and the corresponding twin
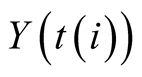 (where
(where
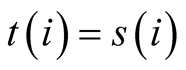 or
or
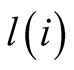 belonging to the set
belonging to the set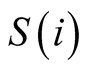 ) or
) or
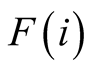 respectively).
respectively).
Assumption 2.2.2. For each
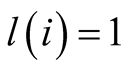 to L, an entity
to L, an entity
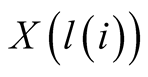 is matched with another twin
is matched with another twin
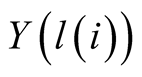 L times in set
L times in set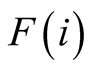 .
.
Assumption 2.2.3. For any consolidated entity or unit, separation means blocking
negative externalities for all matches of the entities representing the unit in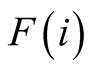 . In other words, discrimination in separation
is not allowed since rules are made for the consolidated entity. However, separation
decisions for negative externalities are not allowed to affect the gains from trade
made by an economic unit in
. In other words, discrimination in separation
is not allowed since rules are made for the consolidated entity. However, separation
decisions for negative externalities are not allowed to affect the gains from trade
made by an economic unit in
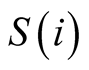 (note that if separation implies separation for all matches both in
(note that if separation implies separation for all matches both in
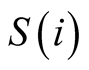 and
and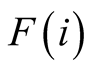 , the case for non-separation is correspondingly
stronger).
, the case for non-separation is correspondingly
stronger).
Assumption 2.2.4. In Case 2, if separation is considered to be optimal then

will be allocated to each set.
The decision criterion for Case 1. Separation is optimal.
The decision criterion for Case 2.
Value from separation:
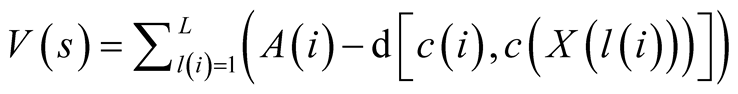 (3)
(3)
Value from non-separation:
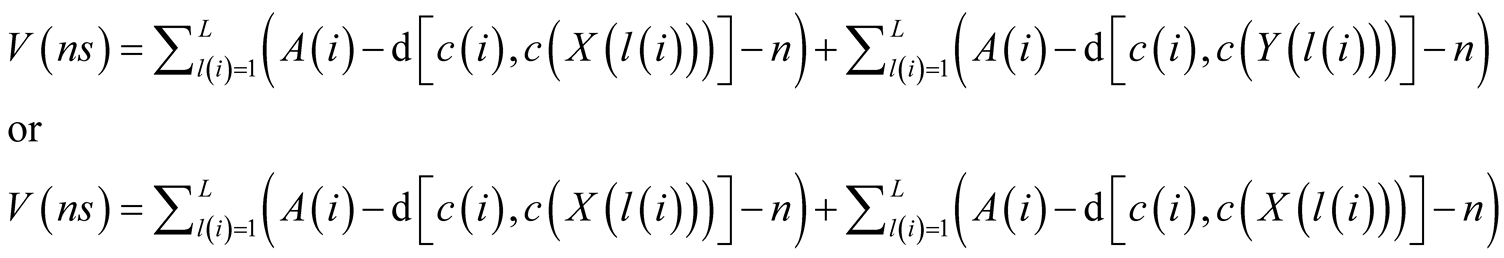 (4)
(4)
Since the centre of each of the twin sets are equidistant from the centre of the neighborhood.
So non-separation is optimal iff: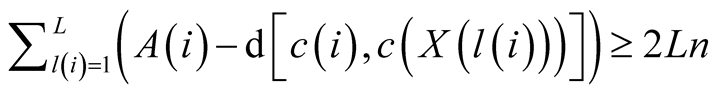 .
.
3. The Decision Problem for a Large Number of Non-Isolated Neighborhoods
The decision problem for a large number of neighborhoods is difficult and I avoid
analysis of an unrestricted domain. Instead, I assume that neighborhoods have a
hierarchical structure (in terms of increasing positive externalities
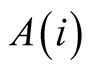 and radii
and radii
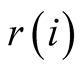 as i increases). This then allows a representation of the space covering the set
of all neighborhoods as a cone CK closed under scalar multiplication.
The cone is convex given the following conditions hold: any of the (closed) set
of points connected by a straight line between any two points in the cone belongs
to a neighborhood and is nonempty (there are activities given externalities everywhere
in any neighborhood) or belongs to the space in the cone which is not belonging
to any neighborhood and is nonempty (there are isolated activities in each point
in that space).
as i increases). This then allows a representation of the space covering the set
of all neighborhoods as a cone CK closed under scalar multiplication.
The cone is convex given the following conditions hold: any of the (closed) set
of points connected by a straight line between any two points in the cone belongs
to a neighborhood and is nonempty (there are activities given externalities everywhere
in any neighborhood) or belongs to the space in the cone which is not belonging
to any neighborhood and is nonempty (there are isolated activities in each point
in that space).
Assumption 3.1. The space that provides a complete cover for all the sets is a convex
cone having the origin as the vertex. It is assumed that
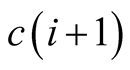 is located to the northwest of set
is located to the northwest of set
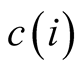 for all i. Further, I assume that for all i,
for all i. Further, I assume that for all i,
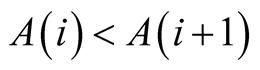 , so that as one moves up northwest, positive
externalities are stronger in the successive neighborhoods. Also,
, so that as one moves up northwest, positive
externalities are stronger in the successive neighborhoods. Also,
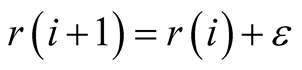 , where ε is an arbitrarily small positive
number.
, where ε is an arbitrarily small positive
number.
Assumption 3.2.
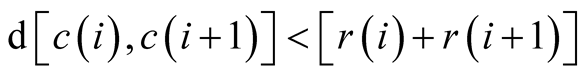 for all i, so intersection does occur between
two adjoining neighborhoods. Further, for all i and
for all i, so intersection does occur between
two adjoining neighborhoods. Further, for all i and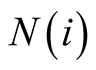 ,
,
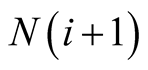 and
and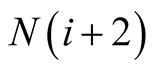 , there is a
restriction on each radius such that the following condition holds:
, there is a
restriction on each radius such that the following condition holds:
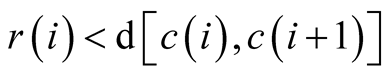 and
and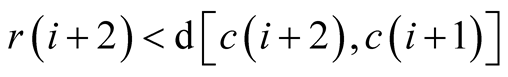 . This will ensure that
for the analysis of the properties of intersection of two adjoining neighborhoods,
no other neighborhood matters.
. This will ensure that
for the analysis of the properties of intersection of two adjoining neighborhoods,
no other neighborhood matters.
Assumption 3.3. For Case 2, if separation is considered to be optimal then
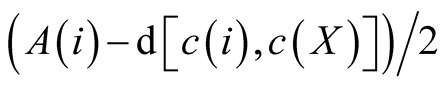 will be allocated to each set.
will be allocated to each set.
3.1. Independent Pair-Wise Contests with Externalities
The decision criterion for Case 1. Separation is optimal.
The decision criterion for Case 2. Let X and Y (a pair of disjoint convex twin sets)
belong to the intersection of
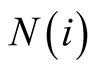 and
and
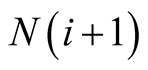 for any i. Now, if the sets X and Y are separated, the positive externality from
for any i. Now, if the sets X and Y are separated, the positive externality from
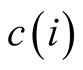 hits one set and the positive externality from
hits one set and the positive externality from
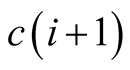 hits the other set given the angularity assumption about separation.
hits the other set given the angularity assumption about separation.
Value from separation:
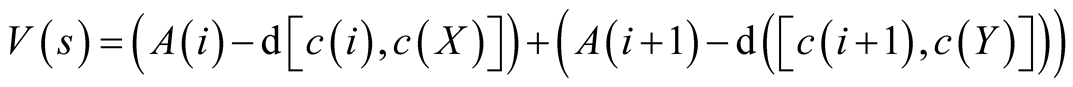 (5)
(5)
Value from non-separation:
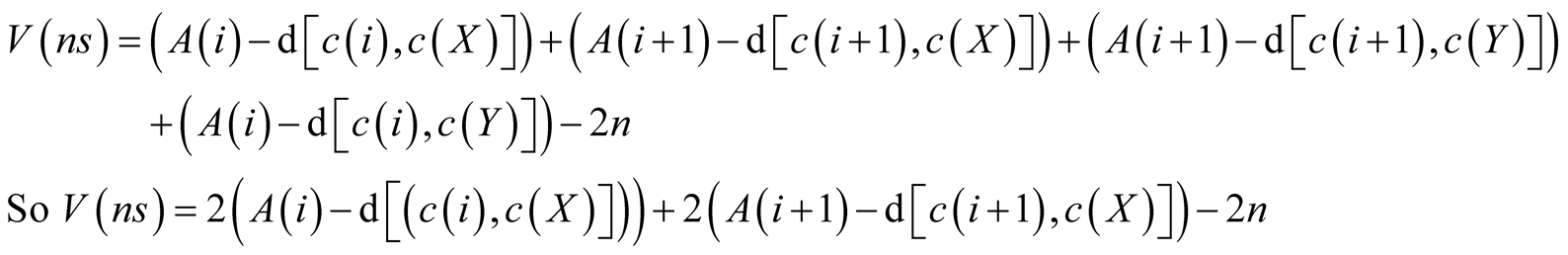 (6)
(6)
Since the centre of each of the twin sets are equidistant from the centre of the relevant neighborhood.
So non-separation is optimal iff: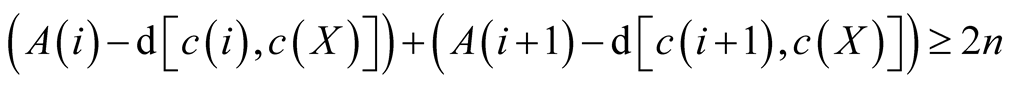 .
.
3.2. Interdependent Pair-Wise Contests with Externalities
The decision criterion for Case 1. Separation is optimal.
The decision criterion for Case 2.
Assumption 3.2.1. Let
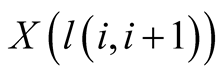 be an economic unit in the intersection of
be an economic unit in the intersection of
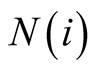 and
and
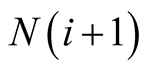 and let it be represented by
and let it be represented by
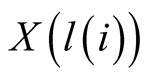 for
for
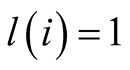 to
to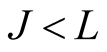 . The same applies for
. The same applies for
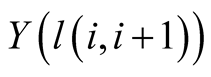 and
and
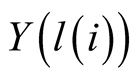
where
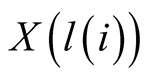 and
and
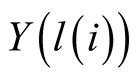 are twins for each
are twins for each
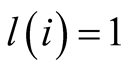 to
to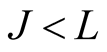 . Separation decision for any pair of twins
imply separation decision between the two corresponding economic units also. Now,
if the twin sets are separated, the positive externality from
. Separation decision for any pair of twins
imply separation decision between the two corresponding economic units also. Now,
if the twin sets are separated, the positive externality from
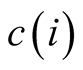 hits one set and the positive externality from
hits one set and the positive externality from
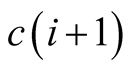 hits the other set given the Case 2.
hits the other set given the Case 2.
Assumption 3.2.2. In Case 2, if separation is considered to be optimal then
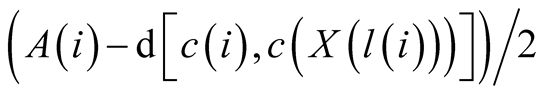 will be allocated to each set.
will be allocated to each set.
Value from separation
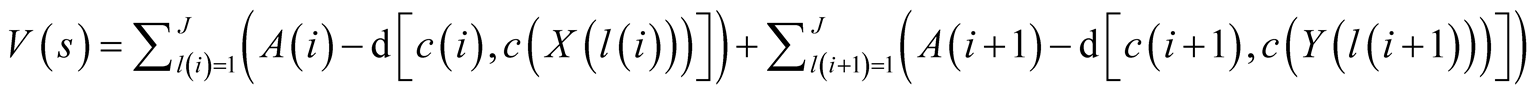 . (7)
. (7)
Value from non-separation:
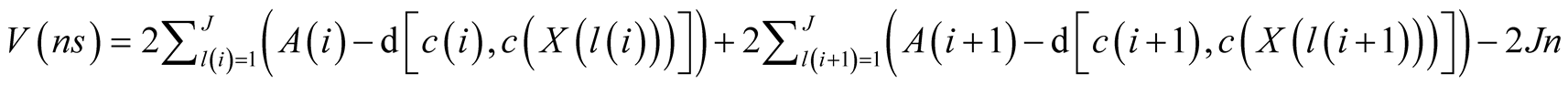 . (8)
. (8)
So non-separation is optimal iff:
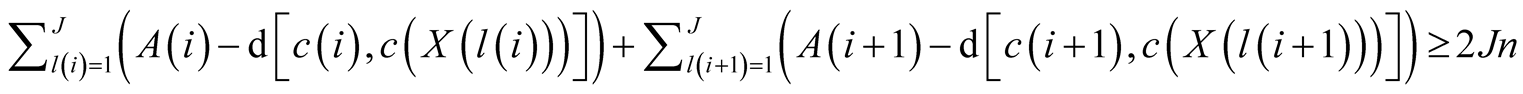 .
.
Since the centre of each of the twin sets are equidistant from the centre of the relevant neighborhood.
4. Conclusions
In this paper, decision criteria have been characterized with respect to the choice of separating or not separating disjoint twin convex sets in small areas of an isolated neighborhood where twins impose potential negative externality on each other and where positive externality comes from the centre of any neighborhood. Wherever there are tradeoffs between blocking negative externality using separation technology and receiving positive externality, the key issue is the distance of the ray travelled from the centre of the neighborhood. When the distance is low relative to other parameters, the positive externality is relatively strong and non-separation is considered to be optimal. On the other hand, when distance is high, positive externality is low and separation becomes optimal. Outliers (belonging far away from centre of a neighborhood) are better candidates for separation. Results are qualitatively same for independent and interdependent pair-wise contests.
I have also considered many neighborhoods in a convex cone under pair-wise intersection of neighborhoods assumption and the decision criteria have been similar but favoring non-separation relatively more since allowing positive externality from two neighborhoods is found more attractive. Otherwise, the distance travelled relative to other parameters is the crucial one. Results are qualitatively same for independent and interdependent pair-wise contests.
A generalization of the present analysis is possible by making the externalities endogenous and ensuring they change over time with each separation decision such that there are also inter-temporal tradeoffs. Another generalization is possible by considering the assumption of large number intersecting and interactive neighborhoods.
Optimization under convexity is an important tool for regulation as has been emphasized here. As mentioned in the beginning, in economic systems, three chief concerns in economic regulation are growth, stability and equitable distribution. Growth results from low capital-output ratios displayed by efficient technologies, technological progress and accumulation of human capital (see [4] ). Instability of a growth path has been noted in some contexts. Financial instability has been discussed in [16] stressing asset risk due to moral hazard and excessive financial innovation (see [15] [25] ) while the financial systemic financial fragility due to some salient properties of liquidity has been analyzed from several viewpoints in [1] [15] [25] . Inequality and poverty are analyzed and discussed in [4] [12] . Inequality is seen as stemming from unequal opportunities, results from lack of trust (see [4] [11] ) through adverse selection and moral hazard, endogenously arise through missing markets and incomplete participation.
Despite important insights, there are problems in the foundations of this literature. Bilateral exchange is as important as organized exchange and even in the organized exchange there are ex ante pair-wise matchings between potential buyers and potential sellers under basic heterogeneities while there is ex post bilateral renegotiation given transaction costs, unforeseeable uncertainties and externalities. At the same time, bilateral bargaining and contracting games proceed in the context of varying and dispersed characteristics of buyers and sellers while histories of games of the past, current play and the future expectations link the bargaining games in an overall dynamic general equilibrium setup. Thus, sellers can be rationed in one class of decentralized pair-wise market leading to lack of effective demand in other decentralized pair-wise market. Other phenomena like delay in investments, slow accumulation of capital, transactions contingent on gradual learning and experimentation, evolution of trading strategies in financial markets and resulting financial innovations and low economic mobility might arise.
The analysis in this paper can be extended for the basic economic problems analyzed as dynamic pair-wise matching and bargaining games. For understanding growth, it is useful to start with the observation that intervention mechanisms for creation of surplus in bilateral bargaining games are necessary. This can be achieved through appropriate provision of public goods like network externalities mechanisms and technology but it should be recognized that fiscal and monetary constraints limit the possibilities. Interdependent pair-wise games can create positive spillovers given mechanisms of positive expectations generated by a policy maker (where the expectations are feasible and can be satisfied under a set of conditions requiring coordination and centralization) with respect to gains from trade. In this way, an increase in economic growth can be coordinated. Successful designs of complementary institutions for pair-wise games also result in endogenous provision of platforms of public goods (like the stock of knowledge, information and network technologies and financial innovations) thus reinforcing the growth process. Financial fragility and instability can be mitigated through certain indirect mechanisms. Regulation of banks, over-the-counter markets, financial innovations and corporate governance through combinations of dynamic screening contracts contingent rules and monitoring allow aggregative regulation as well as regulation of pair-wise matched individual entities which reduces financial fragility and instability. Regulation in the context of economic inequality and poverty can be designed in several ways. The provisions of need based liquidity and finance in combination with developing ability and incentives to repay create conditions for economic surplus and potential gains from trade, government programs for provision of public goods in health and education raises human capital and surplus in bilateral exchange, building trust in trading partners becomes possible in bilateral exchange by information sharing infrastructure and rules embedded in law, and the appropriate institution design of organizations and markets leads to efficient trading rules in bargaining games. Successful learning and experimentation in interdependent pair-wise contests given these interventions bring about the needed inequality reducing innovations.
Acknowledgements
I thank an anonymous reviewer for helpful comments and suggestions.
References
- Allen, F. and Douglas, G. (2007) Understanding Financial Crises. Oxford University Press, Oxford.
- Hahn, F. (1985) Money, Growth and Stability. The MIT Press, Cambridge.
- Keynes, J.M. (1936) The General Theory of Employment, Interest and Money. Macmillan, London.
- Ray, D. (1999) Development Economics. Oxford University Press, New Delhi.
- Fudenberg, D. and Jean, T. (2005) Game Theory. Ane Books, India.
- Gale, D. (2000) Strategic Foundations of General Equilibrium: Dynamic Matching and Bargaining Games. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511492310
- Osborne, M.J. and Ariel, R. (1990) Bargaining and Markets. Academic Press, Inc., San Diego.
- Coase, R.H. (1988) The Firm, the Market and the Law. The University of Chicago Press, Chicago.
- Laffont, J.-J. (1989) The Economics of Uncertainty and Information. The MIT Press, Cambridge.
- Mas-Colell, A., Whinston, M.D. and Green, J.R. (1995) Microeconomic Theory. Oxford University Press, Oxford.
- Bowles, S. (2005) Microeconomics: Behavior, Institutions and Evolution. Oxford University Press, New Delhi.
- Hayami, Y. (2001) Development Economics: From the Poverty to the Wealth of Nations. Oxford University Press, Oxford. http://dx.doi.org/10.1093/0199243972.001.0001
- Azariadis, C. (1993) Intertemporal Macroeconomics. Blackwell Publishers, Cambridge.
- Blanchard, O.J. and Fischer, S. (1989) Lectures on Macroeconomics. The MIT Press, Cambridge.
- Mallick, I. (2002) Strategic Competition in Banking: Theory and Policy. Ph.D. Thesis, Jadavpur University, Kolkata.
- Dewatripont, M. and Tirole, J. (1993) The Prudential Regulation of Banks. The MIT Press, Cambridge.
- Gale, D. (1983) Money: In Disequilibrium. Cambridge University Press, Cambridge.
- Stiglitz, J.E. (1986) Economics of the Public Sector. W. W. Norton & Company, New York.
- Viscusi, W.K., Harrington, J.E. and Vernon, J.M. (2005) Economics of Regulation and Antitrust. The MIT Press, Cambridge.
- Bernard, M. (2012) Conflict, Cooperation and Coordination: Essays in Game Theory and Experimental Economics. Ph.D. Thesis, Stockholm School of Economics, Stockholm.
- Tirole, J. (1988) The Theory of Industrial Organization. The MIT Press, Cambridge.
- Hart, O. (1995) Firms, Contracts, and Financial Structure. Oxford University Press, Oxford.http://dx.doi.org/10.1093/0198288816.001.0001
- Smith, J.M. (1982) Evolution and the Theory of Games. Cambridge University Press, Cambridge.
- Edgeworth, F.Y. (1881) Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences. Kegan Paul, London.
- Duffie, D. (2012) Dark Markets: Asset Pricing and Information Transmission in Over-the-Counter Markets. 3rd Edition, Princeton University Press, Princeton.
- Shavell, S. (2004) Foundations of Economic Analysis of Law. Harvard University Press, Cambridge.
- Milgrom, P. and Roberts, J. (1992) Economics, Organization and Management. Prentice-Hall, Inc., Upper Saddle River.
- Minkowski, H. (1911) Theorie der Konvexen Korper, Insbesondere Begrundung ihres Oberflachenbegriffs. Gessamelte Abhandlungen II, Leipzig.
- Rockafellar, R.T. (1970) Convex Analysis. Princeton University Press, Princeton.
- Gale, D. (1960) The Theory of Linear Economic Models. McGraw-Hill, Inc., New York.
- Luenberger, D.G. (1969) Optimization by Vector Space Methods. Wiley, New York.
- Dixit, A.K. (1990) Optimization in Economic Theory. Oxford University Press, Oxford.
- Rudin, W. (1976) Principles of Mathematical Analysis. McGraw-Hill, Inc., London.

