Advances in Pure Mathematics
Vol.04 No.10(2014), Article ID:51075,15 pages
10.4236/apm.2014.410064
Real-Time Modelling of Dynamic Behaviour for Clinker Rotary Kilns: Learning from Experiment and Theory
Tarasiewicz Stanislaw, Yoboué Guillaume N’zi
Department of Mechanical Engineering, Laval University, Québec, Canada
Email: Stanislaw.Tarasiewicz@gmc.ulaval.ca, nziyob@yahoo.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2014; revised 8 August 2014; accepted 19 August 2014
ABSTRACT
The authors’ objective is to estimate a dynamic behaviour of Clinker Rotary Kiln when the state variables of the process can be measured only at a few locations. These variables (gas, clinker temperatures and clinker mass distributions) are elaborated with the help of heat, pressure and mass balance partial differential equations. The resulting state model, decomposed into five phenomenological zones of CRK, is used as a first step to define a set of Basic Operating Functions. A second step is used to identify a set of Operating Functions. These OFs have also been decomposed into longitudinal distributions of CRK to replace the constant, unknown or unmeasured parameters. Based on the feature of each zone, the OFs are obtained by solving the steady-state model using the standard Newton-Raphson procedure. The CRK is thus characterized by the state variables and intelligent software of the Numerical Estimated Operating Functions and method is proposed to reevaluate the set of the state variables, in adequate space step-size. Consequently, the state variables profiles are linked with the corresponding OFs, which have a direct influence on submitted disturbances for calibration.
Keywords:
Partial Differential Equations, State Variables, Operating Functions, Numerical Estimation

1. Introduction and Background
The Cement Rotary Kiln (CRK) is important equipment used in the chemical, metallurgical industries as well as waste treatment, where it is operated for the continuous process of mixing, heating, incineration, pyrolysis and drying. The basic components of a CRK, (treated as an investigation example) are the steel shell made from a rolled mild steel plate, the refractory material to insulate the steel shell from the high temperatures inside the kiln, a selected burner according to a designed process, supporting tyres and rollers, a driving motor and driving gears. An industrial kiln dimensions can be up to 6 [m] in internal diameter and more than 100 [m] long. Usually it is operated at 1 - 5 [RPM] rotational speed, 1 - 4 [˚] inclination angle and mass flow up to 12,000 [t/d]. A typical CRK with a 3.75 [m] internal diameter and 122.6 [m] long in a clinker production line is shown in Figure 1.
Whether the process is wet or dry, the same chemical reactions take place. Basic chemical reactions are: evaporating all moisture, calcinating the limestone to produce free calcium oxide, and reacting the calcium oxide with the minor materials (sand, shale, clay, and iron). This results in a final black, granular product known as “clinker”.
The study of the particle movement is crucial for the heat transfer from hot gas to the material as well as for process control. Because of the complex nature of the heat transfers, the space varying of the contact surface between the gas, the clinker and the wall is unexplained correctly by using the classical approach. The authors had to find a better way of dealing with this problem. In fact, some of these complex parameters cannot be characterized solely by experimentally measured values. The authors propose an innovative method that creates an intelligent-interface system linking CRK and mainframe computer and capable of working in real-time.
In theoretical approach, some models of the solid flow inside the CRK have been thoroughly investigated by many authors [1] - [14] . Most of them suppose that the CRK parameters are space-invariant. The well-known classical theory of modeling [1] [7] is very useful to investigate the relationship between the temperatures but only in the steady-state conditions. Presently, in modern cement industry, the CRK is often made up of a large number of measured elements, and according to a defined description (see Equations (1) and (2), and Figure 2) the practical investigation [9] - [12] have to be devised to implement numerical simulation techniques. Usually, selected kiln temperatures are very important operational parameters [1] [2] and it is possible to investigate the steady-state conditions by looking at the given relationship between them (see Equations (1) and (2), and Figure 2).
 (1)
(1)
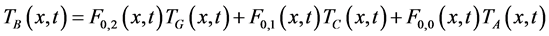 (2)
(2)
where: in particular case, if the CRK is in a steady-state operation,
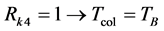 ,
,
Figure 1. CRK of a clinker production is defined by the five phenomenological zones.
Figure 2. Equivalent thermal circuit, i.e., the CRK with a clinker attachment.
and
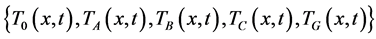
are ambient, shell, brick, clinker and gas temperatures respectively, all 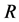 are the thermal resistances of geometry and body, and all
are the thermal resistances of geometry and body, and all 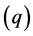 are heat transfers.
are heat transfers.
Once the CRK has been equipped with a system of instrumentations, as the Kiln Shell Temperature Scanner (KSTS), and a few dedicated temperature sensors [12] [15] , then it is possible to estimate the kiln longitudinal temperatures according to the Basic Operating Functions (BOFs), which are
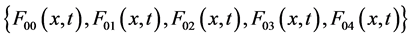 , of the model (see Equations (1) and (2)).
, of the model (see Equations (1) and (2)).
These BOF for the steady-state conditions will be represented by the following forms:
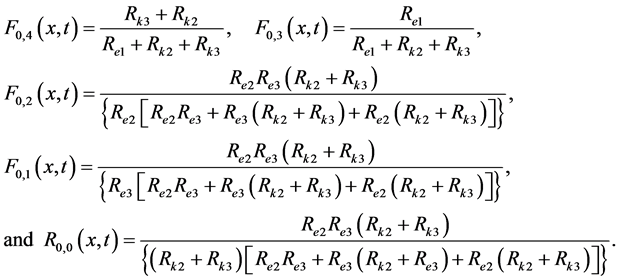
Now the given basic mathematical relationship of the CRK is used as a first step to define the dynamical behaviour which will be represented by a state mathematical model with the space and time-variable parameters [12] [16] .
2. Learning Experiences
The numerical values of the shell and gas temperatures have been collected over two weeks (see Figure 3) to complete the basic data of an operational condition of a full-scale CRK [12] [17] .
As shown in Figure 2 and Equations (1) and (2), the necessary information, estimation and calculation have been used to recreate a particular result of the clinker production process. This computed software has been created, and the computational results have been shown in Figures 4-6.
For the completion of the calculation procedure, by taking into consideration the geometry of CRK, and the longitudinal distribution of the physical phenomena along each zone, the BOFs have been calculated, and the computation can be found in the following diagrams (see Figures 7-9 and Appendix A).
Figure 3. The shell temperatures taken from a full-scale CRK.
Figure 4. Reproduced brick temperature profile from the dedicated sensors.
Figure 5. Reproduced clinker temperature profile from the dedicated sensors.
Figure 6. Reproduced gas temperature profile from the dedicated sensors.

Figure 7. Estimated BOFs: (a)


Figure 8. Estimated BOFs: (a)


Figure 9. Estimated BOFs: (a)
These examples (see Figs. above) illustrate the numerical identification of the BOFs that recreate the steady- state inside temperatures of the CRK (see Figures 4-6).
The author’s objective is to build a uniform mathematical model such as a computer intelligent monitoring system which can reproduce precisely the dynamic behaviour of the CRK with the space and time-variable parameters. In this context, it is necessary that a mathematical structure of a model be described by a set of state equations [9] [12] [16] [17] .
3. Mathematical Structure and Model Concept
Introducing the concept of such a model requires that a small slice 



The preliminary investigations [12] [17] were performed to trace these state variable profiles along the real CRK. The gas, the clinker and the shell temperatures have been measured at a number of specific locations in a steady-state condition. In addition, the raw meal input was stopped for an emergency maintenance. This was an exceptional opportunity to estimate the mass of material (clinker)
The resulting profiles, in the steady-state conditions, are shown in Figure 3, Figure 5, Figure 6, and Figure 8.
It is interesting to note that, in the practical operation of CRK, no general procedure exists for determining a set of the classical model parameters [3] [4] [6] [7] . Consequently, the MS suggests [12] [16] [17] that a set of the constant model parameters will be replaced by a set of the space and time-varying Operating Functions (OFs) for which initial conditions are defined as the BOFs (see Appendix A). Thus, a Fundamental Model (FM) for the CRK is:



Consequently, due to nature of the CRK, this system is constructed by a mixed structure including both distributed and lumped subsystems. To establish the frontiers between them, it is assumed that a set of
is a boundary limit for the kiln which is treated as a distributed subsystem, and the set of
is a boundary limit for the kiln suppliers treated as a lumped subsystem. Therefore, the analysis of the CRK requires that each state variable must be characterized by its boundary and initial conditions.
When the time derivative of each state equation of the FM, is equal zero, i.e.

each steady-state equation of the FM creates an Initial Condition (IC).
In this investigating problem, the steady-state profiles of 
Consequently, the fundamental problem when describing the Boundary Conditions (BCs) is to shift an output of the lumped subsystem with an input of the distributed subsystem, i.e., the output of a lumped subsystem becomes the input of a distributed subsystem 



In accordance with the description of the BCs, the set of the lumped variables will be treated as the control parameters (LV-CP):
and
should be varied to create the optimal conditions inside the CRK. The LV-CV, although treated before as constant, will vary from one time-step to the next in a manner which should be predicted a priori. Additionally, in the optimal operation of CRK, the set of the LV-CV is also called the set of controllability, and will be treated in further research.
For this presentation, (1)-(10) constitute a mathematical model of the dynamic behaviour of the CRK and will be dealt with by a real-time monitoring.
4. Numerical Experiment Evolutions for Standard Air/Fuel Relation
According to the fundamental model proposed by the authors, a simulation procedure consists of a microcomputer-based network of two calculating layers: First: in order to obtain the relationship between the boundary conditions and the resulting state variable profiles, a more elaborate investigation has been proposed, Second: to investigate the local shape of the state variables under various combinations of the Air/Fuel Ration, it was originally suggested to use an analogy of the organization of multi-programmed inputs, which consists of introducing a chemical analyzer into the fuel suppliers and the raw meal supplier.
Now, in the same approach as that of an estimating study of the BOFs (see Figures 7-9), the Standard Air/Fuel Ration (SAFR) has been chosen to obtain the numerical response of FM in the dynamic condition. The simulation tests for the temperature profiles are defined as follows:
Upon examination of the time-space responses of the FM, it can be concluded that using the adjusted OFs (see Appendix B) gives a very good comparison with the measured data. This observation on the model structure (see Figure 10(a) and Figure 11) is rather more interesting than using the classical model [7] [8] [13] .


Figure 10. (a) Temperature reproduced profiles; (b) Distributed mass clinker reproduced profile.


Figure 11. Time-space evolution of the gas and clinker temperatures for SAFR. (a) For gas; (b) For clinker.
5. Conclusions
The paper describes the methodology and estimated results for attempting to build a fundamental model of the CRK which characterizes both the transportation and transformation phenomena. The accuracy of this model is clearly dependent on how correctly and precisely the BOFs have been calibrated. Secondly, the estimation/res- olution of the state variables
Moreover, once the restored-estimated IC has been evaluated, the desired input (which is treated as the control of the CRK) can be more easily found by the proposed model than by simple trial and error method. Using the state variables approach, it is possible to find adequate measurement points to tune the OFs as the function of restored state variables. In summary, the cooperation and coordination in real-time between industrial computers and the CRK allows for the intelligent monitoring and optimization processes, where each specific set of the control variables must be analyzed by its controllability.
References
- Spang, H.A. (1972) Adynamic Model of a Cement Kilns. Automatica, 8, 309-323. http://dx.doi.org/10.1016/0005-1098(72)90050-7
- Bouge, R.H. (1947) The Chemistry of Portland Cement. The Maple Press Company, New York.
- Martins, M.A., Oliveira, M.A. and Franca, L.S. (2002) Modeling and Simulation of Limestone Calcinations in Rotary Kilns, Part 1: Pilot kIln, Part 2: Industrial Rotary Kiln. ZKG International, 4-5, 74-87.
- Guruz, H.K. and Bac, N. (1981) Mathematical Modeling of Rotary Cement Kilns by the Zone Method. The Canadian Journal of Chemical Engineering, 59, 540-548. http://dx.doi.org/10.1016/0005-1098(72)90050-7
- Mastorakos, E., Massias, A., Tsakiroglou, C. D., Goussis, C., Burganos, V. and Payatakes, A.C. (1999) CFD Predictions for Cement kilns Including Flame Modelling, Heat Transfer and Clinker Chemistry. Applied Mathematical Modelling, 23, 57-76. http://dx.doi.org/10.1016/S0307-904X(98)10053-7
- Gorog, J.P., Brimacombe, J.P. and Adams, T.N. (1981) Radiative Heat Transfer in Rotary Kilns. Metallurgical and Materials Transactions B, 12, 55-70.
- Barr, P.V., Brimacombe, J.K. and Watkinson, A.P. (1989) A Heat-Transfer Model for the Rotary Kiln, Part 2: Development of the Cross Section Model. Metallurgical and Materials Transactions B, 20, 403-419.
- Gorog, J.P., Adams, T.N. and Brimacombe, J.K. (1983) Heat Transfer from Flames in a Rotary Kiln. Metallurgical and Materials Transactions B, 14, 411-424.
- Tarasiewicz, S., Gille, J.C., Léger, F. and Vidal, P. (1994) Modelling and Simulation of Complex Mechanical Systems with Applications to a Steam-Generating System, Part 1: Mathematical Modeling. International Journal of Systems Science, 25, 2393-2402. http://dx.doi.org/10.1080/00207729408949360
- Tarasiewicz, S., Vidal, P., Léger, F. and Gille, J.C. (1994) Modelling and Simulation of Complex Mechanical Systems with Applications to a Steam-Generating System, Part 2: Numerical Simulation. International Journal of Systems Science, 25, 2403-2416. http://dx.doi.org/10.1080/00207729408949361
- Tarasiewicz, S., Charette, A. and Bui, R.T. (1983) Modeling the Direct Continuous Dryer. Proceedings of the 14th Annual Pittsburgh Conference, Pittsburgh, 569-580.
- Shahriari, K. and Tarasiewicz, S. (2011) Modeling of a Clinker Rotary Kiln Using Operating Functions Concept. The Canadian Journal of Chemical Engineering, 89, 345-359. http://dx.doi.org/10.1002/cjce.20398
- Incropera, F.P. and DeWitt, D.P. (2007) Fundamentals of Heat and Mass Transfer. 6th Edition, John Wiley & Sons, USA.
- Sonntag, R.-E. and Borgnakke, C. (2007) Introduction to Engineering Thermodynamics. 2nd Edition, John Wiley & Sons, USA.
- Hauser, A. and Walther, T. (1998) Temperature Measurement on Rotary Kiln and Clinker Coolers for Process Control. International Cement Journal, 1-3.
- Tarasiewicz, S. and Ding, F. (1998) Multilevel Control to Complex Systems. Proceeding of the Advances in Systems, Signals, Controls and Computers, Durban, 22-24 September 1998, 437-441.
- Tarasiewicz, S. and Shahriari, K. (2008) Operating Functions Approach to Model Heat Exchange in a Clinker Rotary Kiln: Case Study for Initial and Boundary Conditions. Technical Report, LACM-Laval University, CRIB-Laval University and Lafarge North America Inc., QC, Canada, 1-37.
Nomenclature
In general, subscripts have the following meaning:






















Subscript












Appendix A
The BOFs are decomposed according to the physical parameters of the system and measured state variables (see Figures A1-A5, and Figure B1) according to the physical parameters of the system and measured temperatures
Figure A1. 
Figure A2. 
Figure A3. 
Figure A4. 
Appendix B
B1. Two examples of the OFs which have been decomposed according to the physical parameters of the system and estimated state variables
B2. The numerical solution of the above mentioned FM satisfied the distributed profiles of the space-state variables of the CRK (see Figure 11) with the estimated OFs. According to this approach, the operating functions are:
Figure A5. 


Figure B1. Representation structures of two operating functions and their physical parameters. (a) Hierarchical structure of

Figure B2. Estimated operating functions (OFs) associated with the state variables of the FM.
Figure B3. The estimating linear velocity of the clinker.
Analyzing Figure B2 reveals that the OF profiles vary both with time and space-positions across the CRK. For this case the time-response of the FM provides valuable information relating to prescript physical and chemical phenomena. In addition, transferred energy attributed to the motions and configuration of the CRK also varies particularly between two involved temperatures, the heat transfer area, and the attributed chemical reactions. Thus, instead of choosing the constant coefficients in the model, it may be a requirement to opt for the OFs yielding the best possible values.
Examining once again Figure B2, it is possible to say that knowledge of the measured profile of shell temperatures, and restored temperature profiles of the kiln (see Figures 4-6, and Figure 10) are sufficient to estimate all OFs of the CRK as well as the linear velocity of the clinker (see Figure B3).
The results of preliminary tests justify the Newton-Raphson’s method to account for the numerical simulation of all OFs.


















































