Received 15 July 2014; revised 15 August 2014; accepted 1 September 2014

ABSTRACT

Using the same method that we used in [1] to prove Fermat’s Last Theorem in a simpler and truly marvellous way, we demonstrate that Beal’s Conjecture yields—in the simplest imaginable manner, to our effort to prove it.

Keywords:

Fermat’s Last Theorem, Beal’s conjecture, Proof

1. Introduction

“Simplicity is the ultimate sophistication.”—Leonardo da Vinci (1452-1519).

Beal’s Conjecture is a conjecture in number theory formulated in 1993 while investigating generalizations of Fermat’s Last Theorem set forth in 1997 as a Prize Problem by the United States of America’s Dallas, Texas number theory enthusiast and billionaire banker, Mr. Daniel Andrew Beal [2] . As originally stated, the con- jecture asserts that:

Beal’s Conjecture:

If,

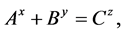(1)

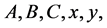and 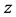are positive integers with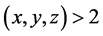, then 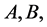and have a common prime factor.

For a correct proof or counterexample published in an internationally renowned and refereed mathematics journal, Mr. Beal initially offered a Prize of 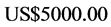in 1997, raising it to 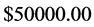over ten years by adding 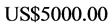each year over the ten-year period [2] . Very recently, Andrew Beal upped the stacks and has raised1 it beyond the initial projection of to.

Herein, we lay down a complete proof of the conjecture not so much for the very “handsome’’ prize money attached to it, but more for the sheer intellectual challenge that the philanthropist—Mr. Andrew Beal, has placed before humanity. We believe that challenges without flinching—must be tackled heard-on, without fear of failure.

From intuition, we strongly believe or feel that a direct proof of the original statement of Beal conjecture as stated in (1) would be difficult if not impossible to procure. We have to recast this statement into an equivalent form and proceed to a proof by way of contradiction. The equivalent statement to (1) is [2] :

Beal’s Conjecture (Recast):

The equation,

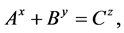(2)

admits no solutions for any positive integers and with 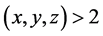for any piecewise co- prime triple 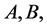and.

In its recast form (2), it becomes clear that Beal’s conjecture is a generalization of Fermat’s Last Theorem [3] where Fermat’s Last Theorem is the special case of Beal’s conjecture where. In the parlance of mathematics, Beal’s conjecture is a corollary to Fermat’s Last Theorem.

The proof that we present demonstrates that the triple can not be co-prime. This is the same method that we used in our “simple, and much more general Proof of Fermat’s Last Theorem’’ [1] . Actually, the present proof is a generalization of the proof of Fermat’s Last Theorem presented in [1] .

The synopsis of this reading is as follows. In §(2), we provide a pivotal lemma that is necessary for our argument. In §(3), we provide the short proof of Beal’s Conjecture and thereafter in §(4), we give a general discussion and the conclusion drawn thereof.

2. Lemma

If where and is one of the prime factors of, then, the following will hold true always:

(3)

The above statement is clearly evident and needs no proof. Below we demonstrate that this statement is true. This demonstration does not constitute a proof.

What this statement really means is that the number (for any and), can always be written as a sum or difference of two numbers and where and are not co-prime, i.e.:

(4)

since one can always find some such that will always be a common factor of, that is to say:

(5)

in which case we will have p = ag and where such that and. If is the set of all the prime factors of, then where. Substituting all this into (5), we will have:

(6)

Setting and, (6) leads us to (3). Therefore, equipped with this simple fact, we will de- monstrate that as we did with Fermat’s Last Theorem, that Beal’s Conjecture yields to a proof in the simplest imaginable manner.

3. Proof

The proof that we are going to provide is a proof by contradiction and this proof makes use of Lemma §(2) whereby we demonstrate that the triple is such that it will always have a common factor if the equation,; is to hold true. We begin by assuming that the statement:

(7)

to be true for some piecewise co-prime triple, the meaning of which is that the greatest common divisor of this triple or any arbitrary pair of the triple is unity i.e.,.

First, we must realise that if just one of the members of the triple is equal to unity for any, then, the other two members of this triple can not be integers, hence, from this it follows that if a solution exists, then, all the members of this triple will be greater than unity i.e..

Now, for our proof, by way of contradiction, we assert that there exists a set of positive integers that satisfies the simple relation for some piecewise co-prime triple. Having made this assumption, if we can show that, then, by way of contradiction Beal’s Conjecture holds true.

If the statement (7) holds true, then—clearly; there must exist some such that, such that, and can be decomposed as follows:

(8)

Now, according to the Lemma §(2), the equation for any and for any, this equation, can always be written such that and for some and is any of the prime factors of; putting everything together, we will have. Substituting and into (8), we will have:

(9)

From (9), it is clear that since there exists a common divisor of the triple

which is, that is to say, is a common divisor of the triple. If, consequently, and this is in complete violation of the critical, crucial

and sacrosanct assumption that.

Alternatively, according to the Lemma §(2), the equation for any and for any,

this equation, can always be written such that and for some and is any of the prime factors of; putting everything together, we will have.

Now, substituting and into (8), we will have:

(10)

Again, from (10), it is clear that since the, that is to say, is a common divisor of triple. From the foregoing, it follows that the prime factors of are common divisors of the triple, the meaning of which is that.

Therefore, by way of contradiction, Beal’s Conjecture is true since we arrive at a contradictory result that. What this effectively means is that the equation for has a solution and this solution is such that the triple always has a common factor as is the case with all those values of, , that satisfy Beal’s Conjecture.

4. Discussion

At present, it appears that there has not been found a general proof of Beal’s conjecture, only partial solutions exist. For example, the case and all its permutations were proven to have only four solutions, none of them involving an even power greater than 2 by Poonen et al. [4] . The case and all its permutations are known to have only three solutions, none of them involving an even power greater than 2 and this was proved by Crandall & Pomerance [5] . There are a number of such cases [6] - [8] where partial proofs have been presented. As-well, there are cases where computer searchers are made [9] . If Beal’s is true as we have shown herein, then, all computer searches will never find a counter-example and the best way to resolved this would be via general proof as we have done here.

Our thrust has been on a direct proof and just as the proof presented in the reading [1] , the proof here provided is simple, general and all-encompassing. It covers all possible cases. Clearly, the present proof applies elementary methods of arithmetic that where available even in the days of Fermat. At this point, if anything, we only await the judgement of the world of mathematics as to whether this proof is correct or not. Without any oversight on our confidence in our proof, allow us to say that, until such a time that evidence to the contrary is brought forth, we are at any rate, convinced of the correctness of the proof here presented.

We have presented another proof of Fermat’s Last Theorem in the reading [10] and this proof makes use of the method of Pythagorean triples. This proof is much longer than the proof using the methods presented herein. We will be presenting a second version of the proof of Beal’s Conjecture using the method of Pythagorean triples used in [10] .

5. Conclusion

We hereby make the following conclusion that if our proof is correct as we strongly believe, then, Beal’s Conjecture seizes to be a conjecture but forthwith transforms into a fully-fledged theorem as a logically and mathematically correct proof has now been supplied.

References

NOTES

¹The Beal Prize, AMS, http://www.ams.org/profession/prizes-awards/ams-supported/beal-prize