Advances in Pure Mathematics
Vol.4 No.5(2014), Article ID:45778,5 pages DOI:10.4236/apm.2014.45024
A Solution of a Problem of I. P. Natanson Concerning the Decomposition of an Interval into Disjoint Perfect Sets
Edgar A. Cohen Jr.
Formerly of the Information Sciences Branch, Naval Surface Warfare Center, White Oak, Silver Spring, MD, USA
Email: edcohenfam@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 March 2014; revised 10 April 2014; accepted 16 April 2014
ABSTRACT
In a previous paper published in this journal, it was demonstrated that any bounded, closed interval of the real line can, except for a set of Lebesgue measure 0, be expressed as a union of c pairwise disjoint perfect sets, where c is the cardinality of the continuum. It turns out that the methodology presented there cannot be used to show that such an interval is actually decomposable into c nonoverlapping perfect sets without the exception of a set of Lebesgue measure 0. We shall show, utilizing a Hilbert-type space-filling curve, that such a decomposition is possible. Furthermore, we prove that, in fact, any interval, bounded or not, can be so expressed.
Keywords:Space-Filling Curve, Perfect Sets, Inverse Image of a Perfect Set, Vertical Line Segments

1. Introduction
In a paper published previously in this journal (see [1] ), it was shown that any bounded, closed interval of the real line can, except for a set of Lebesgue measure 0, be decomposed into c pairwise disjoint perfect sets, where c is the power of the continuum. In this paper we present a proof that such a decomposition is possible without the exception of a set of 0 measure. We are motivated by a problem in a well-known book by I. P. Natanson (see [2] ). There the claim is made that the closed interval [0,1] can be decomposed in this fashion. We utilize a Hilbert-type space-filling curve to show this. The recent work of Nicholas J. Rose (see [3] ) is invoked here in this demonstration.
Furthermore it is shown that any interval, bounded or not, is expressible as the union of c pairwise disjoint perfect sets relative to the interval topology. Then it is proven that the relatively perfect sets can be expressed as a countable union of pairwise disjoint perfect subsets of the real line, and, from that fact, one deduces that any interval is resolvable into c pairwise disjoint perfect sets.
2. Results
Theorem. Any bounded closed interval [a,b] of the real line is expressible as a union of c pairwise disjoint perfect sets.
Proof. First of all, there exists a (continuous) linear map x = L(t) of [a,b] onto [0,1], namely,
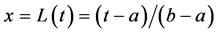 (1)
(1)
Also, one can map [0,1] continuously onto the closed square [0,1] × [0,1] of the xy-plane by invoking a Hilbert-type space-filling curve (see [3] ). We designate the latter curve by
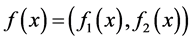 (2)
(2)
where 0 ≤ x ≤ 1. In addition, appealing to Equation (1), let us observe that
 (3)
(3)
is a continuous map of [a,b] onto the square [0,1] × [0,1]. Now a Hilbert-type space-filling curve is of fractal type, meaning that one can divide [0,1] × [0,1] into 4n subsquares, corresponding to 4n equal subintervals of [0,1], each of which is mapped onto one of the 4n subsquares. Furthermore each of these 4n maps is of a nature similar to the initial map (see [3] ).
Next consider the c vertical line segments
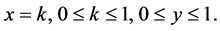 (4)
(4)
Since f(x) is a continuous map and all such line segments are closed, their inverse images are likewise closed (see [4] ). Furthermore, because these vertical segments cover the square, their inverse images cover [0,1] and are pairwise disjoint. Thus we are assured of c pairwise disjoint closed sets which cover [0,1]. To prove that each such set is perfect one need only note that each of the 4n subintervals of [0,1] is dedicated to precisely one of the 4n subsquares, and, as n tends to ∞, the diameter of each of these 4n subintervals and subsquares tends to 0. Therefore, every point of such an inverse image must be an accumulation point.
Finally, consider the linear map x = L(t), as given by Equation (1), and the inverse image under this map of any of the aforementioned perfect subsets of [0,1]. Obviously any such subset is a perfect subset of [a,b], and these subsets form the required decomposition.
Corollary 1. Any subinterval of the real line (including the real line itself) can be decomposed into c pairwise disjoint perfect sets in the relative topology of the subinterval.
Proof. There is always a continuous map of any subinterval of the real line onto the closed subinterval [0,1]. For example, consider the open interval (0,1). Then
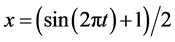 (5)
(5)
maps (0,1) continuously onto [0,1]. Using Equation (5) one can likewise map the half open intervals [0,1) and (0,1] onto the closed interval [0,1]. Although it is not generally true that the inverse image of a perfect subset under the mapping given by Equation (5) is a perfect set in the relative topology of either [0,1) or (0,1], it does turn out (see [3] ) that the perfect subsets of [0,1) engendered by Equation (4) for any k do have inverse images under Equation (5) that are again perfect. This property arises from the very nature of the Hilbert space-filling curve. For example, let us consider the mapping of (0,1] onto [0,1] afforded by Equation (5). We see that
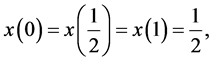 (6)
(6)
and we also observe, from the Rose paper (see [3] ), that
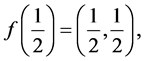 (7)
(7)
i.e., that the point x = 1/2 is mapped to the center of the unit square via Equation (2). On the other hand, since x = 1/2 is at the center of [0,1] and, for each n, we partition [0,1] into 4n equal subintervals, there are certainly points on either side of x = 1/2 which are arbitrarily close to x = 1/2 and whose images under the mapping of Equation (4) with k = 1/2 lie on that designated vertical line segment. Referring once more to Equation (5), together with Equations (6), we see that t = 0, 1/2, and 1 must all be accumulation points of the preimage of the perfect subset of [0,1] corresponding to k = 1/2. Thus, in particular, t = 0 and t = 1 are accumulation points of that closed subset of (0,1] induced by k = 1/2. Ultimately, then, the line segments provided by Equation (4) induce relatively perfect subsets of (0,1] (see [5] ). The other half-open subinterval, viz, [0,1), can be similarly treated. Also, using Equation (5) for the open interval (0,1), one clearly sees that the inverse image is relatively perfect there as well.
As another example, consider the subinterval [0,∞). In this case the function
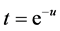 (8)
(8)
will map [0,∞) onto (0,1], and then Equation (5) can be used to map (0,1] onto [0,1]. Finally [0,1] is mapped continuously onto [0,1]×[0,1], and the inverse image of a closed vertical line segment under the composite map provided by Equations (2), (5), and (8) is a perfect subset of [0,∞). In this case, since [0,∞) is a closed subset of the real line, the perfect subset of [0,∞) is also a perfect subset of the real line.
Finally consider the real line (–∞,+∞) and the mapping of the real line onto the open interval (−π/2,π/2) provided by the principal arctan function, namely,
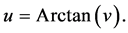 (9)
(9)
Next (–π/2,π/2) can be mapped onto (0,1) utilizing t = L(u) as provided by Equation (1) with a = −π/2 and b = π/2. Then, appealing to Equation (5), one can map (0,1) onto [0,1]. Finally [0,1] is mapped onto the closed unit square using Equation (2). The inverse image of a closed vertical line segment through the closed unit square using the composite function thus formed will then be a perfect subset of (−∞,+∞), as desired.
It should now be clear that any subinterval of the real line can be expressed as a union of c pairwise disjoint perfect subsets in the relative topology of the subinterval. If the subinterval itself is absolutely closed, then we can say that these perfect subsets will themselves be absolutely closed. Corollary 1 is thus established.
Corollary 2. Any relatively perfect set of Corollary 1 can be decomposed into a denumerable number of pairwise disjoint perfect subsets in the usual topology of the real line. Therefore, in fact, any subinterval of the real line is representable as a union of c pairwise disjoint perfect sets of the real line.
Proof. We first establish that the preimages of the closed vertical segments of the unit square [0,1] × [0,1] under the mapping given by Equation (2) are not only perfect sets but also nowhere dense sets, so that they do not contain any intervals. In fact let us refer to the Rose paper (see [3] ), in which it is shown that the coordinate functions f1(x) and f2(x) are nondifferentiable (see Theorem 3 of that paper). If any preimage of a closed vertical line segment as given by Equation (4) were to contain an open interval (x1,x2) of x values, then one has
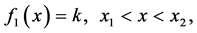 (10)
(10)
and then the derivative  over the interval (x1,x2). However we know that f1(x) is nondifferentiable, so it follows that the preimage is indeed a Cantor type set (contains no intervals).
over the interval (x1,x2). However we know that f1(x) is nondifferentiable, so it follows that the preimage is indeed a Cantor type set (contains no intervals).
Now, if we are considering an interval of the real line which is not closed, then the sets of concern to us are those which do not contain one or both of the interval endpoints. Such endpoints are then accumulation points of one of the sets of interest but do not belong to the set, all other points of the set being limit points belonging to the interval. It is also true that such sets contain no intervals inasmuch as they are derived from preimages of Cantor sets under continuous mappings of the type exhibited by Equations (1), (5), (8), and (9). Such functions are either strictly monotonic or can be decomposed into branches all of which are strictly monotonic. This result then follows from the well-known fact that the image of a connected set under a continuous mapping is again connected (see [4] ).
Suppose then, for the sake of argument, that the interval of concern is the half-closed interval (a,b] and that a is an endpoint of the Cantor type set C of interest. Then, because C contains no intervals, certainly there exists an open interval (a1,b1) contained in (a,b] but not in C, i.e.,
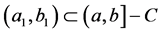 . (11)
. (11)
Let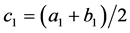 , and observe that c1 does not belong to C. Also, note that
, and observe that c1 does not belong to C. Also, note that
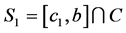 (12)
(12)
is a perfect subset of C. Next consider (a,c1], and choose an open interval (a2,b2) such that
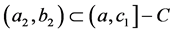 (13)
(13)
and
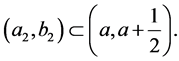 (14)
(14)
Let 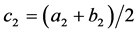 and let
and let
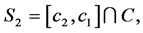 (15)
(15)
a perfect subset of C disjoint from S1 and contained in (a,b]. In general, letting c0 = b, we form
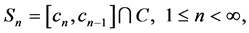 (16)
(16)
where  and
and
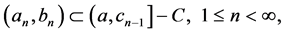 (17)
(17)
together with the requirement that
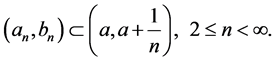 (18)
(18)
Finally,
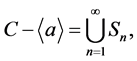 (19)
(19)
where each Sn is a perfect set and the Sn’s are pairwise disjoint. Of course, some of the Sn’s may be empty.
Now, if we consider the Sn’s, together with the other perfect sets which are preimages of the closed vertical line segments of the unit square [0,1] × [0,1], they form our decomposition of (a,b] into c perfect and pairwise disjoint subsets. Other intervals can be treated in a similar fashion. So Corollary 2 is established.
3. Conclusion
It has been shown that any subinterval of the real line can, first of all, be expressed as a union of c pairwise disjoint perfect sets in the subinterval relative topology. This result follows by initially devising s continuous map from the interval onto the closed interval [0,1], followed by a Hilbert space-filling curve from [0,1] onto the closed unit square [0,1] × [0,1]. Then the inverse images of closed vertical line segments through the square yield the perfect sets desired. Finally the relatively perfect sets thus obtained are expressible as a countable union of pairwise disjoint perfect sets, and it follows that any interval is decomposable into c pairwise disjoint perfect sets. Thus, a problem of I. P. Natanson (see [2] ), together with a generalization for arbitrary intervals of the real line, is resolved.
Acknowledgements
The author would like to acknowledge a suggestion of Professor Srinivasa Varadhan, of the Courant Institute of New York University, viz, that of using a space-filling curve as a device for attempting to solve the problem given by I. P. Natanson. It has turned out that one needs to be careful as to the nature of the space-filling curve used. One of Hilbert type appears to satisfy the requirements.
References
- Cohen Jr., E.A. (2013) On the Decomposition of a Bounded Close Interval of the Real Line into Closed Sets. Advances in Pure Mathematics, 3, 405-408. http://dx.doi.org/10.4236/apm.2013.34058
- Natanson, I.P. (1961) Theory of Functions of a Real Variable. Volume 1, Frederick Ungar Publishing Co., Inc., New York, 54.
- Rose, N.J. (2010) Hilbert-Type Space-Filling Curves. http://www4.ncsu.edu/~njrose/pdfFiles/HilbertCurve.pdf
- Hall, D.W. and Spencer II, G.L. (1955) Elementary Topology. John Wiley and Sons, Inc., New York, 72, 78.
- Bourbaki, N. (1971) General Topology. Springer-Verlag, 24.

