ABSTRACT

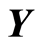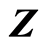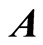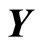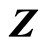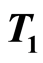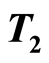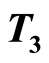The set of continuous functions from topological space to topological space endowed with a topology forms the function space. For subset of, the set of continuous functions from the space to the space forms the underlying function space with an induced topology. The function space has properties of topological space dependent on the properties of the space, such as the, , and separation axioms. 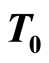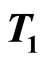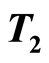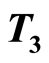In this paper, we show that the underlying function space inherits the, , and separation axioms from the function space, and that these separation axioms are hereditary on function spaces.

Keywords:Function Space; Underlying Function Space; Hereditary Properties

1. Introduction

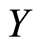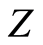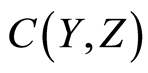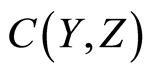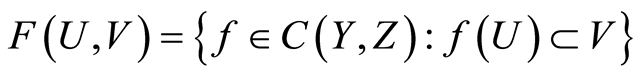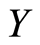The set of continuous functions from the space to the space is denoted by. The set open topology defined on the set generated by the sets of the formwhere the sets and ranges over the class of compact subsets of and 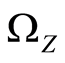class of open subsets of respectively, is called the compact open topology. The sets of the form 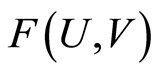forms subbases for the compact open topology 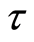on 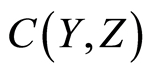(see [1] ). The set open topology 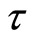defined on the set 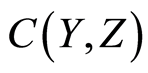generated by the subbases where 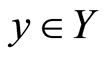and 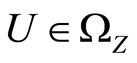is called point open topology (see [2] ).

Let 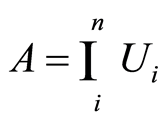for 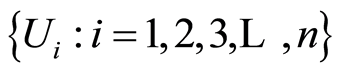family of non-empty open subsets of. The set 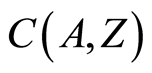consist of continuous functions of the form 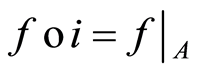where 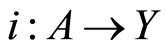is an inclusion mapping (see [3] ).

Let the topological space be a 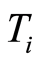-space for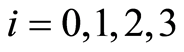, then the function space 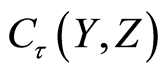with compact open topology 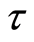inherits the 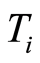-separation axioms for (see [4] and [5] ).

Definition 1.1 For, the sets of the form

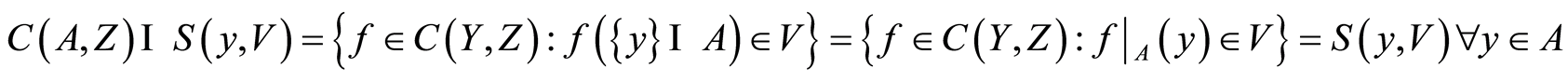as defined in [3] , forms the subbases for point open topology on the set.

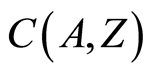Definition 1.2 The sets of the form

where is open in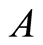, 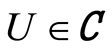and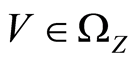, defines the subbases for the set open topology on the set 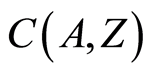(see [3] ). This topology is referred to as open-open topology (see [6] ). If 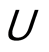is compact, then 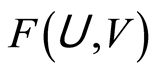defines the subbases for the compact open topology on the set.

The point open topology and the compact open topology are also open-open topologies. The set 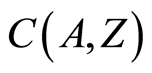endowed with set open topology 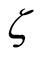is written as 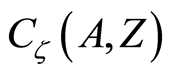and is referred to as the underlying function space of the space 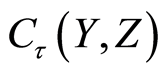(see [3] ).

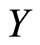Definition 1.3 Let and be open subsets of and 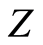respectively. The set forms the subspace of the function space 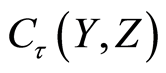with the induced topology generated by the subbases (see [7] ).

The following lemma and theorem are important for our consideration.

Lemma 1.4 In a regular space, if 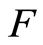is compact, 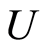an open subset of a regular space and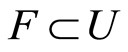, then for some open set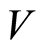, and.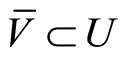

From the above lemma, the following inference is made. Let 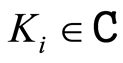where is a class of compact subsets of and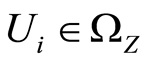. Then for the space 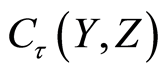with compact open topology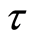, 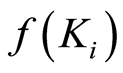is a compact subset of. Since 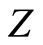is a regular space, there exist open sets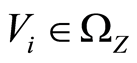, such that 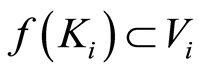and.

This implies that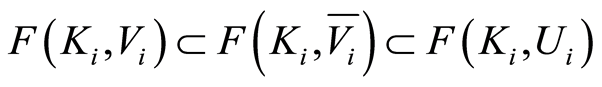, in which the assertion 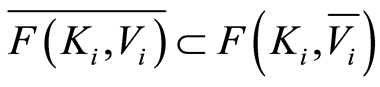can be made (see [5] ).

Theorem 1.5 The function 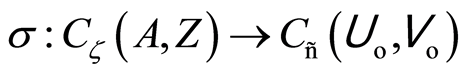defined by 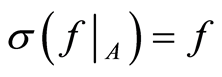is a homeomorphism (see [7] ).

2. Lower Separation Axioms on the Underlying Function Space

In this section, we show that the underlying function space inherits the -separation axioms for 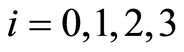from the space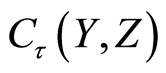. Topologies 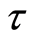and 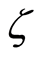are both compact open.

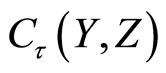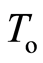Theorem 2.1 Let the function space be a space. The function space 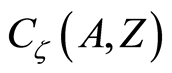for is a 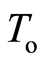space.

Proof. Let 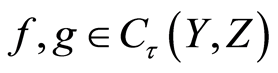be distinct maps such that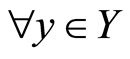,. Then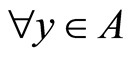, 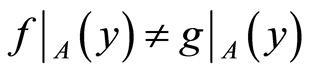. For the open set 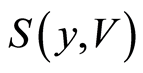containing 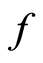but not 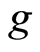in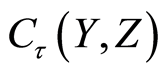, the open set

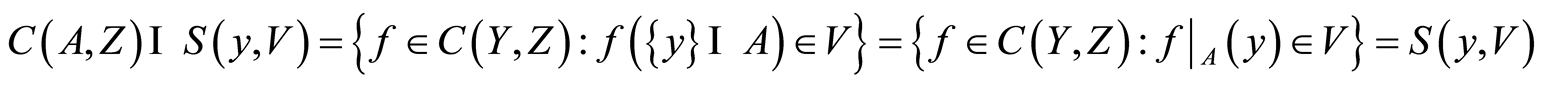in 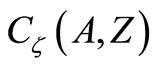contains but not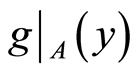. Therefore the space 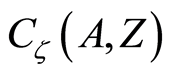is a 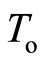space.                       □

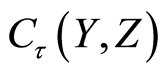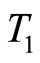Theorem 2.2 Let the function space be a space. The function space 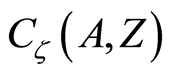for is a 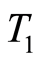space.

Proof. Let 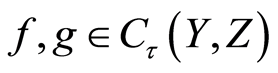be distinct maps such that,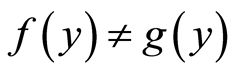. Then,

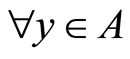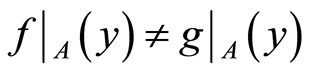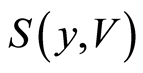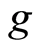. For the open sets containing but not and 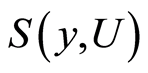containing 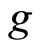but not in, the open sets

and

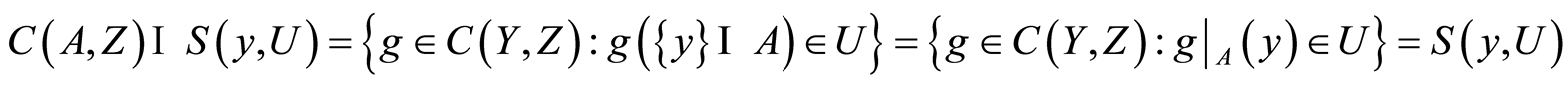
in 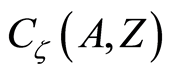are neighborhoods of 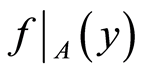but not and but not 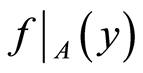respectively. Therefore the space 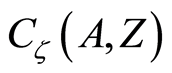is a 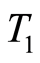space.                                                   □

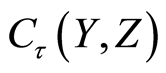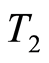Theorem 2.3 Let the function space be a space. The function space 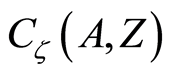for is a 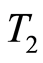space.

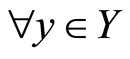Proof. Let be distinct maps such that,. Then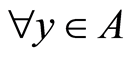,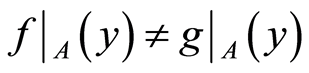. For the disjoint open sets 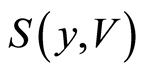and 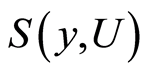neighborhoods of 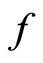and 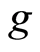respectively in, the open sets

and

in are disjoint neighborhoods of and 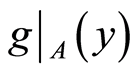respectively. Therefore the space 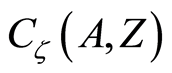is a space.                                                                             □

Theorem 2.4 Let the function space 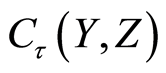be a regular space for a regular space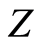. The function space for is a regular space.

Proof. The space is regular for a regular space 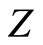if for the open cover 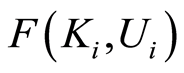of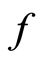, there exist open sets 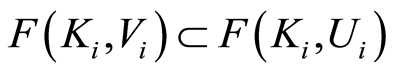neighborhoods of 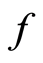such that for 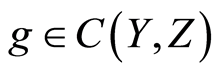and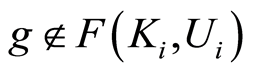, 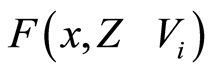for some 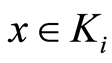is a neighborhood of which does not intersect 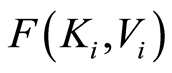and

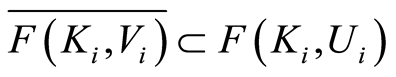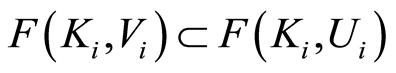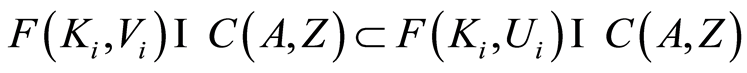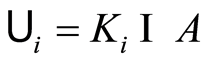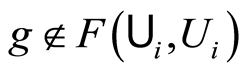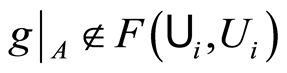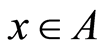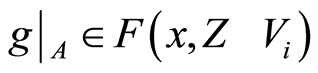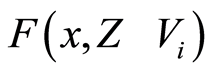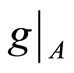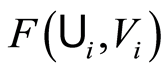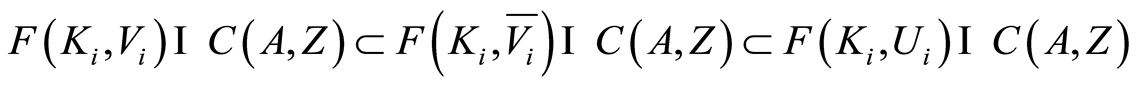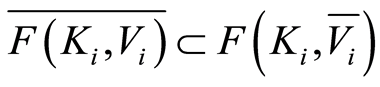. For, implying that, where. For we have that, implying that and for,. Therefore is a neighbourhood of not intersecting. implies that. From the assertion in Lemma 1.4, we have that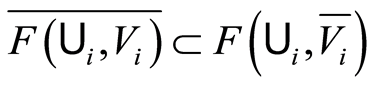. Therefore 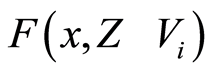and 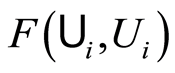are two disjoint open sets neighborhoods of 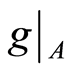and respectively. Hence the set 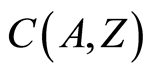with the induced topology 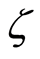is a regular space.                                                                                    □

3. Conclusion

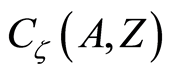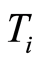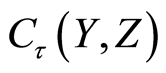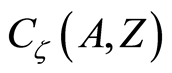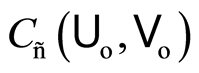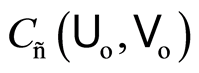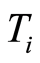The underlying function space inherits the -separation axioms for from the function space. From theorem 1.5, the underlying function space is homeomorphic to the subspace of the function space. This implies that the subspace is a -space for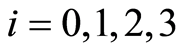, if the function space 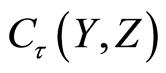is a 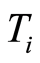-space for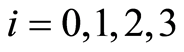. Therefore the 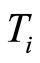-separation axioms for are hereditary on function spaces.

References