Advances in Pure Mathematics
Vol.3 No.9(2013), Article ID:40884,6 pages DOI:10.4236/apm.2013.39096
Nil 3-Armendariz Rings
1Department of Mathematics, Northwest Normal University, Lanzhou, China
2Department of Mathematics, Khartoum University, Omdurman, Sudan
Email: eltiyeb76@gmail.com, ayou1975@yahoo.com, liuzk@nwnu.edu.cn
Copyright © 2013 Eltiyeb Ali et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Eltiyeb Ali et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received November 13, 2013; revised December 13, 2013; accepted December 18, 2013
Keywords: Armendariz Ring; 3-Armendariz Ring; Nil Armendariz Ring; Nil 3-Armendariz Ring
ABSTRACT
We introduce nil 3-Armendariz rings, which are generalization of 3-Armendariz rings and nil Armendaiz rings and investigate their properties. We show that a ring 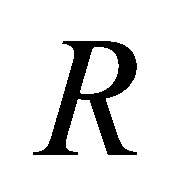 is nil 3-Armendariz ring if and only if for any n Î ℕ,
is nil 3-Armendariz ring if and only if for any n Î ℕ, 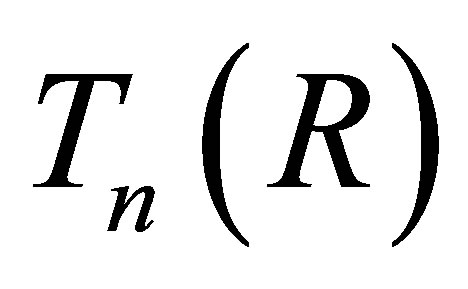 is nil 3-Armendariz ring. Also we prove that a right Ore ring R is nil 3-Armendariz if and only if so is Q, where Q is the classical right quotient ring of
is nil 3-Armendariz ring. Also we prove that a right Ore ring R is nil 3-Armendariz if and only if so is Q, where Q is the classical right quotient ring of . With the help of this result, we can show that a commutative ring
. With the help of this result, we can show that a commutative ring 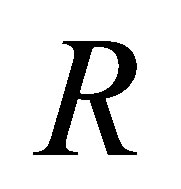 is nil 3-Armendariz if and only if the total quotient ring of
is nil 3-Armendariz if and only if the total quotient ring of  is nil 3-Armendariz.
is nil 3-Armendariz.
1. Introduction
Throughout this article, 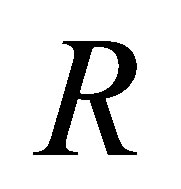 denotes an associative ring, not necessary with identity. Given a ring
denotes an associative ring, not necessary with identity. Given a ring 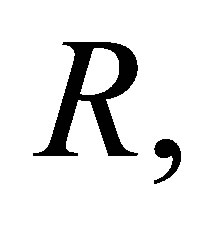 the polynomial ring over
the polynomial ring over  is denoted by
is denoted by  The study of Armendariz ring was initiated by Armendariz [1] and Rege and Chhawchharia [2]. A ring
The study of Armendariz ring was initiated by Armendariz [1] and Rege and Chhawchharia [2]. A ring  is called Armendariz if whenever polynomials
is called Armendariz if whenever polynomials 
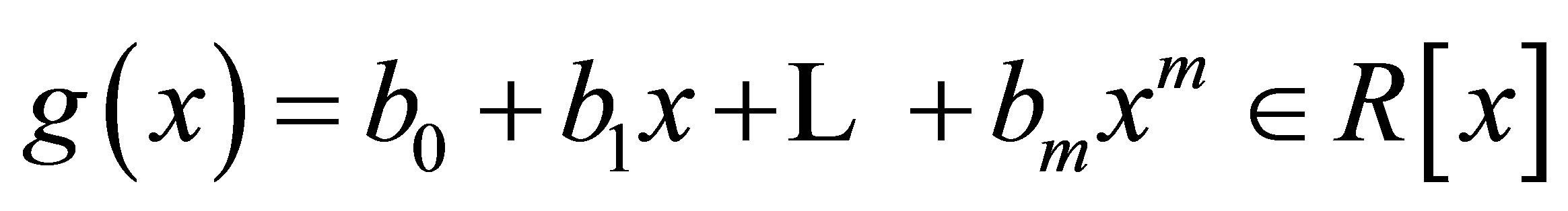 satisfy
satisfy 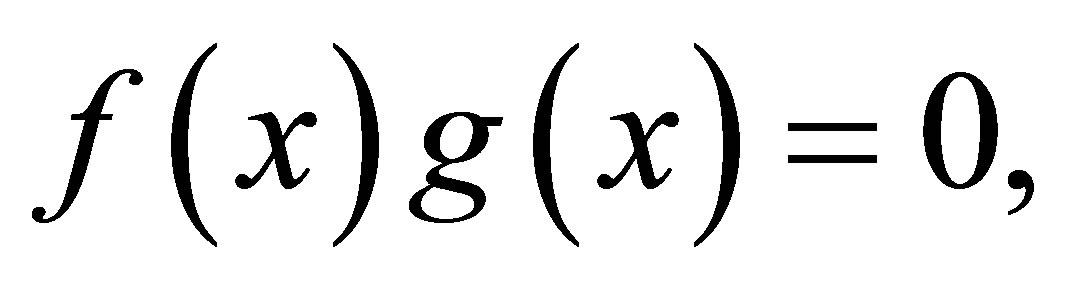 then
then  for all i, j. (The converse is always true.) Some properties of Armendariz rings have been studied in Rege and Chhawchharia [2], Anderson and Camillo [3], Kim and Lee [4], Huh et al. [5], and Lee and Wong [6]. Suiyi [7] introduced the notion of 3-Armendariz ring. A ring
for all i, j. (The converse is always true.) Some properties of Armendariz rings have been studied in Rege and Chhawchharia [2], Anderson and Camillo [3], Kim and Lee [4], Huh et al. [5], and Lee and Wong [6]. Suiyi [7] introduced the notion of 3-Armendariz ring. A ring 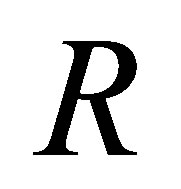 is called a 3-Armendariz if whenever polynomials
is called a 3-Armendariz if whenever polynomials 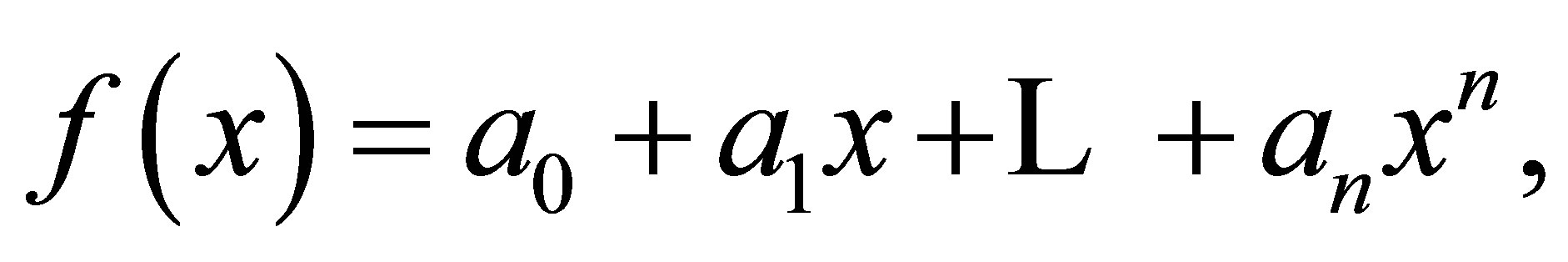
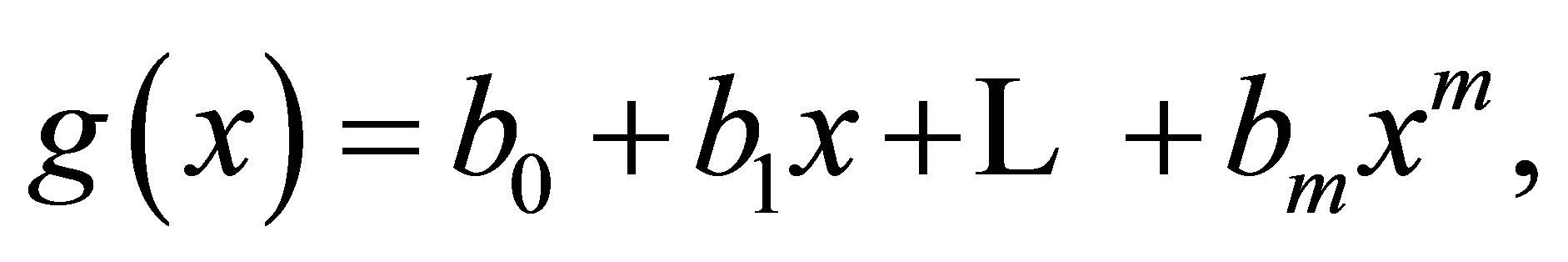
 satisfy
satisfy 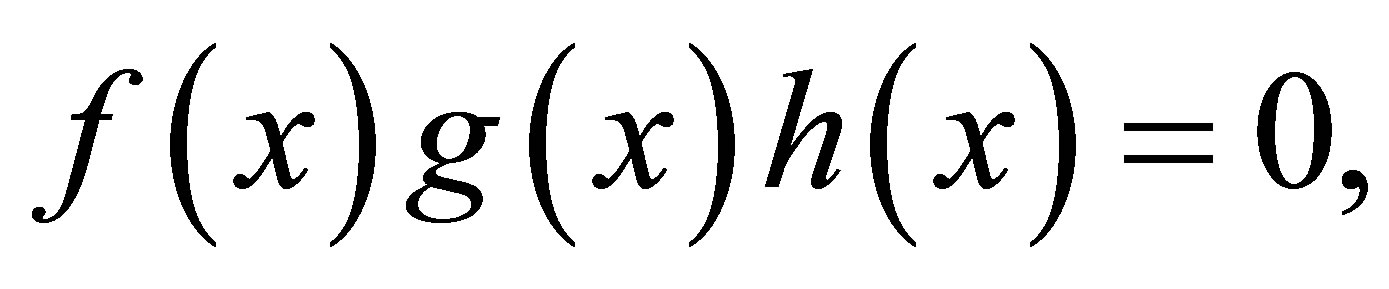 then
then  for all
for all 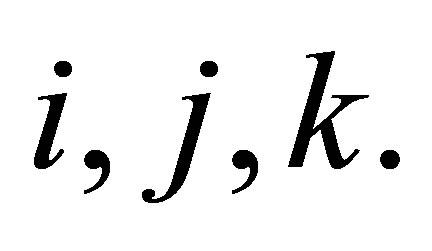 Due to Ramon Antoine [8], a ring
Due to Ramon Antoine [8], a ring 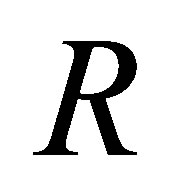 is said to be nil Armendariz if whenever two polynomials
is said to be nil Armendariz if whenever two polynomials 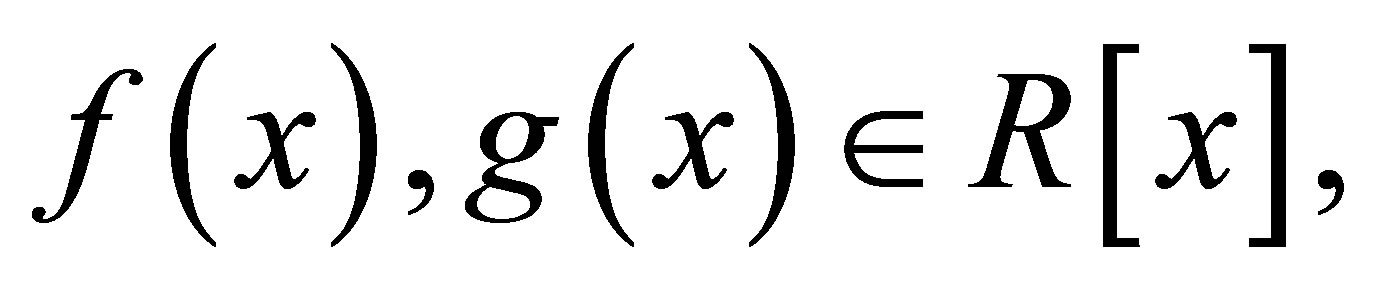 satisfy
satisfy  then
then 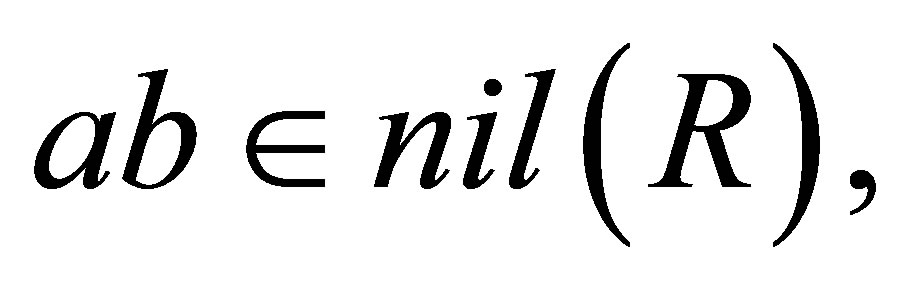 for all
for all  and
and 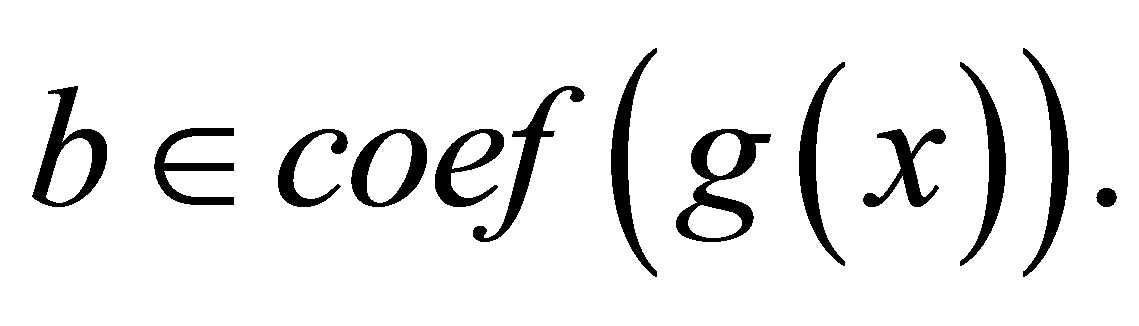 There is a nil Armendariz ring but not Armendaiz by [8, Example 4.11]. A ring
There is a nil Armendariz ring but not Armendaiz by [8, Example 4.11]. A ring 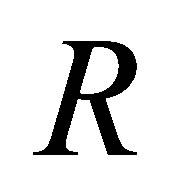 is called reduced if it has no nonzero nilpotent elements. Armendariz rings are thus a generalization of reduced rings, and therefore, nilpotent elements play an important role in this class of rings. There are many examples of rings with nilpotent elements which are Armendariz. In fact, in [3], Anderson and Camillo prove that if
is called reduced if it has no nonzero nilpotent elements. Armendariz rings are thus a generalization of reduced rings, and therefore, nilpotent elements play an important role in this class of rings. There are many examples of rings with nilpotent elements which are Armendariz. In fact, in [3], Anderson and Camillo prove that if  then
then 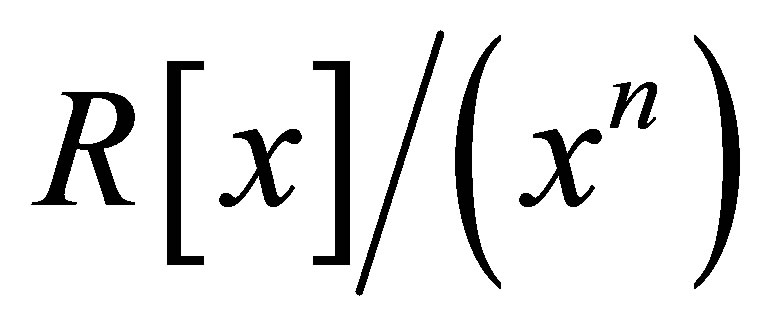 is an Armendariz ring if and only if
is an Armendariz ring if and only if 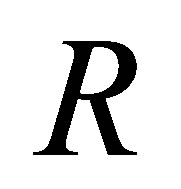 is reduced. In [9], Liu and Zhao introduced weak Armendariz rings as a generalization of Armendariz rings. A ring is weak Armendariz if whenever the product of two polynomials is zero then the product of their coefficients is nilpotent. In [10], Wu Hui-feng introduced the concept of weak 3-Armendariz ring as a generalization of 3-Armendariz rings and weak Armendariz ring and investigated their properties. A ring is weak 3-Armendariz if whenever the product of three polynomials is zero then the product of their coefficients is nilpotent. Motivated by results in Suiyi [7], Liu and Zhao [9], Antoine [8], Kim and Lee [4], Rege and Chhawchharia [2], and Wu Hui-feng [10,11], we investigate a generalization of nil Armendariz rings and 3-Armemdariz rings which we call nil 3-Armendariz rings.
is reduced. In [9], Liu and Zhao introduced weak Armendariz rings as a generalization of Armendariz rings. A ring is weak Armendariz if whenever the product of two polynomials is zero then the product of their coefficients is nilpotent. In [10], Wu Hui-feng introduced the concept of weak 3-Armendariz ring as a generalization of 3-Armendariz rings and weak Armendariz ring and investigated their properties. A ring is weak 3-Armendariz if whenever the product of three polynomials is zero then the product of their coefficients is nilpotent. Motivated by results in Suiyi [7], Liu and Zhao [9], Antoine [8], Kim and Lee [4], Rege and Chhawchharia [2], and Wu Hui-feng [10,11], we investigate a generalization of nil Armendariz rings and 3-Armemdariz rings which we call nil 3-Armendariz rings.
2. Nil 3-Armendariz Rings
If 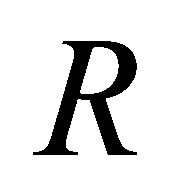 is a ring,
is a ring, 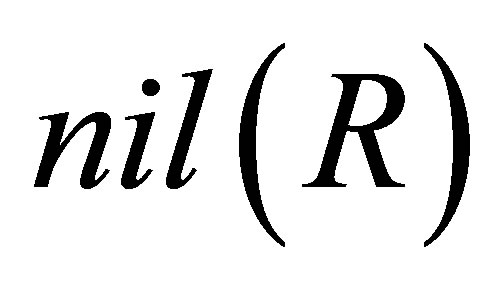 denotes the set of all nilpotent elements in
denotes the set of all nilpotent elements in 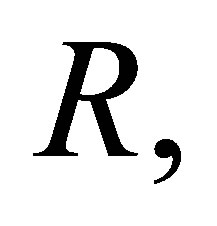 and if
and if 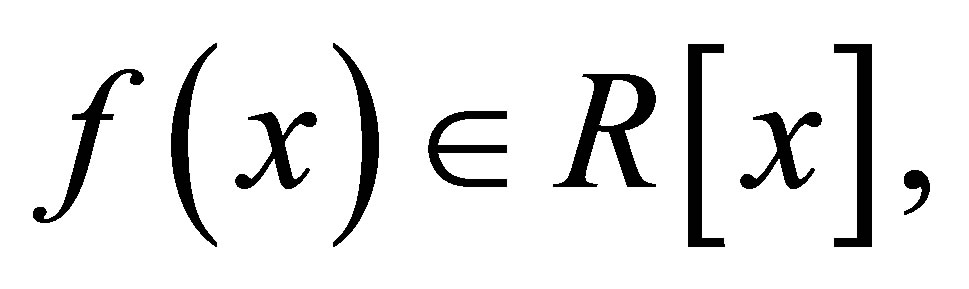
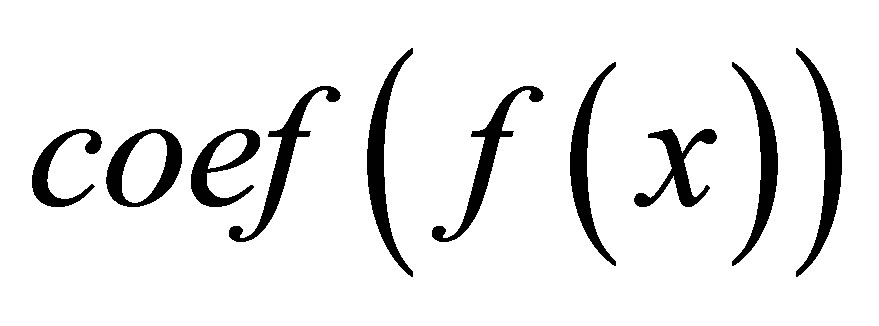 denotes the subset of
denotes the subset of 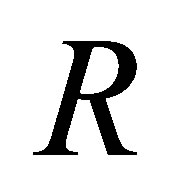 of the coefficients of
of the coefficients of 
Condition (P): For all 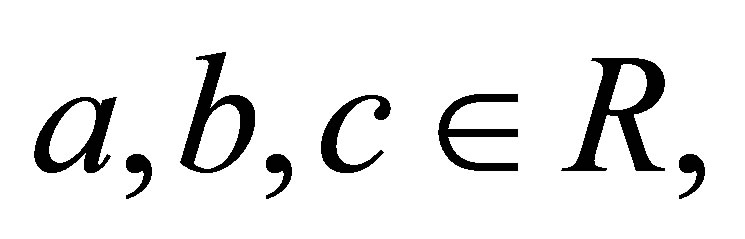 if
if 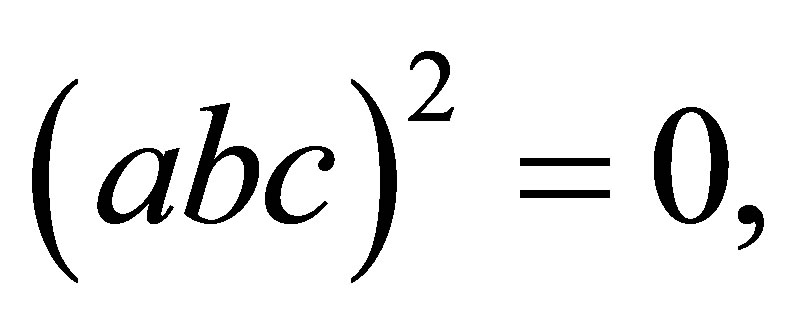 then
then 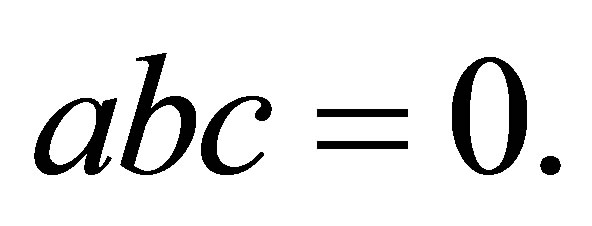 ( See [7])
( See [7])
Lemma 2.1. [11, Proposition 1]. If 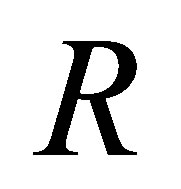 is a reduced ring, then
is a reduced ring, then 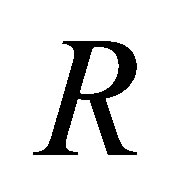 satisfies the condition (P), but the converse is not true.
satisfies the condition (P), but the converse is not true.
Lemma 2.2. [7, Theorem 1]. If a ring  satisfies condition (P), then R is a 3-Armendariz ring.
satisfies condition (P), then R is a 3-Armendariz ring.
Proposition 2.3. Let 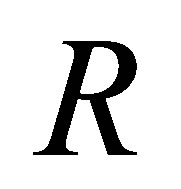 be a ring such that
be a ring such that  If
If  then
then  for all
for all 
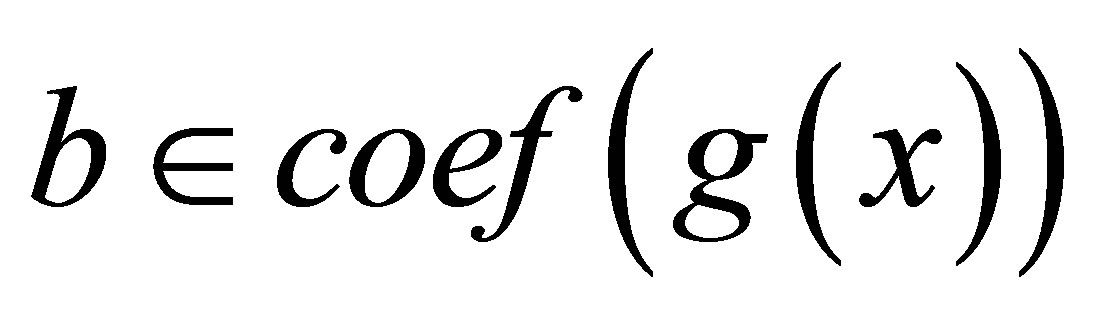 and
and 
Proof. Observe that 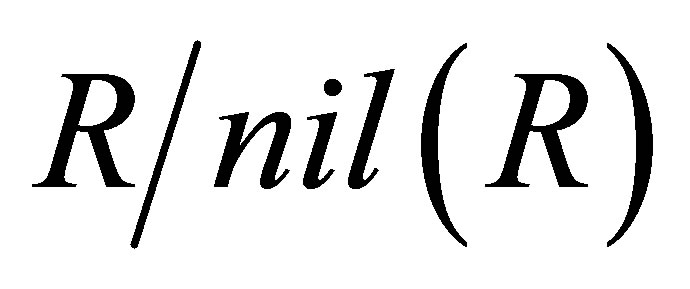 is reduced. By Lemma 2.1,
is reduced. By Lemma 2.1, 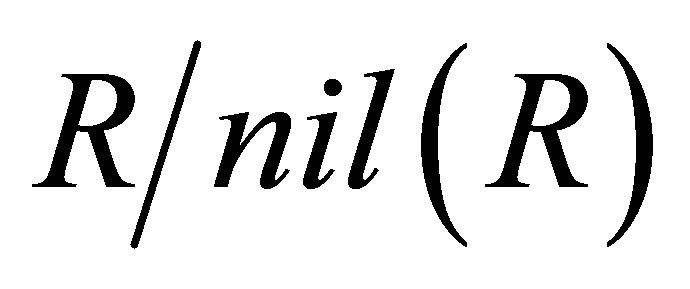 satisfies condition (P) and by Lemma 2.2,
satisfies condition (P) and by Lemma 2.2, 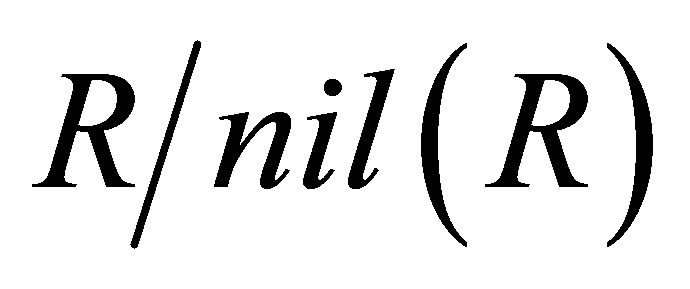 is 3-Armendariz. Suppose
is 3-Armendariz. Suppose  Then, if we denote by
Then, if we denote by  the corresponding polynomials in
the corresponding polynomials in 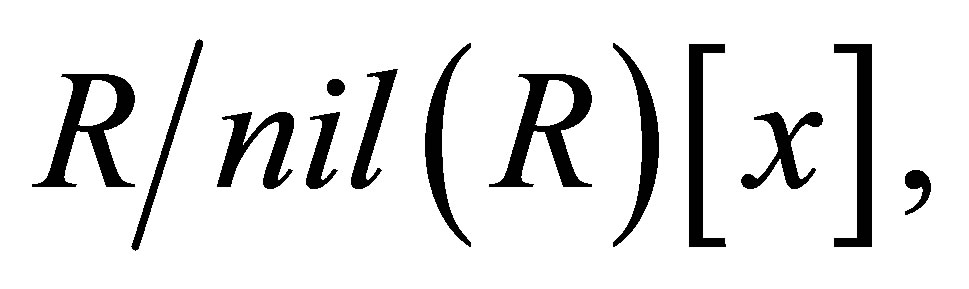
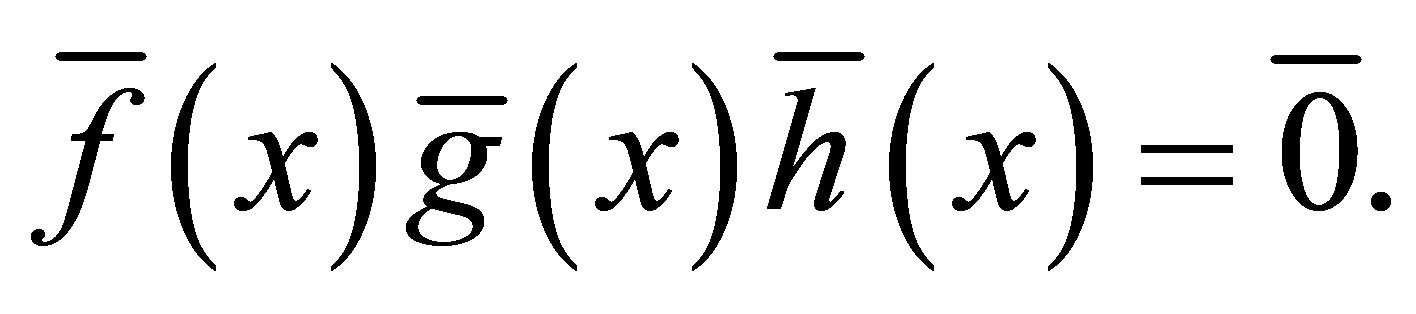 Since
Since  is 3-Armendariz,
is 3-Armendariz, 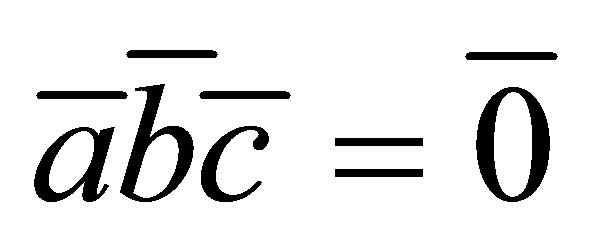 for all
for all 
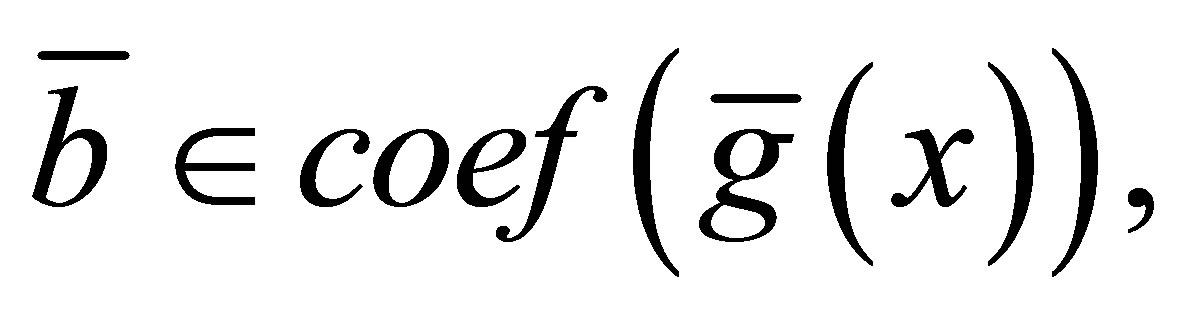 and
and 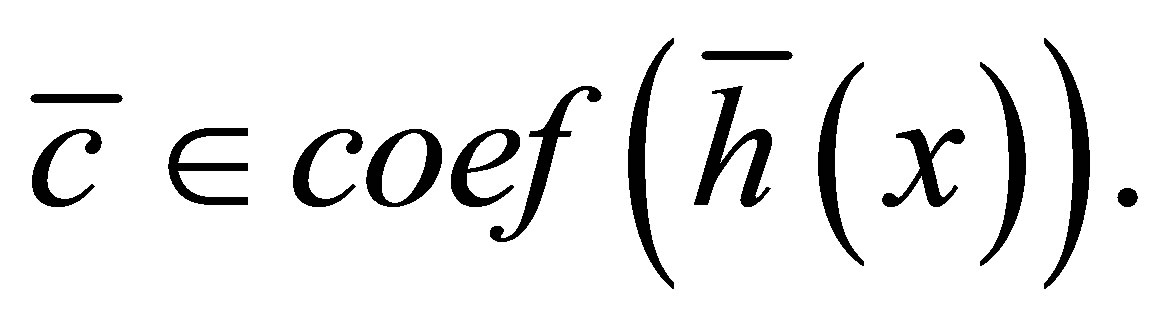 Hence
Hence 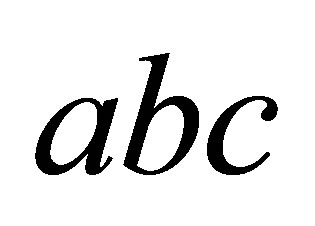 is nil for all
is nil for all 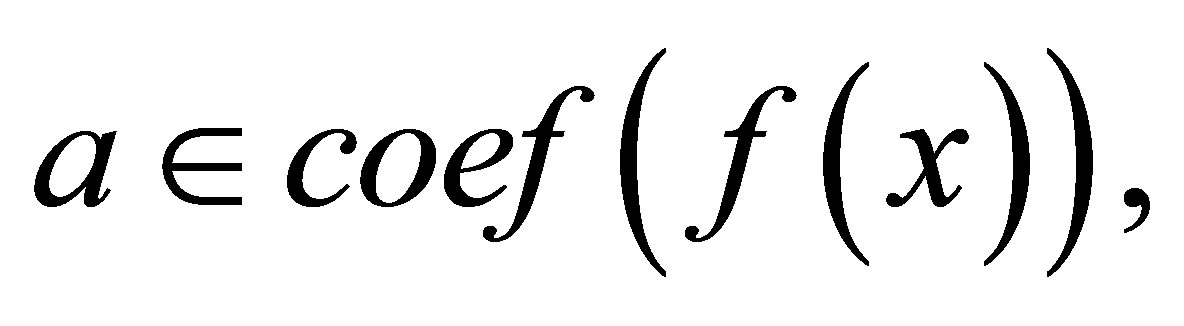
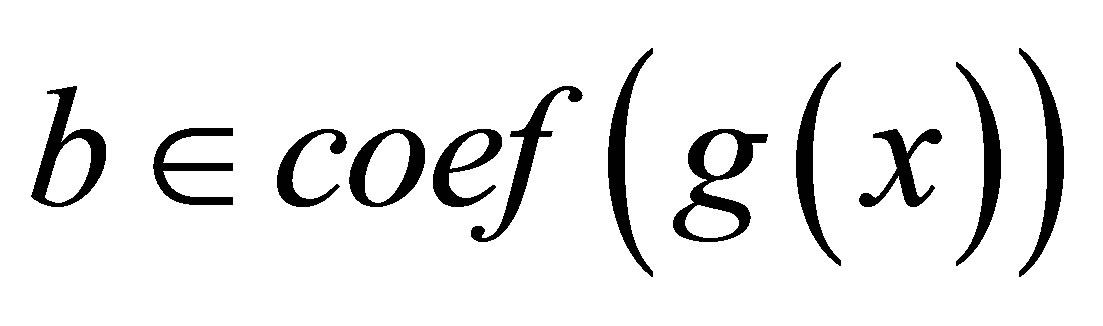 and
and 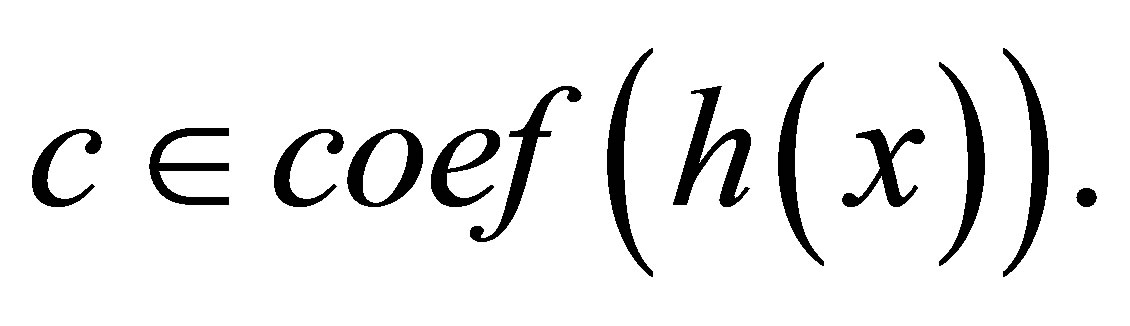
Wu Hui-feng gives the following generalization of 3-Armendariz rings.
Definition 2.4. [10, Definition 1]. A ring  is said to be a weak 3-Armendariz ring if whenever polynomials
is said to be a weak 3-Armendariz ring if whenever polynomials 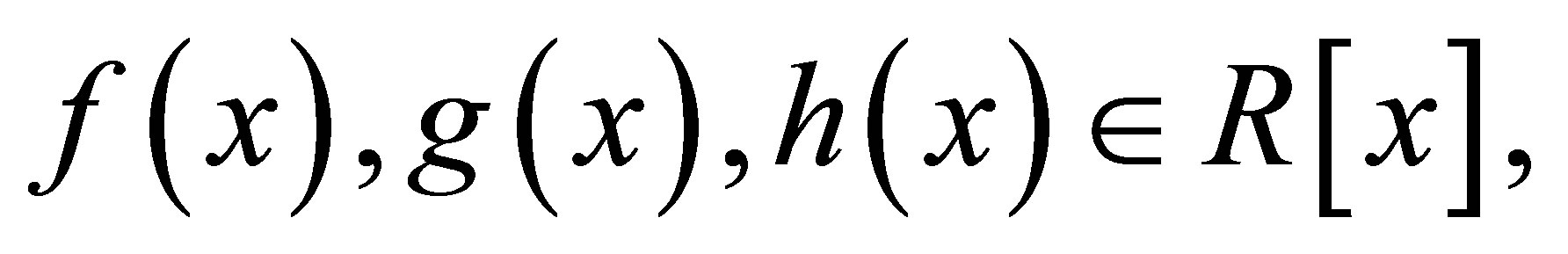 satisfy
satisfy  then
then  for all
for all 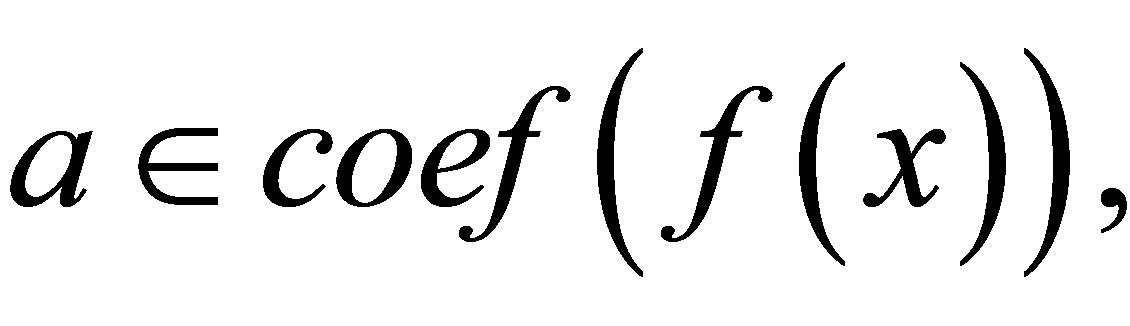
 and
and 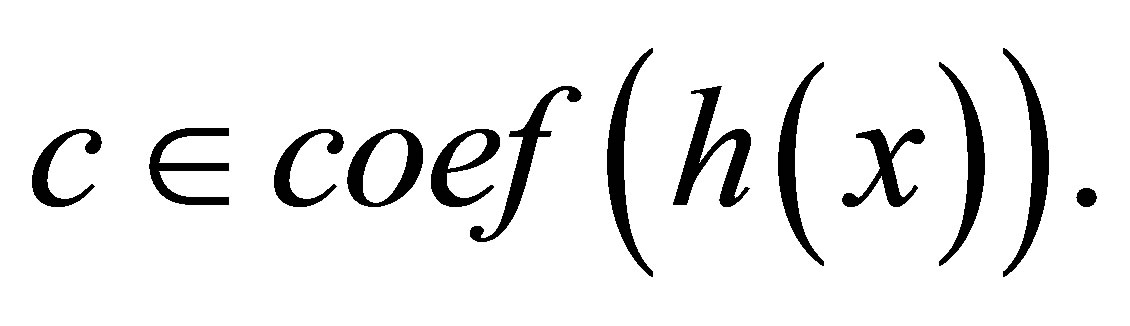
Clearly, 3-Armendariz rings are weak 3-Armendariz. We now present here a stronger condition, given by the property obtained in Proposition 2.3.
Definition 2.5. A ring 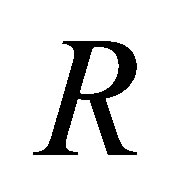 is said to be nil 3-Armendariz if whenever polynomials
is said to be nil 3-Armendariz if whenever polynomials 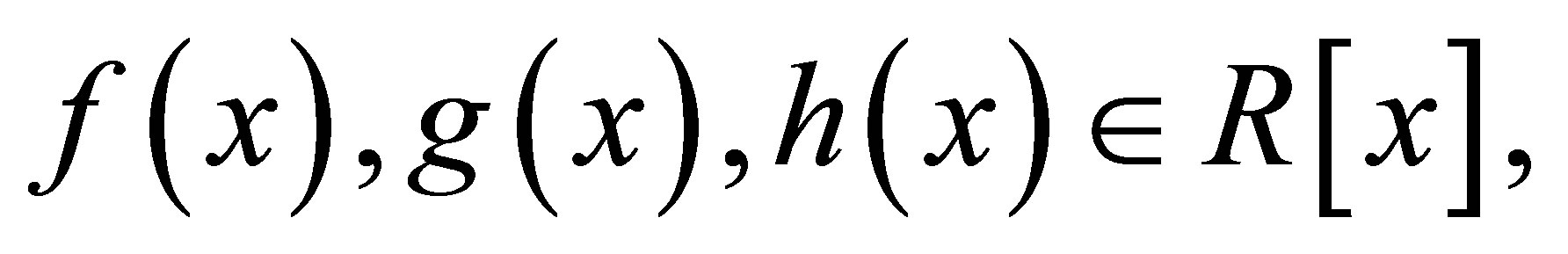 satisfy
satisfy  then
then 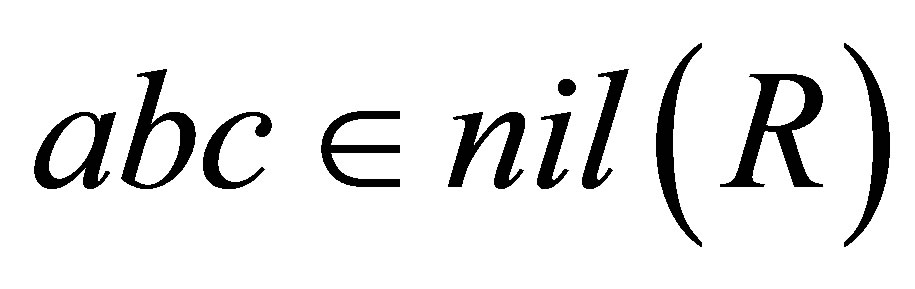 for all
for all 
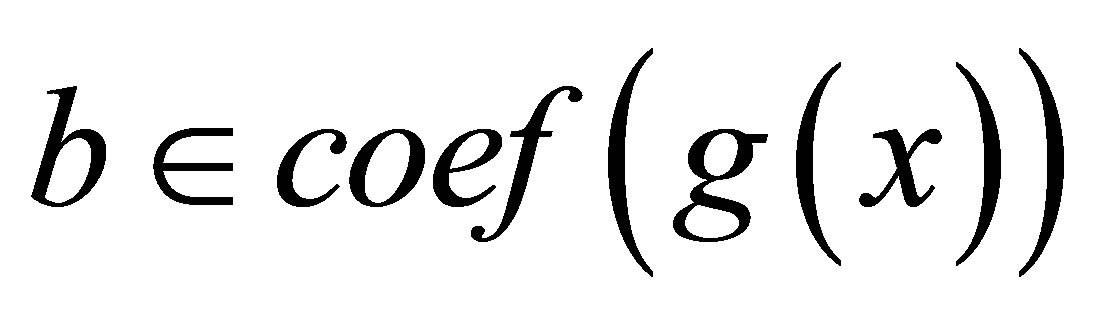 and
and 
Observe that if  then by Proposition 2.3,
then by Proposition 2.3, 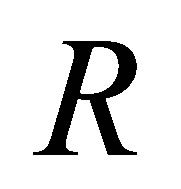 is nil 3-Armendariz. More generally we obtain the following.
is nil 3-Armendariz. More generally we obtain the following.
Proposition 2.6. Let  be a ring that satisfies the condition (P), and
be a ring that satisfies the condition (P), and 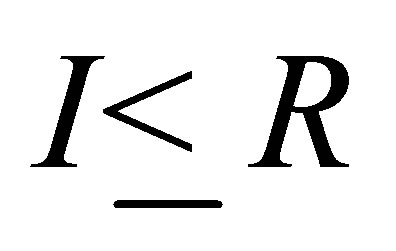 a nil ideal. Then
a nil ideal. Then 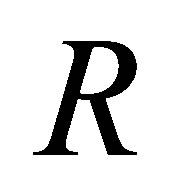 is nil 3-Armendariz if and only if
is nil 3-Armendariz if and only if  is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. We denote 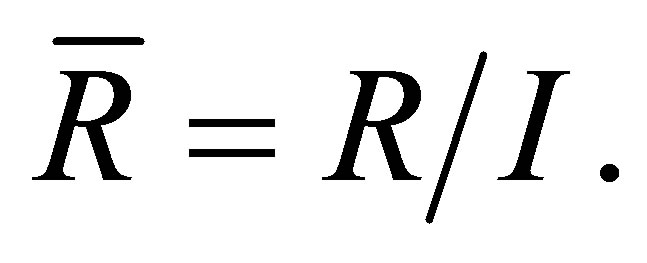 Since
Since  is nil, then
is nil, then 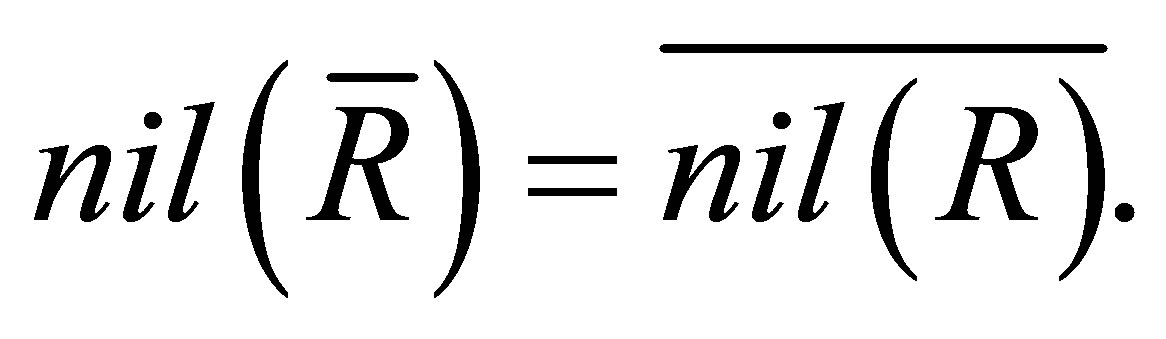 Hence
Hence 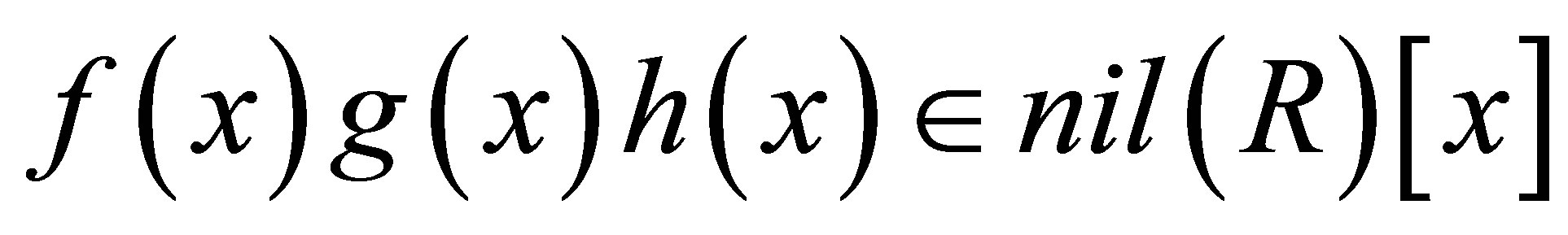 if and only if
if and only if  And, if
And, if 
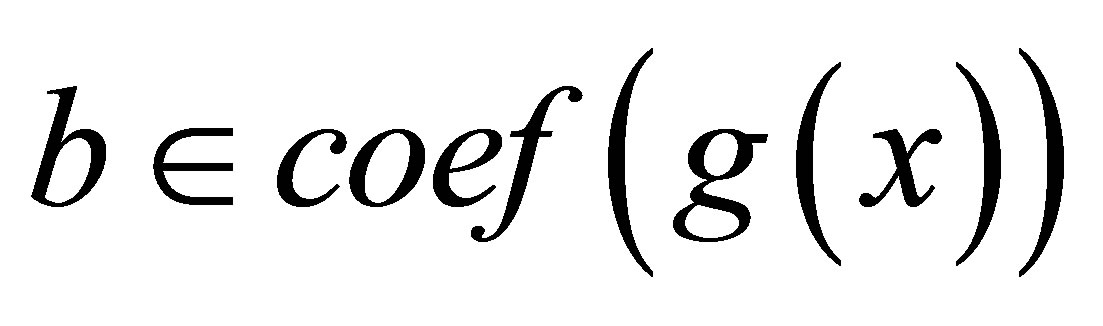 and
and  then
then  if and only if
if and only if 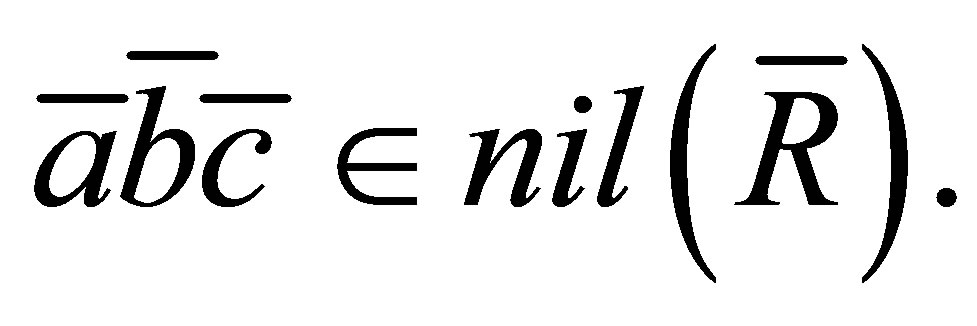 Therefore
Therefore  is nil 3-Armendariz if and only if
is nil 3-Armendariz if and only if 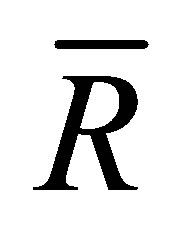 is nil 3-Armendariz.
is nil 3-Armendariz.
The next results can be proved by using the technique used in the proof of [8, Lemma 2.5, Lemma 2.6].
Lemma 2.7. Let 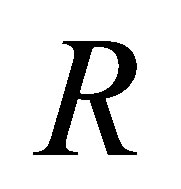 be a nil 3-Armendariz ring and
be a nil 3-Armendariz ring and 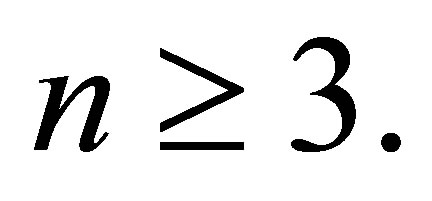 If
If 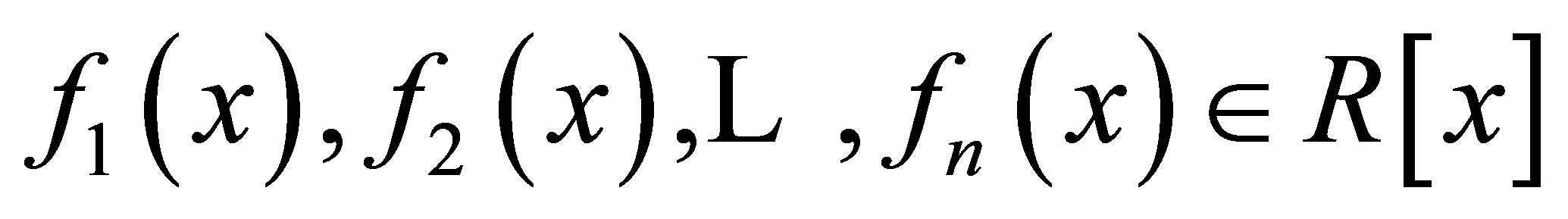 such that
such that  then if
then if  for
for 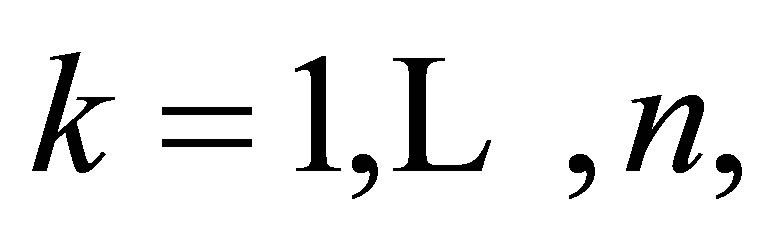 we have
we have 
Lemma 2.8. If  is a 3-Armendariz ring then
is a 3-Armendariz ring then 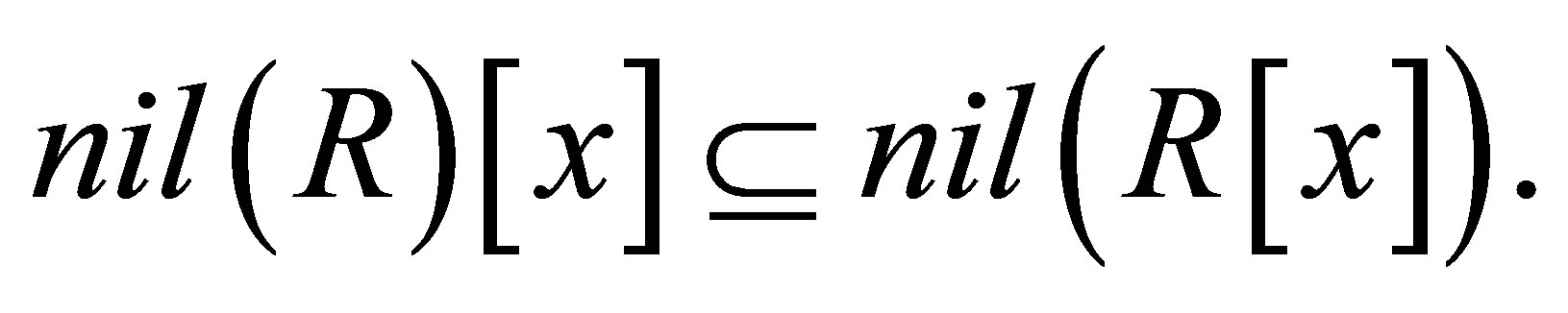
Proposition 2.9. If 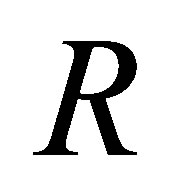 is a 3-Armendariz ring then
is a 3-Armendariz ring then 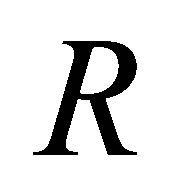 is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. Suppose  be such that
be such that  Since
Since 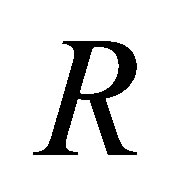 is 3-Armendariz, by Lemma 2.8,
is 3-Armendariz, by Lemma 2.8,  is nilpotent and there exists
is nilpotent and there exists 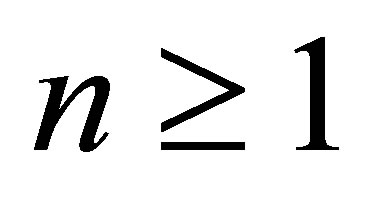 such that
such that  Hence, since
Hence, since  is 3-Armendariz, for all
is 3-Armendariz, for all 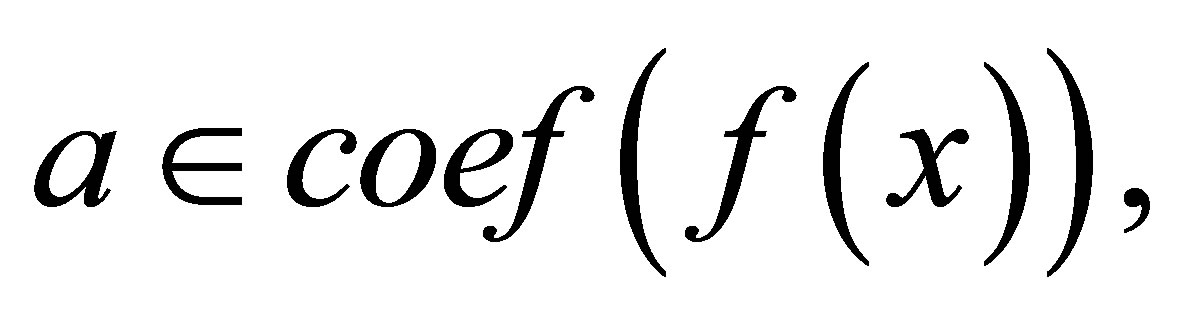
 and
and 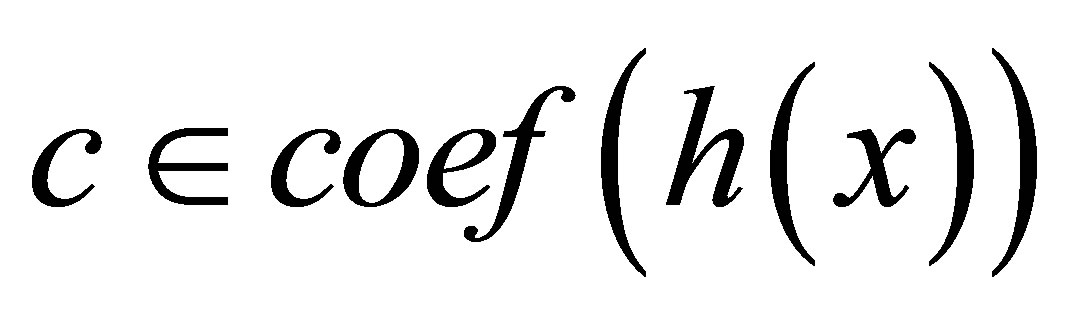 by choosing the corresponding coefficient in each polynomial, we have
by choosing the corresponding coefficient in each polynomial, we have 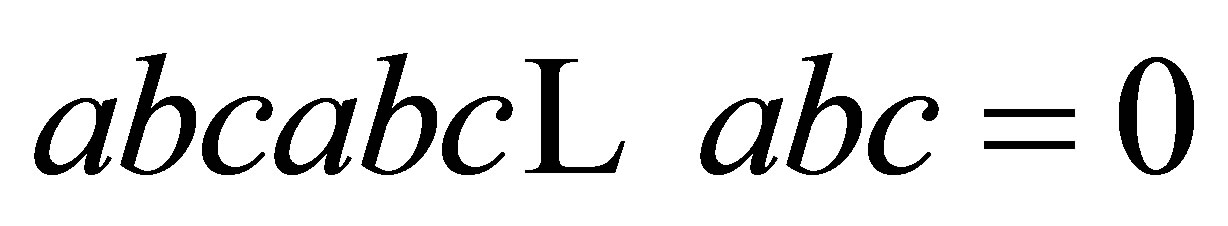 and thus,
and thus, 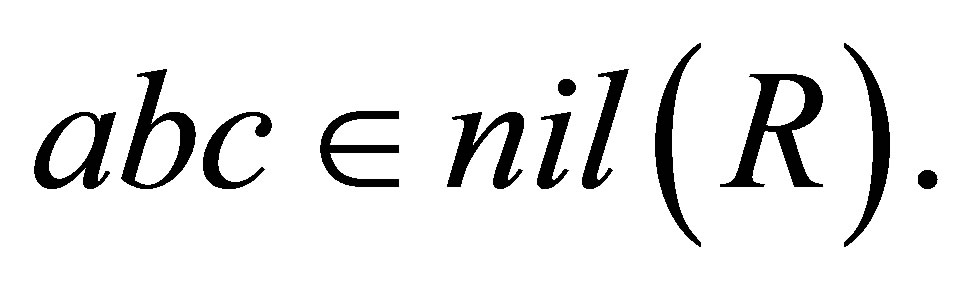 Therefore
Therefore 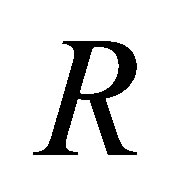 is nil 3-Armendariz.
is nil 3-Armendariz.
Proposition 2.10. The class of nil 3-Armendariz rings is closed under finite direct products.
Proof. Let 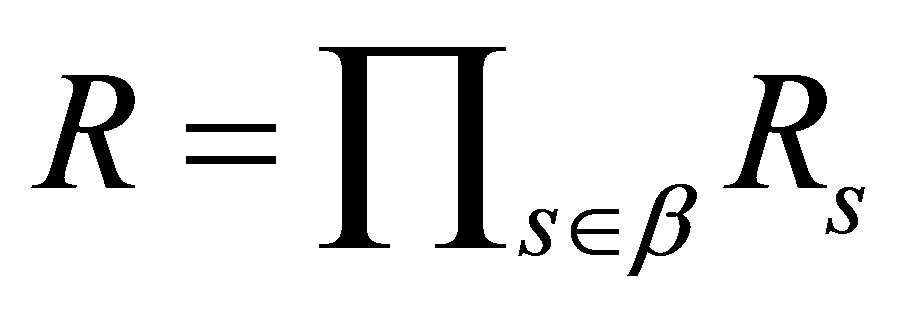 be the finite direct product of
be the finite direct product of 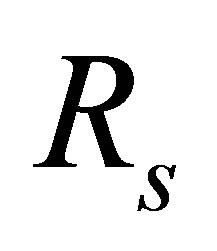 where
where 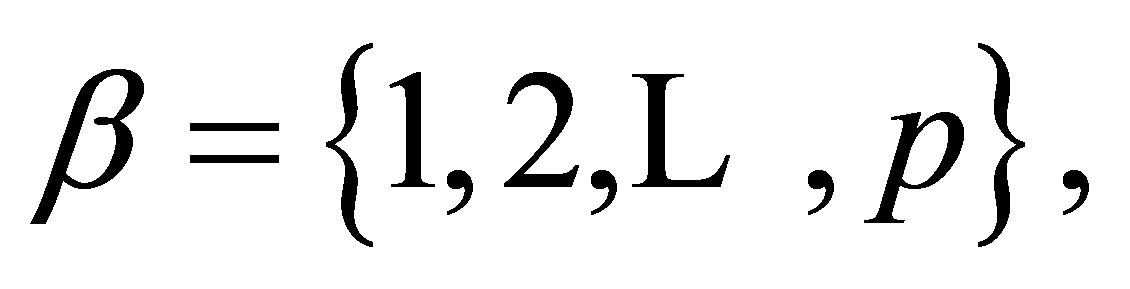
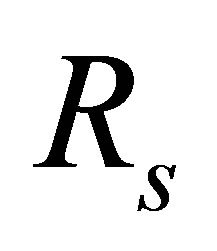 is nil 3-Armendariz. Suppose
is nil 3-Armendariz. Suppose 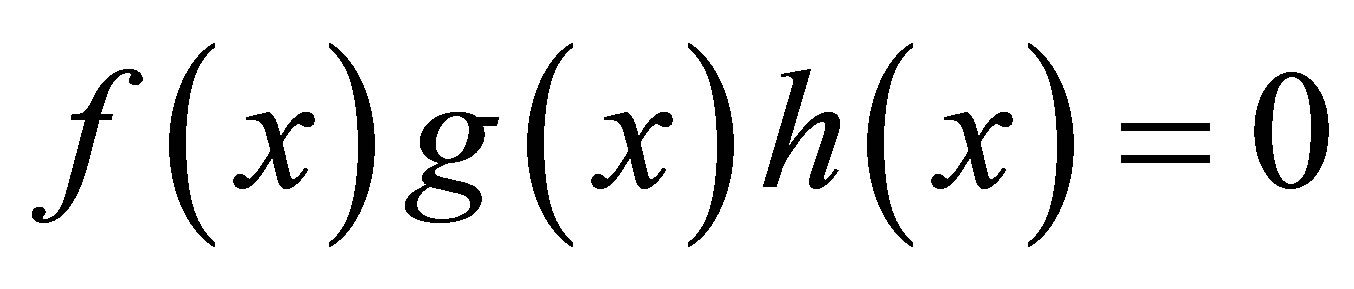 for some polynomials
for some polynomials 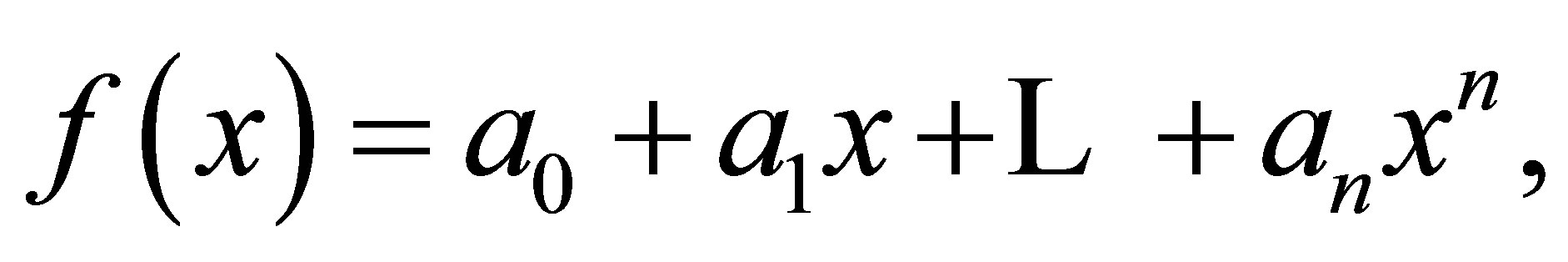
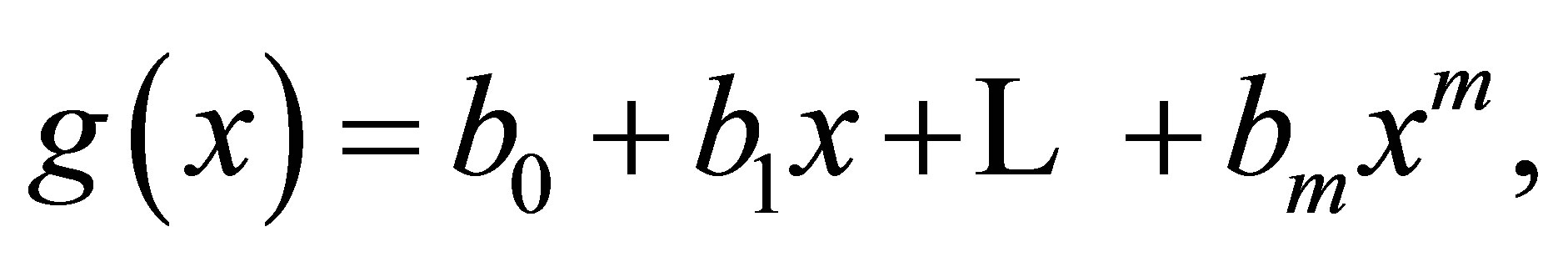
 where
where 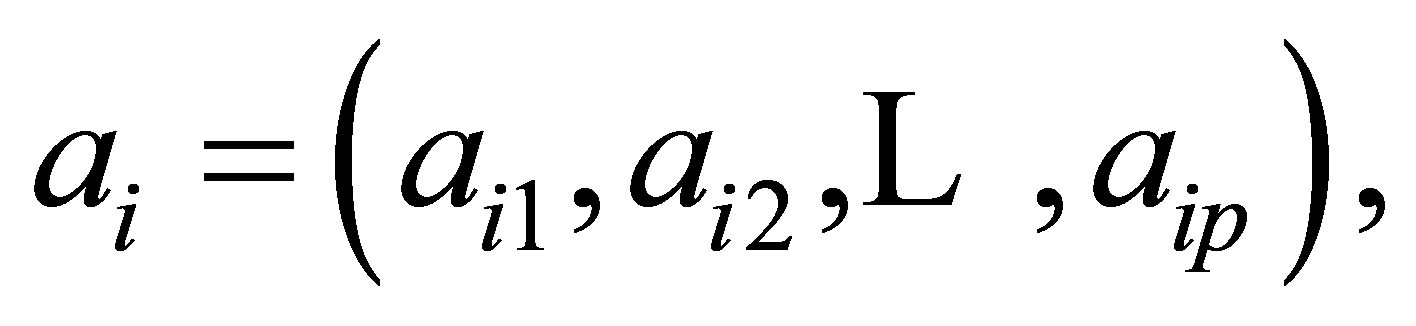

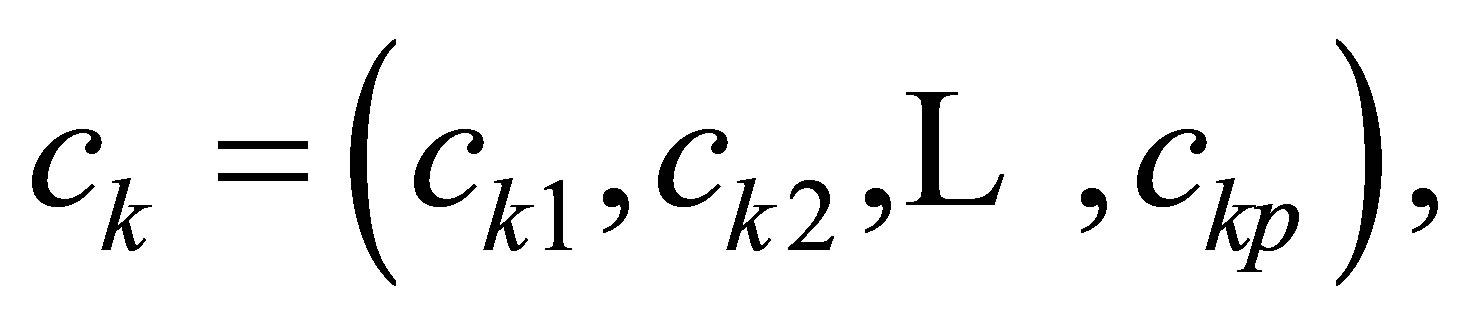 are elements of the product ring
are elements of the product ring
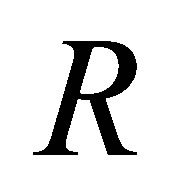 . Set
. Set 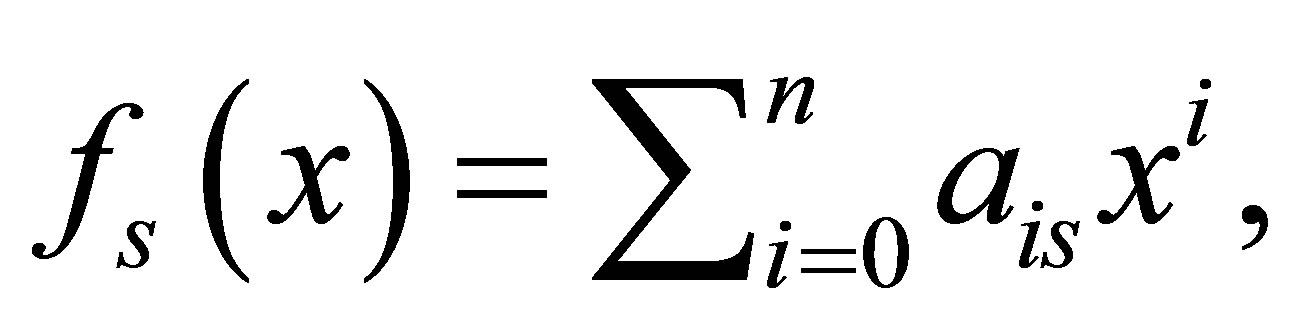
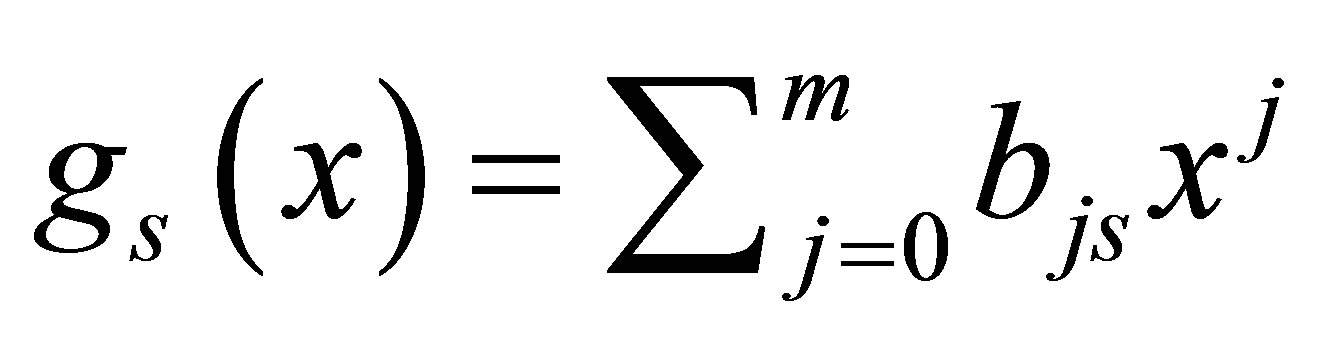 and
and 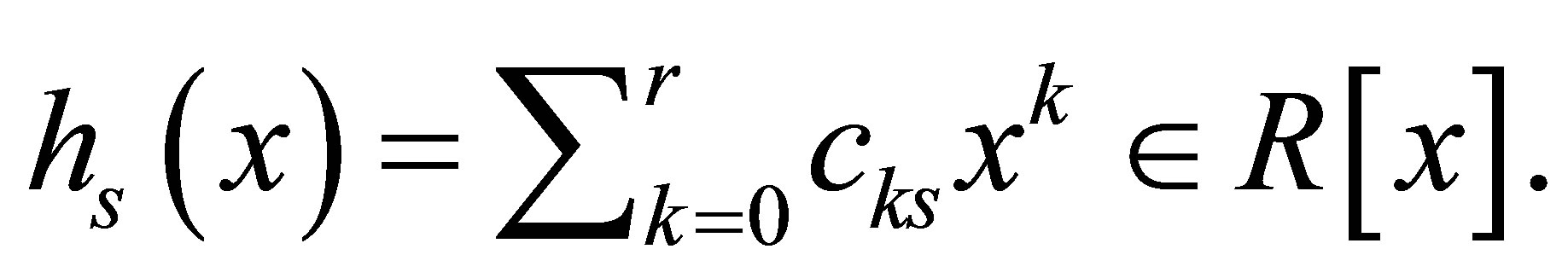 Since
Since  then
then 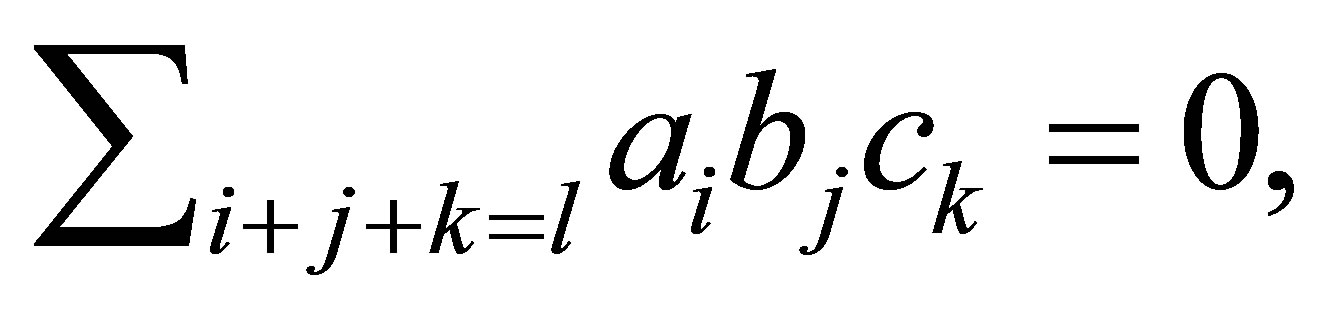
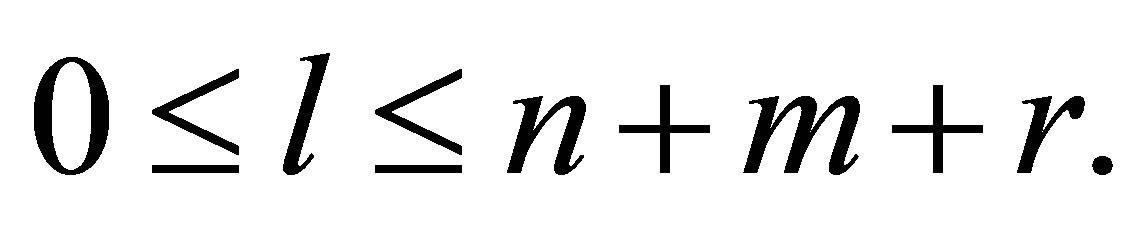 So
So 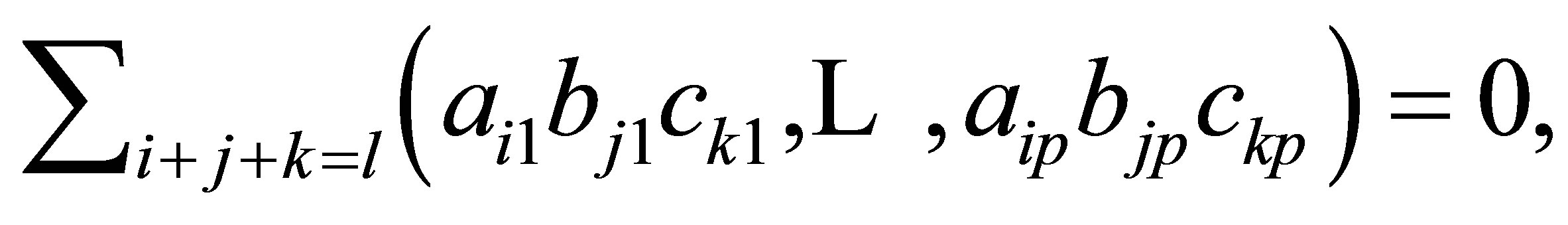 and so
and so 
 Thus
Thus
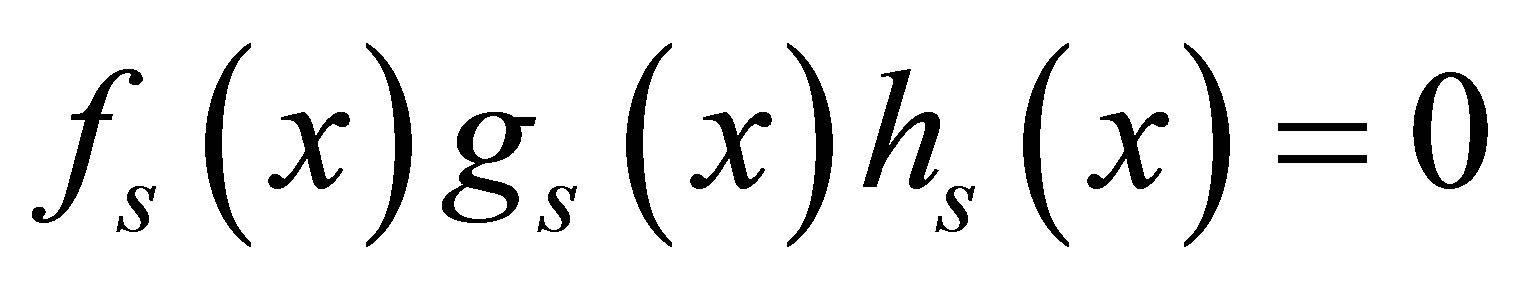 in
in 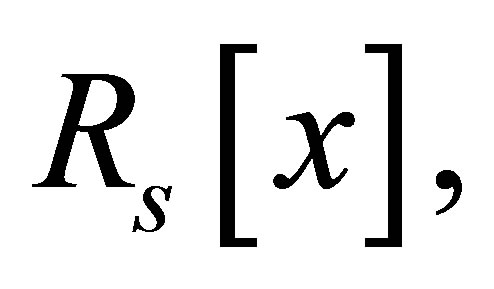
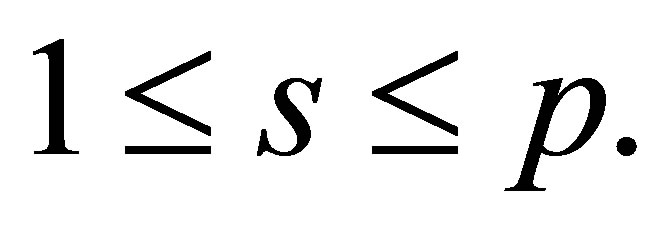 Since
Since  is nil 3-Armendariz, then we have
is nil 3-Armendariz, then we have  Now, for each
Now, for each 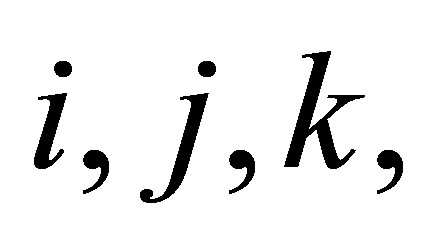 there exist positive integers
there exist positive integers 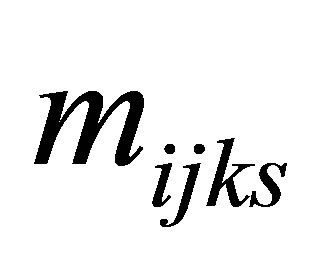
such that  in the ring
in the ring 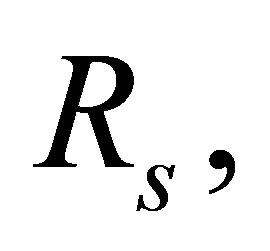
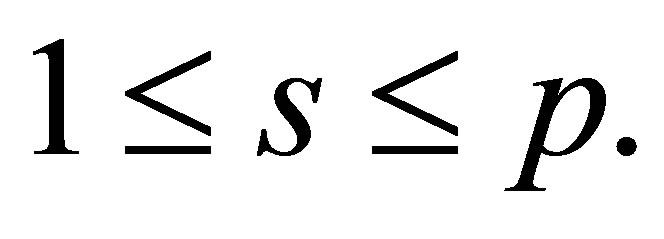 If we take
If we take 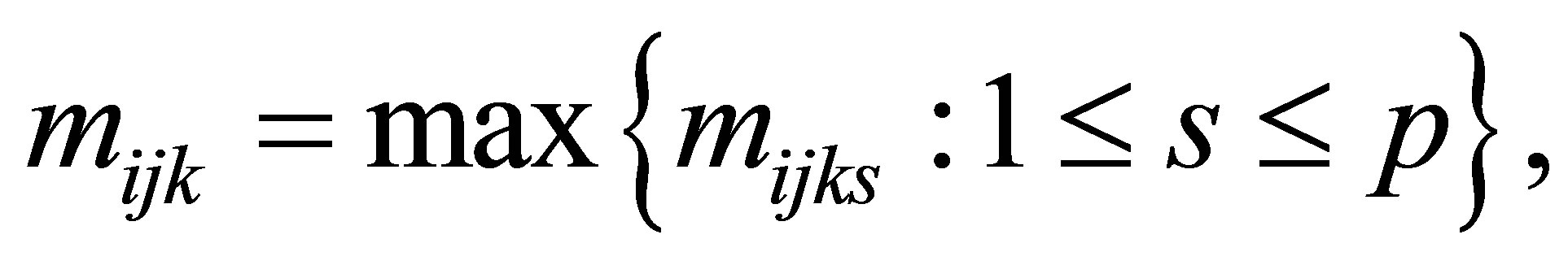 then it is clear that
then it is clear that  Therefore
Therefore 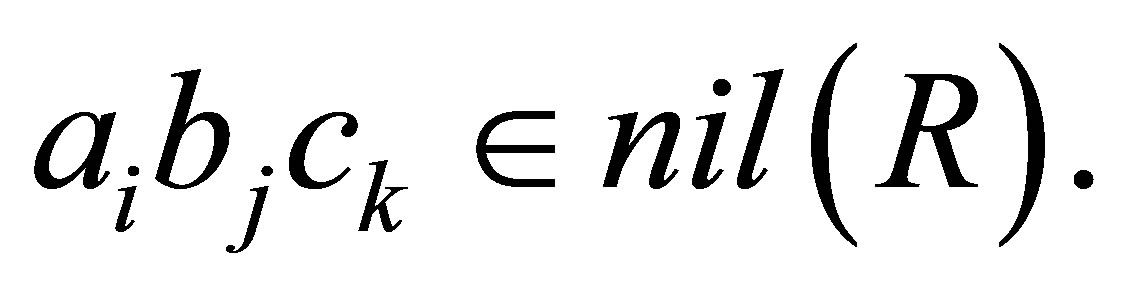 This means that
This means that 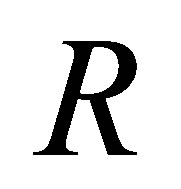 is nil 3-Armendariz.
is nil 3-Armendariz.
Lemma 2.11. Let  be a subring of
be a subring of  If
If 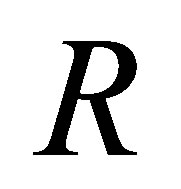 is nil 3-Armendariz. Then so is
is nil 3-Armendariz. Then so is 
Proof. Let  be such that
be such that  Then
Then 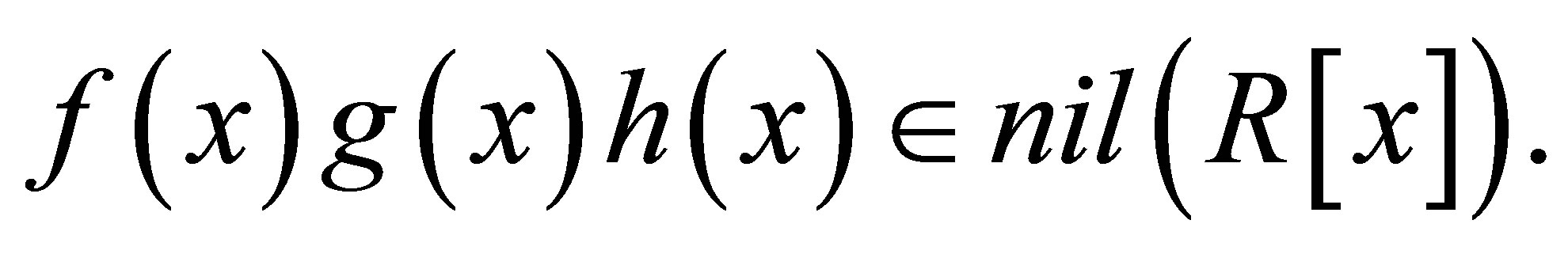 Since
Since 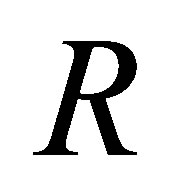 is nil 3-Armendariz, then
is nil 3-Armendariz, then  i.e.,
i.e., 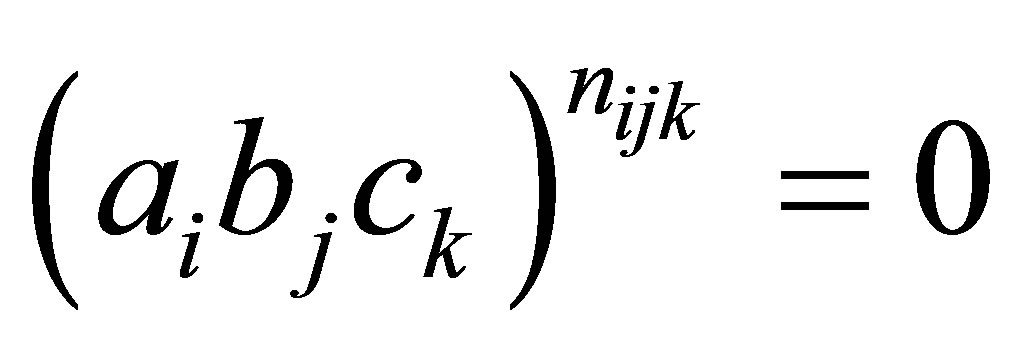
 This means that S is nil 3-Armendariz.
This means that S is nil 3-Armendariz.
We denote by 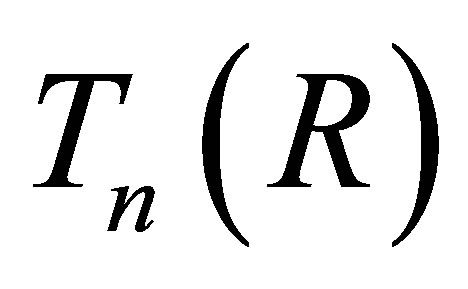 the ring consisting of all n-by-n upper triangular matrices over
the ring consisting of all n-by-n upper triangular matrices over  In [10, Theorem 1], showed that
In [10, Theorem 1], showed that  is a weak 3-Armendariz if and only if
is a weak 3-Armendariz if and only if  is a weak 3-Armendariz ring for all n Î ℕ. Here we have a similar results for nil 3-Armendariz rings.
is a weak 3-Armendariz ring for all n Î ℕ. Here we have a similar results for nil 3-Armendariz rings.
Proposition 2.12. Let  be a ring. The following conditions are equivalent:
be a ring. The following conditions are equivalent:
1)  is nil 3-Armendariz;
is nil 3-Armendariz;
2) for any 
 is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. (2)Þ(1) We note that any subring of nil 3-Armendariz rings is nil 3- Armendariz by Lemma 2.11. Thus if 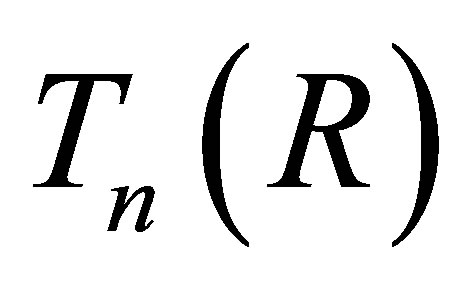 is nil 3-Armendariz ring, then so is
is nil 3-Armendariz ring, then so is 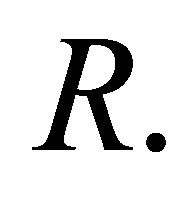 (1)Þ(2) Let
(1)Þ(2) Let 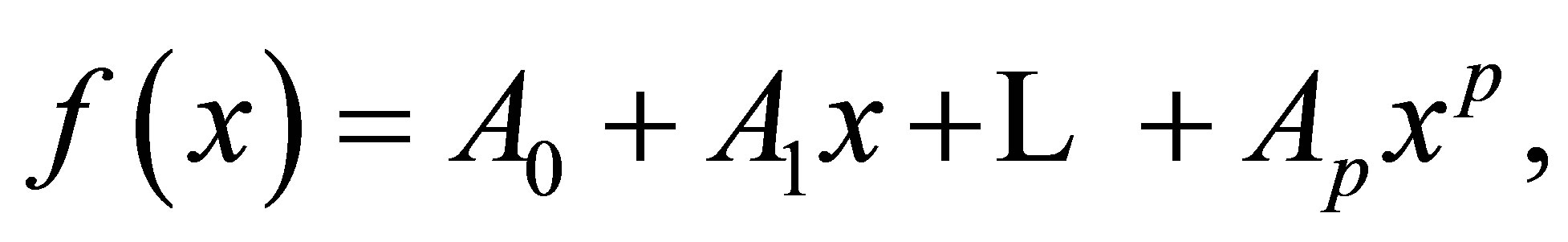
 and
and
 be elements of
be elements of 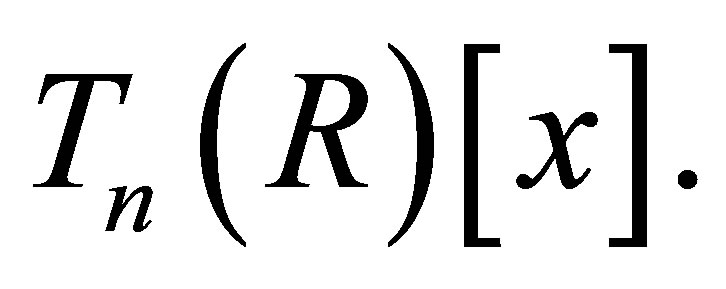 It is easy to see that there exists an isomorphism of rings
It is easy to see that there exists an isomorphism of rings  define by:
define by:
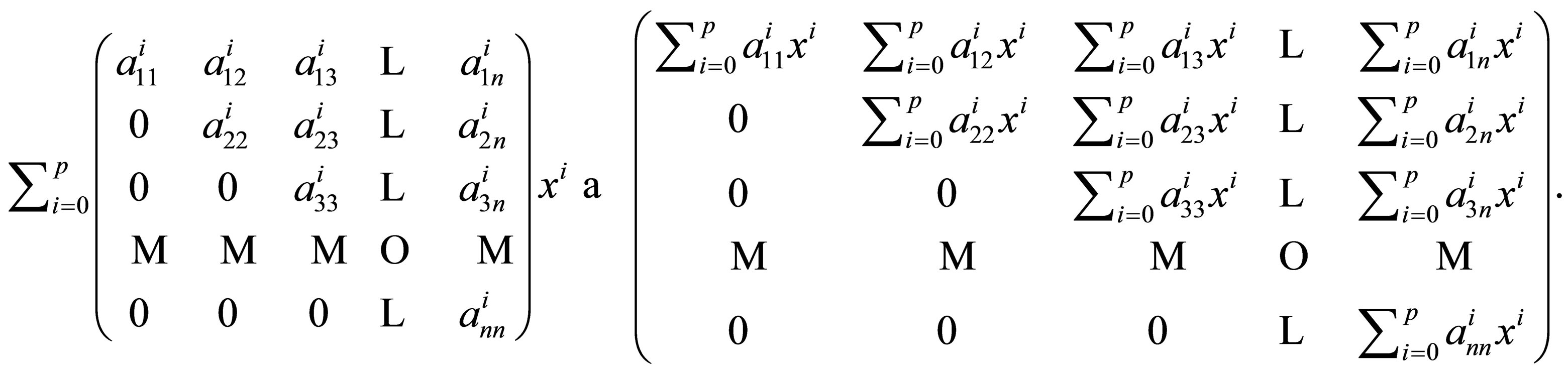
Assume that  Let
Let
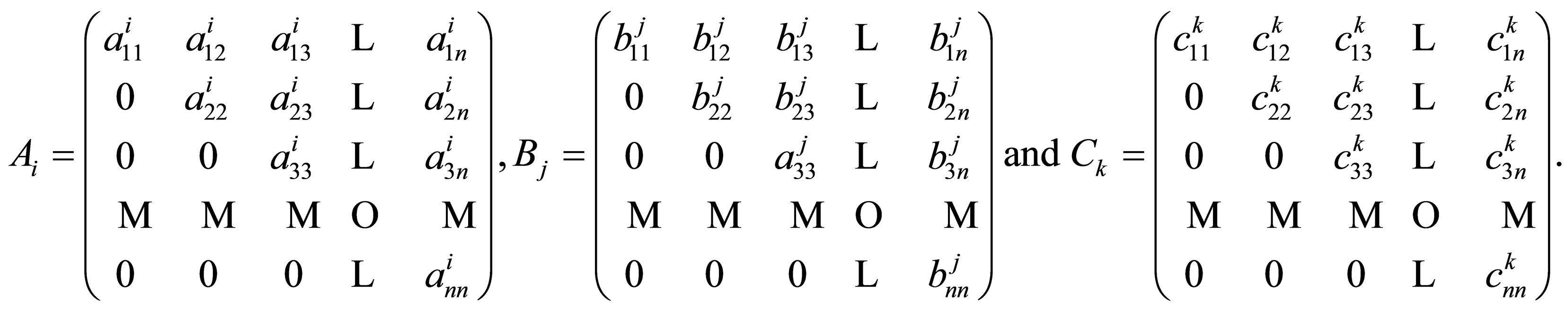
Then

corresponds a polynomial with coefficients in  under the isomorphism
under the isomorphism  Because
Because  and
and

we have

for 
Since  is nil 3-Armendariz, there exists
is nil 3-Armendariz, there exists  such that
such that 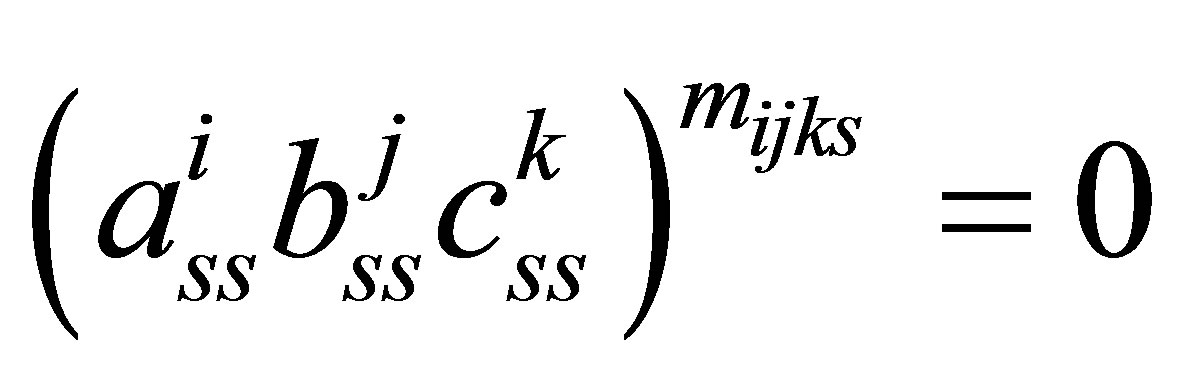 for any
for any  and any
and any 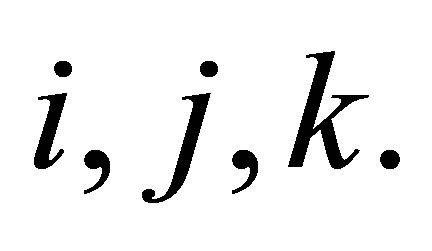 Let
Let  Then
Then
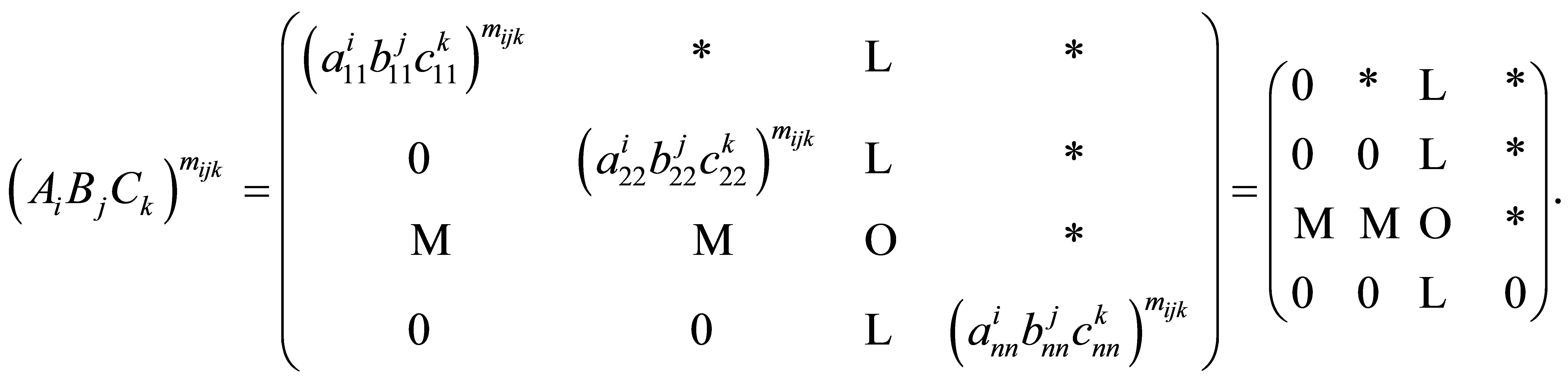
Thus, 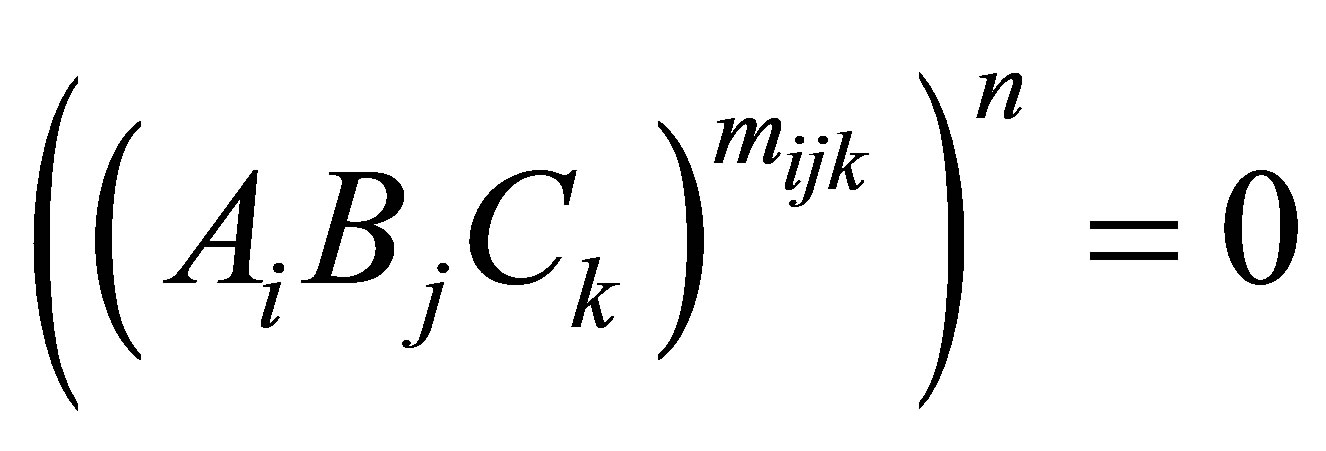 and so
and so
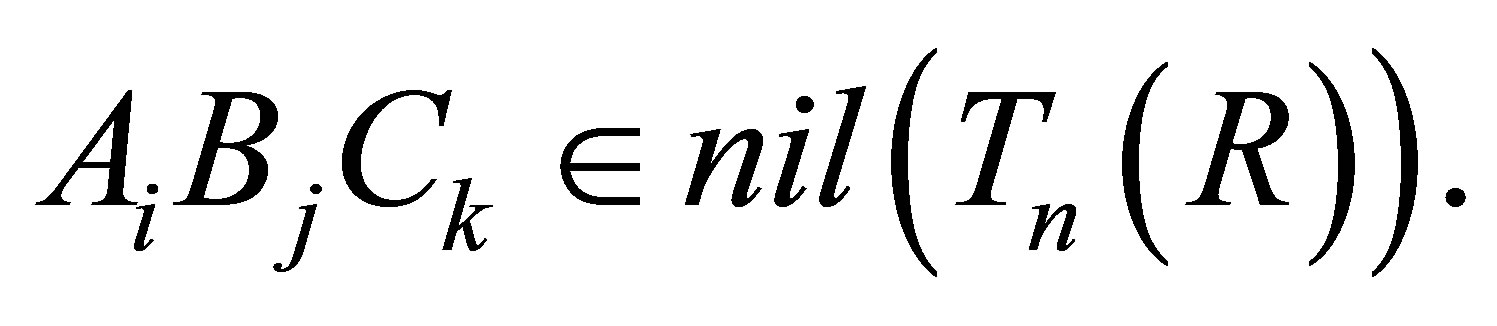 This shows that
This shows that  is nil 3-Armendariz.
is nil 3-Armendariz.
Corollary 2.13. If  is a 3-Armendariz ring, then, for any
is a 3-Armendariz ring, then, for any 
 is nil 3-Armendariz ring.
is nil 3-Armendariz ring.
In [10, Corollary 1], it is shown that a ring is a weak 3-Armendariz ring if and only if  is a weak 3-Armendariz ring, where
is a weak 3-Armendariz ring, where 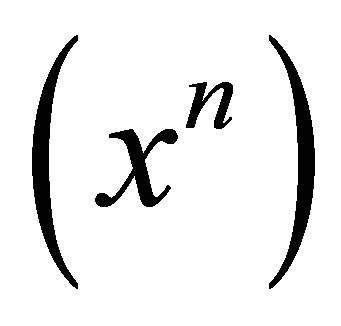 is the ideal of
is the ideal of 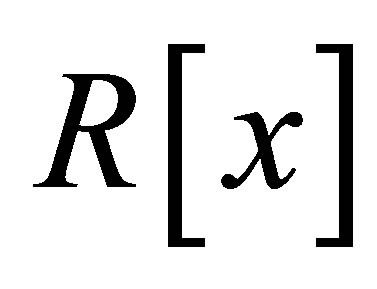 generated by
generated by 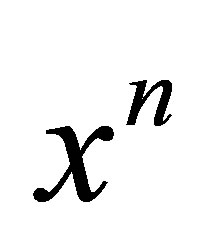 and
and 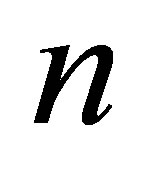 is a positive integer. For nil 3-Armendariz rings, we have the following result.
is a positive integer. For nil 3-Armendariz rings, we have the following result.
Proposition 2.14. Let 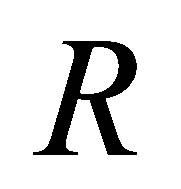 be a ring and
be a ring and 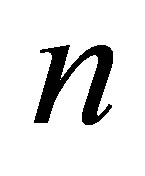 any positive integer. Then
any positive integer. Then  is nil 3-Armendariz if and only if
is nil 3-Armendariz if and only if 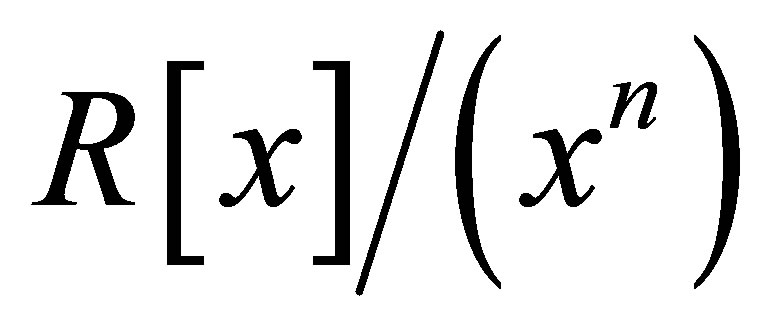 is nil 3-Armendariz, where
is nil 3-Armendariz, where 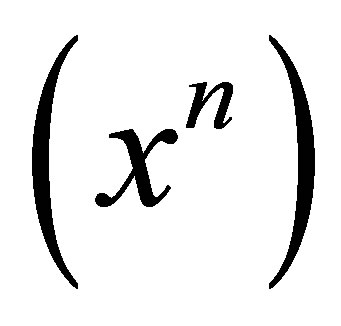 is the ideal of
is the ideal of 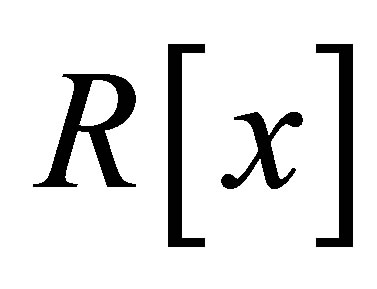 generated by
generated by 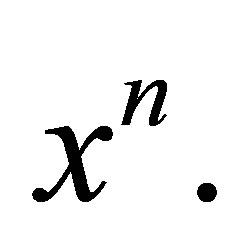
Proof. As 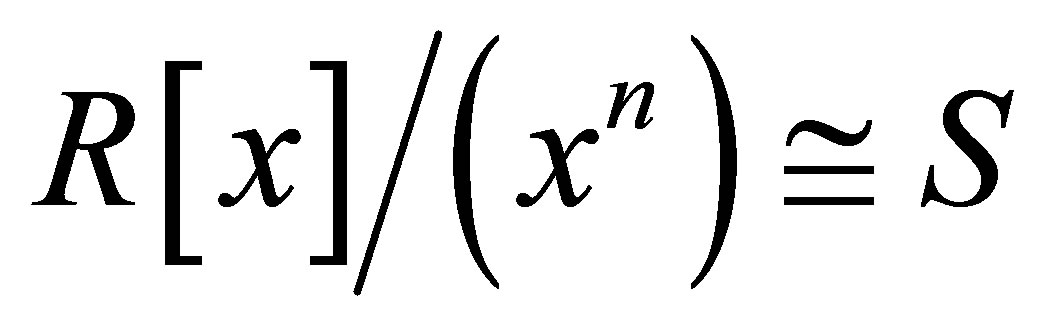 where
where

is a subring of  If
If 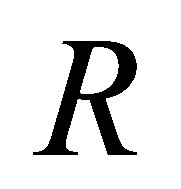 is nil 3-Armendariz, then, by Proposition 2.12, we have that
is nil 3-Armendariz, then, by Proposition 2.12, we have that 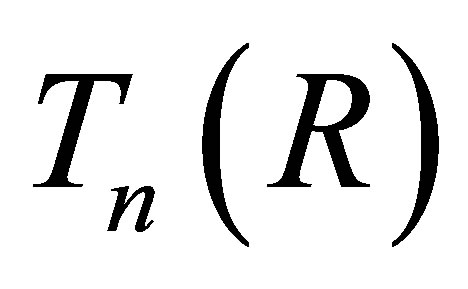 is nil 3-Armendariz, and so is S. Thus,
is nil 3-Armendariz, and so is S. Thus, 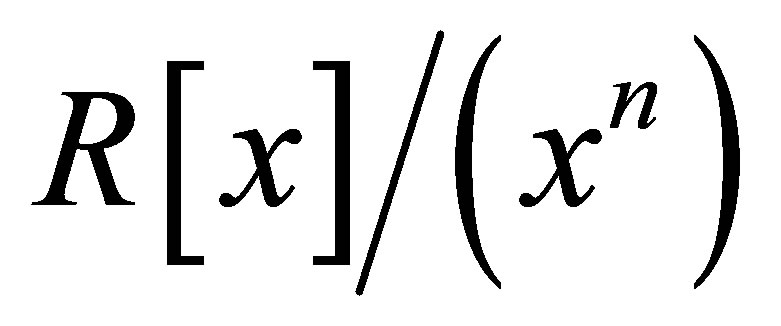 is nil 3-Armendariz. Conversely, if
is nil 3-Armendariz. Conversely, if  is nil 3-Armendariz, then
is nil 3-Armendariz, then 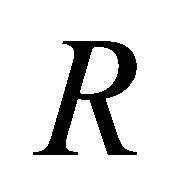 as a subring of
as a subring of  is nil 3- Armendariz too.
is nil 3- Armendariz too.
Corollary 2.15. A ring  is nil 3-Armendariz if and only if the trivial extension
is nil 3-Armendariz if and only if the trivial extension 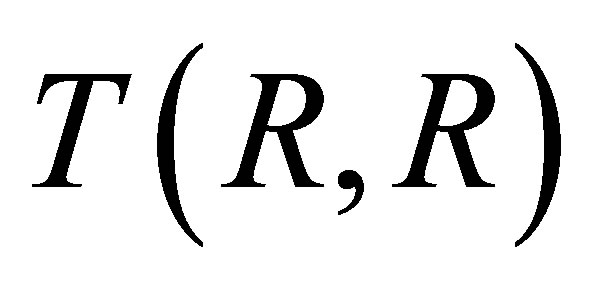 is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. It follows from Proposition 2.12.
From Proposition 2.12, one may suspect that if 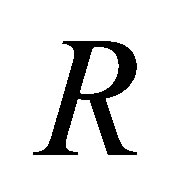 is nil 3-Armendariz then every n-by-n full matrix ring
is nil 3-Armendariz then every n-by-n full matrix ring  over
over 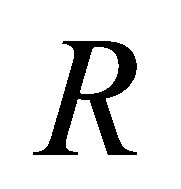 is nil 3-Armendariz, where
is nil 3-Armendariz, where  But the following example erases the possibility.
But the following example erases the possibility.
Example 2.16. Let 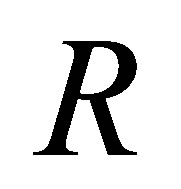 be a ring and let
be a ring and let 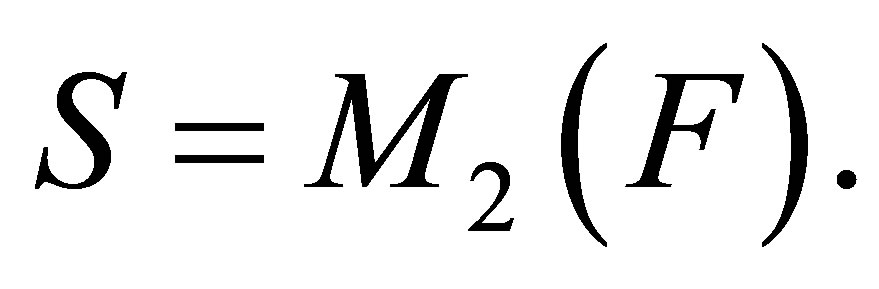 Let
Let
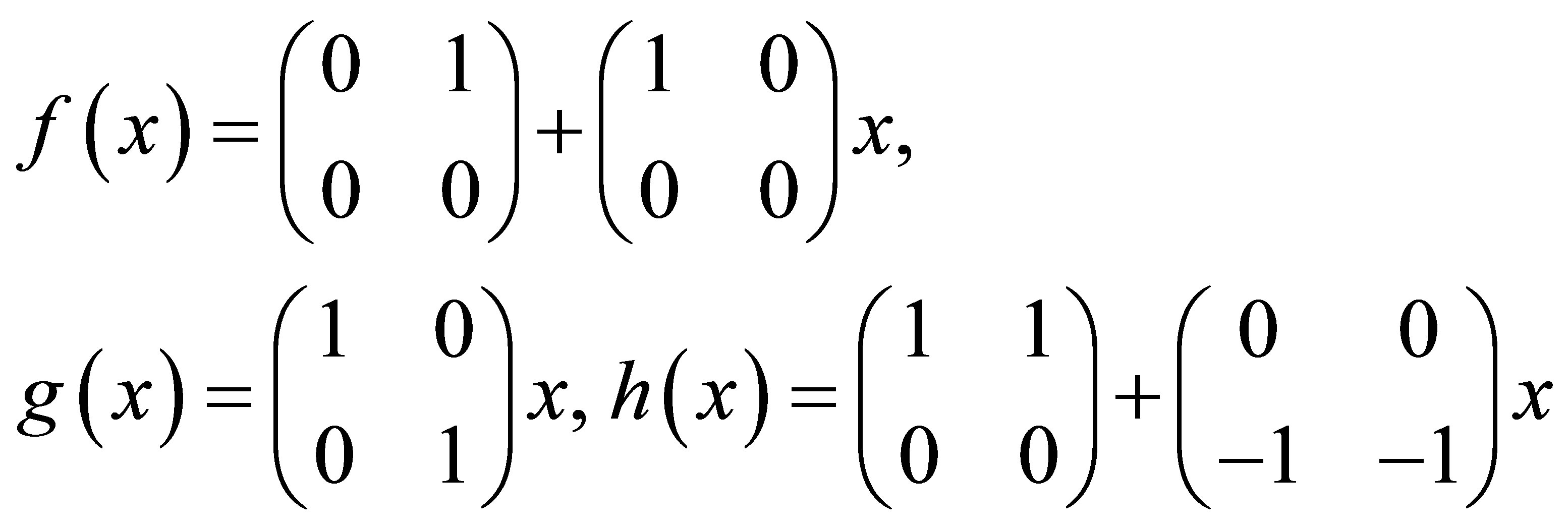
be polynomials in  Then
Then 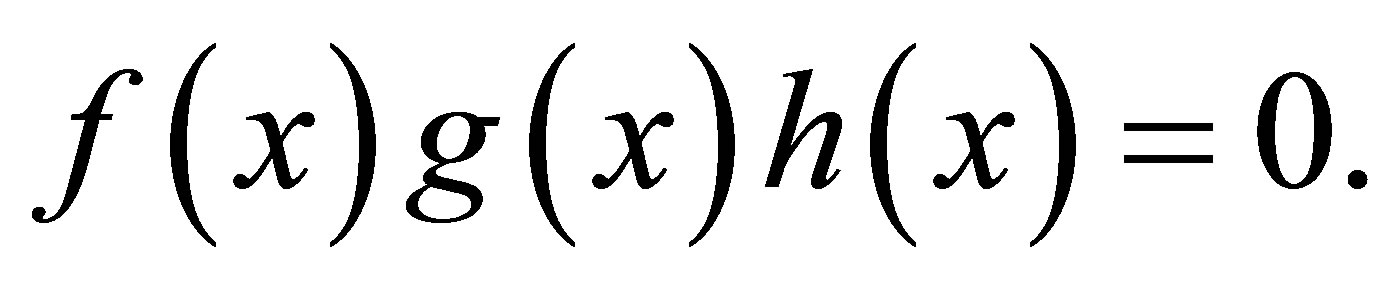 But
But
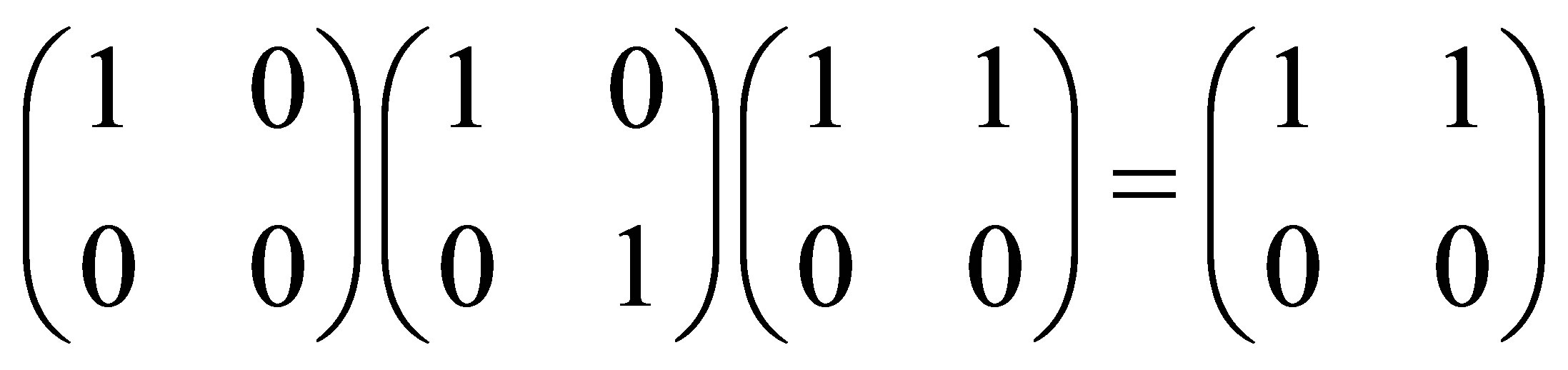
is not nilpotent. Thus 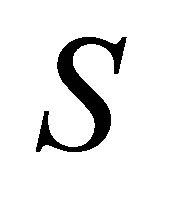 is not nil 3-Armendariz. Now we can give the example of nil 3-Armendariz rings which are not 3-Armendariz.
is not nil 3-Armendariz. Now we can give the example of nil 3-Armendariz rings which are not 3-Armendariz.
Example 2.17. Let 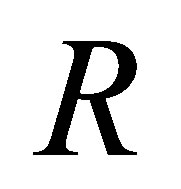 be a nil 3-Armendariz ring. Then the ring
be a nil 3-Armendariz ring. Then the ring
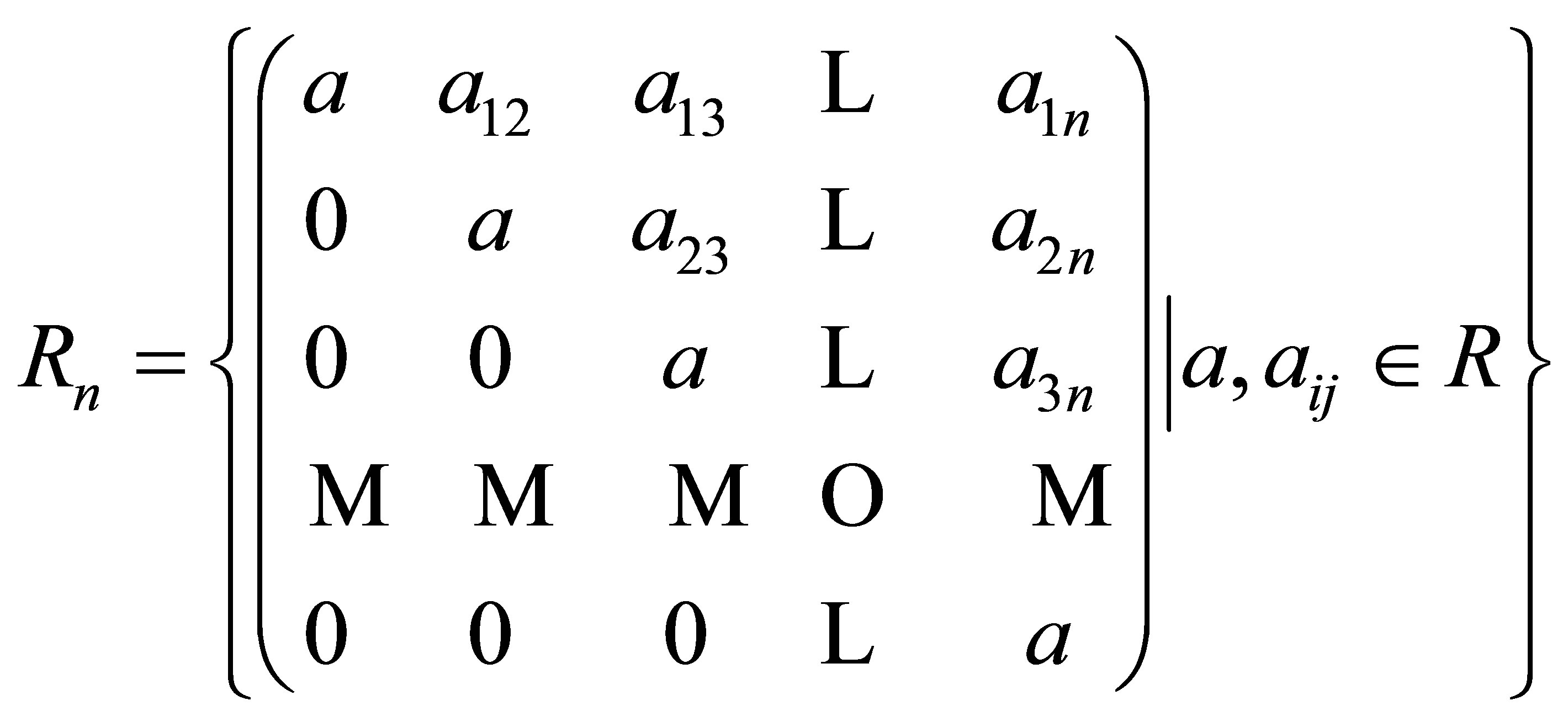
is not 3-Armendariz by [7, Example 4], for 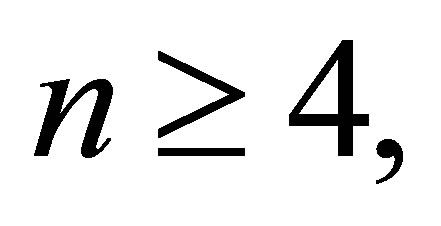 but
but 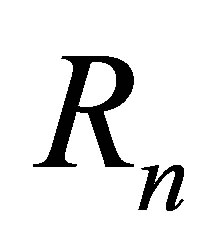 is a nil 3-Armendariz ring by Proposition 2.12, because
is a nil 3-Armendariz ring by Proposition 2.12, because 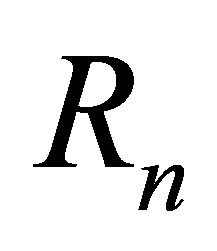 is a subring of
is a subring of 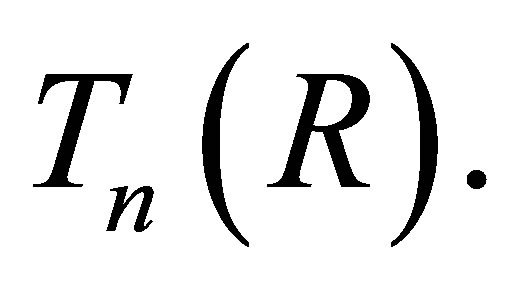
Proposition 2.18. Let 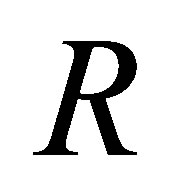 be a ring and
be a ring and  an idempotent of
an idempotent of 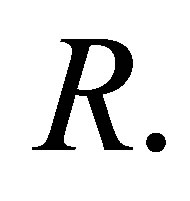 If
If  is central in
is central in 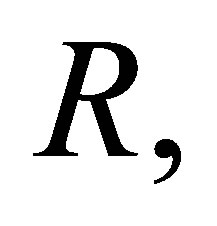 then the following statements are equivalent:
then the following statements are equivalent:
1)  is nil 3-Armendariz;
is nil 3-Armendariz;
2)  and
and 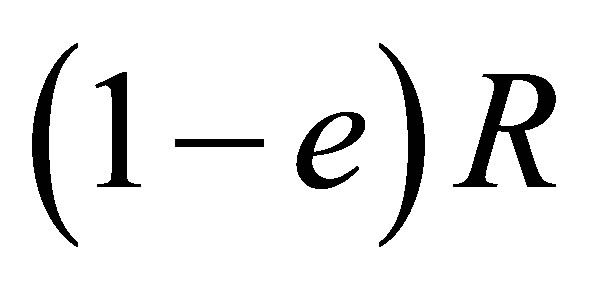 are nil 3-Armendariz.
are nil 3-Armendariz.
Proof. (2)Þ(1). Is obvious since 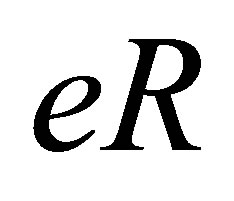 and
and 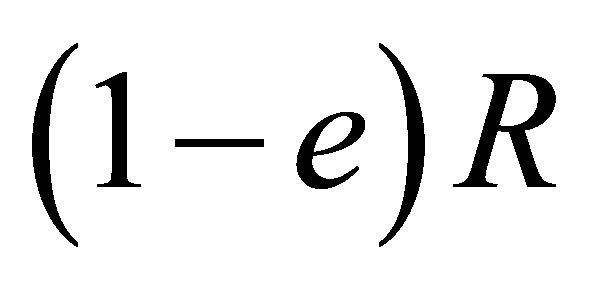 are subrings of
are subrings of 
(1)Þ(2). Note that 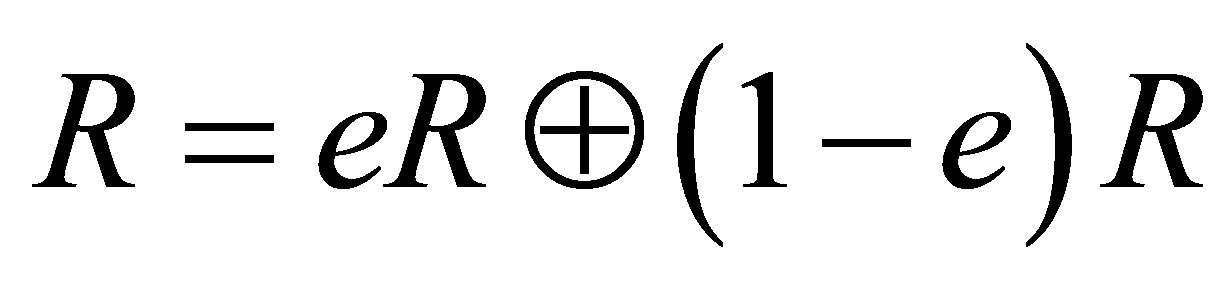 as rings. Thus the result follows from Proposition 2.10.
as rings. Thus the result follows from Proposition 2.10.
In [5, Theorem 11], it was shown that if 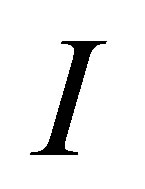 is a reduced ideal of
is a reduced ideal of  such that
such that 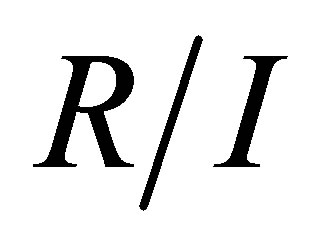 is Armendariz, then
is Armendariz, then  is Armendariz. In [10, Proposition 4], it is shown that if
is Armendariz. In [10, Proposition 4], it is shown that if 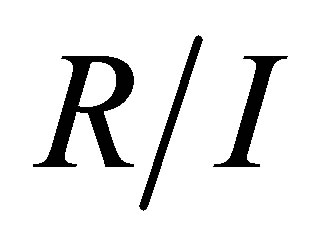 is a weak 3-Armendariz ring, then so is
is a weak 3-Armendariz ring, then so is  where
where 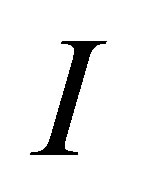 is a nilpotent ideal of
is a nilpotent ideal of  We show that this result also holds for nil 3-Armendariz rings in the following.
We show that this result also holds for nil 3-Armendariz rings in the following.
Proposition 2.19. Let 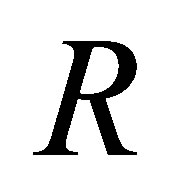 be a ring such that
be a ring such that  is a nil 3-Armendariz ring for some proper ideal
is a nil 3-Armendariz ring for some proper ideal 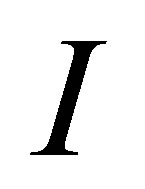 of
of  If
If  then
then 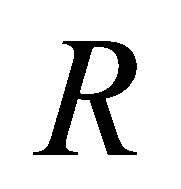 is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. Let 
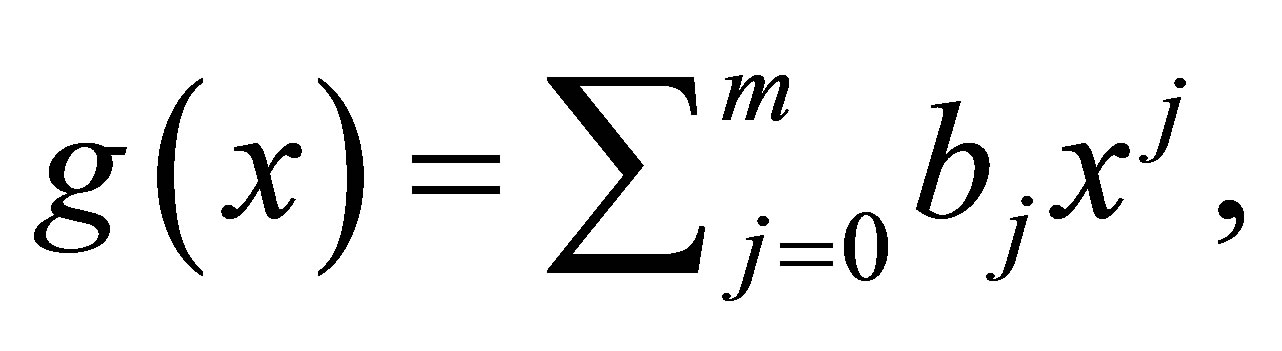
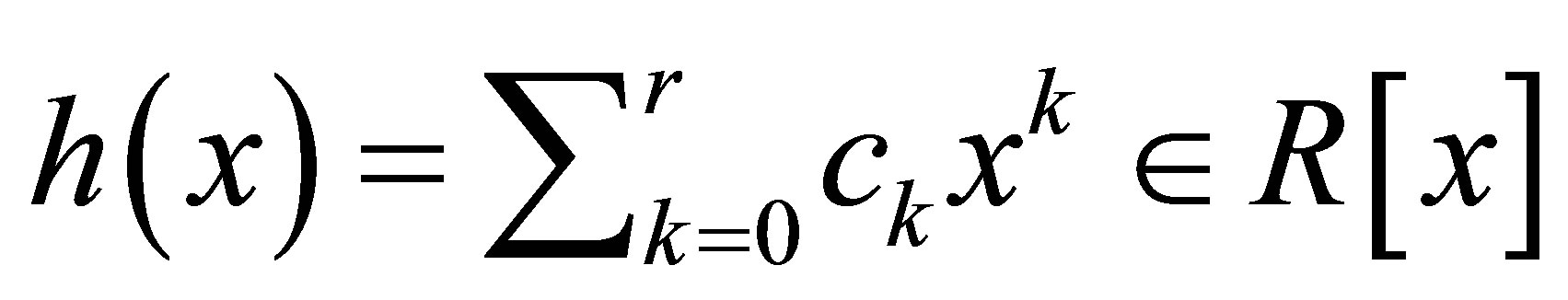 such that
such that 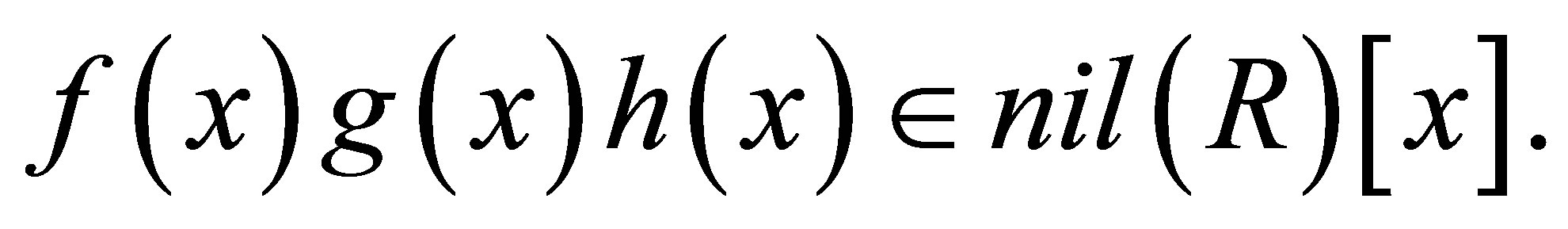 Then
Then 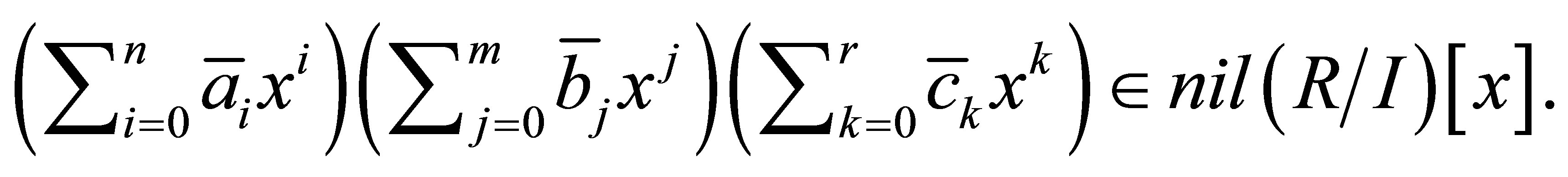
Since 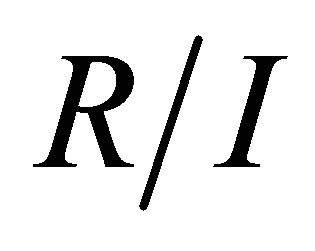 is nil 3-Armendariz, we have that
is nil 3-Armendariz, we have that 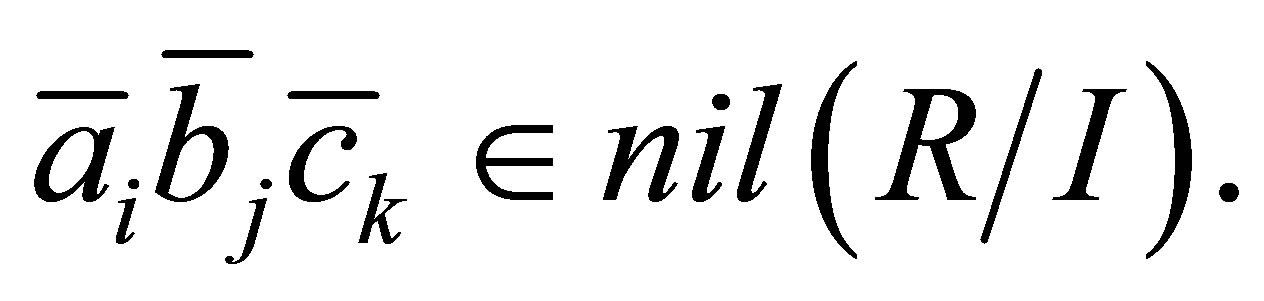 Hence
Hence  Since
Since  then
then 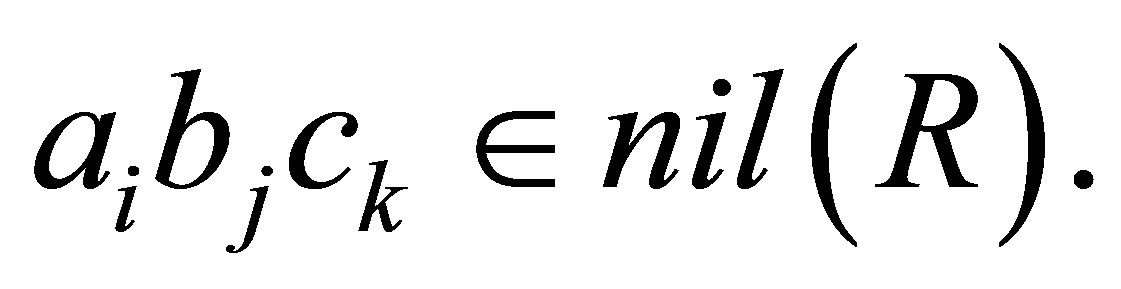 This means that
This means that 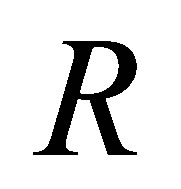 is a nil 3-Armendariz ring.
is a nil 3-Armendariz ring.
Anderson and Camillo in [3, Theorem 2], prove that a ring  is Armendariz if and only if the polynomial ring
is Armendariz if and only if the polynomial ring  is Armendariz. Yang Suiyi [7], prove that a ring
is Armendariz. Yang Suiyi [7], prove that a ring  is 3-Armendariz if and only if the polynomial ring
is 3-Armendariz if and only if the polynomial ring  is 3-Armendariz. In [11], it is shown that if
is 3-Armendariz. In [11], it is shown that if 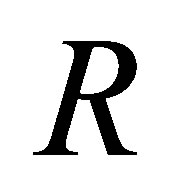 is reduced ring, then
is reduced ring, then 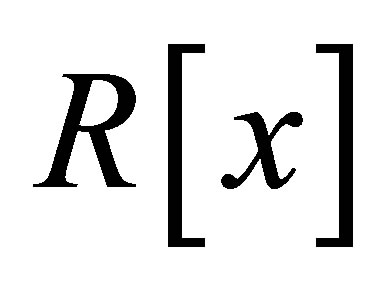 and
and  is 3-Armendariz ring. For nil 3-Armendariz rings we will give the following results.
is 3-Armendariz ring. For nil 3-Armendariz rings we will give the following results.
Proposition 2.20. If 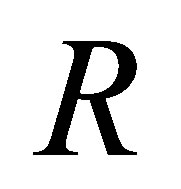 is nil 3-Armendariz, then
is nil 3-Armendariz, then 
Proof. Suppose  and
and 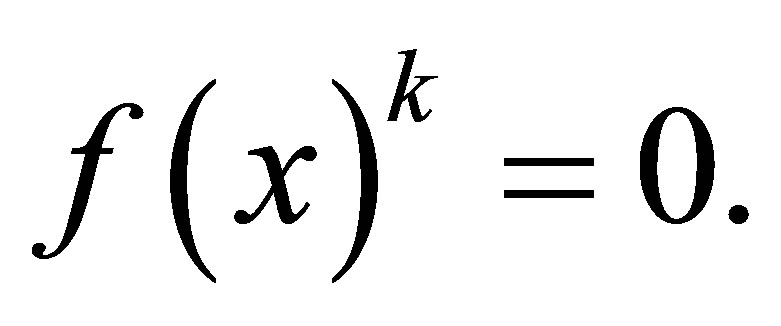 By Lemma 2.7, we have that
By Lemma 2.7, we have that  where
where  for
for 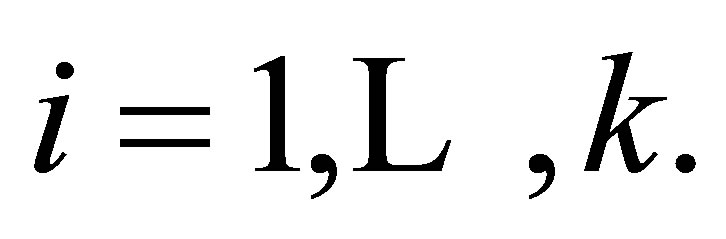 In particular, for every
In particular, for every 
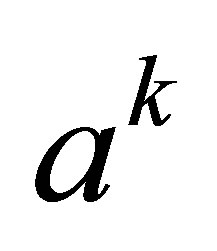 is nilpotent. Therefore
is nilpotent. Therefore 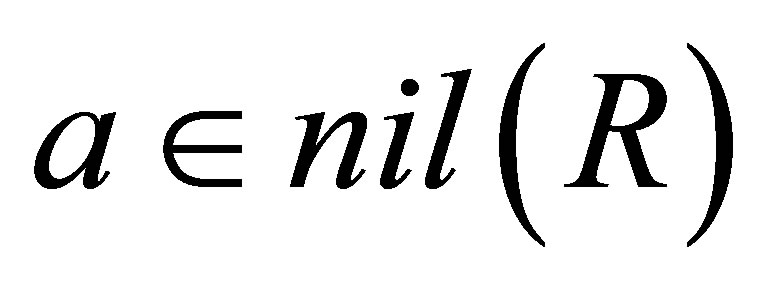 for all
for all 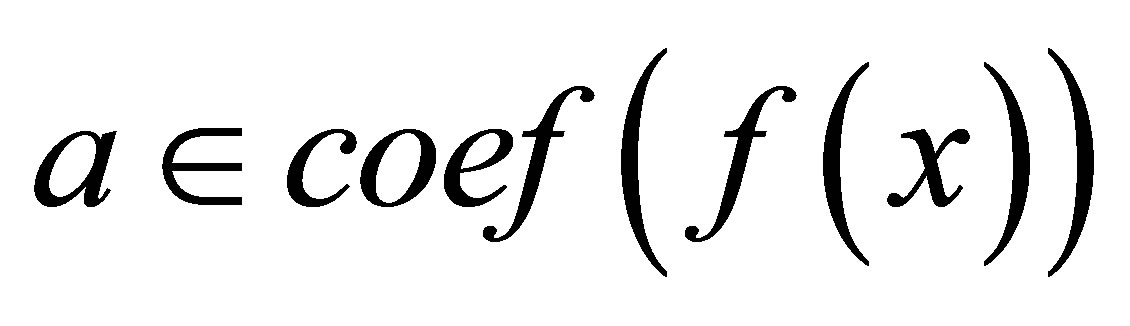 and hence
and hence 
Theorem 2.21. If  is a 3-Armendariz ring, then
is a 3-Armendariz ring, then 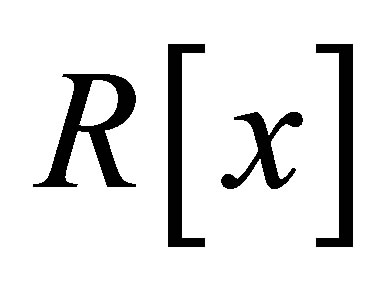 is a nil 3-Armendariz ring.
is a nil 3-Armendariz ring.
Proof. Let 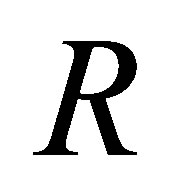 be 3-Armendariz ring. Then by [7, Theorem 3],
be 3-Armendariz ring. Then by [7, Theorem 3], 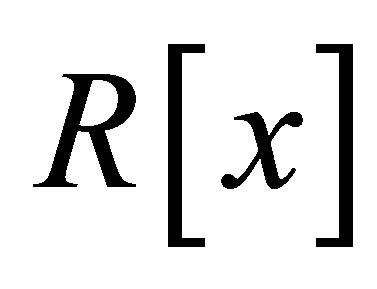 is 3-Armendariz. Thus by Proposition 2.9,
is 3-Armendariz. Thus by Proposition 2.9, 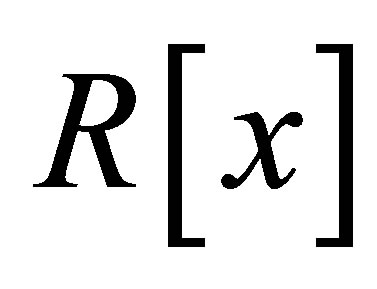 is nil 3-Armendariz.
is nil 3-Armendariz.
Proposition 2.22. Let  be a reduced ring. Then
be a reduced ring. Then  is a nil 3-Armendariz ring.
is a nil 3-Armendariz ring.
Proof. It follows from the method in the proof of [11, Theorem 1].
Corollary 2.23. If 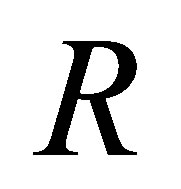 is a reduced ring, then
is a reduced ring, then  is a nil 3-Armendariz ring.
is a nil 3-Armendariz ring.
Recall that an element 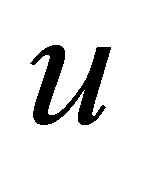 of a ring
of a ring 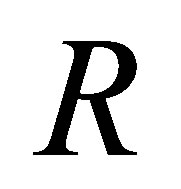 is right regular if
is right regular if  implies
implies 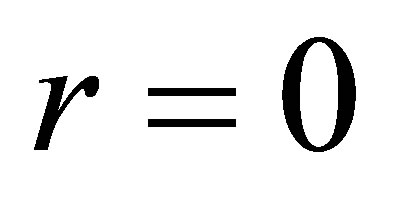 for
for  Similarly, left regular elements can be defined. An element is regular if it is both left and right regular (and hence not a zero divisor).
Similarly, left regular elements can be defined. An element is regular if it is both left and right regular (and hence not a zero divisor).
A ring 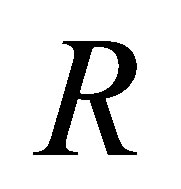 is called right (resp., left) Ore if given
is called right (resp., left) Ore if given  with
with  regular, there exist
regular, there exist 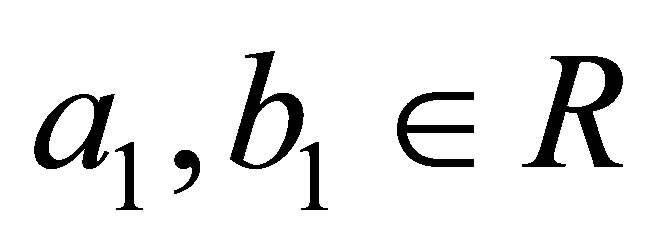 with
with 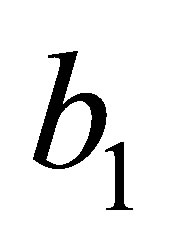 regular such that
regular such that 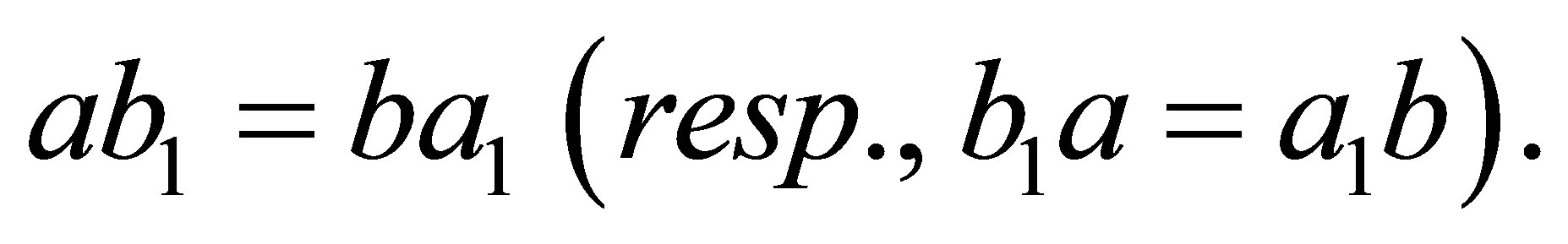 It is a well-known fact that
It is a well-known fact that 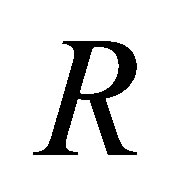 is a right (resp., left) Ore ring if and only if the classical right (resp., left) quotient ring of
is a right (resp., left) Ore ring if and only if the classical right (resp., left) quotient ring of  exists.
exists.
Lemma 2.24. If 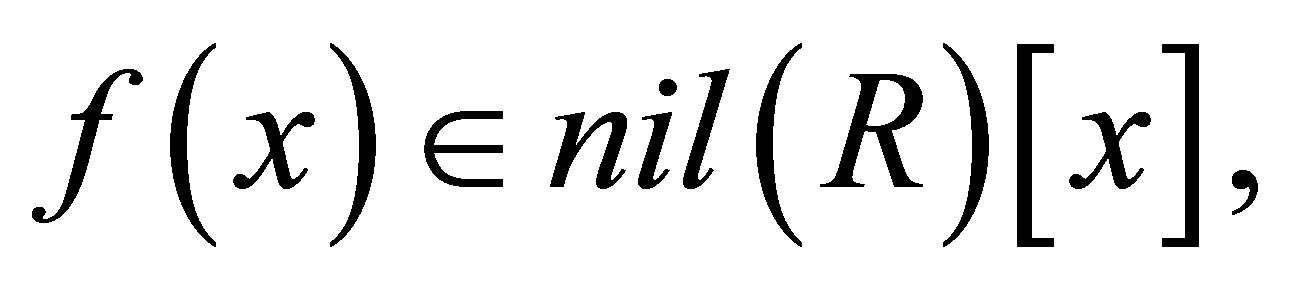 then for any central element
then for any central element 
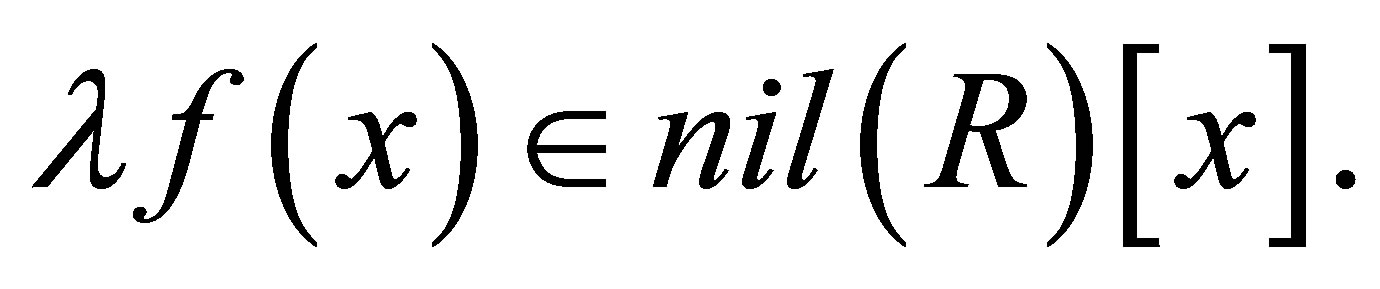
Proof. Set  Then
Then 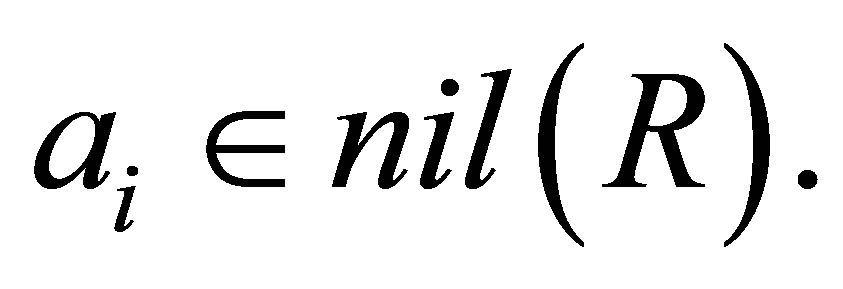 Thus
Thus 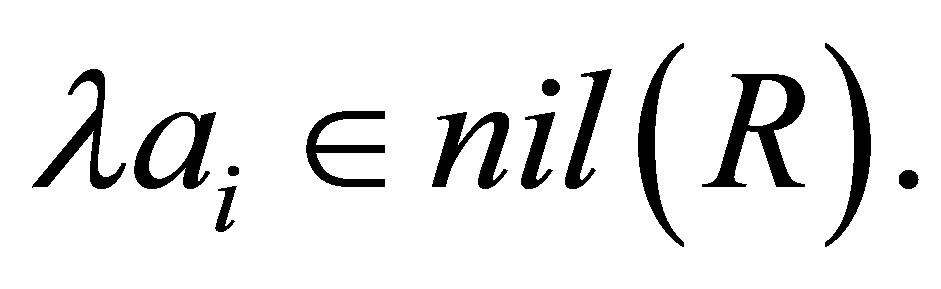 This means that
This means that 
Theorem 2.25. Let 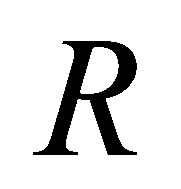 be a right Ore ring with the classical right quotient ring
be a right Ore ring with the classical right quotient ring 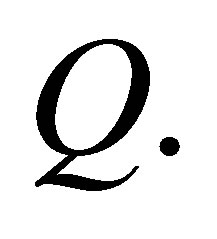 If all right regular elements are central, then
If all right regular elements are central, then  is nil 3-Armendariz if and only if so is
is nil 3-Armendariz if and only if so is 
Proof. It suffices to show by Lemma 2.11, that if 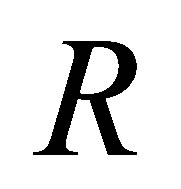 is nil 3-Armendariz rings so is
is nil 3-Armendariz rings so is  We apply the proof of [5, Theorem 12]. Consider
We apply the proof of [5, Theorem 12]. Consider 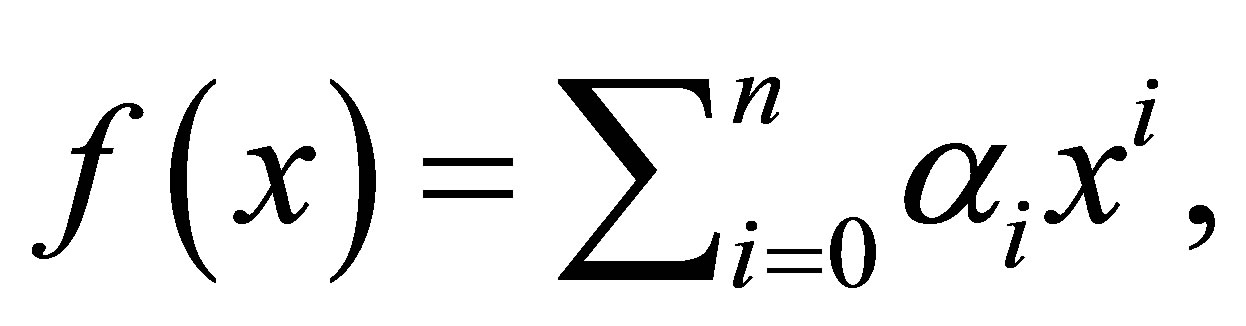

 such that
such that
 By [12, Proposition 2.1.16], we can assume that
By [12, Proposition 2.1.16], we can assume that 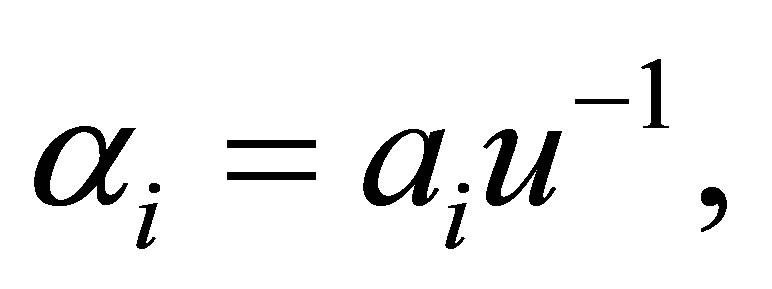
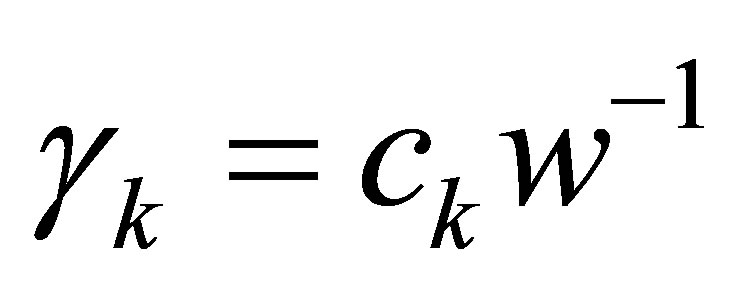
 with
with 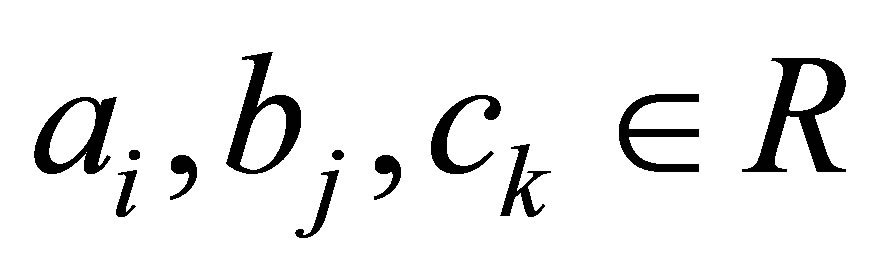 for all
for all  and a right regular elements
and a right regular elements  Put
Put
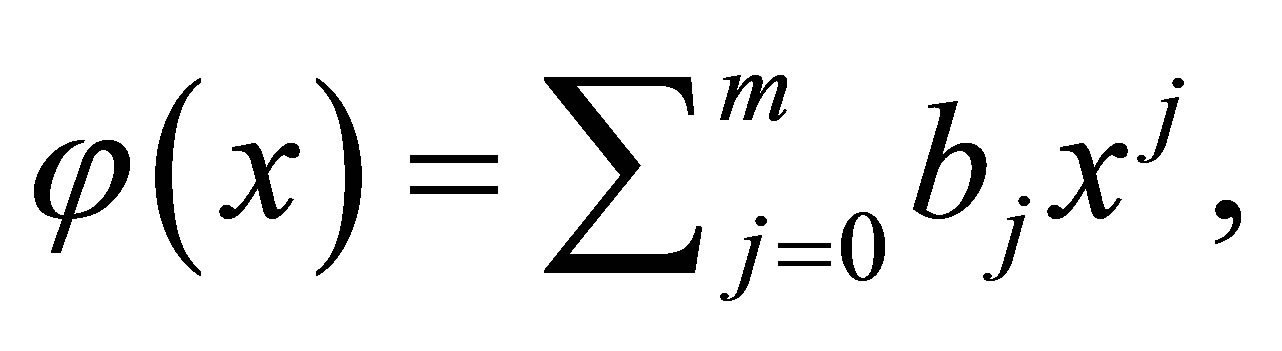

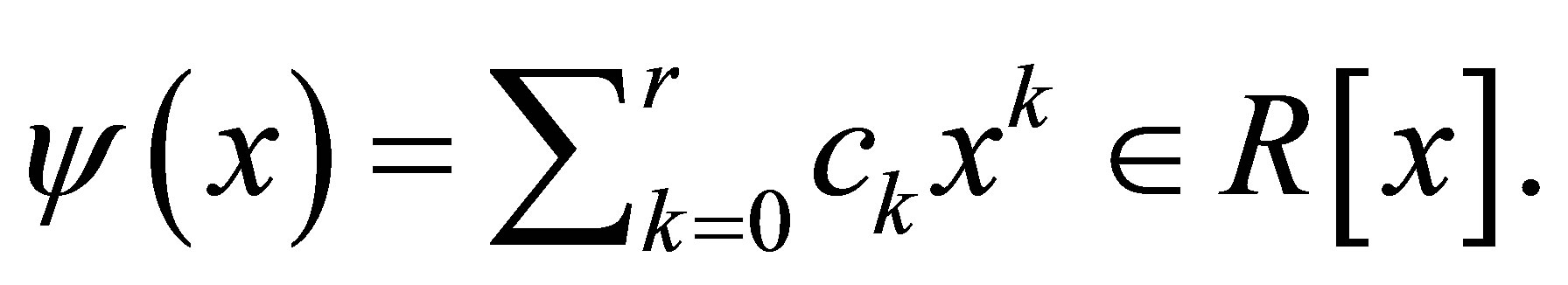 Then we have
Then we have

Since 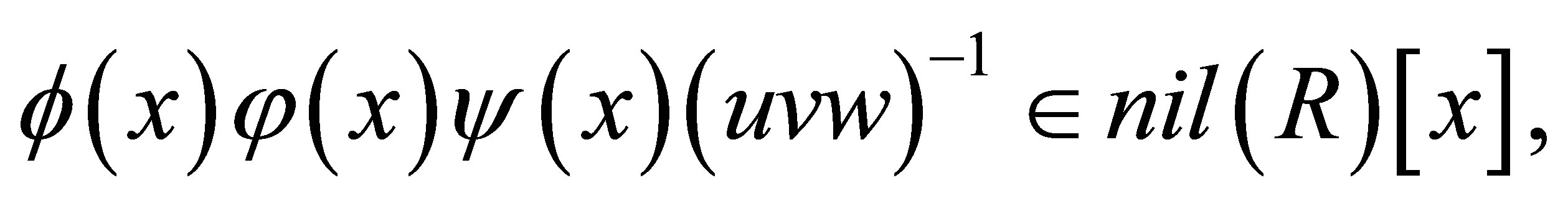 by Lemma 2.24,
by Lemma 2.24, 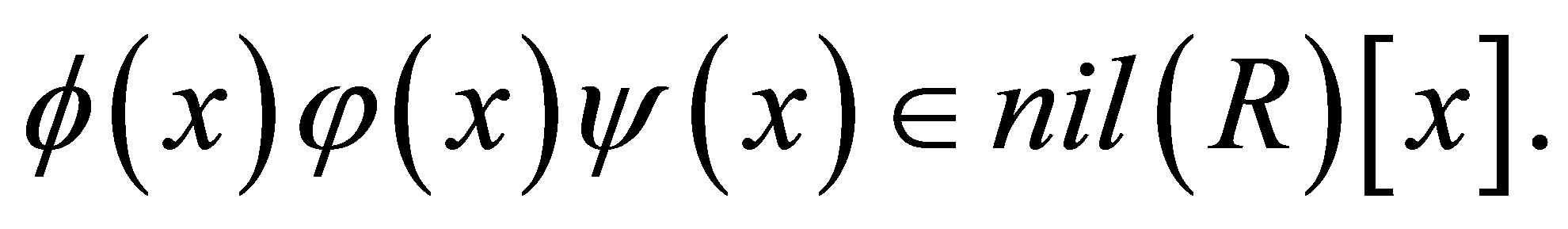 Since
Since 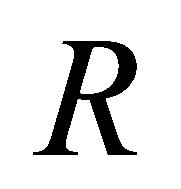 is nil 3-Armendariz,
is nil 3-Armendariz,  for each
for each 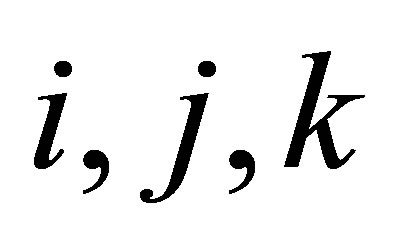 and so
and so 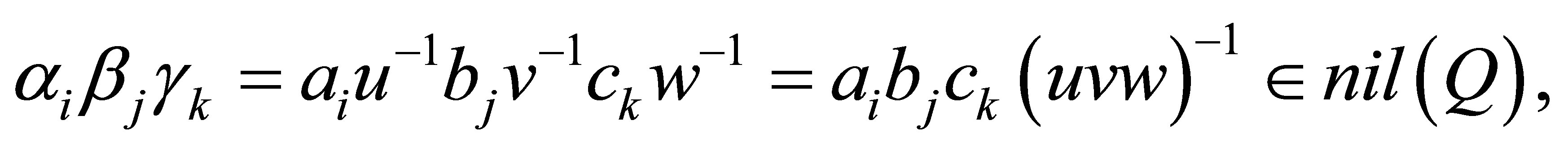 for all
for all  Therefore
Therefore 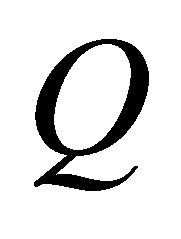 is nil 3-Armendariz ring.
is nil 3-Armendariz ring.
Corollary 2.26. Let 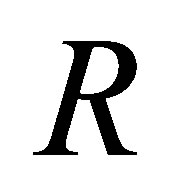 be a ring and
be a ring and  be a multiplicative closed subset in
be a multiplicative closed subset in 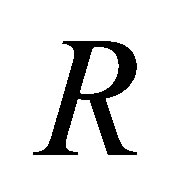 consisting of central regular elements. Then
consisting of central regular elements. Then  is nil 3-Armendariz rings if and only if
is nil 3-Armendariz rings if and only if  is nil 3-Armendariz rings.
is nil 3-Armendariz rings.
Corollary 2.27. A commutative ring  is nil 3-Armendariz if and only if so is the total quotient ring of
is nil 3-Armendariz if and only if so is the total quotient ring of 
Proof. It suffices to show the necessity by Lemma 2.11. Let  be the multiplicative closed subset of all regular elements in
be the multiplicative closed subset of all regular elements in 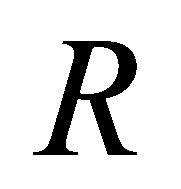 . Then
. Then 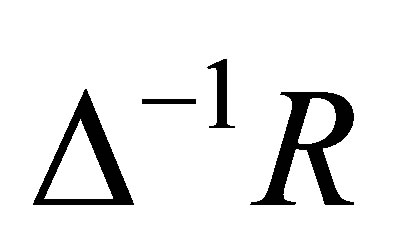 is the total quotient ring of
is the total quotient ring of 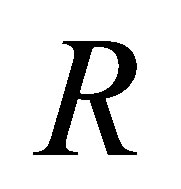 and hence the result holds by Corollary 2.26.
and hence the result holds by Corollary 2.26.
The ring of Laurent polynomials in 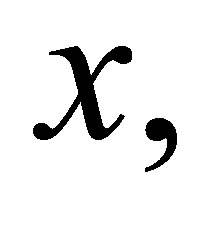 with coefficients in a ring
with coefficients in a ring  consists of all formal sum
consists of all formal sum
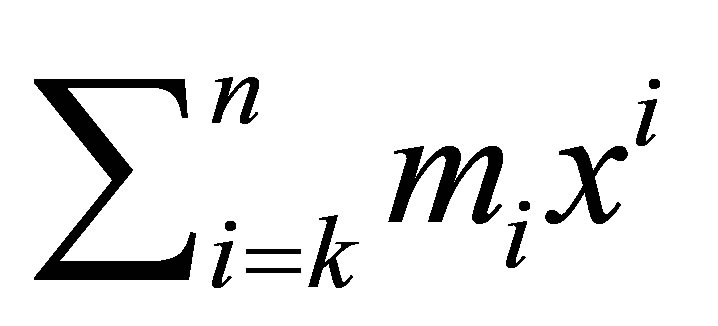 with obvious addition and multiplicationwhere
with obvious addition and multiplicationwhere  and
and 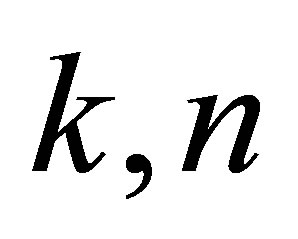 are (possibly negative) integers and denote it by
are (possibly negative) integers and denote it by 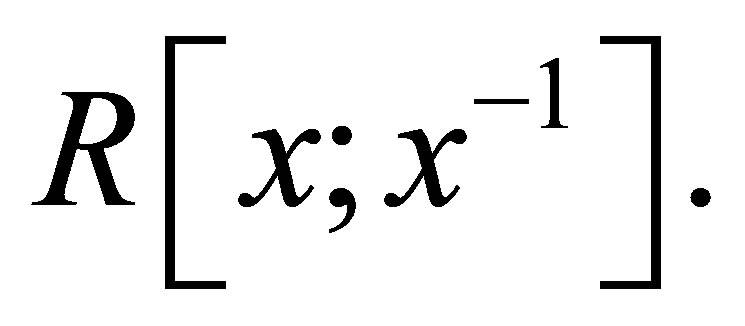
Corollary 2.28. Let  be a ring.
be a ring.  is nil 3- Armendariz if and only if
is nil 3- Armendariz if and only if 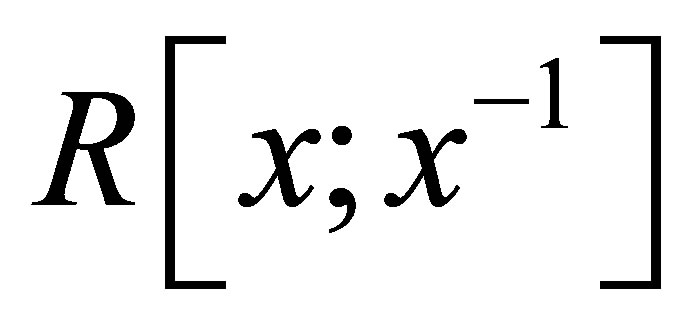 is nil 3-Armendariz.
is nil 3-Armendariz.
Proof. It suffices to establish necessity since  is a subring of
is a subring of  Let
Let  then clearly
then clearly  is a multiplicatively closed subset in
is a multiplicatively closed subset in 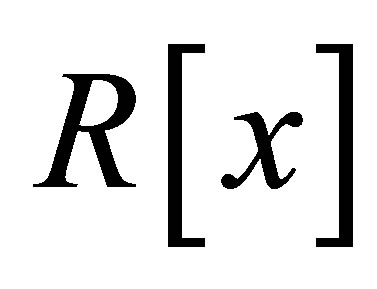 consisting of central regular elements. Note that
consisting of central regular elements. Note that 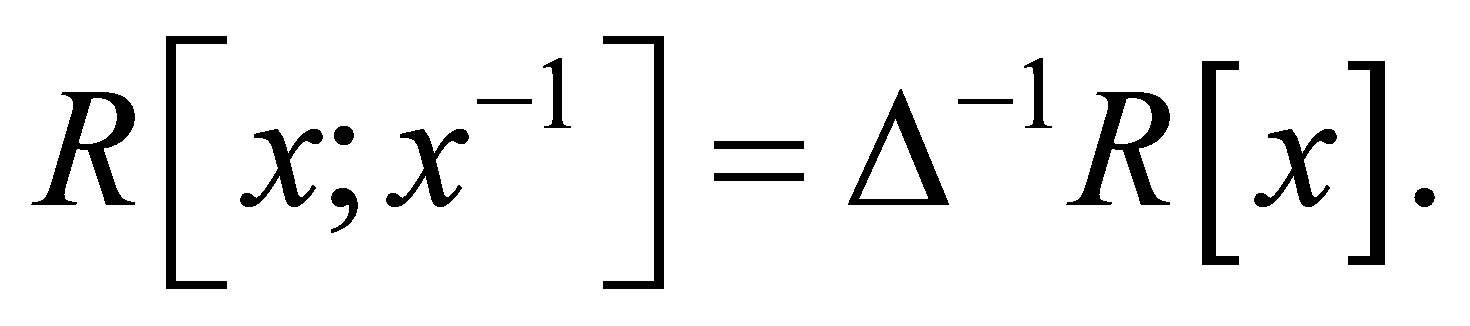 If
If  is nil 3-Armendariz, so is
is nil 3-Armendariz, so is  by Corollary 2.26.
by Corollary 2.26.
3. Acknowledgements
This paper is partially supported by National Natural Science Foundation of China (No.11261050). I also thank the referee for his or her valuable comments.
REFERENCES
- E. P. Armendariz, “A Note on Extensions of Baer and p.p.-Rings,” Journal of the Australian Mathematical Society, Vol. 18, No. 4, 1974, pp. 470-473. http://dx.doi.org/10.1017/S1446788700029190
- M. B. Rege and S. Chhawchharia, “Armendariz Rings,” Proceedings of the Japan Academy, Series A, Mathematical Sciences, Vol. 73, No. 1, 1997, pp. 14-17. http://dx.doi.org/10.3792/pjaa.73.14
- D. D. Anderson and V. Camillo, “Armendariz Rings and Gaussian Rings,” Communications in Algebra, Vol. 26, No. 7, 1998, pp. 2265-2272. http://dx.doi.org/10.1080/00927879808826274
- N. K. Kim and Y. Lee, “Armendariz Rings and Reduced Rings,” Journal of Algebra, Vol. 223, No. 2, 2000, pp. 477-488. http://dx.doi.org/10.1006/jabr.1999.8017
- C. Huh, Y. Lee and A. Smoktunowicz, “Armendariz Rings and Semicommutative Rings,” Communications in Algebra, Vol. 30, No. 2, 2002, pp. 751-761. http://dx.doi.org/10.1006/jabr.1999.8017
- T. K. Lee and T. L. Wong, “On Armendariz Rings,” Houston Journal of Mathematics, Vol. 29, No. 3, 2003, pp. 583-593.
- Y. Suiyi, “On the Extension of Armendariz Rings,” MS Thesis, Lanzhou University, Lanzhou, 2008.
- R. Antoine, “Nilpotent Elements and Armendariz Rings,” Journal of Algebra, Vol. 319, No. 8, 2008, pp. 3128-3140. http://dx.doi.org/10.1016/j.jalgebra.2008.01.019
- Z. K. Liu and R. Y. Zhao, “On Weak Armendariz Rings,” Communications in Algebra, Vol. 34, No. 7, 2006, pp. 2607-2616. http://dx.doi.org/10.1080/00927870600651398
- H. F. Wu, “On Weak 3-Armendariz Rings,” Journal of Hangzhou Normal University (Natural Science Edition), Vol. 11, No. 3, 2012, pp. 241-244.
- H. F. Wu, “Extensions of Reduced Rings,” Journal of Hangzhou Normal University (Natural Science Edition), Vol. 10, No. 5, 2011, pp. 407-410.
- J. C. McConnell and J. C. Robson, “Noncommutative Noetherian Rings,” A Wiley-Interscience Publication, John Wiley and Sons, Ltd., Chichester, 1987.

