Advances in Pure Mathematics
Vol.3 No.9A(2013), Article ID:40870,6 pages DOI:10.4236/apm.2013.39A1004
Identification of Rotor Unbalance as Inverse Problem of Measurement
Faculty of Mechanics & Mathematics, Dnepropetrovsk University, Dnepropetrovsk, Ukraine
Email: Menshikov2003@list.ru
Copyright © 2013 Yuri Menshikov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Yuri Menshikov. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 29, 2013; revised November 29, 2013; accepted December 5, 2013
Keywords: mathematical model; unbalance identification; solution estimation; regularization; numerical test
ABSTRACT
In this paper, the problem of identification of the characteristics of the rotor unbalance on two supports is investigated as the inverse problem of measurement. The vibration of rotor supports in two mutually perpendicular directions used as the initial information. The inverse problem is considered, taking into account the error of the mathematical description of rotor-bearings system. To obtain estimates of real unbalance characteristics, the hypothesis as to the exact solutions is applied. The method of Tikhonov regularization is used to obtain stable results. Test calculations are given to illustrate the proposed approach.
1. Introduction
The constructional differences of rotors and their domains of exploitation led to the creation of special methods of balancing. In many cases, the only criterion of rotor balancing is the absence (or the permissible value) of dynamical responses of supports. The compensation of deflections on length of rotor is considered only as the means to arrive of minimum of main criterion. In other cases, the reach of minimum of its deflections or its bending moment is taken as the criterion of rotor balancing. Such difference in choice of criterion can explain that for each case the parameters that are the main for given type of rotors are chosen. The reactions of supports or corresponding vibrations are taken for criteria of rotors balancing in particular to turbine-generator-building and the rotor deflection axis in jet engine building [1,2].
The basis of the most existing methods of flexible rotors balancing is the measuring of rotor vibrations and its supports, namely measuring of deflection and phases of rotating rotor followed by the choice and putting of trial plummets according to the shape of normal mode of vibrations.
The motion of flexible rotor relative to the rotating together with its coordinate system (one of axis coincides with the geometric axis of rotor) is described by Fredholm equation of the first kind. This equation is substituted for the matrix equation of form:
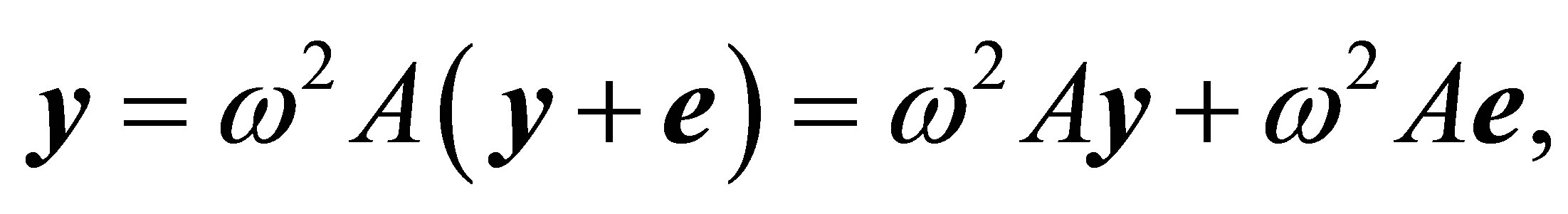
where![]() and
and ![]() are vectors of dimension
are vectors of dimension![]() ;
;  is the quadratic matrix of dimension
is the quadratic matrix of dimension![]() ;
; ![]() is the frequency of rotating. The coefficients of influence
is the frequency of rotating. The coefficients of influence 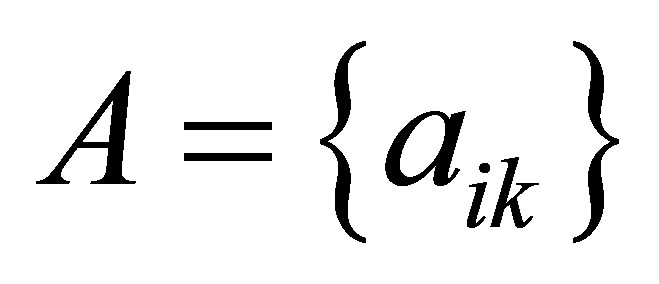 are defined experimentally for each plane of correction by trial starts.
are defined experimentally for each plane of correction by trial starts.
Balancing plummets are calculated with the help of the initial values of vibrations  from condition of remaining amplitudes minimum. The definition of balancing plummets is made by least squares method. The information about experimental complex values of influence coefficients that are obtained by different balancing is neutralized as a rule.
from condition of remaining amplitudes minimum. The definition of balancing plummets is made by least squares method. The information about experimental complex values of influence coefficients that are obtained by different balancing is neutralized as a rule.
The main tendencies of balancing methods development are connected with ways of development of coefficient influence definition [2,3].
Besides, current passive methods do not give the complete information about the position of unbalance if the rotor has a large length along the axis of rotation.
The suggested algorithms of unbalance evaluation use the experimental data about vibrations (accelerations) of two rotors’ support in two mutually perpendicular directions during the work and a few rotor rotations as the initial information. These algorithms do not demand special conditions of work or the installation of trial plummets.
2. Problem Definition
Let us consider a deformable rotor rotating on two non-rigid supports [4,5]. We introduce rectangular righthand coordinates system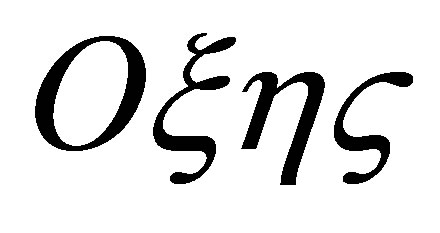 . The axis
. The axis  coincides with axis of the rotating shaft of rotor. The axis
coincides with axis of the rotating shaft of rotor. The axis 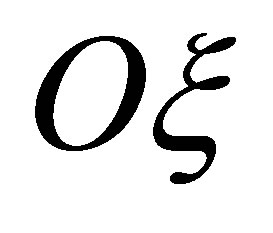 belongs to the plane of rotor in horizontal position. The axis
belongs to the plane of rotor in horizontal position. The axis 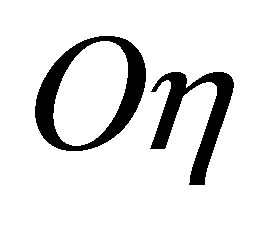 has vertical direction. We obtain equations of rotor motion in the following [4,5]:
has vertical direction. We obtain equations of rotor motion in the following [4,5]:
1) Weight’s centers and stiffness’s centers of crosssection of rotor coincide;
2) Eccentricity of rotor’s disk is one-order infinitesimal with a displacement under vibrations.
The motion of rotor on two non-region supports is described by system of ordinary differential equations of 18th order [4,5]. Unbalance of rotor is modeled by some external load (EL). The value of this EL and the place of its action is it necessary to find. It is assumed that the vibrations of rotor supports in two mutual perpendicular directions are obtained from experiment. Let us suppose that the functions 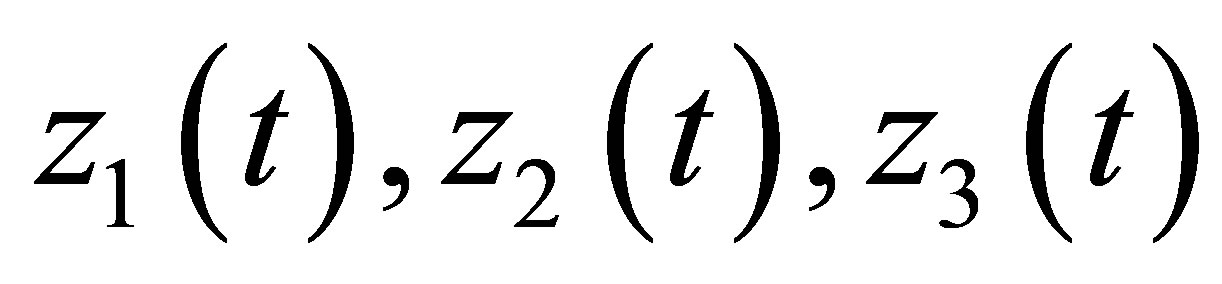 characterize the unbalance of rotor (EL)
characterize the unbalance of rotor (EL)

where 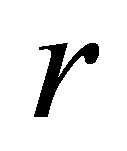 is the radius of rotor,
is the radius of rotor, 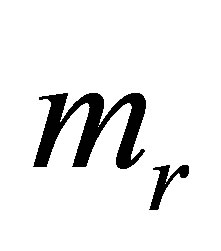 is the mass of unbalance reducing to a surface of rotor,
is the mass of unbalance reducing to a surface of rotor, ![]() is the angular velocity of rotation,
is the angular velocity of rotation, 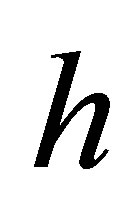 is unbalance arm,
is unbalance arm, ![]() is angular deviation of the factor of EL with respect to correction plane. If the unbalance is absent then the functions
is angular deviation of the factor of EL with respect to correction plane. If the unbalance is absent then the functions  will be equal to zero. We suppose that with the help of acceleration transducers the function have been recorded (
will be equal to zero. We suppose that with the help of acceleration transducers the function have been recorded (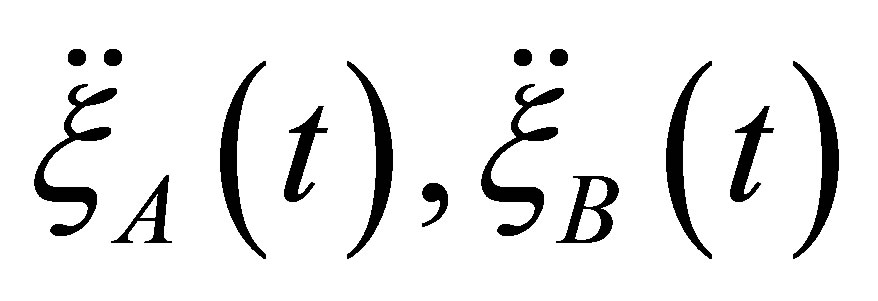 are the acceleration of supports in horizontal direction,
are the acceleration of supports in horizontal direction, 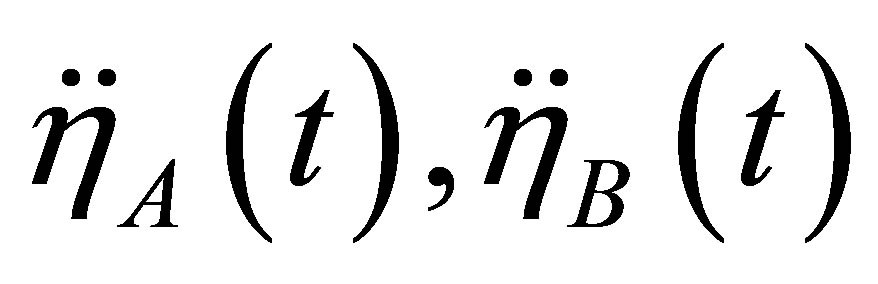 are the acceleration of supports in vertical direction). As an example, we consider the equation for the unknown function
are the acceleration of supports in vertical direction). As an example, we consider the equation for the unknown function  only.
only.
Then the problem of unbalance measurement is reduced to the solution of integral equations of Volltera first kind
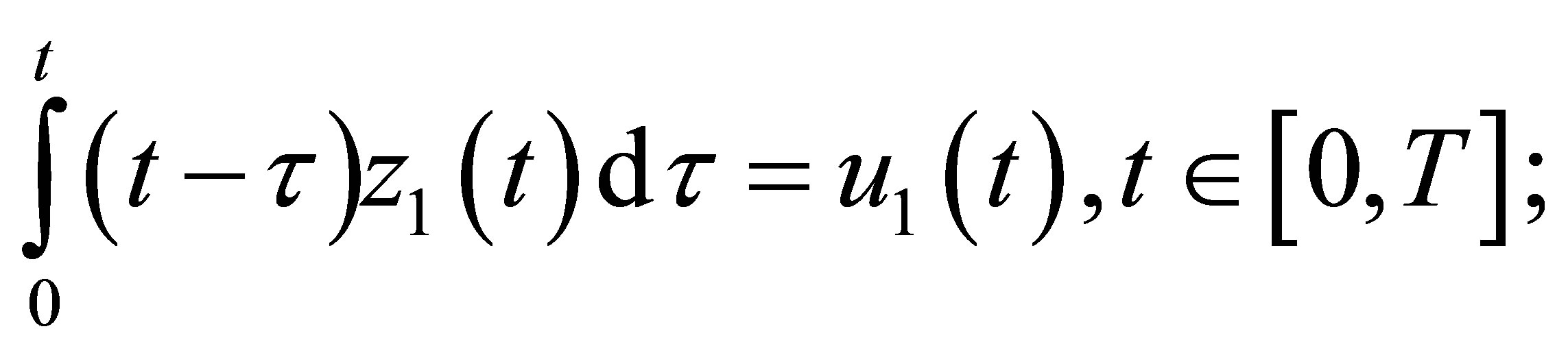
or
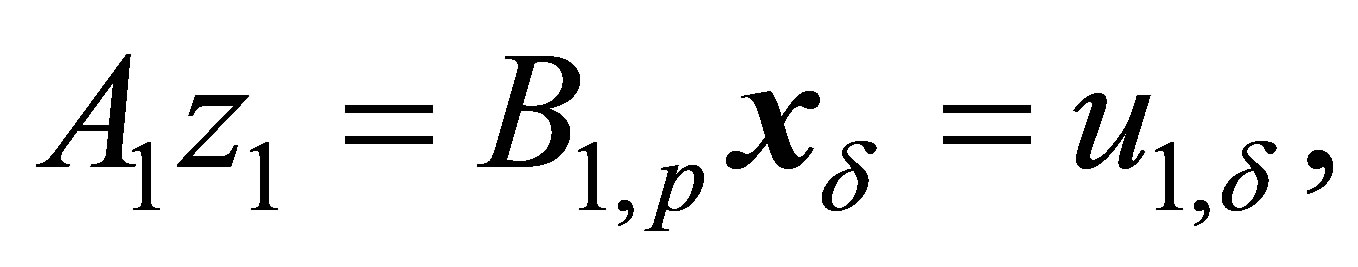 (1)
(1)
where 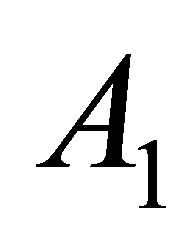 is a linear integral operator
is a linear integral operator ,
, ![]() is the searched characteristic of EL,
is the searched characteristic of EL,  is a linear irreversible operator
is a linear irreversible operator 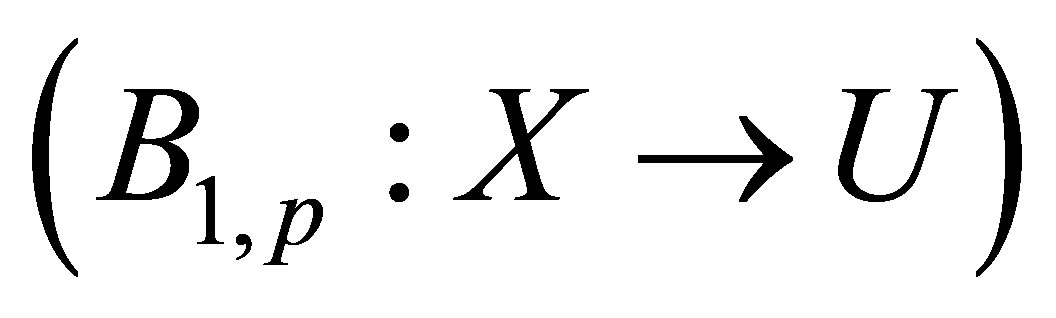 depending on vector parameters of mathematical model (MM) of “rotorsupports” system
depending on vector parameters of mathematical model (MM) of “rotorsupports” system 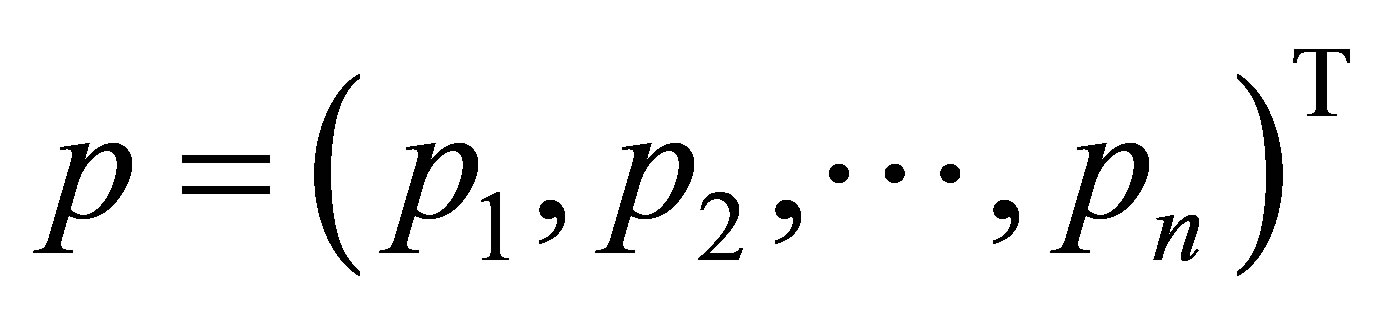 (
(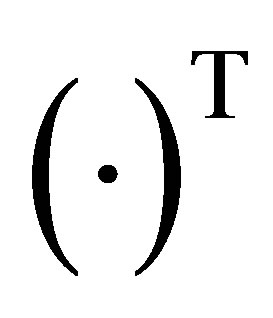 is the sign of transposition);
is the sign of transposition); 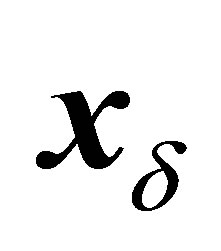 is the vector-function of initial data. Subjective factors influence on the definition of parameters of system “rotor-supports” MM and therefore the parameters are supposed to have their values within certain limits:
is the vector-function of initial data. Subjective factors influence on the definition of parameters of system “rotor-supports” MM and therefore the parameters are supposed to have their values within certain limits: ,
, . In this way the vector
. In this way the vector ![]() can be changed inside the known closed region
can be changed inside the known closed region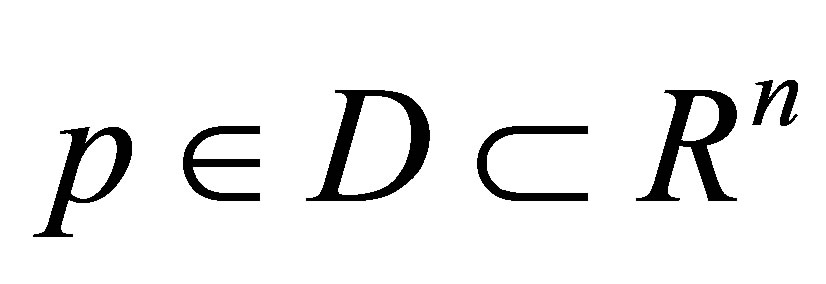 .
.
The equations for required functions  will be similar to the Equation (1).
will be similar to the Equation (1).
For a rotor on two supports for function 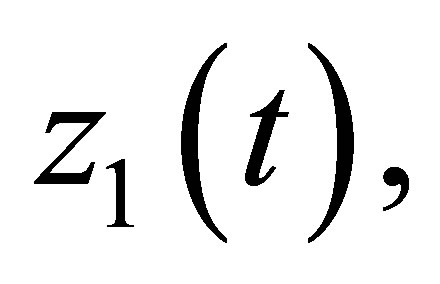
 the vector parameters
the vector parameters  of MM has a kind
of MM has a kind
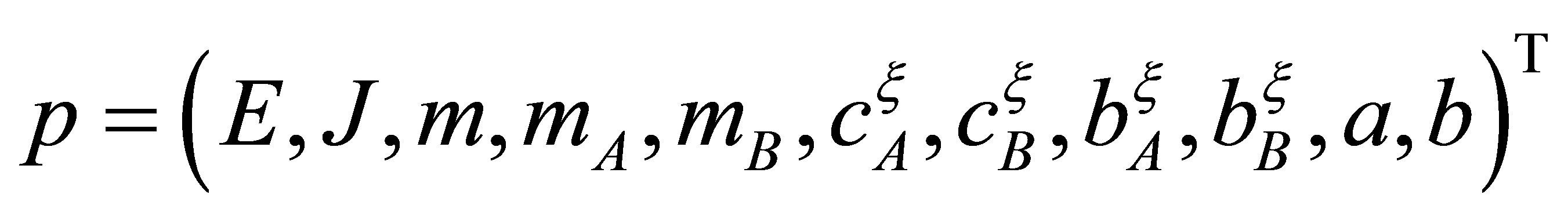 where E is module of Jung of rotor material, m is the mass of rotor, mA is the mass of the A support, mB is the mass of the B support;
where E is module of Jung of rotor material, m is the mass of rotor, mA is the mass of the A support, mB is the mass of the B support;  are the stiffness of supports A and B with respect to the horizontal and vertical direction;
are the stiffness of supports A and B with respect to the horizontal and vertical direction; 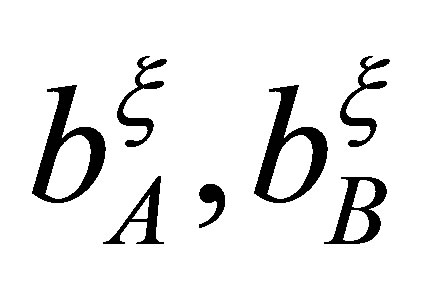 are the coefficients of external friction; a is the distance of gravity centre of rotor to the A support, a + b = l is the shaft length of rotor.
are the coefficients of external friction; a is the distance of gravity centre of rotor to the A support, a + b = l is the shaft length of rotor.
The vector function  is obtained using the experimental data (vibrations of supports) where the noise is present. Therefore it is convenient to think that each component of vector function
is obtained using the experimental data (vibrations of supports) where the noise is present. Therefore it is convenient to think that each component of vector function  and function
and function 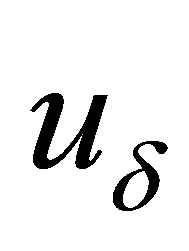 belongs to L2 [0, T]. Under this conditions the problem of equation (1) solution belongs to ill-posed problems if the searched functions
belongs to L2 [0, T]. Under this conditions the problem of equation (1) solution belongs to ill-posed problems if the searched functions  belong to
belong to 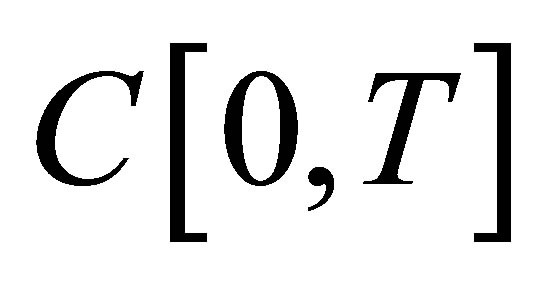 as the operator A in (1) is completely continuous [6].
as the operator A in (1) is completely continuous [6].
The value of function deviation 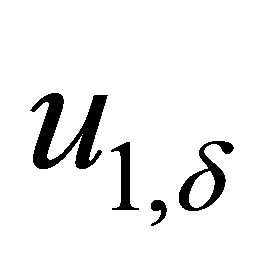 from the exact function
from the exact function 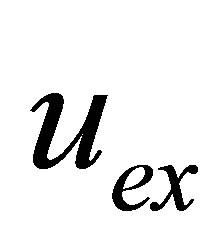 is given (if exact operator
is given (if exact operator 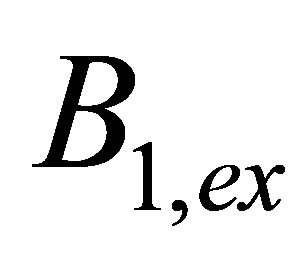 is linear):
is linear):
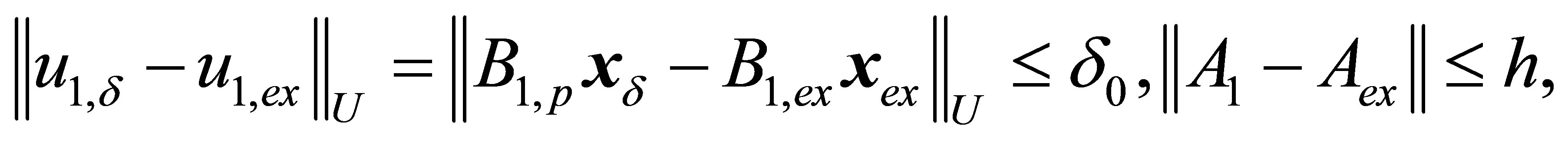
where
 ;
;
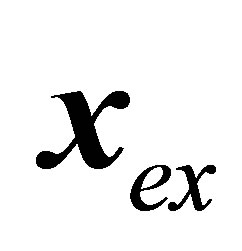 is the exact vector function of initial data;
is the exact vector function of initial data; 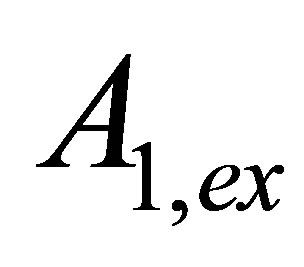
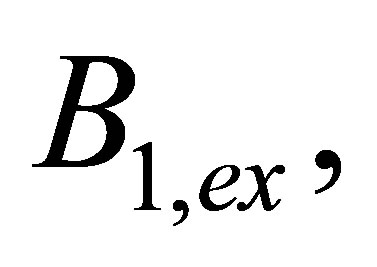 are the exact operators; d, b0, d,
are the exact operators; d, b0, d, 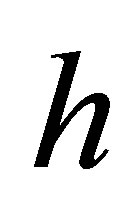 are given values.
are given values.
3. Statements of Identification Problem as Inverse Problem of Measurement
Let us consider the set of possible solutions of Equation (1) with account of whole error of initial data
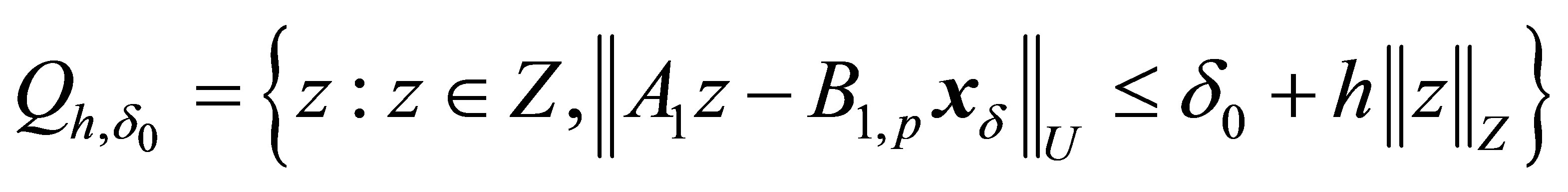 .
.
The set  is unbounded for any
is unbounded for any 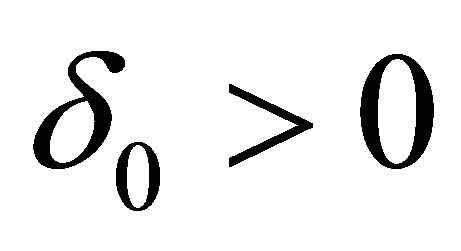 as this problem is ill-posed [6].
as this problem is ill-posed [6].
For definition of stable approximate solution is used the regularization method of Tikhonov [6]. This way is based on the search of following extreme problem solution:
 , (2)
, (2)
where  is the stabilizing functional which is defined on
is the stabilizing functional which is defined on  (
( is the everywhere dense set into Z).
is the everywhere dense set into Z).
The functional 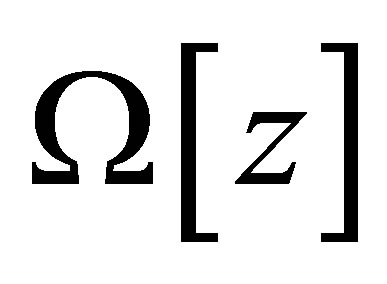 is chosen as follows
is chosen as follows
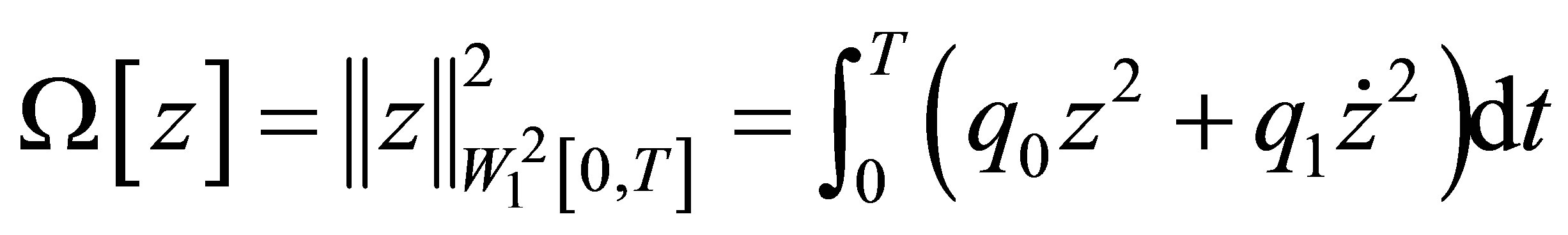 where
where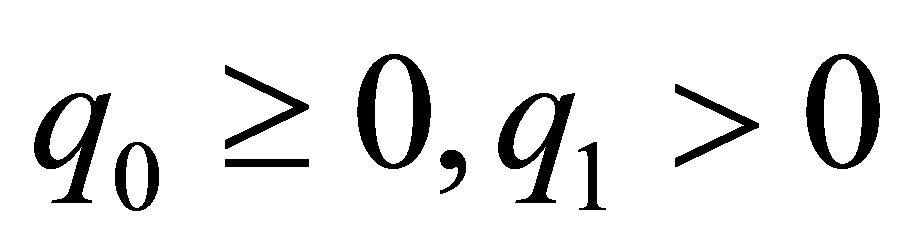 .
.
The choice such functional is explained by the following reasons:
• The solution  of an extreme problem (2) least will deviate zero and to have least first derivative in root-mean-square sense;
of an extreme problem (2) least will deviate zero and to have least first derivative in root-mean-square sense;
• The solution 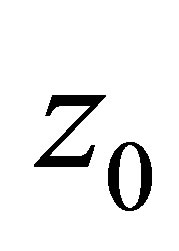 will give an estimation from below of exact solution
will give an estimation from below of exact solution 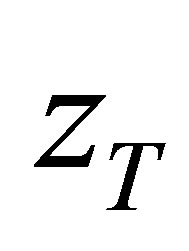 of equation (1)
of equation (1)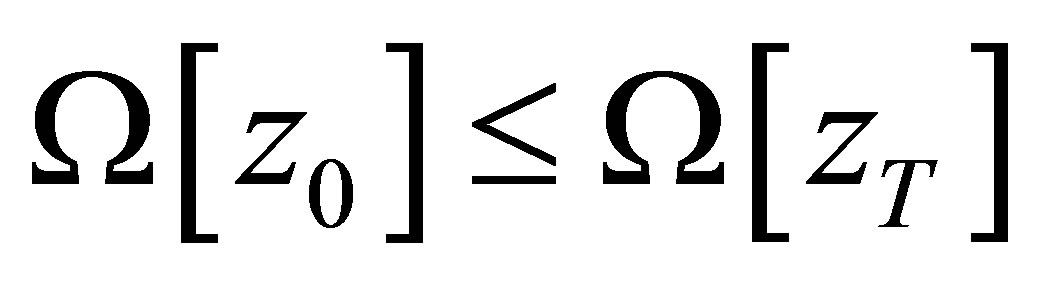 .
.
From the practical point of view the function  gives a guaranteed estimation from below sizes of real of a rotor in sense of functional
gives a guaranteed estimation from below sizes of real of a rotor in sense of functional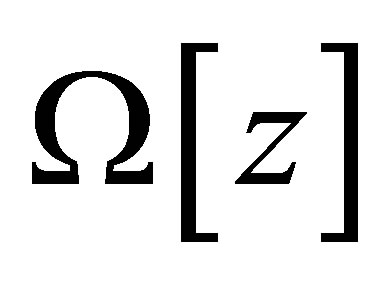 . If
. If 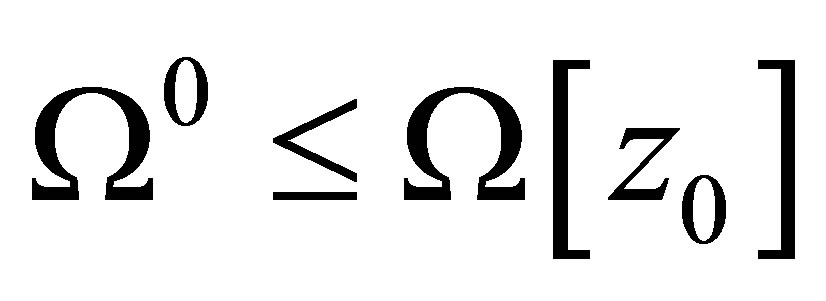 (
( there is known limiting an allowable size for the given type of rotor machine) then the rotor is working in emergency operation with guarantee.
there is known limiting an allowable size for the given type of rotor machine) then the rotor is working in emergency operation with guarantee.
If the inequality  is carried out, then no objective conclusions can be made. We will be named the solution of extreme problem (2) as estimation from below of real unbalance.
is carried out, then no objective conclusions can be made. We will be named the solution of extreme problem (2) as estimation from below of real unbalance.
In work [7] regularizing algorithm was suggested for equation (1) with approximate linear operator  for Banach spaces
for Banach spaces , which based on the regularization method [6].
, which based on the regularization method [6].
The solution of problem (1) is reduced to the solution of following extreme problem:
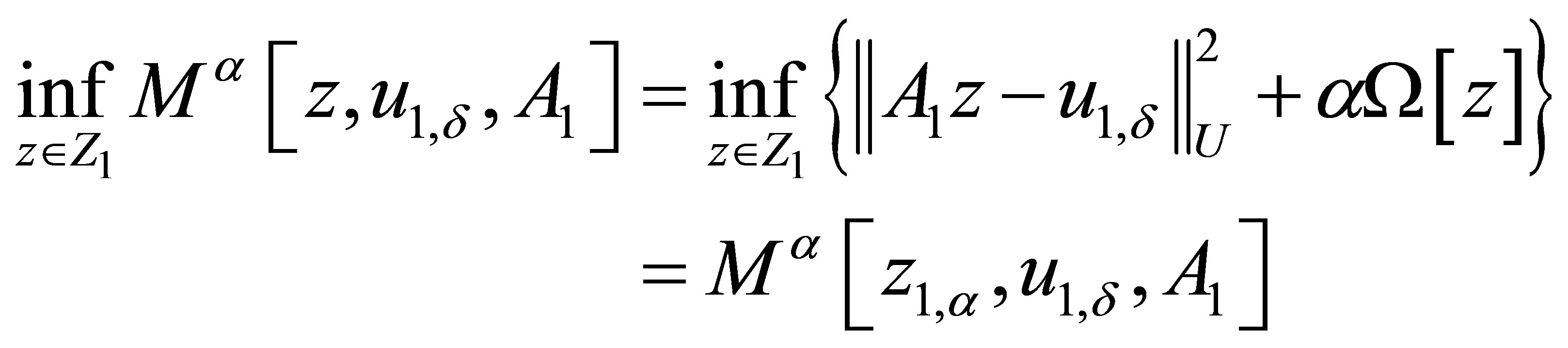 , (3)
, (3)
where 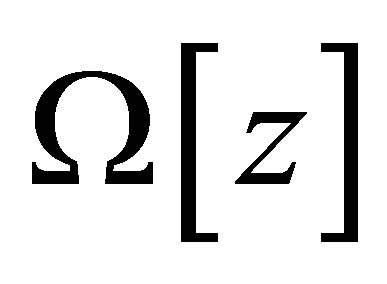 is stabilizing functional for equation (1) which defined on
is stabilizing functional for equation (1) which defined on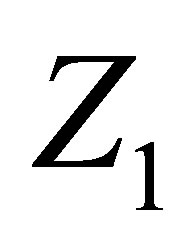 , the set
, the set 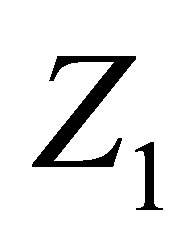 is everywhere dense into
is everywhere dense into .
.
Regularization parameter ![]() can be obtained from equation of general discrepancy:
can be obtained from equation of general discrepancy:
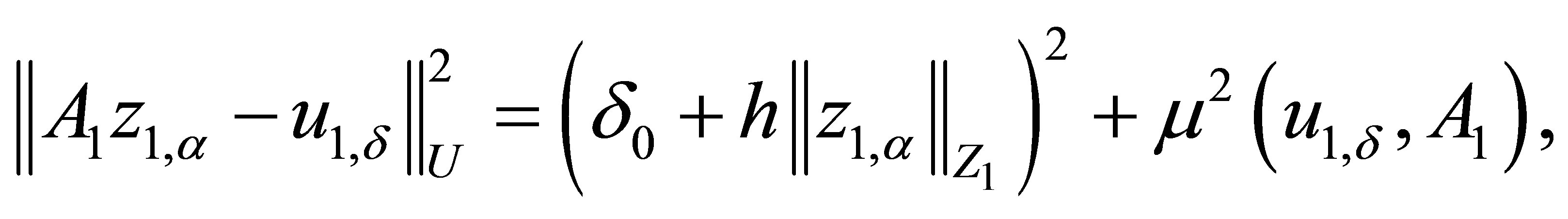 (4)
(4)
where  is measure of discrepancy.
is measure of discrepancy.
However at realization of such approach there are large difficulties at definition of size d, h as the absolute exact operators  are unknown and basically they cannot be constructed. However at realization of such approach there are large difficulties at definition of size d, h as the absolute exact operators
are unknown and basically they cannot be constructed. However at realization of such approach there are large difficulties at definition of size d, h as the absolute exact operators  is unknown and basically it cannot be constructed. Therefore size d is determined with the large overestimate and in set
is unknown and basically it cannot be constructed. Therefore size d is determined with the large overestimate and in set  the “extraneous” functions get, that considerably reduces accuracy of the regularized solution.
the “extraneous” functions get, that considerably reduces accuracy of the regularized solution.
So in this paper the estimation of inverse problem solution instead of solution of equation (1) is suggested. The following hypothesis is assumed for this purpose [8,9]: the such inequality is valid
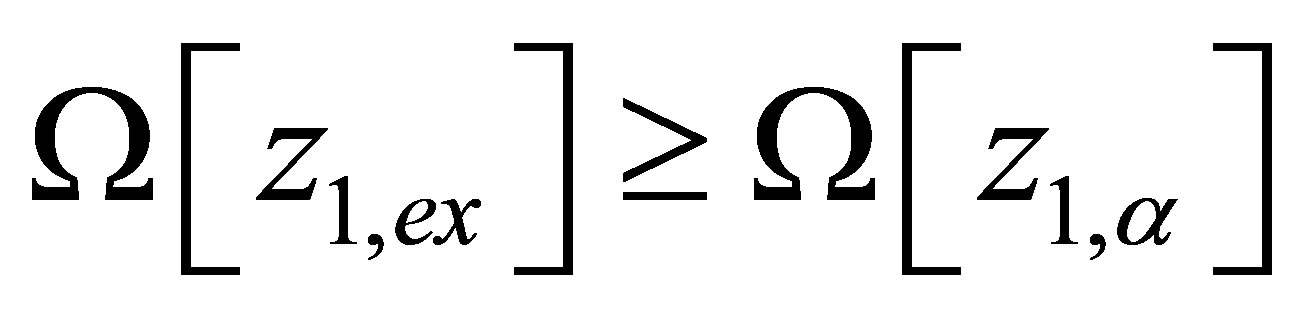 (5)
(5)
for any approximate operators 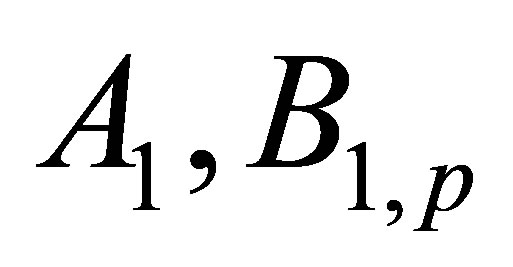 in equation (1) which corresponding to adequate mathematical description of vibration process [10];
in equation (1) which corresponding to adequate mathematical description of vibration process [10]; 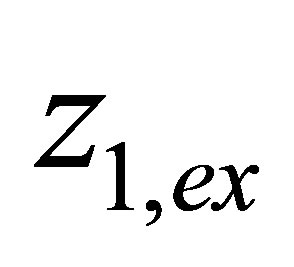 is the solution of equation (1) with exact right part
is the solution of equation (1) with exact right part 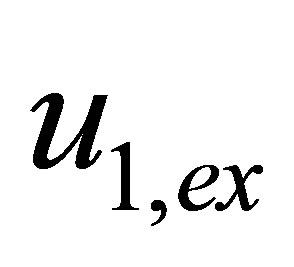 and exact operator
and exact operator . The exact operators
. The exact operators  can are nonlinear.
can are nonlinear.
The inequality (5) is evident if the exact operators are linear one.
In the given work it is supposed, that all approximate operators 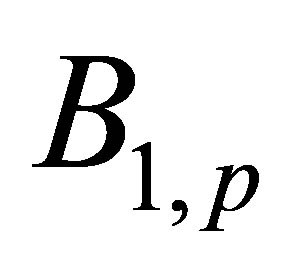 in (1) have the same structures which depend from some vector parameters
in (1) have the same structures which depend from some vector parameters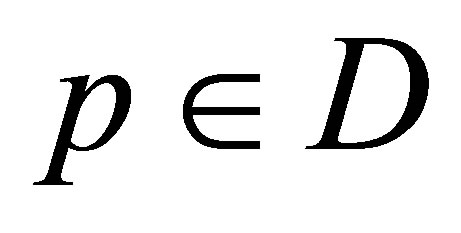 . In this case extreme problem (2) can be replaced by the following extreme problem [11]:
. In this case extreme problem (2) can be replaced by the following extreme problem [11]:
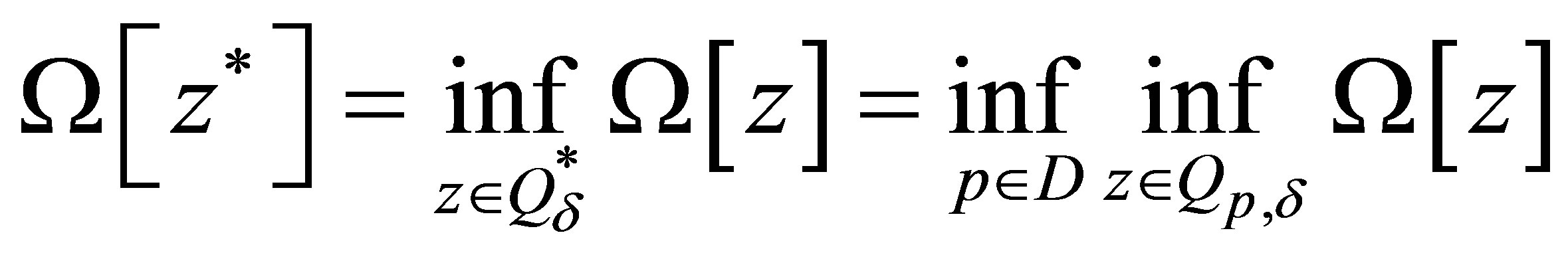 , (6)
, (6)
where 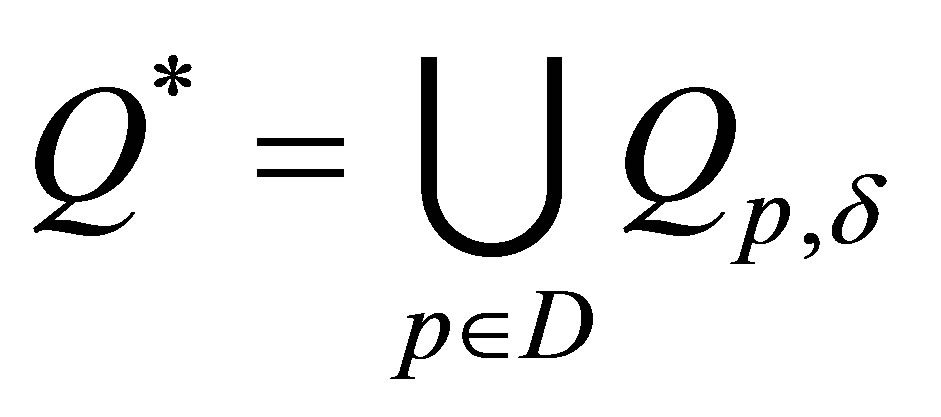 (
( is the union).
is the union).
Now in set of the possible solutions “the extraneous functions” have not got.
It is evident that 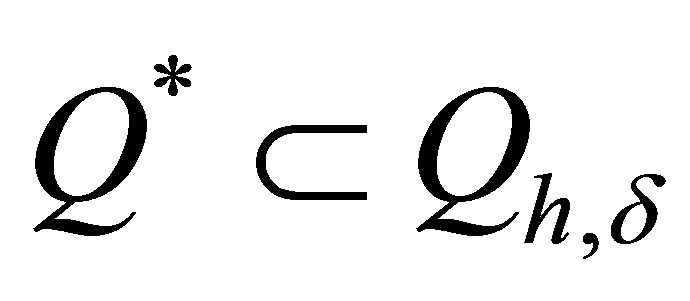 for any d > 0, h > 0, d > 0. Therefore the use of the set
for any d > 0, h > 0, d > 0. Therefore the use of the set  instead of
instead of 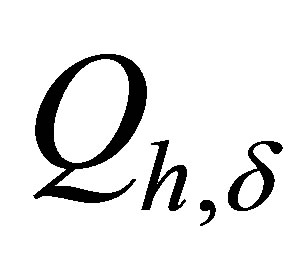 allows obtaining the most “thin” solution.
allows obtaining the most “thin” solution.
From the practical point of view the solution  of an extreme problem (6) has the same meaning, as well as
of an extreme problem (6) has the same meaning, as well as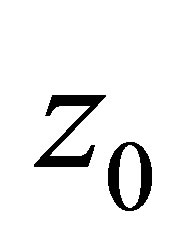 , but gives an exacter estimation from below. We will be named the solution of extreme problem (6) as estimation from below of real unbalance also. But the inequality
, but gives an exacter estimation from below. We will be named the solution of extreme problem (6) as estimation from below of real unbalance also. But the inequality 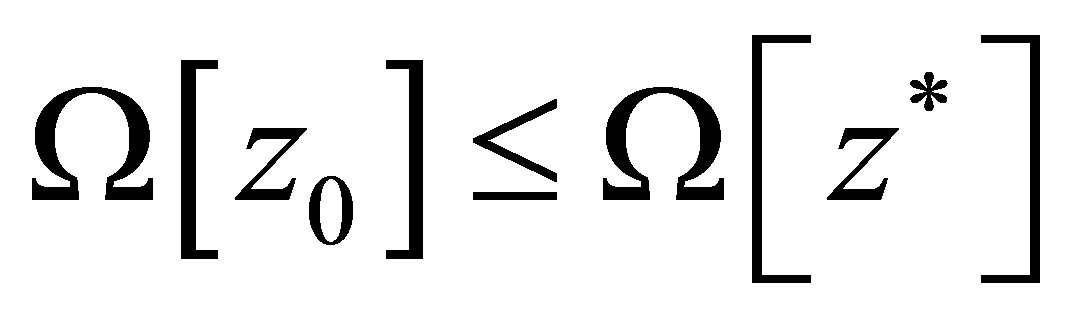 is valid.
is valid.
For the solution of an extreme problem (6) it is offered to use a method of a choice of the minimal special mathematical model of system “rotor-supports” [11,12]. It allows getting more exact estimation of exact solution.
For the realization of such approach it is necessary to choose within the vectors 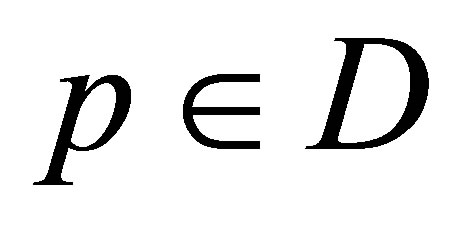 some vector
some vector 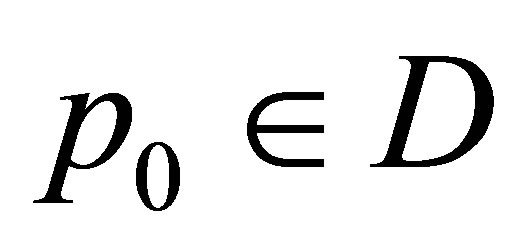 such that
such that

for all possible  and all
and all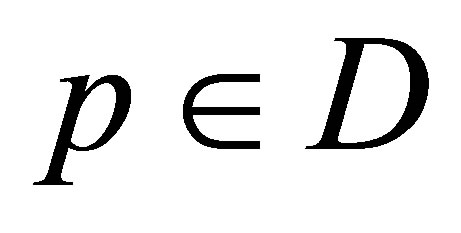 . The operator
. The operator 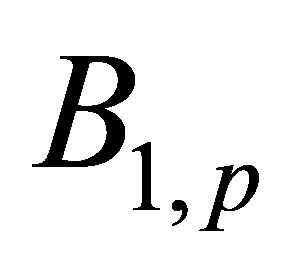 with parameter
with parameter 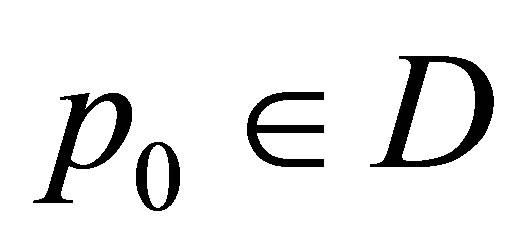 will be called the minimal operator. Appropriate to this operator the model is named as the minimal MM [12,13].
will be called the minimal operator. Appropriate to this operator the model is named as the minimal MM [12,13].
If the minimal MM exists, then the extreme problem (6) can be replaced by an equivalent simpler extreme problem:
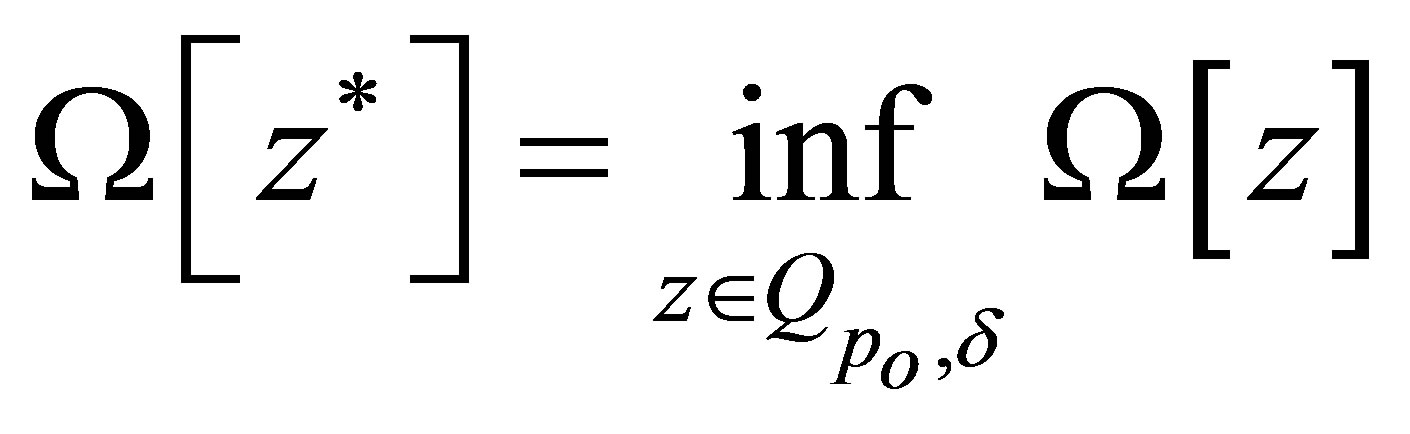 . (7)
. (7)
Let’s consider the problem on existence of the minimal MM in a problem of unbalance identification.
From physical sense of a problem follows, that the vibrations of support of a rotor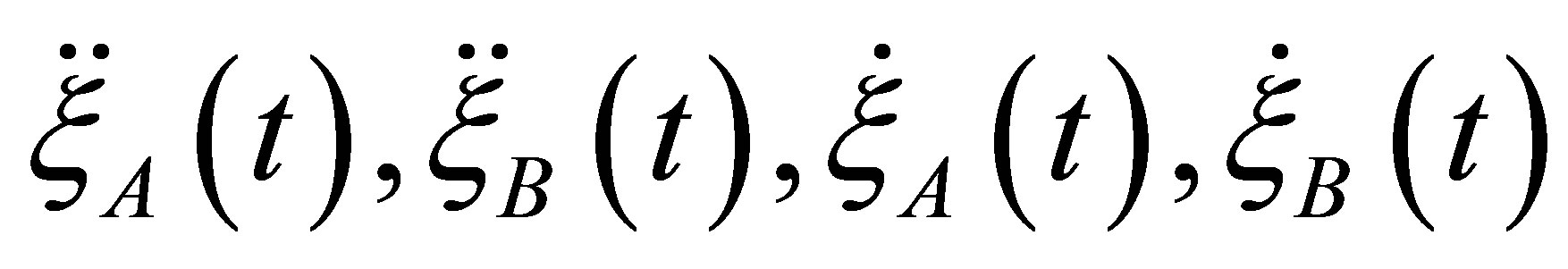 ,
, 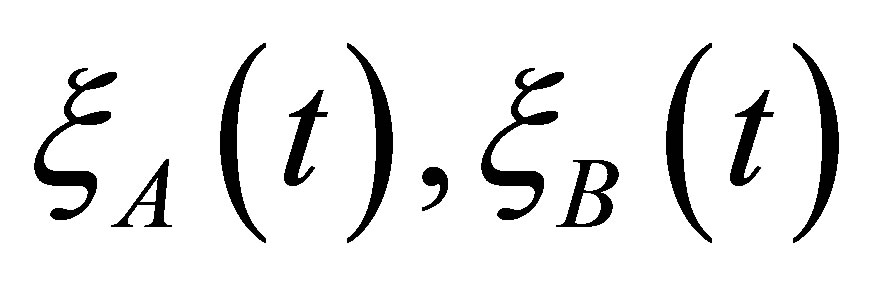 at constant speed of rotation of a rotor w and at constant size of unbalance in time
at constant speed of rotation of a rotor w and at constant size of unbalance in time 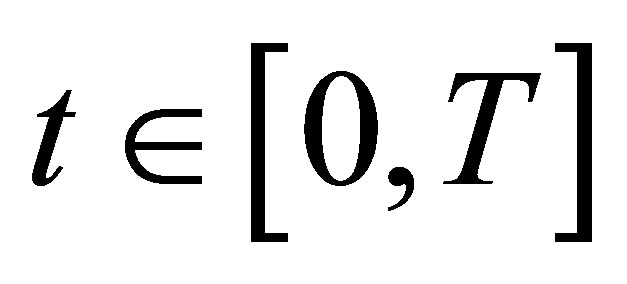 are periodic functions with zero average for the minimal period
are periodic functions with zero average for the minimal period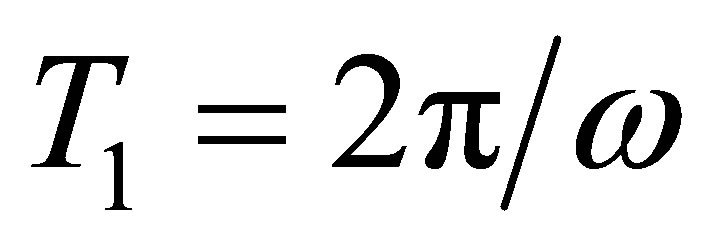 .
.
The function 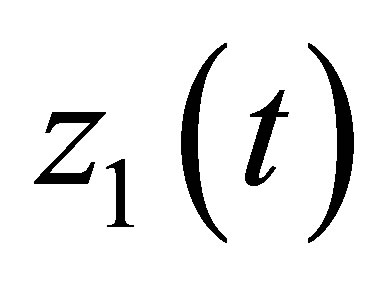 on physical sense represents also periodic function of a type
on physical sense represents also periodic function of a type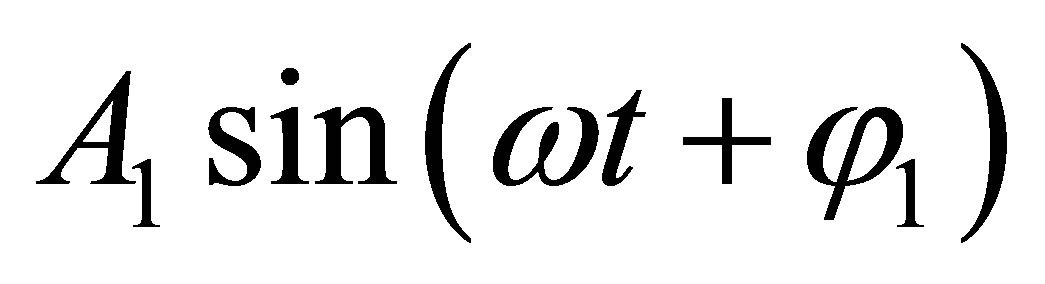 . At
. At ![]() = const and at constant size of unbalance between functions
= const and at constant size of unbalance between functions 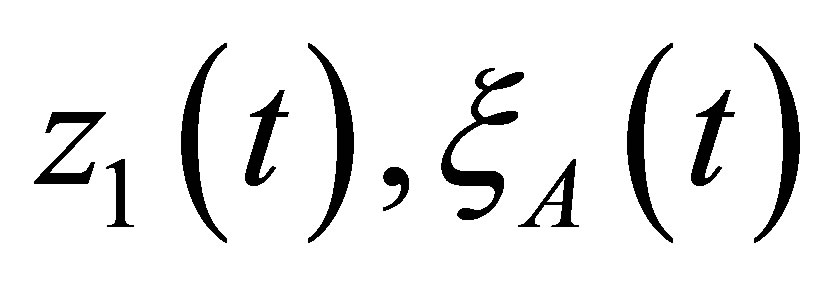 and
and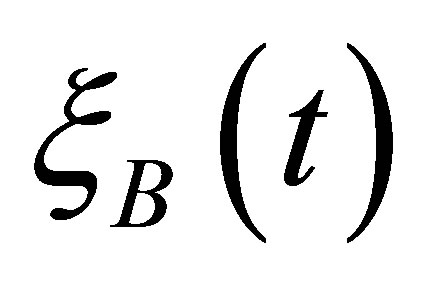 , also there is a connection
, also there is a connection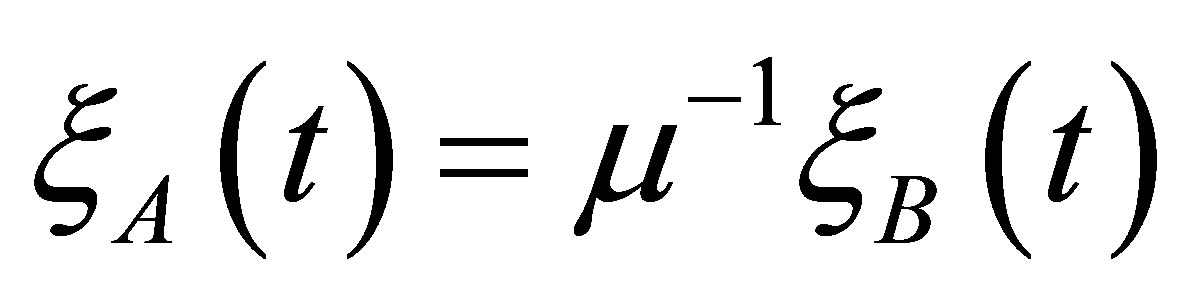 , where m-Const, m > 0.
, where m-Const, m > 0.
Then the identity is valid
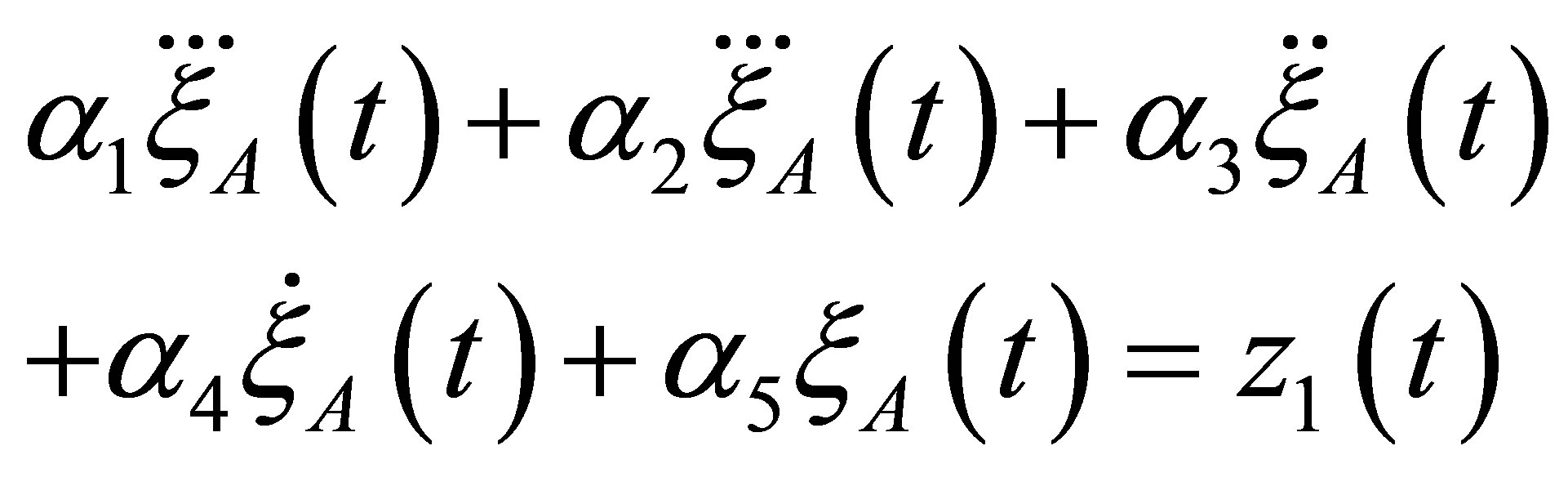 , (8)
, (8)
where 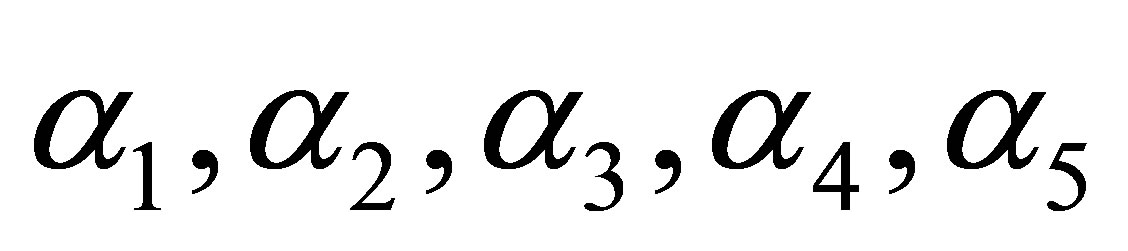 are the function from T and p.
are the function from T and p.
In this case function 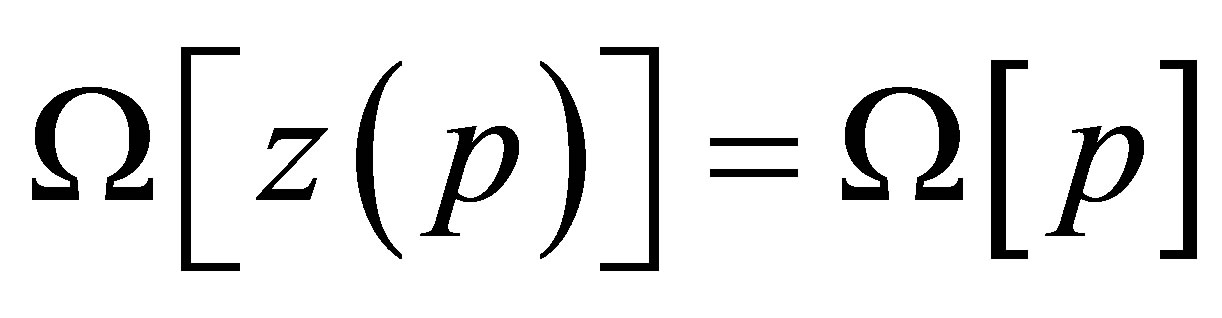 at the fixed functions
at the fixed functions 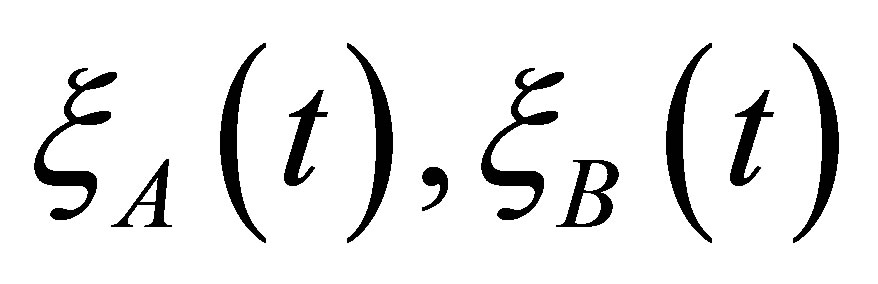 is continuous on components of a vector p. Under the well-known theorem of Weierstrass the function
is continuous on components of a vector p. Under the well-known theorem of Weierstrass the function  reaches on the convex closed set D of the greatest lower bound.
reaches on the convex closed set D of the greatest lower bound.
Let’s calculate partial derivatives of function  on parameters (in the dimensionless form):
on parameters (in the dimensionless form):
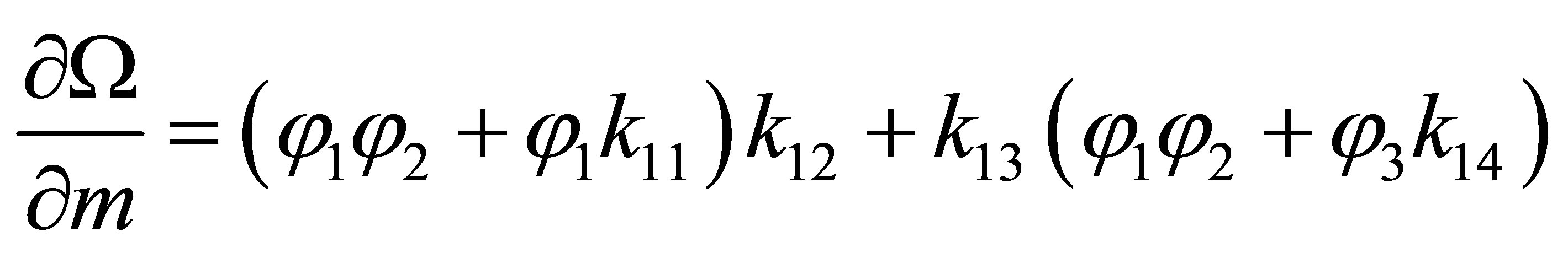 ,
,
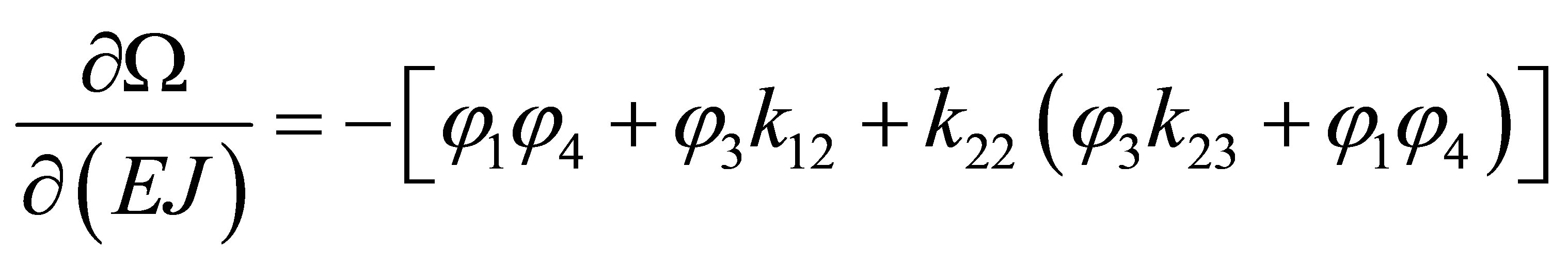 , (9)
, (9)
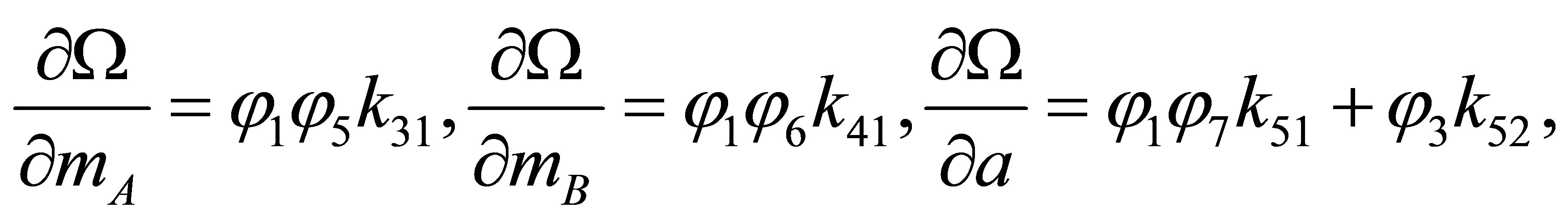

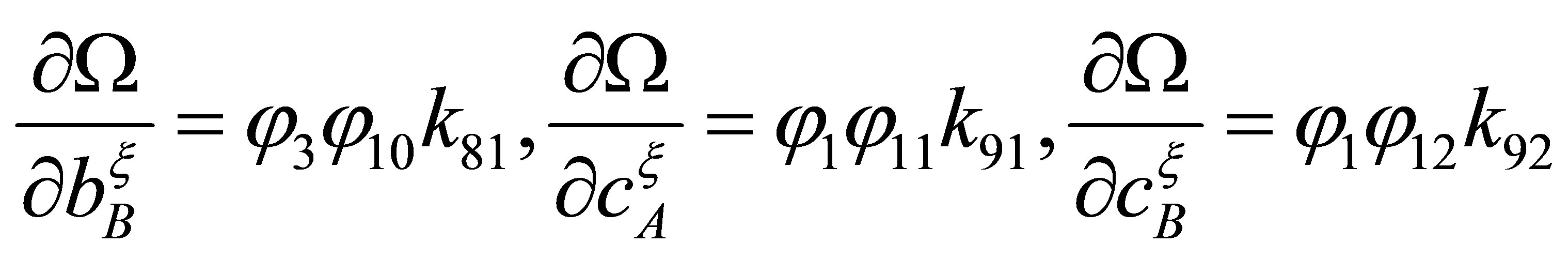 ;
;
where  are positive constants.
are positive constants.
The signs of the partial derivatives are determined by signs and sizes of functions 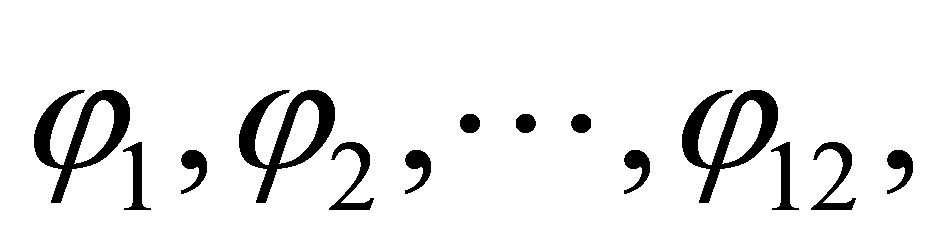 which depend on angular speed of rotation of a rotor w , parameters p of MM and size of T:
which depend on angular speed of rotation of a rotor w , parameters p of MM and size of T: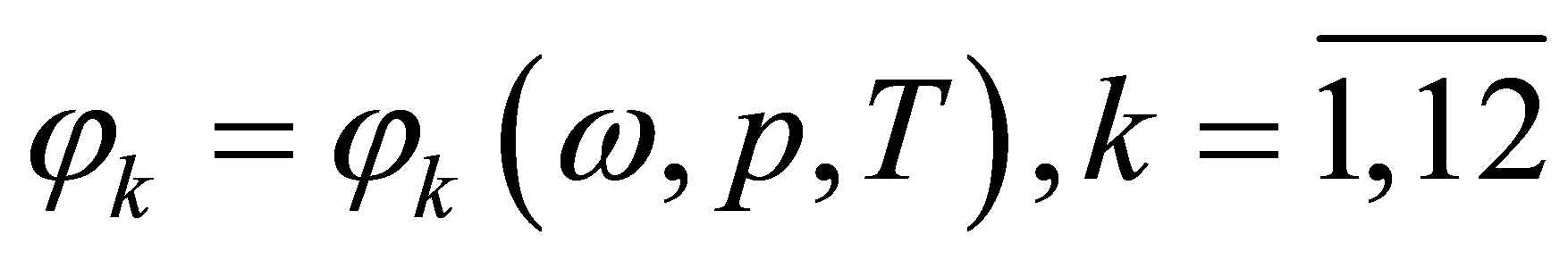 .
.
The functions 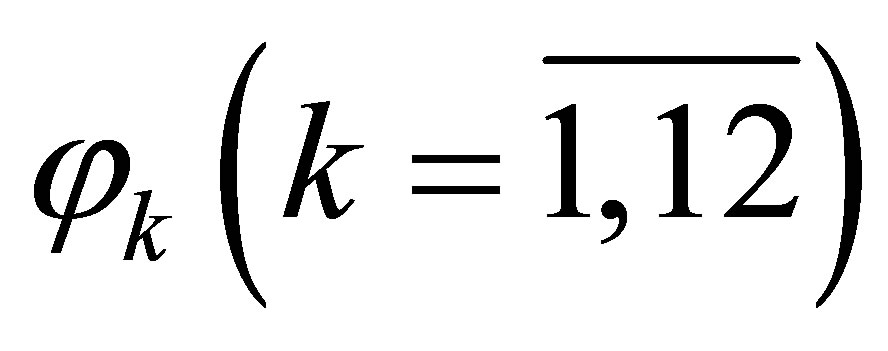 from variable
from variable  are either square-law or linear. Therefore their signs are enough easily determined.
are either square-law or linear. Therefore their signs are enough easily determined.
At rather small Т the minimal operator for (1) exists and associated the corner point of D.
In a problem of modeling of fluctuations in ventilator of the furnace the parameters of MM were the following [14]:
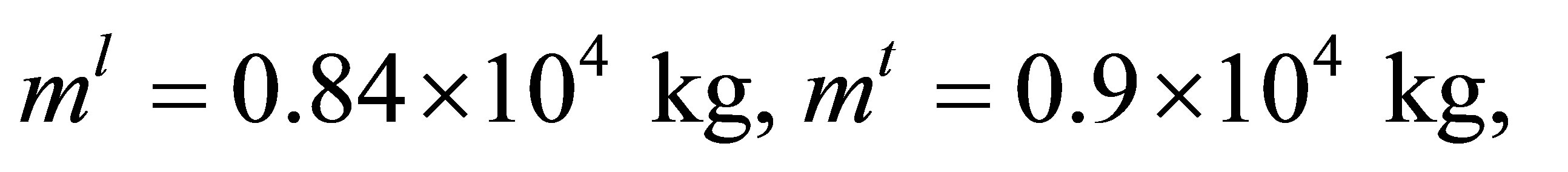




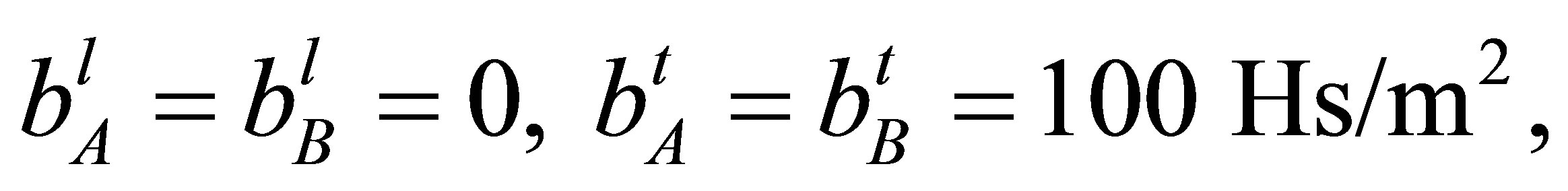
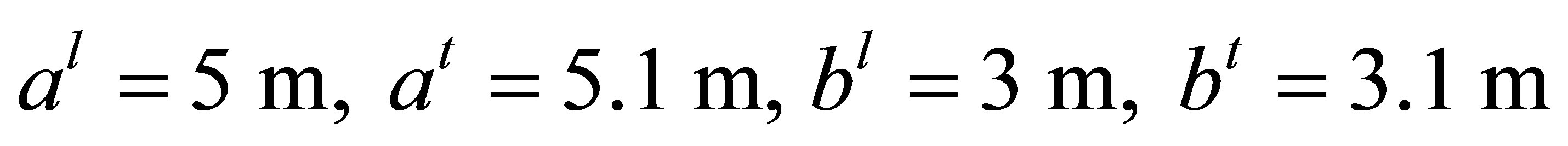 .
.
At  and
and 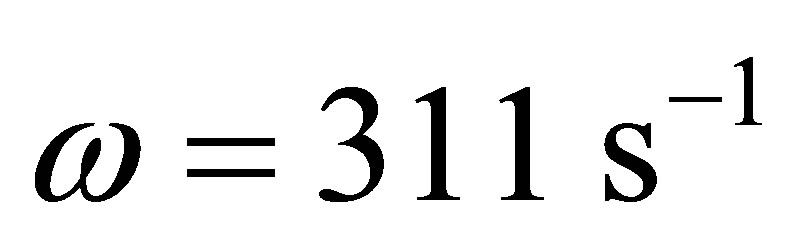 the value
the value  has appeared less least roots of the equations
has appeared less least roots of the equations  (in view of allowable disorder of parameters). Therefore, in this example of function jk have signs:
(in view of allowable disorder of parameters). Therefore, in this example of function jk have signs:
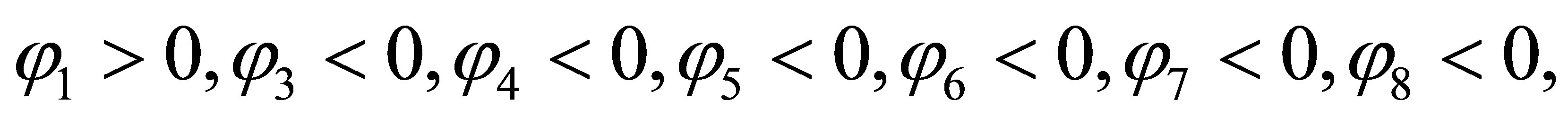
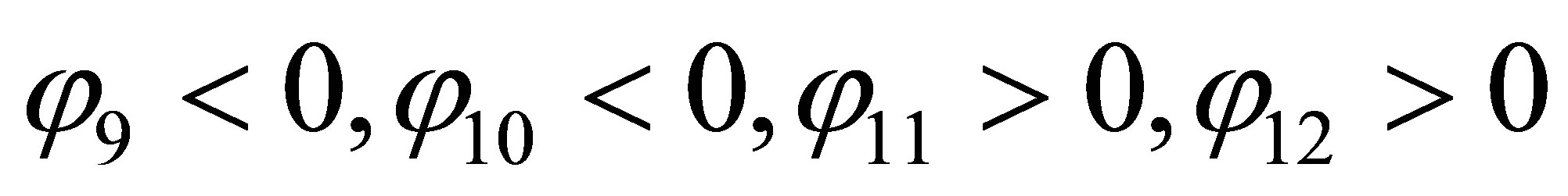 .
.
Then, taking into account expressions (6), it is possible to conclude, that

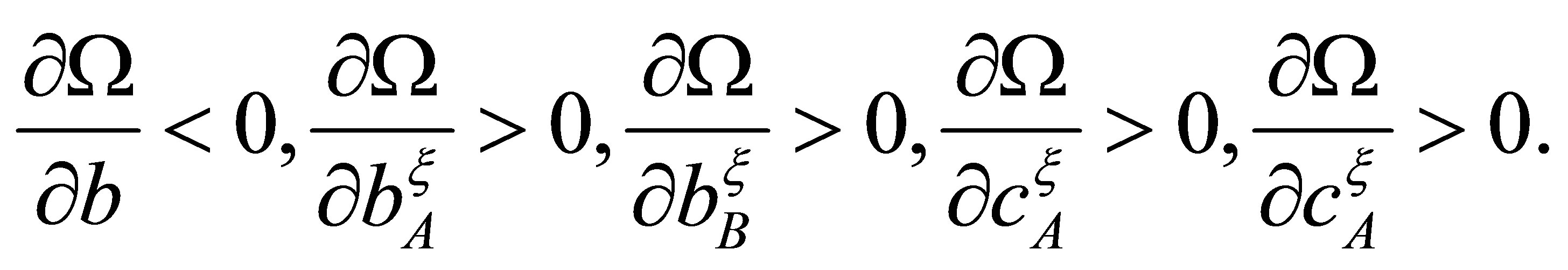
Hence, in a considered example the minimal model exists and corresponds to a vector
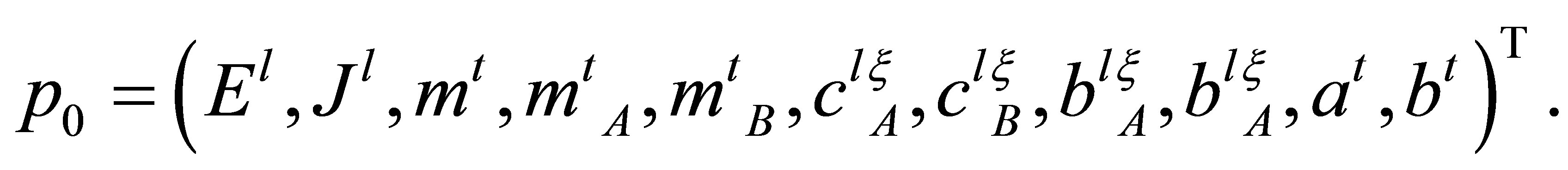
It is possibly that the size of 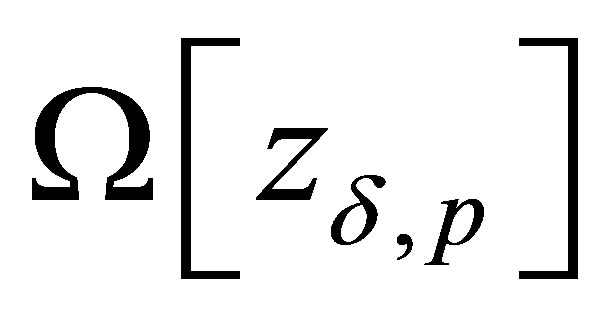 for function
for function 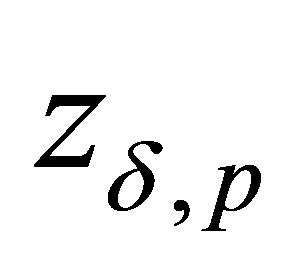 from the some set
from the some set 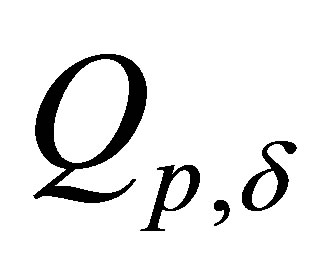 which satisfies to equality
which satisfies to equality

exceeds admissible size of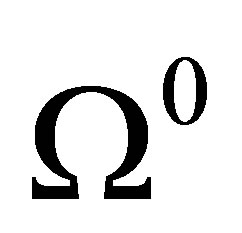 . But the vector parameters p of MM is given with error. To make this conclusion about a similar situation with a guarantee it is necessary to consider all possible sets
. But the vector parameters p of MM is given with error. To make this conclusion about a similar situation with a guarantee it is necessary to consider all possible sets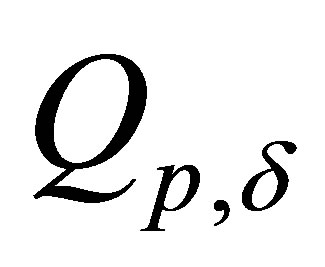 , then in them to find all functions
, then in them to find all functions 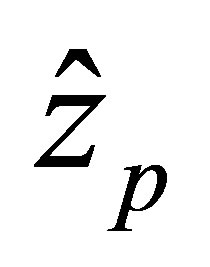 which minimize
which minimize 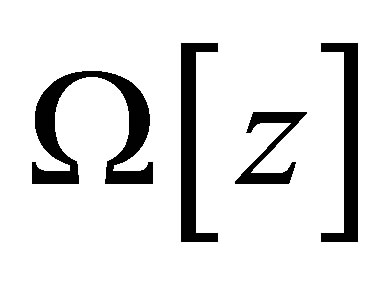 on
on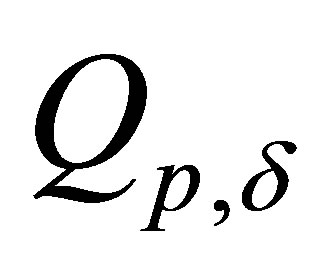 , further among them to find greatest in sense of functional value
, further among them to find greatest in sense of functional value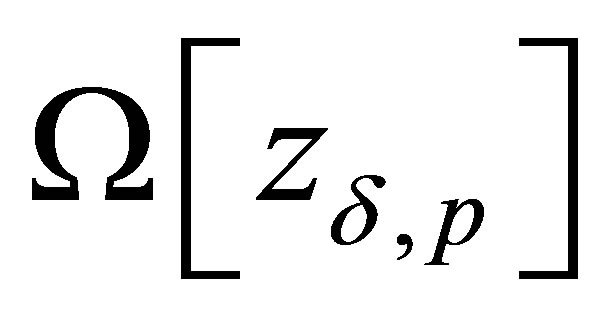 . Thus we are getting to necessity of statement of the following problem:
. Thus we are getting to necessity of statement of the following problem:
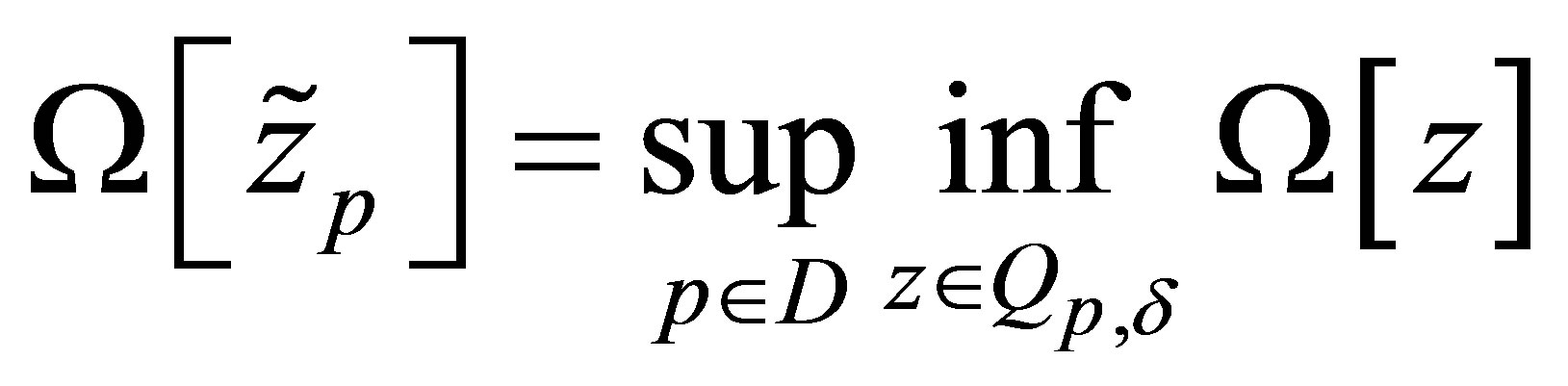 . (10)
. (10)
It is obvious that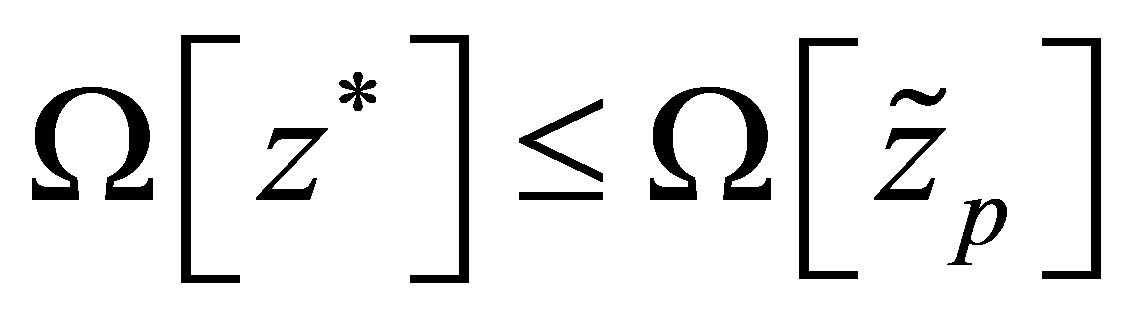 . If
. If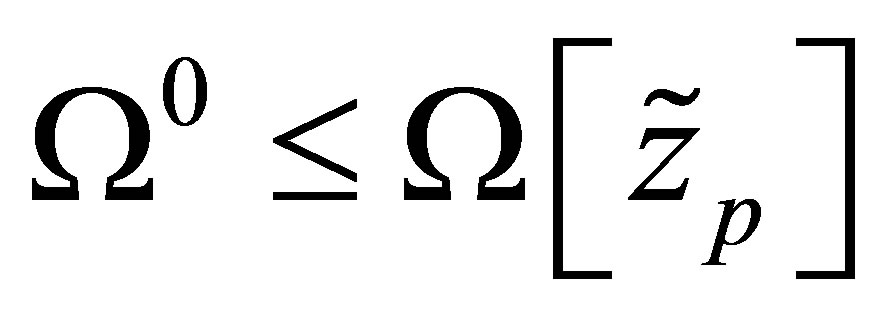 , then the machine probably works in emergency operation. If
, then the machine probably works in emergency operation. If , then no certain conclusions can be made.
, then no certain conclusions can be made.
For the solution of an extreme problem (10) it is offered to use a method of a choice of the special maximal MM of system “rotor-supports”.
It is possible to show that the solution of an extreme problem (10) under some conditions always exists.
For the realization of such approach it is necessary to choose within the vectors 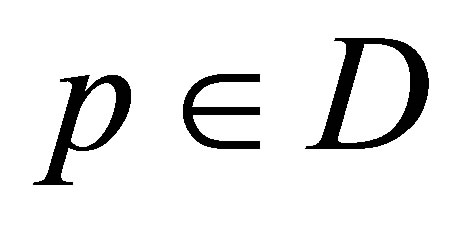 some vector
some vector  such that
such that
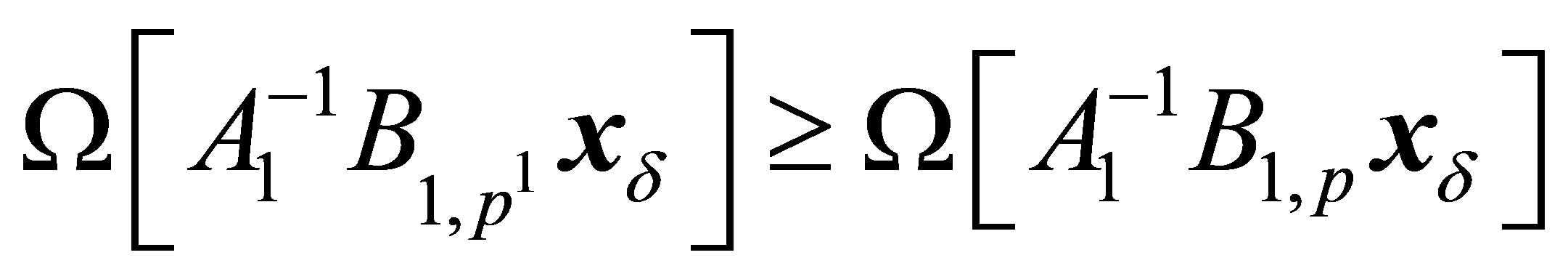
for all possible  and all
and all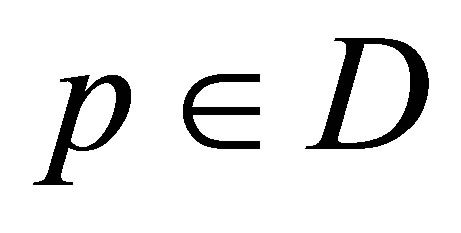 . The operator
. The operator 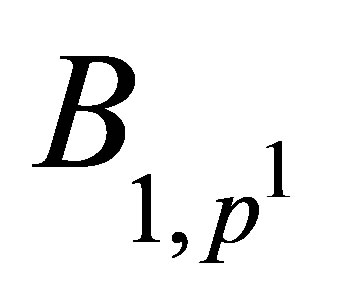 with parameter
with parameter 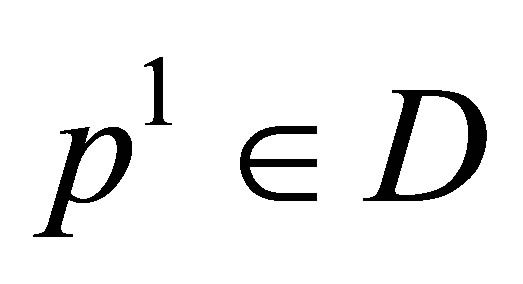 will be called the special maximal operator. Appropriate to this operator the model is named as the special maximal MM [9,10].
will be called the special maximal operator. Appropriate to this operator the model is named as the special maximal MM [9,10].
If the special maximal MM exists then the solution of an extreme problem (10) will coincide with the solution of the following extreme problem:
 . (11)
. (11)
For considered before an example the special maximal MM exists, unique and corresponds to a vector
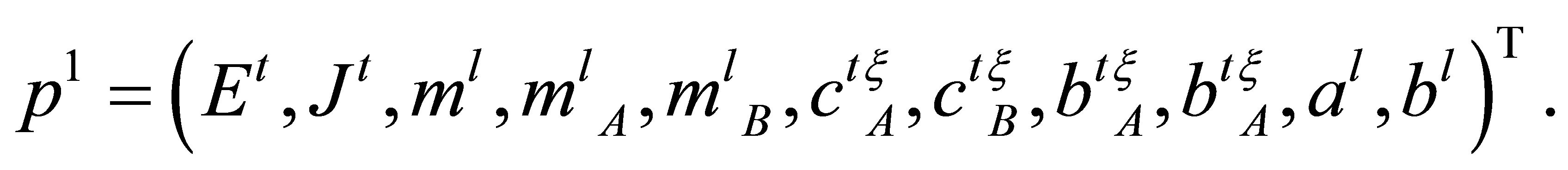
If at a vector parameters p is inexact the part of parameters is given only then a situation essentially to not change but only the vector parameters p will have only smaller dimension. In a number of cases it is possible to carry out a choice of the special minimal or special maximal MM only in part of parameters of a vector p. And in this case it is possible to receive some prize in accuracy of the approximate estimation.
Let us consider the following statement of a problem of rotor unbalance identification: to find the function 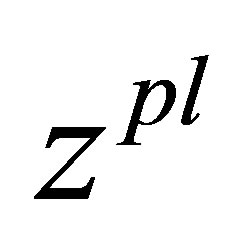 among set of the possible solutions of the equation (1) which would give the least maximal deviation from the experimentally measured vibrations of support of a rotor for all operators
among set of the possible solutions of the equation (1) which would give the least maximal deviation from the experimentally measured vibrations of support of a rotor for all operators . Such statement is reduced to the solution of the following extreme problem:
. Such statement is reduced to the solution of the following extreme problem:
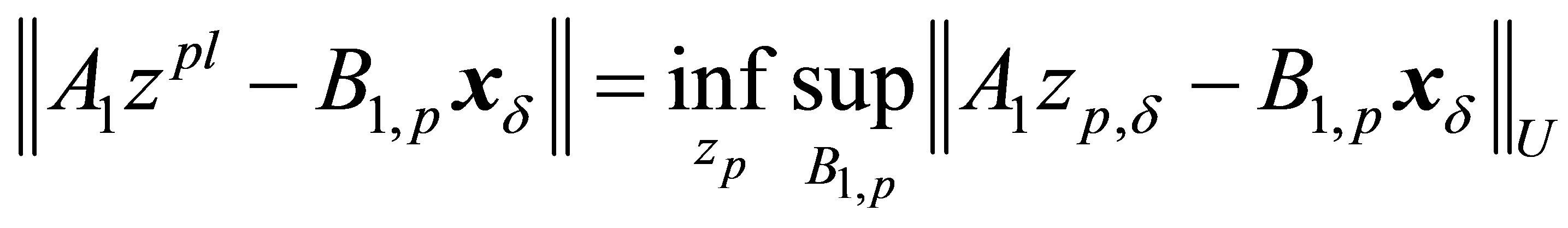 , (12)
, (12)
where 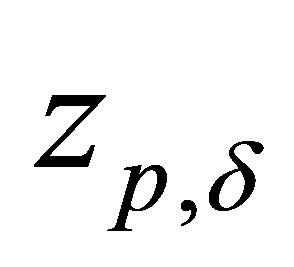 is the solution of extreme problem (11) on set
is the solution of extreme problem (11) on set .
.
As all operators  it is possible to consider equivalent within the limits of the specified accuracy, it is possible to consider function
it is possible to consider equivalent within the limits of the specified accuracy, it is possible to consider function 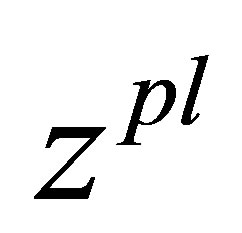 as the most probable solution of a problem of unbalance identification. The function
as the most probable solution of a problem of unbalance identification. The function 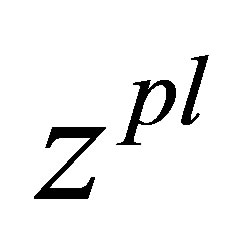 will be call the most plausible estimation of unbalance. The most probable estimation
will be call the most plausible estimation of unbalance. The most probable estimation 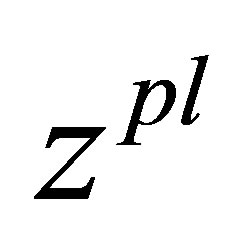 will coincide with classical regularizing the solution of an inverse problem of unbalance identification of a rotor if there is the one operator
will coincide with classical regularizing the solution of an inverse problem of unbalance identification of a rotor if there is the one operator 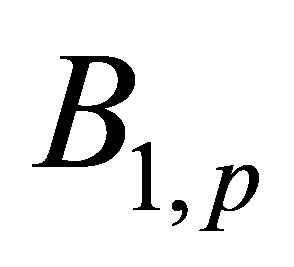 only. The function
only. The function 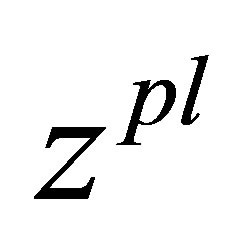 is the best approximation of real unbalance characteristics and also is steady to small deviations of the initial data.
is the best approximation of real unbalance characteristics and also is steady to small deviations of the initial data.
Suggested algorithm can be used in case if the exact operator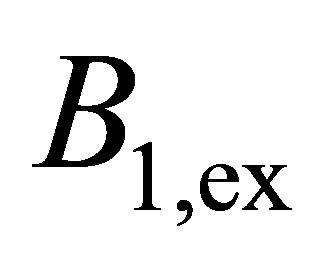 does not belong to set of operators
does not belong to set of operators 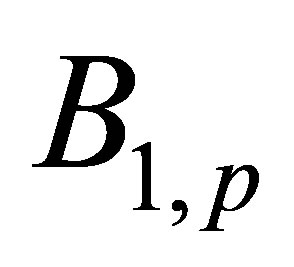 and the operator
and the operator 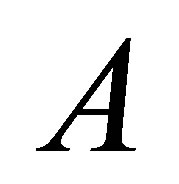 does not coincide with exact operator
does not coincide with exact operator .
.
4. Test Calculation
For suggested algorithm examination of unbalance characteristics’ evaluation, there was a calculated case when functions 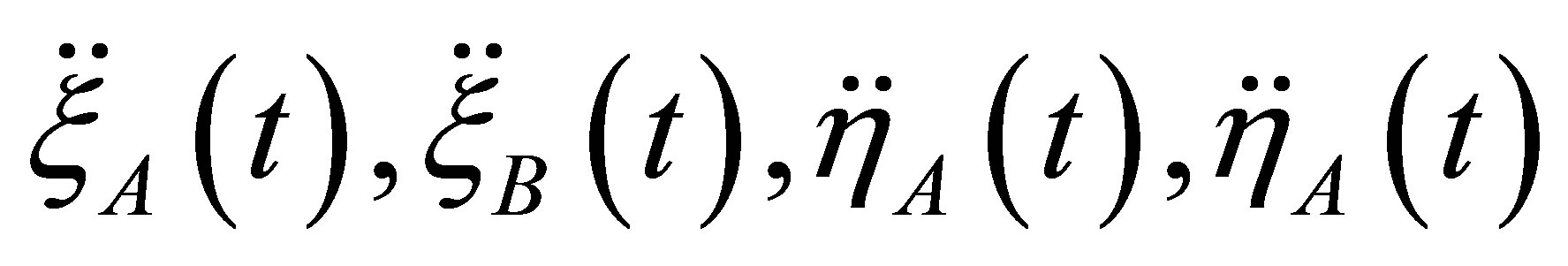 are the results of mathematical simulation of rotor vibrations with given unbalance. The parameters of rotor unbalance were chosen as:
are the results of mathematical simulation of rotor vibrations with given unbalance. The parameters of rotor unbalance were chosen as:
 by
by 
The values of initial data inaccuracy were chosen after filtering as the following:

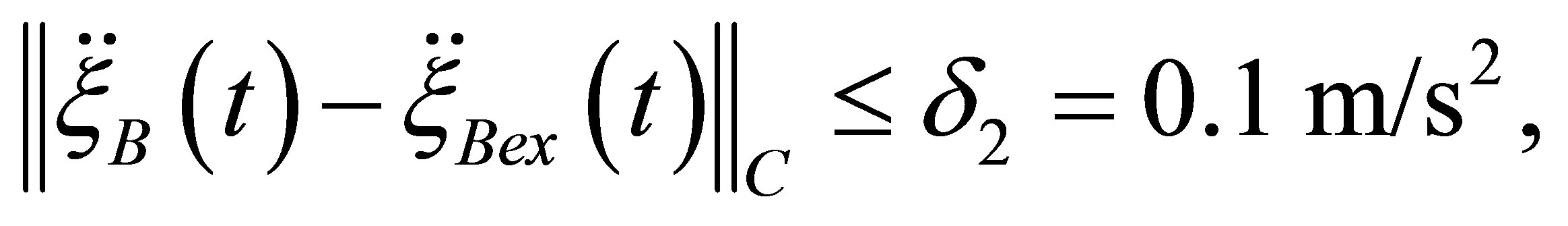
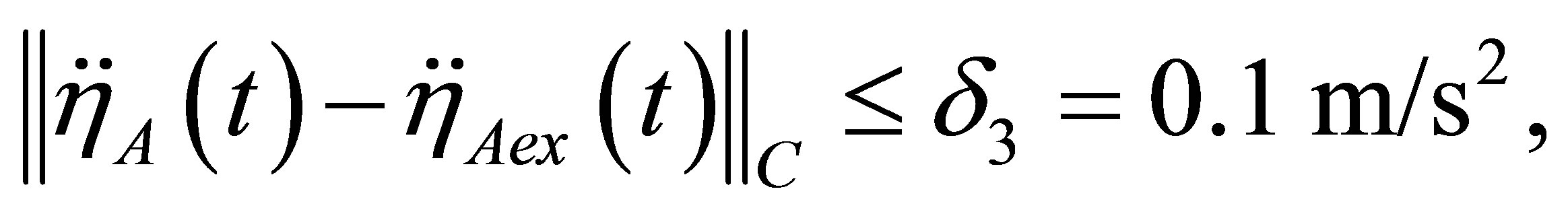

The whole inaccuracy of function  in equation (1) is
in equation (1) is 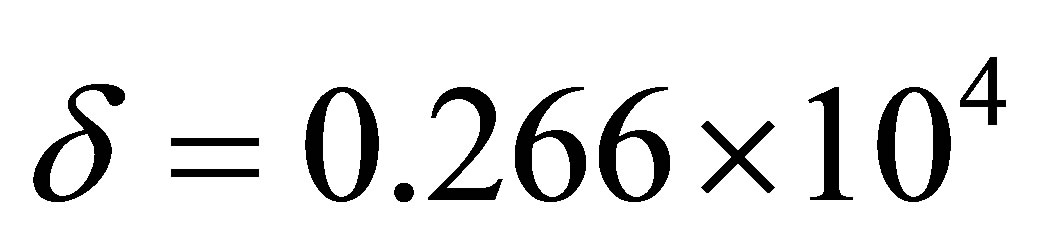 by chosen inaccuracy of initial data. The discrepancy method defined the parameter of regularization a [7].
by chosen inaccuracy of initial data. The discrepancy method defined the parameter of regularization a [7].
The functions 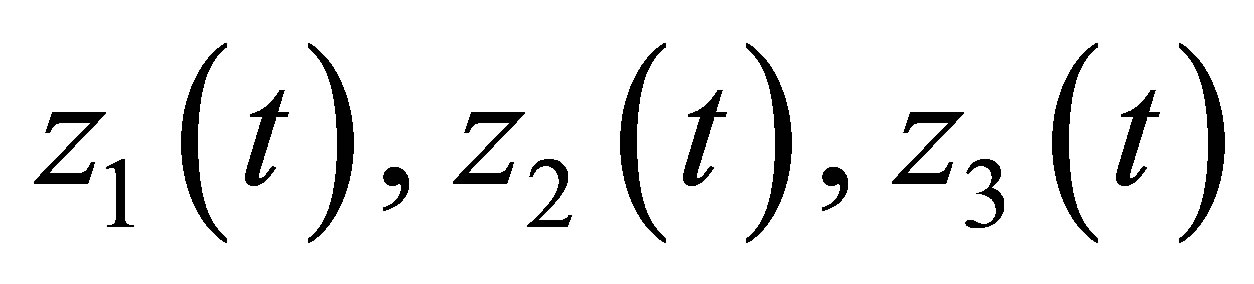 with parameters
with parameters  are the results of identification as solution of extreme problem (2).
are the results of identification as solution of extreme problem (2).
The results of identification with using the special minimal MM are followings:
 .
.
The results of identification with using the special maximal MM are followings:
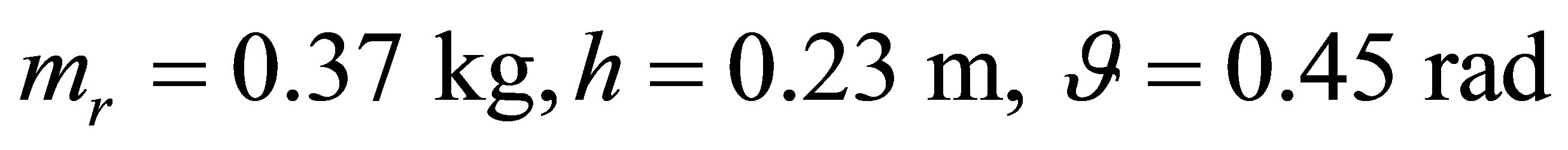 .
.
The solution of extreme problem (12) gives the results:
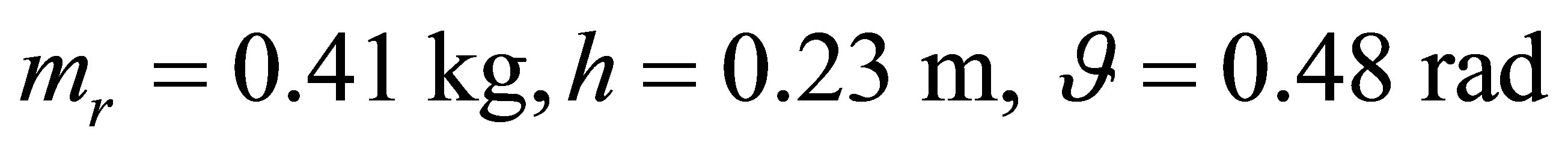 .
.
If the parameters of unbalance don’t change during the 3 - 4 turns round, the axis of rotation is used for the parametric statement of problem. It permits to shorten the time of calculation of initial data about 10 times.
Efficiency of suggested algorithm was also shown on other tests [1,3,12,15].
REFERENCES
- A. W. Lees and M. I. Friswell, “The Evaluation of Rotor Imbalance in Flexibly Mounted Machines,” Journal of Sound and Vibration, Vol. 208, No. 5, 1997, pp. 671-683. http://dx.doi.org/10.1006/jsvi.1997.1260
- M. G. Smart, M. I. Friswell and A. W. Lees, “Estimating Turbogenerator Foundation Parameters: Model Selection and Regularization,” Proceedings of the Royal Society of London A, Vol. 456, 2000, pp. 1583-1607. http://dx.doi.org/10.1098/rspa.2000.0577
- M. S. Darlow, “Balancing of High-Speed Machinery: Theory, Methods and Experimental Results,” Mechanical Systems and Signal Processing, Vol. 1, No. 1, 1982, pp. 105-134. http://dx.doi.org/10.1016/0888-3270(87)90087-2
- Yu. L. Menshikov and N. V. Polyakov, “Operative Evaluation of Unbalance Characteristics of a Deformable Rotor,” Proceedings of 8th International Symposium on Technical Diagnostics (IMEKO), Dresden, 23-25 September 1992, pp. 399-408.
- Yu. L. Menshikov and N. V. Polyakov, “The New Statement of Problem of Unbalance Identification,” Proceedings of ICTAM 2004, Warsaw, 15-21 August 2004.
- A. N. Tikhonov and V. Y. Arsenin, “The Methods of Solution of the Incorrectly Formulated Problems,” Science, Moscow, 1979.
- A. V. Goncharskij, A. C. Leonov and A. G. Yagola, “About One Regularized Algorithm for Ill-Posed Problems with Approximate Given Operator,” Journal of Computational Mathematics and Mathematical Physics, Vol. 12, No. 6, 1972, pp. 1592-1594.
- Yu. L. Menshikov, “Useful Hypothesis in Inverse Problems of Interpretation,” Proceedings of International Conference Inverse Problems and Applications (IPA2013), Linkoping University, Linköping, 2-6 April 2013.
- Yu. L. Menshikov, “Solution Estimations of Measurement’s Inverse Problem,” Proceedings of 4th Inverse Problems, Design and Optimization Symposium (IPDO-2013), Book of Abstracts, Albi, 26-28 June 2013.
- Yu. L. Menshikov, “Synthesis of Adequate Mathematical Description as Solution of Special Inverse Problems,” European Journal of Mathematical Sciences, Vol. 2, No 3, 2013, pp. 256-271.
- Yu. L. Menshikov, “The Reduction of Initial Date Inaccuracy in Ill-Posed Problems,” Proceedings of 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Vol. VI, Berlin, 24-29 August 1997, pp. 577-582.
- Yu. L. Menshikov, “Identification of Optimal Mathematical Model of External Impacts,” Proceedings of MATHMOD 03, Vienna, 5-7 February 2003.
- Yu. L. Menshikov, “Some New Statements of Inverse Problems of Recognition,” 10th International Conference on Mathematical Methods in Electromagnetic Theory, Kharkov, 14-17 September 2004, pp. 464-466.
- Yu. L. Menshikov, “Recognition of Rotor Machines Unbalance,” Differential Equations and Their Appendices in Physics. The Collection of the Proceedings, Dnepropetrovsk, 1988, pp. 44-56.
- Yu. L. Menshikov, “Identification of Rotor Unbalance in Minimax Statement,” 13th International Congress on Sound and Vibration, Vienna, 2-6 July 2006, pp. 345-352.

