Advances in Pure Mathematics
Vol.04 No.01(2014), Article ID:42178,8 pages
10.4236/apm.2014.41004
S-Injective Modules and Rings
Nasr A. Zeyada1,2
1Department of Mathematics, Faculty of Science, Cairo University, Cairo, Egypt 2Department of Mathematics, Faculty of Science, King Abdulaziz University, KSA
Email: nasmz@yahoo.com
Copyright © 2014 Nasr A. Zeyada. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Nasr A. Zeyada. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Received October 7, 2013; revised November 7, 2013; accepted November 15, 2013
We introduce and investigate the concept of s-injective modules and strongly s-injective modules. New characte- rizations of SI-rings, GV-rings and pseudo-Frobenius rings are given in terms of s-injectivity of their modules.
Keywords:
S-Injective Module; Kasch Ring; Pseudo Frobenius Ring
1. Introduction
In this paper we introduce and investigate the notion of s-injective Modules and Rings. A right R-module M is called right s-N-injective, where N is a right R-module, if every R-homomorphism  extends to
extends to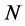 , where K is a submodule of the singular submodule
, where K is a submodule of the singular submodule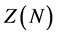 . M is called strongly s-injective if M is s-N-injective for every right R-module N. The connection between this new injectivity condition and other injectivity conditions has been established, and examples are provided to distinguish s-injectivity from other injectivity concepts such as mininjectivity, soc-injectivity. Several properties of this new class of injectivity are highlighted.
. M is called strongly s-injective if M is s-N-injective for every right R-module N. The connection between this new injectivity condition and other injectivity conditions has been established, and examples are provided to distinguish s-injectivity from other injectivity concepts such as mininjectivity, soc-injectivity. Several properties of this new class of injectivity are highlighted.
Throughout this paper all rings are associative with identity, and all modules are unitary R-modules. For a right R-module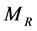 , we denoted
, we denoted ,
, 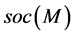 , and
, and  by the Jacobson radical, the socle and the singular submodule of
by the Jacobson radical, the socle and the singular submodule of , respectively.
, respectively.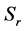 ,
, 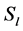 ,
, 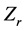 ,
,  and
and  are used to indicate the right socle, the left socle, the right singular ideal, the left singular ideal, and the Jacobson radical of
are used to indicate the right socle, the left socle, the right singular ideal, the left singular ideal, and the Jacobson radical of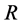 , respectively. For a submodule
, respectively. For a submodule 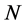 of
of , the notations
, the notations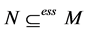 ,
, 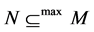 and
and 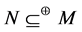 mean, respectively, that N is essential, maximal, and direct summand. If
mean, respectively, that N is essential, maximal, and direct summand. If 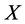 is a subset of a right R-module
is a subset of a right R-module![]() , right annihilators will be denoted by
, right annihilators will be denoted by![]() , with a similar definition of left annihilators
, with a similar definition of left annihilators![]() . Multiplication maps
. Multiplication maps ![]() and
and ![]() will be denoted by
will be denoted by ![]() and
and![]() , respectively. If M and N are right R-modules, then M is called N-injective if every R-homomorphism from a submodule of N into M can be extended to an R-homomorphism from N into M. Mod-R indicates the category of right R-modules. We refer to [1-3] for all the undefined notions in this paper.
, respectively. If M and N are right R-modules, then M is called N-injective if every R-homomorphism from a submodule of N into M can be extended to an R-homomorphism from N into M. Mod-R indicates the category of right R-modules. We refer to [1-3] for all the undefined notions in this paper.
2. Strongly S-Injective Modules
Definition 1 A right R-module M is called s-N-injective if every R-homomorphism ![]() extends to
extends to![]() , where
, where ![]() is a submodule of the singular submodule
is a submodule of the singular submodule![]() . M is called s-injective if
. M is called s-injective if ![]() is s-R-injective.
is s-R-injective. ![]() is called strongly s-injective, if
is called strongly s-injective, if ![]() is s-N-injective for all right R-modules
is s-N-injective for all right R-modules![]() .
.
For example every nonsingular R-module is strongly s-injective. In particular, the ring of integers ![]() is strongly s-injective, but not injective.
is strongly s-injective, but not injective.
Proposition 1
1) Let ![]() be a right R-module and
be a right R-module and ![]() a family of right R-modules. Then the direct product
a family of right R-modules. Then the direct product ![]()
is s-N-injective if and only if each ![]() is s-N-injective,
is s-N-injective, ![]()
2) Let M, ![]() , and
, and ![]() be right R-modules with
be right R-modules with ![]() If M is s-N-injective, then M is s-K-injective.
If M is s-N-injective, then M is s-K-injective.
3) Let M, ![]() , and
, and ![]() be right R-modules with
be right R-modules with ![]() If
If ![]() is s-M-injective, then
is s-M-injective, then ![]() is s-M-injective.
is s-M-injective.
4) Let ![]() be a right R-module and
be a right R-module and ![]() a family of right R-modules. Then
a family of right R-modules. Then ![]() is
is ![]() injective
injective
if and only if ![]() is
is ![]() injective,
injective, ![]()
5) A right R-module ![]() is s-injective if and only if
is s-injective if and only if ![]() is s-P-injective for every projective right R-module
is s-P-injective for every projective right R-module![]() .
.
6) Let M, ![]() , and
, and ![]() be right R-modules with
be right R-modules with ![]() If
If ![]() is s-K-injective, then
is s-K-injective, then ![]() is s-K- injective.
is s-K- injective.
7) If![]() ,
, ![]() , and
, and ![]() are right R-modules,
are right R-modules, ![]() and
and ![]() is s-A-injective, then
is s-A-injective, then ![]() is s-B-injective.
is s-B-injective.
Proof. The proofs of 1) through 4) are routine.
5). This follows from 4).
6). Let ![]() be an R-homomorphism where
be an R-homomorphism where ![]() is singular submodule of
is singular submodule of![]() . Then the map
. Then the map ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism![]() , where
, where ![]() the inclusion map. Now, the map
the inclusion map. Now, the map ![]() is an extension of
is an extension of![]() , where
, where ![]() the natural projection map into
the natural projection map into![]() .
.
7). Let ![]() be an R-isomorphism, and
be an R-isomorphism, and ![]() an R-homomorphism where
an R-homomorphism where ![]() is a singular submodule of
is a singular submodule of![]() . The restriction of
. The restriction of ![]() to
to ![]() induces an isomorphism
induces an isomorphism ![]() By hypothesis, the map
By hypothesis, the map ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism ![]() Now, the map
Now, the map ![]() is an extension of
is an extension of![]() . □
. □
The next two corollaries are immediate consequences of the above proposition.
Corollary 1 Let ![]() be a right R-module. Then the following statements are true:
be a right R-module. Then the following statements are true:
1) A finite direct sum of s-N-injective modules is again s-N-injective. In particular a finite direct sum of s-injective (strongly s-injective) modules is again s-injective (strongly s-injective).
2) A summand of s-N-injective (s-injective, strongly s-injective) module is again s-N-injective (s-injective, strongly s-injective) module.
Corollary 2
1) Let ![]() be a right R-module and
be a right R-module and ![]() in
in![]() , where the
, where the ![]() are orthogonal idempotents. Then
are orthogonal idempotents. Then ![]() is s-injective if and only if
is s-injective if and only if ![]() is
is ![]() injective for each
injective for each![]() ,
, ![]()
2) Assume that ![]() and
and ![]() are idempotents of
are idempotents of![]() ,
, ![]() and
and ![]() is
is ![]() injective. Then
injective. Then ![]() is s-fN-injective.
is s-fN-injective.
Proposition 2 If ![]() is a finitely generated right R-module, then the following conditions are equivalent:
is a finitely generated right R-module, then the following conditions are equivalent:
1) Any direct sum of s-N-injective modules is s-N-injective.
2) Any direct sum of injective modules is s-N-injective.
3) ![]() is noetherian.
is noetherian.
Proof. 1) ![]() 2). Clear.
2). Clear.
2) ![]() 3). Consider a chain
3). Consider a chain ![]() of singular submodules of
of singular submodules of ![]() and
and![]() . Let
. Let ![]() be the injective hull of
be the injective hull of![]() ,
, ![]() and
and ![]() be a map defined by
be a map defined by![]() . Since,
. Since, ![]() is s-N-injective,
is s-N-injective, ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism ![]() Since
Since ![]() is finitely generated,
is finitely generated, ![]() for some
for some ![]() then
then ![]() and
and ![]() for
for
every![]() . Hence
. Hence ![]() is noetherian.
is noetherian.
3) ![]() 1). Let
1). Let ![]() be a direct sum of s-N-injective modules, and
be a direct sum of s-N-injective modules, and ![]() be a homomorphism of
be a homomorphism of
right R-modules where![]() . Since
. Since ![]() is noetherian,
is noetherian, ![]() for some finite subset
for some finite subset ![]()
Since finite direct sums of s-N-injective modules is s-N-injective, ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism ![]() □
□
The second singular submodule of a right R-module![]() , denoted by
, denoted by![]() , is defined by the equality
, is defined by the equality![]() . We see that a
. We see that a ![]() is closed submodule of
is closed submodule of ![]() and
and ![]() is non-singular. A right R-module is Goldie torsion if
is non-singular. A right R-module is Goldie torsion if![]() .
.
Lemma 1 Let ![]() and
and ![]() be right R-modules such that
be right R-modules such that ![]() is injective. Then every homomorphism
is injective. Then every homomorphism ![]() where
where ![]() extends to
extends to![]() .
.
Proof. Let ![]() where
where ![]() is injective and
is injective and![]() . If
. If ![]() is a homomor- phism where
is a homomor- phism where ![]() such that
such that![]() , then
, then ![]() is singular. So
is singular. So ![]() extendable
extendable
to![]() . Now suppose that
. Now suppose that![]() , so
, so ![]() is singular which is a contradiction. Thus
is singular which is a contradiction. Thus
![]() . Suppose that
. Suppose that ![]() where
where ![]() and
and![]() ,
,![]() . So
. So ![]() and the kernal of the map
and the kernal of the map ![]() by
by ![]() is essential in
is essential in ![]() which is a contradiction. Then every homomorphism
which is a contradiction. Then every homomorphism ![]() where
where ![]() extends to
extends to![]() . □
. □
Proposition 3 The following statements are equivalent:
1) ![]() is strongly s-injective.
is strongly s-injective.
2) ![]() is
is ![]() injective, where
injective, where ![]() is the injective hull of
is the injective hull of![]() .
.
3)![]() , where
, where ![]() is nonsingular and
is nonsingular and ![]() is injective with
is injective with![]() .
.
4) ![]() is injective.
is injective.
5) ![]() is G-injective for every Goldie torsion module
is G-injective for every Goldie torsion module![]() .
.
6) ![]() is I-injective, where
is I-injective, where ![]() is the injective hull of
is the injective hull of![]() .
.
Proof. 1) ![]() 2). Clear.
2). Clear.
2) ![]() 3). If
3). If![]() , we are done. Assume that
, we are done. Assume that ![]() and consider the following diagram:
and consider the following diagram:
![]()
where ![]() and
and ![]() are inclusion maps and
are inclusion maps and ![]() is injective closure of
is injective closure of ![]() in
in![]() . Since
. Since ![]() is
is ![]() injective,
injective, ![]() is s-D-injective. So there exists an R-homomorphism
is s-D-injective. So there exists an R-homomorphism ![]() which extends
which extends ![]() Since
Since![]() ,
, ![]() is an embedding of
is an embedding of ![]() in
in![]() . If we write
. If we write ![]() then
then ![]() for some submodule
for some submodule ![]() of
of ![]() because
because ![]() is injective. Finally
is injective. Finally ![]() is nonsingular because
is nonsingular because![]() .
.
3) ![]() 4). Since
4). Since ![]() is singular and
is singular and ![]() is singular submodule of
is singular submodule of![]() , so
, so ![]() and
and ![]() for some submodule
for some submodule ![]() of
of![]() . Then
. Then ![]()
![]() and
and ![]() is injective.
is injective.
4) ![]() 5). Let
5). Let ![]() be a Goldie torsion right R-module and
be a Goldie torsion right R-module and ![]() is a submodule of
is a submodule of![]() . Using the above Lemma, every homomorphism
. Using the above Lemma, every homomorphism ![]() extends to
extends to![]() .
.
5) ![]() 6). If
6). If ![]() is the injective hull of
is the injective hull of![]() , then
, then ![]() and
and ![]() is Goldie torsion.
is Goldie torsion.
6) ![]() 1). Let
1). Let ![]() be a right R-module and
be a right R-module and ![]() be a singular submodule of
be a singular submodule of![]() . Consider the diagram
. Consider the diagram
![]()
where![]() ,
, ![]() , and
, and ![]() are the inclusion maps. Since
are the inclusion maps. Since ![]() is I-injective and
is I-injective and ![]() is injective. So, there exist R- homomorphisms
is injective. So, there exist R- homomorphisms ![]() and
and ![]() such that
such that ![]() and
and![]() . Thus
. Thus![]() . Hence
. Hence ![]() is strongly s-injective. □
is strongly s-injective. □
Corollary 3 Let ![]() a Goldie torsion right R-module. Then
a Goldie torsion right R-module. Then ![]() is injective if and only if
is injective if and only if ![]() is strongly s-injective.
is strongly s-injective.
Proposition 4 For a ring![]() , the following conditions are equivalent:
, the following conditions are equivalent:
1) ![]() is strongly s-injective.
is strongly s-injective.
2) ![]() is s-I(RR)-injective, where
is s-I(RR)-injective, where ![]() is the injective hull of
is the injective hull of![]() .
.
3) ![]() where
where ![]() is injective and
is injective and ![]() is nonsingular. Moreover, if
is nonsingular. Moreover, if![]() , then
, then![]() , and in this case
, and in this case ![]() and
and ![]() are relatively injective.
are relatively injective.
4) ![]() is injective.
is injective.
5) ![]() is G-injective for every Goldie torsion right R-module
is G-injective for every Goldie torsion right R-module![]() .
.
6) ![]() is G-injective, where
is G-injective, where ![]() is the injective hull of
is the injective hull of![]() .
.
7) Every finitely generated projective right R-module is strongly s-injective.
Proof. The equivalence between 1), 2), 3), 4), 5) and 6) is from Proposition 3.
1) ![]() 7) Since a finite direct sum of s-N-injective is s-N-injective for every right R-module
7) Since a finite direct sum of s-N-injective is s-N-injective for every right R-module ![]() (Corollary 1), so every finitely generated free right R-module is strongly s-injective. But a direct summand of strongly s-injective is strongly s-injective (Corollary 1). Therefore every finitely generated projective module is strongly s-injective. The converse is clear. □
(Corollary 1), so every finitely generated free right R-module is strongly s-injective. But a direct summand of strongly s-injective is strongly s-injective (Corollary 1). Therefore every finitely generated projective module is strongly s-injective. The converse is clear. □
The following examples show that the two classes of strongly s-injective rings and of soc-injective rings are different.
Example 1 Let ![]() be the field of two elements,
be the field of two elements, ![]() for
for![]() ,
, ![]() ,
, ![]() If
If ![]()
is the subring of ![]() generated by
generated by ![]() and
and ![]() then
then ![]() is a von Neumann regular ring with
is a von Neumann regular ring with![]() , and hence
, and hence ![]() and
and ![]() is strongly s-injective. However, the map
is strongly s-injective. However, the map ![]() given by
given by ![]() cannot be extended to an R-homomorphism from
cannot be extended to an R-homomorphism from ![]() into
into ![]() (suppose that
(suppose that ![]() for some
for some![]() . Then for every
. Then for every![]() ,
, ![]() which is impossible), and so
which is impossible), and so ![]() is not a soc-injective ring.
is not a soc-injective ring.
Example 2 Let ![]() where
where ![]() for all
for all ![]()
![]() for all
for all ![]() and
and ![]() for all
for all ![]() and
and ![]() Then
Then ![]() is a commutative, semiprimary, local ring with
is a commutative, semiprimary, local ring with ![]() and
and ![]() has simple essential socle
has simple essential socle![]() . It is not difficult to see that
. It is not difficult to see that ![]() is right soc-injective. However the R-homomorphism
is right soc-injective. However the R-homomorphism ![]() defined by
defined by ![]() for all
for all ![]() can not be extended to an endomorphism of
can not be extended to an endomorphism of![]() , and so
, and so ![]() is not s-injective ring.
is not s-injective ring.
Definition 2 A ring ![]() is called a right generalized V-ring (right GV-ring) if every simple singular right R-module is injective.
is called a right generalized V-ring (right GV-ring) if every simple singular right R-module is injective.
Proposition 5 A ring ![]() is right GV-ring if and only if every simple right R-module is strongly s-injective.
is right GV-ring if and only if every simple right R-module is strongly s-injective.
Proof. Let ![]() be a right GV-ring and
be a right GV-ring and ![]() be a simple right R-module. The module
be a simple right R-module. The module ![]() is either projective or singular, so
is either projective or singular, so ![]() is strongly s-injective. Conversely, if
is strongly s-injective. Conversely, if ![]() is a simple singular right R-module, then
is a simple singular right R-module, then ![]() is strongly s-injective. Thus
is strongly s-injective. Thus ![]() is injective by Proposition 3. □
is injective by Proposition 3. □
Lemma 2 For a right R-module ![]() the following conditions are equivalent:
the following conditions are equivalent:
1) ![]() satisfies
satisfies ![]() on essential submodules.
on essential submodules.
2) ![]() is noetherian.
is noetherian.
Proof. Assume that ![]() has
has ![]() on essential submodules. Then
on essential submodules. Then ![]() is noetherian for every submodule
is noetherian for every submodule ![]()
![]() where
where ![]() is an intersection complement of
is an intersection complement of ![]() and
and ![]() is noetherian). In particular, every uniform submodule of
is noetherian). In particular, every uniform submodule of ![]() is noetherian. Let
is noetherian. Let ![]() be an intersection complement of
be an intersection complement of ![]()
![]() (see Kasch [2] p.112). Then
(see Kasch [2] p.112). Then ![]() is noetherian. So, to prove that
is noetherian. So, to prove that ![]() is noetherian it is enough to show that
is noetherian it is enough to show that ![]() is noetherian. Assume that
is noetherian. Assume that ![]() contains an infinite direct sum
contains an infinite direct sum ![]() of nonzero submodules
of nonzero submodules![]() . Since
. Since![]() , each
, each ![]() contains a proper essential submodule
contains a proper essential submodule ![]() and
and ![]() is essential in
is essential in![]() . But this gives that
. But this gives that ![]() is noetherian which is impossible because
is noetherian which is impossible because ![]() with each
with each ![]() nonzero. Then
nonzero. Then ![]() contains
contains ![]() independent uniform submodules
independent uniform submodules ![]() such that
such that ![]() is essential in
is essential in![]() . Thus
. Thus ![]() and
and ![]() are noetherian. Hence
are noetherian. Hence ![]() is noetherian. □
is noetherian. □
It is well-known that, a ring ![]() is right noetherian if and only if all direct sums of injective right R-modules are injective. In the next Proposition we obtain a characterization of ring which has
is right noetherian if and only if all direct sums of injective right R-modules are injective. In the next Proposition we obtain a characterization of ring which has ![]() on essential right ideals in terms of strongly s-injective right R-modules.
on essential right ideals in terms of strongly s-injective right R-modules.
Proposition 6 The following conditions on a ring ![]() are equivalent:
are equivalent:
1) Every direct sum of strongly s-injective right R-modules is strongly s-injective.
2) Every direct sum of injective right R-modules is strongly s-injective.
3) Every finitely generated right R-module has ![]() on essential submodules.
on essential submodules.
4) ![]() is noetherian.
is noetherian.
Proof. 1) ![]() 2). Clear.
2). Clear.
2) ![]() 3). Consider a chain
3). Consider a chain ![]() of essential submodules of a finitely generated right R-module
of essential submodules of a finitely generated right R-module
![]() and
and![]() . Let
. Let ![]() be the injective hull of
be the injective hull of ![]()
![]() and
and ![]() be a map defined by
be a map defined by![]() . Since
. Since ![]() is strongly s-injective and
is strongly s-injective and ![]() has an essential singular submodule, so
has an essential singular submodule, so ![]() is injective and
is injective and ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism ![]() Then
Then ![]() for some
for some ![]() and
and![]() . Thus
. Thus ![]()
for every![]() . Hence
. Hence ![]() has
has ![]() on essential submodules.
on essential submodules.
3) ![]() 4). Above Lemma.
4). Above Lemma.
4) ![]() 1). Let
1). Let ![]() be a direct sum of injective Goldie torsion modules. Then
be a direct sum of injective Goldie torsion modules. Then![]() ,
, ![]() , may be
, may be
considered as an injective R/Sr-module. Thus ![]() is an injective R/Sr-module. Now, suppose that
is an injective R/Sr-module. Now, suppose that ![]()
is a nonzero map where ![]() is simple right ideal, so
is simple right ideal, so ![]() is a singular right ideal and
is a singular right ideal and ![]() where
where ![]() is finite. Thus
is finite. Thus ![]() extends to
extends to![]() . Then
. Then ![]() which is a contradiction
which is a contradiction
with![]() . Hence any homomorphism
. Hence any homomorphism ![]() where
where ![]() is a right ideal of
is a right ideal of ![]() induces a map
induces a map ![]() with
with![]() . The map
. The map ![]() extends to a homomorphism
extends to a homomorphism![]() . Then the map
. Then the map ![]() where π is the natural epimorphism
where π is the natural epimorphism![]() , extends
, extends![]() . Hence
. Hence ![]() is injective. Therefore, every direct sum of strongly s-injective right R-modules is strongly s-injective. □
is injective. Therefore, every direct sum of strongly s-injective right R-modules is strongly s-injective. □
If ![]() is an ideal of
is an ideal of![]() ,
, ![]() is called I-semiperfect if for every right ideal
is called I-semiperfect if for every right ideal![]() , there is a decomposition
, there is a decomposition ![]() such that
such that ![]() and
and ![]() [4].
[4].
Lemma 3 If ![]() is Zr-semiperfect, then the following statements hold:
is Zr-semiperfect, then the following statements hold:
1) A module ![]() is s-injective if and only if
is s-injective if and only if ![]() is injective.
is injective.
2) ![]() for all singular right ideals
for all singular right ideals ![]() of
of ![]() if and only if
if and only if ![]() for all right ideals
for all right ideals ![]() of
of![]() .
.
Proof. 1) Let ![]() be s-injective, and
be s-injective, and ![]() be an R-homomorphism where
be an R-homomorphism where ![]() is a right ideal of
is a right ideal of![]() . Then
. Then![]() where
where ![]() Let
Let ![]() be an extension of the restriction map
be an extension of the restriction map ![]() Define
Define ![]() by
by ![]() for all
for all ![]() Clearly,
Clearly, ![]() is an extension of
is an extension of![]() , and so
, and so ![]() is injective by the Baer's Criterion.
is injective by the Baer's Criterion.
2) Let ![]() be a right ideal of
be a right ideal of![]() . Since
. Since ![]() is right
is right ![]() -semiperfect, then
-semiperfect, then ![]() where
where ![]()
and![]() . So
. So ![]() and
and![]() . If
. If
![]() , then
, then ![]() and so
and so
![]() . The last equality is because that
. The last equality is because that ![]() is a singular right ideal of
is a singular right ideal of![]() . Write
. Write ![]() where
where![]() . Then
. Then![]() . Therefore,
. Therefore,![]() . □
. □
Proposition 7 Let ![]() be a right R-module.
be a right R-module. ![]() is semisimple summand of
is semisimple summand of ![]() if and only if every right R-module is s-M-injective.
if and only if every right R-module is s-M-injective.
Proof. If ![]() is semisimple summand of
is semisimple summand of![]() , then every right R-module
, then every right R-module ![]() is s-M-injective. Conversely, if every right R-module is s-M-injective, then every identity map
is s-M-injective. Conversely, if every right R-module is s-M-injective, then every identity map ![]() where
where ![]() is singular submodule of
is singular submodule of ![]() extends to
extends to![]() . Thus
. Thus ![]() is a summand of
is a summand of![]() . Hence
. Hence ![]() is a semisimple summand of
is a semisimple summand of![]() . □
. □
Corollary 4 A ring ![]() is right nonsingular if and only if every right R-module is s-injective.
is right nonsingular if and only if every right R-module is s-injective.
A ring ![]() is called a right (left)
is called a right (left) ![]() ring if every singular right (left) R-module is injective.
ring if every singular right (left) R-module is injective. ![]() rings were initially introduced and investigated by Goodearl [5]
rings were initially introduced and investigated by Goodearl [5]
Theorem 1 The following statements are equivalent:
1) ![]() is right
is right ![]() ring.
ring.
2) Every right R-module is strongly s-injective.
3) Every singular right R-module is strongly s-injective.
Proof. Clear from Proposition 3. □
A module ![]() is said to satisfy the C2-condition, if
is said to satisfy the C2-condition, if ![]() and
and ![]() are submodules of
are submodules of![]() ,
, ![]() and
and ![]() then
then ![]() We also say
We also say ![]() satisfies the C3-condition if
satisfies the C3-condition if ![]() and
and ![]() are submodules of
are submodules of ![]() with
with ![]()
![]() and
and ![]() then
then ![]() is a summand of
is a summand of![]() . It is a well-know fact that the C2-condition implies the C3-condition. In the next proposition we show that s-quasi-injective modules inherit a weaker version of these conditions.
. It is a well-know fact that the C2-condition implies the C3-condition. In the next proposition we show that s-quasi-injective modules inherit a weaker version of these conditions.
Proposition 8 Suppose ![]() is a s-quasi-injective right R-module.
is a s-quasi-injective right R-module.
1) ![]() If
If ![]() and
and ![]() are singular submodules of
are singular submodules of![]() ,
, ![]() and
and ![]() then
then ![]()
2) ![]() Let
Let ![]() and
and ![]() be singular submodules of
be singular submodules of ![]() with
with ![]() If
If ![]() and
and ![]() then
then ![]() is a summand of
is a summand of![]() .
.
Proof. 1) Since ![]() and
and ![]() is s-injective, being a summand of the s-quasi-injective right R-module
is s-injective, being a summand of the s-quasi-injective right R-module ![]()
![]() is s-injective. If
is s-injective. If ![]() is the inclusion map, the identity map
is the inclusion map, the identity map ![]() has an extension
has an extension ![]() such that
such that ![]() and so
and so ![]() is a summand of
is a summand of![]() .
.
2) Since ![]() and
and ![]() are summands of
are summands of![]() , and
, and ![]() is s-quasi-injective, both
is s-quasi-injective, both ![]() and
and ![]() are s-M- injective. Thus the singular module
are s-M- injective. Thus the singular module ![]() is s-M-injective, and so is a summand of
is s-M-injective, and so is a summand of![]() . □
. □
It is a well-known fact that the C2-condition implies the C3-condition.
Proposition 9 If a module ![]() has s-C2-condition, then
has s-C2-condition, then ![]() has s-C3-condition.
has s-C3-condition.
Proof. Consider singular summands ![]() and
and ![]() of
of ![]() such that
such that![]() . Write
. Write ![]() and let π denote the projection
and let π denote the projection![]() . Then
. Then![]() . If
. If![]() ,
, ![]() where
where
![]() and
and ![]() and
and![]() ,
, ![]() and
and![]() . Then
. Then ![]() is a mono-
is a mono-
morphism; so ![]() is a summand of
is a summand of ![]() by
by ![]() -
-![]() . As
. As![]() ,
,![]() .
.
Proposition 10 Let ![]() and
and ![]() be Morita-equivalent rings with category equivalence
be Morita-equivalent rings with category equivalence ![]() Let
Let![]() ,
, ![]() , and
, and ![]() be right R-modules. Then
be right R-modules. Then
1) ![]() is singular if and only if
is singular if and only if ![]() is singular.
is singular.
2) ![]() is s-N-injective if and only if
is s-N-injective if and only if ![]() is s-injective.
is s-injective.
Proof. There is a natural isomorphisms ![]() and
and![]() . This means that for each
. This means that for each ![]() there is an isomorphism
there is an isomorphism ![]() in
in ![]() such that for each
such that for each![]() ,
, ![]() in
in ![]() and each
and each ![]() in
in![]() , the following diagram commutes
, the following diagram commutes
![]()
1). The right R-module ![]() is singular if and only if there is an exact sequence of right R-modules
is singular if and only if there is an exact sequence of right R-modules ![]() with essential monomorphism
with essential monomorphism![]() . But using [6, Proposition 21.4 and Proposition 21.6] the sequence
. But using [6, Proposition 21.4 and Proposition 21.6] the sequence ![]() is exact with essential monomorphism
is exact with essential monomorphism ![]() if and only if the sequence
if and only if the sequence ![]() of right S-modules is exact with essential monomorphism
of right S-modules is exact with essential monomorphism![]() . So
. So ![]() is singular if and only if
is singular if and only if ![]() is singular.
is singular.
2). Let ![]() be a s-N-injective and
be a s-N-injective and ![]() be a singular submodule of
be a singular submodule of![]() . Let
. Let ![]() be a homomorphism. Since
be a homomorphism. Since ![]() is singular,
is singular, ![]() is a monomorphism and the maps
is a monomorphism and the maps ![]() and
and ![]() are isomorphisms ( we may assume that
are isomorphisms ( we may assume that ![]() is a submodule of
is a submodule of![]() ), then we have the commutative diagram
), then we have the commutative diagram
![]()
So the following diagram
![]()
is commutative where ![]() is
is ![]() injective. The converse is similarly. □
injective. The converse is similarly. □
As for right self-injectivity, right strongly s-injectivity turns out to be a Morita invariant.
Theorem 2 Right strong s-injectivity is a Morita invariant property of rings.
Proof. Let ![]() and
and ![]() be Morita-equivalent rings with category equivalences
be Morita-equivalent rings with category equivalences ![]() and
and![]() . Let
. Let![]() , and
, and ![]() be right R-modules.
be right R-modules. ![]() is finitely generated projective R-module if and only if
is finitely generated projective R-module if and only if ![]() is finitely generated projective S-module [6, Propositions
is finitely generated projective S-module [6, Propositions ![]() and
and![]() ]. Also
]. Also ![]() is s-N-injective if and only if
is s-N-injective if and only if ![]() is s-F(N)-injective (Proposition 10) and then
is s-F(N)-injective (Proposition 10) and then ![]() is strongly s-injective if and only if
is strongly s-injective if and only if ![]() is strongly s-injective. Then, every finitely generated projective right R-module is strongly s-injective if and only if every finitely generated projective right S-module is strongly s-injective. Therefore right strong s-injectivity is a Morita invariant property of rings. □
is strongly s-injective. Then, every finitely generated projective right R-module is strongly s-injective if and only if every finitely generated projective right S-module is strongly s-injective. Therefore right strong s-injectivity is a Morita invariant property of rings. □
Proposition 11 For a projective right R-module![]() , the following conditions are equivalent:
, the following conditions are equivalent:
1) Every homomorphic image of a s-M-injective right R-module is s-M-injective.
2) Every homomorphic image of an injective right R-module is s-M-injective.
3) Every singular submodule of ![]() is projective.
is projective.
Proof. 1) ![]() 2) Obvious.
2) Obvious.
2) ![]() 3) Consider the following diagram:
3) Consider the following diagram:
![]()
Where ![]() is a singular submodule of
is a singular submodule of![]() ,
, ![]() and
and ![]() are right R-modules with
are right R-modules with ![]() injective,
injective, ![]() an R-epimorphism, and
an R-epimorphism, and ![]() an R-homomorphism. Since
an R-homomorphism. Since ![]() is s-injective,
is s-injective, ![]() can be extended to an R-homomo- rphism
can be extended to an R-homomo- rphism ![]() Since
Since ![]() is projective,
is projective, ![]() can be lifted to an R-homomorphism
can be lifted to an R-homomorphism ![]() such that
such that ![]() Now, define
Now, define ![]() by
by ![]() Clearly,
Clearly, ![]() and hence
and hence ![]() is projective.
is projective.
3) ![]() 1) Let
1) Let ![]() and
and ![]() be right R-modules with
be right R-modules with ![]() an R-epimorphism,
an R-epimorphism, ![]() is a singular submodule of
is a singular submodule of ![]() and
and ![]() is s-M-injective. Consider the following diagram:
is s-M-injective. Consider the following diagram:
![]()
Since ![]() is projective,
is projective, ![]() can be lifted to an R-homomorphism
can be lifted to an R-homomorphism ![]() such that
such that ![]()
![]() Since
Since ![]() is s-injective,
is s-injective, ![]() can be extended to an R-homomorphism
can be extended to an R-homomorphism ![]() Clearly,
Clearly, ![]() extends
extends![]() . □
. □
Corollary 5 The following conditions are equivalent:
1) Every quotient of s-injective right R-module is s-injective.
2) Every quotient of an injective right R-module is s-injective.
3) Every singular right ideal is projective.
Proposition 12 The following conditions are equivalent:
1) Every strongly s-injective right R-module is injective.
2) Every nonsingular right R-module is semisimple injective.
3) For every right R-module![]() ,
, ![]() where
where ![]() semisimple injective.
semisimple injective.
4) ![]() is
is ![]() semiperfect.
semiperfect.
Proof. 1) ![]() 2) If
2) If ![]() is nonsingular right R-module, then
is nonsingular right R-module, then ![]() is strongly s-injective. Thus
is strongly s-injective. Thus ![]() is semisimple injective.
is semisimple injective.
2) ![]() 3) Let
3) Let ![]() be a right R-module. If
be a right R-module. If ![]() is Goldie torsion, we are done. Now suppose that
is Goldie torsion, we are done. Now suppose that ![]() is not essential in
is not essential in ![]() and
and ![]() be a maximal submodule
be a maximal submodule ![]() with respect to
with respect to![]() . Then
. Then ![]() is semisimple injective and
is semisimple injective and![]() . It is clear that
. It is clear that![]() .
.
3) ![]() 4). Let
4). Let ![]() be a right ideal of
be a right ideal of![]() . Then
. Then ![]() where
where ![]() is semisimple injective. We have
is semisimple injective. We have ![]() and
and ![]() is a summand of
is a summand of ![]() and generated by an idempotent. Hence
and generated by an idempotent. Hence ![]() is
is ![]() semiperfect.
semiperfect.
4) ![]() 1). Let
1). Let ![]() be a strongly s-injective and
be a strongly s-injective and ![]() be an R-homomorphism where
be an R-homomorphism where ![]() is a right ideal of
is a right ideal of ![]() By
By ![]() where
where ![]() and
and ![]() Using Proposition 3 let
Using Proposition 3 let ![]() be an extension of the restriction map
be an extension of the restriction map ![]() Define
Define ![]() by
by ![]() for all
for all ![]() Clearly,
Clearly, ![]() is an extension of
is an extension of![]() , and so
, and so ![]() is injective by the Baer's Criterion. □
is injective by the Baer's Criterion. □
Theorem 3 The following are equivalent for a ring![]() :
:
1) ![]() is a right PF-ring.
is a right PF-ring.
2) ![]() is Zr-semiperfect, right strongly s-injective ring with essential right socle.
is Zr-semiperfect, right strongly s-injective ring with essential right socle.
3) ![]() is semiperfect, right min-C2, right strongly s-injective ring with essential right socle.
is semiperfect, right min-C2, right strongly s-injective ring with essential right socle.
4) ![]() is semiperfect with
is semiperfect with![]() , right strongly s-injective ring with essential right socle.
, right strongly s-injective ring with essential right socle.
5) ![]() is right finitely cogenerated, right min-C2, right strongly s-injective ring.
is right finitely cogenerated, right min-C2, right strongly s-injective ring.
6) ![]() is a right Kasch, right strongly s-injective ring.
is a right Kasch, right strongly s-injective ring.
7) ![]() is a right strongly s-injective ring and the dual of every simple left R-module is simple.
is a right strongly s-injective ring and the dual of every simple left R-module is simple.
Proof. 1) ![]() 2). Clear.
2). Clear.
2) ![]() 1). Clear by Lemma 2.
1). Clear by Lemma 2.
1) ![]() 3). Clear.
3). Clear.
3) ![]() 4). Suppose that
4). Suppose that ![]() is a non singular simple right ideal in
is a non singular simple right ideal in![]() , so
, so ![]() for some simple right ideal
for some simple right ideal ![]() with
with![]() . Thus
. Thus ![]() and
and ![]() is a summand which is a contradiction. Then
is a summand which is a contradiction. Then![]() . The other inclusion is clear.
. The other inclusion is clear.
4) ![]() 1). Let
1). Let ![]() be semiperfect and right strongly s-injective ring with essential right socle and
be semiperfect and right strongly s-injective ring with essential right socle and![]() . Then
. Then ![]() where
where ![]() is injective and
is injective and![]() . Thus
. Thus ![]() and
and![]() . The right ideal
. The right ideal ![]() may be considered as an R/J-module. Let
may be considered as an R/J-module. Let ![]() be a map where
be a map where ![]() is a right ideal of
is a right ideal of![]() ,
, ![]() induces a map
induces a map ![]() given by
given by![]() . Since
. Since ![]() is injective as an R/J-module so
is injective as an R/J-module so ![]() extends to
extends to![]() . The map
. The map![]() , where π is the natural epimorphism
, where π is the natural epimorphism![]() , extends
, extends ![]() and
and ![]() is injective. Therefore
is injective. Therefore ![]() is right selfinjective and
is right selfinjective and ![]() is right
is right![]() .
.
1) ![]() 5). Clear.
5). Clear.
5) ![]() 1). Since
1). Since ![]() is right strongly s-injective ring, it follows from Proposition 3 that
is right strongly s-injective ring, it follows from Proposition 3 that![]() , where
, where ![]() is injective and
is injective and ![]() is nonsingular. If
is nonsingular. If ![]() is simple right ideal in
is simple right ideal in ![]() such that
such that![]() , then, by the proof of 3)
, then, by the proof of 3) ![]() 1)
1) ![]() and every simple right ideal in
and every simple right ideal in ![]() is a summand of
is a summand of![]() . Since
. Since ![]() is right finitely cogenerated,
is right finitely cogenerated, ![]() has a finitely generated essential socle. Thus
has a finitely generated essential socle. Thus ![]() is semisimple. Hence
is semisimple. Hence ![]() is injective and
is injective and ![]() is right
is right ![]() ring.
ring.
1) ![]() 6) Proposition 3 and [7, Theorem 5]
6) Proposition 3 and [7, Theorem 5]
1) ![]() 7). Assume that
7). Assume that ![]() is right strongly s-injective and the dual of every simple left R-module is simple. If
is right strongly s-injective and the dual of every simple left R-module is simple. If ![]() is a nonsingular simple right ideal, then
is a nonsingular simple right ideal, then ![]() for some simple right ideal
for some simple right ideal ![]() with
with![]() . But
. But ![]() is
is![]() , so
, so ![]() and
and ![]() is a summand. Thus
is a summand. Thus ![]() is right min-CS, so by [3, Theorem 4.8]
is right min-CS, so by [3, Theorem 4.8] ![]() is semiperfect with essential right socle. Hence
is semiperfect with essential right socle. Hence ![]() is right
is right ![]() by 3). □
by 3). □
The following is an example of a right perfect, left Kasch ring and right strongly s-injective which is not right self-injective ring.
Example 3 Let ![]() be a field and let
be a field and let ![]() be the ring of all upper triangular, countably infinite square matrices over
be the ring of all upper triangular, countably infinite square matrices over ![]() with only finitely many off-diagonal entries. Let
with only finitely many off-diagonal entries. Let ![]() be the K-subalgebra of
be the K-subalgebra of ![]() generated by
generated by ![]() and
and ![]() Then
Then ![]() is a right perfect, left Kasch (
is a right perfect, left Kasch (![]() has only one simple left R-module
has only one simple left R-module ![]() up to isomorphism. So
up to isomorphism. So![]() ) such that
) such that ![]() whereas
whereas ![]() is neither left perfect nor right self-injective because it is not right finite dimensional.
is neither left perfect nor right self-injective because it is not right finite dimensional.
Remark 1 Note that the ring of integers ![]() is an example of a commutative noetherian strongly s-injective ring which is not quasi-Frobenius.
is an example of a commutative noetherian strongly s-injective ring which is not quasi-Frobenius.
Definition 3 A ring ![]() is called right CF-ring (FGF-ring) if every cyclic (finitely generated) right R-module embeds in a free module. It is not known whether right CF-rings (FGF-rings) are right artinian (quasi- Frobenius). In the next result we provide a positive answer if we assume in addition that the ring
is called right CF-ring (FGF-ring) if every cyclic (finitely generated) right R-module embeds in a free module. It is not known whether right CF-rings (FGF-rings) are right artinian (quasi- Frobenius). In the next result we provide a positive answer if we assume in addition that the ring ![]() is strongly right s-injective.
is strongly right s-injective.
Proposition 13 Every right ![]() right strongly s-injective ring is quasi-Frobenius.
right strongly s-injective ring is quasi-Frobenius.
Proof. Theorem 3 and [7, Theorem 5] □
3. S-CS Modules and Rings
A module ![]() is said to satisfy C1-condition or called
is said to satisfy C1-condition or called ![]() module if every submodule of
module if every submodule of ![]() is essential in a direct summand of
is essential in a direct summand of![]() .
.
Definition 4 A right R-module ![]() is called s-CS module if every singular submodule of
is called s-CS module if every singular submodule of ![]() is essential in a summand of
is essential in a summand of![]() .
.
For example, every nonsingular module is s-CS. In particular, the ring of integers ![]() is s-CS but not
is s-CS but not ![]()
Proposition 14 For a right R-module![]() , the following statements are equivalent:
, the following statements are equivalent:
1) The second singular submodule ![]() is
is ![]() and a summand of
and a summand of![]() .
.
2) ![]() is s-CS.
is s-CS.
Proof. 1) ![]() 2). If the second singular submodule
2). If the second singular submodule ![]() of
of ![]() is
is ![]() and a summand of
and a summand of![]() , then every singular submodule of
, then every singular submodule of ![]() is a summand of
is a summand of ![]() and a summand of
and a summand of![]() .
.
2) ![]() 1). Let
1). Let ![]() be s-CS and
be s-CS and ![]() is a submodule of
is a submodule of![]() . Then
. Then ![]() where
where ![]() is a sum-
is a sum-
mand of ![]() and
and![]() . But
. But ![]() is closed, so
is closed, so![]() . Since
. Since ![]() and
and ![]() is closed in
is closed in![]() , so
, so ![]() and
and ![]() is
is![]() . In particular,
. In particular, ![]() is the only closure of
is the only closure of![]() . Thus
. Thus ![]() is a summand of
is a summand of![]() . □
. □
A module is called s-continuous if it satisfies both the s-C1- and s-C2-conditions, and a module is called quasi-s-continuous if it satisfies the s-C1- and s-C3-conditions, and ![]() is called a right s-continuous ring (right quasi-s-continuous ring) if
is called a right s-continuous ring (right quasi-s-continuous ring) if ![]() has the corresponding property. Clearly every strongly s-injective is s-continuous.
has the corresponding property. Clearly every strongly s-injective is s-continuous.
Proposition 15 If every singular simple right R-module embeds in ![]() and
and ![]() is s-CS, then
is s-CS, then ![]() is finitely cogenerated.
is finitely cogenerated.
Proof. Let ![]() be a s-CS and every singular simple right R-module embeds in
be a s-CS and every singular simple right R-module embeds in![]() . Then
. Then ![]() is a
is a ![]() and summand of
and summand of ![]() by above Proposition. Also
by above Proposition. Also ![]() cogenerats every simple quotient of
cogenerats every simple quotient of ![]() then by [3, Theorem 7.29],
then by [3, Theorem 7.29], ![]() is finitely cogenerated.
is finitely cogenerated.
Proposition 16 Let ![]() be a ring. Then
be a ring. Then ![]() is a right PF-ring if and only if
is a right PF-ring if and only if ![]() is a cogenerator and
is a cogenerator and ![]() is
is![]() .
.
Proof. Every right PF-ring is right self-injective and is a right cogenerator by [3, 1.56]. Conversely, if ![]() is a
is a ![]() and
and ![]() is cogenerator then
is cogenerator then ![]() has finitely generated, essential right socle by Proposition 15. Since
has finitely generated, essential right socle by Proposition 15. Since ![]() is right finite dimensional and
is right finite dimensional and ![]() is a cogenerator, let
is a cogenerator, let ![]() and
and ![]() be the injective hull of
be the injective hull of![]() , then there exists an embedding
, then there exists an embedding ![]() for some set
for some set![]() . Then
. Then ![]() for some projection
for some projection![]() , so
, so ![]() and hence is monic. Thus
and hence is monic. Thus ![]() is monic, and so
is monic, and so ![]() where
where ![]() is nonsingular. So
is nonsingular. So ![]() is a right PF-ring by Theorem 3. □
is a right PF-ring by Theorem 3. □
Proposition 17 If every simple singular right R-module embeds in ![]() and
and ![]() is continuous, then
is continuous, then ![]() is semiperfect.
is semiperfect.
Proof. Let ![]() be continuous and every simple singular right R-module embeds in
be continuous and every simple singular right R-module embeds in![]() . Then
. Then ![]() has a finitely generated essential socle by Proposition 15. Thus, by hypothesis, there exist simple submodules
has a finitely generated essential socle by Proposition 15. Thus, by hypothesis, there exist simple submodules
![]() of
of ![]() such that
such that ![]() is a complete set of representatives of the isomorphism classes of
is a complete set of representatives of the isomorphism classes of
simple singular right R-modules. Since ![]() is
is![]() , there exist submodules
, there exist submodules ![]() of
of ![]() such that
such that ![]() is a direct summand of
is a direct summand of ![]() and
and ![]() for
for![]() . Since
. Since ![]() is an indecomposable continuous R-module, it has a local endomorphism ring; and since
is an indecomposable continuous R-module, it has a local endomorphism ring; and since ![]() is projective,
is projective, ![]() is maximal and small in
is maximal and small in ![]() by [3, 1.54]. Then
by [3, 1.54]. Then ![]() is a projective cover of the simple module
is a projective cover of the simple module![]() . Note that
. Note that ![]() clearly implies
clearly implies![]() ; and the converse also holds because every module has at most one projective cover up to isomorphism. But it is clear that
; and the converse also holds because every module has at most one projective cover up to isomorphism. But it is clear that ![]() if and only if
if and only if ![]() if and only if
if and only if![]() . Moreover, every
. Moreover, every ![]() is singular. Thus,
is singular. Thus, ![]() is a complete set of representatives of the isomorphism classes of simple singular right R-modules. Hence every simple singular right R-module has a projective cover. Since every non-singular simple right R-module is projective, we conclude that
is a complete set of representatives of the isomorphism classes of simple singular right R-modules. Hence every simple singular right R-module has a projective cover. Since every non-singular simple right R-module is projective, we conclude that ![]() is semiperfect. □
is semiperfect. □
References
- C. Faith, “Algebra II Ring Theory,” Springer-Verlag, Berlin, 1976. http://dx.doi.org/10.1007/978-3-642-65321-6
- F. Kasch, “Modules and Rings,” L.M.S. Monograph No. 17. Academic Press, New York, 1982.
- W. K. Nicholson and M. F. Yousif, “Quasi-Frobenius Rings,” In: Cambridge Tracts in Mathematics, Vol. 158, Cambridge University Press, Cambridge, 2003. http://dx.doi.org/10.1017/CBO9780511546525
- M. F. Yousif and Y. Zhou, “Semi-Regular, Semi-Perfect and Perfect Rings Relative to an Ideal,” Rocky Mountain Journal of Mathematics, Vol. 32, No. 4, 2002, pp. 1651-1671. http://dx.doi.org/10.1216/rmjm/1181070046
- K. R. Goodearl, “Singular Torsion and the Splitting Properties,” Memoirs of the American Mathematical Society, Vol. 124, 1972.
- F. W. Anderson and K. R. Fuller, “Rings and Categories of Modules,” Springer-Verlag, Berlin/New York, 1974. http://dx.doi.org/10.1007/978-1-4684-9913-1
- M. F. Yousif, Y. Zhou and N. Zeyada, “On Pseudo-Frobenius rings,” Canadian Mathematical Bulletin, Vol. 48, No. 2, 2005, pp. 317-320. http://dx.doi.org/10.4153/CMB-2005-029-5
 extends to
extends to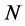 , where K is a submodule of the singular submodule
, where K is a submodule of the singular submodule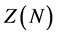 . M is called strongly s-injective if M is s-N-injective for every right R-module N. The connection between this new injectivity condition and other injectivity conditions has been established, and examples are provided to distinguish s-injectivity from other injectivity concepts such as mininjectivity, soc-injectivity. Several properties of this new class of injectivity are highlighted.
. M is called strongly s-injective if M is s-N-injective for every right R-module N. The connection between this new injectivity condition and other injectivity conditions has been established, and examples are provided to distinguish s-injectivity from other injectivity concepts such as mininjectivity, soc-injectivity. Several properties of this new class of injectivity are highlighted.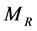 , we denoted
, we denoted ,
, 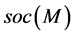 , and
, and  by the Jacobson radical, the socle and the singular submodule of
by the Jacobson radical, the socle and the singular submodule of , respectively.
, respectively.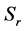 ,
, 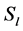 ,
, 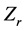 ,
,  and
and  are used to indicate the right socle, the left socle, the right singular ideal, the left singular ideal, and the Jacobson radical of
are used to indicate the right socle, the left socle, the right singular ideal, the left singular ideal, and the Jacobson radical of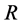 , respectively. For a submodule
, respectively. For a submodule 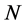 of
of , the notations
, the notations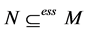 ,
, 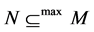 and
and 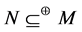 mean, respectively, that N is essential, maximal, and direct summand. If
mean, respectively, that N is essential, maximal, and direct summand. If 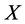 is a subset of a right R-module
is a subset of a right R-module


























































































































































































































































































































































































































































































































































































































































































































































































































































































































