Advances in Pure Mathematics
Vol.3 No.2(2013), Article ID:28584,5 pages DOI:10.4236/apm.2013.32036
The Ricci Operator and Shape Operator of Real Hypersurfaces in a Non-Flat 2-Dimensional Complex Space Form
1Department of Mathematics, Hankuk University of Foreign Studies, Seoul, Republic of Korea
2Department of Mathematics, Yeungnam University, Kyongbuk, Republic of Korea
Email: dhlnys@hufs.ac.kr, mathsohn@ynu.ac.kr, hsong@hufs.ac.kr
Received November 8, 2012; revised December 15, 2012; accepted January 2, 2013
Keywords: real hypersurface; η-parallel shape operator; η-parallel Ricci operator; Hopf hypersurface; ruled real hypersurfaces
ABSTRACT
In this paper, we study a real hypersurface M in a non-at 2-dimensional complex space form M2(c) with η-parallel Ricci and shape operators. The characterizations of these real hypersurfaces are obtained.
1. Introduction
A complex ![]() -dimensional Kaeherian manifold of constant holomorphic sectional curvature
-dimensional Kaeherian manifold of constant holomorphic sectional curvature  is called a complex space form, which is denoted by
is called a complex space form, which is denoted by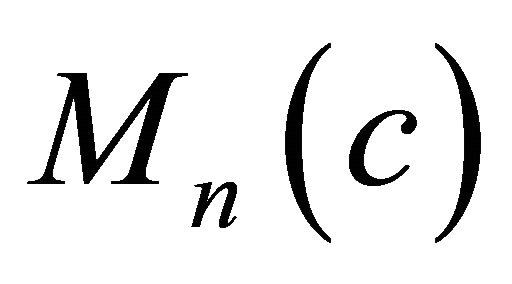 . As is well-known, a complete and simply connected complex space form is complex analytically isometric to a complex projective space
. As is well-known, a complete and simply connected complex space form is complex analytically isometric to a complex projective space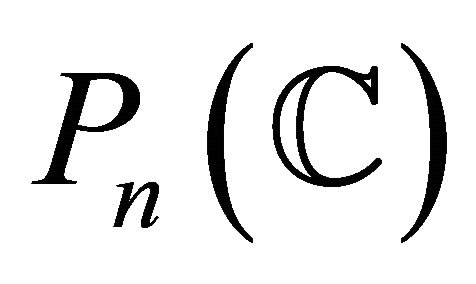 , a complex Euclidean space
, a complex Euclidean space 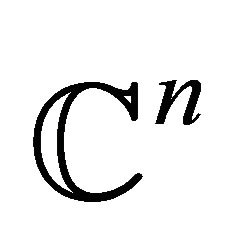 or a complex hyperbolic space
or a complex hyperbolic space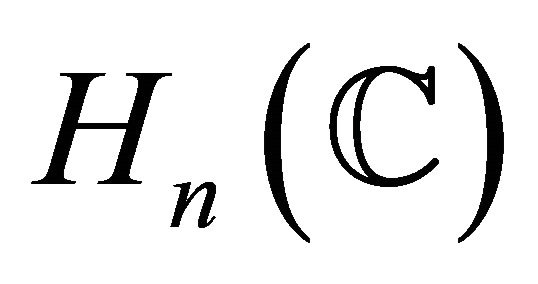 , according to
, according to 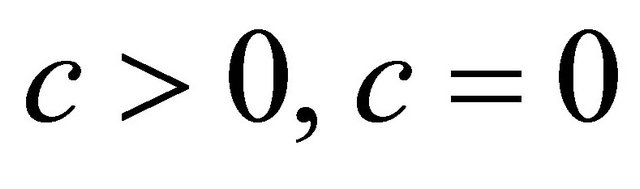 or
or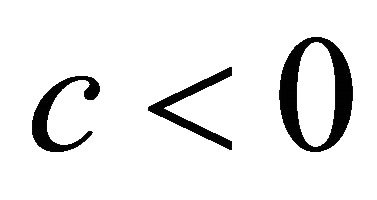 .
.
In this paper we consider a real hypersurface 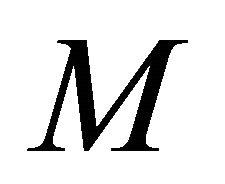 in a complex space form
in a complex space form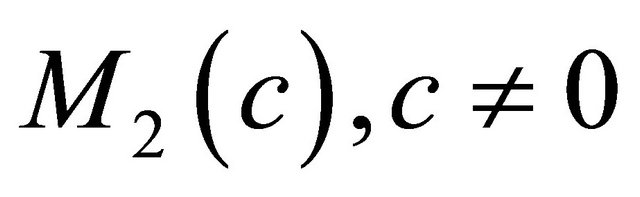 . Then
. Then 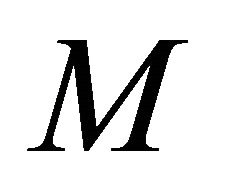 has an almost contact metric structure
has an almost contact metric structure 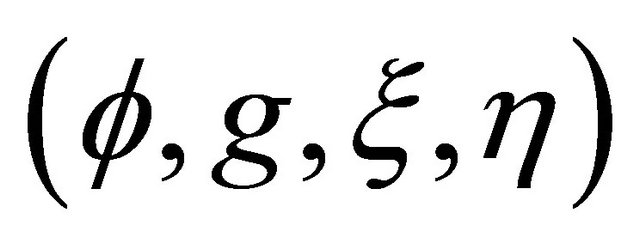 induced from the Kaehler metric and complex structure
induced from the Kaehler metric and complex structure  on
on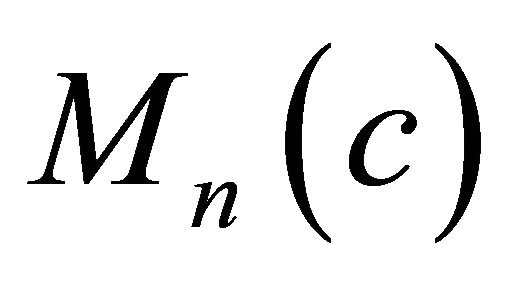 . The structure vector field
. The structure vector field  is said to be principal if
is said to be principal if 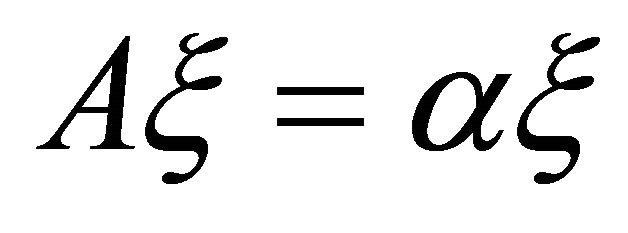 is satisfied, where
is satisfied, where  is the shape operator of
is the shape operator of 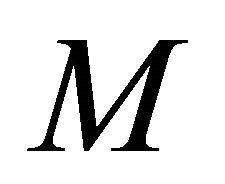 and
and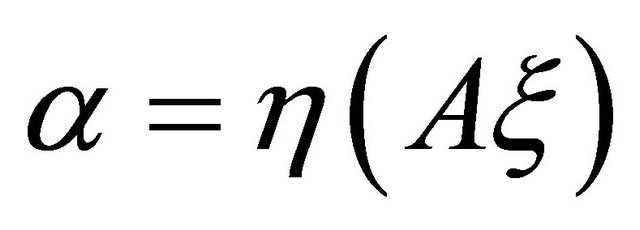 . In this case, it is known that
. In this case, it is known that 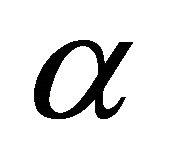 is locally constant ([1]) and that
is locally constant ([1]) and that 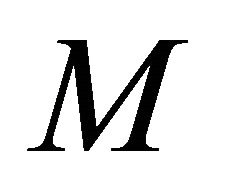 is called a Hopf hypersurface.
is called a Hopf hypersurface.
Typical examples of Hopf hypersurfaces in 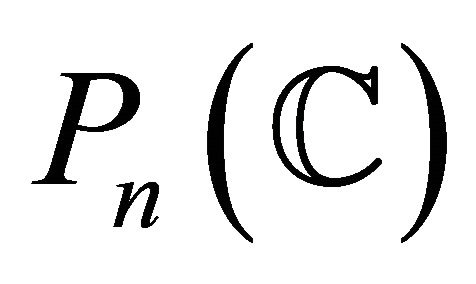 are homogeneous ones, R. Takagi [2] and M. Kimura [3] completely classified such hypersurfaces as six model spaces which are said to be
are homogeneous ones, R. Takagi [2] and M. Kimura [3] completely classified such hypersurfaces as six model spaces which are said to be 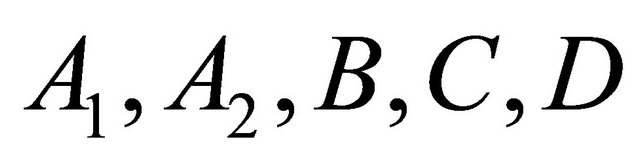 and
and . On the other hand, real hypersurfaces in
. On the other hand, real hypersurfaces in 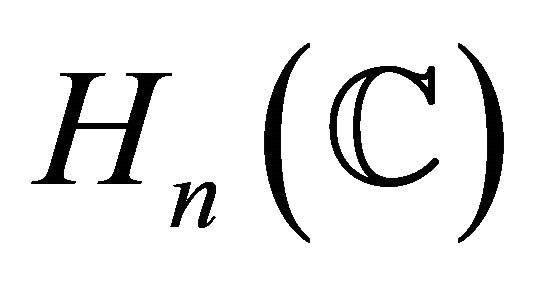 have been investigated by J. Berndt [4], S. Montiel and A. Romero [5] and so on. J. Berndt [4] classified all homogeneous Hopf hyersurfaces in
have been investigated by J. Berndt [4], S. Montiel and A. Romero [5] and so on. J. Berndt [4] classified all homogeneous Hopf hyersurfaces in 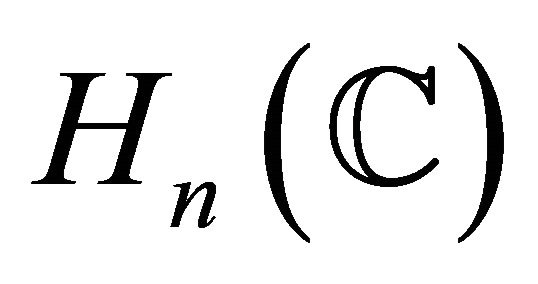 as four model spaces which are said to be
as four model spaces which are said to be 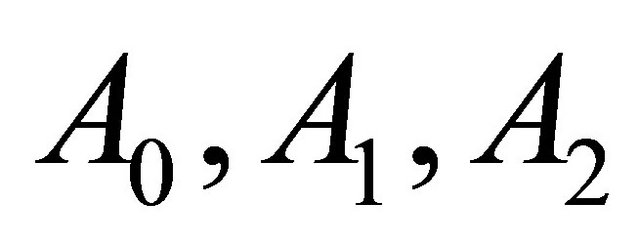 and
and . Further, Hopf hypersurfaces with constant principal curvatures in a complex space form have been completely classified as follows:
. Further, Hopf hypersurfaces with constant principal curvatures in a complex space form have been completely classified as follows:
Theorem 1.1. ([2]) Let 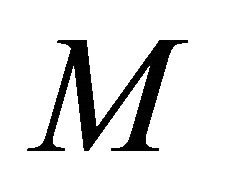 be a homogeneous real hypersurface of
be a homogeneous real hypersurface of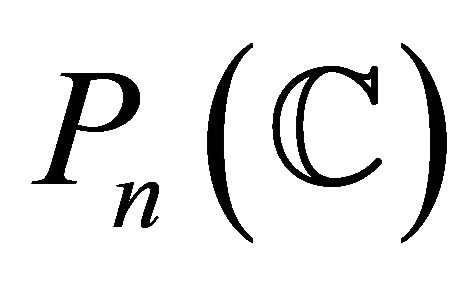 . Then
. Then 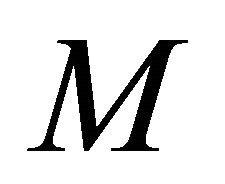 is tube of radius
is tube of radius 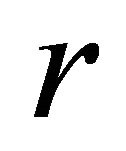 over one of the following Kaeherian submanifolds:
over one of the following Kaeherian submanifolds:
(A1) a hyperplane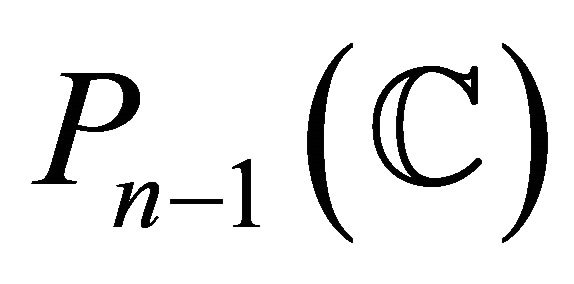 , where
, where ;
;
(A2) a totally geodesic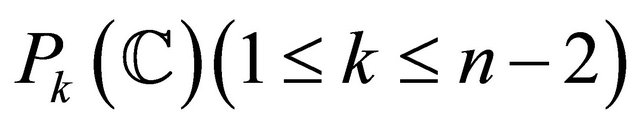 , where
, where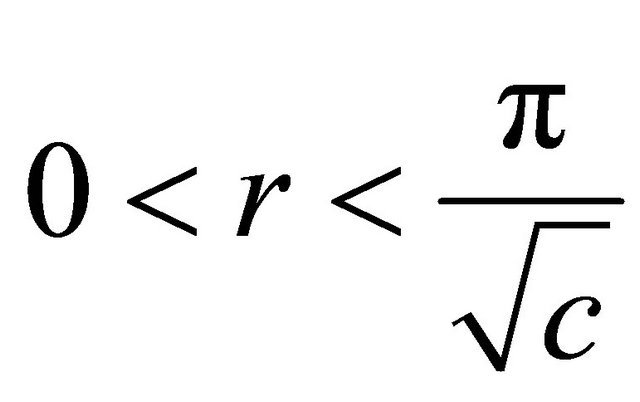 ;
;
(B) a complex quadric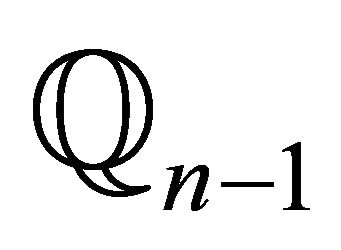 , where
, where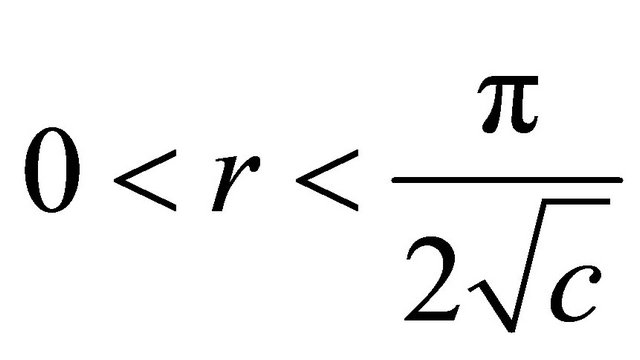 ;
;
(C)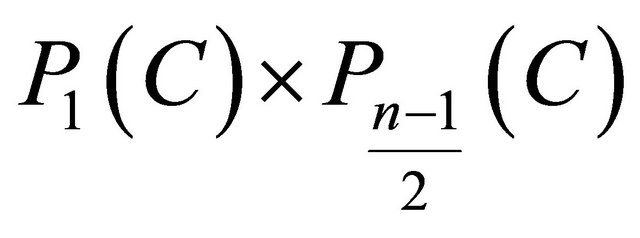 , where
, where 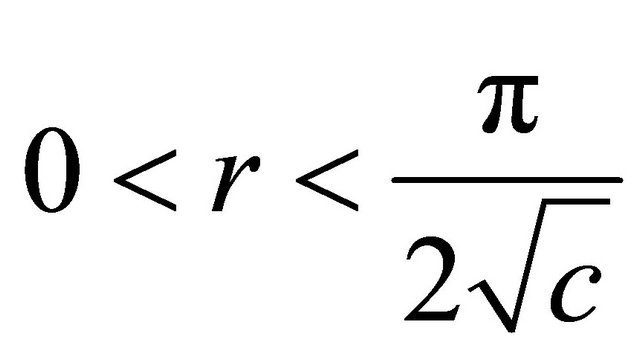 and
and 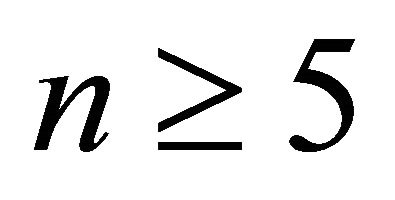 is odd;
is odd;
(D) a complex Grassmann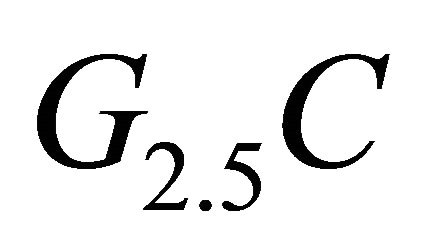 , where
, where 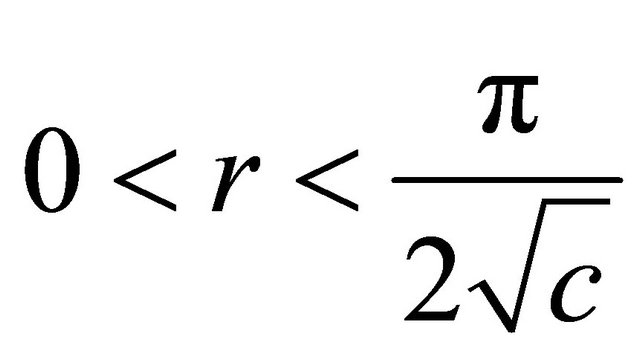 and
and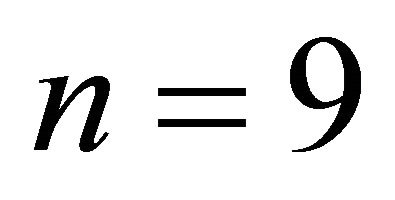 ;
;
(E) a Hermitian symmetric space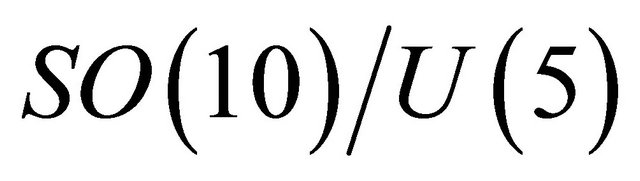 , where
, where 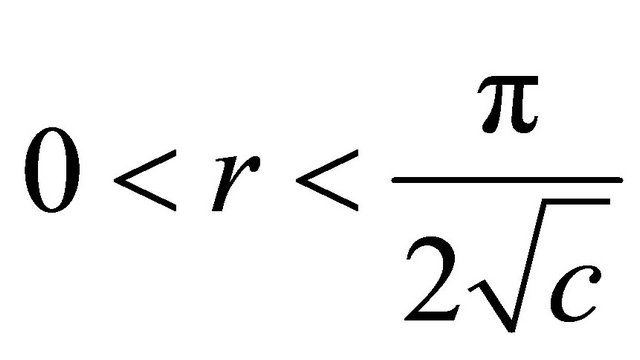 and
and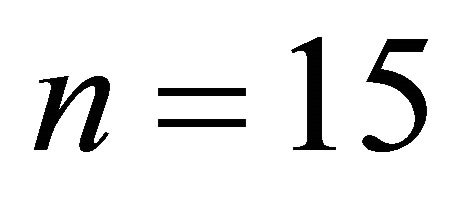 .
.
Theorem 1.2. ([4]) Let 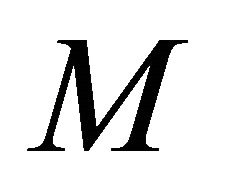 be a real hypersurface in
be a real hypersurface in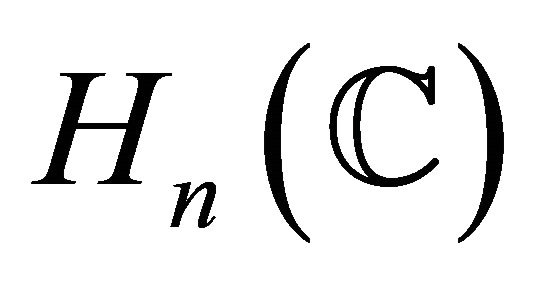 . Then
. Then 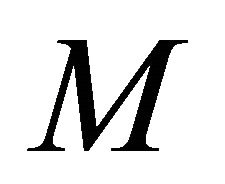 has constant principal curvatures and
has constant principal curvatures and  is principal if and only if
is principal if and only if 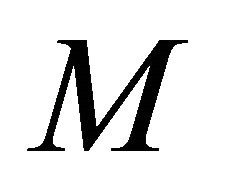 is locally congruent to one of the followings:
is locally congruent to one of the followings:
(A0) a self-tube, that is, a horosphere;
(A1) a geodesic hypersphere;
(A2) a tube over a totally geodesic 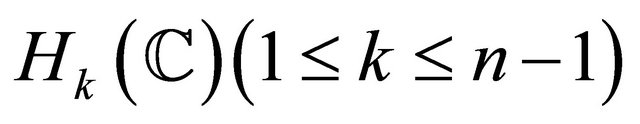 ;
;
(B) a tube over a totally real hyperbolic space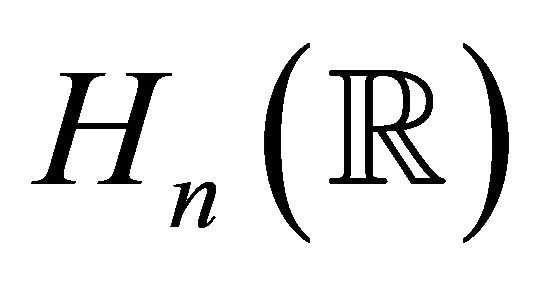 .
.
A real hypersurface of type  or
or 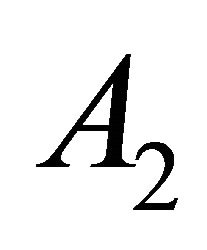 in
in 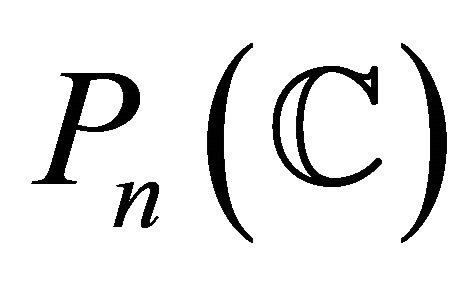 or type
or type 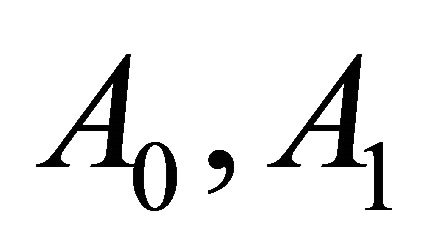 or
or 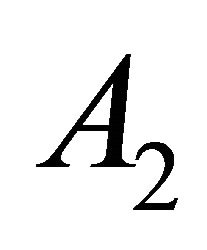 in
in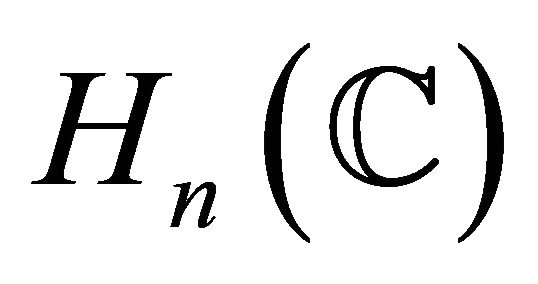 , then
, then 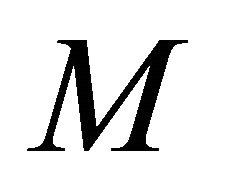 is said to be of type
is said to be of type  for simplicity. As a typical characterization of real hypersurfaces of type
for simplicity. As a typical characterization of real hypersurfaces of type , in a complex space form
, in a complex space form 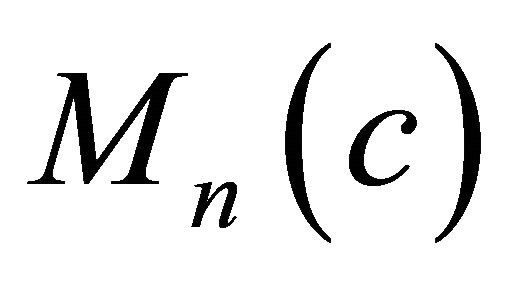 was given under the condition
was given under the condition
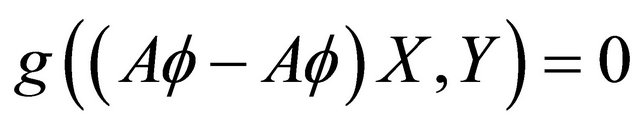 , (1.1)
, (1.1)
for any tangent vector fields 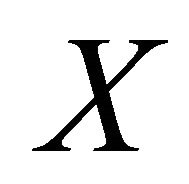 and
and 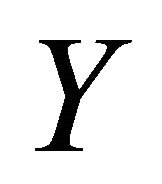 on
on  by M. Okumura [5] for
by M. Okumura [5] for 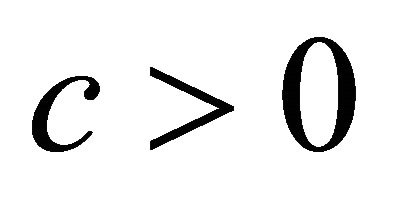 and S. Montiel and A. Romero [6] for
and S. Montiel and A. Romero [6] for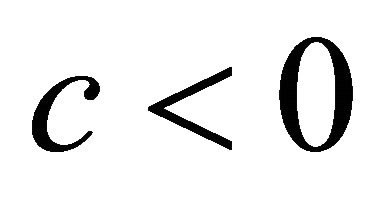 . Namely Theorem 1.3. ([5,6]) Let
. Namely Theorem 1.3. ([5,6]) Let 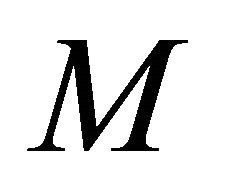 be a real hypersurface in
be a real hypersurface in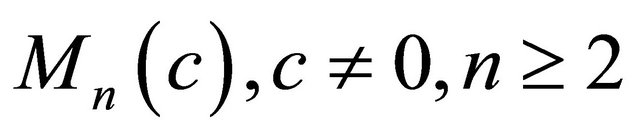 . It satisfies (1.1) on
. It satisfies (1.1) on 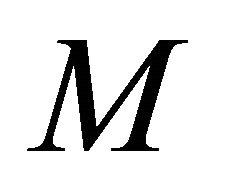 if and only if
if and only if 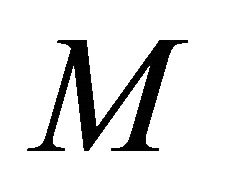 is locally congruent to one of the model spaces of type A.
is locally congruent to one of the model spaces of type A.
The holomorphic distribution 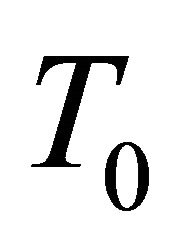 of a real hypersurface
of a real hypersurface  in
in 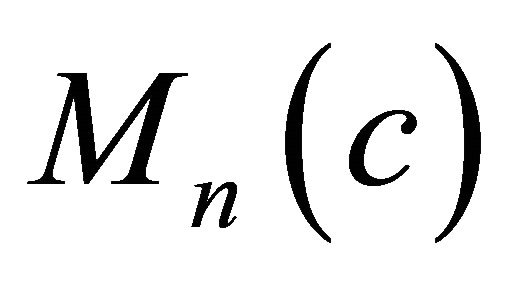 is defined by
is defined by
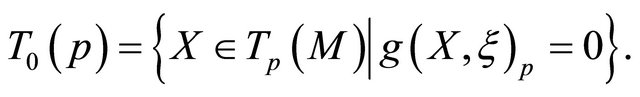 (1.2)
(1.2)
The following theorem characterizes ruled real hypersurfaces in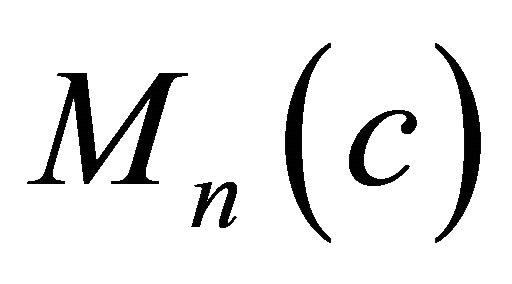 .
.
Theorem 1.4. ([7]) Let  be a real hypersurface in
be a real hypersurface in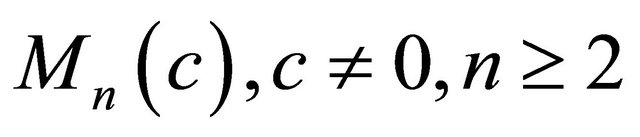 . Then
. Then 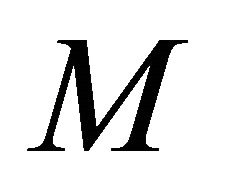 is a ruled real hypersurfaces if and only if
is a ruled real hypersurfaces if and only if 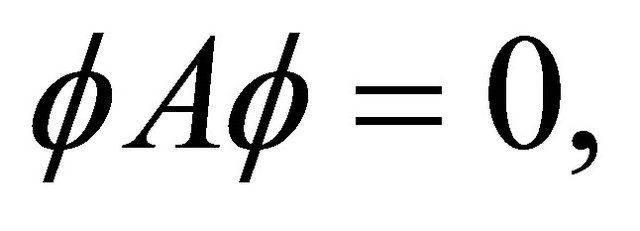 or equivalently
or equivalently 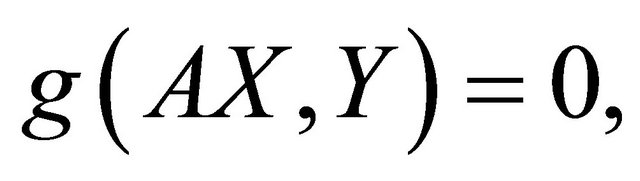 for any
for any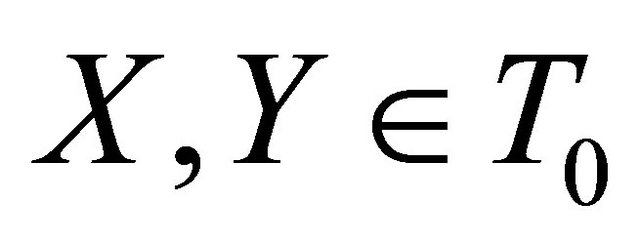 .
.
A (1,1) type tensor field 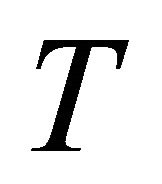 of
of 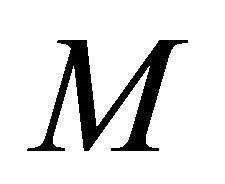 is said to be
is said to be 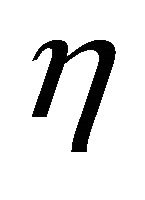 -parallel if
-parallel if
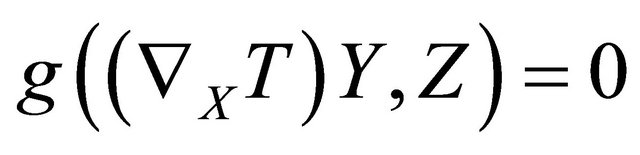 (1.3)
(1.3)
for any vector fields 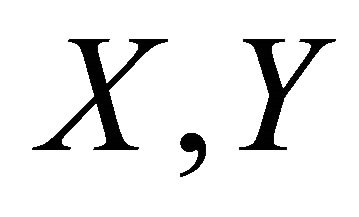 and
and 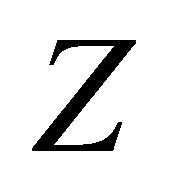 in
in . Real hypersurfaces with
. Real hypersurfaces with 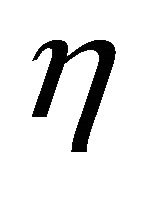 -parallel shape operator or Ricci operator have been studied by many authors (see [13]). Nevertheless, the classification of real hypersurfaces with
-parallel shape operator or Ricci operator have been studied by many authors (see [13]). Nevertheless, the classification of real hypersurfaces with 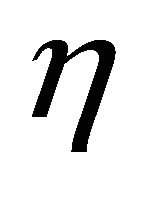 -parallel shape operator or Ricci operator in
-parallel shape operator or Ricci operator in 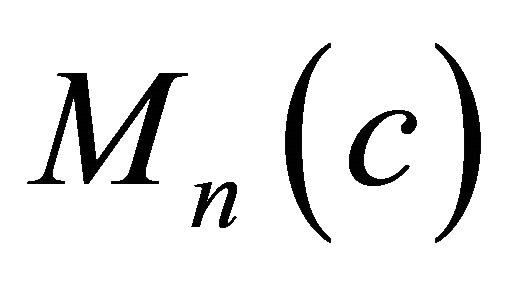 remains open up to this point. Recently, S.H. Kon and T.H. Loo ([9]) investigated the conditions
remains open up to this point. Recently, S.H. Kon and T.H. Loo ([9]) investigated the conditions  -parallel shape operator.
-parallel shape operator.
Theorem 1.5. ([9]) Let 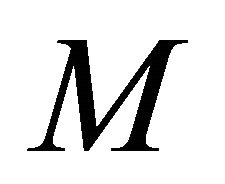 be a real hypersurface of
be a real hypersurface of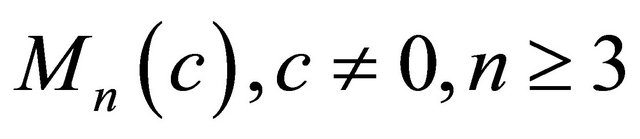 . Then the shape operator
. Then the shape operator  is
is 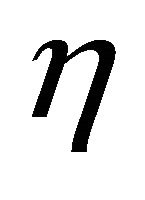 -parallel if and only if
-parallel if and only if 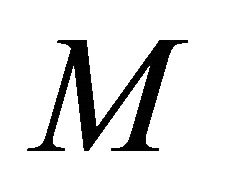 is locally congruent to a ruled real hypersurface, or a real hypersurface of type
is locally congruent to a ruled real hypersurface, or a real hypersurface of type  or
or .
.
Also, M. Kimura and S. Maeda ([10]) and Y.J. Suh ([11]) investigated the conditions 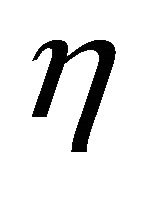 -parallel Ricci operator.
-parallel Ricci operator.
Theorem 1.6. ([10,11]) Let 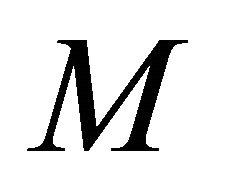 be a real hypersurface in a complex space form
be a real hypersurface in a complex space form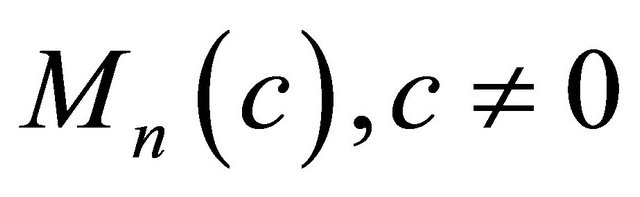 . Then the Ricci operator of
. Then the Ricci operator of 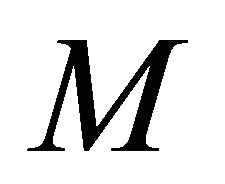 is
is 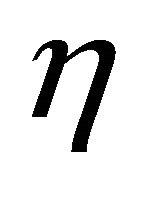 -parallel and the structure vector field
-parallel and the structure vector field  is princial if and only if
is princial if and only if 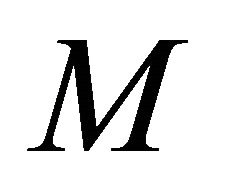 is locally congruent to one of the model spaces of type
is locally congruent to one of the model spaces of type  or type
or type .
.
As for the structure tensor field , shape operator
, shape operator  and
and 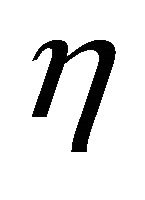 -parallel, I.-B. Kim, K. H. Kim and one of the present authors ([12]) have proved the following.
-parallel, I.-B. Kim, K. H. Kim and one of the present authors ([12]) have proved the following.
Theorem 1.7. ([12]) Let 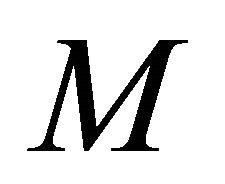 be a real hypersurface in a complex space form
be a real hypersurface in a complex space form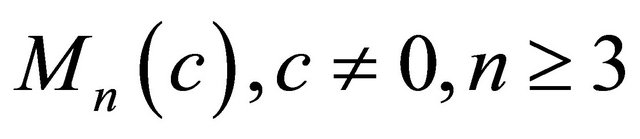 . If
. If 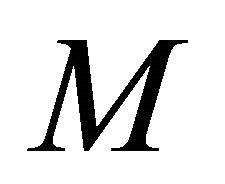 has the cyclic
has the cyclic 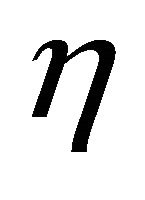 -parallel shape operator (resp. Ricci operator) and satisfies
-parallel shape operator (resp. Ricci operator) and satisfies
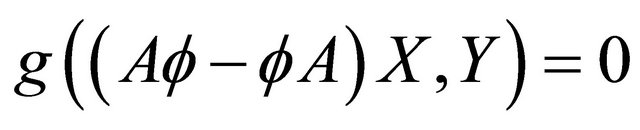 (1.4)
(1.4)
for any 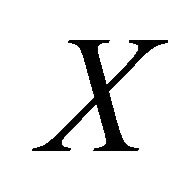 and
and 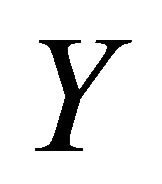 in
in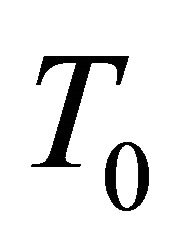 , then
, then 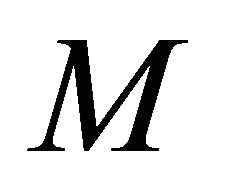 is locally congruent to either a real hypersurface of type
is locally congruent to either a real hypersurface of type  or a ruled real hypersurface (resp.
or a ruled real hypersurface (resp. 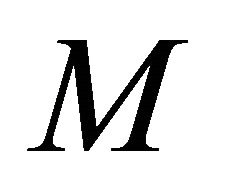 is locally congruent to a real hypersurface of type
is locally congruent to a real hypersurface of type ).
).
The purpose of this paper is to give some characterizations of real hypersurface satisfying (1.4) and having the 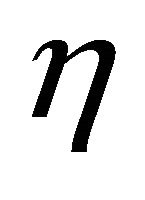 -parallel shape operator or Ricci operator in
-parallel shape operator or Ricci operator in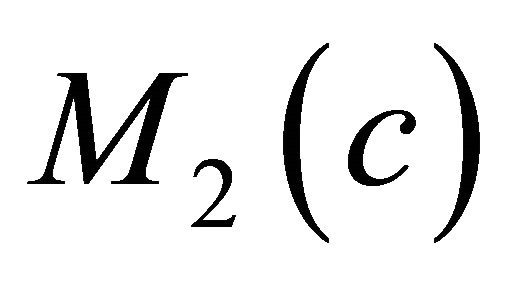 . We shall prove the following.
. We shall prove the following.
Theorem 1.8. Let  be a real hypersurface in a complex space form
be a real hypersurface in a complex space form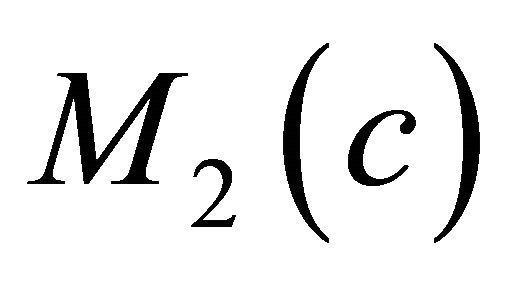 ,
, 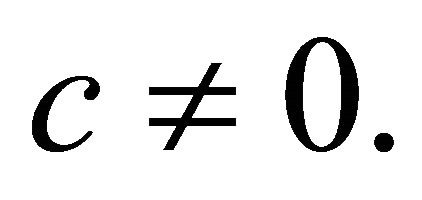 If
If 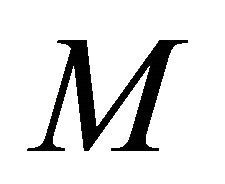 has the
has the 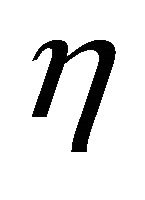 - parallel shape operator and satisfies (1.4), then
- parallel shape operator and satisfies (1.4), then 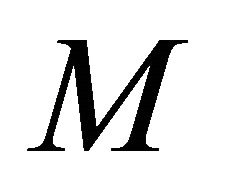 is locally congruent a ruled real hypersurface.
is locally congruent a ruled real hypersurface.
Theorem 1.9. Let 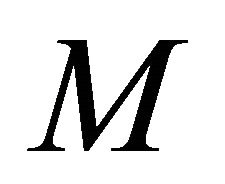 be a real hypersurface in a complex space form
be a real hypersurface in a complex space form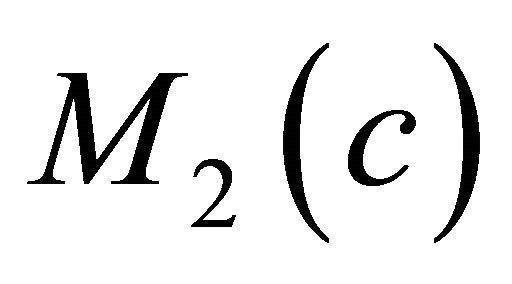 ,
, 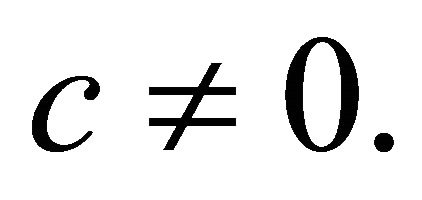 If
If 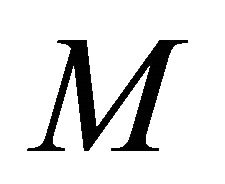 has the
has the 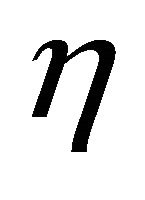 - parallel Ricci operator and satisfies (1.4), then
- parallel Ricci operator and satisfies (1.4), then 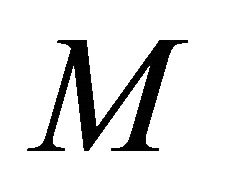 is locally congruent to a real hypersurface of type
is locally congruent to a real hypersurface of type .
.
All manifolds in the present paper are assumed to be connected and of class 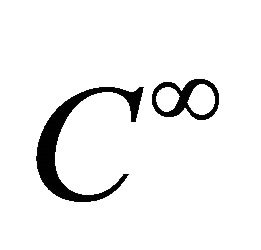 and the real hypersurfaces are supposed to be orientable.
and the real hypersurfaces are supposed to be orientable.
2. Preliminaries
Let 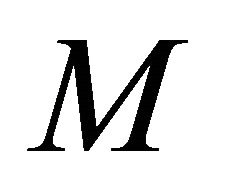 be a real hypersurface immersed in a complex space form
be a real hypersurface immersed in a complex space form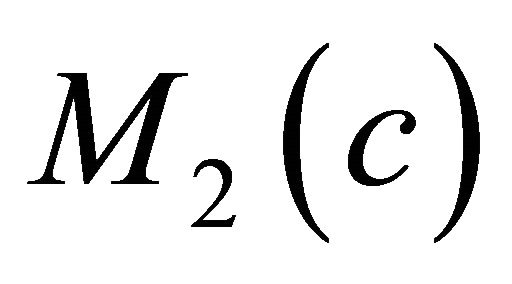 , and
, and 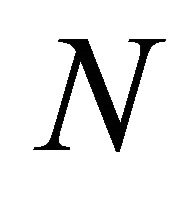 be a unit normal vector field of
be a unit normal vector field of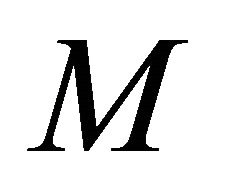 . By
. By  we denote the Levi-Civita connection with respect to the Fubini-Study metric tensor
we denote the Levi-Civita connection with respect to the Fubini-Study metric tensor 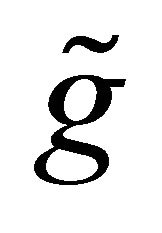 of
of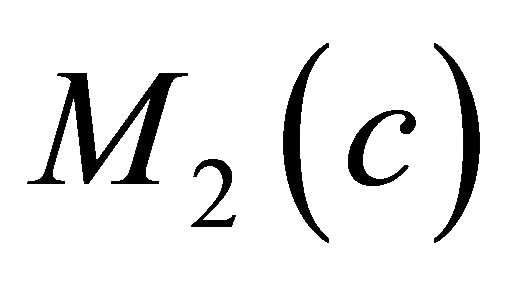 . Then the Gauss and Weingarten formulas are given respectively by
. Then the Gauss and Weingarten formulas are given respectively by
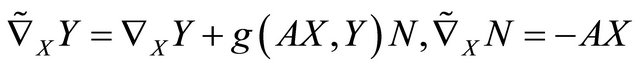
for any vector fields 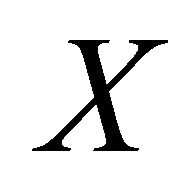 and
and 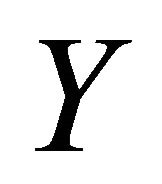 tangent to
tangent to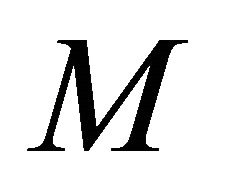 , where
, where 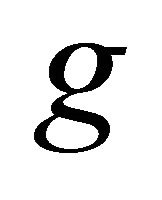 denotes the Riemannian metric tensor of
denotes the Riemannian metric tensor of 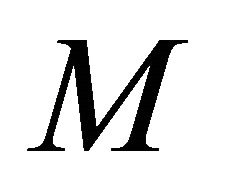 induced from
induced from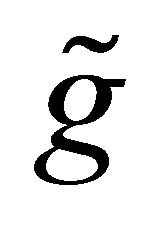 , and
, and  is the shape operator of
is the shape operator of 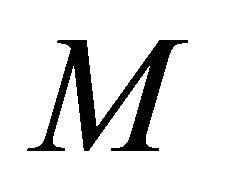 in
in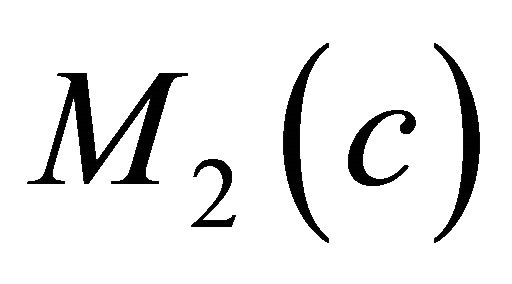 . For any vector field
. For any vector field 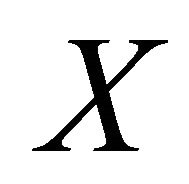 on
on 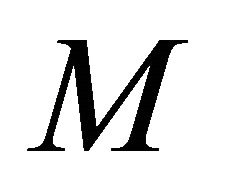 we put
we put
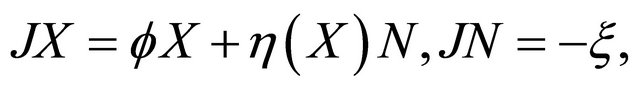
where  is the almost complex structure of
is the almost complex structure of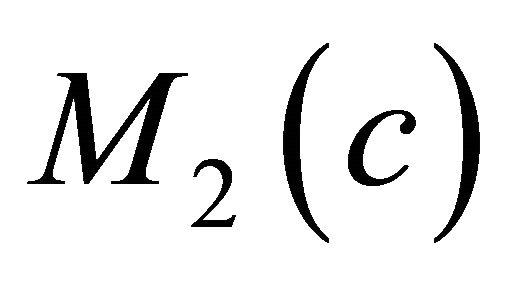 . Then we see that
. Then we see that 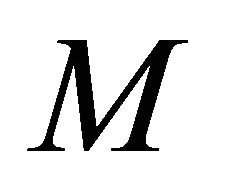 induces an almost contact metric structure
induces an almost contact metric structure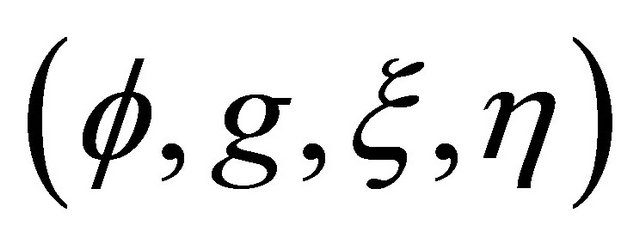 , that is,
, that is,
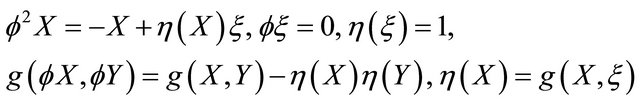 (2.1)
(2.1)
for any vector fields 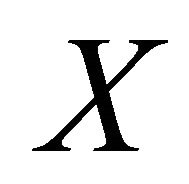 and
and 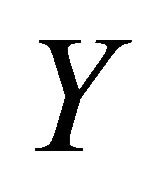 on
on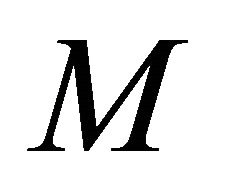 . Since the almost complex structure
. Since the almost complex structure  is parallel, we can verify from the Gauss and Weingarten formulas the followings:
is parallel, we can verify from the Gauss and Weingarten formulas the followings:
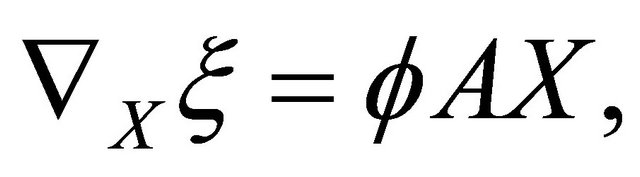 (2.2)
(2.2)
 (2.3)
(2.3)
Since the ambient manifold is of constant holomorphic sectional curvature , we have the following Gauss and Codazzi equations respectively:
, we have the following Gauss and Codazzi equations respectively:
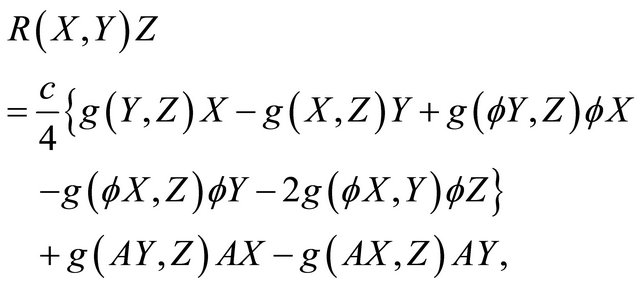 (2.4)
(2.4)
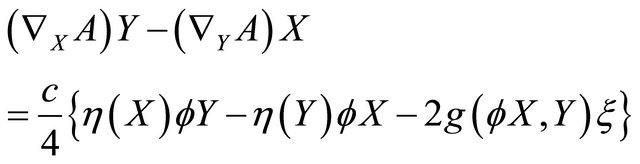 (2.5)
(2.5)
for any vector fields 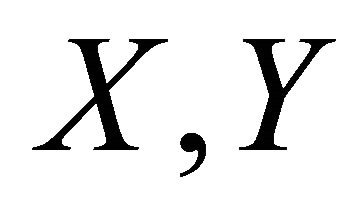 and
and 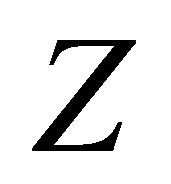 on
on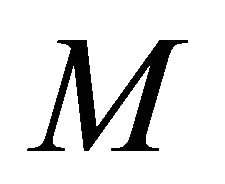 , where
, where 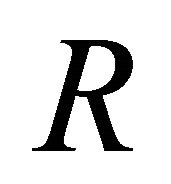 denotes the Riemannian curvature tensor of
denotes the Riemannian curvature tensor of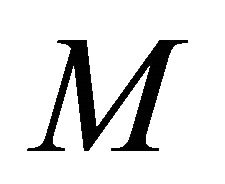 . From (1.3), the Ricci operator
. From (1.3), the Ricci operator 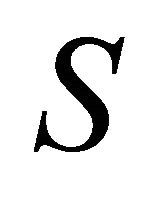 of
of 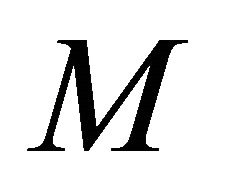 is expressed by
is expressed by
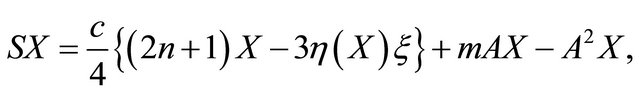 (2.6)
(2.6)
where  is the mean curvature of
is the mean curvature of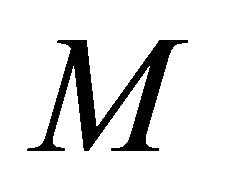 , and the covariant derivative of (2.5) is given by
, and the covariant derivative of (2.5) is given by
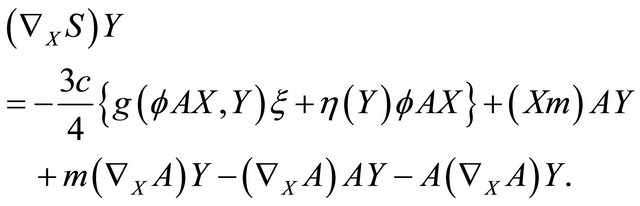 (2.7)
(2.7)
Let U be a unit vector field on 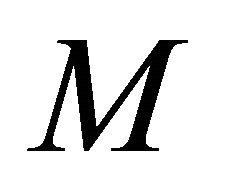 with the same direction of the vector field
with the same direction of the vector field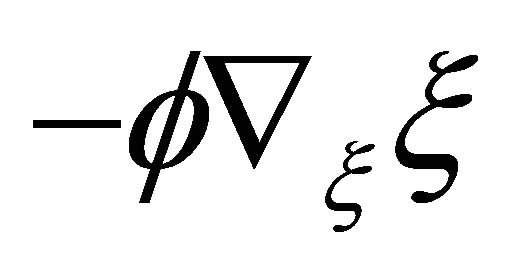 , and let
, and let 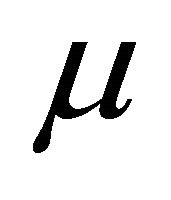 be the length of the vector field
be the length of the vector field 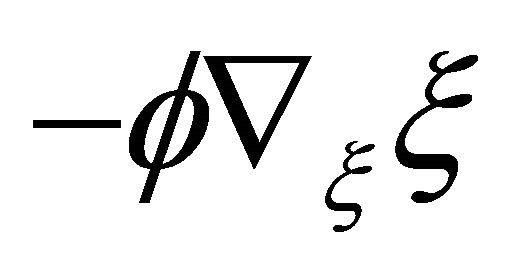 if it does not vanish, and zero (constant function) if it vanishes. Then it is easily seen from (1.1) that
if it does not vanish, and zero (constant function) if it vanishes. Then it is easily seen from (1.1) that
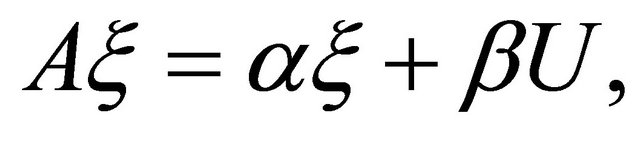 (2.8)
(2.8)
where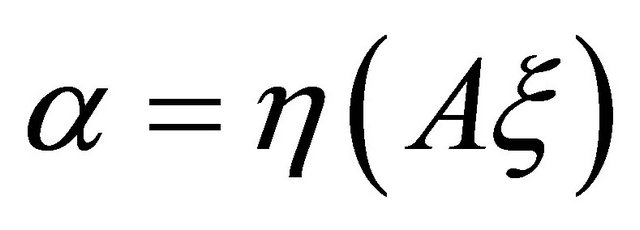 . We notice here that
. We notice here that 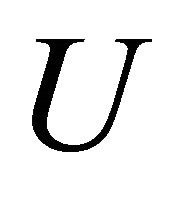 is orthogonal to
is orthogonal to . We put
. We put
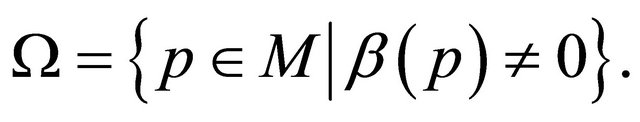 (2.9)
(2.9)
Then  is an open subset of
is an open subset of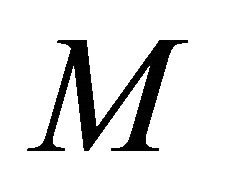 .
.
3. Some Lemmas
In this section, we assume that  is not empty, then there are sclar fields
is not empty, then there are sclar fields 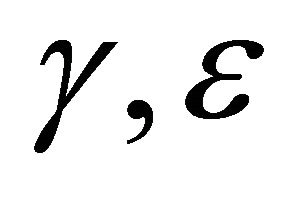 and
and  and a unit vector field
and a unit vector field 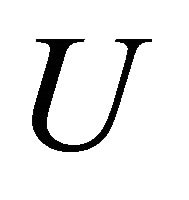 and
and 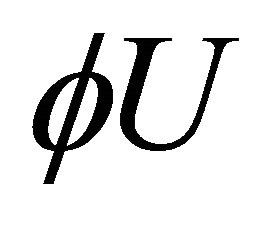 orthogonal to
orthogonal to  such that
such that
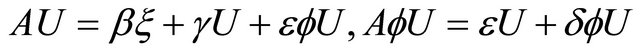 (3.1)
(3.1)
and
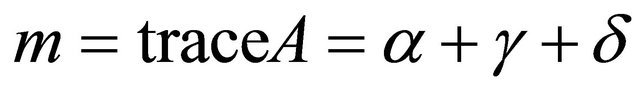 (3.2)
(3.2)
in 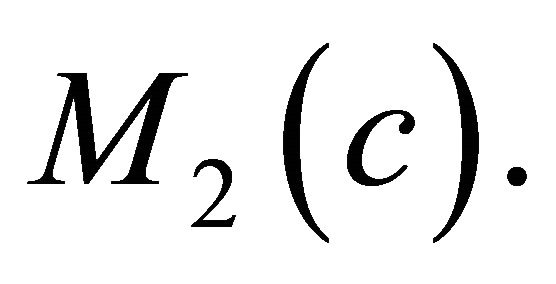 We shall prove the following Lemmas.
We shall prove the following Lemmas.
Lemma 3.1. Let 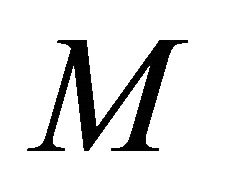 be a real hypersurface in a complex space form
be a real hypersurface in a complex space form 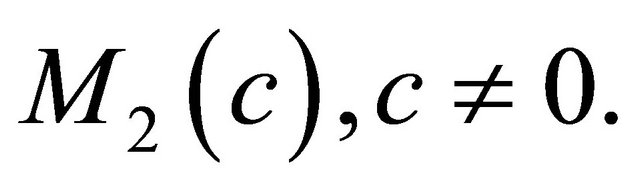 If
If  satisfies (1.4), then we have
satisfies (1.4), then we have 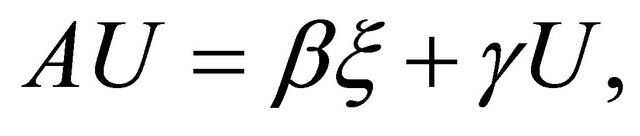
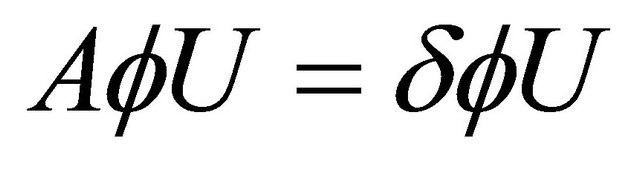 and
and 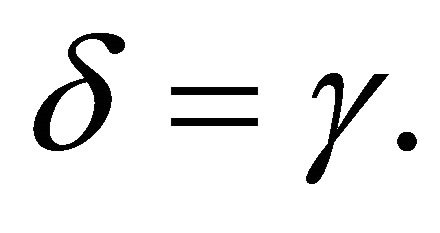
Proof. If we put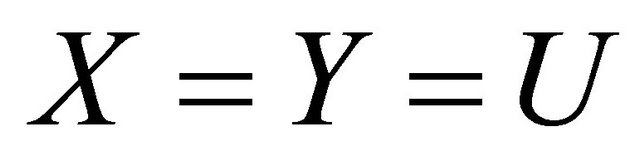 , or
, or 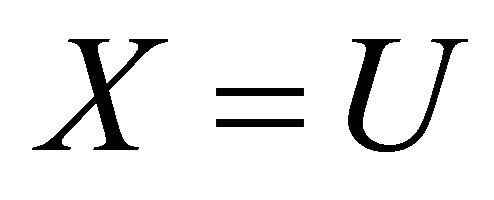 and
and 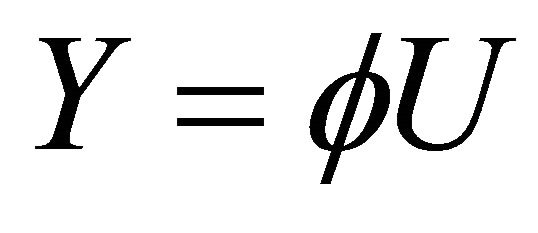 into (1.4) and make use of (3.1), then we have
into (1.4) and make use of (3.1), then we have
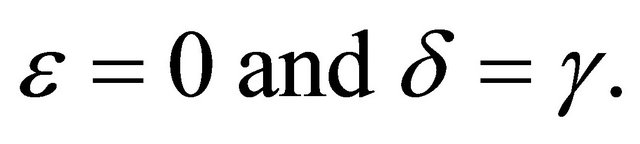 (3.3)
(3.3)
Therefore, it follows that 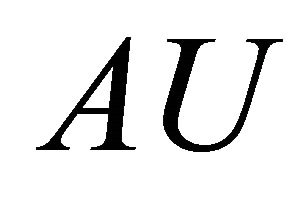 is expressed in terms of
is expressed in terms of  and
and 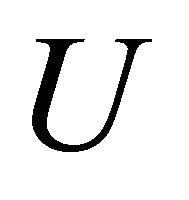 only and
only and 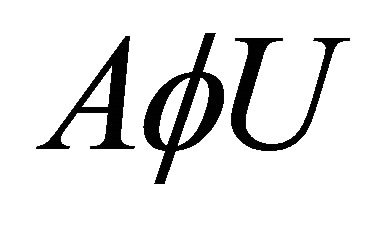 given by
given by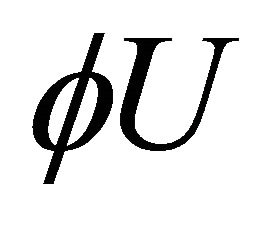 . □
. □
It follows from (2.6), (2.8) and Lemma 3.1 that
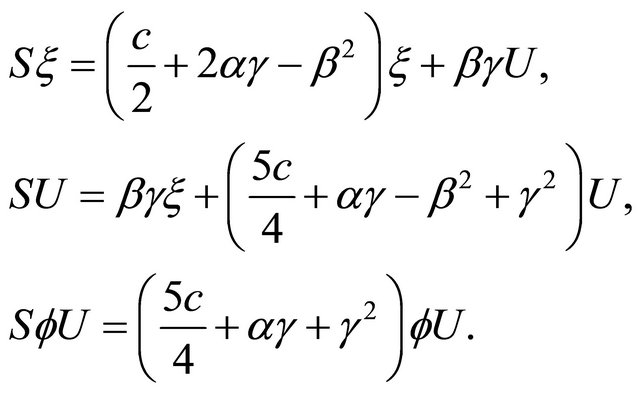 (3.4)
(3.4)
Lemma 3.2. Under the assumptions of Lemma 3.1. If 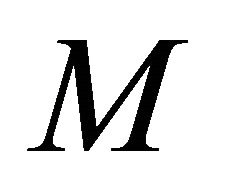 has the
has the 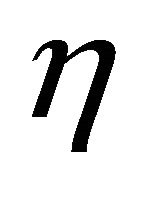 -parallel Ricci operator
-parallel Ricci operator 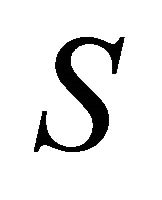 then we have
then we have 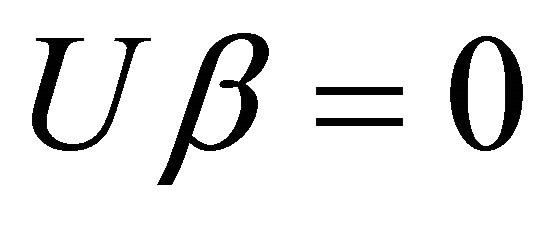 and
and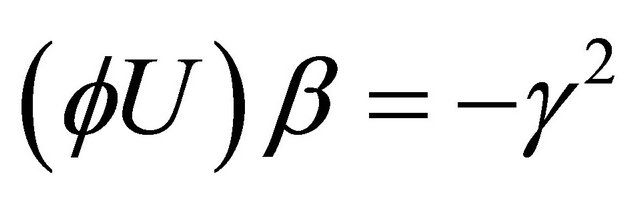 .
.
Proof. Differentiating the second of (3.4) covariantly along vector field 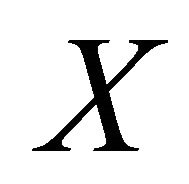 in
in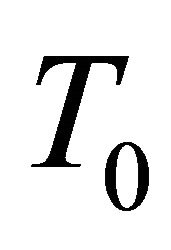 , we obtain
, we obtain
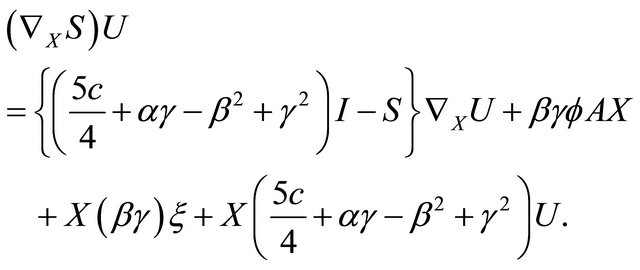 (3.5)
(3.5)
Taking inner product of (3.5) with 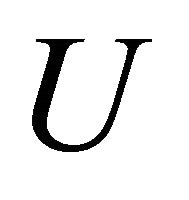 and
and 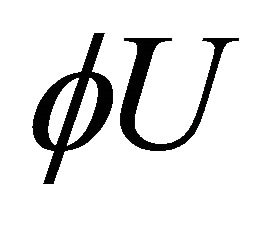 and making use of (3.5) and Lemma 3.1, we have
and making use of (3.5) and Lemma 3.1, we have
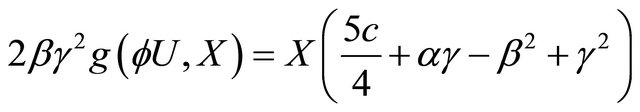 (3.6)
(3.6)
and
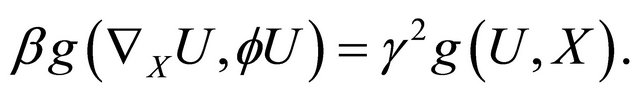 (3.7)
(3.7)
If we put 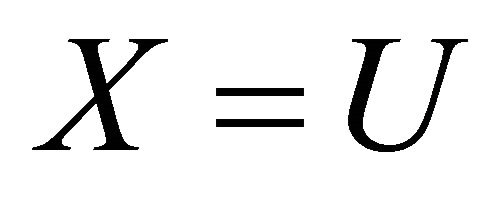 and
and 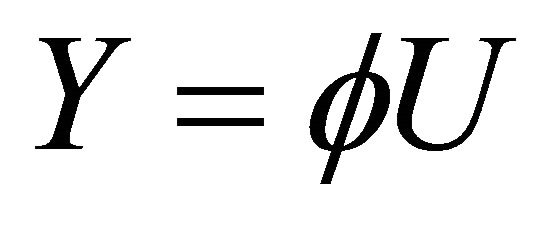 into (3.6) then we have
into (3.6) then we have
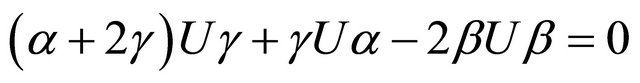 (3.8)
(3.8)
and
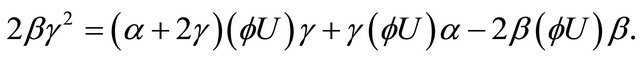 (3.9)
(3.9)
Putting 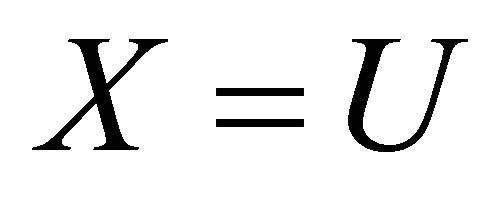 and
and 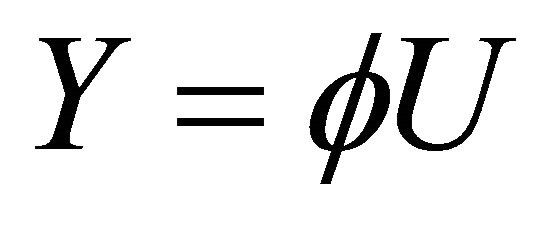 into (3.7), then we obtain
into (3.7), then we obtain
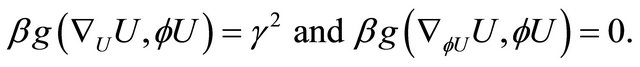 (3.10)
(3.10)
If we differentiate the third of (3.4) covariantly along vector field 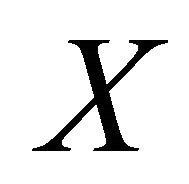 in
in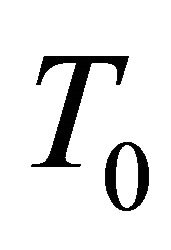 , we obtain
, we obtain
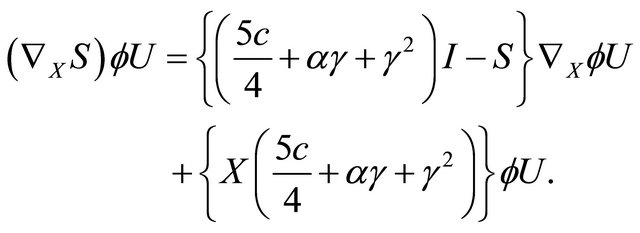 (3.11)
(3.11)
If we take inner product of 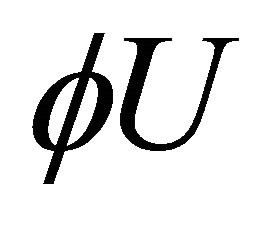 and using (3.4), then we have
and using (3.4), then we have
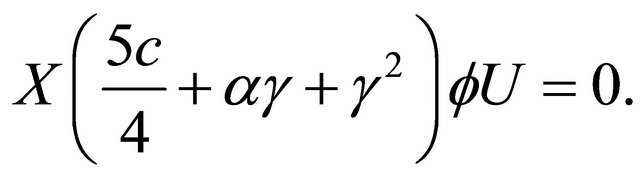 (3.12)
(3.12)
Substituting 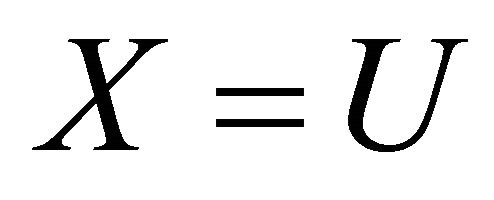 and
and 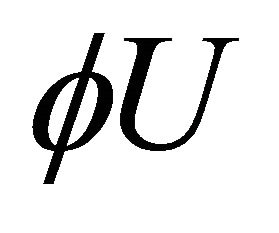 into (3.12), we obtain
into (3.12), we obtain
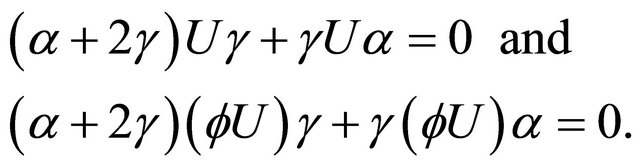 (3.13)
(3.13)
By comparing (3.8) and (3.9) with (3.13), we have 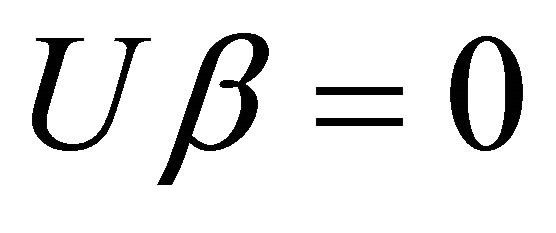 and
and 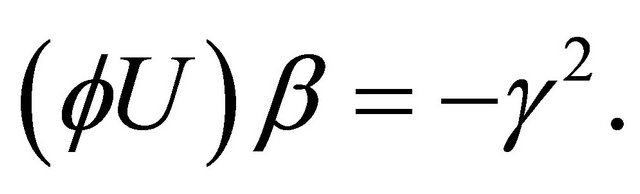 □
□
Lemma 3.3. Under the assumptions of Lemma 3.2, we have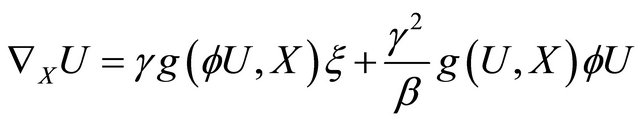 .
.
Proof. Since we have 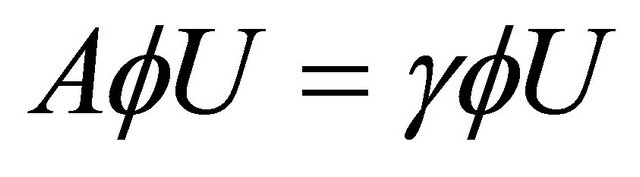 and using (3.7), we get
and using (3.7), we get
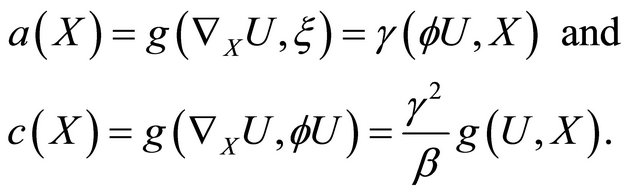 (3.14)
(3.14)
Thus, it follows from (3.14) that
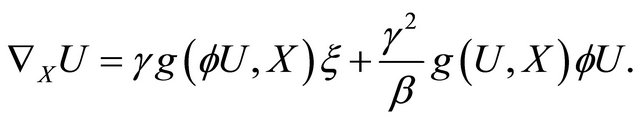 □
□
Lemma 3.4. Under the assumptions of Lemma 3.2, we have 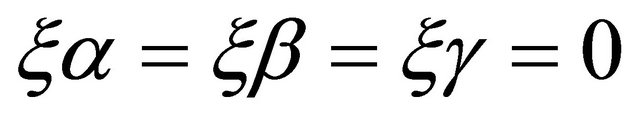 and
and 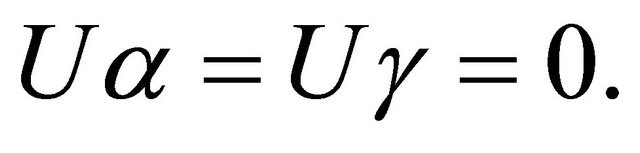
Proof. Differentiating the smooth function 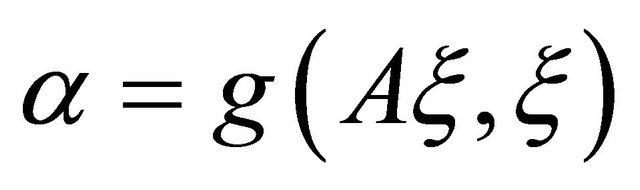 along any vector field
along any vector field 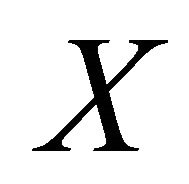 on
on  and using (2.2) and (2.5) and Lemma 3.1, we have
and using (2.2) and (2.5) and Lemma 3.1, we have
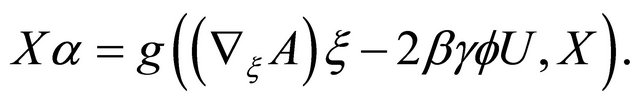 (3.15)
(3.15)
Since we have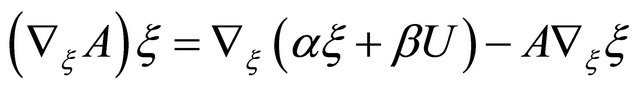 , we see from this equation above that the gradient vector field
, we see from this equation above that the gradient vector field 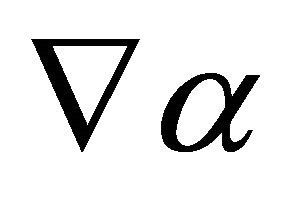 of
of 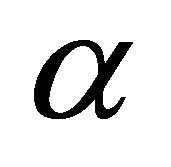 is given by
is given by
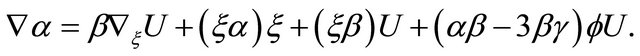
If we put 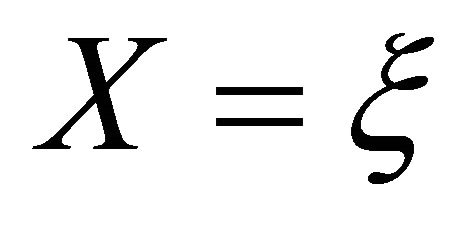 into Lemma 3.3, then we have
into Lemma 3.3, then we have
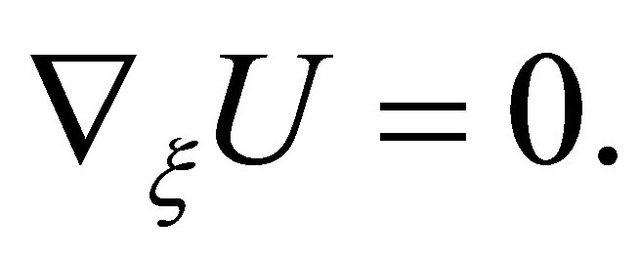 (3.16)
(3.16)
Thus, the above equation is reduced to
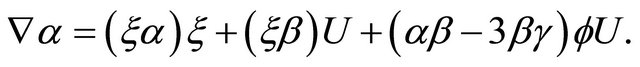 (3.17)
(3.17)
Taking inner product of this equation with 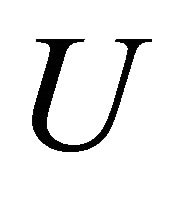 and
and 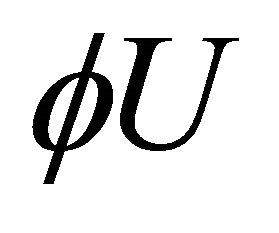 respectively, we obtain
respectively, we obtain
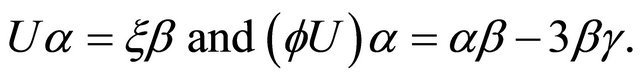 (3.18)
(3.18)
If we differentiate the smooth function 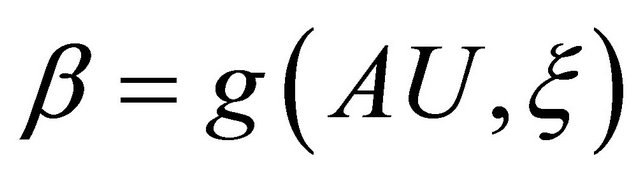 along any vector field
along any vector field  on
on 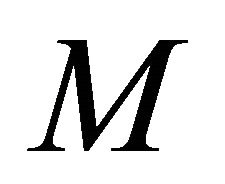 and using (2.2), (2.5) and (2.8) and Lemma 3.2, we have
and using (2.2), (2.5) and (2.8) and Lemma 3.2, we have
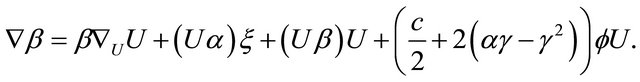 (3.19)
(3.19)
Putting 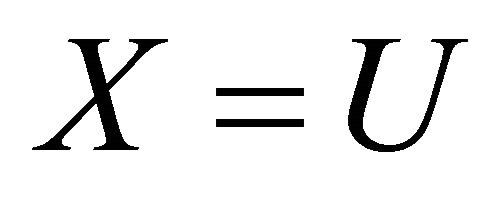 into Lemma 3.3, then we have
into Lemma 3.3, then we have
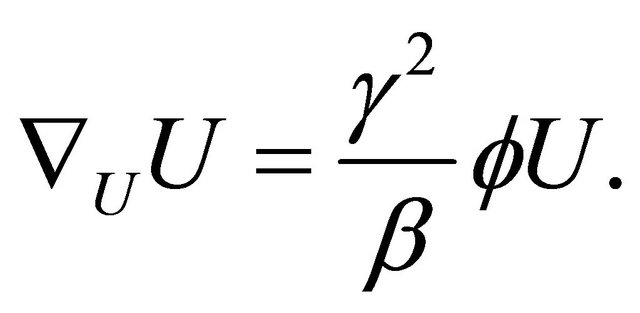 (3.20)
(3.20)
If we substitute (3.20) into (3.19), then we obtain
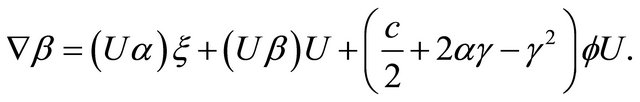 (3.21)
(3.21)
If we take inner product of this equation with 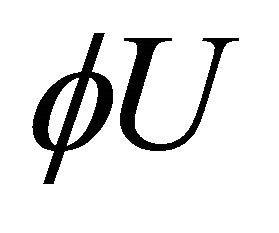 and using
and using 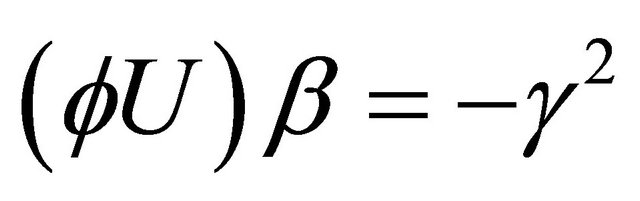 in Lemma 3.2, then we have
in Lemma 3.2, then we have
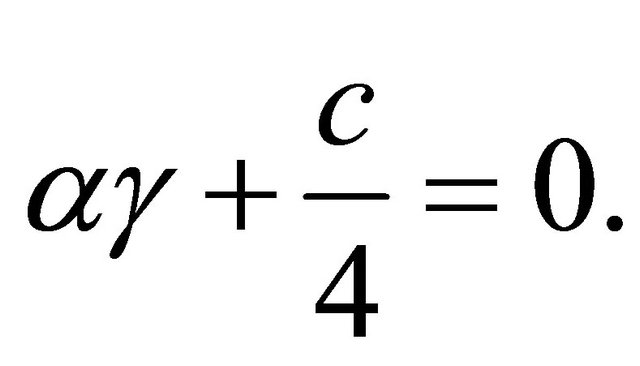 (3.22)
(3.22)
As a similar argument as the above, we can verify that the gradient vector fields of the smooth function
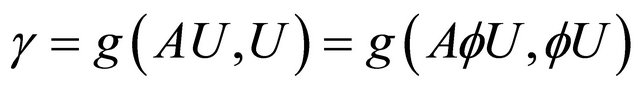 is given respectively by
is given respectively by
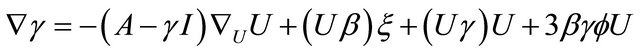 (3.23)
(3.23)
and
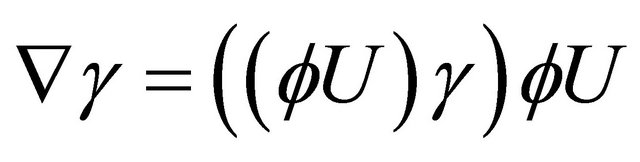 (3.24)
(3.24)
by virtue of (2.3) and Lemma 3.2.
If we substitute (3.24) into (3.23) and make use of (3.20) and Lemma 3.1, then we obtain
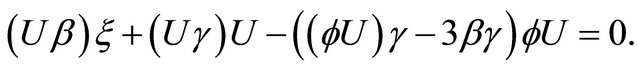 (3.25)
(3.25)
If we take inner product of this equation with 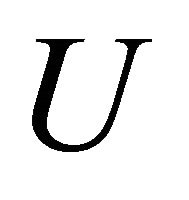 and
and 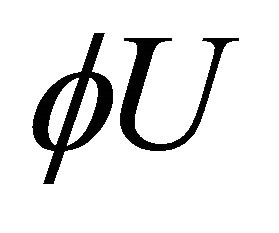 respectively, then we have
respectively, then we have
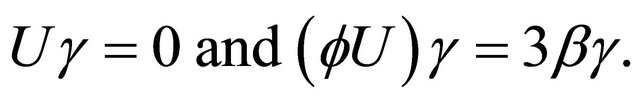 (3.26)
(3.26)
If we substitute (3.26) into (3.14) and take account of (3.21), then we have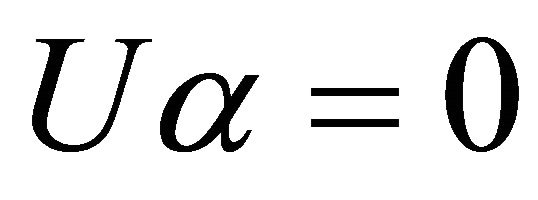 . Also, if we differentiate (3.21) along any vector field
. Also, if we differentiate (3.21) along any vector field , then we have
, then we have
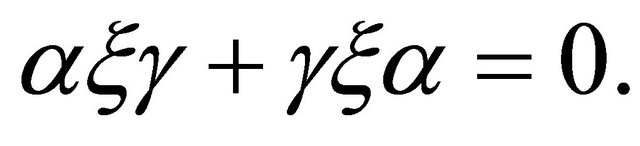 (3.27)
(3.27)
Taking inner product of (3.23) with  and using (3.18), we get
and using (3.18), we get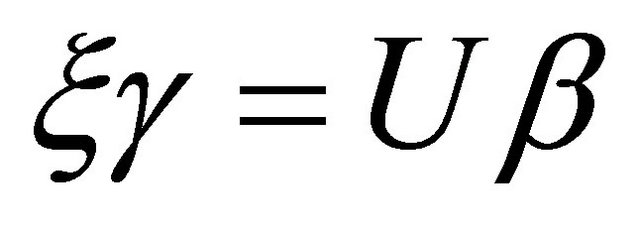 . Since
. Since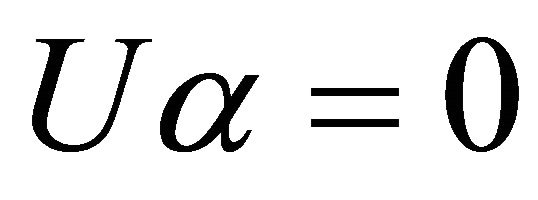 , we see from (3.27) and the first of (3.18) that
, we see from (3.27) and the first of (3.18) that 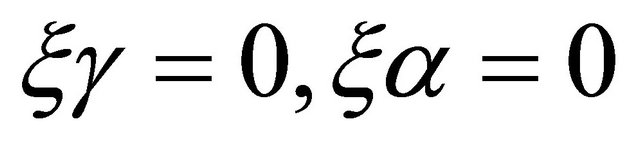 and
and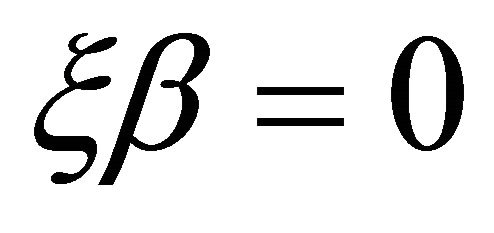 . □
. □
4. Proofs of Theorems
Proof Theorem 1.8. If (1.4) is given in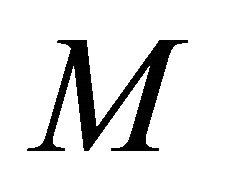 , then we see that Lemma 3.1 holds on
, then we see that Lemma 3.1 holds on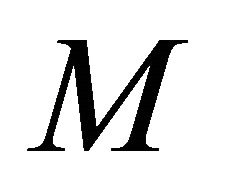 . If we differentiate (1.3) along any vector field
. If we differentiate (1.3) along any vector field 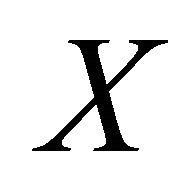 in
in 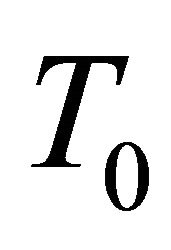 and using (2.3) and (2.8), then we have
and using (2.3) and (2.8), then we have
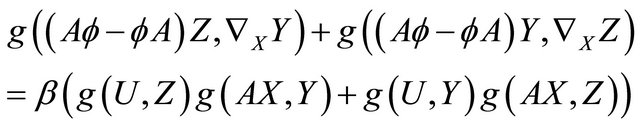 (4.1)
(4.1)
for any vector fields 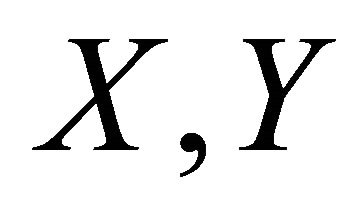 and
and 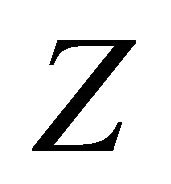 on
on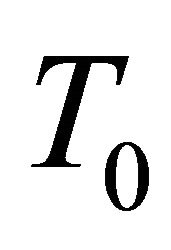 . Putting
. Putting 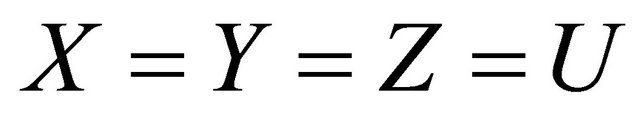 into (4.1) and using Lemma 3.1 and 3.3, then we have
into (4.1) and using Lemma 3.1 and 3.3, then we have
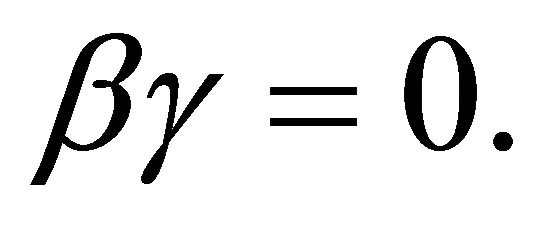 (4.2)
(4.2)
Since  is not empty, we have
is not empty, we have 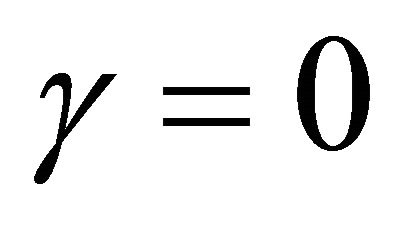 hold on
hold on . It follows from (2.8) and Lemma 3.1 that
. It follows from (2.8) and Lemma 3.1 that
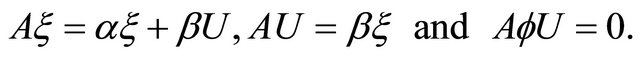
Thus  is locally congruent to ruled real hypersurface (see [7]). □
is locally congruent to ruled real hypersurface (see [7]). □
Proof Theorem 1.9. Assume that the open set 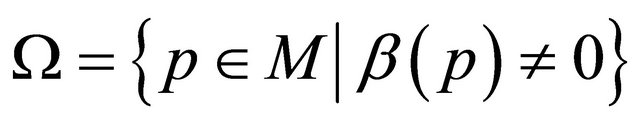 is not empty. Then we consider from Lemma 3.2 and 3.3 that
is not empty. Then we consider from Lemma 3.2 and 3.3 that 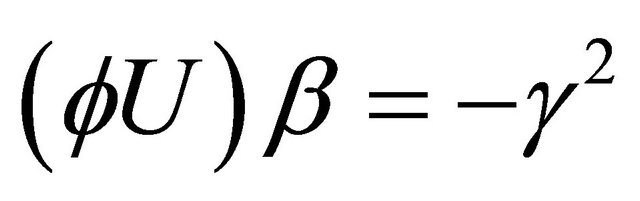 and
and
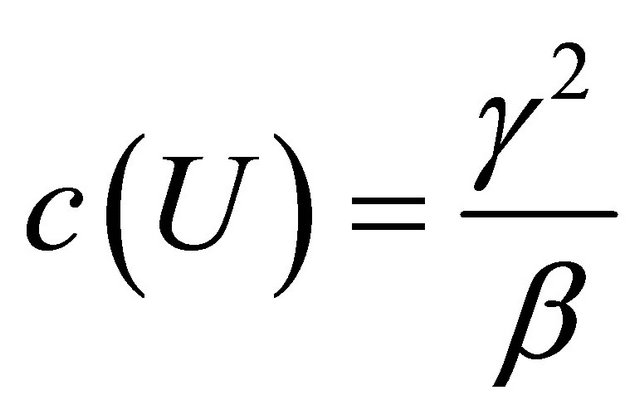 . If we differentiate the smooth function
. If we differentiate the smooth function
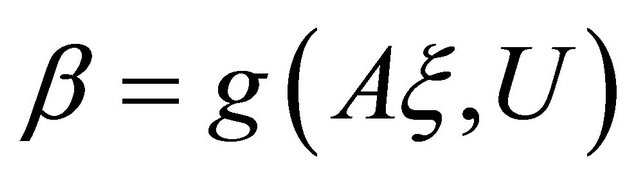 along vector field
along vector field 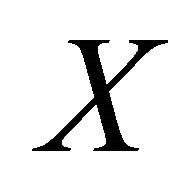 on
on 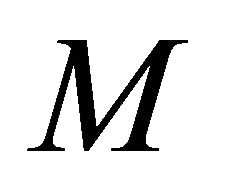 and (2.2), (2.5) and (2.8), we have
and (2.2), (2.5) and (2.8), we have
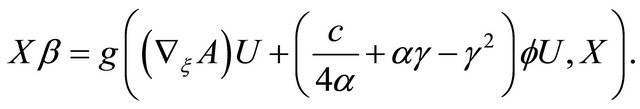 (4.3)
(4.3)
Since we have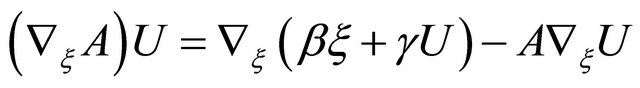 , we see from this equation above that gradient vector field
, we see from this equation above that gradient vector field  of
of  is given by
is given by
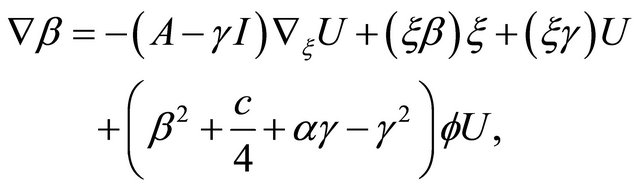 (4.4)
(4.4)
where 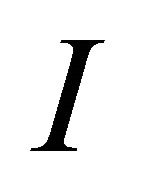 indicates the identity transformation on
indicates the identity transformation on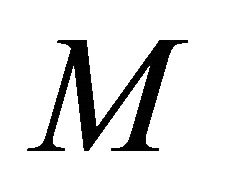 . If we substitute (3.16) into (4.4) and using Lemma 3.4, then we obtain
. If we substitute (3.16) into (4.4) and using Lemma 3.4, then we obtain
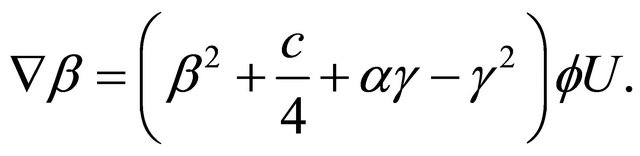 (4.5)
(4.5)
Since we have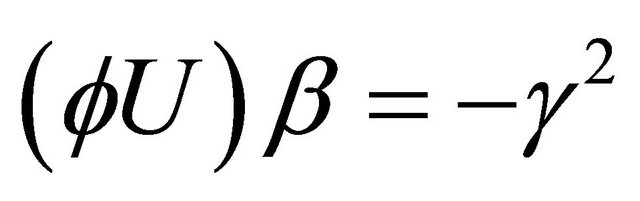 , we get
, we get
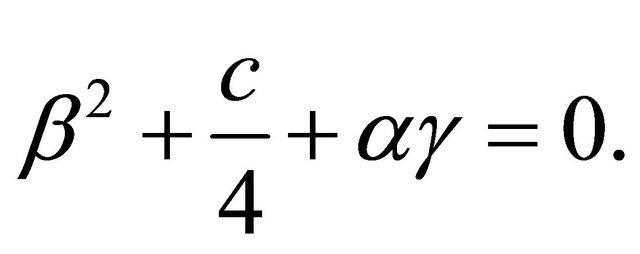 (4.6)
(4.6)
By (4.6) and (3.22), we have 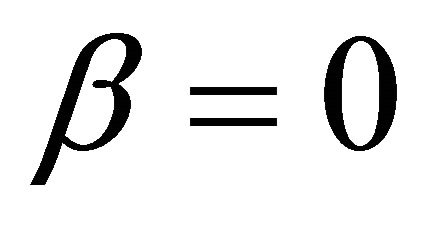 and hence it is a contradiction. Thus the set
and hence it is a contradiction. Thus the set 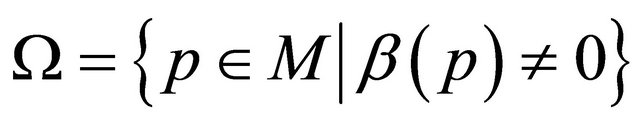 is empty, and hence
is empty, and hence 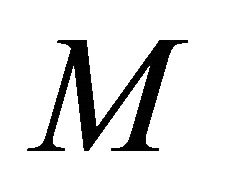 is a Hopf hypersurface. Since
is a Hopf hypersurface. Since 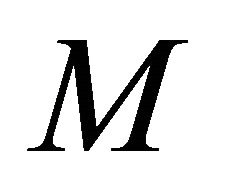 is a Hopf hypersurface, we see from (2.1) and (2.8) that
is a Hopf hypersurface, we see from (2.1) and (2.8) that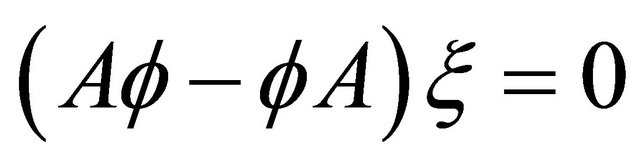 , which together with our assumption (1.4) implies (1.1), that is
, which together with our assumption (1.4) implies (1.1), that is 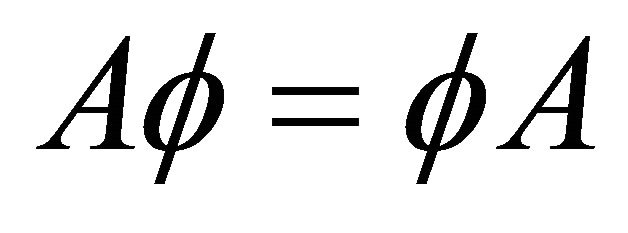 on
on . Thus, Theorem 1.9 shows that
. Thus, Theorem 1.9 shows that  is locally congruent to a real hypersurface of type
is locally congruent to a real hypersurface of type . □
. □
5. Acknowledgements
The authors would like to express their sincere gratitude to the refree who gave them valuable suggestions and comments.
REFERENCES
- U.-H. Ki and Y. J. Suh, “On Real Hypersurfaces of a Complex Space Form,” Mathematical Journal of Okayama University, Vol. 32, 1990, pp. 207-221.
- R. Takagi, “On Homogeneous Real Hypersurfaces in a Complex Projective Space,” Osaka Journal of Mathematics, Vol. 10, 1973, pp. 495-506.
- M. Kimura, “Real Hypersurfaces and Complex Submanifolds in Complex Projective Space,” Transactions of the American Mathematical Society, Vol. 296, 1986, pp. 137- 149. doi:10.1090/S0002-9947-1986-0837803-2
- J. Berndt, “Real Hypersurfaces with Constant Principal Curvatures in Complex Hyperbolic Space,” Journal Für Die Reine und Angewandte Mathematik, Vol. 1989, No. 395, 1989, pp. 132-141.
- M. Okumura, “On Some Real Hypersurfaces of a Complex Projective Space,” Transactions of the American Mathematical Society, Vol. 212, 1975, pp. 355-364. doi:10.1090/S0002-9947-1975-0377787-X
- S. Montiel and A. Romero, “On Some Real Hypersurfaces of a Complex Hyperbolic Space,” Geometriae Dedicata, Vol. 20, No. 2, 1986, pp. 245-261. doi:10.1007/BF00164402
- S. Maeda and T. Adachi, “Integral Curves of Characteristic Vector Fields of Real Hypersurfaces in Nonflat Complex Space Forms,” Geometriae Dedicata, Vol. 123, No. 1, 2006, pp. 65-72. doi:10.1007/s10711-006-9100-1
- W. H. Sohn, “Characterizations of Real Hypersurfaces of Complex Space Forms in Terms of Ricci Operators,” Bulletin of the Korean Mathematical Society, Vol. 44, No. 2007, pp. 195-202. doi:10.4134/BKMS.2007.44.1.195
- S. H. Kon and T. H. Loo, “Real Hypersurfaces of a Complex Space Form with η-Parallel Shape Operator,” Mathematische Zeitschrift, Vol. 269, No. 1-2, 2011, pp. 47-58. doi:10.1007/s00209-010-0715-4
- M. Kimura and S. Maeda, “On Real Hypersurfaces of a Complex Projective Space,” Mathematische Zeitschrift, Vol. 202, No. 3, 1989, pp. 299-311. doi:10.1007/BF01159962
- Y. J. Suh, “On Real Hypersurfaces of a Complex Space Form with η-Parallel Ricci Tensor,” Tsukuba Journal of Mathematics, Vol. 14, 1990, pp. 27-37.
- I.-B. Kim, K. H. Kim and W. H. Sohn, “Characterizations of Real Hypersurfaces in a Complex Space Form,” Canadian Mathematical Bulletin, Vol. 50, 2007, pp. 97-104. doi:10.4153/CMB-2007-009-5

