Advances in Pure Mathematics
Vol.3 No.3(2013), Article ID:31228,4 pages DOI:10.4236/apm.2013.33047
An Elementary Proof of the Mean Inequalities
Department of Statistics, George Mason University, Fairfax, USA
Email: iizmirl2@gmu.edu
Copyright © 2013 Ilhan M. Izmirli. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 24, 2012; revised December 30, 2012; accepted February 3, 2013
Keywords: Pythagorean Means; Arithmetic Mean; Geometric Mean; Harmonic Mean; Identric Mean; Logarithmic Mean
ABSTRACT
In this paper we will extend the well-known chain of inequalities involving the Pythagorean means, namely the harmonic, geometric, and arithmetic means to the more refined chain of inequalities by including the logarithmic and identric means using nothing more than basic calculus. Of course, these results are all well-known and several proofs of them and their generalizations have been given. See [1-6] for more information. Our goal here is to present a unified approach and give the proofs as corollaries of one basic theorem.
1. Pythagorean Means
For a sequence of numbers 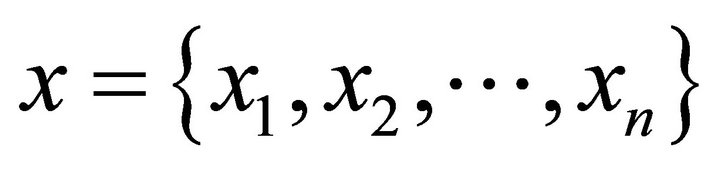 we will let
we will let
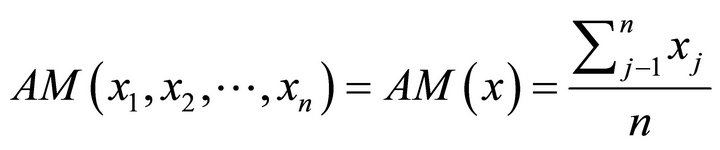

and
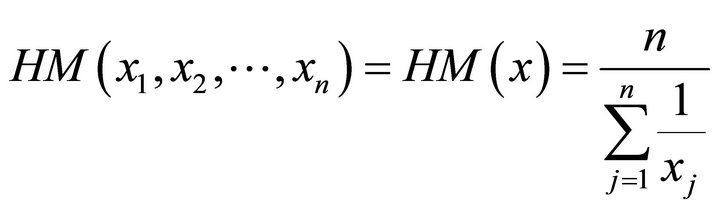
to denote the well known arithmetic, geometric, and harmonic means, also called the Pythagorean means .
.
The Pythagorean means have the obvious properties:
1) 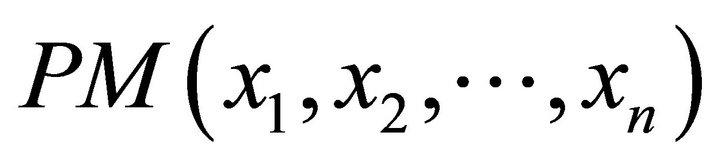 is independent of order 2)
is independent of order 2) 
3) 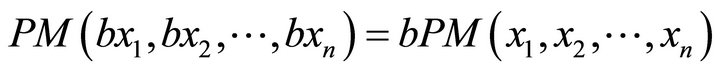
4)  is always a solution of a simple equation. In particular, the arithmetic mean of two numbers
is always a solution of a simple equation. In particular, the arithmetic mean of two numbers 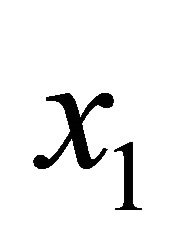 and
and 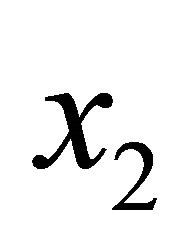 can be defined via the equation
can be defined via the equation
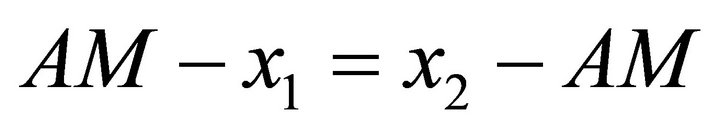
The harmonic mean satisfies the same relation with reciprocals, that is, it is a solution of the equation
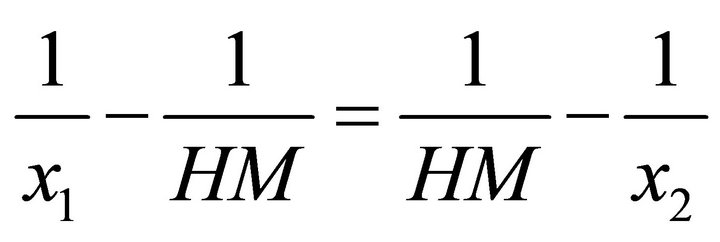
The geometric mean of two numbers 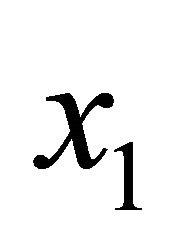 and
and 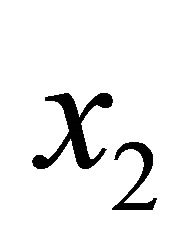 can be visualized as the solution of the equation
can be visualized as the solution of the equation

1) 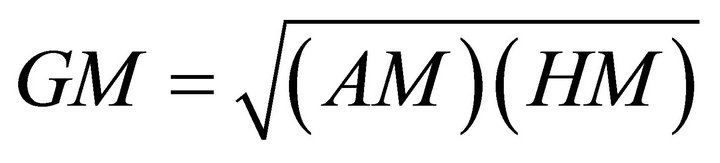
2) 
3) 
This follows because

2. Logarithmic and Identric Means
The logarithmic mean of two non-negative numbers 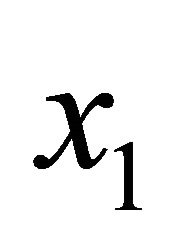 and
and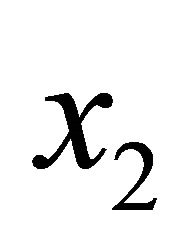 is defined as follows:
is defined as follows:
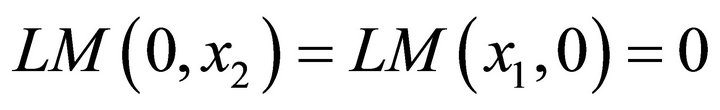
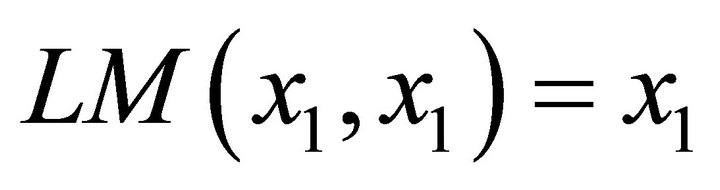
and for positive distinct numbers 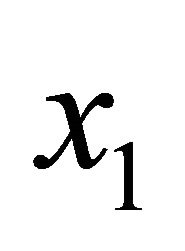 and
and 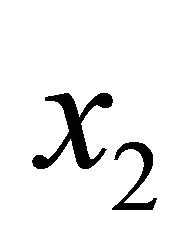
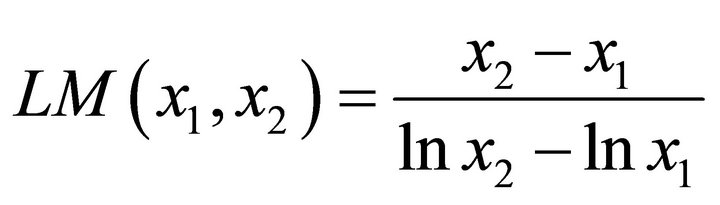
The following are some basic properties of the logarithmic means:
1) Logarithmic mean 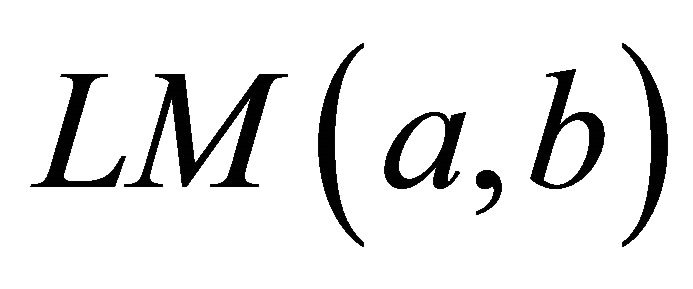 can be thought of as the mean-value of the function
can be thought of as the mean-value of the function 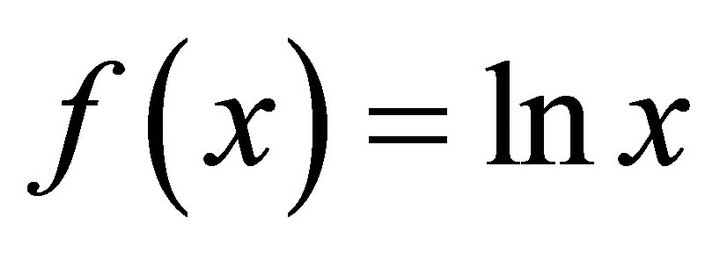 over the interval
over the interval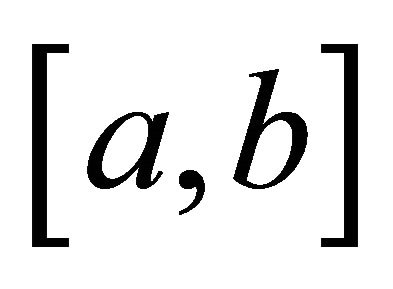 .
.
2) The logarithmic mean can also be interpreted as the area under an exponential curve.
Since
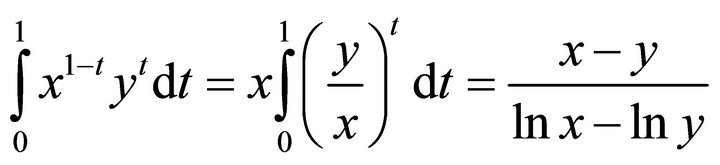
We also have the identity

Using this representation it is easy to show that
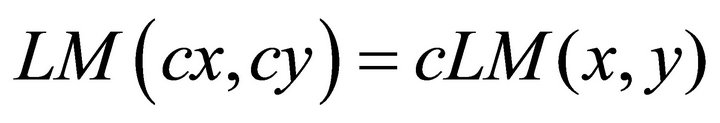
1) We have the identity
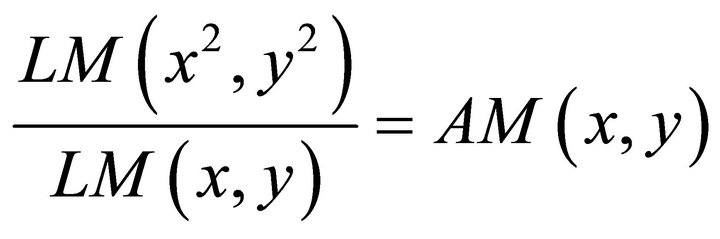
which follows easily:

To define the logarithmic mean of positive numbers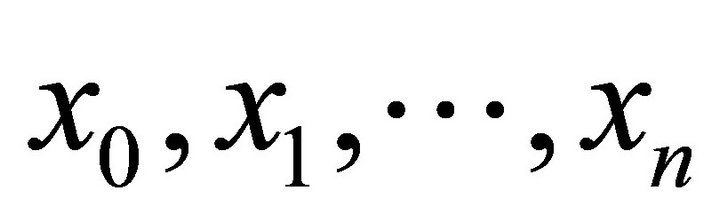 , we first recall the definition of divided differences for a function
, we first recall the definition of divided differences for a function 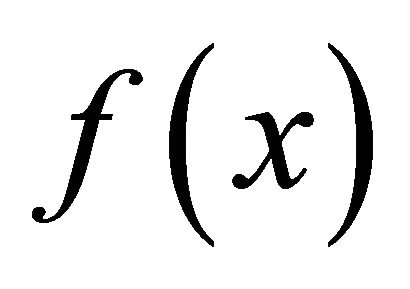 at points
at points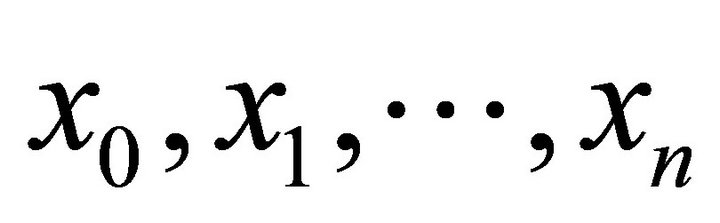 , denoted as
, denoted as
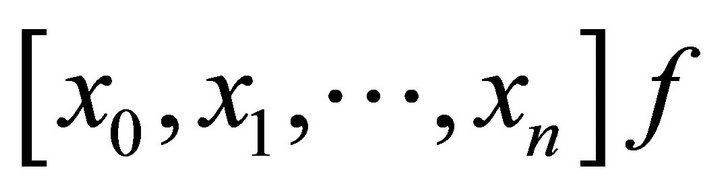
For 

and for  and
and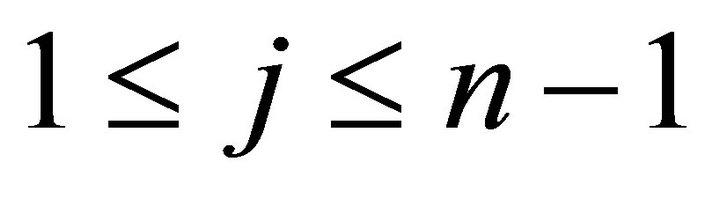 ,
,
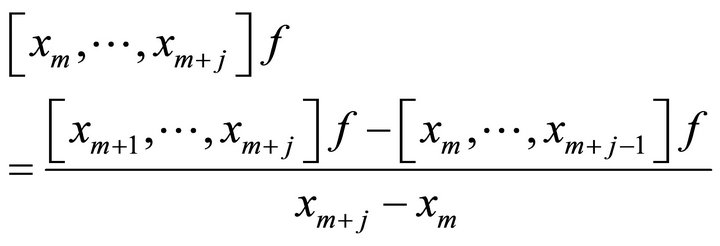
We now define
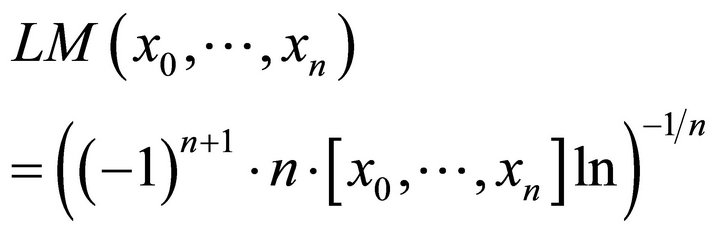
So for example for n = 2, we get
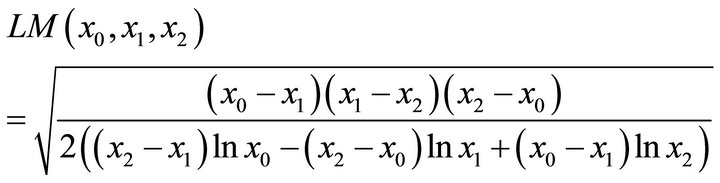
The identric mean of two distinct positive real numbers 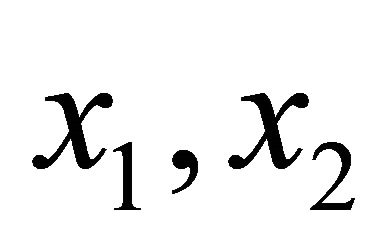 is defined as:
is defined as:
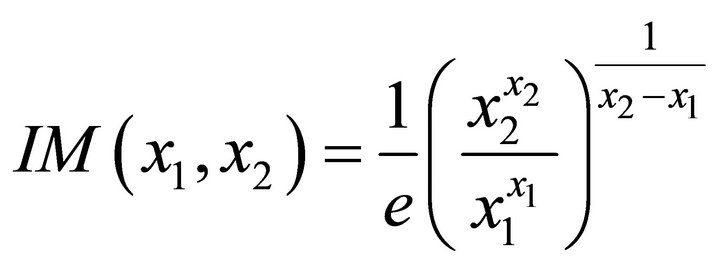
with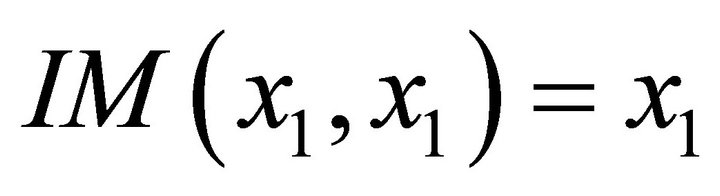 .
.
The slope of the secant line joining the points
 and
and 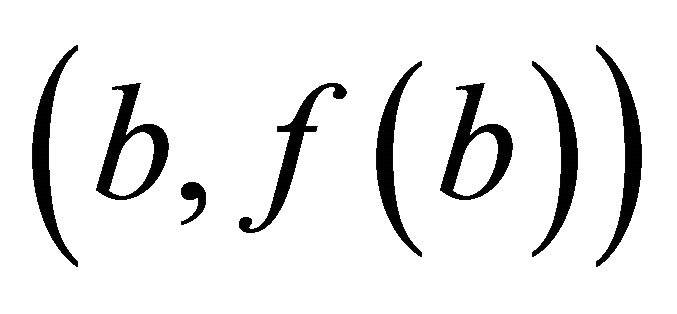 on the graph of the function
on the graph of the function
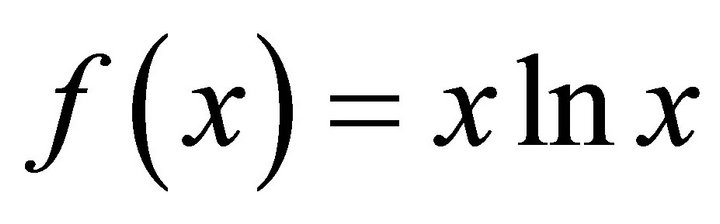 is the natural logarithm of
is the natural logarithm of .
.
It can be generalized to more variables according by the mean value theorem for divided differences.
3. The Main Theorem
Theorem 1. Suppose 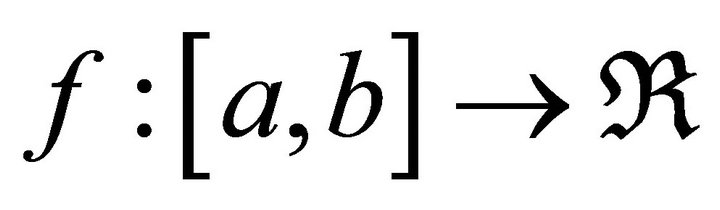 is a function with a strictly increasing derivative. Then
is a function with a strictly increasing derivative. Then

for all 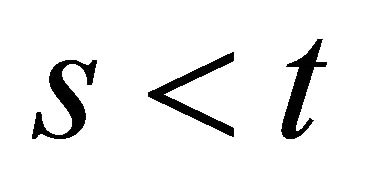 in
in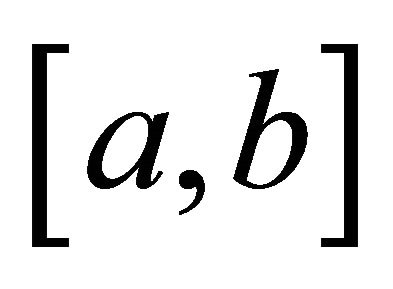 .
.
Let 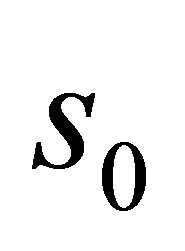 be defined by the equation
be defined by the equation
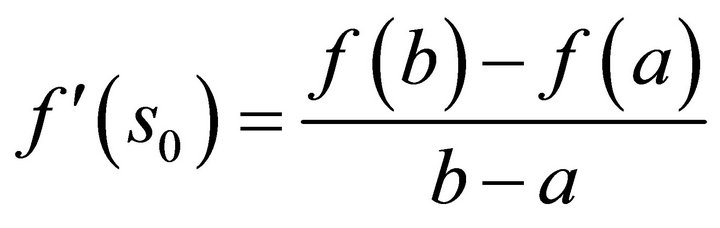
Then,

is the sharpest form of the above inequality.
Proof. By the Mean Value Theorem, for all  in
in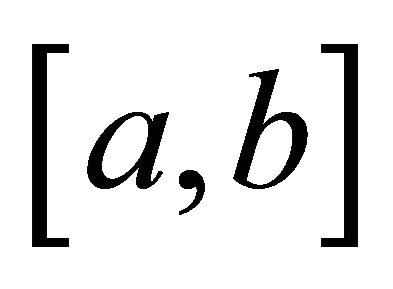 , we have
, we have
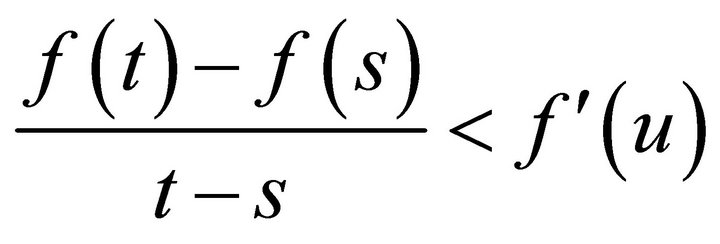
for some ![]() between
between ![]() and
and . Assuming without loss of generality
. Assuming without loss of generality 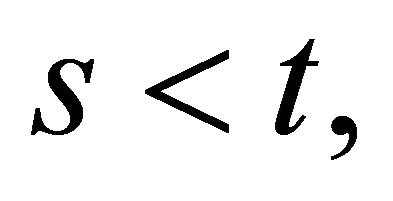 by the assumption of the theorem we have
by the assumption of the theorem we have
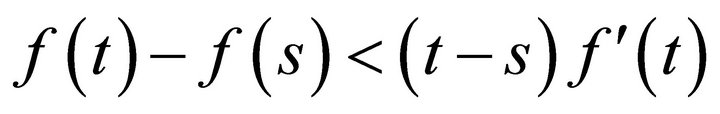
Integrating both sides with respect to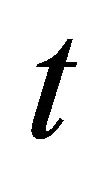 , we have
, we have
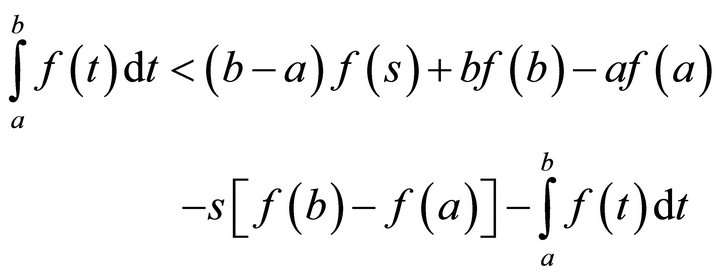
and the inequality of the theorem follows.
Let us now put
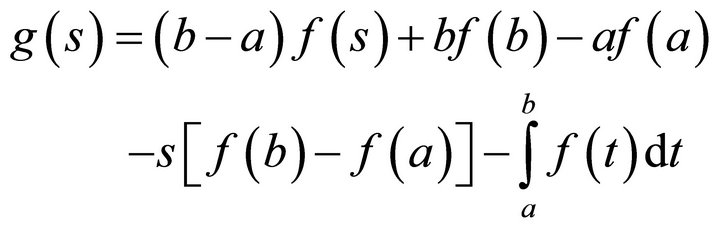
Note that
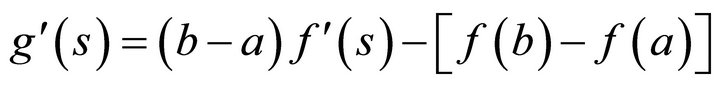
Moreover, since
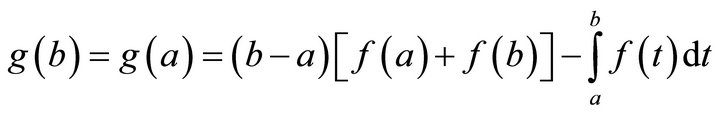
there exists an 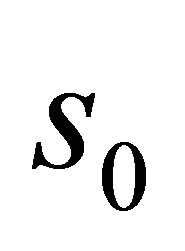 in
in 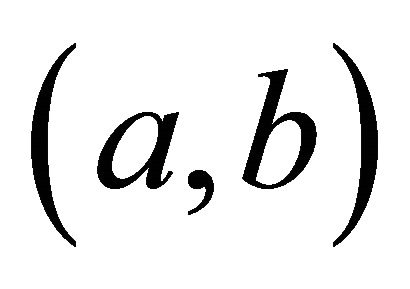 such that
such that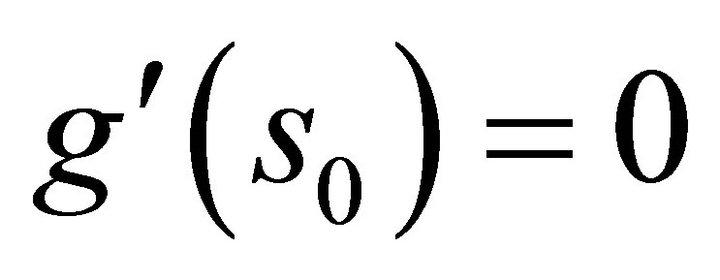 .
.
Since 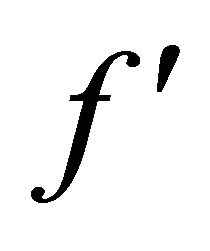 is strictly increasing, we have
is strictly increasing, we have

for 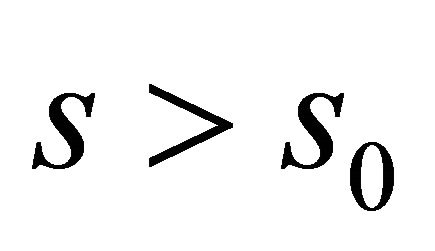
and

for 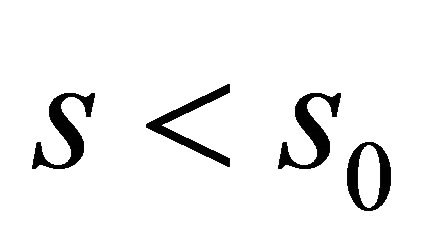
Thus, 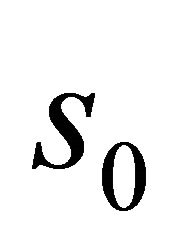 is a minimum of
is a minimum of ![]() and
and 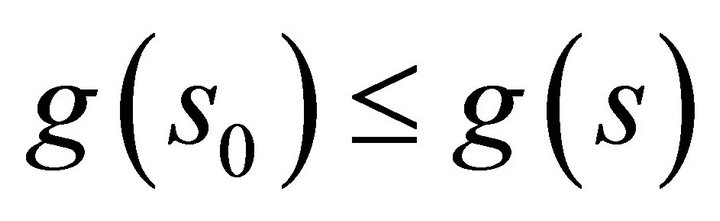 for all
for all 
4. Applications to Mean Inequalities
We will extend the well-known chain of inequalities
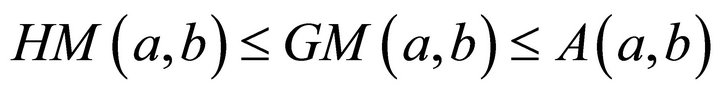
to the more refined
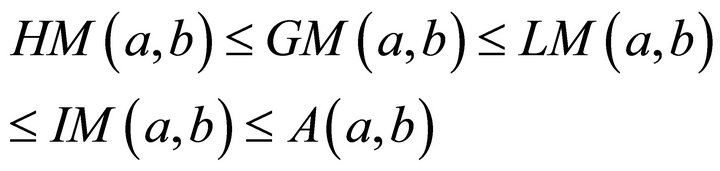
using nothing more than the mean value theorem of differential calculus. All of these are strict inequalities unless, of course, the numbers are the same, in which case all means are equal to the common value of the two numbers.
Let us now assume that 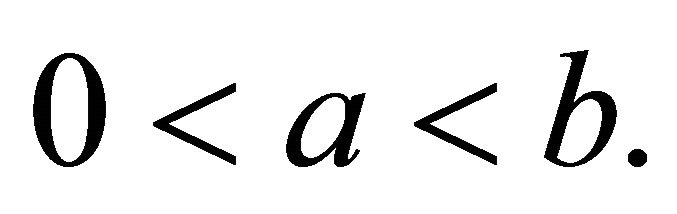
Let us let 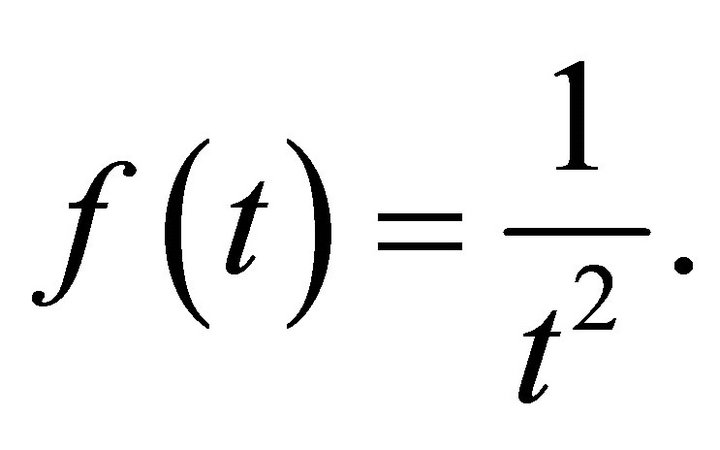 The condition of the Theorem 1 is satisfied. Solving the equation
The condition of the Theorem 1 is satisfied. Solving the equation
we find
where 
Hence the left-hand side of the inequality becomes
Thus we have
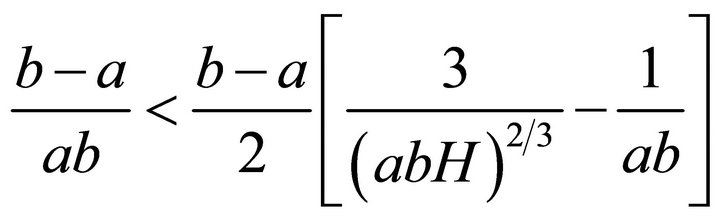
implying
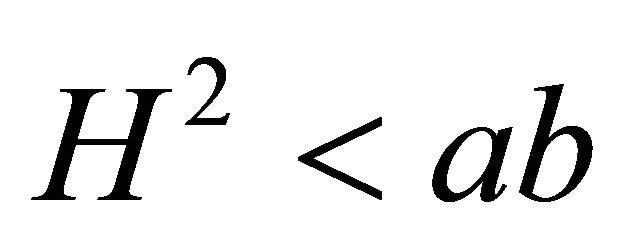
or
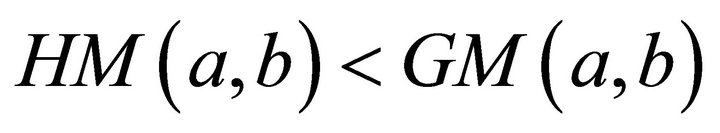
Let us let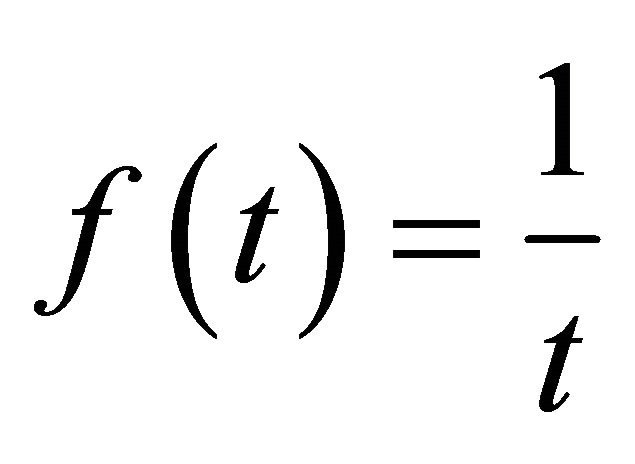 . The condition of Theorem 1 is satisfied. We can easily compute the
. The condition of Theorem 1 is satisfied. We can easily compute the  of the theorem from the equation
of the theorem from the equation
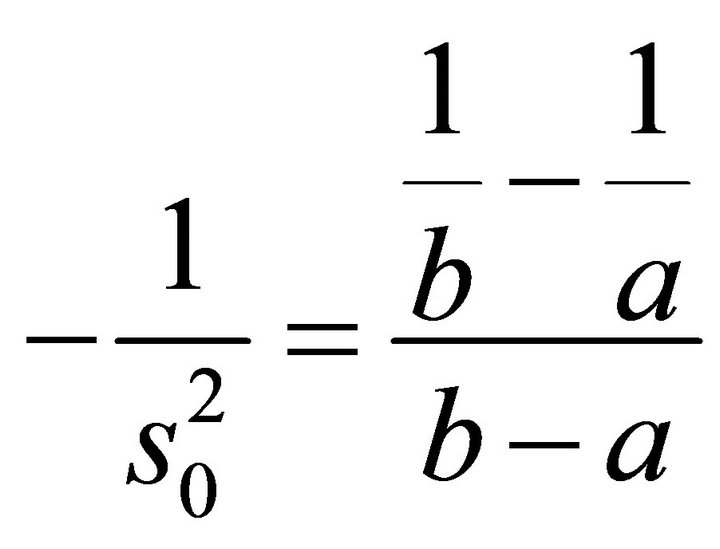
as
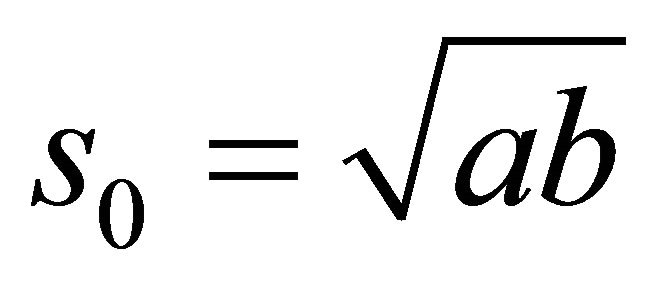
Our inequality becomes
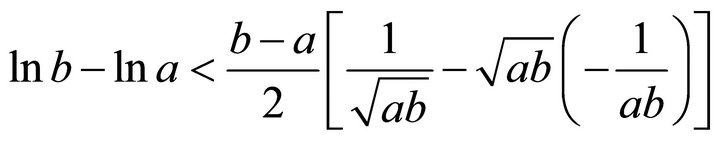
Implying,
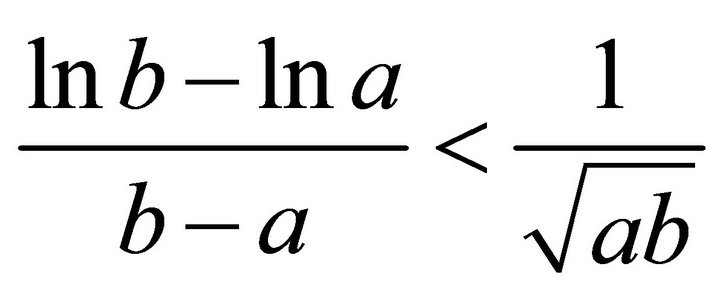
that is
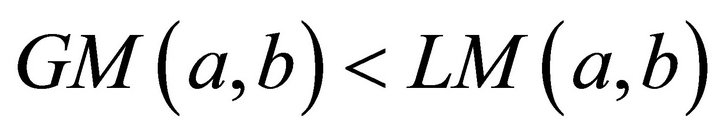
Now let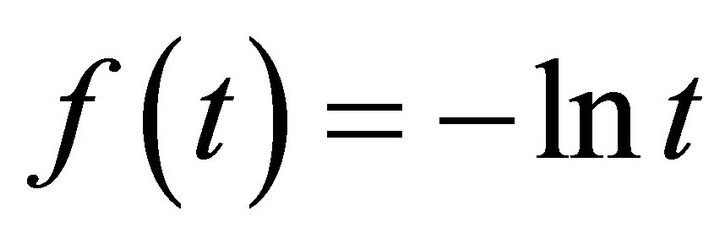 . Again the condition of Theorem 1 is satisfied. The
. Again the condition of Theorem 1 is satisfied. The 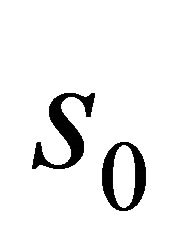 of the theorem can be computed from the equation
of the theorem can be computed from the equation

as
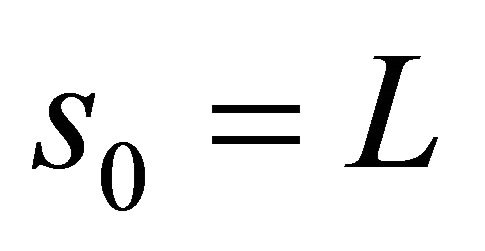
where 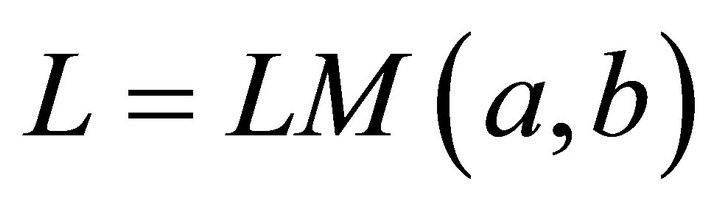
Since

Thus,

where 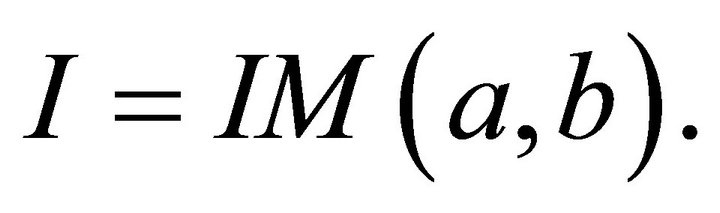
Consequently our inequality becomes
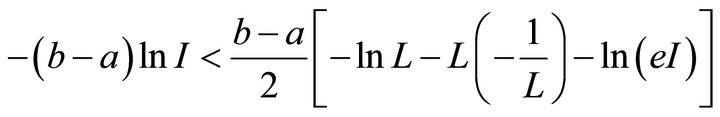
implying

that is,
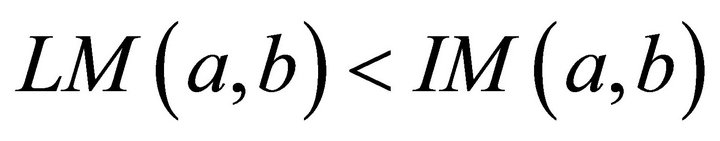
Finally, let us put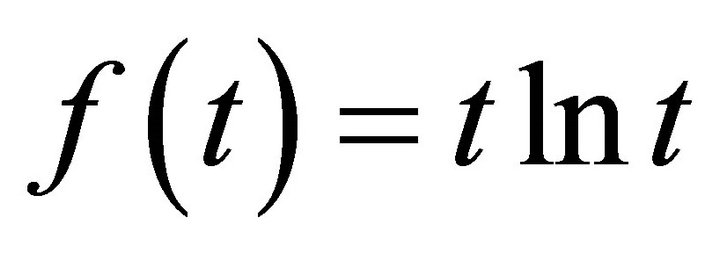 . Again the condition of Theorem 1 is satisfied. Since in this case
. Again the condition of Theorem 1 is satisfied. Since in this case
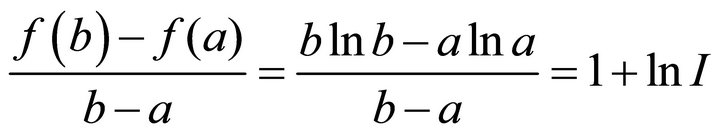
the  of the theorem can be computed as
of the theorem can be computed as

The right-hand side of the inequality becomes
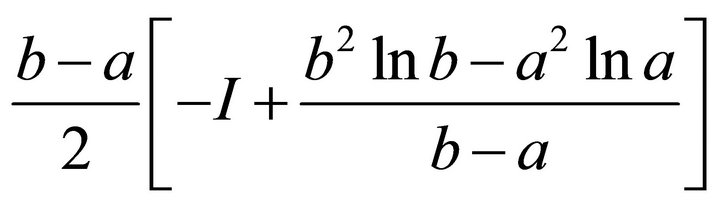
The integral on the left-hand side of our inequality yields
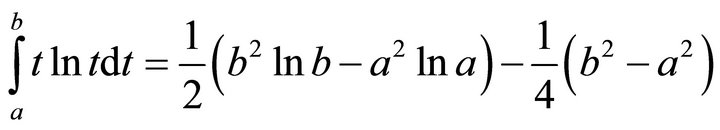
implying

or
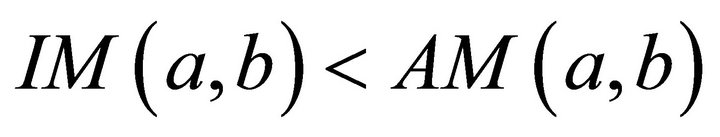
Thus, we now have for 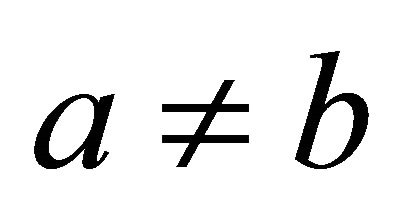
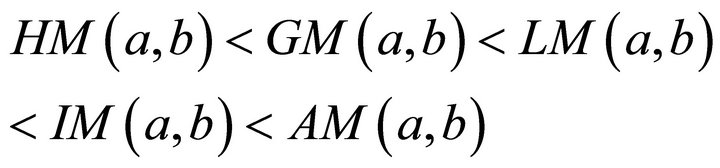
REFERENCES
- G. H. Hardy, J. E. Littlewood and G. Pólya, “Inequalities,” 2nd Edition, Cambridge University Press, London, 1964.
- B. C. Carlson, “A Hypergeometric Mean Value,” Proceedings of the American Mathematical Society, Vol. 16, No. 4, 1965, pp. 759-766. doi:10.1090/S0002-9939-1965-0179389-6
- B. C. Carlson and M. D. Tobey, “A Property of the Hypergeometric Mean Value,” Proceedings of the American Mathematical Society, Vol. 19, No. 2, 1968, pp. 255-262. doi:10.1090/S0002-9939-1968-0222349-X
- E. F. Beckenbach and R. Bellman, “Inequalities,” 3rd Edition, Springer-Verlag, Berlin and New York, 1971.
- H. Alzer, “Übereinen Wert, der zwischendemgeometrischen und demartihmetischen Mittelzweier Zahlenliegt,” Elemente der Mathematik, Vol. 40, 1985, pp. 22-24.
- H. Alzer, “Ungleichungenfür
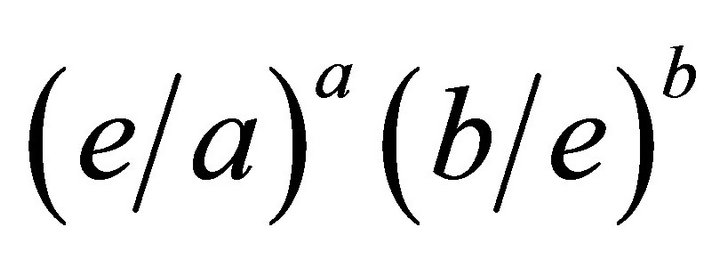 ,” Elemente der Mathematik, Vol. 40, 1985, pp. 120-123.
,” Elemente der Mathematik, Vol. 40, 1985, pp. 120-123.

