Advances in Pure Mathematics
Vol.3 No.1A(2013), Article ID:27539,6 pages DOI:10.4236/apm.2013.31A024
Poincaré Problem for Nonlinear Elliptic Equations of Second Order in Unbounded Domains
LMAM, School of Mathematical Sciences, Peking University, Beijing, China
Email: wengc@math.pku.edu.cn
Received September 27, 2012; revised November 2, 2012; accepted November 10, 2012
Keywords: Poincaré Boundary Value Problem; Nonlinear Elliptic Equations; Unbounded Domains
ABSTRACT
In [1], I. N. Vekua propose the Poincaré problem for some second order elliptic equations, but it can not be solved. In [2], the authors discussed the boundary value problem for nonlinear elliptic equations of second order in some bounded domains. In this article, the Poincaré boundary value problem for general nonlinear elliptic equations of second order in unbounded multiply connected domains have been completely investigated. We first provide the formulation of the above boundary value problem and corresponding modified well posed-ness. Next we obtain the representation theorem and a priori estimates of solutions for the modified problem. Finally by the above estimates of solutions and the Schauder fixed-point theorem, the solvability results of the above Poincaré problem for the nonlinear elliptic equations of second order can be obtained. The above problem possesses many applications in mechanics and physics and so on.
1. Formulation of the Poincaré Boundary Value Problem
Let D be an 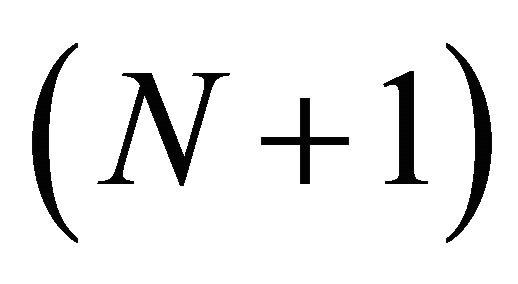 -connected domain including the infinite point with the boundary
-connected domain including the infinite point with the boundary 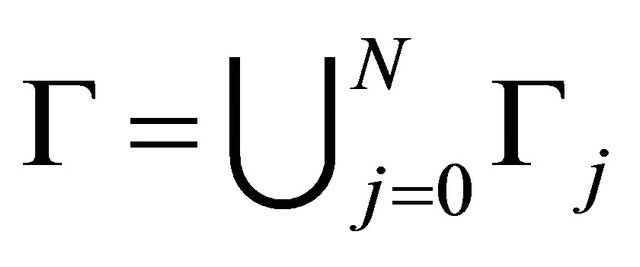 in
in where
where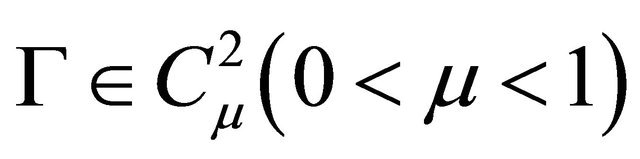 . Without loss of generality, we assume that D is a circular domain in
. Without loss of generality, we assume that D is a circular domain in , where the boundary consists of
, where the boundary consists of 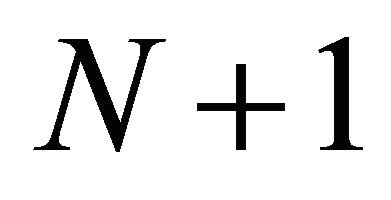 circles
circles ,
, 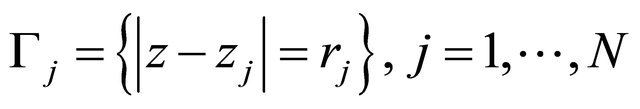 and
and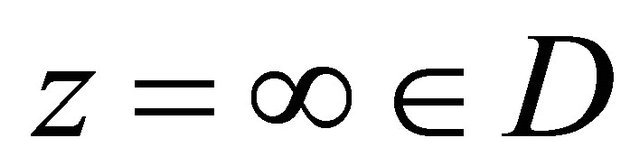 . In this article, the notations are as the same in References [1-8]. We consider the second order equation in the complex form
. In this article, the notations are as the same in References [1-8]. We consider the second order equation in the complex form
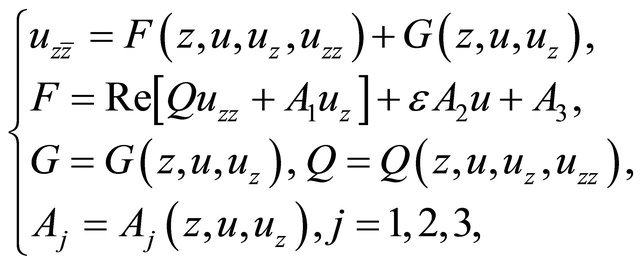 (1.1)
(1.1)
satisfying the following conditions.
Condition C. 1)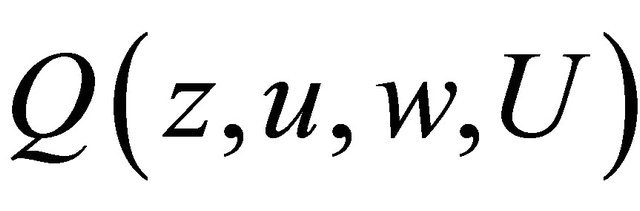 ,
, 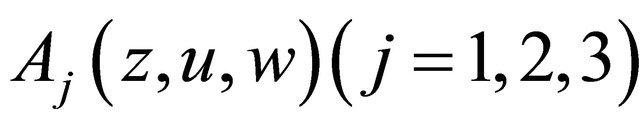 are continuous in
are continuous in  for almost every point
for almost every point 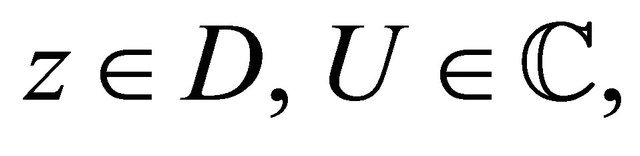 and
and 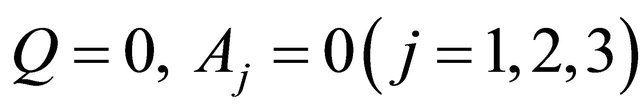 for
for 
2) The above functions are measurable in  for all continuous functions
for all continuous functions 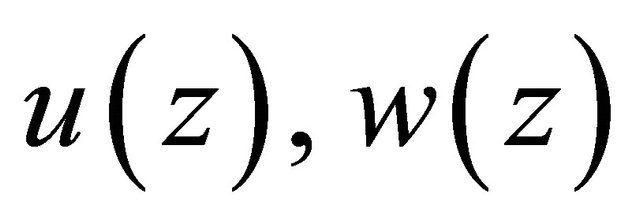 in
in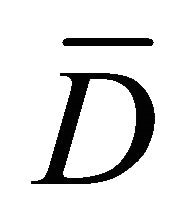 , and satisfy
, and satisfy
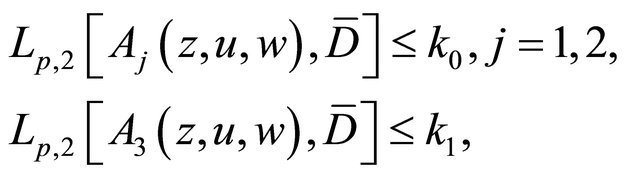 (1.2)
(1.2)
in which 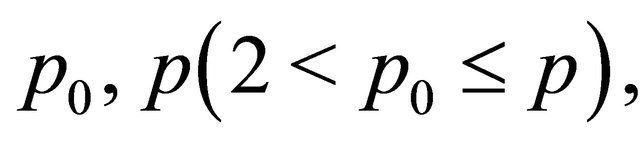
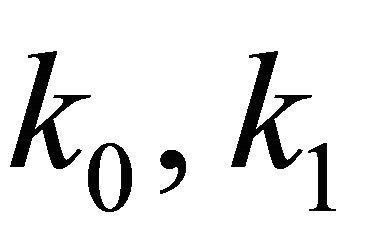 are non-negative constants.
are non-negative constants.
3) The Equation (1.1) satisfies the uniform ellipticity condition, namely for any number  and w, U1,
and w, U1,  the inequality
the inequality
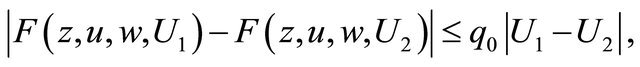
for almost every point  holds, where
holds, where 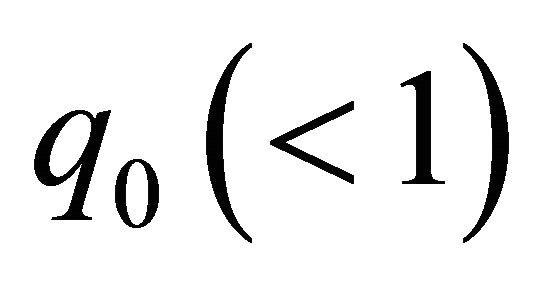 is a non-negative constant.
is a non-negative constant.
4) For any function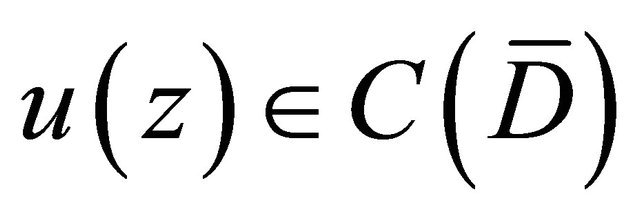 ,
, 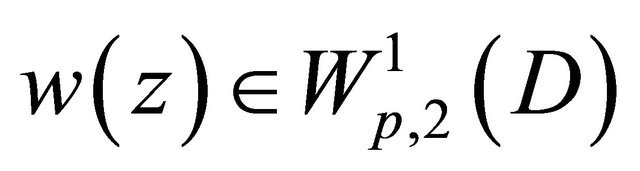 ,
, 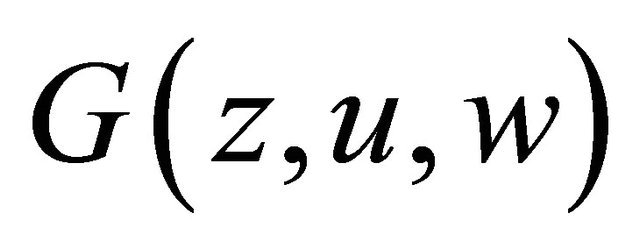 satisfies the condition
satisfies the condition
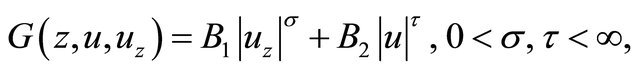
in which 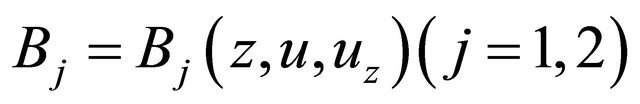 satisfy the condition
satisfy the condition
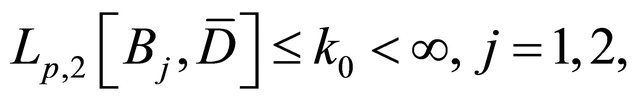 (1.3)
(1.3)
with a non-negative constant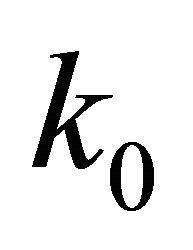 .
.
Now, we formulate the Poincaré boundary value problem as follows.
Problem P. In the domain D, find a solution 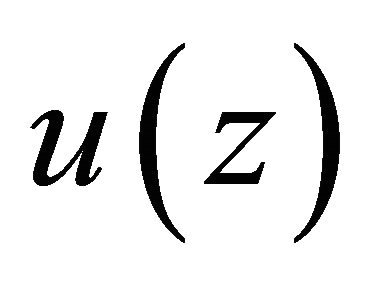 of Equation (1.1), which is continuously differentiable in
of Equation (1.1), which is continuously differentiable in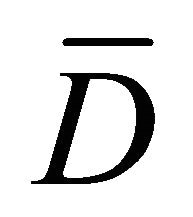 , and satisfies the boundary condition
, and satisfies the boundary condition
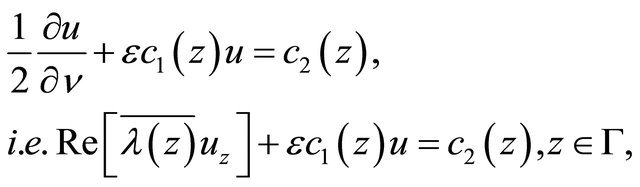 (1.4)
(1.4)
in which 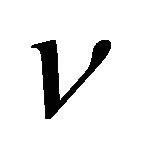 is any unit vector at every point on
is any unit vector at every point on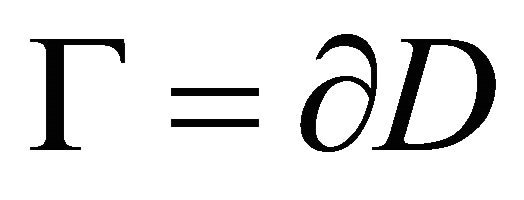 ,
, 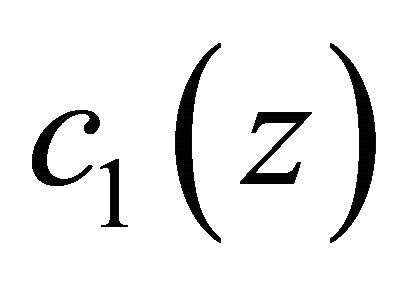
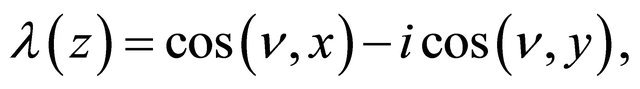 and
and 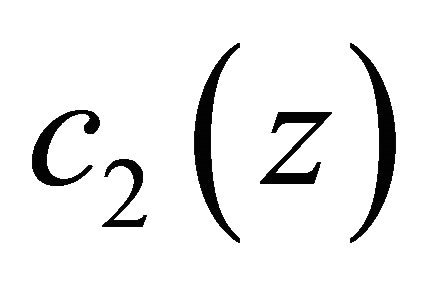 are known functions satisfying the conditions
are known functions satisfying the conditions
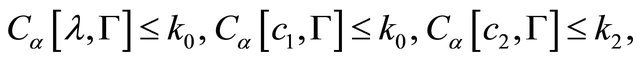 (1.5)
(1.5)
where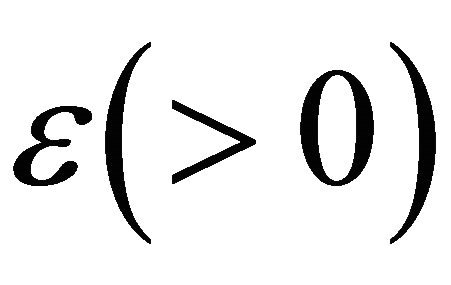 ,
,  ,
, 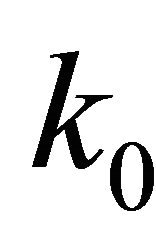 ,
, 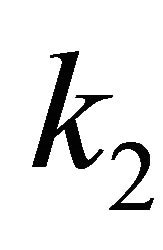 are non-negative constants.
are non-negative constants.
If 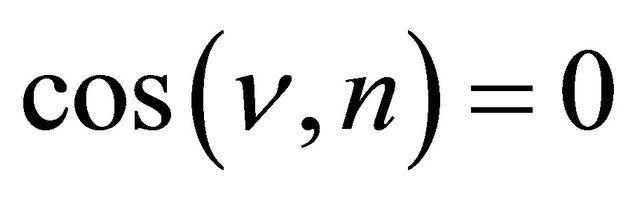 and
and 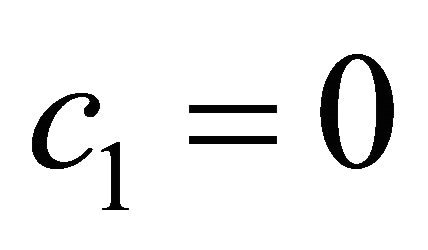 on
on , where n is the outward normal vector on
, where n is the outward normal vector on , then Problem P is the Dirichlet boundary value problem (Problem D). If
, then Problem P is the Dirichlet boundary value problem (Problem D). If 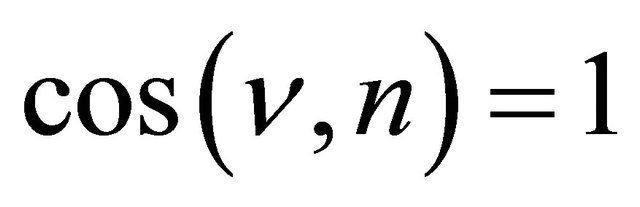 and
and 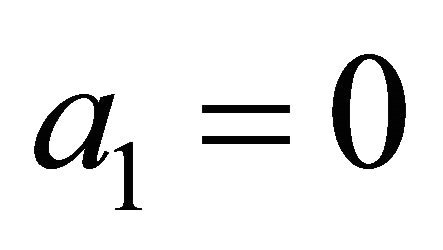 on
on , then Problem P is the Neumann boundary value problem (Problem N), and if
, then Problem P is the Neumann boundary value problem (Problem N), and if , and
, and 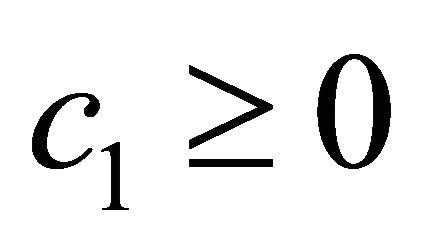 on
on , then Problem P is the regular oblique derivative problem, i.e. the third boundary value problem (Problem III or O). Now the directional derivative may be arbitrary, hence the boundary condition is very general.
, then Problem P is the regular oblique derivative problem, i.e. the third boundary value problem (Problem III or O). Now the directional derivative may be arbitrary, hence the boundary condition is very general.
The integer
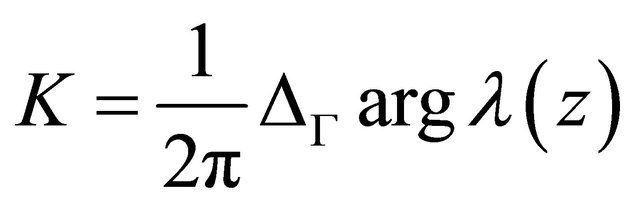
is called the index of Problem P. When the index 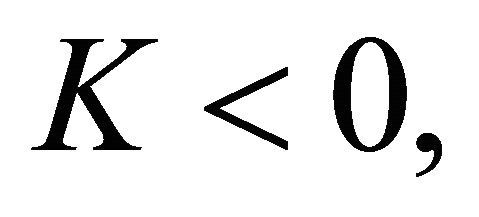 Problem P may not be solvable, and when
Problem P may not be solvable, and when 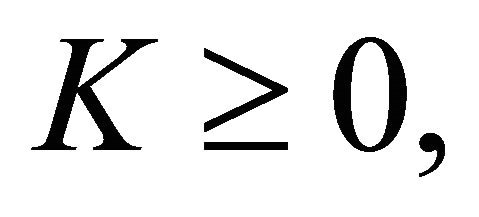 the solution of Problem P is not necessarily unique. Hence we consider the well-posedness of Problem P with modified boundary conditions.
the solution of Problem P is not necessarily unique. Hence we consider the well-posedness of Problem P with modified boundary conditions.
Problem Q. Find a continuous solution 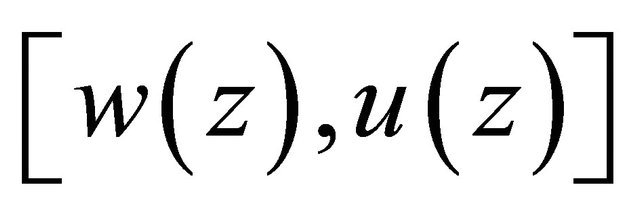 of the complex equation
of the complex equation
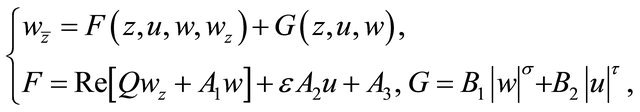 (1.6)
(1.6)
satisfying the boundary condition
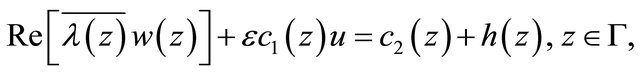 (1.7)
(1.7)
and the relation
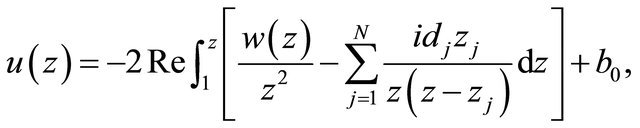 (1.8)
(1.8)
where 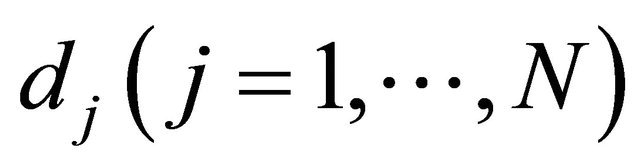 are appropriate real constants such that the function determined by the integral in (1.8) is single-valued in
are appropriate real constants such that the function determined by the integral in (1.8) is single-valued in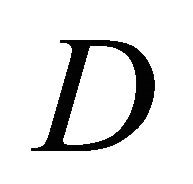 , and the undetermined function
, and the undetermined function 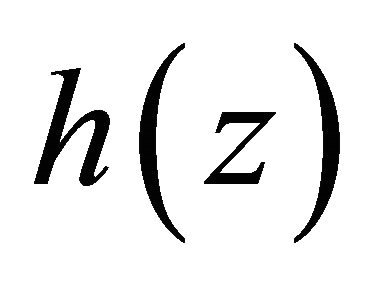 is as stated in
is as stated in
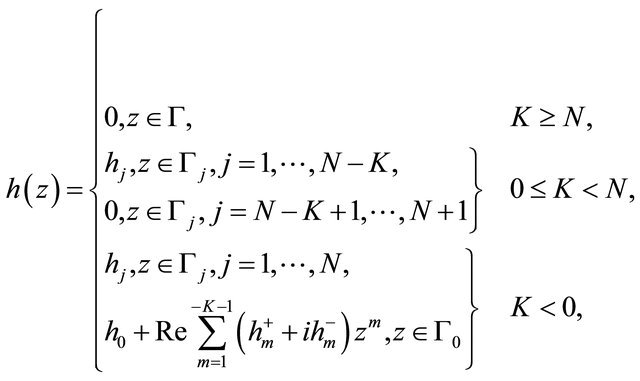
in which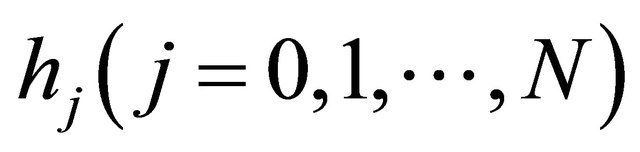 ,
, 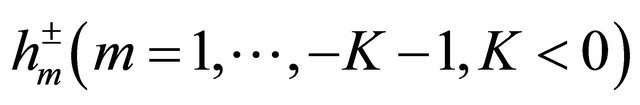 are unknown real constants to be determined appropriately. In addition, for
are unknown real constants to be determined appropriately. In addition, for 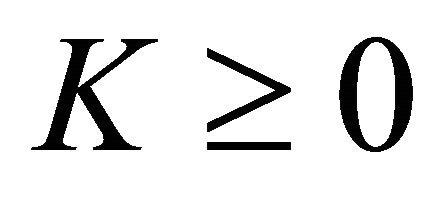 the solution
the solution 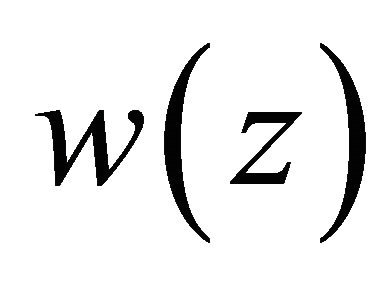 is assumed to satisfy the point conditions
is assumed to satisfy the point conditions
 (1.9)
(1.9)
where

are distinct points, and 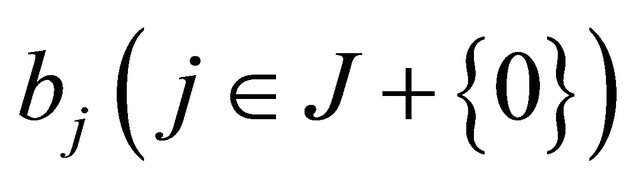 are all real constants satisfying the conditions
are all real constants satisfying the conditions
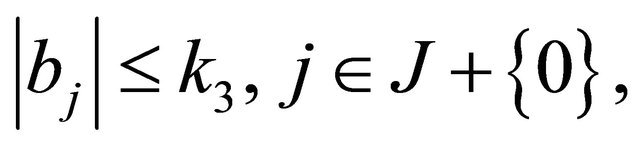 (1.10)
(1.10)
for a non-negative constant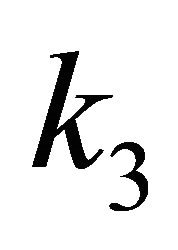 .
.
2. Estimates of Solutions for the Poincaré Boundary Value Problem
First of all, we give a prior estimate of solutions of Problem Q for (1.6).
Theorem 2.1. Suppose that Condition C holds and ε = 0 in (1.6) and (1.7). Then any solution 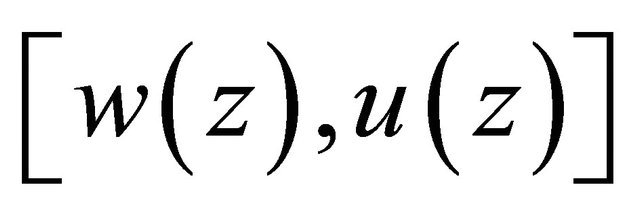 of Problem Q for (1.6) satisfies the estimates
of Problem Q for (1.6) satisfies the estimates
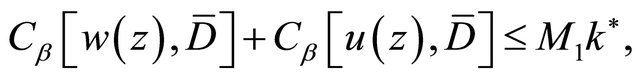 (2.1)
(2.1)
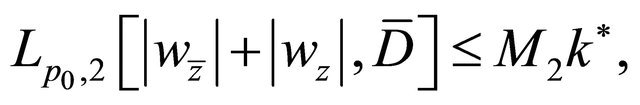 (2.2)
(2.2)
in which
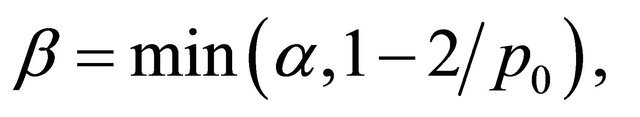
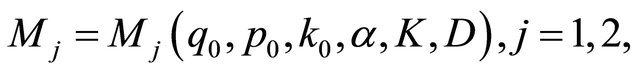
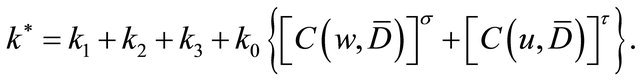
Proof. Noting that the solution 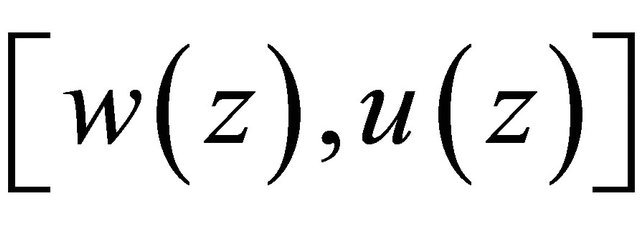 of Problem Q satisfies the equation and boundary conditions
of Problem Q satisfies the equation and boundary conditions
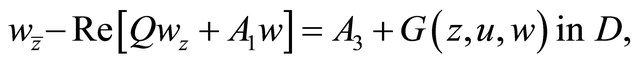 (2.3)
(2.3)
 (2.4)
(2.4)
 (2.5)
(2.5)
according to the method in the proof of Theorem 4.3, Chapter II, [2] or Theorem 2.2.1, [5], we can derive that the solution 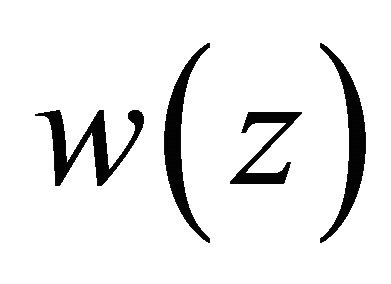 satisfies the estimates
satisfies the estimates
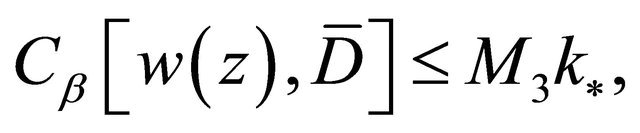 (2.6)
(2.6)
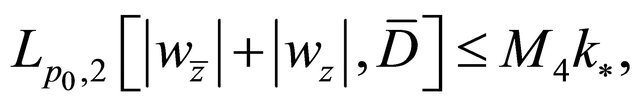 (2.7)
(2.7)
where

and

From (1.8), it follows that
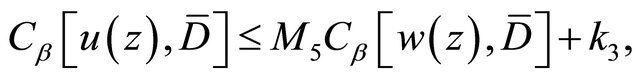 (2.8)
(2.8)
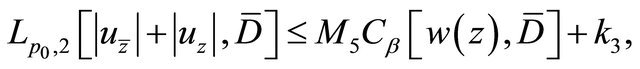 (2.9)
(2.9)
in which 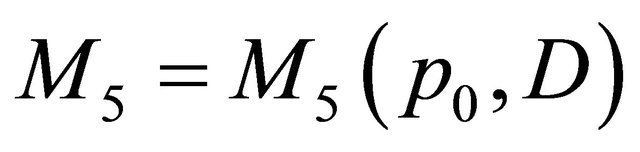 is a non-negative constant. Moreover, it is easy to see that
is a non-negative constant. Moreover, it is easy to see that
 (2.10)
(2.10)
Combining (2.6)-(2.10), the estimates (2.1) and (2.2) are obtained.
Theorem 2.2. Let the Equation (1.6) satisfy Condition C and 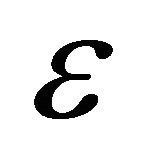 in (1.6)-(1.7) be small enough. Then any solution
in (1.6)-(1.7) be small enough. Then any solution 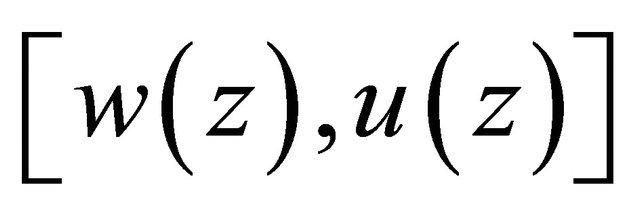 of Problem Q for (1.6) satisfies the estimates
of Problem Q for (1.6) satisfies the estimates
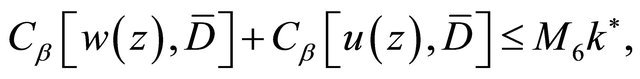 (2.11)
(2.11)
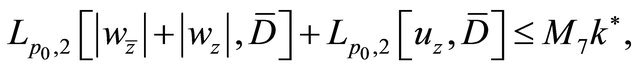 (2.12)
(2.12)
here  are as stated in Theorem 2.1,
are as stated in Theorem 2.1,
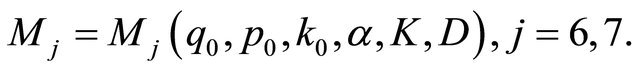
Proof. It is easy to see that 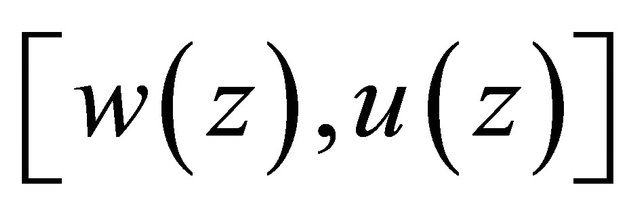 satisfies the equation and boundary conditions
satisfies the equation and boundary conditions
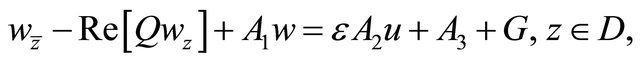 (2.13)
(2.13)
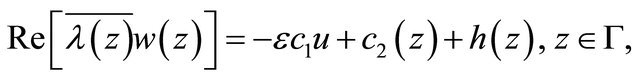 (2.14)
(2.14)
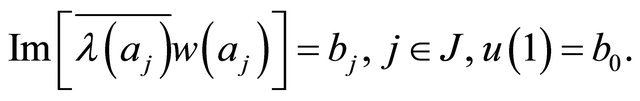 (2.15)
(2.15)
Moreover from (2.6) and (2.7), we have
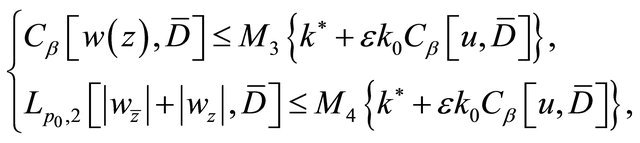 (2.16)
(2.16)
and from (2.8)-(2.10), it follows that
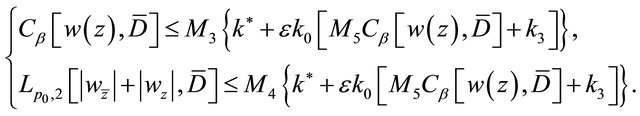 (2.17)
(2.17)
If the positive constant 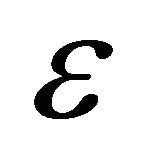 is small enough such that
is small enough such that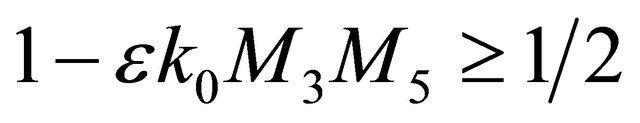 , then the first inequality in (2.17) implies that
, then the first inequality in (2.17) implies that
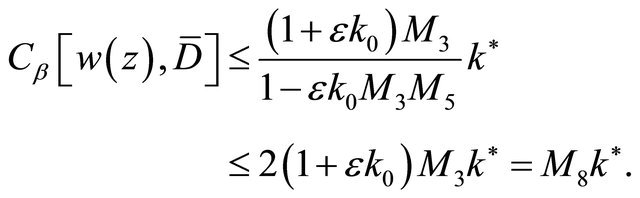 (2.18)
(2.18)
Combining (2.8) and (2.18), we obtain
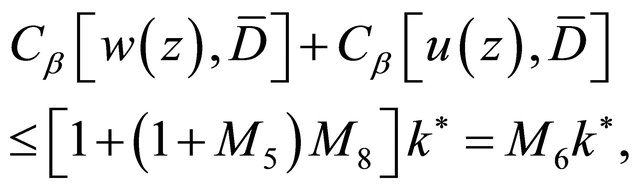 (2.19)
(2.19)
which is the estimate (2.11). As for (2.12), it is easily derived from (2.9) and the second inequality in (2.17), i.e.
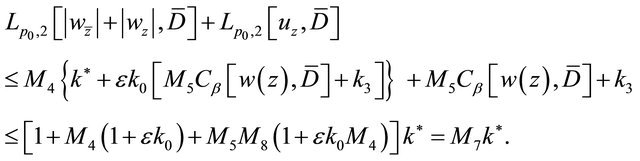 (2.20)
(2.20)
3. Solvability Results of the Poincaré Boundary Value Problem
We first prove a lemma.
Lemma 3.1. If 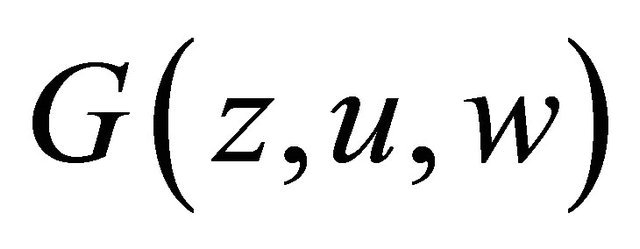 satisfies the condition stated in Condition C, then the nonlinear mapping G:
satisfies the condition stated in Condition C, then the nonlinear mapping G:
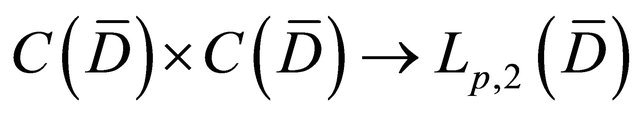
defined by 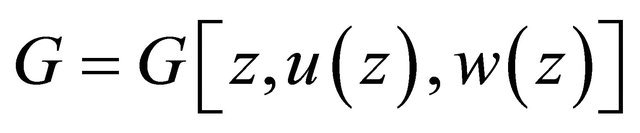 is continuous and bounded
is continuous and bounded
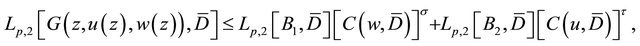 (3.1)
(3.1)
where 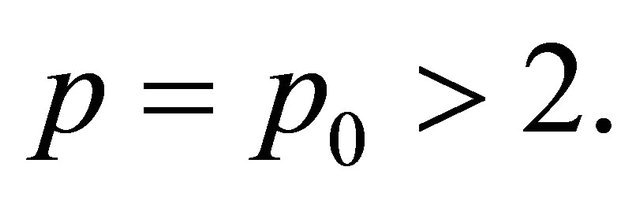
Proof. In order to prove that the mapping :
:
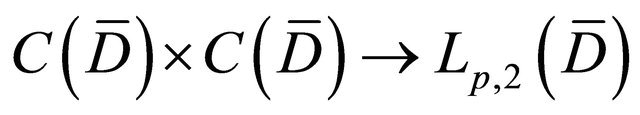
Defined by 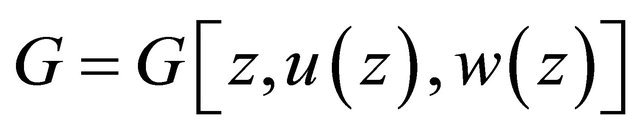 is continuous, we choose any sequence of functions
is continuous, we choose any sequence of functions 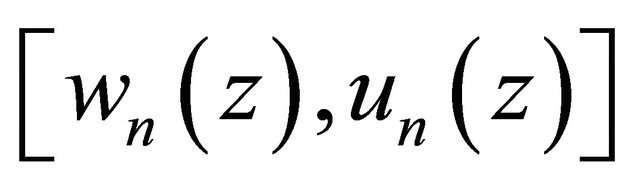
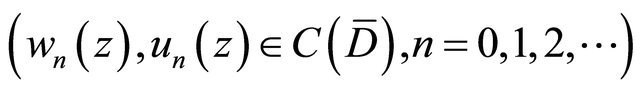
such that
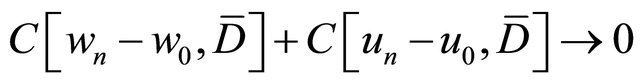
as  Similarly to Lemma 2.2.1, [5], we can prove that
Similarly to Lemma 2.2.1, [5], we can prove that
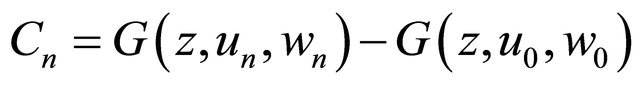
possesses the property
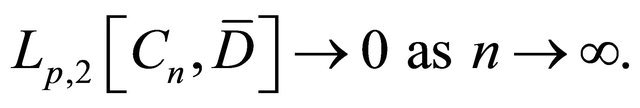 (3.2)
(3.2)
And the inequality (3.1) is obviously true.
Theorem 3.2. Let the complex Equation (1.1) satisfy Condition C, and the positive constant 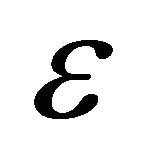 in (1.6) and (1.7) is small enough.
in (1.6) and (1.7) is small enough.
1) When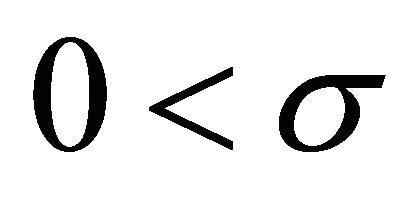 ,
, 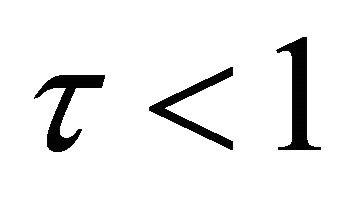 , Problem Q for (1.6) has a solution
, Problem Q for (1.6) has a solution , where
, where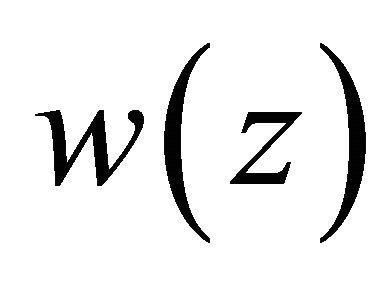 ,
,  ,
, 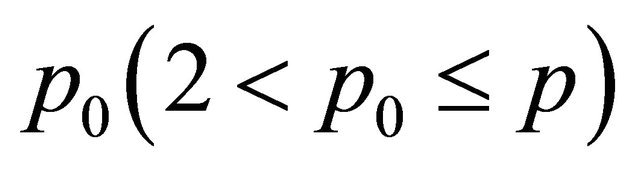 is a constant as stated before.
is a constant as stated before.
2) When 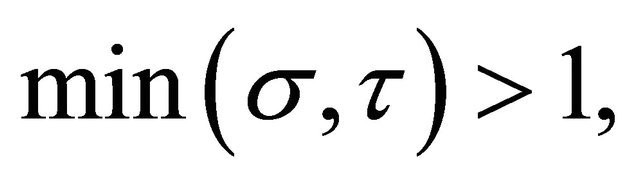 Problem Q for (1.6) has a solution
Problem Q for (1.6) has a solution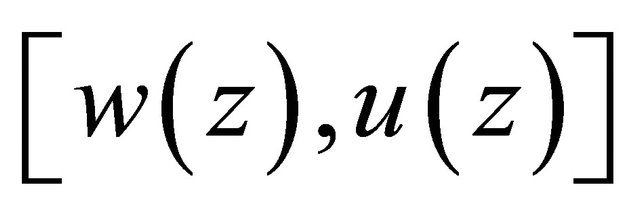 , where
, where 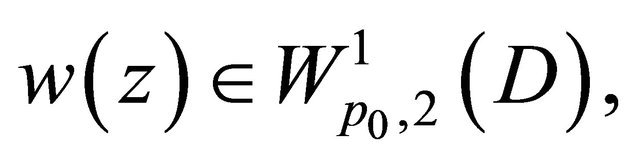 provided that
provided that
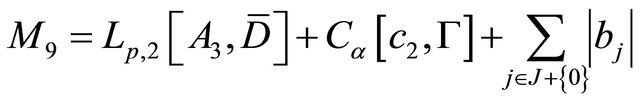 (3.3)
(3.3)
is sufficiently small.
3) If 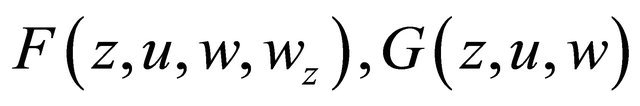 satisfy the conditions, i.e. Condition C and for any functions
satisfy the conditions, i.e. Condition C and for any functions 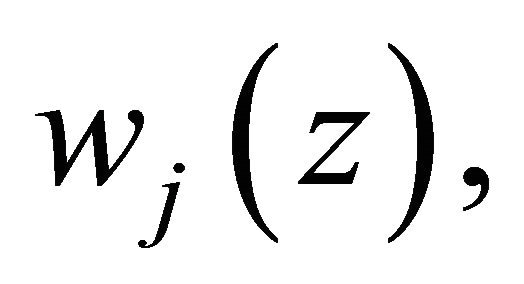
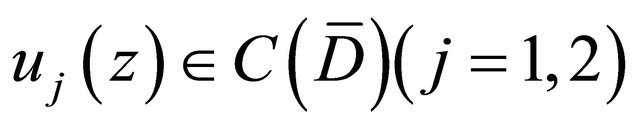 and
and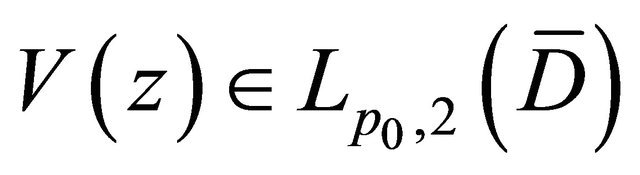 , there are
, there are
 (3.4)
(3.4)
where
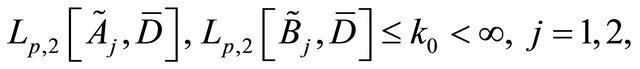
 is a sufficiently small positive constant, then the above solution of Problem Q is unique.
is a sufficiently small positive constant, then the above solution of Problem Q is unique.
Proof. 1) In this case, the algebraic equation for t is as follows
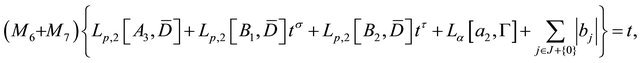 (3.5)
(3.5)
where M6, M7 are constants as stated in (2.11) and (2.12). Because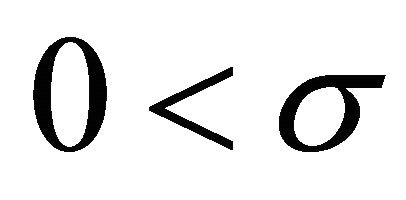 ,
, 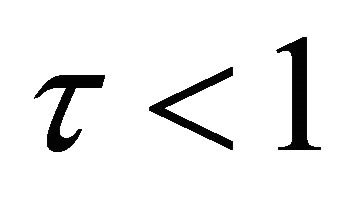 , the Equation (3.5) has a unique solution
, the Equation (3.5) has a unique solution 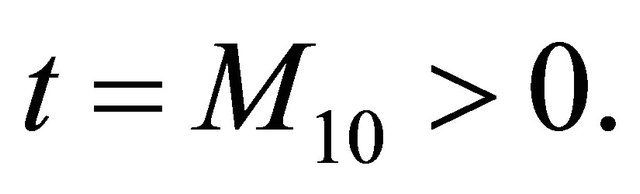 Now we introduce a bounded, closed and convex subset B* of the Banach space
Now we introduce a bounded, closed and convex subset B* of the Banach space 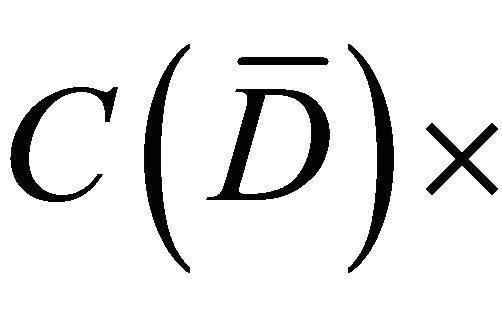
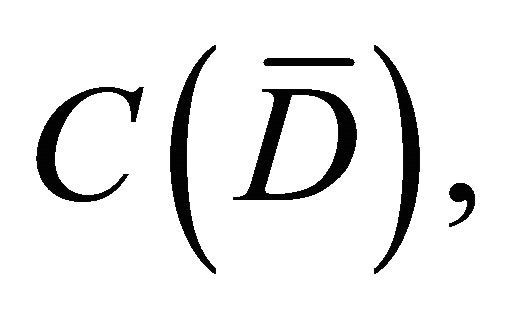 whose elements are of the form
whose elements are of the form 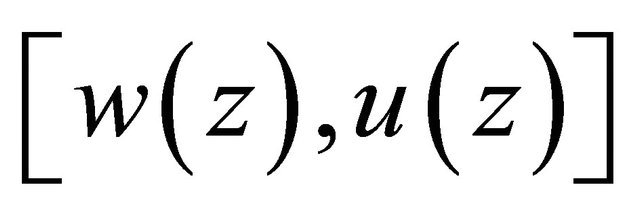 satisfying the condition
satisfying the condition
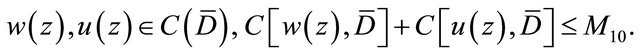 (3.6)
(3.6)
We choose a pair of functions  and substitute it into the appropriate positions of
and substitute it into the appropriate positions of
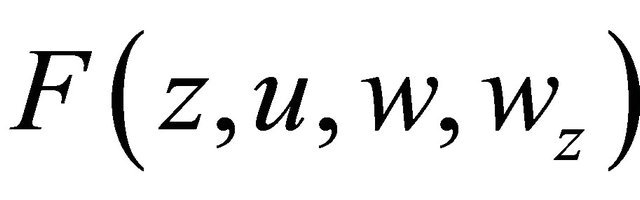 ,
, 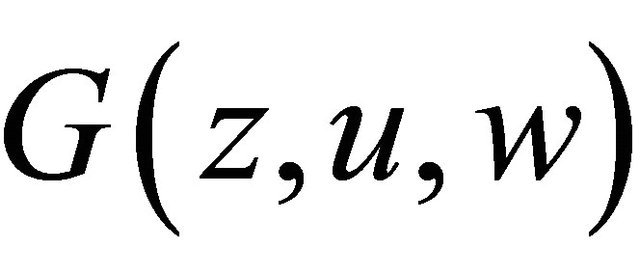 in (1.6) and the boundary condition (1.7), and obtain
in (1.6) and the boundary condition (1.7), and obtain
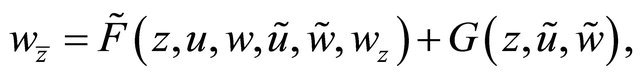 (3.7)
(3.7)
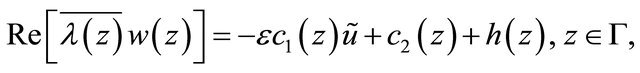 (3.8)
(3.8)
where
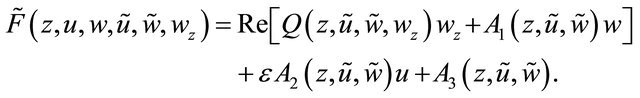
In accordance with the method in the proof of Theorem 1.2.5, [5], we can prove that the boundary value problem (3.7), (3.8) and (1.6) has a unique solution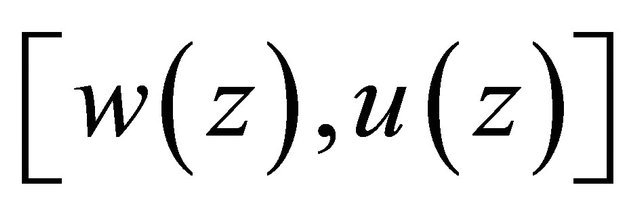 . Denote by
. Denote by 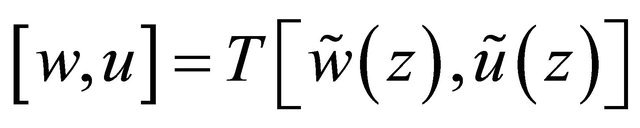 the mapping from
the mapping from 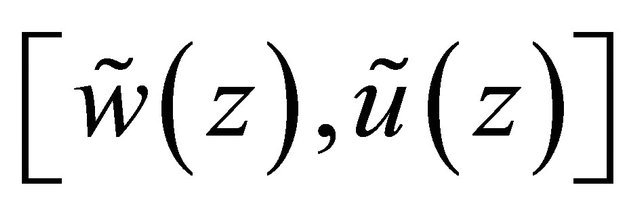 to
to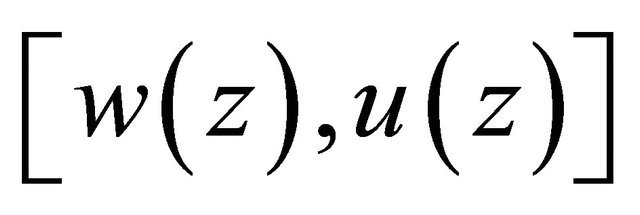 . Noting that
. Noting that
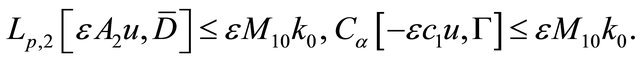
provided that the positive number  is sufficiently small, and noting that the coefficients of complex Equation (3.7) satisfy the same conditions as in Condition C, from Theorem 2.2, we can obtain
is sufficiently small, and noting that the coefficients of complex Equation (3.7) satisfy the same conditions as in Condition C, from Theorem 2.2, we can obtain
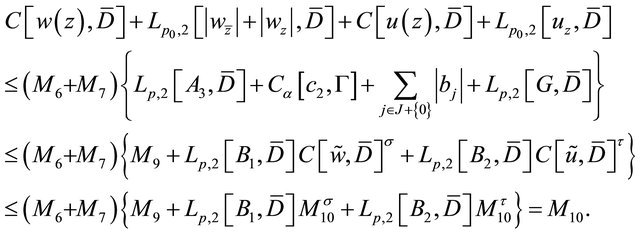 (3.9)
(3.9)
This shows that T maps B* onto a compact subset in B*. Next, we verify that T in B* is a continuous operator. In fact, we arbitrarily select a sequence 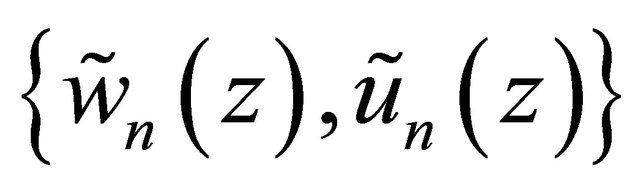 in B*, such that
in B*, such that
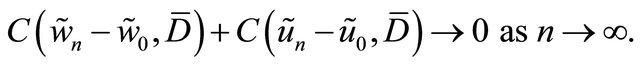 (3.10)
(3.10)
By Lemma 3.1, we can see that
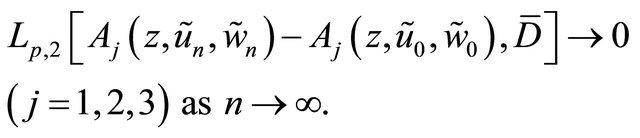 (3.11)
(3.11)
Moreover, from
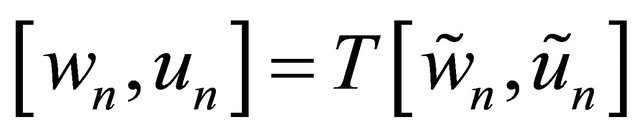 ,
,
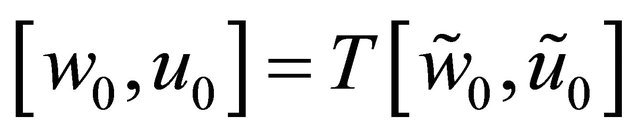 it is clear that
it is clear that 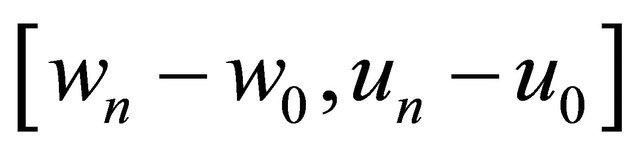 is a solution of Problem Q for the following equation
is a solution of Problem Q for the following equation
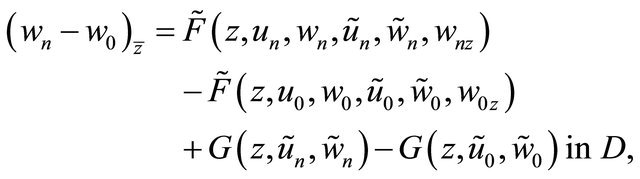 (3.12)
(3.12)
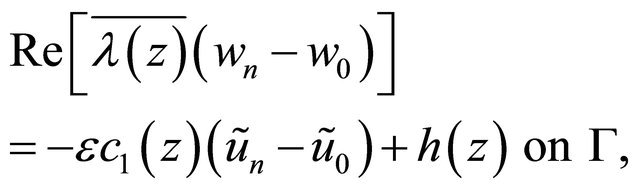 (3.13)
(3.13)
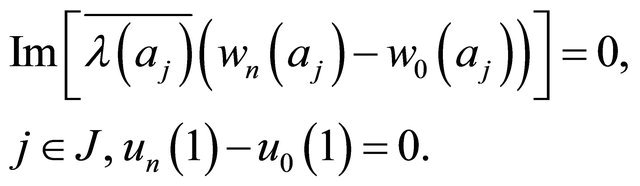 (3.14)
(3.14)
In accordance with the method in proof of Theorem 2.2, we can obtain the estimate
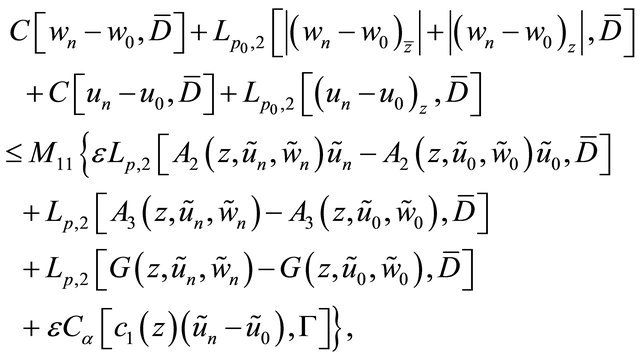 (3.15)
(3.15)
in which 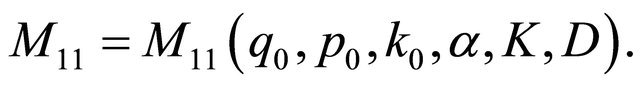 From (3.10), (3.11) and the above estimate, we obtain
From (3.10), (3.11) and the above estimate, we obtain
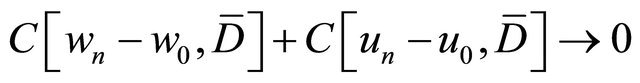 as
as 
On the basis of the Schauder fixed-point theorem, there exists a function 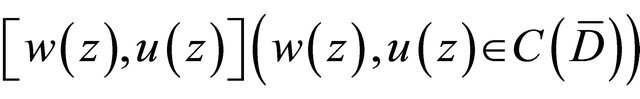 such that
such that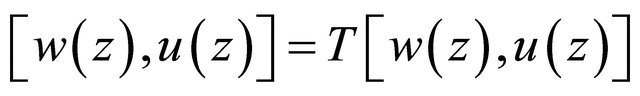 , and from Theorem 2.2, it is easy to see that
, and from Theorem 2.2, it is easy to see that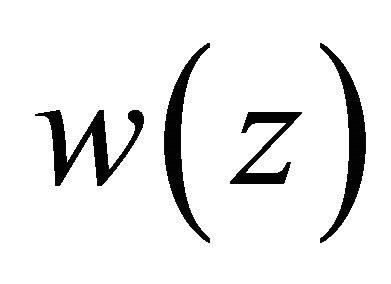 ,
, 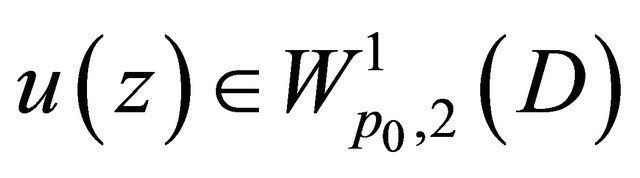 , and
, and
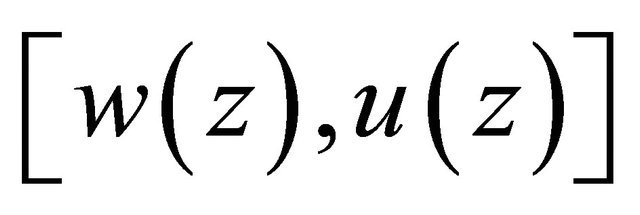 is a solution of Problem Q for the Equation (1.6) and the relation (1.8) with the condition
is a solution of Problem Q for the Equation (1.6) and the relation (1.8) with the condition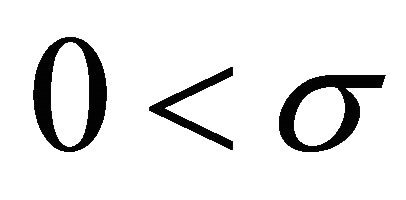 ,
,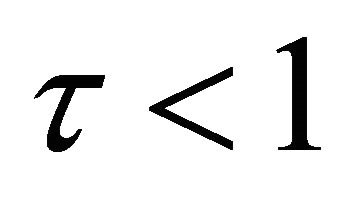 .
.
In addition, if 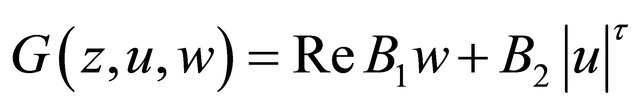 in
in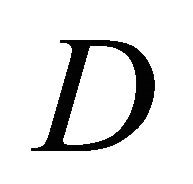 where
where 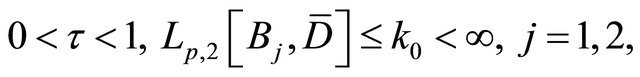 then the above solvability result still hold by using the above similar method.
then the above solvability result still hold by using the above similar method.
2) Secondly, we discuss the case: 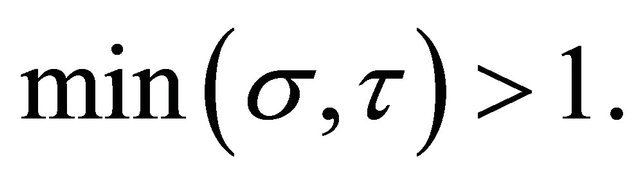 In this case, (3.5) has the solution
In this case, (3.5) has the solution 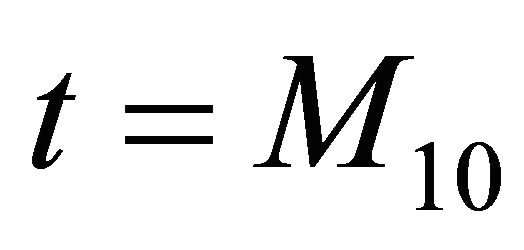 provided that M9 in (3.3) is small enough. Now we consider a closed and convex subset
provided that M9 in (3.3) is small enough. Now we consider a closed and convex subset  in the Banach space
in the Banach space 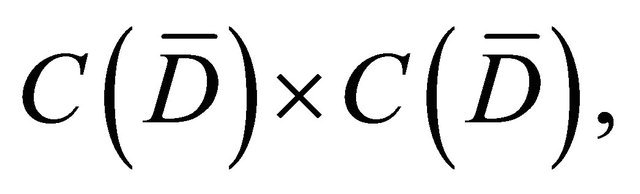 i.e.
i.e.
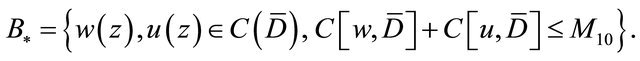 (3.16)
(3.16)
Applying a method similar as before, we can verify that there exists a solution
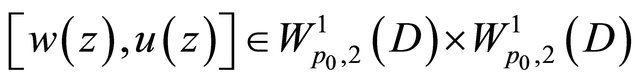
of Problem Q for (1.6) with the condition 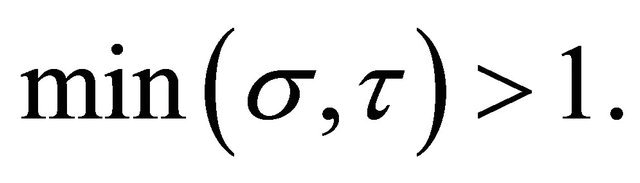
Moreover, if 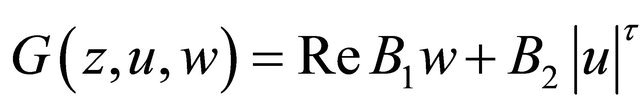 in D, where
in D, where
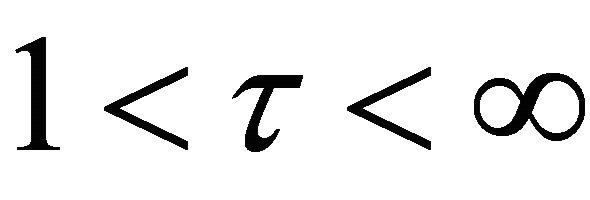 ,
,  , j = 1, 2. Under the same condition, we can derive the above solvability result by the similar method.
, j = 1, 2. Under the same condition, we can derive the above solvability result by the similar method.
3) When 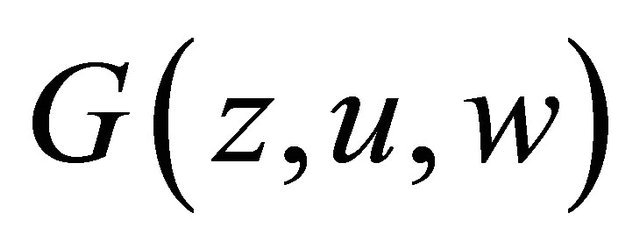 satisfies the condition (3.4), we can verify the uniqueness of solutions in this theorem. In fact, if
satisfies the condition (3.4), we can verify the uniqueness of solutions in this theorem. In fact, if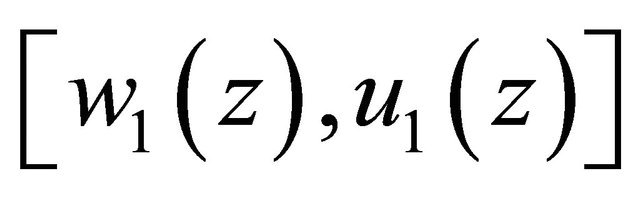 ,
, 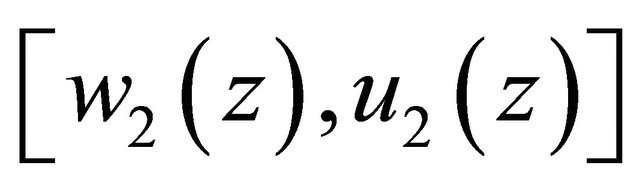 are two solutions of Problem Q for the Equation (1.6), then
are two solutions of Problem Q for the Equation (1.6), then
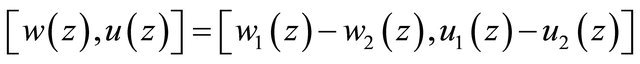
satisfies the equation and boundary conditions
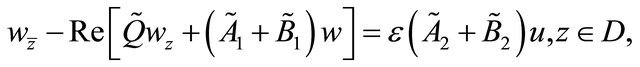 (3.17)
(3.17)
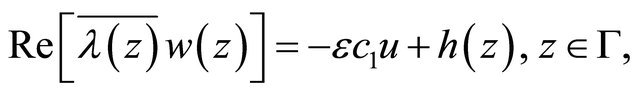 (3.18)
(3.18)
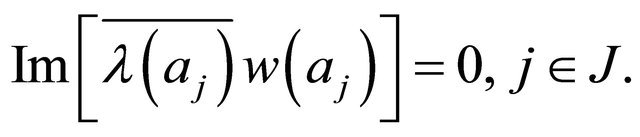 (3.19)
(3.19)
in which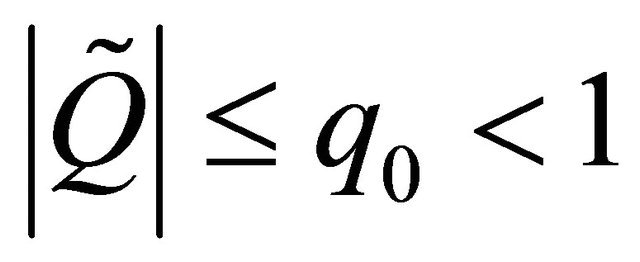 . Similarly to Theorem 2.2, we can derive the following estimates of the solution
. Similarly to Theorem 2.2, we can derive the following estimates of the solution 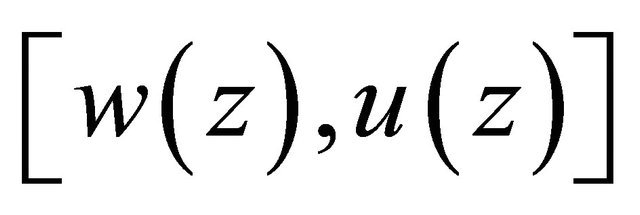 for complex Equation (3.17):
for complex Equation (3.17):
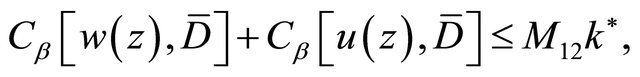 (3.20)
(3.20)
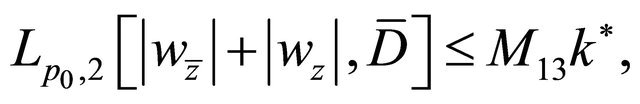 (3.21)
(3.21)
where
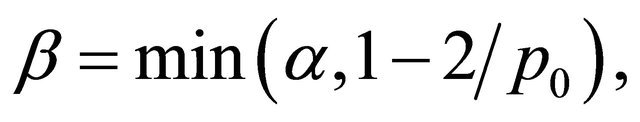
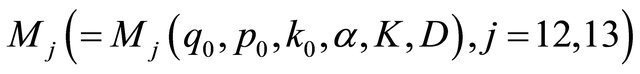
are two non-negative constants, 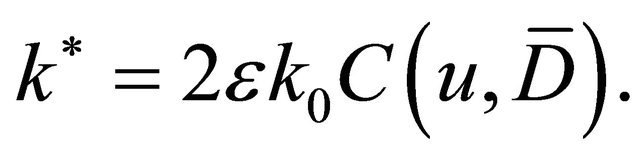 Moreover the estimate
Moreover the estimate
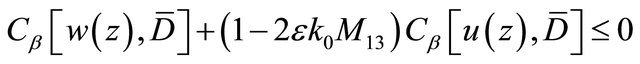 (3.22)
(3.22)
can be derived. Provided that the positive constant 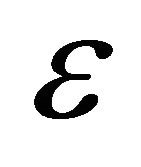 is small enough such that
is small enough such that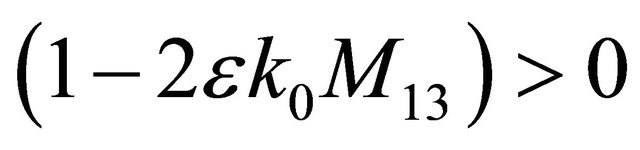 , from (3.22) it follows
, from (3.22) it follows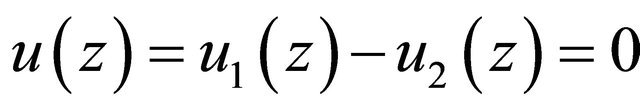 , i.e.
, i.e. 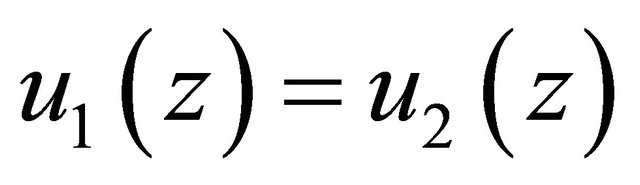 in D. This completes the proof of the theorem.
in D. This completes the proof of the theorem.
From the above theorem, the next result can be derived.
Theorem 3.3. Under the same conditions as in Theorem 3.2, the following statements hold.
1) When the index K > N, Problem P for (1.1) has N solvability conditions, and the solution of Problem P depends on 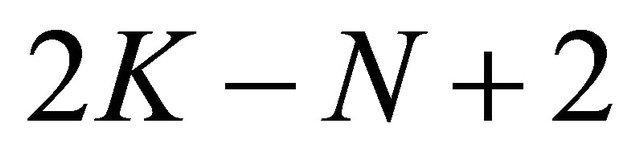 arbitrary real constants.
arbitrary real constants.
2) When 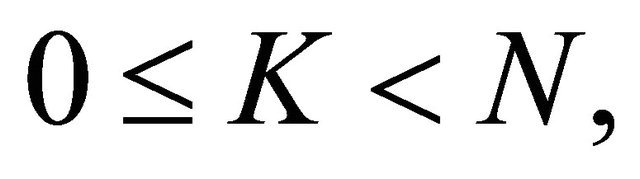 Problem P for (1.1) is solvable, if
Problem P for (1.1) is solvable, if 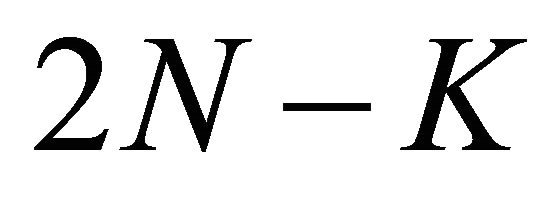 solvability conditions are satisfied, and the solution of Problem P depends on
solvability conditions are satisfied, and the solution of Problem P depends on 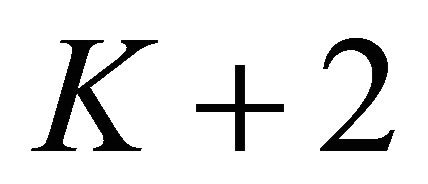 arbitrary real constants.
arbitrary real constants.
3) When K < 0, Problem P for (1.1) is solvable under 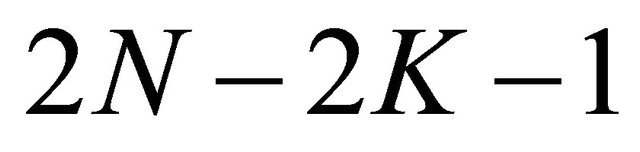 conditions, and the solution of Problem P depends on 1 arbitrary real constant.
conditions, and the solution of Problem P depends on 1 arbitrary real constant.
Moreover, we can write down the solvability conditions of Problem P for all other cases.
Proof. Let the solution 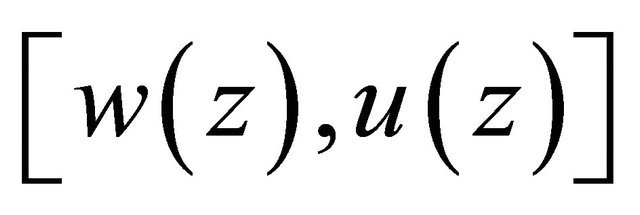 of Problem Q for (1.6) be substituted into the boundary condition (1.7) and the relation (1.8). If the function
of Problem Q for (1.6) be substituted into the boundary condition (1.7) and the relation (1.8). If the function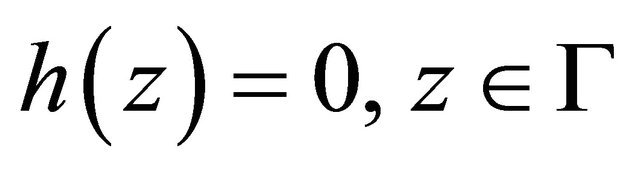 , i.e.
, i.e.
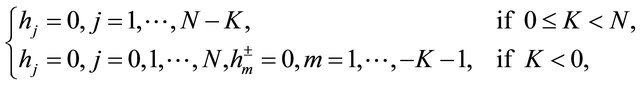
and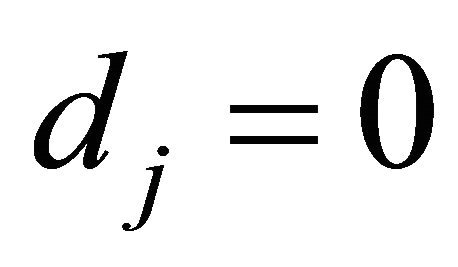 ,
,  , then we have
, then we have  in D and the function
in D and the function 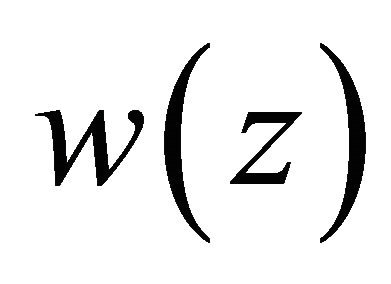 is just a solution of Problem P for (1.1). Hence the total number of above equalities is just the number of solvability conditions as stated in this theorem. Also note that the real constants b0 in (1.8) and
is just a solution of Problem P for (1.1). Hence the total number of above equalities is just the number of solvability conditions as stated in this theorem. Also note that the real constants b0 in (1.8) and 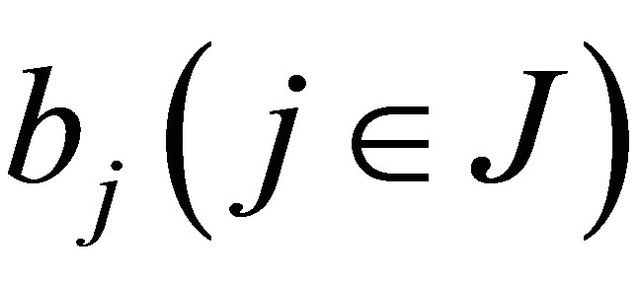 in (1.9) are arbitrarily chosen. This shows that the general solution of Problem P for (1.1) includes the number of arbitrary real constants as stated in the theorem.
in (1.9) are arbitrarily chosen. This shows that the general solution of Problem P for (1.1) includes the number of arbitrary real constants as stated in the theorem.
REFERENCES
- I. N. Vekua, “Generalized Analytic Functions,” Pergamon, Oxford, 1962.
- G. C. Wen and H. Begehr, “Boundary Value Problems for Elliptic Equations and Systems,” Longman Scientific and Technical Company, Harlow, 1990.
- A. V. Bitsadze, “Some Classes of Partial Differential Equations,” Gordon and Breach, New York, 1988.
- G. C. Wen, “Conformal Mappings and Boundary Value Problems,” Translations of Mathematics Monographs 106, American Mathematical Society, Providence, 1992.
- G. C. Wen, D. C. Chen and Z. L. Xu, “Nonlinear Complex Analysis and Its Applications,” Mathematics Monograph Series 12, Science Press, Beijing, 2008.
- G. C. Wen, “Approximate Methods and Numerical Analysis for Elliptic Complex Equations,” Gordon and Breach, Amsterdam, 1999.
- G. C. Wen, “Linear and Quasilinear Complex Equations of Hyperbolic and Mixed Type,” Taylor & Francis, London, 2002. doi:10.4324/9780203166581
- G. C. Wen, “Recent Progress in Theory and Applications of Modern Complex Analysis,” Science Press, Beijing, 2010.

