World Journal of Mechanics
Vol. 1 No. 6 (2011) , Article ID: 9100 , 6 pages DOI:10.4236/wjm.2011.16036
Unsteady Boundary Layer Flow and Heat Transfer Due to a Stretching Sheet by Quasilinearization Technique
Department of Mathematics, Osmania University, Hyderabad, India
E-mail: wubshetib@yahoo.com, bandarishanker@yahoo.co.in
Received September 10, 2011; revised October 16, 2011; accepted November 4, 2011
Keywords: Quasi-Linearization Technique, Stretching Sheet, Boundary-Layer, Unsteady Flow, Heat Transfer
ABSTRACT
In this paper, the problem of unsteady laminar boundary-layer flow and heat transfer of a viscous incomepressible fluid over stretching sheet is studied numerically. The unsteadiness in the flow and temperature is caused by the time-dependent stretching velocity and surface temperature. A similarity transformation is used to reduce the governing boundary-layer equations to couple higher order non-linear ordinary differential equations. These equations are numerically solved using quasi-linearization technique. The effect of the governing parameters unsteadiness parameter and Prandtl number on velocity and temperature profile is discussed. Besides, the numerical results for the local skin friction coefficient and local Nusselt number are presented. The computed results are compared with previously reported work.
1. Introduction
The study of heat transfer over stretching surface has a significant importance in a number of engineering applications. For more than three decades, researchers were studying the flow over stretching sheet because of its wide applications in different areas of industrial manufacturing processes, such as in Aerodynamics, extrusion of plastic sheets, the boundary-layer along a liquid film, condensation process of metallic plate in a cooling bath and glass blowing, polymer industries, paper production, metal spinning, drawing plastic films and artificial fibres. In all such applications the final product depends on the rate of cooling and boundary layer flow near the stretching surface.
Crane[1] studied the boundary-layer flow due to a moving stretching surface with a constant surface temperature in an ambient fluid. He gave a similarity solution in closed analytical form for steady two dimensional incompressible boundary layer flow. The study considered the case when velocity varies linearly with distance from a fixed point. Furthermore, Carragher and Crane [2] studied the influence of heat transfer on the flow over a stretching surface in the case when the temperature difference between the surface and the ambient fluid is proportional to a power of distance from the fixed point. Other studies, for example, Dutta [3], Grubka and Bobba [4], discussed the temperature field in the flow over a stretching surface when a uniform heat flux is exerted to the surface.
Furthermore, Elbashbeshy [5] conducted a numerical study of steady heat transfer over a stretching surface with a variable surface heat flux and uniform heat flux subjected to injection and suction. The findings show that suction increases heat transfer from the surface, where as injection causes a decrease in heat transfer. In all the above studies, the researchers considered the case of steady flow and heat transfer. However, Elbashbeshy and Bazid [6] extended the previous work of Elbashybesh [5] to unsteady flow and heat transfer over a stretching sheet in laminar boundary-layer. Further, Sharidan et al. [7] investigated the unsteady boundary layer flow and heat transfer due to stretching sheet for the especial distribution of the stretching velocity and surface temperature. Moreover, Ishak et al. [8] extended the dimension of the problem of heat transfer due to stretching sheet to unsteady laminar mixed convection boundary layer flow and heat transfer due to a stretching vertical surface. They discussed the effects of unsteadiness parameter, buoyancy parameter and Prandtl number on the flow characteristic. They found that the heat transfer rate at the surface increases with unsteadiness parameter, buoyancy parameter and Prandtl number. In all the above studies the influence of heat source or sink concept was not considered. However, Elbashbeshy and Aldawody [9] incorporated the idea of heat source and sink and studied unsteady boundary layer flow and heat transfer of an incompressible fluid over stretching surface with variable heat flux in the presence of heat source or sink. Their numerical result shows that an increase in the heat source or sink parameter leads to an increase in the surface temperature and a decrease in the local Nusslet number.
In this study, quasi-linearization technique is used to solve unsteady boundary-layer flow and heat transfer due to a stretching sheet. This technique was introduced in 1965 by Bellman and Kalaba [10]. Since then different authors [11-16] have employed the technique to solve different types of non-linear equations and higher order differential equations arising in the fields of engineering, science, fluid dynamics, solid mechanics and heat and mass transfer. This proves that the method used in the present study is widely used and is believed to be valid and effective for the study of our problem.
The objective of the present study is to find numerical solution for unsteady boundary-layer and heat transfer due to stretching sheet by quasi-linearization technique. The analytic solution of same problem was obtained by Rashid and Mohimanian [17] by using homotopy analysis method. Accordingly, the present study tries to solve the same problem numerically using quasi-linearization technique. It presents results for velocity and temperature profiles graphically.
2. Mathematical Formulation
Consider a two-dimensional, unsteady flow and heat transfer of a viscous incompressible fluid past a semiinfinite stretching sheet in the region y > 0, as shown in Figure 1.
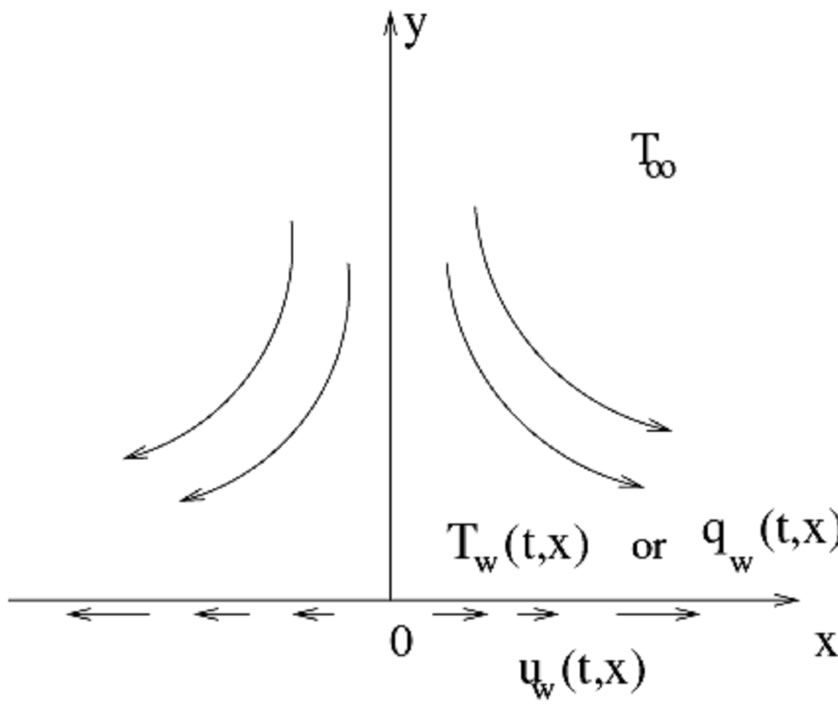
Figure 1. Physical flow model of the problem.
The flow is generated due to stretching sheet caused by the simultaneous application of two equal and opposite forces which are suddenly applied along the x-axis and results in stretching of the sheet. Its speed varies linearly with the distance from the origin x = 0, keeping the origin fixed. At the same time, the wall temperature
 of the sheet is suddenly raised from
of the sheet is suddenly raised from  to
to
 or there is a suddenly imposed heat flux
or there is a suddenly imposed heat flux
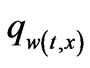 at the wall. VHF denotes variable heat flux and VWT denotes variable wall temperature. Under the boundary-layer approximation, the continuity, momentum and energy equation are given by
at the wall. VHF denotes variable heat flux and VWT denotes variable wall temperature. Under the boundary-layer approximation, the continuity, momentum and energy equation are given by
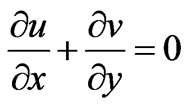 (1)
(1)
 (2)
(2)
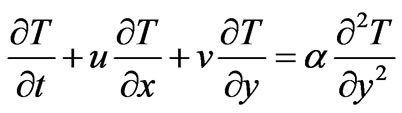 (3)
(3)
Subjected to boundary conditions
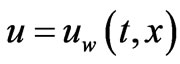 v = 0 at y = 0(4)
v = 0 at y = 0(4)
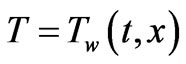 for (VWT) or
for (VWT) or  for (VHF) at y =0(5)
for (VHF) at y =0(5)
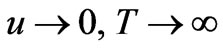 at
at 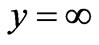 (6)
(6)
where t is the time, u and v are the velocity components along the x and y-axis respectively, T is the temperature, 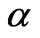 is the thermal diffusivity,
is the thermal diffusivity, 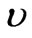 is the kinematics viscosity and k is the thermal conductivity.
is the kinematics viscosity and k is the thermal conductivity.
The velocity of the sheet 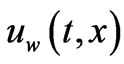 , the sheet temperature
, the sheet temperature 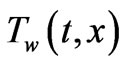 and the heat flux
and the heat flux 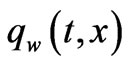 are defined as
are defined as
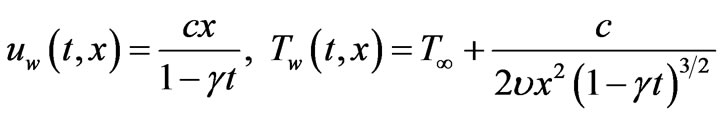 and
and
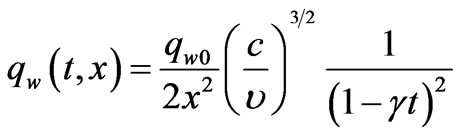 (7)
(7)
where c is the stretching rate being a positive constant, 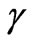 is positive constant, which measures the unsteadiness and
is positive constant, which measures the unsteadiness and is a characteristics heat transfer quantity. The mathematical analysis of the problem is simplified by introducing the following similarity transforms due to [7]
is a characteristics heat transfer quantity. The mathematical analysis of the problem is simplified by introducing the following similarity transforms due to [7]
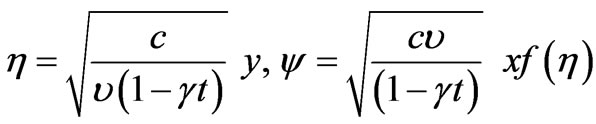
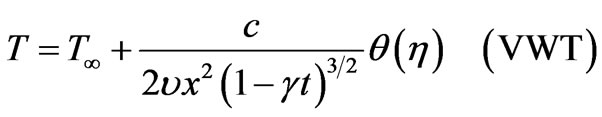
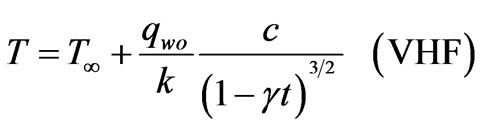
where 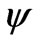 is the stream function and is defined as
is the stream function and is defined as 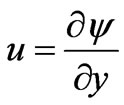 and
and 
Using the similarity transformation quantity, the governing Equations (1)-(3) are transformed to the non-dimensional form as follows:
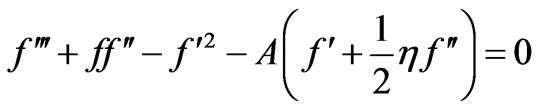 (9)
(9)
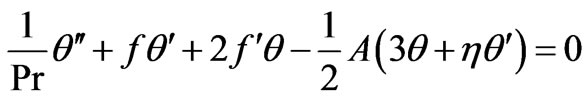 (10)
(10)
with the boundary condition
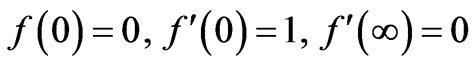
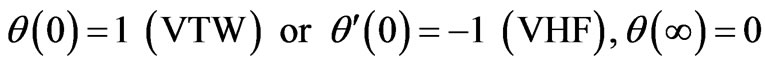 (11)
(11)
where Pr is the Prandtl number,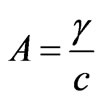 , is non-dimensional constant which measures unsteadiness of the flow and heat transfer and the prime denotes the differentiation with respect to the similarity variable
, is non-dimensional constant which measures unsteadiness of the flow and heat transfer and the prime denotes the differentiation with respect to the similarity variable .
.
The skin friction coefficient 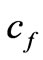 and the local Nusselt number
and the local Nusselt number are the two important physical quantities and are defined as
are the two important physical quantities and are defined as
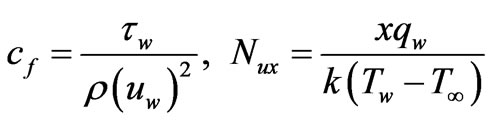 (12)
(12)
where the skin friction 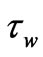 and the heat transfer from the sheet
and the heat transfer from the sheet  are given by
are given by
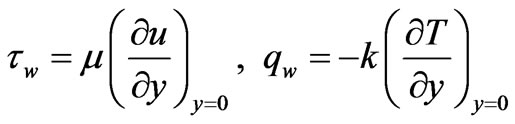 (13)
(13)
And 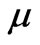 is the dynamic viscosity. By using Equation (7) and (8), we get
is the dynamic viscosity. By using Equation (7) and (8), we get
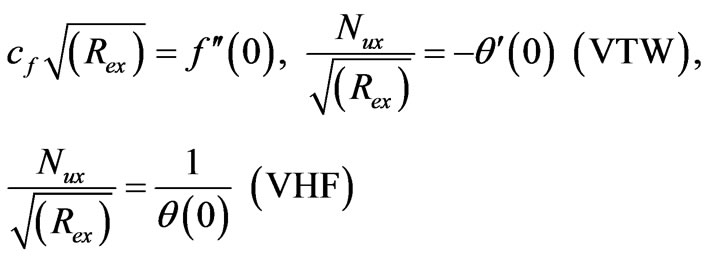 (14)
(14)
where is the local Reynolds number.
is the local Reynolds number.
3. Numerical Solution
The numerical solution for the above equations for different values of unsteadiness parameter A and Prandtl number Pr are developed using quasi-linearization technique. The quasi-linearization technique applied for solving the Equations (9) and (10) is as follows:
Equations (9) and (10) can be expressed as
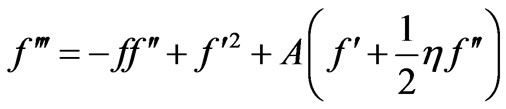
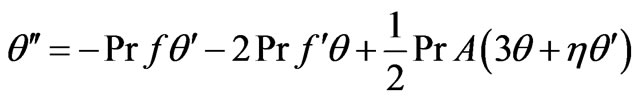 (15)
(15)
Now defining new variables by the equation
 (16)
(16)
The two coupled higher order differential equations and the boundary conditions may be transformed to five equivalent first order differential equation and boundary conditions respectively as given below
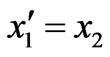


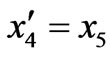
 (17)
(17)
And the boundary conditions are
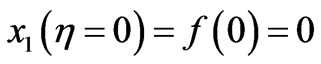
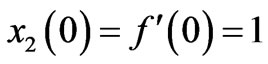
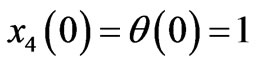
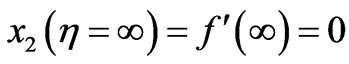 (18)
(18)
The above equation (17) is in the form of
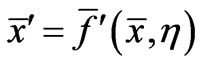 (19)
(19)
By performing the Taylor’s series expansion of differential equation (17), we obtain the following equations expressed in matrix form
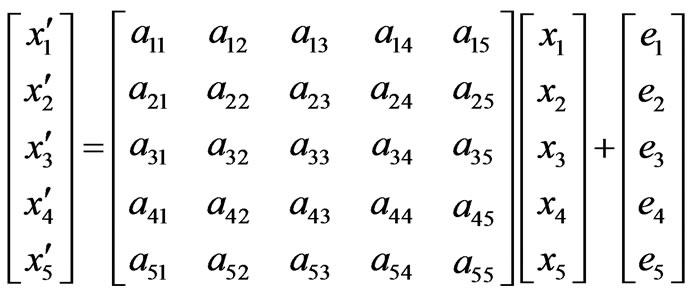 (20)
(20)
where 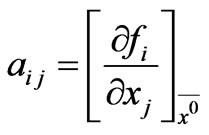 for i = 1 to 5 and j = 1 to 5
for i = 1 to 5 and j = 1 to 5
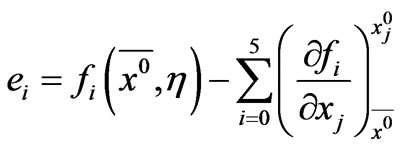 (21)
(21)
The element of the matrices are thus obtained as given below
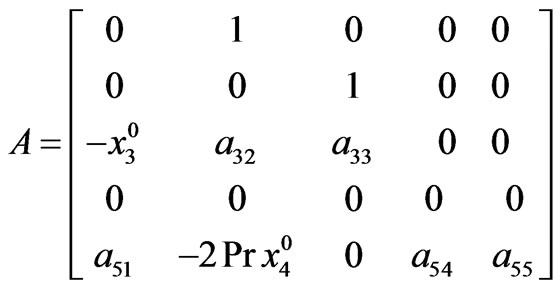
where


The coefficient 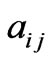 and
and 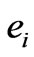 are dependent on the nominal trajectories
are dependent on the nominal trajectories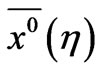 .
.
Hence, depending on the initial guess of nominal trajectories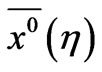 , the solution of (20) yields the neighbouring trajectories
, the solution of (20) yields the neighbouring trajectories . These neighbouring trajectories are treated as nominal trajectories and next neighbouring trajectories are obtained. This process is continued until the convergence is obtained. The solution said to be convergent when the following stopping criteria norm is satisfied where
. These neighbouring trajectories are treated as nominal trajectories and next neighbouring trajectories are obtained. This process is continued until the convergence is obtained. The solution said to be convergent when the following stopping criteria norm is satisfied where
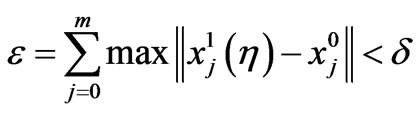 (22)
(22)
It may be noted that the 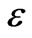 defined in the equation (22) is the sum of maximum absolute difference between the nominal trajectories and neighbouring trajectories of all the dependent variables. If the value of
defined in the equation (22) is the sum of maximum absolute difference between the nominal trajectories and neighbouring trajectories of all the dependent variables. If the value of  falls below a prescribed number
falls below a prescribed number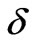 , the iterative procedure may be stopped and the sequence of solutions of the approximate linear differential equations may be converged. The value of
, the iterative procedure may be stopped and the sequence of solutions of the approximate linear differential equations may be converged. The value of 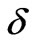 = 0.001 is chosen in the current solution. The coupled Equation (20) can be solved by numerical integration called Runge-Kutta fourth order scheme following the quasi-linearization procedures.
= 0.001 is chosen in the current solution. The coupled Equation (20) can be solved by numerical integration called Runge-Kutta fourth order scheme following the quasi-linearization procedures.
4. Results and Discussion
The transformed momentum equation (9) and energy equation (10) subjected to the boundary condition equation (11) were numerically solved by means of quasilinearization technique as described by Bellman and Kalaba [10]. We have obtained velocity and temperature graph for different values of unsteadiness parameter A and Prandtl number Pr. The results obtained are presented through the graphs as shown in Figures 2-5.
Figure 2 represents the variation of velocity with respect to the similarity variable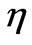 . It indicates that the velocity for any fixed
. It indicates that the velocity for any fixed 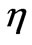 decreases with an increase in unsteadiness parameter A. The velocity graph in Figure 2 also shows that the boundary layer thickness decreases monotonically when unsteadiness parameter A increases.
decreases with an increase in unsteadiness parameter A. The velocity graph in Figure 2 also shows that the boundary layer thickness decreases monotonically when unsteadiness parameter A increases.
Figure 3 shows the variation of temperature with respect to the similarity variable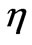 . This reveals that the temperature for fixed value of
. This reveals that the temperature for fixed value of 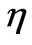 decreases with the increase of values of
decreases with the increase of values of . The temperature graph indicates that
. The temperature graph indicates that 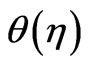 decreases with the increase in
decreases with the increase in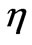 . Moreover, the graph shows that the thermal boundary layer thickness decreases with an increase in Prandtl number Pr, for all unsteadiness parameters. It is possible to see that the temperature
. Moreover, the graph shows that the thermal boundary layer thickness decreases with an increase in Prandtl number Pr, for all unsteadiness parameters. It is possible to see that the temperature 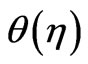 at the surface of a sheet is invariant with respect to unsteadiness parameter A. We also observe that as the distance from the stretching sheet within dynamic region increases, temperature field decreases as unsteadiness increases. Physically, when unsteadiness increases the sheet looses more heat which causes decrease in temperature.
at the surface of a sheet is invariant with respect to unsteadiness parameter A. We also observe that as the distance from the stretching sheet within dynamic region increases, temperature field decreases as unsteadiness increases. Physically, when unsteadiness increases the sheet looses more heat which causes decrease in temperature.
Figure 4 stands for the variation of temperature with respect to Prandtl number Pr. It is possible to see that the temperature decreases as the Prandtl number Pr increases for a fixed value of 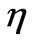 i.e. the temperature decrease as the distance away from the sheet increases and it become almost zero at
i.e. the temperature decrease as the distance away from the sheet increases and it become almost zero at 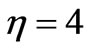 which ends the boundary layer thickness. The temperature field attains maximum value at the surface of the stretching sheet. The temperature decreases within the boundary layer for all values of the Prandtl number Pr. This is consistent with the fact that the thermal boundary layer thickness decreases with increasing in Prandtl number.
which ends the boundary layer thickness. The temperature field attains maximum value at the surface of the stretching sheet. The temperature decreases within the boundary layer for all values of the Prandtl number Pr. This is consistent with the fact that the thermal boundary layer thickness decreases with increasing in Prandtl number.
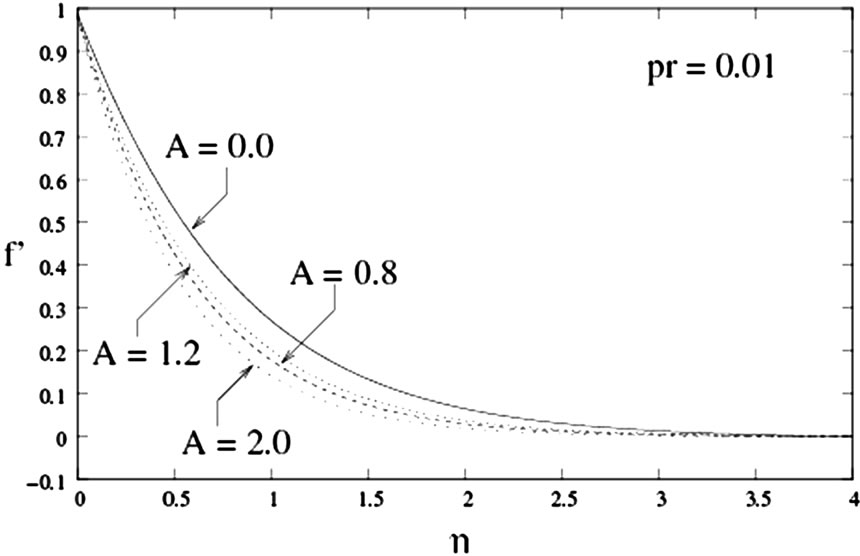
Figure 2. Velocity graph for Pr = 0.01 and for different values of A.
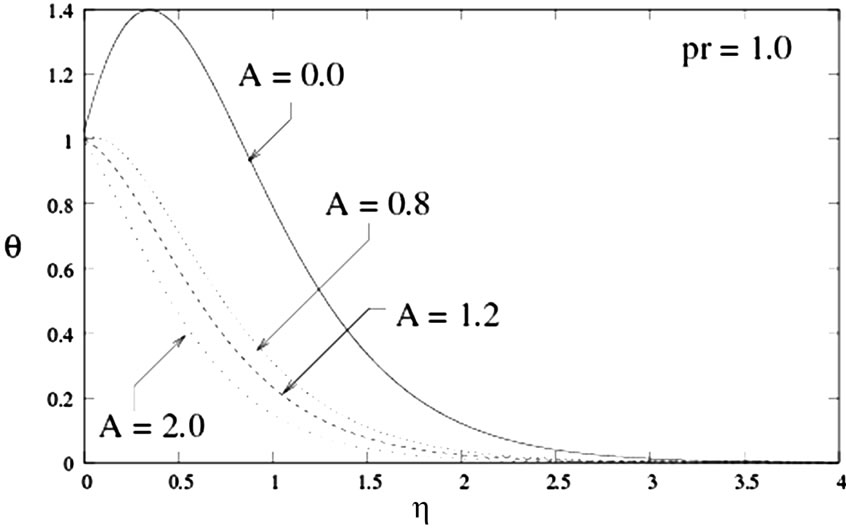
Figure 3. Temperature graph for different values of A when Pr = 1.0.
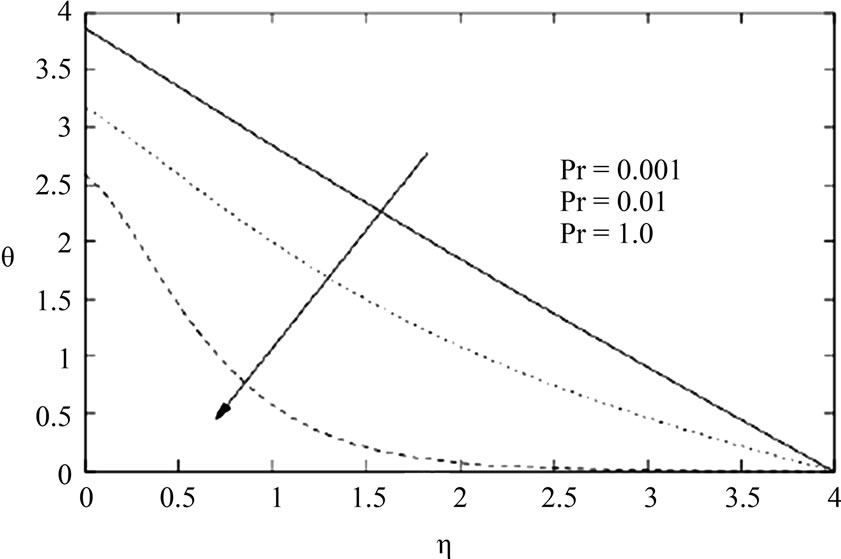
Figure 4. Temperature graph for different values of Pr when A = 1.2.
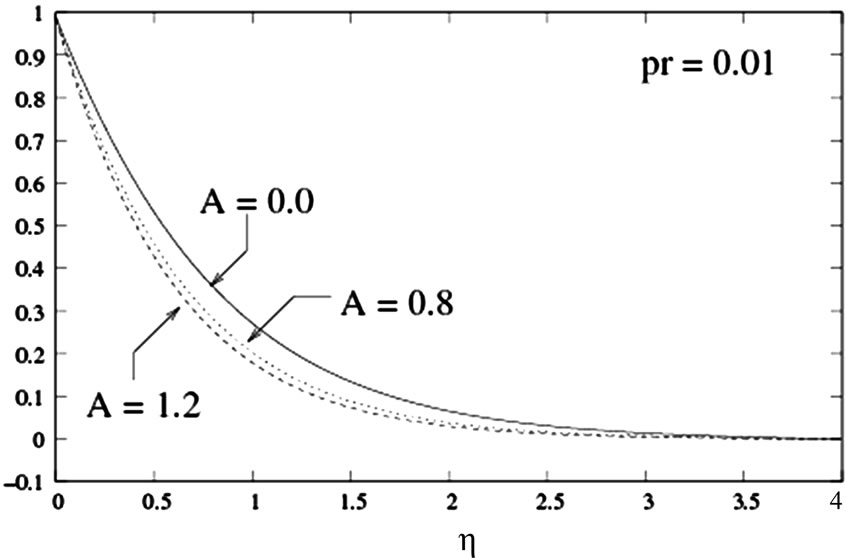
Figure 5. velocity graph for different values of A (VHF) for Pr = 0.01.
Figure 5 shows the velocity graph for different values of unsteadiness parameter A for (VHF) at a fixed Prandtl number Pr = 0.01. The velocity graph decreases monotonically as unsteadiness parameter increases. From the graph, we can also observe that the velocity boundary layer thickness decreases as the distance from the sheet increases.
When we compare the velocity and temperature graphs of this study with the result obtained by analytic method of previous study, our results are in good agreement with them. Furthermore, heat transfer at the surface for different values of unsteadiness parameter A and Prandtl number Pr of this study has shown similarity with the study conducted by Sharidan et al. [7].
Table 1 shows the values of heat transfer  and skin friction coefficient –
and skin friction coefficient –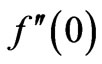 , for various values of unsteadiness parameter A and Pr. From the table, it is possible to see that heat transfer rate at the surface
, for various values of unsteadiness parameter A and Pr. From the table, it is possible to see that heat transfer rate at the surface 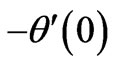 increases with unsteadiness parameter A. However, when the value of unsteadiness parameter A = 0.8, the heat transfer rate at the surface
increases with unsteadiness parameter A. However, when the value of unsteadiness parameter A = 0.8, the heat transfer rate at the surface 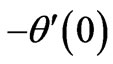 decreases as the values of Prandtl number Pr increases. The table further shows that at the values of Prandtl number Pr = 1.2 and Pr = 2, the heat transfer rate at the surface
decreases as the values of Prandtl number Pr increases. The table further shows that at the values of Prandtl number Pr = 1.2 and Pr = 2, the heat transfer rate at the surface  increases. It is also indicated that skin friction coefficient
increases. It is also indicated that skin friction coefficient 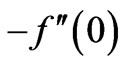 increases with the increase in the values of unsteadiness parameter A and Pr .
increases with the increase in the values of unsteadiness parameter A and Pr .
Table 2 shows the values of the heat transfer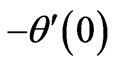 , temperature on the wall
, temperature on the wall 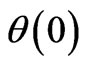 and skin friction coefficient
and skin friction coefficient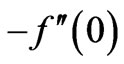 , for various values of A and Pr from the previous study of Shardian [7] for comparison purpose.
, for various values of A and Pr from the previous study of Shardian [7] for comparison purpose.
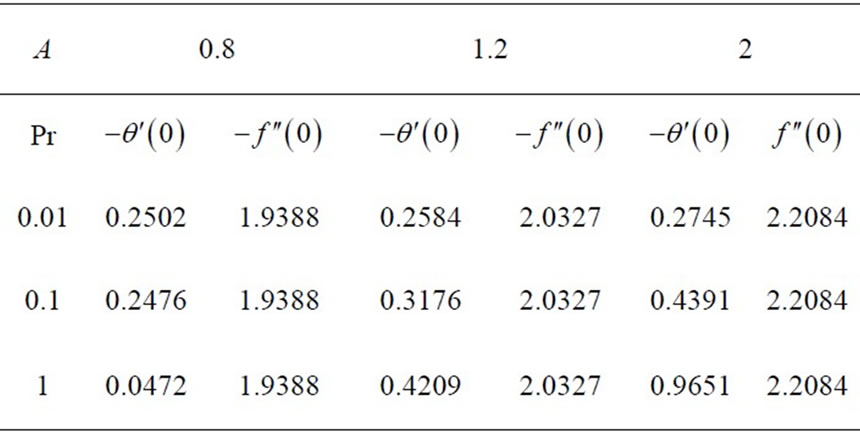
Table 1. Results for the values of heat transfer  and skin friction
and skin friction 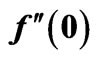 for various values of A and Pr for the present study.
for various values of A and Pr for the present study.
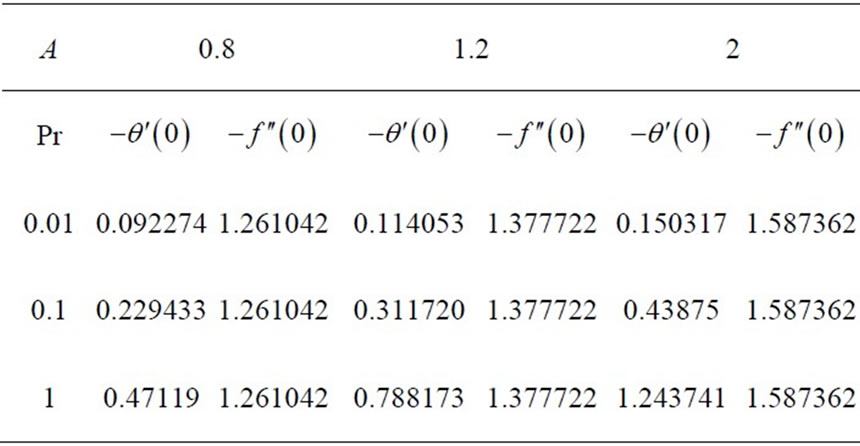
Table 2. Results for the values of the heat transfer and skin friction coefficient
and skin friction coefficient  for various values of A and Pr from previous study [7].
for various values of A and Pr from previous study [7].
5. Conclusions
A numerical method has been employed to study unsteady flow and heat transfer in the laminar flow of an incompressible fluid over stretching sheet. The effect of the unsteadiness parameter A and Prandtl number Pr on the heat transfer were studied. The numerical results indicate the following.
1) The thickness of velocity boundary layer decreases with increasing unsteadiness parameter.
2) The thickness of thermal boundary layer decreases with increasing unsteadiness parameter.
3) An increment in unsteadiness parameter A increases the skin friction coefficients and decreases the local Nusslet number.
4) Temperature decreases with an increasing in the value of unsteadiness parameter A.
5) Increasing the Prandtl number Pr leads to a decrease in the surface temperature.
REFERENCES
- L. J. Crane, “Flow Past a Stretching Plate,” Journal of Applied Mathematic and Physics (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- P. Carragher and L. J. Crane, “Heat Transfer on a Continuous Stretching Sheet,” Journal of Applied Mathematic and Mechanics, Vol. 62, No. 10, 1982, pp. 564-565.
- B. K. Dutta, P. Roy and A. S. Gupta, “Temperature Field in Flow over a Stretching Surface with Uniform Heat Flux,” International Communication in Heat Mass Transfer, Vol. 12, No. 1, 1985, pp. 89-94. doi:10.1016/0735-1933(85)90010-7
- L. J. Grubka and K. M. Bobba, “ Heat Transfer Characteristic of a Continuous Stretching Surface with Variable Temperature,” Journal of Heat Transfer, Vol. 107, No. 1, 1985, pp. 248-250. doi:10.1115/1.3247387
- E. M. A. Elbashbeshy, “Heat Transfer over a Stretching Surface with Variable Surface Heat Flux,” Journal of Physics D: Applied Physics, Vol. 31, No. 16, 1998, pp. 1951- 1954. doi:10.1088/0022-3727/31/16/002
- E. M. A. Elbashbeshy and M. A. A. Bazid, “Heat Transfer over an Unsteady Stretching Surface,” Journal of Heat and Mass Transfer, Vol. 41, No. 1, 2004, pp. 1-4. doi:10.1007/s00231-004-0520-x
- S. Sharidan, T. Mahood and I. Pop, “Similarity Solutions for The Unsteady Boundary Layer Flow and Heat Transfer Due to A Stretching Sheet,” International Journal of Applied Mechanics and Engineering, Vol. 11, No. 3, 2006, pp. 647-654
- A. Ishak, R. Nazar and I. Pop, “Boundary Layer Flow and Heat Transfer over Unsteady Stretching Vertical Surface,” Meccanica, Vol. 44, No. 4, 2009, pp. 369-375. doi:10.1007/s11012-008-9176-9
- E. M. A. Elbashbeshy and D. A. Aldawody, “Heat Transfer over an Unsteady Stretching Surface with Variable Heat Flux in the Presence of Heat Source or Sink,” Computers and Mathematics with Applications, Vol. 60, No. 10, 2010, pp. 2806-2811. doi:10.1016/j.camwa.2010.09.035
- R. E. Bellman and R. E. Kalaba, “Quasilinearization and Nonlinear Boundary Value Problems,” American Elsevier, New York, 1965.
- M. Massoudi and C. E. Maneschy, “Numerical Solution to the Flow of a Second Grade Fluid over a Stretching Sheet Using the Method of Quasilinearization,” Journal of Applied Mathematics and Computation, Vol. 149, No. 1, 2004, pp. 165-173
- T. Hymavathi and B. shanker, “A Quasilinearization Approach to Heat Transfer in MHD Visco-Elastic Fluid Flow,” Journal of Applied Mathematics and Computation, Vol. 215, No. 6, 2009, pp. 2045-2054
- R. Bhargava, L. Kumar and H. S. Takhar, “Numerical Solution of Free Convection MHD Micropolar Fluid Flow between Two Parallel Porous Vertical Plates,” International Journal of Engineering Science, Vol. 41, No. 2, 2003, pp. 123-136. doi:10.1016/S0020-7225(02)00157-X
- D. Srinivasacharya and M. Shiferaw, “Numerical Solution to the MHD Flow of Micro Polar Fluid between Two Concentric Porous Cylinders,” International Journal of Applied Mathematics and Mechanics, Vol. 4, No. 2, 2008, pp. 77-86.
- C. L. Huang, “Application of Quasi-Linearization Technique to the Vertical Channel Flow and Heat Convection,” International Journal of Non-Linear Mechanics, Vol. 13, No. 2, 1978, pp. 55-60. doi:10.1016/0020-7462(78)90015-X
- C.-L. Hunge, “Applying Quasi-Linearization to the Problem of Flow through an Annulus with Porous Walls of Different Permeability,” Journal of Applied scientific Research, Vol. 29, No. 1,1974, pp. 145-158.
- M. M. Rashidi and S. A. Mohimanian Pour, “Analytic Approximate Solutions for Unsteady Boundary-Layer and Heat Transfer Due to a Stretching Sheet by Homotopy Analysis Method,” Non-linear Analysis: Modelling and Control, Vol. 15. No. 1, 2010, pp. 83-95.

