World Journal of Mechanics
Vol.05 No.12(2015), Article ID:62115,8 pages
10.4236/wjm.2015.512025
Stability Analysis of a SDOF Mechanical Model with Distinct Critical Points: II. Catastrophe Theory Approach
Dimitrios S. Sophianopoulos, Vasiliki S. Pantazi
Department of Civil Engineering, University of Thessaly, Volos, Greece

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 October 2015; accepted 19 December 2015; published 22 December 2015
ABSTRACT
In a recent publication [1] , the fully nonlinear stability analysis of a Single-Degree-of Freedom (SDOF) model with distinct critical points was dealt with on the basis of bifurcation theory, and it was demonstrated that this system is associated with the butterfly singularity. The present work is the companion one, tackling the problem via the Theory of Catastrophes. After Taylor expanding the original potential energy function and introducing Padè approximants of the trigonometric expression involved, the resulting truncated potential is a universal unfolding of the original one and an extended canonical form of the butterfly catastrophe potential energy function. Results in terms of equilibrium paths, bifurcation sets and manifold hyper-surface projections fully validate the whole analysis, being in excellent agreement with the findings obtained via bifurcation theory.
Keywords:
Mechanical Models, Nonlinear Stability, Critical Points, Catastrophe Theory, Butterfly Singularity

1. Introduction
Problems in Non-Linear Buckling, where various phenomena may arise, such as discontinuities, singularities and instabilities, can be efficiently treated by using Catastrophe Theory [2] - [4] , and a better insight on them can be readily gained. Due to its topological character, this particular Theory allows for the establishment of universal solutions and the direct production of qualitative results, since it deals with various forms of potential energy functions incorporating the behavior of classes of complex systems.
The Theory of Catastrophes supplies the tools for comprehension and detection of numerous types of bifurcations and it has been proven highly efficient as far as potential discrete or continuous systems are concerned. Among the former type of systems, mechanical models (original ones or products of adequate discretization of the latter systems) with a few degrees of freedom are included, which, despite their geometrical and overall simplicity, may exhibit a quite complicated post-buckling response, associated with all kinds of distinct critical points. Their treatment via the foregoing Theory however is not an easy task, and this remark is fully justified from the admittedly limited relevant publications [5] - [13] .
Aiming to contribute a further step towards the goal of using Catastrophe Theory in achieving universal results on the buckling and post-buckling of a simple model, the present work reconsiders the single DOF system dealt with in [1] , utilizing advanced mathematical tools [14] . After Taylor expansions and Padé approximations of trigonometric functions, the universal unfolding of the system’s original potential energy yields the butterfly singularity, in full accordance with the findings of the Theory of Bifurcations [1] .
2. Single DOF System and Its Truncated Total Potential Energy Function
We reconsider the single DOF mechanical model studied in the companion paper [1] , depicted in Figure 1.
The system consists of a weightless rigid bar of length ℓ, partially pinned at its base via a linear rotational spring of stiffness c; its tip is connected via an inclined linear extensional spring of stiffness k, the angle of inclination a of which is always constant, since the other end of the spring freely slides along an equally inclined support. The tip of the bar (point A) is acted upon by a gravitational force P. Hence, the single degree of freedom (active coordinate) characterizing the foregoing model is the rotation θ. Τhis model is considered generally imperfect, by introducing an initial rotation ε. Before the action of the loading P the springs are considered unstressed. Angle α is measured (i.e. is positive) from the horizontal line passing through point A clockwise, while both rotations θ and ε are measured from the vertical line through the base again clockwise.
After the introduction of the dimensionless parameters 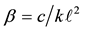 and
and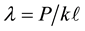 , the non-dimensional total potential energy function governing the system is given by
, the non-dimensional total potential energy function governing the system is given by
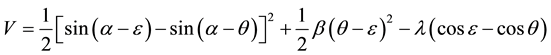 . (1)
. (1)
Aiming to explore the nature of the above potential and classify the system to one of the seven Elementary Catastrophes [4] if possible, we perform a Taylor series expansion of the function given in Expression (1) up to the 6th order and introduce in the outcome of this process Padé approximations of the trigonometric functions involved (associated only with a and ε), given in general by:
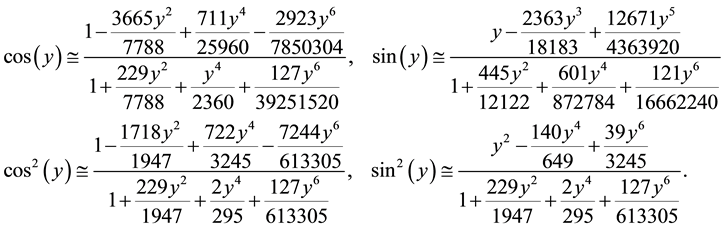 (2a-d)
(2a-d)
Figure 1. Single DOF mechanical model dealt with herein.
After cumbersome symbolic manipulations in Mathemetica [14] , the truncated potential of the foregoing model takes a 6th-order polynomial form with respect to θ, given by
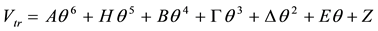 . (3)
. (3)
where coefficients Α, Β, Γ, Δ, Ε, Ζ and H are strongly nonlinear functions of the four parameters a, β, λ, ε; their general form is given below:
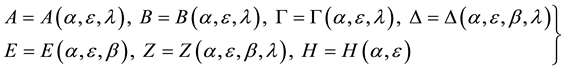 . (4)
. (4)
The exact expressions of these coefficients are enormously lengthy, and so they will not be given herein for reasons of brevity. Following standard procedures (monomials, k-jets and so on) described in [6] , it was found that the truncated potential given above is a universal unfolding of the original one, since it has a co-dimension equal to four and a determinacy equal to six. These procedures however were extremely time-consuming and literally almost exhausted our computer resources.
Evidently,  has one active variable and resembles the standard form of the potential associated with the Butterfly Singularity. There are however three distinguished differences/obstacles, which do not allow us to fully classify it among the seven elementary Catastrophes, namely: (a) the “constant” term Z, which has a negligible influence [4] [6] , since Catastrophe Manifolds (equilibria) and Bifurcation Sets (critical states), associated with 1st and 2nd order derivatives of
has one active variable and resembles the standard form of the potential associated with the Butterfly Singularity. There are however three distinguished differences/obstacles, which do not allow us to fully classify it among the seven elementary Catastrophes, namely: (a) the “constant” term Z, which has a negligible influence [4] [6] , since Catastrophe Manifolds (equilibria) and Bifurcation Sets (critical states), associated with 1st and 2nd order derivatives of 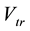 with respect to the active variable θ, are not affected by its presence, (b) the 5th order term related to coefficient H, which however does not depend on the external load, remaining constant as λ is varied, and (c) the effect of the presence of coefficient A on the truncated potential.
with respect to the active variable θ, are not affected by its presence, (b) the 5th order term related to coefficient H, which however does not depend on the external load, remaining constant as λ is varied, and (c) the effect of the presence of coefficient A on the truncated potential.
We initially address the latter of the aforementioned obstacles. The standard perturbation of the germ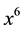 , associated with the butterfly singularity, is of the form
, associated with the butterfly singularity, is of the form 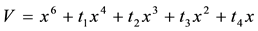 [5] , with four unfolding parameters. The presence of A initially reveals a fifth unfolding parameter, which would not allow the sought classification. However, within accepted ranges of the parameters α, ε and λ (on which A depends), if its mean value is independent of these parameters, then one could easily consider A as a quasi-constant. Consequently, the whole analysis could in this case be continued smoothly, overcoming this particular drawback.
[5] , with four unfolding parameters. The presence of A initially reveals a fifth unfolding parameter, which would not allow the sought classification. However, within accepted ranges of the parameters α, ε and λ (on which A depends), if its mean value is independent of these parameters, then one could easily consider A as a quasi-constant. Consequently, the whole analysis could in this case be continued smoothly, overcoming this particular drawback.
Indeed, after cumbersome symbolic and algebraic calculations [14] , it was found than the mean value of A, for a ranging from −π/2 to 3π/2, ε ranging from −π/2 to π/2 and λ ranging from −5 to 10, it was found that A varies from 0.025 to −0.10, with a mean value −0.0375 and a negliblibly small standard deviation. Consequently, the presence of A does not affect our classification effort whatsoever.
Considering at this point the second of the above obstacles, the following are valid. Within the range of values of the angular parameters α and ε, on which H is dependent, given above, one may plot the surface , which is depicted in Figure 2. Its absolute maximum value does not exceed 0.0695, implying that the term
, which is depicted in Figure 2. Its absolute maximum value does not exceed 0.0695, implying that the term
Figure 2. Variation, via 3D plot, of the value of coeffient H within accepted ranges of values of control parameters α and ε.
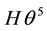 becomes negligibly small for values of θ smaller than 1, while for the extreme model deformation of θ equal to −π/2 or π/2 this term remains smaller than 0.7. These preliminary findings are a strong initial indication that the above term may be omitted from the expression of the truncated potential and hence one may assume that the related Singularity is indeed of the Butterfly type. The qualitative analysis that follows will provide strong evidence and justification of the above, taking also into account the local nature of the whole approach. and the Splitting Lemma of the Theory of Catastrophes [4] .
becomes negligibly small for values of θ smaller than 1, while for the extreme model deformation of θ equal to −π/2 or π/2 this term remains smaller than 0.7. These preliminary findings are a strong initial indication that the above term may be omitted from the expression of the truncated potential and hence one may assume that the related Singularity is indeed of the Butterfly type. The qualitative analysis that follows will provide strong evidence and justification of the above, taking also into account the local nature of the whole approach. and the Splitting Lemma of the Theory of Catastrophes [4] .
3. Qualitative Analysis
Based on the preceding findings, the qualitative analysis that follows consists of two steps. In the 1st step, a brief description of the theoretical background is presented, while the 2nd step concerns symbolic manipulations for the computation of Catastrophe Manifolds (CMs) and Bifurcation Sets (BSs).
Thereafter, verification, validation and proof of the existence of the Butterfly Singularity via a parametric comparative study of the CMs, BSs (and related projections) of the system are given in the Numerical Results and Discussion section.
3.1. Theoretical Background
For any given gradient system, governed by a potential V, which is associated with one state (independent) variable?active coordinate, say x, and four control parameters, defined by ri (i = 1 − 4), i.e. V = V(x; ri), Nonlinear Stability and Bifurcation Theory dictates that the equilibrium configurations are the solutions of Equation (5a), while the critical states should also satisfy Equation (5b).
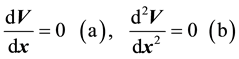 . (5a,b)
. (5a,b)
We assume that U is a universal unfolding of V, being a product of adequate Taylor expansion and truncation. We also assume that U is a 6th order polynomial of the most general form with respect to x (as the one shown in Equation (3)), the coefficients of which are known functions of ri, implying that the unfolding parameters are directly dependent on the control parameters of V. Hence, instead of seeking equilibria, critical states and bifurcations (ought to infinitesimal changes of one or more of ri, individually or in an combined manner) of the original system, it is convenient to apply Catastrophe Theory on the truncated system and afterwards compare the results with those of Nonlinear Stability Theory. Aiming to present qualitative proof that the original system, governed by V, is associated with the Butterfly Catastrophe, a short reminder of the salient features of this Singularity is given below:
・ Depending on the parameter values, the potential function may have three, two, or one different local minima, separated by the loci of fold bifurcations. At the butterfly point, the different 3-surfaces of fold bifurcations, the 2-surfaces of cusp bifurcations, and the lines of swallowtail bifurcations all meet up and disappear, leaving a single cusp structure remaining.
・ The set of critical points of the U-unfolding is the so-called four-dimensional Catastrophe Manifold CMU, given by [5]

・ The set of the singular (degenerate) critical points SU is a four-dimensional Sub-Manifold of the previous one, satisfying [5] :

・ The projection of the above Manifold in the space of the control parameters, which forms the Bifurcation Set BSU, should combine Equations (6) and (7) yielding:

・ This Bifurcation Set constitutes a hyper-surface in the four-dimensional control space, and thus its graphic representation is impossible in the three-dimensional physical space. Only 3D sections of this hyper-surface can be drawn as 3D contour plots or bifurcation diagrams, for some characteristic combinations of the control parameters, with at least one of them kept constant. Furthermore, it should be noted that pioneer publications on the subject [2] [4] [6] have revealed the immense difficulty of the sought representations, since it is valid that: (a) the BS is made of fold hyper-surfaces (lines on a 2D slice of control space) which meet on surface of cusp points which themselves meet on lines of swallowtail points, (b) these lines of swallowtail points meet together at a butterfly point and (c) at this point in control space, potential curve (germ) has only one minimum which corresponds to the collapse of three minimums and two maximums. Furthermore, the potential energy described by U will have in general an odd number of minima and an even number of maxima, and therefore, in some regions of the Catastrophe Manifold (and for some orientation of the surface) there will be up to five layers of the CMU overlying each other.
3.2. Computation of Catastrophe Manifolds and Bifurcation Sets via Elimination Scheme
From the One-Dimensional Elementary Catastrophes (Cuspoids), the Butterfly (A5 according to the classification of Thom [4] ), possesses the highest degree of complexity and moreover it rarely appears in the Theory of Elastic Stability [5] ; however, it has been found to occur in other engineering disciplines, as for instance in the mesophase stability response of external magnetic or electric fields [7] .
In order to show that the one-dimensional system studied herein exhibits the Butterfly Singularity, one may either use Equations (6) and (8) or employ and extend the alternative elimination procedure of Deng [8] . The main drawback of the latter method lies on the fact that, both CM and BS, seem to depend on all the parameters involved, namely λ, β, θ, ε and a. Hence, the former scheme will be employed hereafter.
After computing the Catastrophe Manifold, the Bifurcation Set is evaluated, by symbolically eliminating favorably either λ or β (due to their apparent linear presence). In the foregoing analysis β was eliminated, based either on the original potential, given in Equation (1), or on the truncated one with H = 0 from Equation (3). The expression governing the BS of the original system is given in Equation (9), while the one of the truncated system is extremely lengthy and will not be presented for brevity.

In the sequel, one may produce reliable results in terms of equilibrium paths, bifurcation diagrams and bifurcation sets, and qualitatively justify that the system dealt with is governed by the Butterfly Singularity, in agreement with the findings of the companion paper [1] .
4. Numerical Results and Discussion
Our first goal is to compare 3D Contour Plots of the Bifurcation Set, as products (a) of the original potential, and (b) of the truncated potential, with H = 0. The corresponding plots, for two characteristic values of imperfection parameter ε, are illustrated in Figure 3 and Figure 4.
Comparing the contents of the above figures, it is evident that the plots of the two cases are almost identical. This result verifies to a certain extent the validity of the approximate Catastrophe Theory approach adopted in this work. Further validation and evidence will be provided in what follows, by reproducing equilibrium paths and bifurcation diagrams of the system, based on its truncated potential with H = 0.
As far as equilibrium paths are concerned, the cases of β ≠ 0, α, ε = 0 and β, ε ≠ 0, α = 0 where chosen. The corresponding plots are shown in Figure 5 and Figure 6 respectively.
These paths are identical with the ones presented in the companion paper, via a Nonlinear Stability analysis.
Furthermore, several Bifurcation Diagrams (imperfection sensitivity plots) are presented, as products of the present analysis. These correspond to α = 0, shown in Figure 7, to a = 0.10, β = 0, shown in Figure 8, and to a = 0.20, β = 0.20, shown in Figure 9.
Once again, full accordance with the relevant findings of the companion paper is identified.
From all the above results and the preceding analysis, it is proven that the model exhibits the Butterfly Singularity.
Figure 3. Bifurcation Sets based on the original potential.
Figure 4. Bifurcation Sets based on the truncated potential with H = 0.
Figure 5. Equilibrium paths for β ≠ 0, α, ε = 0, based on the truncated potential with H = 0.
5. Concluding Remarks
The single degree-of-freedom model analyzed herein, although quite simple, is associated with all kinds of dis-
Figure 6. Equilibrium paths for β, ε≠0, α = 0, based on the truncated potential with H = 0.
Figure 7. Bifurcation diagrams for α = 0, based on the truncated potential with H = 0.
Figure 8. Bifurcation diagrams for a = 0.10, β = 0, based on the truncated potential with H = 0.
tinct critical points and related to the Butterfly Catastrophe, a situation scarcely encountered in Structural Mechanics. The use of the truncated potential, within reasonable parameter ranges, lead to results in excellent
Figure 9. Bifurcation diagrams for a = 0.20, β = 0.20, based on the truncated potential with H = 0.
agreement with ones obtained from the original potential in terms of equilibria, imperfection sensitivity and Bifurcation Sets, as also reported in the companion paper.
Cite this paper
Dimitrios S.Sophianopoulos,Vasiliki S.Pantazi, (2015) Stability Analysis of a SDOF Mechanical Model with Distinct Critical Points: II. Catastrophe Theory Approach. World Journal of Mechanics,05,266-273. doi: 10.4236/wjm.2015.512025
References
- 1. Sophianopoulos, D.S. (2013) Stability Analysis of a Single-Degree-of-Freedom Mechanical Model with Distinct Critical Points: I. Bifurcation Theory Approach. World Journal of Mechanics, 3, 62-81.
http://dx.doi.org/10.4236/wjm.2013.31005 - 2. Woodcock, A.E.R. and Poston, T. (1974) A Geometrical Study of the Elementary Catastrophes. Springer, New York.
http://dx.doi.org/10.1007/BFb0068967 - 3. Stewart, I.A. (1980) Catastrophe Theory and Equations of State: Conditions for a Butterfly Singularity. Mathematical Proceedings of the Cambridge Philosophical Society, 88, 429-449.
http://dx.doi.org/10.1017/S0305004100057789 - 4. Gilmore, R. (1981) Catastrophe Theory for Scientists and Engineers. Dover, New York.
- 5. Theocaris, P.S. (1984) Instability of Cantilever Beams with Non-Linear Elements: Butterfly Catastrophe. International Journal of Mechanical Sciences, 26, 265-275.
http://dx.doi.org/10.1016/0020-7403(84)90047-X - 6. Steindl, H. and Troger, A. (1991) Nonlinear Stability and Bifurcation Theory. Springer, New York.
- 7. Pershin, K.Vl. (1992) The Butterfly Catastrophe and Mesophase Stability in an External Field. Physics Letters A, 161, 510-516.
http://dx.doi.org/10.1016/0375-9601(92)91083-4 - 8. Deng, C.-G. (1994) Equations of Bifurcation Sets of Three-Parameter Catastrophes and Application in Imperfection Sensitivity Analysis. International Journal of Engineering Science, 32, 1811-1822.
http://dx.doi.org/10.1016/0020-7225(94)90110-4 - 9. Lignos, X.A., Parke, G.A.R., Harding, J.E. and Kounadis, A.N. (2002) A Comprehensive Catastrophe Theory for Non-Linear Buckling of Simple Systems Exhibiting Fold and Cusp Catastrophes. International Journal of Numerical Methods in Engineering, 54, 175-193.
http://dx.doi.org/10.1002/nme.416 - 10. Lignos, X., Ioannidis, G. and Kounadis, A.N. (2003) Non-Linear Buckling of Simple Models with Tilted Cusp Catastrophe. International Journal of Nonlinear Mechanics, 38, 1163-1172.
http://dx.doi.org/10.1016/S0020-7462(02)00061-6 - 11. Lengyel, A. and You, Z. (2004) Bifurcations of SDOF Mechanisms Using Catastrophe Theory. International Journal of Solids and Structures, 41, 559-568.
http://dx.doi.org/10.1016/j.ijsolstr.2003.09.024 - 12. Raftoyiannis, I.G., Constantakopoulos, T.G., Michaltsos, G.T. and Kounadis, A.N. (2006) Dynamic Buckling of a Simple Geometrically Imperfect Frame Using Catastrophe Theory. International Journal of Mechanical Sciences, 48, 1021-1030.
http://dx.doi.org/10.1016/j.ijmecsci.2006.05.010 - 13. Sophianopoulos, D.S. (2007) Bifurcations and Catastrophes of a Two-Degrees-of-Freedom Nonlinear Model Simulating the Buckling and Postbuckling of Rectangular Plates. Journal of the Franklin Institute, 344, 463-488.
http://dx.doi.org/10.1016/j.jfranklin.2006.02.012 - 14. Wagon, S. (2010) Mathematica® in Action: Problem Solving Through Visualization and Computation. Springer, New York.
http://dx.doi.org/10.1007/978-0-387-75477-2










