World Journal of Mechanics
Vol.4 No.6(2014), Article
ID:47456,5
pages
DOI:10.4236/wjm.2014.46020
Kinematics of a 2D Asymmetric Nonlinear Oscillator
Haiduke Sarafian
Pennsylvania State University, University College, York, USA
Email: has2@psu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 8 May 2014; accepted 4 June 2014
Abstract
Motion of a point-like massive particle under the influence of two nonidentical linear springs conducive to an irregular planar oscillation is analyzed. For a two dimensional oscillations the equation of motion is a coupled highly nonlinear differential equation. The set of equations cannot be solved analytically. Utilizing a Computer Algebra System (CAS) such as Mathematica [1] we solve the equations numerically. Kinematics of the particle is presented. For a comprehensive visual understanding the oscillations are simulated. We also include an extended atlas of useful two-dimensional time-folded diagrams.
Keywords:2D Nonlinear Oscillator, Computer Algebra System, Mathematica

1. Introduction and Objectives
In our previous investigation [2] we analyzed the impact of nonlinear position dependent forces, specifically a cubic, a quintic and their respective combinations on the characteristics of a one dimensional oscillator. We devised a prototype composed of two identical linear light springs resulting in one dimensional oscillation for a point-like massive object. Aside from the main objective, i.e., the analysis of oscillations, we proposed also a fresh method for solving the associated equation of motion. This article with two major modifications is the extension of our previous work. First, by deploying a somewhat similar empirical setting we consider asymmetric linear light springs, and, second we allow two dimensional oscillations. The latter complicates the analysis; this is because the movement of the point-like object comes from combination of in-tangled motions along two independent directions. The latter even becomes more challenging considering the asymmetry of the springs. These equations may not be untangled, and the coupled ODE may not be solved analytically. This project is an excellent forum to promote the application of Computer Algebra System (CAS). In the analysis section we detail the procedure. To address the issues at hand, we craft a paper composed of four sections. In addition to Introduction and Objectives, in Section 2 we outline the physics problem. In Section 3 we present the results including an atlas of useful graphs of kinematics. We close the paper with concluding remarks.
2. The Physics of the Problem
Figure 1 is the schematic of the assembly of the problem at hand. One end of each asymmetric spring is fastened to a support and the other ends are tied to a massive marble. The entire setup is placed on a level surface, so that gravity has no impact. Pulling the marble from its original rest position, O, to an arbitrary position P (x, y) on the xy-plane brings about the restoration forces F1 and F2 along the springs as shown. The motion of the marble after release is subject to these forces. Resolving these forces along two independent coordinates x, y yields the corresponding equation of motions.
Assuming the springs are linear the force components along the x and y axes are:
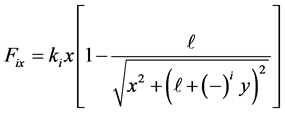 (1)
(1)
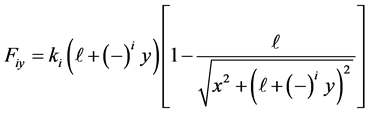 (2)
(2)
Here i = 1, 2 and  is the relaxed length of the springs; k1 and k2 are the stiffness of the first and the second spring, respectively.
is the relaxed length of the springs; k1 and k2 are the stiffness of the first and the second spring, respectively.
Utilizing Equations (1 & 2) the corresponding equations of motion are:
 (3)
(3)
 (4)
(4)
Where m is the marble’s mass and double-dots indicate the second order derivatives with respect t. The set of Equations (3 & 4) are coupled, and are highly nonlinear differential equations. We were unable to solve them analytically, so did Mathematica. What follows are the output of the numeric solutions of these equations. Based on our previous reported experience [2] , we utilize  = 6.0 cm and m = 10.0 g. We pull the mass from its initial relaxed position to an arbitrary point on the xy-plane, and then release it freely. We compose a simulation program in Mathematica such that the stiffness of the springs and the initial coordinate of the mass are input parameters. Solution of above equations are implicitly time dependent. By suppressing the time variable we construct the geometric trajectory of the marble. Following the same strategy we construct various useful phase diagrams.
= 6.0 cm and m = 10.0 g. We pull the mass from its initial relaxed position to an arbitrary point on the xy-plane, and then release it freely. We compose a simulation program in Mathematica such that the stiffness of the springs and the initial coordinate of the mass are input parameters. Solution of above equations are implicitly time dependent. By suppressing the time variable we construct the geometric trajectory of the marble. Following the same strategy we construct various useful phase diagrams.
3. Results
Simulation template of the aforementioned strategy is shown in Figure 2.The left column is the adjustable sliders for the stiffness, and initial coordinate of the marble, the last slider controls the run time of the simulation. The right panel displays the x and y coordinates of the marble vs. time. For the chosen values of the displayed parameters one learns about the impact of the asymmetry of the stiffness and the initial coordinate one frameat-a-time. For instance although the vibrations along the y-axis are somewhat harmonically regular, the x-component displays an exotic behavior.
Plots of the coordinate of the marble vs. time as shown in Figure 2 are useful and informative. With the flexible features built into the simulation program, one may adjust the values of the relevant parameters to analyze the impact of each individual parameter on the movement of the marble. It is also desirable to view the actual movement of the marble. To accomplish this goal, we compose another simulation program; its template is shown in Figure 3. The engine of this simulation contains a feature that eliminates the implicit time-dependent
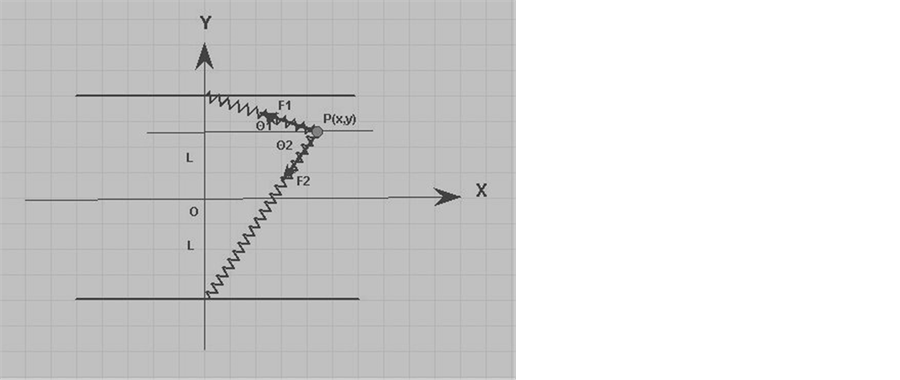
Figure 1. Two light asymmetric springs are tied to a common massive marble. The setup is assembled on a horizontal table. The initial position of the marble P (x, y) and the spring forces F1 and F2 are shown.

Figure 2. Display of the simulation template with the control sliders on the left, and coordinate of the marble vs. time on the right.

Figure 3. Simulation template of the motion of the marble along with its 166 cumulative traced trajectories.
solution of the set of ODEs [Equations (3 & 4)] and plots the associated coordinate (x, y) along with the trace of the connected curves between adjacent coordinates. The simulation template has two built-in frames/second speed control buttons allowing displaying the position and associated traces one frame at a time making the analysis of the motion useful and meaningful. Figure 3 displays a collection of 166 such frames. Parameters associated with this plot are: k1 = 5.0, k2 = 3.0, and the marble initially was place in the second quadrant; units are all in MKS. For visual purposes the marble, the top and the bottom springs are colored in green, blue and red, respectively.
As in the previous simulation template one may select different values for the stiffness and initial position of the marble to analyze their impact on the trajectory. The author created an atlas of such trajectories. Because of the space limitation only one case is included.
In the rest of the paper we display various time-suppressed diagrams. The traditional phase diagram is a plot of speed vs. position. The marble moves in a 2D space so there are two such diagrams, one per dimension. As we reported in our previous investigation [3] in addition to the traditional phase diagrams one may also plot useful non-traditional time-suppressed diagrams as well, such as position vs. acceleration and speed vs. acceleration. Also because of the 2D motion one may plot time-folded mixed variables, such as the position coordinate along one axis vs. the speed along the second dimension. The list of such combinations is quite long. Following this road map, in Figure 4 we display a set of three such plots. These are plots of kinematic variables associated with the x-axis.
Similarly, Figure 5 displays plots of kinematic quantities along the y-axis.
Figure 6 is a display of selected mixed kinematic quantities. The left plot is the display of x variable vs. the speed along the y-axis. Its adjacent plot displays the x position vs. the acceleration along the y-axis. As mentioned earlier the plots of the mixed mode variables are long, and because of the space limitation only two such graphs are included. Interested readers may try analyzing the problem beyond what we included here.
A word of caution: For the sake of clarity horizontal and vertical axes of all the plots in Figures 4-6 are scaled. We have applied appropriately chosen scale factors making the plots readable. However, all the graphs are in SI units.
4. Conclusion
It is the objective of this investigation to augment the scope of our previous work [2] . We accomplish this uti
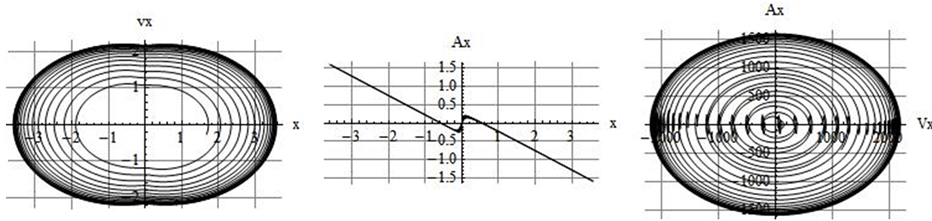
Figure 4. Time-suppressed display of various kinematic quantities along the x-axis. The left diagram is the traditional phase plot. The middle and the right plots are non-traditional. For the sake of clarity the axes are scaled.
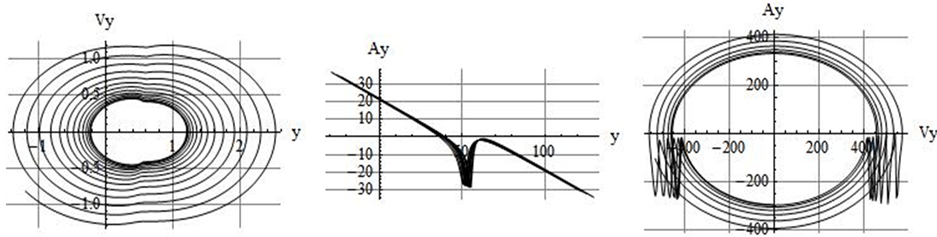
Figure 5. Time-folded display of various kinematic quantities along the y-axis. The left diagram is the traditional phase plot. The middle and the right plots are non-traditional. For the sake of clarity the axes are scaled.
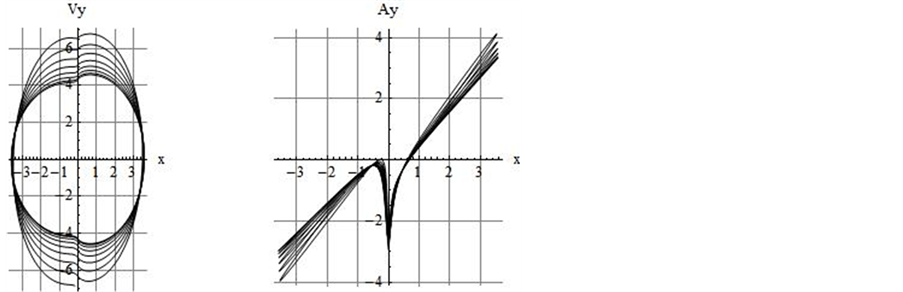
Figure 6. Time-suppressed display of various mixed kinematic quantities along the x and y-axes. For the sake of clarity the axes are scaled.
lizing a CAS, specifically Mathematica [1] . The author believes without deploying a CAS the features of this 2D motion would have stayed unresolved. This report includes a numeric solution of coupled highly nonlinear differential equations. The solutions of these equations are used to simulate the motion of a massive particle in a 2D space. We also include a list of useful time-suppressed diagrams. The asymmetry of the setup due to nonidentical linear springs is well highlighted. We also provide a guideline so that interested readers may launch his/her own investigation.
References
- (2012) Mathematica, V9.0, a Computational Software Program to Do Scientific Computation. Wolfram Research.
- Sarafian, H. (2013) Linear, Cubic and Quintic Coordinate-Dependent Forces and Kinematic Characteristics of a Spring-Mass System. World Journal of Mechanics, 3, 265-269. http://dx.doi.org/10.4236/wjm.2013.36027
- Sarafian, H. (2011) Nonlinear Oscillations of a Magneto Static Spring-Mass. Journal of Electromagnetic Analysis and Applications, 3, 133-139. http://dx.doi.org/10.4236/jemaa.2011.35022

