World Journal of Mechanics
Vol. 3 No. 6 (2013) , Article ID: 37346 , 6 pages DOI:10.4236/wjm.2013.36030
Hydrodynamic Limitations of Microchannel Fischer-Tropsch Reactor Operation
1Moscow State Technical University by N.E. Bauman, Moscow, Russian Federation
2Federal State Institution “Technological Institute for Superhard and Novel Carbon Materials”, Troitsk, Russian Federation
3INFRA Technology Ltd., Moscow, Russian Federation
Email: *DerevichIgor@gmail.com
Copyright © 2013 Igor V. Derevich et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 14, 2013; revised August 16, 2013; accepted September 12, 2013
Keywords: Fischer-Tropsch; Microchannel; Liquid; Pressure; Annular; Catalysis; Resistance; Conversion
ABSTRACT
The pressure drop in a microchannel Fischer-Tropsch reactor was investigated by means of a fluid dynamics model developed by the authors. The developed model takes into account roughness of the microchannel wall induced by catalyst particle deposition on the surface of the microchannel. The presented simulation procedure takes into account the variation of the synthesis product composition and the variation of thermal properties of the liquid and gas phases along the microchannel length as functions of pressure, temperature, conversion rate and chain growth coefficient. Liquid and gaseous products down flow are modeled in the annular flow approximation. The obtained results are presented for two general types of microchannels, i.e. for rough-walled and for smooth-walled microchannels. It is shown that fluid dynamics in rough-walled and smooth-walled microchannels are dramatically different. It is established that a mean critical diameter can be introduced. The microchannels with diameter below the mean critical value can experience operation difficulty due to by high aerodynamic resistance or can even become completely flooded.
1. Introduction
The Fischer-Tropsch synthesis is a key step in the process of synthetic crude production from natural gas or other carbon-containing feedstock. The chemistry of the process includes conversion of syngas (CO and H2 mixture) into hydrocarbons over Co metal or Fe metal catalyst. The molecular mass distribution of produced hydrocarbons obeys Anderson-Schulz-Flory law [1]. The maximum of the distribution is determined by chain growth coefficient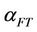 . For higher value of
. For higher value of 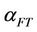 the heavier hydrocarbons dominate the product. It is attractive to run the Fischer-Tropsch reaction at
the heavier hydrocarbons dominate the product. It is attractive to run the Fischer-Tropsch reaction at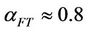 , which gives the molecular mass distribution close to that of diesel fuel.
, which gives the molecular mass distribution close to that of diesel fuel.
Currently are realized two types of Fischer-Tropsch reactors in industrial practice, namely slurry-bed reactors and fixed-bed reactors. Both types of the reactors possess certain advantages and drawbacks related with thermal stability, diffusion limitations and aerodynamic resistance.
The recent successes in microchannel fabrication technologies have led to very active research and development of microchannel systems for Fischer-Tropsch synthesis as a challenge to conventional slurry-bed and fixed-bed reactors [2-6]. Cobalt catalyst microparticles of 50 - 300 µm size get deposited on the inner surface of a microchannel thus forming a randomly roughed inner surface. Such micro reactors promise easy transport of syngas to catalyst surface and excellent heat removal conditions. The efficiency of a microchannel system increases with decrease in the microchannel diameter. However, the hydrodynamic resistance can ruin the reactor operation even at very good diffusion and hat removal efficiencies. The importance of hydrodynamic resistance cannot be overestimated. It is difficult, however, to estimate this value.
Indeed, experimental measurements must be carried out with the use of gas-liquid mixtures of proper composition, which changes along the channel, otherwise the results cannot be correct. The computational methods available in literature are good for modeling flow in smooth channel, without taking into account evolution of properties and composition along the channel [7-9]. It is necessary to note that hydrodynamics of smooth-walled and rough-walled channels can be dramatically different even for laminar flow. Another important factor is that literature computational methods suggest that gas flow and liquid film flow are considered as independent, which results in substantial error in liquid film thickness value [10].
This work is devoted to investigation of hydrodynamic resistance in microchannel Fischer-Tropsch reactors and its influence on the reactor operation. Theoretical model was published in our previous work [11], where conjugated flow of gaseous and liquid Fischer-Tropsch products of variable composition was considered. The gaseous and liquid flows were modeled in annular flow approximation, while inertia, surface tension and hydrodynamic interaction of phases at interphase boundary are taken into account. Presented work models the randomly roughed internal surface of microchannels in accordance with the technology of catalyst microparticles deposition. The difference in modeling of smooth-walled and rough-walled channels is investigated. The dependencies of hydrodynamic resistance on syngas flow rate, chain growth coefficient , conversion rate, temperature and pressure are modeled. The limitations of microreactor operation are studied, up to determination of conditions for complete flooding of a microchannel.
, conversion rate, temperature and pressure are modeled. The limitations of microreactor operation are studied, up to determination of conditions for complete flooding of a microchannel.
2. Formulation of the Problem. The Basic Equations
It is consider a vertical cylindrical microchannel. Procedure of numerical generation a random surface inside the ceramic microchannel is carried out in accordance with the technical method of coating the channel walls by catalyst microparticles. It is selected the average number of spherical particles per unit length of the microchannel. For cylindrical coordinate system microparticles are modeled as random rings located on the perimeter of the cylinder. The distance between the micro inclusions and the height of the roughness are also independent random variables. The number of particles is recalculated in order to preserve a given volume fraction of particulate catalyst inside the microchannel. Volume fraction of cobalt particles is in the range 20% - 30%.
Figure 1 illustrates sketch of an element of the channel with random roughness and with a liquid film. The liquid film flows down along inner surface of a cylindrical microchannel, and the gas moves inside a cylinder of liquid formed by the outer surface of the film. Film velocity is determined by the force of gravity and shear stresses on the gas-liquid interface boundary. Shear stress at the gas-liquid boundary depends on the thickness and diameter of the gas stream. The pressure gradient in the channel is determined by the combined flow of the liquid
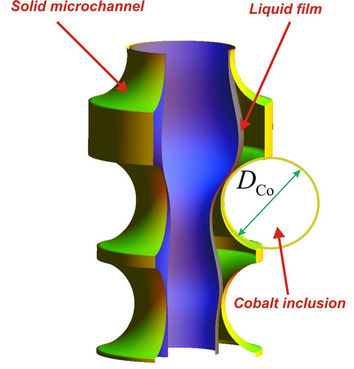
Figure 1. Element of a microchannel with roughness formed by sedimentation of cobalt microparticles at walls of the channel and liquid film.
and gas, and can be found only by solving the conjugate problem, which taking into account the velocity and shear stress at the gas-liquid interface boundary.
A random micro inclusion inside the channel causes a significant change in film thickness, which leads to the appearance of capillary effects. The capillary forces are making a significant contribution to the dynamics of the liquid film and influence on the pressure drop in the microchannel. All of these complicating factors must be taken into account when developing of annular flow model of synthesis liquid and gaseous products in a microchannel. Taking into account the low rate of catalytic reactions, the thermodynamic parameters and thermophysical properties of liquid and gaseous products are calculated for the equilibrium case. Modeling of the liquid film and gas hydrodynamics is based on the balance equations of axial momentum components [12]. Taking into account the viscous shear stress at the gas-liquid interface boundary and surface tension force, and integrate the Navier-Stokes equations over the cross section of the microchannel, one can derive the system of momentum balance equations for liquid and gaseous products [11]
 (1)
(1)
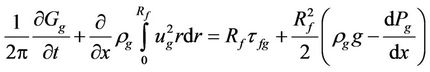 . (2)
. (2)
Here 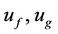 are liquids film and gas axial components of velocities,
are liquids film and gas axial components of velocities,  is gravitational acceleration,
is gravitational acceleration,  are mass flow rate of liquid and gaseous synthetic products, x is axial coordinate,
are mass flow rate of liquid and gaseous synthetic products, x is axial coordinate, 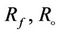 are radii of the outer surface of the film and the inner surface of the random channel,
are radii of the outer surface of the film and the inner surface of the random channel,  is coefficient of surface tension at gas-liquid interphase boundary,
is coefficient of surface tension at gas-liquid interphase boundary,  are viscous stresses at gas-liquid interphase boundary and at solid wall of the microchannel,
are viscous stresses at gas-liquid interphase boundary and at solid wall of the microchannel,  are densities of liquid and gaseous mixtures,
are densities of liquid and gaseous mixtures, 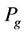 is pressure in the gaseous phase, the coordinate system and direction of movement of liquid and gaseous products are shown in Figure 2.
is pressure in the gaseous phase, the coordinate system and direction of movement of liquid and gaseous products are shown in Figure 2.
The system of Equations (1), (2) describes the hydrodynamics of liquid and gas in the annular flow approximation. Calculation of shear stresses at the gas-liquid interface boundary and at the solid wall of the channel require the approximation of liquid and gas velocities in the channel. Assumption about thermodynamic equilibrium leads to the dependence of mass flow rates of liquid and gaseous products on conversion rate of carbon dioxide KCO.
The distribution of velocity in the liquid film flowing on a cylindrical surface is approximated by the expression
 . (3)
. (3)
Fluid velocity (3) turns to zero on the solid surface of the channel. The parameters 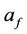 and
and 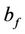 related to fluid flow rate and shear stress between gas and liquid at the interphase boundary
related to fluid flow rate and shear stress between gas and liquid at the interphase boundary
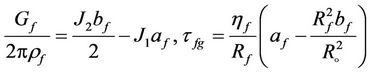 . (4)
. (4)
Here coefficients 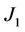 and
and  depend on the radii of the channel and liquid-gas interface boundary
depend on the radii of the channel and liquid-gas interface boundary
 ,
, .
.
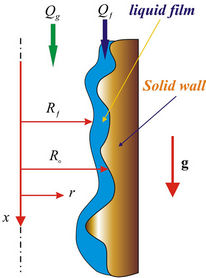
Figure 2. Coordinate frame, mass flow rates of liquid and gaseous products, radii of liquid film and an internal surface of rough-walled channel.
From (3) and (4) an expression for the difference between shear stresses in Equation (1) it is follows
 . (5)
. (5)
Velocity (3) distribution of gaseous mixture flowing within the cylinder bounded by the surface of the liquid film is approximated as
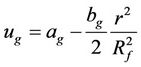 . (6)
. (6)
Equation (6) satisfies the symmetry condition at the center of a cylindrical channel. The distribution parameters 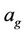 and
and 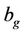 in (6) are associated with mass flow of gaseous products and the gas velocity at the gas-liquid interface boundary
in (6) are associated with mass flow of gaseous products and the gas velocity at the gas-liquid interface boundary 
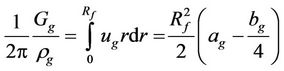 , (7)
, (7)
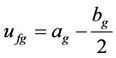 . (8)
. (8)
The expression for the shear stress at the gas-liquid interface boundary from the gas side follows from the velocity distribution (6)
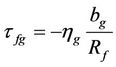 . (9)
. (9)
The terms describing the inertial effects in the liquid (1) and gas (2) equations, are modeled as follows
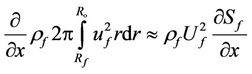 , (10)
, (10)
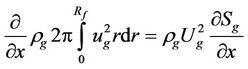 . (11)
. (11)
Here 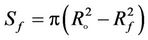 is area of liquid film cross section,
is area of liquid film cross section, 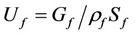 is mean velocity of liquid,
is mean velocity of liquid,  is area of the gas cross section, and
is area of the gas cross section, and 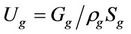 is mean velocity of the gas.
is mean velocity of the gas.
Coupled hydrodynamics of liquid and gaseous products of the synthesis is described by the closed system of Equations (1)-(11).
3. Calculation Results
The composition of the synthesis products is modeled as paraffin hydrocarbons. The product distribution of hydrocarbons is described by the Anderson-Schulz-Flory formula [1]. Calculations of thermodynamic equilibrium in hydrocarbon mixtures in liquid and vapor phases and thermophysical properties of paraffins composition are realized on the methods outlined by the authors [13,14].
Figure 3 presents mass fraction of liquid and gaseous synthetic products as a function of CO conversion. Calculation results correspond with temperature TR = 220˚C and pressure PR = 20 bar.
The Figure 3 shows that for large values of the chain growth coefficient 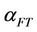 it is increased the liquid fraction in the products of synthesis.
it is increased the liquid fraction in the products of synthesis.
In calculation the length of the microchannel is equal HR = 600 mm. Volume flow rate of synthesis gas specified as the gas volume entering into the reactor per unit time per unit mass of catalyst under normal conditions. The mass flow rate of syngas at the inlet of a microchannel is calculated as follows. The mass of catalyst mCo is proportional to the volume of the microchannel
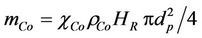 .
.
Here 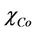 is volume fraction of cobalt particles on the surface of the microchannel,
is volume fraction of cobalt particles on the surface of the microchannel,  is density of cobalt.
is density of cobalt.
The mass flow rate of syngas at the inlet of the channel is
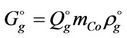 .
.
where  is density of syngas under normal conditions.
is density of syngas under normal conditions.
For example, when the volume fraction of cobalt particles is 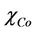 = 20% and volume flow rate of syngas is
= 20% and volume flow rate of syngas is 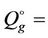 5000 cm3/(gm∙hour) molar flow rate is equal to 0.108 mole/(gm∙s). Under normal conditions and the length of the microchannel HR = 600 mm, the volume flow rate of synthesis gas leads to the linear velocity of 0.833 m/s.
5000 cm3/(gm∙hour) molar flow rate is equal to 0.108 mole/(gm∙s). Under normal conditions and the length of the microchannel HR = 600 mm, the volume flow rate of synthesis gas leads to the linear velocity of 0.833 m/s.
It is supposed that the degree of CO conversion varies linearly from zero to one along the length of the microchannel. Figure 4 shows the distributions of the radii of the inner surface of random wall of a microchannel and radius of the liquid film flowing along the channel wall. The shape of gas-liquid interface boundary weakly correlated with the shape of random surface of the channel. This is explained by action surface tension and inertia forces.
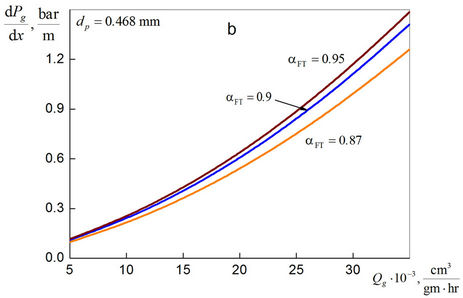
Figure 5 gives representation about dependence of the mean pressure gradient on syngas volume flow rate in the

Figure 3. Mass fractions of liquid and gaseous products as a function of conversion of CO.
microchannels with different average diameters. It is seen that decrease of the mean diameter of the channel significantly increases the pressure gradient of syngas. For the microchannels with average diameter less than 0.3 mm, the pressure gradient becomes so significant that it can cause a hydraulic blocking of the microchannel.
Figure 6 illustrates the qualitative difference in the distribution of the liquid film thickness along the length of a smooth channel in contrast with microchannel with random roughness surface. A comparison of Figures 4 and 6 shows that in the case of a smooth microchannel role of surface tension is low. Figure 7 shows the average pressure gradient in a smooth microchannel as a function of syngas volume flow rate. From Figure 7 and 5 one can conclude that smooth channel approximation can be almost ten times underestimating the pressure drop compared with the real microchannel.
4. Conclusions
For the first time the hydrodynamics of flows of gaseous and liquid products in rough-walled microchannel Fischer-Tropsch reactor was modeled in details, which allow calculation of operational characteristic values without use of empirical information. In the study is employed technique for derivation of the equations of film flows described, for example, in [12].
The analysis of the calculation results allowed us to establish the following:
1) Equilibrium composition and thermophysical properties of both liquid and gas phases are determined by conversion rate, chain growth coefficient, temperature and pressure.
2) The flow of liquid film and flow of gas phase are conjugated. It is necessary to take random roughness of the channel internal surface into account while calculating pressure drop along the channel.
3) The geometry of the interphase surface of the liquid

Figure 4. Radii of random surfaces of a microchannel and gas-liquid interphase boundary.
 (a)
(a)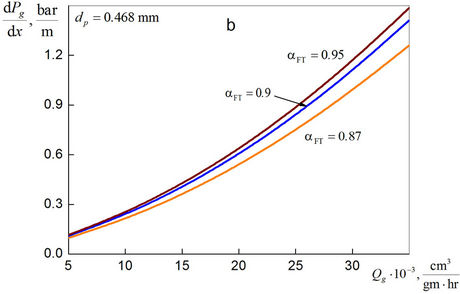 (b)
(b)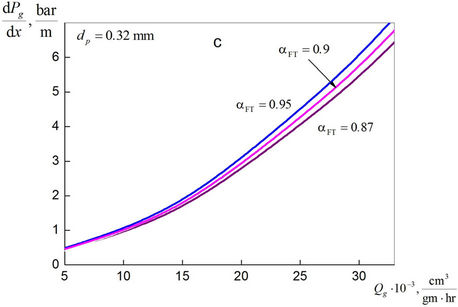 (c)
(c)
Figure 5. Mean gradient of syngas pressure in microchannels with different averaged diameters.
film is determined by inertia and surface tension. The outer profile of the liquid film correlates weakly with the profile of the random rough surface of the channel wall.
4) It has been shown that the pressure drop rises significantly with the channel diameter decrease. A phenomenon of complete hydraulic locking of a channel becomes highly probable for the rough-walled channels with diameter below 0.4 mm. It is shown that fluid dynamics in rough-walled and smooth-walled microchannels are dramatically different, which can lead to significant errors if the smooth-wall model is used for the pres-

Figure 6. Thickness of liquid film in the smooth-walled microchannel: 1— 10,000 cm3/(gm∙hr); 2—20,000; 3— 35,000.
10,000 cm3/(gm∙hr); 2—20,000; 3— 35,000.
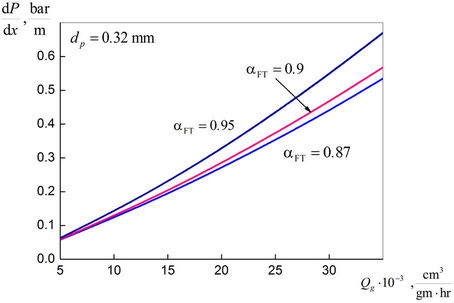
Figure 7. Mean gradient of syngas pressure in smooth-walled microchannel.
sure drop calculation.
5. Acknowledgements
This work was partly supported by the Russian Ministry of science and education, contract No 16.552.11.7014 and by the Russian Foundation for Basic Research (RFBR), grant number 11-08-00645-a.
REFERENCES
- P. Steynberg, M. E. Dry, B. H. Davis and B. B. Breman, “Fischer-Tropsch Reactors Studies,” In: A. Steynberg and M. Dry, Eds., Surface Science and Catalysis, Elsevier B.V., Amstelredam, 2004.
- L. Wei, J. Hu and Y. Wang, “Fischer-Tropsch Synthesis on Ceramic Monolith-Structured Catalysts,” Catalysis Today, Vol. 140, No. 3-4, 2009, pp. 142-148. doi:10.1016/j.cattod.2008.10.015
- R. Myrstad, S. Eri, P. Pfeifer, E. Rytter and A. Holmen, “Fischer-Tropsch Synthesis in a Microstructured Reactor,” Catalysis Today, Vol. 147S, 2009, pp. S301-S304. doi:10.1016/j.cattod.2009.07.011
- C. G. Visconti, E. Tronconi, L. Lietti, G. Groppi, P. Forzatti, C. Cristiani, R. Zennaro and S. Rossini, “An Experimental Investigation of Fischer-Tropsch Synthesis over Washcoated Metallic Structured Supports,” Applied Catalysis A: General, Vol. 370, No. 1-2, 2009, pp. 93-101. doi:10.1016/j.apcata.2009.09.023
- S. Saisorn and S. Wongwises, “A Review of Two-Phase Gas-Liquid Adiabatic Flow Characteristics in MicroChannels,” Renewable and Sustainable Energy Reviews, Vol. 12, No. 3, 2008, pp. 824-838. doi:10.1016/j.rser.2006.10.012
- J. Knochen, R. Guttel, C. Knobloch and T. Turek, “Fischer-Tropsch Synthesis in Milli-Structured FixedBed Reactors: Experimental Study and Scale-Up Considerations,” Chemical Engineering and Processing, Vol. 49, No. 9, 2010, pp. 958-964. doi:10.1016/j.cep.2010.04.013
- K. Mogalicherla and D. Kunzru, “Performance of Monolithic Reactors in Film Flow,” Chemical Engineering Research and Design, Vol. 88, No. 8, 2010, pp. 1057-1066. doi:10.1016/j.cherd.2010.01.032
- T. Bauer, R. Guettel, S. Roy, M. Schubert, M. Al-Dahhan and R. Lange, “Modelling and Simulation of the Monolithic Reactor for Gas-Liquid-Solid Reactions,” Chemical Engineering Research and Design, Vol. 83, No. 7, 2005, pp. 811-819. doi:10.1205/cherd.04335
- R. Guettel and T. Turek, “Comparison of Different Reactor Types for Low Temperature Fischer-Tropsch Synthesis: A Simulation Study,” Chemical Engineering Science, Vol. 64, No. 5, 2009, pp. 955-964. doi:10.1016/j.ces.2008.10.059
- G. Hetsroni, A. Mosyak, E. Pogrebnyak and L. P. Yarin, “Fluid Flow in Micro-Channels,” International Journal of Heat Mass Transfer, Vol. 48, No. 10, 2005, pp. 1982- 1998. doi:10.1016/j.ijheatmasstransfer.2004.12.019
- I. V. Derevich, V. S. Ermolaev and V. Z. Mordkovich, “Modeling of Hydrodynamics in Microchannel Reactor for Fischer-Tropsch Synthesis,” International Journal of Heat Mass Transfer, Vol. 55, No. 5-6, 2012, pp. 1695- 1708. doi:10.1016/j.ijheatmasstransfer.2011.11.024
- S. V. Alekseenko, V. G. Nakoraykov and B. G. Pokusaev, “Wave Flows of Liquid Films,” The Siberian Book-Publishing Firm, VO Nauka, Novosibirsk, 1992.
- I. V. Derevich, V. S. Ermolaev, N. V. Zolnikova and V. Z. Mordkovich, “Modeling the Thermal and Physical Properties of Liquid and Gas Mixtures of Fischer-Tropsch Synthesis Products,” Theoretical Foundation of Chemical Engineering, Vol. 45, No. 2, 2011, pp. 221-226. doi:10.1134/S0040579511020060
- I. V. Derevich, V. S. Ermolaev and V. Z. Mordkovich, “Liquid-Vapor Thermodynamic Equilibrium in FischerTropsch Synthesis Products,” Theoretical Foundation of Chemical Engineering, Vol. 42, No. 2, 2008, pp. 216-219. doi:10.1134/S0040579508020152
NOTES
*Corresponding author.

