World Journal of Mechanics
Vol. 3 No. 5A (2013) , Article ID: 36189 , 11 pages DOI:10.4236/wjm.2013.35A004
Analytical Solutions of a Symmetrical Dynamic Crack Model of Bridging Fibers in Unidirectional Composites
1School of Material Science and Engineering, Shenyang Ligong University, Shenyang, China
2Department of Civil Engineering, Northeastern University, Shenyang, China
3College of Mechanical Engineering, Liaoning Technical University, Fuxin, China
4Department of Astronautics and Mechanics, Harbin Institute of Technology, Harbin, China
Email: lnc_65@163.com, cyh_neu@163.com, wyt234@163.com, chengjin@ hit.edu.cn
Copyright © 2013 Nianchun Lü et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 23, 2013; revised April 30, 2013; accepted May 27, 2013
Keywords: Composite materials; Bridging fibers; Analytical solutions; Crack; Variable loads
ABSTRACT
When composite materials occur crack, their fibrous locations will produce bridging fibers. A symmetrical dynamic crack model of bridging fibers in unidirectional composite materials are not probed as deeply by virtue of the complexity, cockamamie and difficulty in mathematical operations. In the light of the theory of complex variable functions, the problems discussed can be facilely translated into Remann-Hilbert problems. Analytical solutions of the displacements, stresses and stress intensity factors under the action of variable loads Pt6/x6, Px6/t5 are attained, respectively. After those analytical solutions were used by superposition theorem, the solutions of arbitrary complex problems were acquired.
1. Introduction
It is well known that the matrix cracking as well as fracture course of the bridging fibers is one of the significant mechanisms of crack extension in fiber-reinforced composite materials, such as unidirectional fiberreinforced brittle matrix composites [1,2], and threedimensional fiber-reinforced composites with an orthogonal fibrous structure [3,4]. It is necessary to consider the mechanical analyses of matrix cracking with bridging fibers in order to assess the distribution of the axis traction force in each fiber. When composite materials appear a crack, they necessarily occur bridging fibers, and this is an inevitable phenomenon. Composites are universally referred to as orthotropic anisotropic bodies in macrostructure by virtue of their fibrous directions, moreover bridging fibers play a vital role in studies. Consequently, bridging fibers queries of composite materials are one of the most significant advanced tasks of mechanics of composite materials [5,6]. Because bridging fibers of composite materials are very complicated, which are nearly researched on their static problems by so far. Most researchers, such as Bowic, Woo, Lee, Ji and Tsai [7-11] etc., have studied the crack problem of bridging fibers by boundary collocation measure, but all of them almost researched static problems of composite materials, moreover, gained only numerical solutions. Nevertheless, the fractures of composite materials often arise in dynamic conditions, so it is extremely significant to study their fracture dynamics problems. Recently, Piva and Viola [11,12] as well as De [13] et al. gained a closed solution of elastodynamic crack problems in an orthotropic medium. All the dynamic crack problems mentioned above were not concerned with fracture course of the bridging fibers of composite materials. When a crack extends at high speed, bridging fiber phenomenon still exists. Because bridging fibers can conduce crack arresting, studying fracture dynamics problems is very important.
The problem under consideration is that of a crack, running in one plane, postulated to initiate from an infinitesimally small micro-crack with maximum velocity. This symmetrical crack, moving with constant velocity V in both the positive and negative directions of the x-axis, has been considered by Broberg [15] and Craggs [16]. Both considered motion in composite materials, which were presumed to be homogeneous and isotropic, both as regards stress-strain relations and fracturing characters. If the fiber failure is governed by maximum tensile stress, which appears at the crack plane, the fiber breaks and hence the crack expansion should occur in the format of self-similarity. The fiber breaks along a transverse line and therefore present a notch [9,17]. When a crack runs in high speed, bridging fibers still exist in the dynamic situations of composite materials, which are more significant than those in the statics. Since bridging fibers can lead to stabilizing effect on crack moving problems along the original notch plane, the effect of dynamic fracture of bridging fibers will be expressed in detail, at the same time, stresses and displacements as well as stress intensity factors are deducted appropriately.
In this paper, the symmetrical dynamic expansion problems of an internal central crack with bridging fibers of unidirectional composite materials are analyzed by means of Keldysh-Sedov mixed boundary value queries, and that analytic solutions of stresses and displacements as well as stress intensity factors for unidirectional reinforced materials with fibers parallel to the free surface are shown. First, the solution of a unique dislocation in an elastically half-plane is derived by the use of complex variable analysis. The crack is then expressed in terms of a continuous distribution of dislocation. This solution in conjunction with a bridging fiber force gives rise to a system of self-similar functions with dislocation density as unknown units. Then selfsimilar functions are solved analytically by means of Keldysh-Sedov approaches. The work in this paper is how to conveniently acquire analytical solutions using the self-similar functions under the action of variable loads Pt6/x6, Px6/t5, respectively.
2. A Symmetrical Dynamic Crack Model of Bridging Fibers
Postulating that a crack nucleates from zero, and spreads symmetrically in self-similar high speed along the positive and negative directions of x-axis with constant velocity in the matrix, but bridging fibers don’t break in the vicinity of the crack tips, moreover the others break at the central region of the crack. When the crack runs, its fibers break uninterruptedly, fiber fracture velocity presumed is α, as illustrated in Figure1. The fibers and the matrix are taken to be linearly elastic, and it is further assumed that the fibers have a much higher elastic modulus in the axial direction than the matrix, hence the fibers are taken as supporting all of the axial load in composite materials. In order to analyze expediently, the fiber fracture location is postulated to occur along a sole plane, in short, the fiber fracture could be the modality of self-similarity and therefore presents a notch. In Figure 1, the crack area in the matrix is in the realm of y = 0, |x| < Vt; while fibers break at the interval of |x| < αt. The bridging fiber segment lies in the domain of y = 0, αt < |x| < Vt, [3].
Obviously, the dynamic crack model of bridging fibers in Figure 1 is shown by that in Figure 2. At y = 0, closed forces act in the section of αt < |x| < Vt, which represent

Figure 1. A dynamic crack model of bridging fiber contour.

Figure 2. The dynamic crack model of bridging fibers.
bridging fiber tensions; bridging fibers are usually collocated tightly, so bridging fiber tensions are supposed to distribute continuously. It is evident that traction forces are larger near the point of αt, and they are smaller close to the point of Vt [5-7,18,19]. As the crack moves at high speed, its dimension will correlate to variables x and t, then the edges of crack subjected to loads must also relate to x and t. In short, traction forces of bridging fibers are homogenous in this segment, whose magnitude is P according to assumption. On the other hand, when the crack moves with high speed, its magnitude will increase with time t; the longer the crack runs, the more fibers break. The above analyses presume bridging fibers distribute uniformly in the matrix, and each bridging fiber has the identical strength, while bridging fibers and matrix break simultaneously along a sole plane [5-7,18,19].
3. Universal Expressions of Elastodynamic Equations for Orthotropic Anisotropy
In order to solve efficaciously fracture dynamics queries of bridging fibers of composite materials, solutions will be attained under the action of point forces for mode I motive crack. In terms of the theorem of generalized functions, the problems dealt with unlike boundary conditions will be facilely translated into Reimann-Hilbert mixed boundary value problem by means of self-similar functions, then correlative solutions will be obtained.
Postulate at y = 0 that there are any number of loaded segments and displacement segments along the x-axis, and the ends of these sections are running with different constant velocity. At the initial moment t = 0, the halfplane is at rest. In these ranges the loads and displacements are discretional linear compages of the following functions [15-23]:
 . (1)
. (1)
where
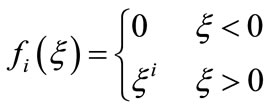 (2)
(2)
here k, k1 and s, s1 are discretionary integer positive numbers [15-23].
A discretional successive function of two variables x and t may be shown as a linear superposition of Equation (1), therefore resolving loads or displacements with the form of Equation (2) will possess significance in principle. Introduce the linear differential operator as well as inverse:
 inverse:
inverse:
 (3)
(3)
here + m + n, – m – n and 0 represent the (m + n)th order derivative, the (m + n)th order integral and function’s self. It is facile to prove that there exist constants m and n, when L is put into Equations (1), (2), homogeneous functions of x and t of zeroth dimension (homogeneous) are gained. The coefficients m, n will be called the indices of self-similarity [15-23].
For the case when function Lv is homogeneous [5,6]:
 (4)
(4)
For the case when function Lσy is homogeneous:
 (5)
(5)
The relative self-similar functions are as [15-23]:
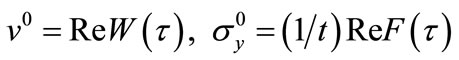 (6)
(6)
where: v0 and 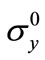 in Equations (4)~(6) are the notation in [15-17,20-23], and they are relevant variables τ and t which directly work out displacements and stresses by the course of respective calculations in Equation (7).
in Equations (4)~(6) are the notation in [15-17,20-23], and they are relevant variables τ and t which directly work out displacements and stresses by the course of respective calculations in Equation (7).
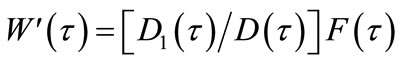 (7)
(7)
Where: τ = x/t, F(τ), W(τ) are self-similar functions. The values of D1(τ)/D(τ) can be ascertained from Appendix 1 of literatures [15-17,20-23], indicated here are only: D1(τ)/D(τ) in the neighborhood of the subsonic speeds is purely imaginary for the considered values. Thus, elastodynamics problems for an orthotropic anisotropic body studied can be changed into seeking the sole unknown function problems of F(τ) and W(τ) for which must meet the boundary-value conditions. In the universal case this is Riemann-Hilbert problem in the theory of complex variable functions while for the simplest situation, which is the Keldysh-Sedov or Dirchlet problem [24,25].
4. Radical Solution of Symmetrical Dynamic Running Problem on Mode I Crack
At the initial moment t = 0, a micro-crack is supposed to appear in an orthotropic anisotropy. Let the Cartesian coordinate axes align with the axes of elastic symmetry of the body. The problem considered is restricted to motion in the x-y-plane. The crack is moving symmetrically with constant velocity V along the positive and negative directions of x-axis respectively. The problems will be changed into the following boundary condition queries:
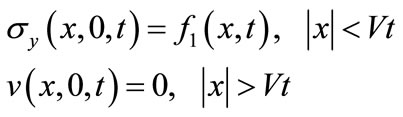 (8)
(8)
Introducing the variable τ = x/t. By means of the above correlative expressions and  in the theory of generalized functions [26-28], the boundary conditions can be transformed as:
in the theory of generalized functions [26-28], the boundary conditions can be transformed as:
 (9)
(9)
In terms of the relationship of F(τ) and W(τ) in Equation (7) and the previous conditions, the format of sole unbeknown function W′(τ) can be confirmed:
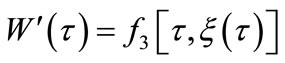 (10)
(10)
The problems can reduce to Keldysh-Sedov problem:
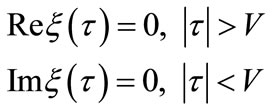 (11)
(11)
Considering symmetry and the infinite point of the plane corresponding to the origin of coordinates of the physical plane as well as singularities of the stress at the crack tip [29,30], the solution in the above problems can be readily deducted by literatures [15,16,20] as:
 (12)
(12)
Using Equations (6) or (7), we will easily obtain the stress, the displacement and the stress intensity factor under the conditions of mode I crack extension problems.
5. The Solutions of Real Problems
In order to resolve effectively symmetrical dynamics queries with bridging fibers of composite materials, solutions will be found under the actions of unlike loads for mode I motive crack. In terms of the theorem of generalized functions, the unlike boundary condition problems will be changed into Keldysh-Sedov mixed boundary value problem by self-similar functions, and the solutions will be gained under the plane strain states.
5.1. Displacements are Homogeneous Functions
Postulate at the initial moment t = 0 a crack occurs at the coordinate origin and begins to run at constant velocity  in both directions along the x-axis. The edges of the crack are subjected to normal point force Pt6/x6, moving at a constant velocity β along the positive direction of x-axis, where β < V; at t < 0 the half-plane was at rest. The boundary conditions of the problem will be as:
in both directions along the x-axis. The edges of the crack are subjected to normal point force Pt6/x6, moving at a constant velocity β along the positive direction of x-axis, where β < V; at t < 0 the half-plane was at rest. The boundary conditions of the problem will be as:
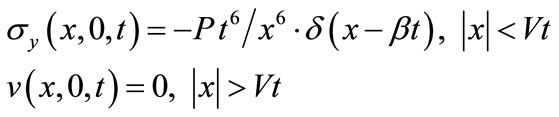 (13)
(13)
In which L = 1, utilizing τ = x/t and the theory of generalized functions [25-27] and Equations (4) and (6), the first of Equation (13) can be written as:
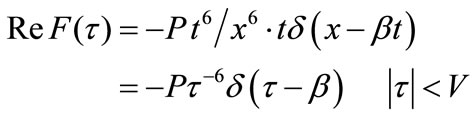 (14)
(14)
In the light of Equation (7), boundary conditions (14) will be further rewritten:
 (15)
(15)
Deducting from the mentioned-above formulae, the unique solution of W′(τ) must have the modality:
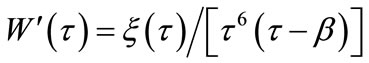 (16)
(16)
ξ(τ) has no singularity in the domain of |τ| < V, while D1(τ)/D(τ) is purely imaginary for the subsonic speeds, consequently ξ(τ) must be purely real in this segment. Thus, question (15) can conduce the following problems:
 (17)
(17)
According to symmetry and the conditions of the infinite point of the plane corresponding to the origin of coordinates of the physical plane as well as singularities of the stress of the crack tips [27-29], the sole solution of the Keldysh-Sedov problem (17) must have the form:
 (18)
(18)
where A is an unknown constant.
Inserting Equation (18) into (16), (7), one can gain:
 (19)
(19)
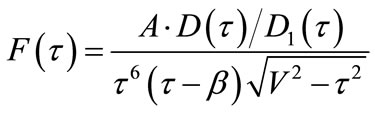 (20)
(20)
Then putting Equation (20) into (14), at τ→β, constant A can be determined from that
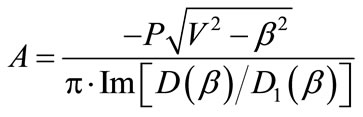 (21)
(21)
Substituting Equation (20) into (6) and (4), at the surface y = 0, the stress σy, the displacement v and the stress intensity factor K1(t) are acquired, respectively:
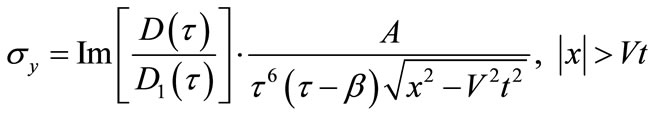 (22)
(22)
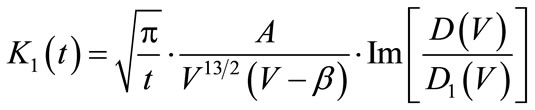 (23)
(23)
Replacing Equation (19) into (4), (6), after integrating with respective to τ one can obtain the displacement v (see Equation (24) below):
Utilizing correlative integral formulas [30] to yield:
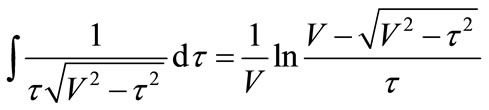
 (25)
(25)
 (26)
(26)
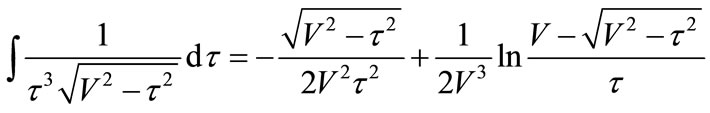 (27)
(27)

 (28)
(28)
 (29)
(29)
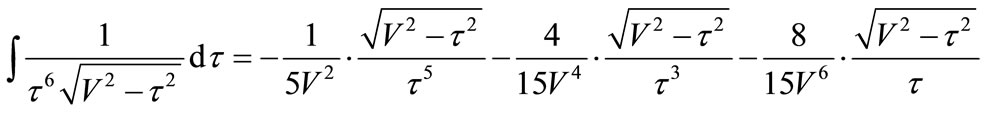 (30)
(30)
 (31)
(31)
In order to show expediently, constant C was omitted in Equations (25)-(31).
The crack extends along the x-axis, therefore W(τ) can be worked out in the operation of the definite integral, we take constant C = 0. Then putting Equations (25)-(31) into (24), the displacement  is given as follows:
is given as follows:
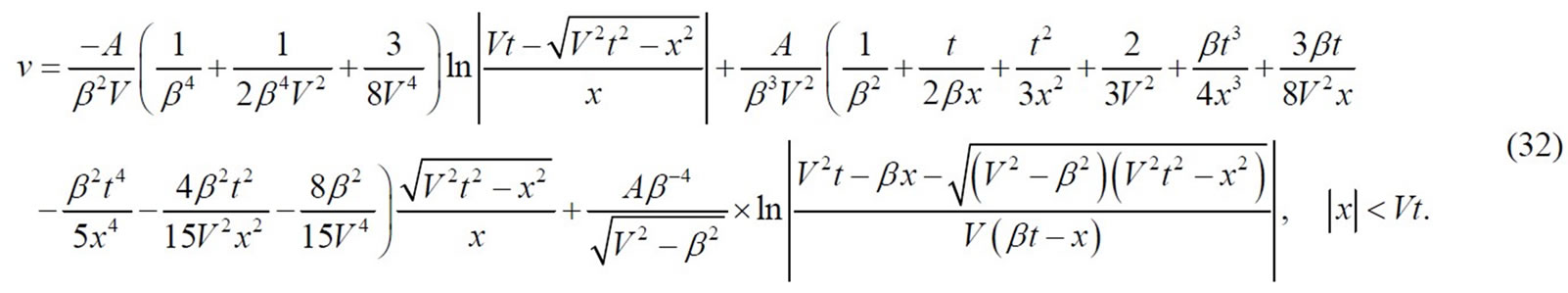
By means of the solution of Equation (32), the bridging fiber fracture speed α can be facilely acquired:
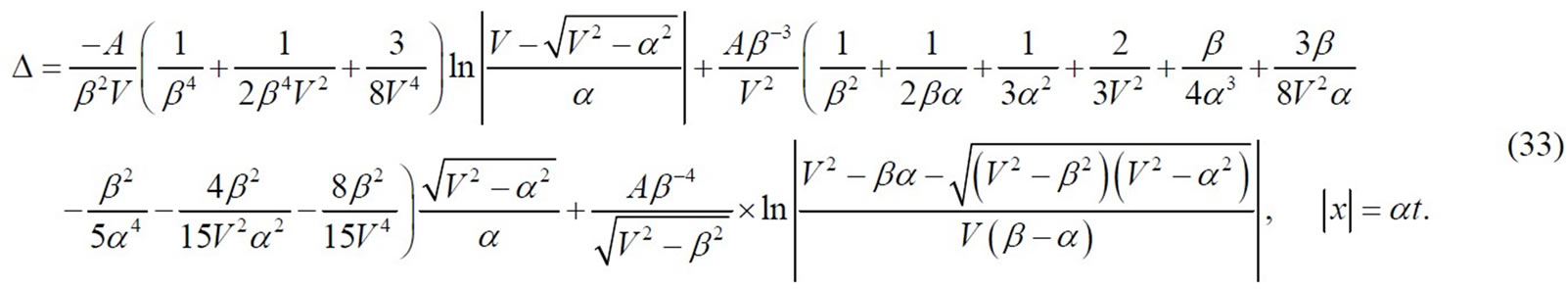
 Each fibre has equal strength [15-17,20-22] in the light of presumption, hence the bridging fiber fracture strength must be same. Where Δ can be ascertained by an axial tensile test of bridging fibers of composite materials with V and ß regarded as known constants, respectively. In terms of this measure, the bridging fiber fracture speed α can be only attained numerical solution, because it can not be represented in the modality of explicit function.
Each fibre has equal strength [15-17,20-22] in the light of presumption, hence the bridging fiber fracture strength must be same. Where Δ can be ascertained by an axial tensile test of bridging fibers of composite materials with V and ß regarded as known constants, respectively. In terms of this measure, the bridging fiber fracture speed α can be only attained numerical solution, because it can not be represented in the modality of explicit function.
5.2. Stresses are Homogeneous Functions
With all conditions holding the same as those in the above sample, the applied loads become variational loads Px6/t5. The boundary conditions of the query will be as:
 (34)
(34)
In which L=1, utilizing τ=x/t and the theory of generalized functions [25-27] and Equations (4) and (6), the first of Equation (34) can be written as follows:
 (35)
(35)
On account of the derivative of Dirac’s function equaling zero at x ≠ βt, the above representation will be easily deducted.
In terms of Equation (7), boundary conditions (35) will be further rewritten:
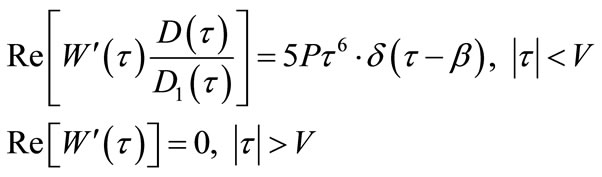 (36)
(36)
Known from the above, the sole solution of W′(τ) is:
 (37)
(37)
ξ(τ) has no singularity in the domain of |τ|
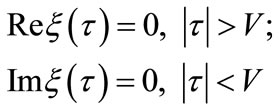 (38)
(38)
In the light of the symmetrical conditions and singularities of the stress as well as the infinite point of the plane corresponding to the coordinate origin of the physical plane, the sole solution of Keldysh-Sedov problem (38) takes the form as:
 (39)
(39)
where A is an unknown constant.
Putting Equation (39) into (37), (7), one can attain:
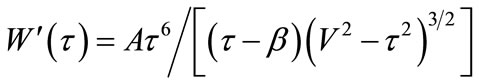 (40)
(40)
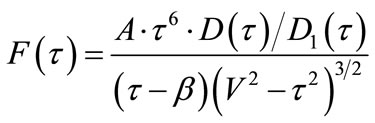 (41)
(41)
Then replacing Equation (41) into (35), at τ→β, constant A can be determined from that
 (42)
(42)
In an orthotropic isotropic body, the disturbance range of elastic wave can be shown by the circular area of radius c1t and c2t. Here c1 and c2 are the velocities of longitudinal and transverse waves (c1 > c2) of elastic bodyrespectively. In an orthotropic anisotropic body, the disturbance range of elastic wave is not the circular area and can not exceed threshold value
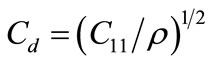
of elastic body, where C11 is an elastic constant of materials. At |x| > Cdt, with
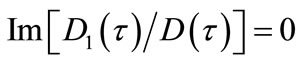 thus displacements and stresses are zero with the initiate cases; and this shows that disturbance of elastic wave can not exceed Cdt.
thus displacements and stresses are zero with the initiate cases; and this shows that disturbance of elastic wave can not exceed Cdt.
Afterwards inserting Equation (41) into (6) and (4), at the surface y = 0, the stress σy and the intensity factor K1(t) are obtained, respectively:
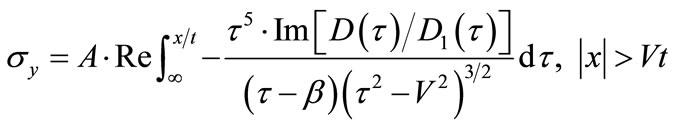 (43)
(43)
 (44)
(44)
The limit of Equation (44) belongs to the format 0·∞, which should be only changed into the type of ∞/∞, the result can be computed by means of L’Hospital theorem.
In order to represent expediently, Equation (40) can rewrite as follows
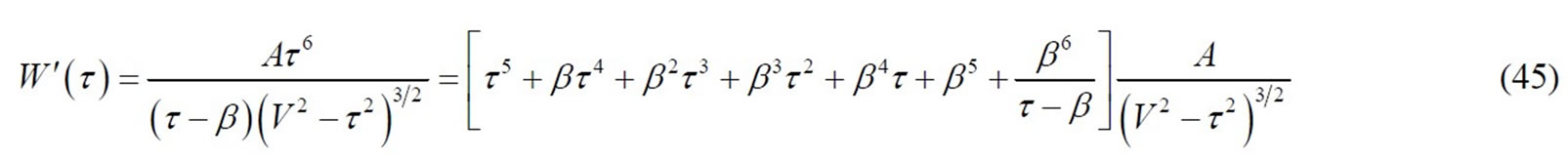
Integrating Equation (45), one will attain W(τ). But it has seven items, separate denotation is more convenient, then integral formulas can be utilized in literature [30], now postulating:
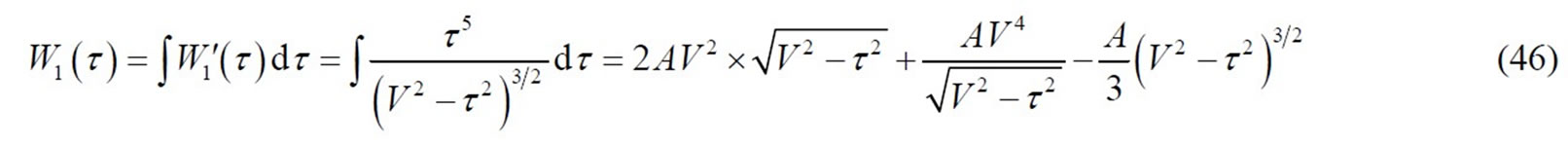
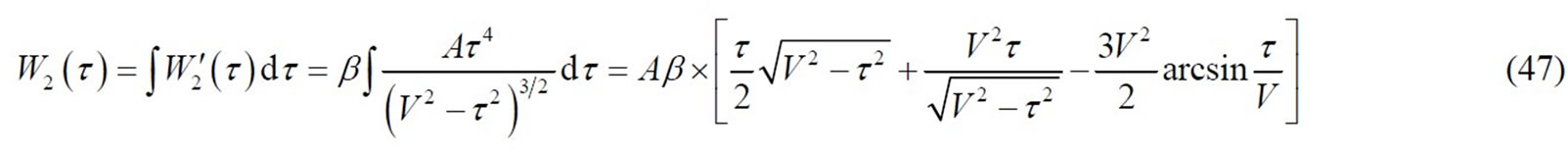
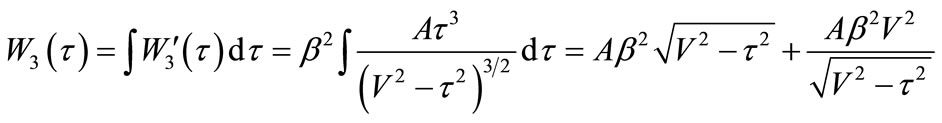 (48)
(48)
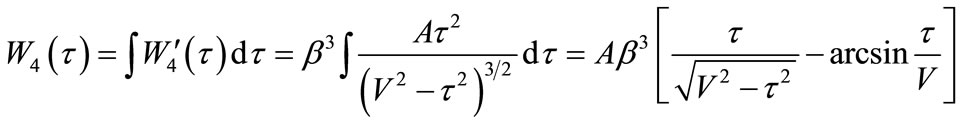 (49)
(49)
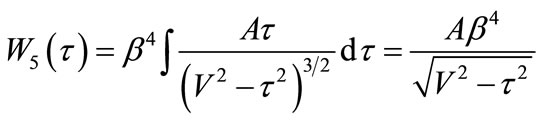 (50)
(50) 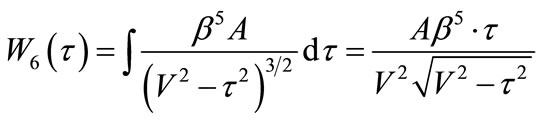 (51)
(51)
Denominator in Equation (46) contains this term
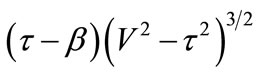 calculation will not be preformed in the light of integral formulae, hence integral format must be translated into integral which can be fulfilled.
calculation will not be preformed in the light of integral formulae, hence integral format must be translated into integral which can be fulfilled.
For the sake of conveniency, we assume: 
By variable replacement: , this term X can be rewritten as follows:
, this term X can be rewritten as follows:
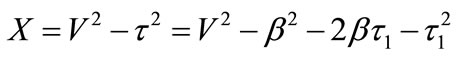 (52)
(52)
Known from it, the following relationship in literature [30] is:
 ,
, 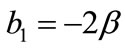 ,
,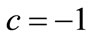 ,
,

Integrating the seventh term of Equation (45) in terms of relevant formulae in [30], we will acquire W7(τ) as:
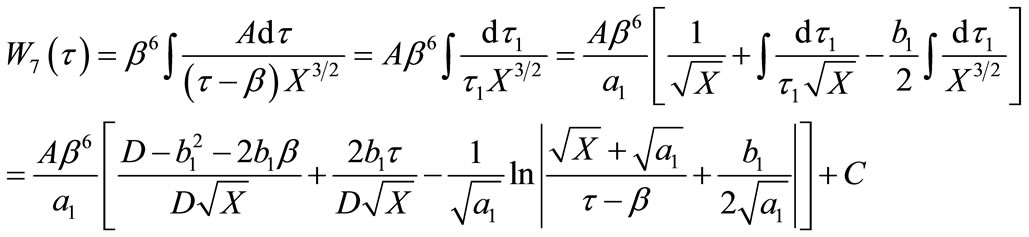 (53)
(53)
Known from Equation (45):
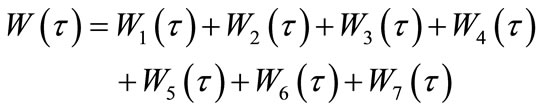 .
.
The crack runs along x-axis, consequently W(τ) comprising Equations (46)-(51) and (53) can be performed inthe definite integral operation, one takes constant C = 0.
Making use of relative integral formulas [30] to yield:
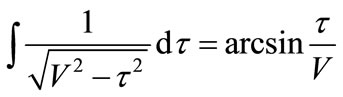 (54)
(54)
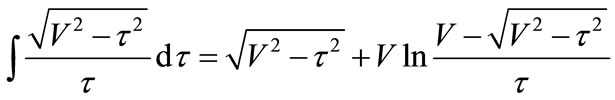 (55)
(55)
 (56)
(56)
 (57)
(57)
Putting Equation (46) into (6), (5), the divisional displacement v1 will be obtained as:

Now replacing Equations (56), (26), (57) into (58), there results the divisional displacement v1:
 (59)
(59)
Inserting Equation (47) into (6), (5), the divisional displacement v2 will be attained as:
 (60)
(60)
Putting Equations (55), (26) into (60), there results the divisional displacement v2:
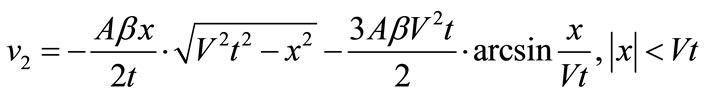 (61)
(61)
Inserting Equations (48) into (6), (5), by means of Equations (56), (26), the sub-displacement v3 will be as:
 (62)
(62)
Replacing Equation (49) into (6), (5), by application of Equation (25), there results sub-displacement v4:
 (63)
(63)
Putting Equation (50) into (6), (5), by means of Equation (26), there results the divisional displacement v5:
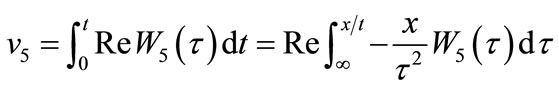
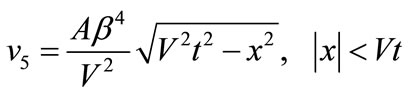 (64)
(64)
Then inserting Equation (51) into (6), (5), by means of Equation (25), there results the sub-displacement v6 as:
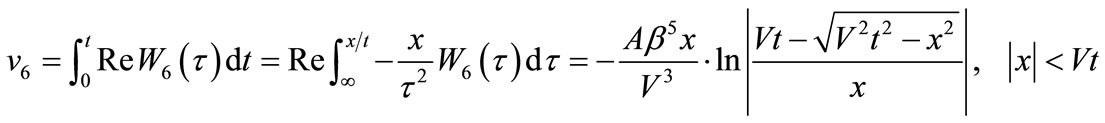 (65)
(65)
Substituting Equation (53) into (6), (5), there results the divisional displacement v7 as follows:
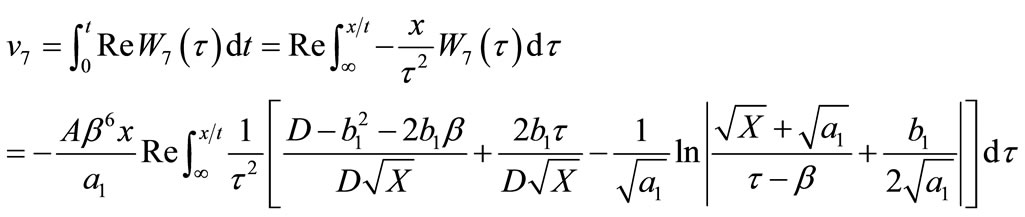 (66)
(66)
Integral of the second term of Equation (66) without comprising coefficient can be written as:
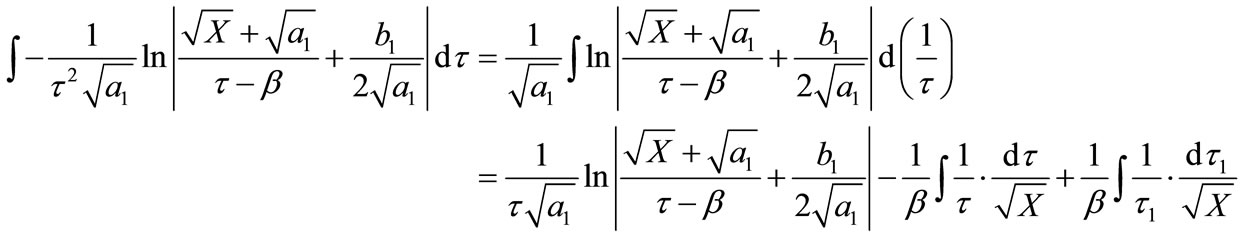 (67)
(67)
Using integral formulas in Literature [30], one gains:
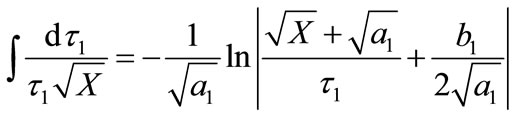 (68)
(68)
where: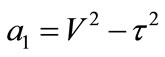 ,
,  ,
,  ,
, .
.
Putting Equations (68), (25) into (67), the following representation is given as:
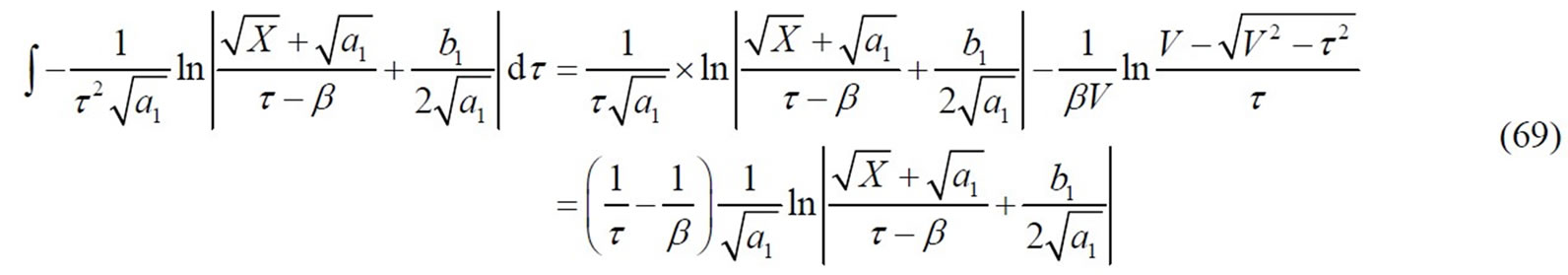
Inserting Equations (69), (26) into (66), the divisional displacement v7 will be obtained as follows:

The displacement v is the sum of divisional displacement: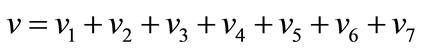 .
.
Afterwards the addition of Equations (59), (61)-(65) and (70), the displacement  is acquired as follows:
is acquired as follows:
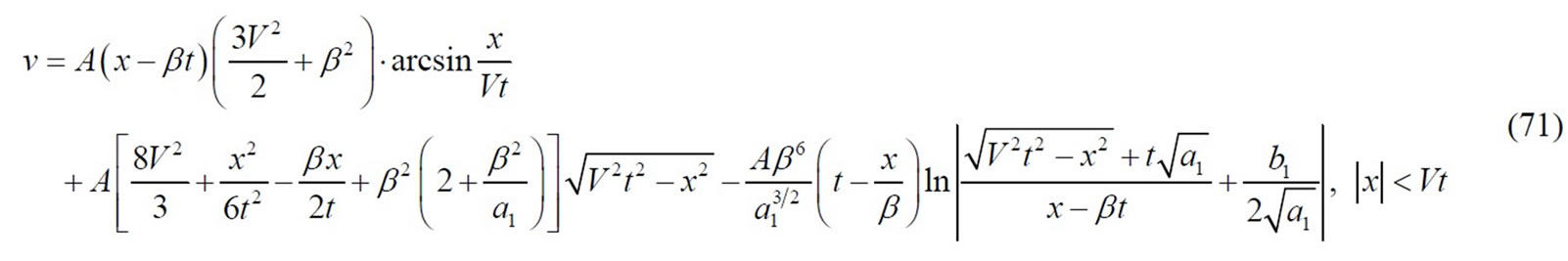
Using the similar ways as that for finding Equation (33), put |x| = αt into (71) while regarding V, β and t as known constants, respectively. Bridging fiber fracture speed α can be only gained numerical solution, because it can also not be shown in the form of explicit function.
6. Rule of Dynamic Stress Intensity Factor
According to real cases of concrete problems, variational rule of dynamic stress intensity factor should be shown better. The corresponding parameters are substituted into Equations (23), (44) to plot K1(t) as a function of time t, and their numerical solutions are facilely obtained. The following constants are as follows [8,17,21-23,33-36]:
C11 = 19.24 GPa; C12 = 1.25 GPa; C11 = 17.83 GPa; P = 200 N; C66 = 1.00 GPa; V = 300 m/s; β = 200 m/s; ρ = 4.9 × 1000 N/m3
Known from Equation (23), dynamic stress intensity factor K1(t) reduces tardily and has instinct singularity by virtue of unique variable t in its denominator, and the rest units are referred to as real constants. Such a current is shown by the curve in Figure 1. This variable tendency is similar to the result of Literatures [8,17,21-23,33-38].
It is known from Equation (45) that dynamic stress intensity factor K1(t) escalates from zero and even reaches or surpasses fracture toughness of this material, because unique variable t locates in its numerator, while the rest quantities are also regarded as real constants. This result must lead to the structural destruction, as represented in Figure 2. This trend is similar to the aftermath in references [8,17,21-23,33-36,38-42], hence it is also right.
The relative numerical values between dynamic stress intensity factor K1(t) and time t are expressed in Tables 1 and 2 in terms of curves in Figures 3 and 4, respectively.
7. Conclusions
By the ways of relevant expression:
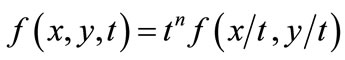 where n is an integral number, and the problem considered can be readily translated into homogeneous function of x and t of zeroth dimension, namely self-similar functions. All suffice the relationship of this function, thus the analytical solutions can be attained by Equations (4)-(7) with homogeneous function of variable τ. This approach can utilize not only in elastodynamics [15-20, 22,23,34,35], but also in elastostatics [24,30,43,44] and even in other regions [30,44,45].
where n is an integral number, and the problem considered can be readily translated into homogeneous function of x and t of zeroth dimension, namely self-similar functions. All suffice the relationship of this function, thus the analytical solutions can be attained by Equations (4)-(7) with homogeneous function of variable τ. This approach can utilize not only in elastodynamics [15-20, 22,23,34,35], but also in elastostatics [24,30,43,44] and even in other regions [30,44,45].
Analytic solutions of the symmetrical dynamic crack

Table 1. Relative numerical values between K1(t) versus t.

Table 2. Relative numerical values between K1(t) versus t.
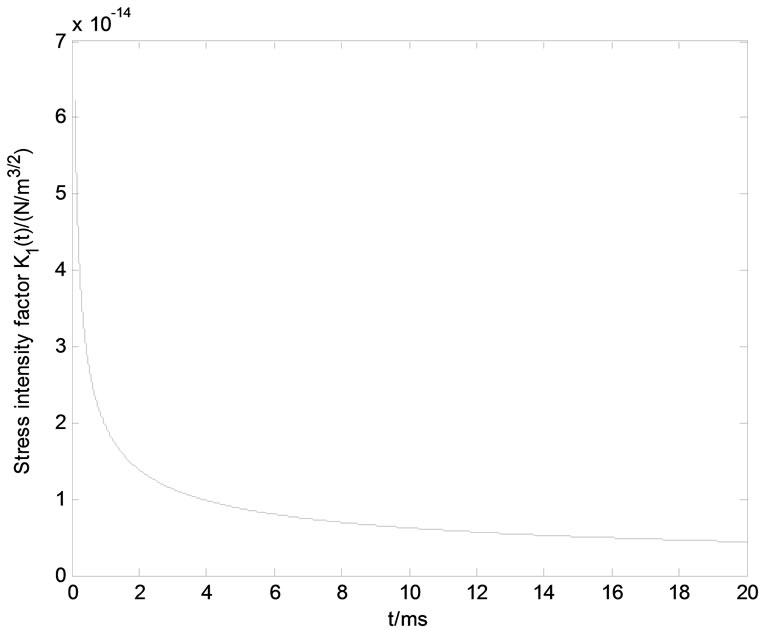
Figure 3. Stress intensity factor K1(t) versus time t.
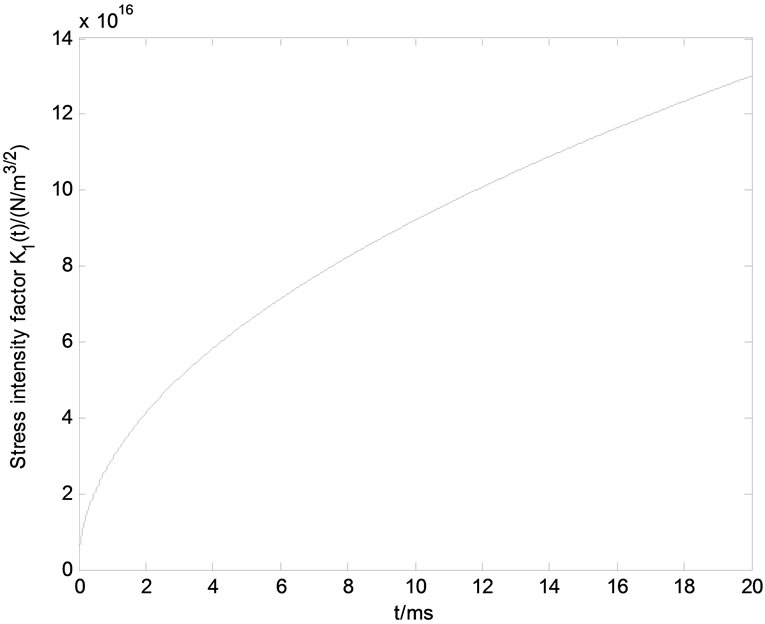
Figure 4. Stress intensity factor K1(t) versus time t.
expansion model for bridging fibers in unidirectional composite materials were found by way of the theoretical application of a complex variable function. The technique developed in this paper based on the methods of the self-similar functions makes it probable to obtain the concrete solution of this model and bridging fiber fracture velocity α. The fundamental solution of symmetrical dynamic crack extension problems is derived based on the self-similar functions. In the light of the concrete boundary conditions, self-similar function W′(τ) can be facilely deducted by the approaches of corresponding to variable τ, consequently analytical solutions of stresses, displacements and dynamic stress intensity factors will be readily worked out. This is regarded as the analogous class of dynamic problem of the elasticity theory. However, the present solution occurs to be the simplest and intuitive of all alternative methods appeared by so far. Indeed, we have succeeded in a mixed Keldysh-Sedov boundary value problem on a half-plane. The problem is of adequate real interest, since all of the members of structures in which fractures may propagate are of finite dimensions and are frequently in the modality of long strips. The approach of solution is based exclusively on techniques of analytical-function theory and is straightforward and compendious. By making some observations regarding the solution of the mixed boundary value problem we have rather decreased the amount of the computative work needed to resolve such a crack exte sion query. The techniques of self-similar functions are still applicable in studies of mode I semi-infinite crack [21-23,46], mode Ⅲ crack [47,48] and mode Ⅲ interface crack [49] as well as axially crack [18,19,50].
8. Acknowledgements
Project is supported by the postdoctoral foundation of China (No. 2005038199), HeiLongJiang provincial nature science foundation of China (ZJG04-08).
REFERENCES
- D. B. Marshall, B. N. Cox and A. G. Evens, “The Mechanics of Matrix Cracking in Brittle-Matrix Fiber Composites,” Acta Metallurgical, Vol. 33, No. 11, 1985, pp. 2013-2021. doi:10.1016/0001-6160(85)90124-5
- B. Budiansky, J. W. Hutchinson and A. G. Evens, “Matrix Fracture in Fiber-Reinforced Ceramics,” Journal of the Mechanics and Physics of Solids. Vol. 34, No. 2, 1986, pp. 167-189. doi:10.1016/0022-5096(86)90035-9
- M. Ji and H. Ishikawa, “Analysis of an Internal Central Crack with Bridging Fibers in a Finite Orthotropic Plate,” International Journal of Engineering Science, Vol. 35, No. 4, 1997, pp. 549-560.
- D. B. Marshall and B. N. Cox, “Tensile Fracture of Brittle Matrix Composites: Influence of Fiber Strength,” Acta Metallurgica, Vol. 35, No. 11, 1987, pp. 2607-2619. doi:10.1016/0001-6160(87)90260-4
- Z.-M. Wang, “Mechanics and Structural Mechanics of Composite Materials,” Publisher of Machinery Industry, Beijing, 1991, (in Chinese).
- G.-L. Shen, “Mechanics of Composite Materials,” Tsinghua University Press, Beijing, 1996, (in Chinese).
- C. W. Woo and Y. H. Wang, “Analysis of an Internal Crack in a Fine Anisotropic Plate,” International Journal of Fracture, Vol. 62, No. 2, 1993, pp. 203-208. doi:10.1016/0955-7997(93)90038-M
- J. C. Lee, “Analysis of Fiber Bridged Crack near a Free Surface in Ceramic Matrix Composites,” Engineering Fracture Mechanics, Vol. 37, No. 2, 1990, pp. 209-219. doi:10.1016/0013-7944(90)90344-G
- W. T. Tsai and I. R. Dharani, “Non Self-Similar Fiber Fracture in Unidirectional Composites,” Engineering Fracture Mechanics, Vol. 44, No. 1, 1993, pp. 43-49. doi:10.1016/0013-7944(93)90080-C
- W. N. Liu, “Stress ahead of the Tip of a Finite-Width Center-Crack in Fiber-Reinforced Composite Specimens: Subjected to Non-Linearly Distributed Bridging Stresses,” International Journal of Fracture, Vol. 70, No. 1, 1994, pp. 31-35. doi:10.1016/0013-7944(94)90092-2
- K. Liao and K. Reifsnider, “A Tensile Strength Model for Unidirectional Fiber-reinforced Brittle Matrix Composite,” International Journal of Fracture, Vol. 106, No. 1, 2000, pp. 95-115. doi:10.1016/S1359-835X(02)00143-4
- V. Tamuzs, S. Tarasovs and U. Vilks, “Progressive Delamination and Fibre Bridging Modeling in Double Cantilever Beam Composite Specimens,” Engineering Fracture Mechanics, Vol. 68, No. 5, 2001, pp. 513-525. doi:10.1016/S0013-7944(00)00131-4
- A. Piva and E. Viola, “Crack Propagation in An Orthotropic Media,” Engineering Fracture Mechanics, Vol. 29, No. 5, 1988, pp. 535-547. doi:10.1016/0013-7944(88)90179-8
- J. De and B. Patra, “Elastodynimic Crack Problems in An Orthotrpic Medium through Complex Variable Approach,” Engineering Fracture Mechanics, Vol. 41, No. 5, 1998, pp. 895-909.
- K. B. Broberg, “The Propagation of a Brittle Crack,” Arkiv för Fysik, Vol. 18, No. 2, 1960, pp. 159-192. doi:10.1016/0022-5096(60)90006-5
- Y. W. Craggs, “The Growth of a Disk-Shaped Crack,” International Journal of Engineering Science, Vol. 4, No. 2, 1966, pp. 113-124. doi:10.1016/0013-7944(80)90086-7
- J. G. Goree and R. S. Gross, “Analysis of a Unidirectional Composite Containing Broken Fibers and Matrix Damage,” Engineering Fracture Mechanics, Vol. 33, No. 3, 1979, 2001, pp. 55-578. doi:10.1016/0020-7225(66)90019-X
- G. P. Cherepanov and E. F. Afanasov, “Some Dynamic Problems of the Theory of Elasticity—A Review,” International Journal of Engineering Science, Vol. 12, No. 8, 1974, 665-690. doi:10.1016/0020-7225(74)90043-3
- G. P. Charepanov, “Mechanics of Brittle Fracture,” Nauka, Moscow City, 1973.
- C. Atkinson, “The Propagation of a Brittle Crack in Anistropic Material,” International Journal of Engineering Science, Vol. 3, No. 1, 1965, pp. 77-91. doi:10.1016/0020-7225(65)90018-2
- N.-C. Lü, X.-G. Li, Y.-H. Cheng and J. Cheng, “Fracture Dynamics Problem on Mode I Semi-Infinite Crack,” Archive of Applied Mechanics, Vol. 81, No. 9, 2011, pp. 1181-1193 doi:10.1016/j.amc.2011.04.028
- N. C, Lü, Y. H. Cheng. X. G. Li and J. Cheng, “Dynamic Propagation Problem of Mode Ⅰ Semi-Infinite Crack Subjected to Superimpose Loads,” Fatigue & Fracture of Engineering Materials & Structures. Vol. 33, No. 3, 2010, pp. 141-148.
- N. C. Lü, Y. H. Cheng, X. G. Li and J. Cheng, “An Asymmetrical Dynamic Model for Bridging Fiber PullOut of Unidirectional Composite Materials,” Meccanica, Vol. 47, No. 5, 2012, pp. 1247-1260. doi:10.1016/j.tafmec.2012.05.007
- N. I. Muskhlishvili, “Singular Integral Equations,” Nauka, Moscow City, 1968.
- N. I. Muskhlishvili, “Some Fundamental Problems in the Mathematical Theory of Elasticity,” Nauka, Moscow City, 1966.
- F. D. Gakhov, “Boundary-Value Problems,” Fitzmatigiz, Moscow City, 1963.
- R. F. Hoskins, “Generalized Functions,” Horwood, Ellis, 1979.
- X. S Wang, “Singular Functions and Their Applications in Mechanics,” Scientific Press, Beijing, 1993 (in Chinese).
- G. C. Sih, “Mechanics of Fracture 4. Elastodynamics Crack Problems,” Noordhoff, Leyden, 1977.
- R. P. Kanwal and D. L. Sharma, “Singularity Methods for Eastostatics,” Journal of Elasticity, Vol. 6, No. 4, 1976, pp. 405-418.
- Editorial Group of Mathematics Handbook, “Mathematical Handbook,” Advanced Education Press, Beijing, 2002 (in Chinese).
- Teaching Office of Mathematics of Tongji University, “Advanced Mathematics,” Advanced Education Press, Beijing, 1994 (in Chinese).
- K. C. Wu, “Dynamic Crack Growth in Anisotropic Material,” International Journal of Fracture, Vol. 106, No. 1, 2000, pp. 1-12. doi:10.1016/S0022-5096(00)00012-0
- X.-G. Li, Y.-H. Cheng, N.-C. Lü, G.-D. Hao and J. Cheng, “A Dynamic Asymmetrical Crack Model of Bridging Fiber Pull-Out in Uniderectional Composite Materials,” Journal of Mechanical Science and Technoogy, Vol. 25, No. 9, 2011, pp. 2297-2309. doi:10.1016/j.ymssp.2011.07.013
- N. C, Lü, Y. H. Cheng. H. L. Si and J. Cheng, “Dynamics of Asymmetrical Crack Propagation in Composite Materials,” Theoretical and Applied Fracture Mechanics, Vol. 47, No. 3, 2007, pp. 260-273. doi:10.1016/j.tafmec.2007.01.004
- N. C. Lü, Y. H. Cheng and J. Cheng, “Mode I Crack Tips Propagating at Different Speeds under Differential Surface Tractions,” Theoretical and Applied Fracture Mechanics, Vol. 46, No. 3, 2006, pp. 262-275.
- A. S. Kobayashi, “Dynamic Fracture Analysis by Dynamic Finite Element Method. Generation and Prediction Analyses,” In: Nonlinear and Dynamic Fracture Mechanics, New York Publisher, New York, 1979, pp. 19- 36.
- J. F. Kalthof, J. Beinert and S. Winkler, “Measurements of Dynamic Stress Intensity Factors for Fast Running and Arresting Cracks in Double-Cantilever-Beam Specimens,” In: Fast Fracture and Crack Arrest, PA Publisher, Philadelphia, 1977, pp. 161-176.
- K. Ravi-Chandar and W. G. Knauss, “An Experimental Investigation into Dynamic Fracture: Part 1, Crack Initiation and Arrest,” International Journal of Fracture, Vol. 25, No. 41, 1984, pp. 247-262,
- K. Ravi-Chandar and W. G. Knauss, “An Experimental Investigation into Dynamic Fracture: Part 2, Microstructural Aspects,” International Journal of Fracture, Vol. 18, No. 7, 1984, pp. 735-738. doi:10.1016/0036-9748(84)90330-2
- K. Ravi-Chandar and W. G. Knauss, “An Experimental Investigation into Dynamic Fracture: Part 3, on SteadyState Crack Propagation and Crack Branching,” International Journal of Fracture, Vol. 26, No. 2, 1984, pp. 141- 152.
- L. B. Freund, “Crack Propagation in an Elastic Solid Subjected to General Loading—I. Constant Rate of Extension,” Journal of the Mechanics and Physics of Solids, Vol. 20, No. 3, 1972, pp. 129-140. doi:10.1016/0022-5096(72)90006-3
- N. I. Sneddon, “Fourier Transform,” McGraw-Hill, New York, 1951.
- N. I. Muskhelishvili, “Some Basic Problems of the Mathematical Theory of Elasticity,” Noordoff, Groningen, 1953.
- L. A. Galin, “Contact Problems in Elasticity Theory,” GITTL, Moscow City, 1953.
- N.-C. Lü, Y.-H. Cheng, X. G. Li and J. Cheng, “Fracture Dynamics Problem on Mode I Semi-Infinite Crack for Anisotropic Orthotropic Body,” Nonlinear Dynamics, Vol. 67, No. 4, 2012, pp. 2381-2396.
- N.-C. Lü, Y.-H. Cheng, Y.-T. Wang and J. Cheng, “Dynamic Extension Problems Concerning Asymmetrical Mode III Crack,” Applied Mathematical Modelling, Vol. 35, No. 5, 2011, pp. 2499-2507. doi:10.1016/j.apm.2010.11.058
- N.-C. Lü, Y.-H. Cheng, Y.-T. Wang and J. Cheng, “Fracture Dynamics Problems of Orthotropic Solids under Anti-Plane Shear Loading,” Nonlinear Dynamics, Vol. 63, No. 4, 2011, pp. 793-806.
- N.-C. Lü, Y.-H. Cheng, X. G. Li and J. Cheng, “Asymmetrical Dynamic Propagation Problems Concerning Mode Ⅲ Interface Crack,” Composite Interfaces, Vol. 17, No. 1, 2010, pp. 37-48.
- N.-C. Lü, J. Cheng and Y.-H. Cheng, “Self-Similar Solutions of Fracture Dynamics Problems on Axially Symmetry,” Applied Mathematical and Mechanics, Vol. 22, No. 12, 2001, pp. 1429-1435.

