World Journal of Mechanics
Vol.2 No.1(2012), Article ID:17683,7 pages DOI:10.4236/wjm.2012.21004
A Fatigue Analysis of a Hydraulic Francis Turbine Runner
1Centro de Investigación en Ingeniería y Ciencias Aplicadas, CIICAp, Universidad Autónoma del Estado de Morelos, Cuernavaca, México
2Centro Nacional de Investigación y Desarrollo Tecnológico, Cuernavaca, México
Email: miriam_flores@uaem.mx
Received October 20, 2011; revised November 22, 2011; accepted January 7, 2012
Keywords: Hydraulic Francis Turbine; Crack; Finite Element; Modal Analysis; Fluid-Structure Interaction
ABSTRACT
In this work, the estimation of crack initiation life of a hydraulic Francis turbine runner is presented. The life prediction is based on the local strain approach to predict the initiation life. First, the analysis is carried out in air and in water condition and the runner’s natural frequencies were calculated using the finite element (FE) method. The analysis in air is compared with experimental analysis in order to have a representative model of real runner and subsequently the numerical analysis was perform in water. In the case of the runner immersed in water, the added mass effect due to the fluid structure interaction (FSI) is considered. Second, the static and dynamic stresses were calculated according to life estimation. For the calculation of static stresses, the pressure distribution of water and the centrifugal forces were applied to the runner. The dynamic stresses were estimated for interactions between the guide vane and the runner. Lastly, the estimation of the crack initiation life of the runner was obtained.
1. Introduction
The tendency of higher power concentration in hydraulic turbines, bring as a consequence an increase in both the load and hydraulic forces in the machine. These conditions produce major stresses in runners and possible vibration problems that could cause fatigue and fracture the blades. The fracture begins in small cracks, brought about by critical operation conditions of the machine over long periods, until failure.
In the most of hydroelectric power plants around the World, turbines have operated for decades and in many of them, the current operating conditions are different from the original design specified, these operations cause vibrations and some have presented cracks in the runners produced by fatigue [1,2].
The fatigue cracks normally are present in regions that have a metallurgical or structural discontinuity and were subjected to higher stresses [3]. The concept of local strains and stresses are the most promising approach to predict the crack initiation growth in a structure subjected to fatigue loads [4]. These concepts are used in this work, and the following procedure is adopted for the estimation of crack initiation growth life of a Hydraulic Francis Turbine Runner that is installed in a Mexican hydroelectric power plant.
2. Modal Analysis
In the actual operating conditions, Francis runners are surrounded by water. For the prediction of the dynamical characteristics of the structure at these conditions, it must be taken into account the effect of the fluid that surrounds it. The system had to be treated as a problem of fluid-structure interactions, where the equation of dynamic structure has to be coupled with the fluids equations. It is well known that the equation of the dynamic structure could be formulated as follows:
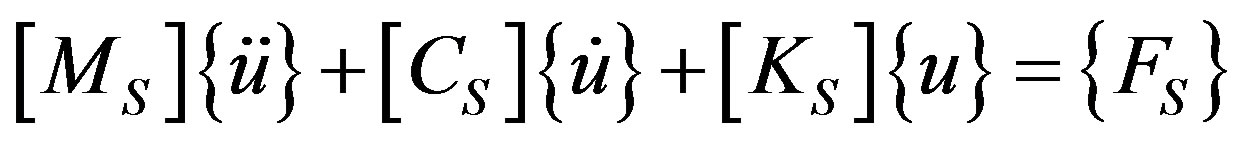 (1)
(1)
where [Ms] is the structural mass matrix; [Cs], the structural damping matrix; [Ks], the structural stiffness matrix; {Fs}, the applied load vector and {u}, the nodal displacement vector. In the case of the coupled model of the structure-water, the behavior of the water pressure could be described with the acoustic wave equation, known as the Helmholtz equation.
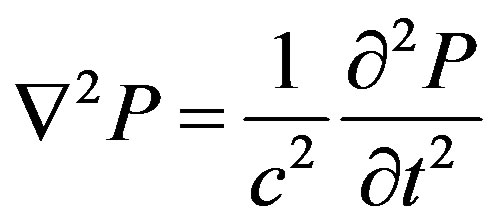 (2)
(2)
where P is the fluid’s pressure, c the sound velocity in the fluid’s media, t is the time and Ñ2 the Laplace operator. Equation (2) comes from the Navier-Stokes movement equation and the continuity equation considering the following assumptions [5]:
Ÿ The fluid is a compressible fluid (the density change because of the pressure variations)
Ÿ The fluid has no viscosity.
Ÿ There are no flow on the fluid The density and pressure are uniform in the fluid.
In the interface between the solid runner and water, the relation between the normal pressure gradient of the fluid and the normal acceleration of the structure gives the equation [6]:
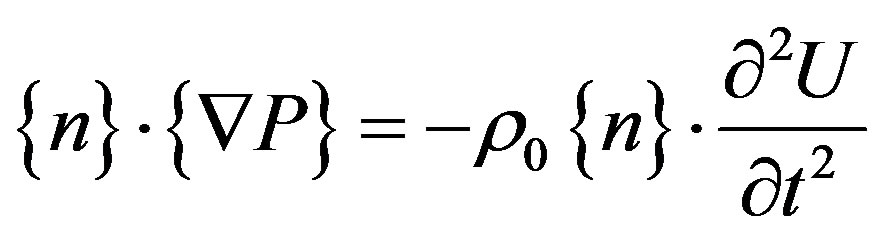 (3)
(3)
where U is the displacement vector of the structure’s interface, and r0 the density of the fluid. Considering the pressure of the fluid that acts in the interface, (1) for the structural dynamics can be described by the form:
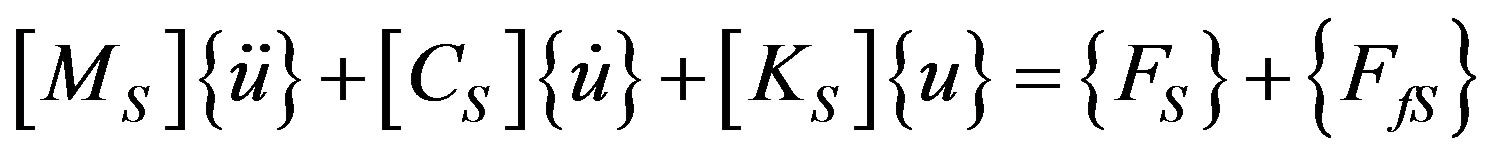 (4)
(4)
where {FfS} is the load vector because of the fluid’s pressure acting in the interface. The finite element discretized equations for the fluid-structure interaction problem were described as:
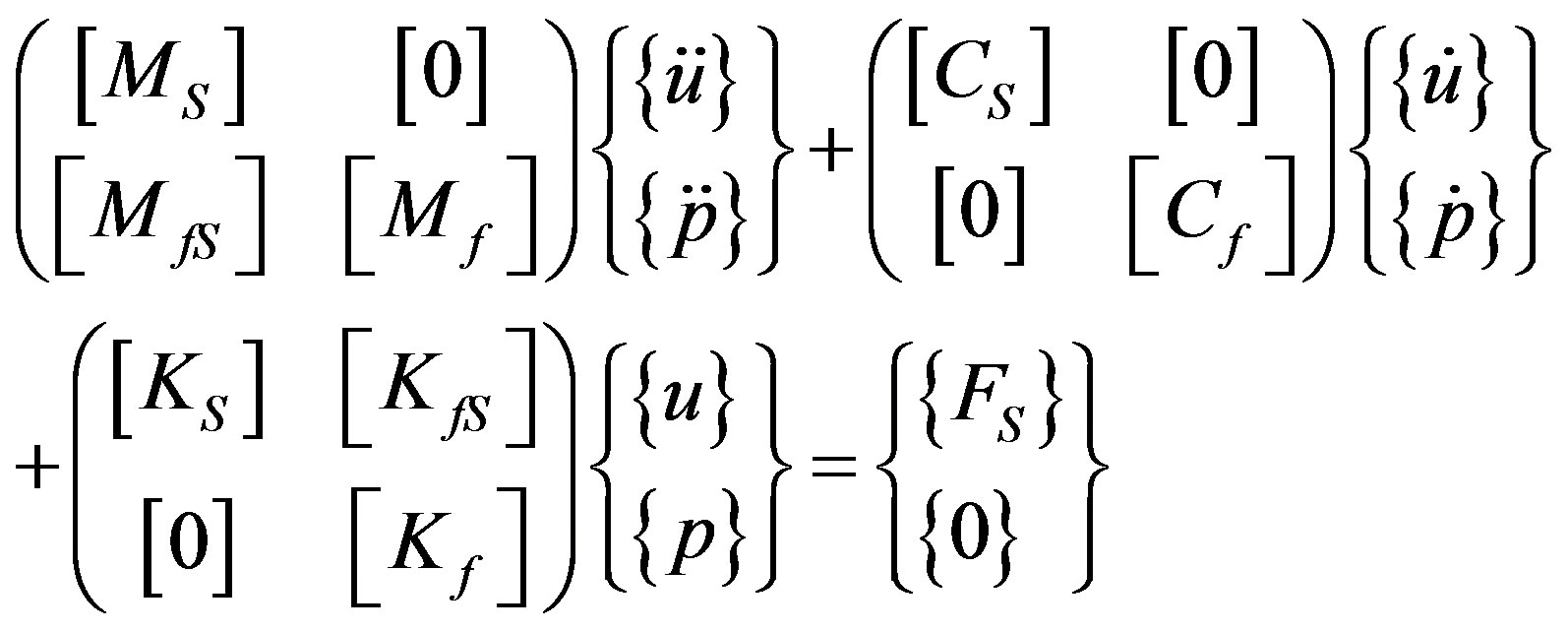 (5)
(5)
where [MfS] is the mass equivalent matrix in the interface and [KfS] is the stiffness equivalent matrix in the interface. The solution of the finite element modal analysis from the runner-water coupled model gives as a result the natural frequencies and the modal shapes of the structure.
3. Crack Initiation Life
3.1. Cyclic Strain in Fatigue
The range of total deformation (De) is the addition of the elastic strain (ee) and the plastic strain (ep):
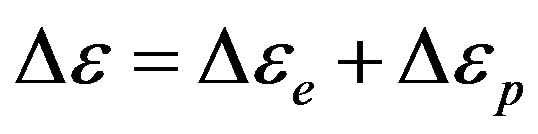 (6)
(6)
For a stable hysteresis curve, it is suggested [7] that it can be described by a cycle of deformation being the sum of the elastically and plastically ranges, so:
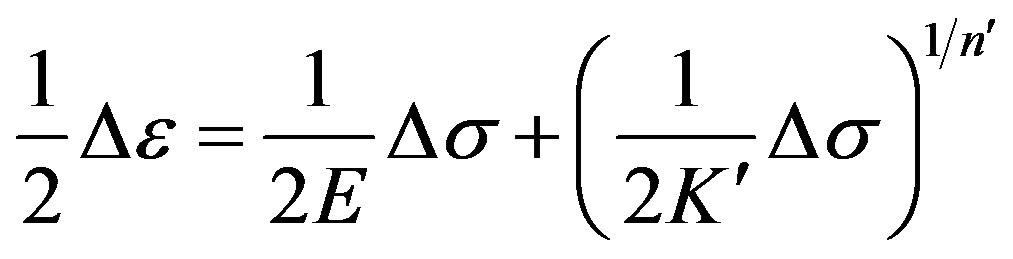 (7)
(7)
where: E is the elastic module, Ds is the real range of stress, K' is the cyclic strength coefficient, and n' is the cyclic strain hardening exponent.
3.2. Neuber’s Rule
The Neuber’s rule expresses the relation between the nominal stress range DS, and the true stress; and the nominal deformation in the elastic region in the vicinity of the defect in the specimen [8]. This is the nominal deformation in the elastic region in the vicinity of the defect in a specimen. That is:
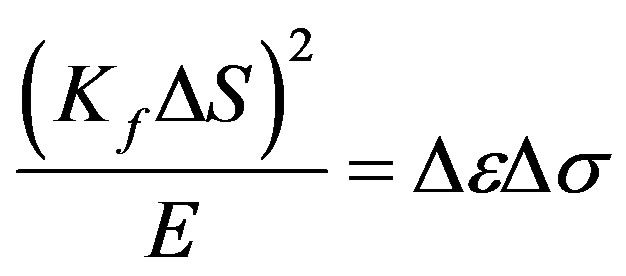 (8)
(8)
Equation (7) is used in the equation of the Neuber’s rule (8), obtaining (first approximation):
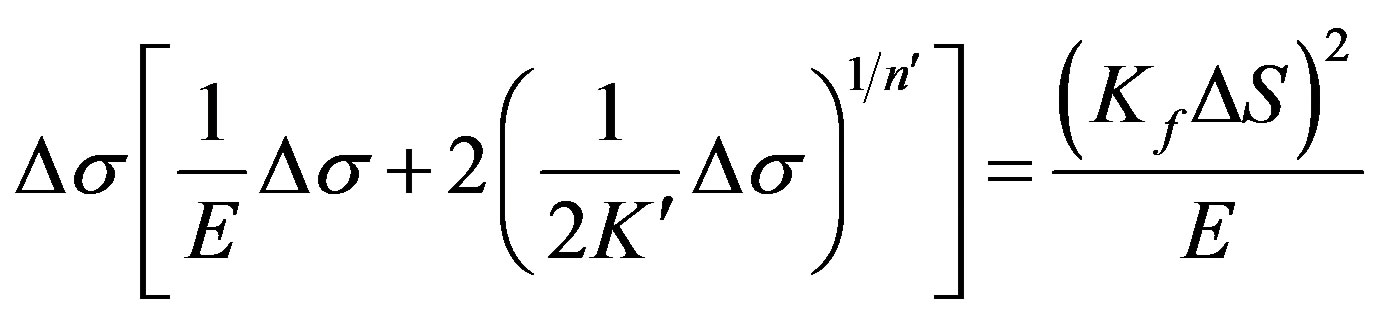 (9)
(9)
3.3. Fatigue Life
The stress life (S-N) data can be plotted linearly on a log-log scale. The total strain amplitude is the sum of elastic strain amplitude and plastic strain amplitude. The stress life for the elastic part of the strain amplitude is determined by:
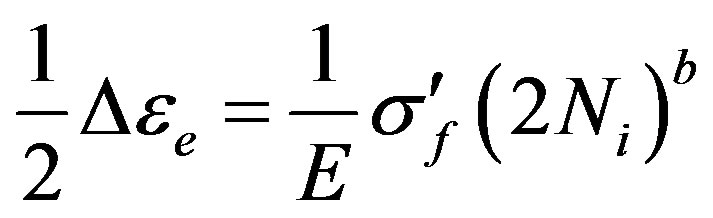 (10)
(10)
where s'f is the fatigue strength coefficient. The plastic strain life in the log-log plot is
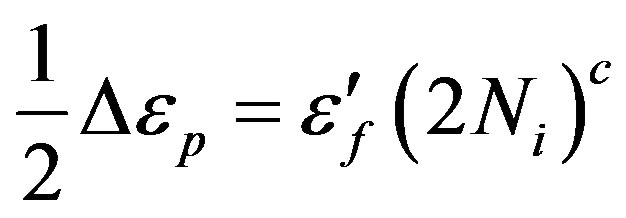 (11)
(11)
where e'f is the fatigue ductility coefficient, and c is the fatigue ductility exponent. The total strain amplitude is the strain life equation (include the effect of mean stress sm), as follows:
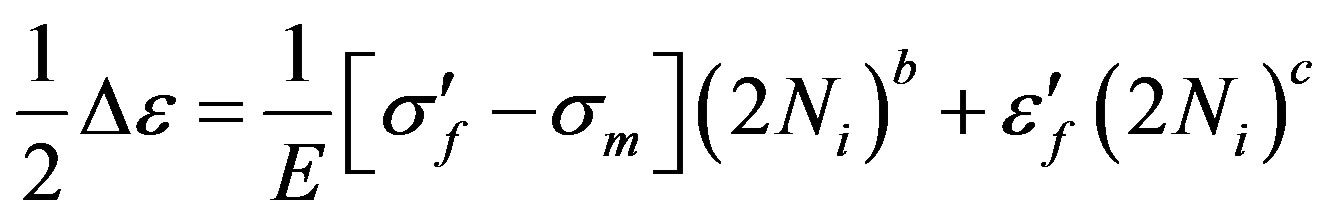 (12)
(12)
4. Case Study
The case study presented was performed for a Francis turbine runner of 38.5 MW with an operation velocity of 180 rpm and it consists of 13 blades. The runner’s metallic material is 13.4CrNi stainless steel with elastic module E = 206 GPa, yield strength Sys = 590 MPa, Poisson ratio m = 0.288 and density r = 7700 kg/m3. The adopted procedure for the runner analysis is as follows:
1) The model of the runner was constructed as a FE model to perform the modal and the static stress analysis. The simulations were performed using the commercial software ANSYS.
2) The modal analysis was realized for air and water. The numerical analysis in air is compared with the vibration experimental results obtained for air. The runner’s analysis in water considers the interaction of the structure and the fluid to obtain the natural frequencies. Also, the relation of the frequencies reduction was obtained due to the water that surrounds the runner.
3) The static stress of the runner was calculated taken into account the loads in the operational conditions caused by the centrifugal forces and the fluids static pressure. For the calculation of the dynamical stress, an excitation force was considered for blades passing the guide vanes. The numbers of the guide vanes in this case is 24.
4) With the nominal stresses (from the stress analysis), the estimation of the cracking initiation growth on the runner was calculated.
4.1. FE Model
Based on the characteristic of cyclic symmetry for the structure, it was used a runner’s sector conformed by a blade and an angle of 360/13 degrees of the crown and the band to run the simulation. The model was discretized with 3D solid structure elements with 20 nodes for the blade, and 3D structural solid elements tetrahedral with 10 nodes for crown and band. In the analysis it was established the conditions of the cyclic analysis. The results were expanded to the whole runner. Figure 1 shows the model of the runner sector, which is formed by 20894 nodes and 10374 elements. Figure 2 shows the discretized model of the complete runner. The modal characteristics of runner were obtained using the modal analysis for cyclic geometry of ANSYS using the Block-Lanczos method.
4.2. Modal Analysis
The theoretical and experimental study of the structures immersed in water, indicates that the natural frequencies are reduced because of the interaction of this fluid with the structure [9-11]. It is important to determine the natural frequencies of the runner in air and establish if there is a reduction of them when the runner is sur-

Figure 1. FE model of runner section.
rounded by water.
The modal characteristics of a free vibration in air were obtained from a numerical and experimental procedure [12], the results were presented in Table 1. The modal shapes of the runner in air were shown in Figure 3" target="_self"> Figure 3.
For comparison of the numerical and experimental results in air, the variation (D%) is calculated between them, indicating the concordance between both analyses.
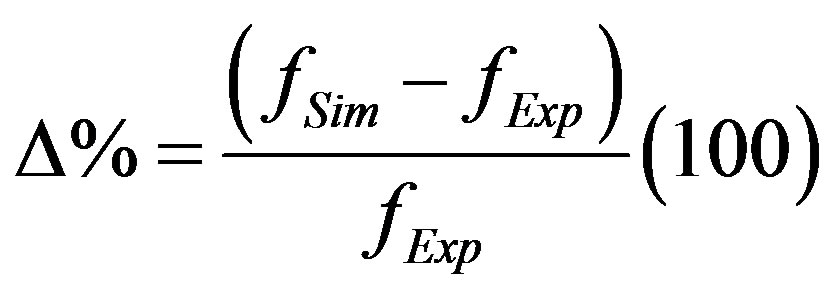 (13)
(13)
It is observed a variation between ±1.29% and ±3.5%, depending on the frequency, showing a good correlation between the simulation and the experimental results. From this air simulation model, the simulation of the runner in water is performed.
For the runner’s simulation in water, the FE model was modified extending the mesh of the structure, the fluid mesh considers that the runner was surrounded by the fluid. Both dominions share the same nodes group in the interface. 3D acoustic fluid elements were used specifying the elements of the fluids-structure interface and 3D infinite acoustic elements for the wall absorption. Figure 4 showed the mesh model of the complete runner surrounded by water. The water properties under environmental temperature and atmospheric pressure were: density r = 1000 kg/m3 and sound speed in water v = 1483 m/s. The obtained frequencies in this analysis were presented in Table 2. The modes of vibration observed
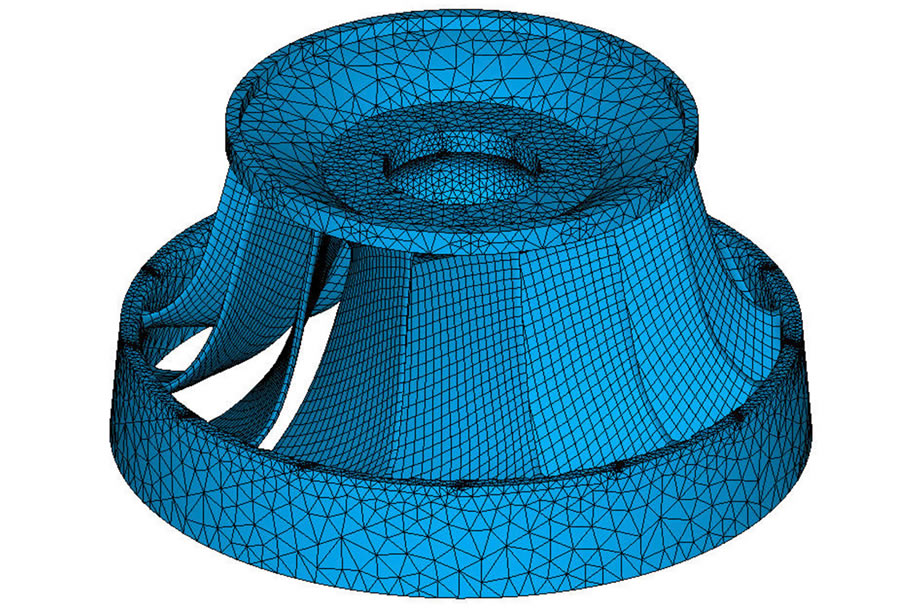
Figure 2. The whole runner model of the Francis turbine.
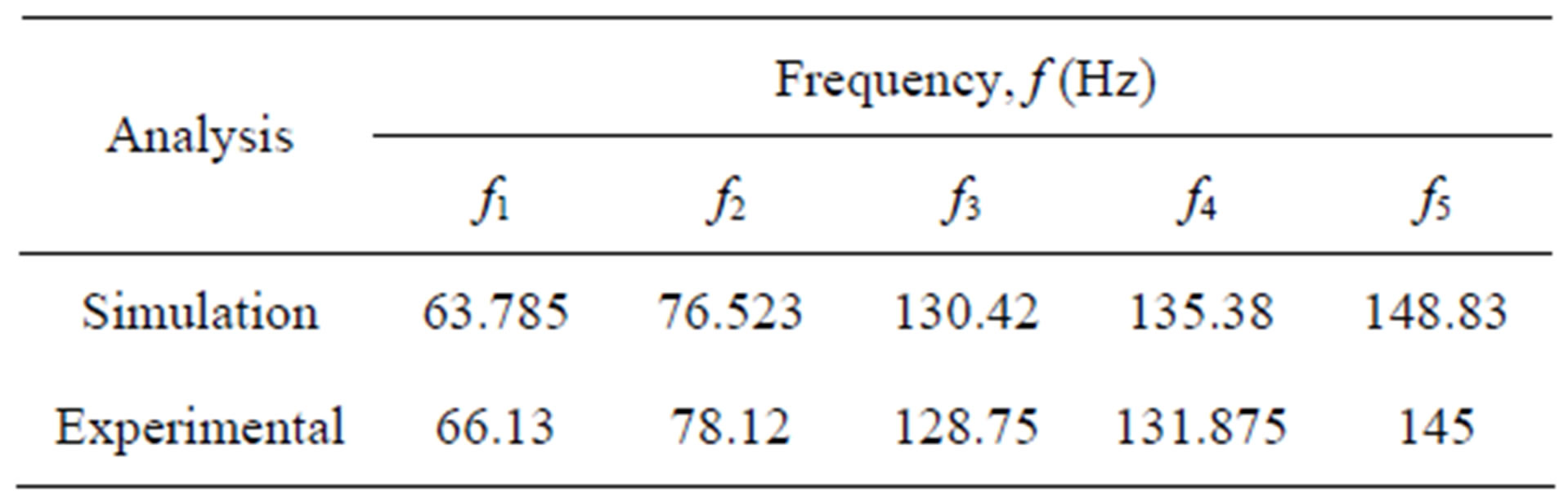
Table 1. Natural frequencies of the runner in air.
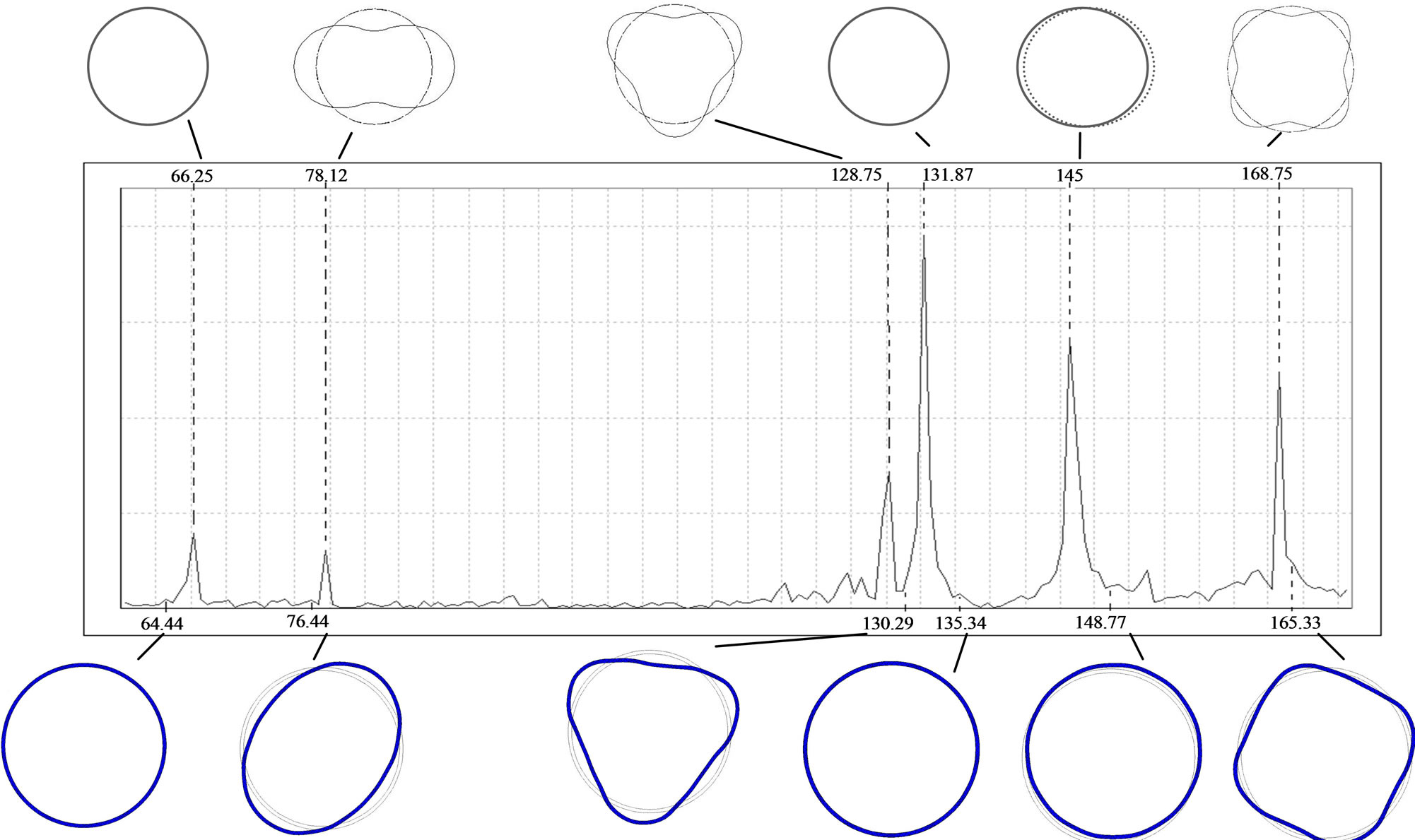
Figure 3. Vibration modes of the runner in air calculated by the experimental analysis (top) and numerical analysis (bottom) of first to sixth natural frequencies.

Table 2. Natural frequencies of the runner in water.
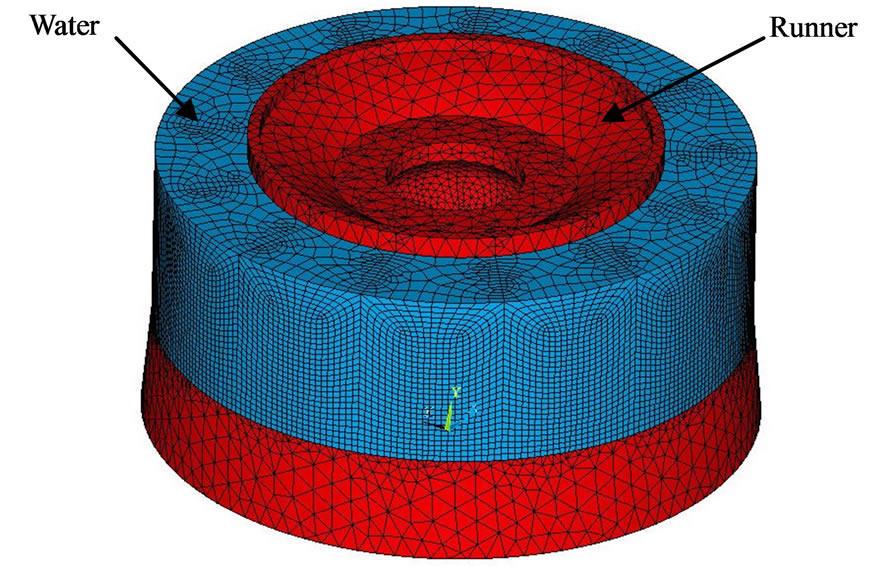
Figure 4. Mesh model of the complete runner surround of water.
were similar to the ones presented before, for the simulation of the runner in air. Figure 5 shows the natural frequencies of the runner in air and water.
When the obtained results in the runner’s simulations in air and submerged in water are compared, it was observed that a decrease in the natural frequencies do exist,

Figure 5. Natural frequencies in air and water.
because of the water that surrounds the structure. The above mentioned is estimated by the ratio of frequencies reduction given by:
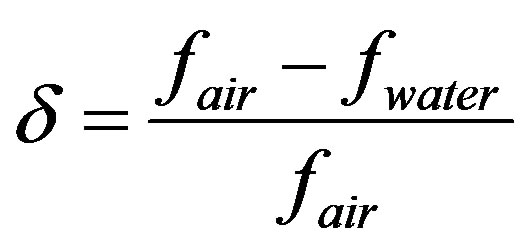 (14)
(14)
where fair and fwater are the natural frequencies in air and water respectively. The ratios frequencies reduction d, are shown in Table 3.
It was observed that the ratio of frequencies reduction varies from 0.152 to 0.324 depending on the frequencies. These values of d approach to those presented in different works, for example: Tanaka [4] gave an empiric value of 0.2, and Rodríguez [11] and Liang [13] realized a theoretical and experimental investigation modeling the runner in water with simplifications, and presenting for d, values that vary from 0.1 to 0.39.
It was observed that the ratio of frequencies reduction varies from 0.152 to 0.324 depending on the frequencies. These values of d approach to those presented in different works, for example, Tanaka [4] gave an empiric value of 0.2, and Rodríguez [11] and Liang [13] realized a theoretical and experimental investigation modeling the runner in water with simplifications, and presenting for d, values that vary from 0.1 to 0.39.
4.3. Stress Analysis
For the static stresses analysis of the runner under operating conditions, it was necessary to include the force of inertia and pressure fluid on the runner. The load in relation with the static pressure of the fluid on the sides of the pressure and suction of the runner’s blades were obtained by the Computational Fluids Dynamic (CFD) analysis [12] which uses the finite volume method to solve the Navier-Stokes equations. This load was allocated for the FE model for the stress analysis. The calculation was realized with the Von Mises criteria. The stress distribution was shown in Figure 6. The peak stress was found at 56.1 MPa and the average stress was 19.7 MPa. The maximum stress was localized in the blade near the band, close to the runner’s axis. The dynamical stresses come from the possible resonance of the harmonic from the guide vanes with the runner’s frequency. The calculation of the frequency of the blades passing the guide vanes, fz, caused by the external force that acts on the blades, having a frequency of:
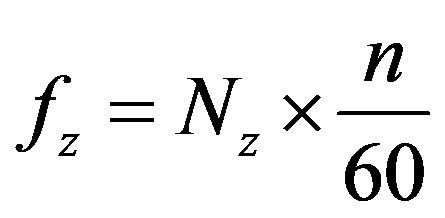 (15)
(15)
where Nz is the blades passing the guide vanes number, and n is the operation velocity of the turbine. The corresponding frequencies of the first and second harmonics for the blades passing the guide vanes were 72 and 144 Hz. From these results, it is shown that the second natural frequency of the runner in water was very close to the

Table 3. Ratio frequencies reduction of the runner.
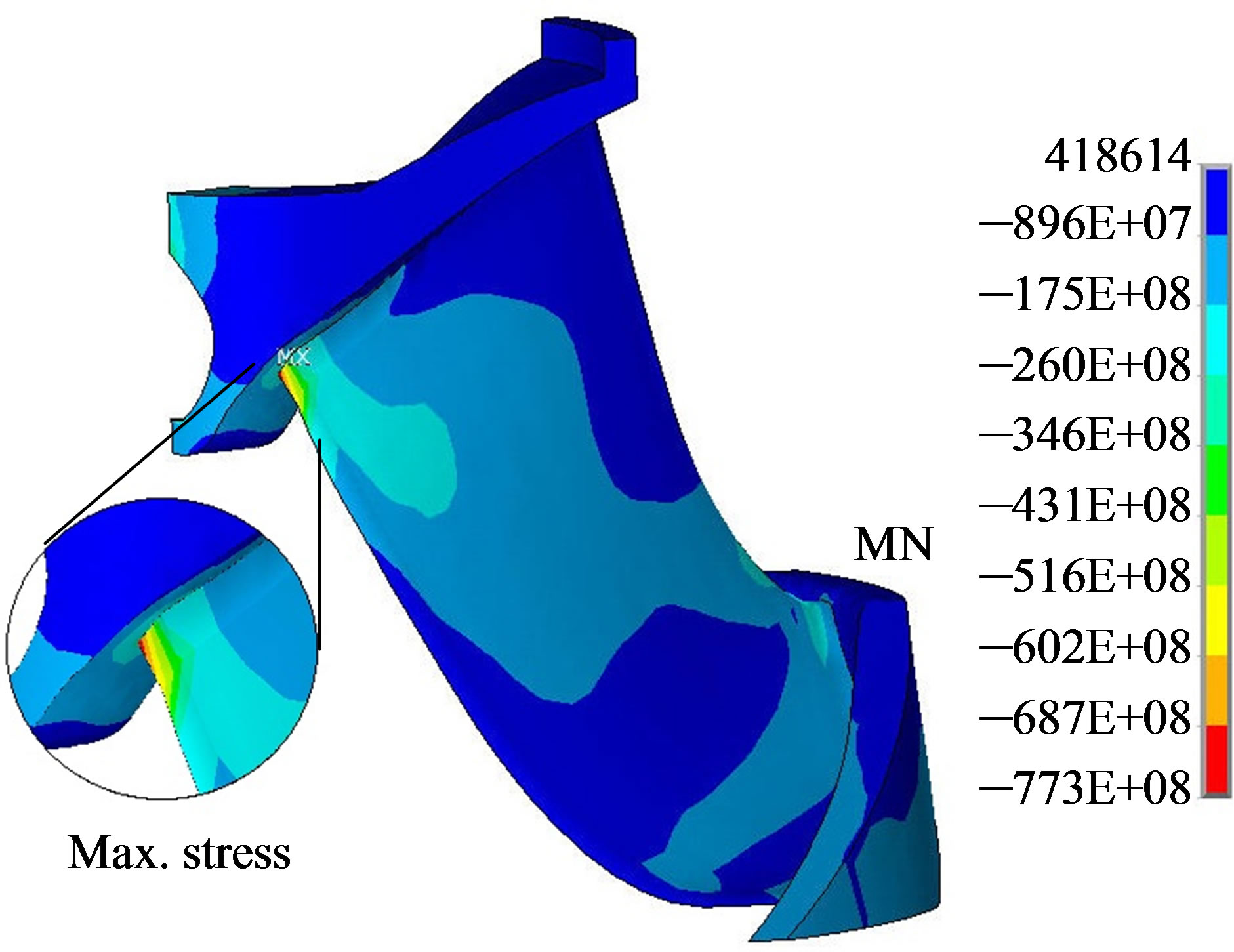
Figure 6. Stress distribution to the centrifuge forces and the static pressure of the fluid.
frequency of the first harmonic for the blades passing the guide vanes, producing a possible resonance effect.
The force of excitation comes from the first harmonic from the guide vanes and was a maximum at 10% of the stable force, taking the stress of Von Mises in the runner as 19.7 MPa as the stable load. Assuming that the damping ratio was 0.02, the quality factor for the fundamental bending is 25. Because of this, the dynamical stresses were very close to the union zone of the crown and the blade being 49.25MPa.
4.4. Crack Initiation
For the estimation of the crack initiation growth in the chosen runner’s hydraulic turbine, the equations were solved with the values obtained in the previous analysis. The material fatigue properties as: ultimate tensile strength Su = 735 MPa, cyclic strength coefficient K' = 1730 MPa, cyclic strain hardening exponent n' = 0.14, fatigue strength exponent b = –0.076 and fatigue ductility exponent c = –0.62 were useful for the calculation of crack initiation growth [14,15]. The nominal stress range DS was obtained from the dynamical stresses calculated, with their value as 49.25 MPa, so DS = 98.5 MPa. The real range of stress Ds was determined by Equation (9). The stress concentration factor K equals 5 and was considered that Kf = K, and because of this Ds = 492 MPa. The local strain range from the Neuber’s rule (8), was obtained as De = 0.002553.
The crack initiation growth was estimated from the equation for the total amplitude of deformation in the deformation life (12). The mean stress sm is considered equal to 0. The fatigue strength coefficient s'f, can be approximated equal to the true stress at fracture, s'f = sf. For steel with Brineel hardness up to 500 it may be approximated as s'f @ Su + 345 MPa, so s'f = 1080 MPa.
The fatigue ductility coefficient e’f, is approximated by the true fracture ductility (13)
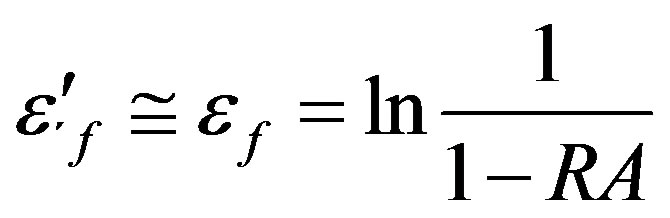 (16)
(16)
where RA is reduction in area. The number of cycles of crack initiation growth is obtained from (12). The life of the blade under resonance conditions is calculated by equation:
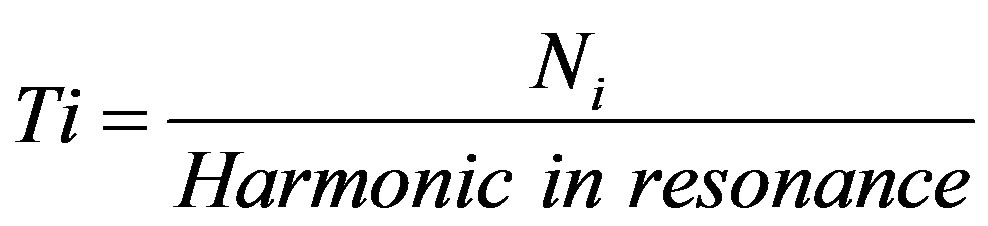 (17)
(17)
In operation conditions, the dynamic stresses induced in the runner are present for possible resonance. In these conditions, the resonance is accumulative and if the machine exceeds the crack initiation life of 23 days, the fracture initiation will occur.
5. Conclusion
A modal analysis was realized and the estimation of crack initiation growth life was calculated, for a Francis turbine runner. A FE model was built for the numerical, modal and static stress analysis. In the modal analysis, the natural frequencies and the modal shapes of the runner in air and surrounded by water, were determined. The simulation results in air as compared with the experimentally obtained, present a maximum variation of ±3.5% and shows a good correlation between them. In the submerged in water runner analysis, it was considered the runner surrounded by this fluid, and also the interface between the fluid and the structure. It was observed a decrease in the natural frequencies of the runner in air and surrounded by water. The modal shapes in both cases were similar. A static analysis was realized in operation loads obtaining the Von Mises stresses. The maximum stress was localized in the blade near to the band, close to the runner axis. The dynamical stresses were calculated from the possible resonance that exists between the second natural frequencies of the runner and the first harmonic of the guide vanes. If the machine operates under these conditions of resonance and dynamical stress, exceeding the time of crack initiation growth of 23 days, the crack initiation growth will occur. The method used in this work for the runner analysis could be used for the dynamical behavior analysis for other turbine runners and crack initiation growth estimation.
6. Acknowledgements
This paper is dedicated to the memory of Dr. Janusz Kubiak Szyszka (Centro de Investigación en Ingeniería y Ciencias Aplicadas, Universidad Autónoma del Estado de Morelos) who left us in April 2009.
REFERENCES
- R. Xiao, et al., “Study on Dynamic Analysis of the Francis Turbine Runner,” Large Electric Machine and Hydraulic Turbine, Vol. 7, 2001, pp. 41-43.
- S. Rao, P. K. Nimbekar, R. Misra and A. K. Singh, “Application of Local Stress-Strain Approach to Predict Fracture Initiation of a Francis Turbine Runner Blade,” 7th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Hawaii, 22-26 February 1998, pp. 22-26.
- S. Rao, “Turbine Blade Life Estimation,” Alpha Science International Ltd., Pangbourne, 2000.
- H. Tanaka, “Vibration Behavior and Dynamic Stress of Runners of Very High Head Reversible Pump-Turbine,” 15th International Association of Hydraulic Engineering & Research, Symposium on Hydraulic Machinery and Systems, Belgrade, 1990, pp. 289-306.
- L. E. Kinsler, et al., “Fundamentals of Acoustics,” John Wiley and Sons, New York, 1982.
- O. C. Zienkiewicz, and R. E. Newton, “Coupled Vibrations of a Structure Submerged in a Compressible Fluid,” Symposium on Finite Element Techniques, Stuttgart, 1-15 May 1969, pp. 360-378.
- J. F. Martin, T. H. Topper and G. M. Sinclair, “Computer Based Simulation of Cyclic Stress Strain Behavior,” T. &A. M. Report No. 326, University of Illinois, Urbana, 1969.
- H. Neuber, “Theory of Stress Concentration for ShearStrained Prismatical Bodies with Arbitrary Nonlinear Stress-Strain Law,” Journal of Applied Mechanics, Vol. 28, No. 4, 1961, pp. 544-550. doi:10.1115/1.3641780
- A. Coutu, H. Aunemo, B. Badding and O. Velagandula, “Dynamic Behavior of High Head Francis Turbine,” Hydro 2005, Villach, 17-20 October 2005.
- C. Monette, A. Coutu and O. Velagandula, “Francis Runner Natural Frequency and Mode Shape Predictions,” Waterpower XV, Chattanooga, 23-26 July 2007.
- C. G. Rodríguez, E. Egusquiza, X. Escaler, M. Farhat, Q. W. Liang and F. Avellan, “Experimental Investigation of Added Mass Effect on a Francis Turbine Runner,” Journal of Fluids and Structures, Vol. 22, No. 5, 2006, pp. 699-712. doi:10.1016/j.jfluidstructs.2006.04.001
- M. Flores, “Fluid-Structure Interaction Study of a Hydraulic Francis Turbine Runner,” Ph.D. Dissertation, University Autonomous of Morelos State, Mexico, 2009.
- Q. W. Liang, C. G. Rodríguez, E. Egusquiza, X. Escaler and F. Avellan, “Modal Response of Hydraulic Turbine Runners,” 23th International Association of Hydraulic Engineering & Research, Symposium on Hydraulic Machinery and Systems, Yokohama, October 2006.
- ASM International, “Mechanical Testing and Evaluation,” ASM Handbook, Vol. 8, 2000.
- D. F. Socie, M. R. Mitchell and E. M. Caulfield, “Fundamentals of Modern Fatigue Analysis,” Fracture Control Program Report No. 26, University of Illinois, Urbana, 1977.
Nomenclature
r: Density of the fluid d: Ratio of frequencies reduction De: Strain range Ds: Stress range DS: Nominal stress range e'f : Fatigue ductility coefficient s'f : Fatigue strength coefficient sm: Mean stress B: Fatigue Strength Exponent
C: Damping c: Fatigue Ductility Exponent E: Young’s Modulus F: Applied load f: Frequency K: Stiffness K: Factor of stress concentration K': Cyclic Strength Coefficient
Kf Fatigue stress concentration factor M: Mass n: Nominal speed n': Cyclic Strain Hardening Exponent Ni: Number of cycles of crack initiation Nz: Number of guide vanes P: Pressure Su: Ultimate Tensile Strength Sys Yield Strength
Ti: Crack initiation life u: Displacement U: Displacement in the structure interface v: Sound velocity in the fluid media

