World Journal of Mechanics
Vol. 1 No. 2 (2011) , Article ID: 4671 , 6 pages DOI:10.4236/wjm.2011.12006
Thermal Bending of Circular Plates for Non-Axisymmetrical Problems
1School of Mechanics and Civil Engineering, China university of Mining and Technology, Xuzhou, China
2East-China Research Institute of Computer Technology, Shanghai, China
3Changzhou No. 1 Construction Group Co., Ltd, Changzhou, China
E-mail: dongzhengzhu@hotmail.com
Received February 17, 2011; revised March 30, 2011; accepted April 12, 2011
Keywords: Thermal Bending Problems, Circular Plate, Boundary Integral Formula, Natural Boundary Integral Equation
ABSTRACT
Using the Green function, the boundary integral formula and natural boundary integral equation for thermal elastic problems are obtained. Then based on bending solutions to circular plates subjected to the non-axisymmetrical load, by utilizing the Fourier series and convolution formulae, the bending solutions under nonaxisymmetrical thermal conditions have been obtained. The calculating process is simple. Examples show the discussed methods are effective.
1. Introduction
Due to the complexity of the thermoelasticity problems, analytic solutions can be obtained only for axisymmetrical problems and simply problems [1-6]. For general non-axisymmetrical loads and general non-axisymmetrical boundary conditions, the numerical computation is the main method [7,8,9]. For bending problems of solid circular plates, Fu Bao-lian adopted the reciprocal theorem and took the solution of the clamped circular plate as the basic solution to discuss some bending solutions under axis-symmetrical loads [10]. Wang An-wen introduced the point source function to discuss the nonsymmetrical bending problems under the concentrated force [11,12]. Yu De-hao discussed bending problems of plates with the natural boundary element method [13,14]. Using the above methods, Li Shun-cai discussed the bending problems of solid circular plates under the boundary loads [15-17]. On the basis of the same method, using Fourier series and several convolution formulae, the boundary integral formula and natural boundary integral equation for the thermal bending of circular plates are obtained. The calculating process is simple. Examples show that the discussed methods are effective.
2. Boundary Integral Formula and Natural Boundary Integral Equation
The differential equation of elastic plate bending problems is
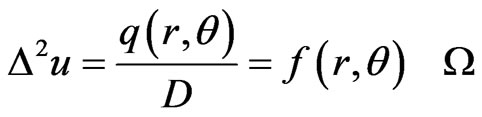 (1)
(1)
where, 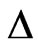 is the Laplacian operator, u is the deflection of the plate, q is the surface density of external loads, D is the bending rigidity of the plate,
is the Laplacian operator, u is the deflection of the plate, q is the surface density of external loads, D is the bending rigidity of the plate,  is the plate in a circle domain. For convenient, suppose the circle is a unit circle.
is the plate in a circle domain. For convenient, suppose the circle is a unit circle.
Using the Green formula of the bending problems for thin plates, we get
 (2)
(2)
Let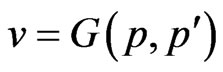 , which is the Green function of the biharmonic equation in
, which is the Green function of the biharmonic equation in , and then the Poisson integral equation of the bending problem of the plate can be found
, and then the Poisson integral equation of the bending problem of the plate can be found
 (3)
(3)
where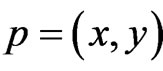 ,
, 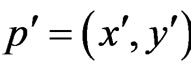 ,
, 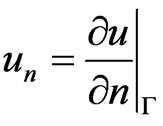 ,
, 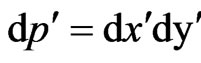 ,
,
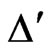 is the Laplacian operator related to
is the Laplacian operator related to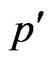 . The Green function in the unit circular domain can be obtained from the basic solution of the biharmonic equation
. The Green function in the unit circular domain can be obtained from the basic solution of the biharmonic equation
 (4)
(4)
where, 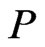 and
and 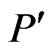 represent the polar coordinate
represent the polar coordinate 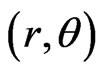 and
and 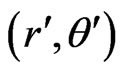 respectively. Thus
respectively. Thus
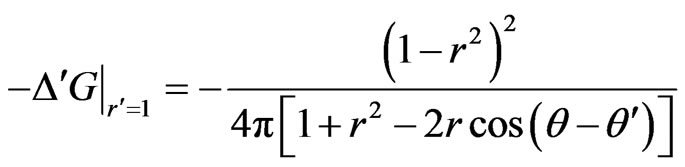
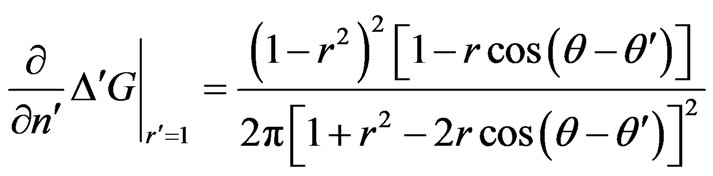
Hence, the Poisson integral formula of the bending circular plates can be obtained as
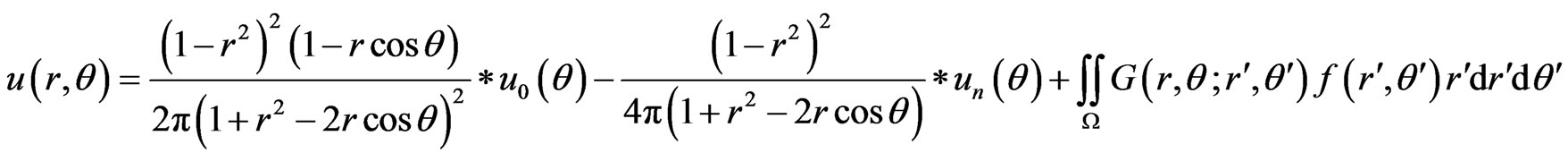
where, * is the convolution with regard to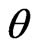 ,
,  ,
, 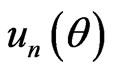 denote the deflection and slope at the edge respectively. For the supported edge,
denote the deflection and slope at the edge respectively. For the supported edge,  , the above equation will be educed to
, the above equation will be educed to
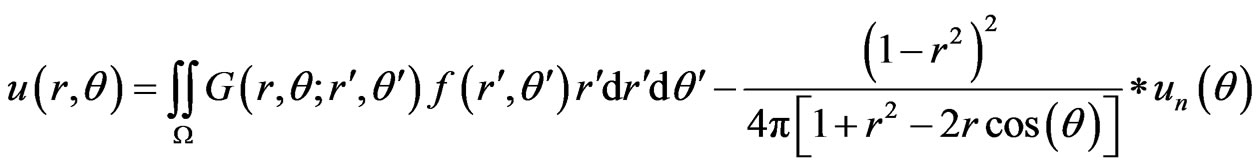 (5)
(5)
Suppose M is the differential boundary operator in the polar coordinate system, the bending moment Mu
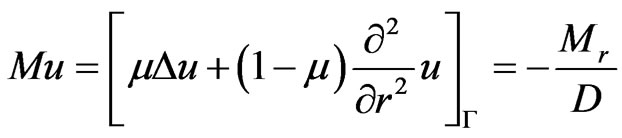 (6)
(6)
where, 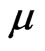 is Poisson ratio. Let the boundary operator acts on Equation (5), and use the limit formula of generalized function
is Poisson ratio. Let the boundary operator acts on Equation (5), and use the limit formula of generalized function

The natural boundary integral equation of the bending problems can be obtained as
 (7)
(7)
here

3. Thermoelasticity Equation and Boundary Conditions
The steady-state thermoelasticity equation is
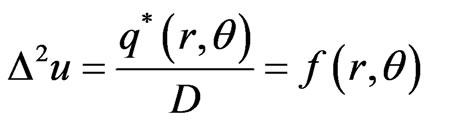
where q* is the surface distribution density of the thermoelasticity equivalent load over the plate. Suppose h is the thickness of the plate, E is elastic modulus, α is the thermal expansion coefficient and D is the bending rigidity of the plate. In general, suppose the thermal distribution is linear along the plate thickness, the equivalent load
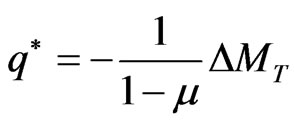

where
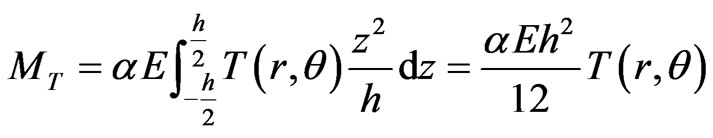
T(r, θ) is the thermal distribution function on the surface of the plate.
The equivalent boundary conditions of the clamped bending plate are ,
, . The equivalent boundary conditions of the simply bending plate are
. The equivalent boundary conditions of the simply bending plate are
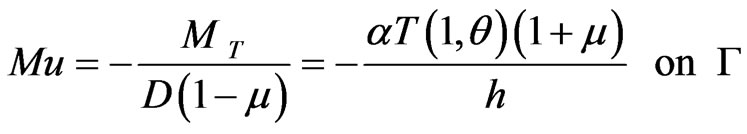
If in the plate there are no internal heat sources, then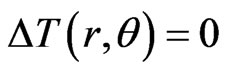 , q* = 0, for the simply plate,
, q* = 0, for the simply plate,  , Equations (5) and (6) will be reduced to
, Equations (5) and (6) will be reduced to
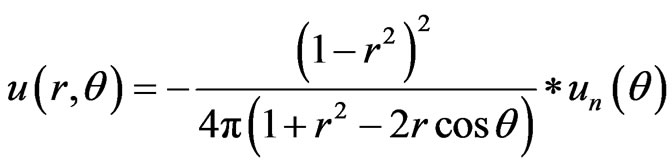 (8)
(8)
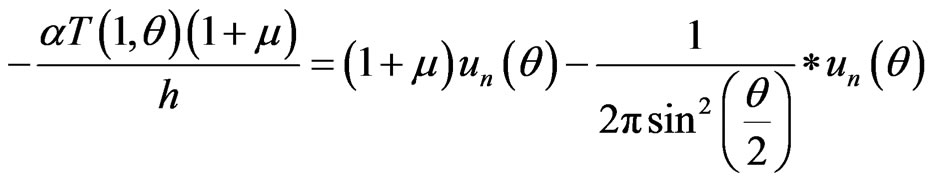 (9)
(9)
4. Heat Sources on the Plate
Firstly consider internal heat sources in the plate. The solution process is discussed through some examples.
Example 1 For comparison, suppose the thermal distribution function on the surface of the plate is axisymmetrical, 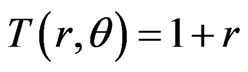
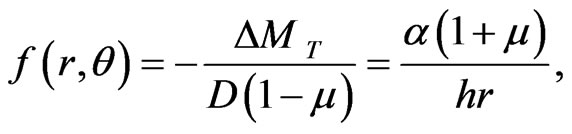
For the clamped plate, from (5)
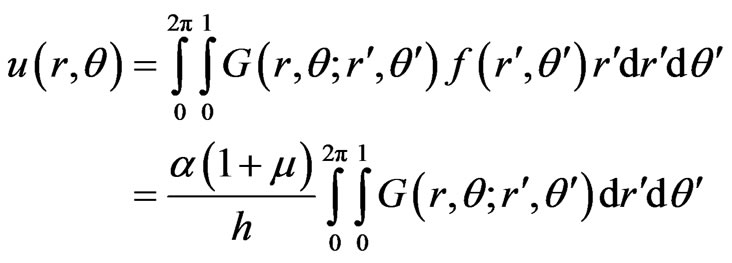
This solution is according to the axisymmetrical solution
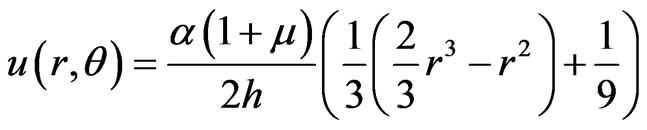
For the simply plate, firstly from the Equation (7) to get un which is a constant in axisymmetrical problems. Using the convolution formula [18,19]

if k = 0, we have

From (7), we get

So that
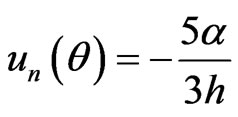
Substituting it into (8) and using the convolution formula
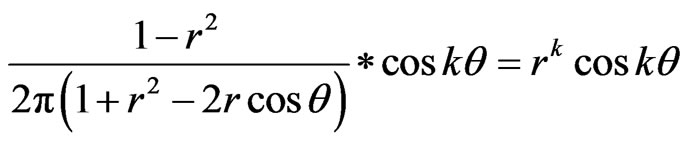
We get
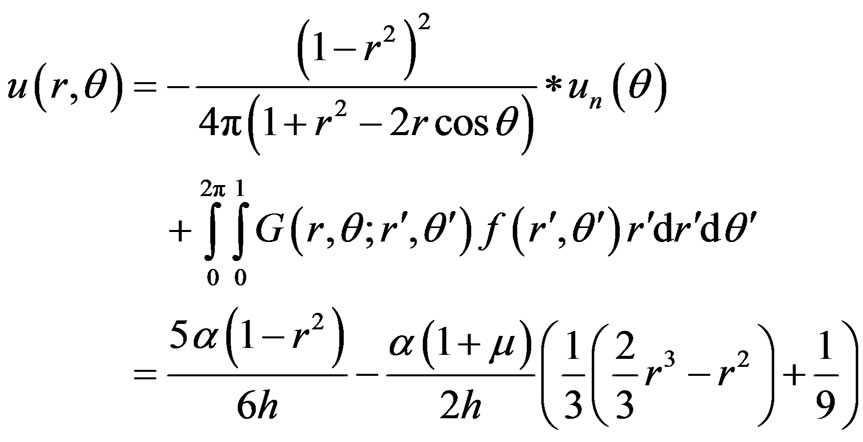
The solution is according to the axisymmetrical solution.
Example 2 Suppose the center of the thermal distribution function 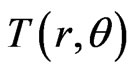 is in the point
is in the point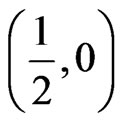 . This is a non-axisymmetrical problem.
. This is a non-axisymmetrical problem.
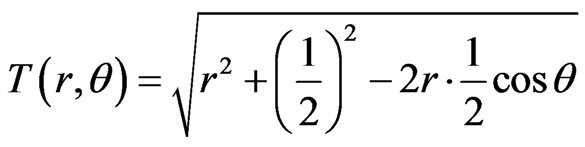
and
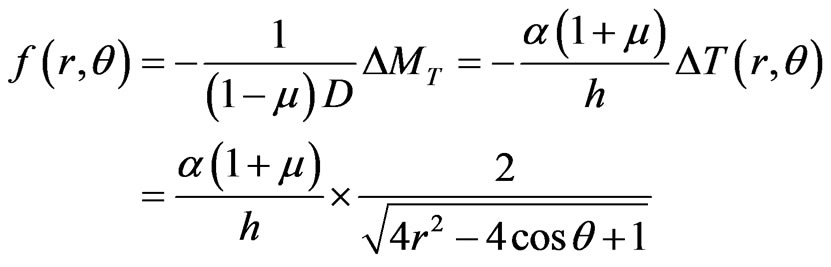
For the clamped plate, from (5)
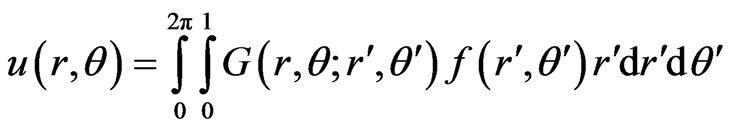
Suppose μ = 0.3, D = 1, α/h = 1, by the numerical calculation, the deflections of the plate are shown as Figure 1.
The center deflection of the plate is 0.046 and the maximum deflection is 0.048.
For the simply plate, firstly using Equation (7) to get un , suppose
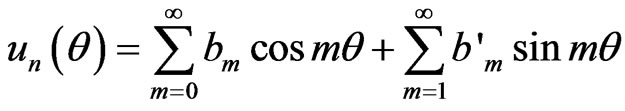
Then suppose μ = 0.3, D = 1, α/h = 1, the left expression of (7) is expanded to Fourier series
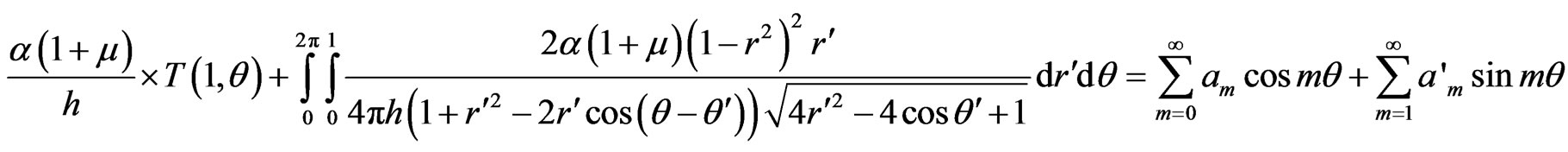
Substituting it into (8) which is an integral with a strongly singular Poisson kernel, and using the convolution formula, we get
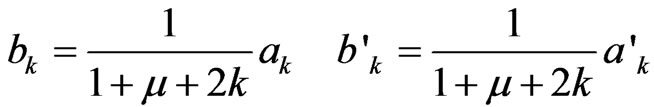
Then

The deflections of the plate are shown as Figure 2.
The center deflection of the plate is 0.669 and the maximum deflection is 0.67.
5. No Heat Sources on the Plate
When there are no heat sources on the plate, T(r,θ) satisfies harmonic equation,  , thus, q* = 0. For the clamped plate, there is no bending deflections on the plate. For the simply plate, (5) and (7) will be reduced to
, thus, q* = 0. For the clamped plate, there is no bending deflections on the plate. For the simply plate, (5) and (7) will be reduced to
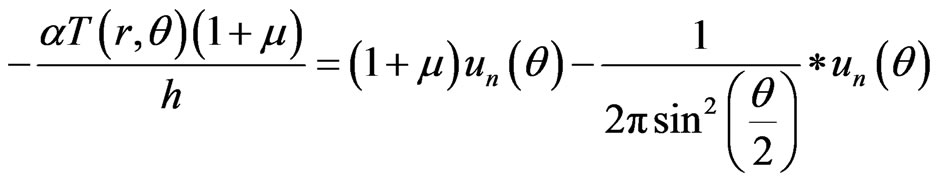
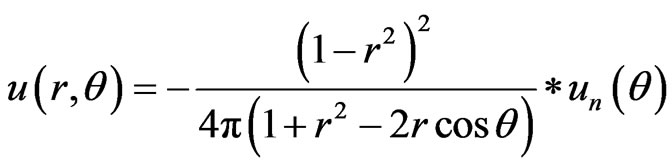
Example 3 On the boundary of a simply plate, T(1,θ) = sin2θ, in the plate T(r, θ) = r2 sin2θ.
Suppose
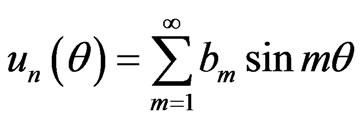
Then using the convolution formula
 s We get
s We get
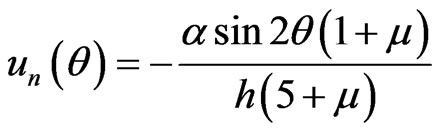
Substituting it into (8) and using the convolution formula
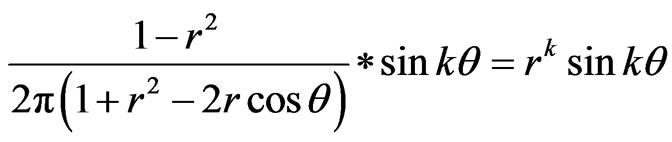
We have
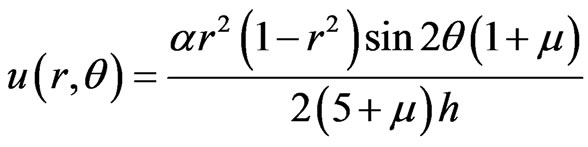
From above equation, we get

Suppose μ = 0.3, D = 1, α/h = 1, the bending deflections and the bending resultants are as Figure 3 and Figure 4:
6. Conclusions
Based on the Green function method, the boundary integral formula and natural boundary integral equation with
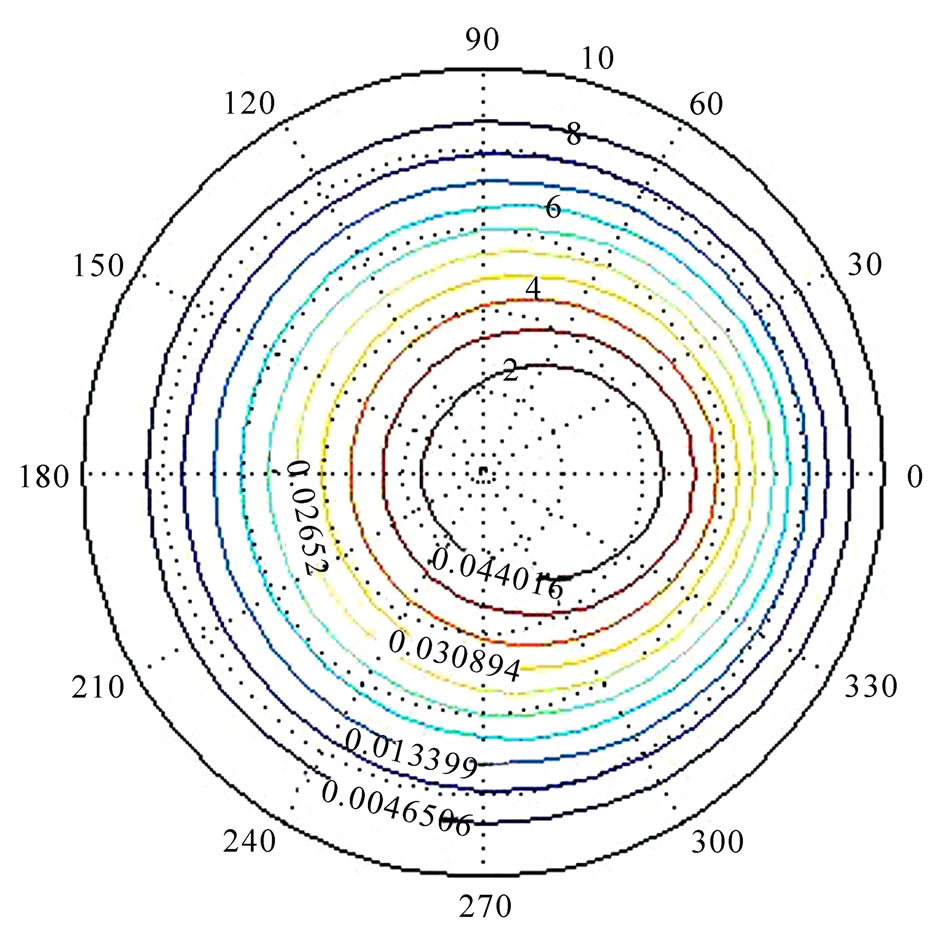
Figure 1. Deflections of the clamped circular plate.
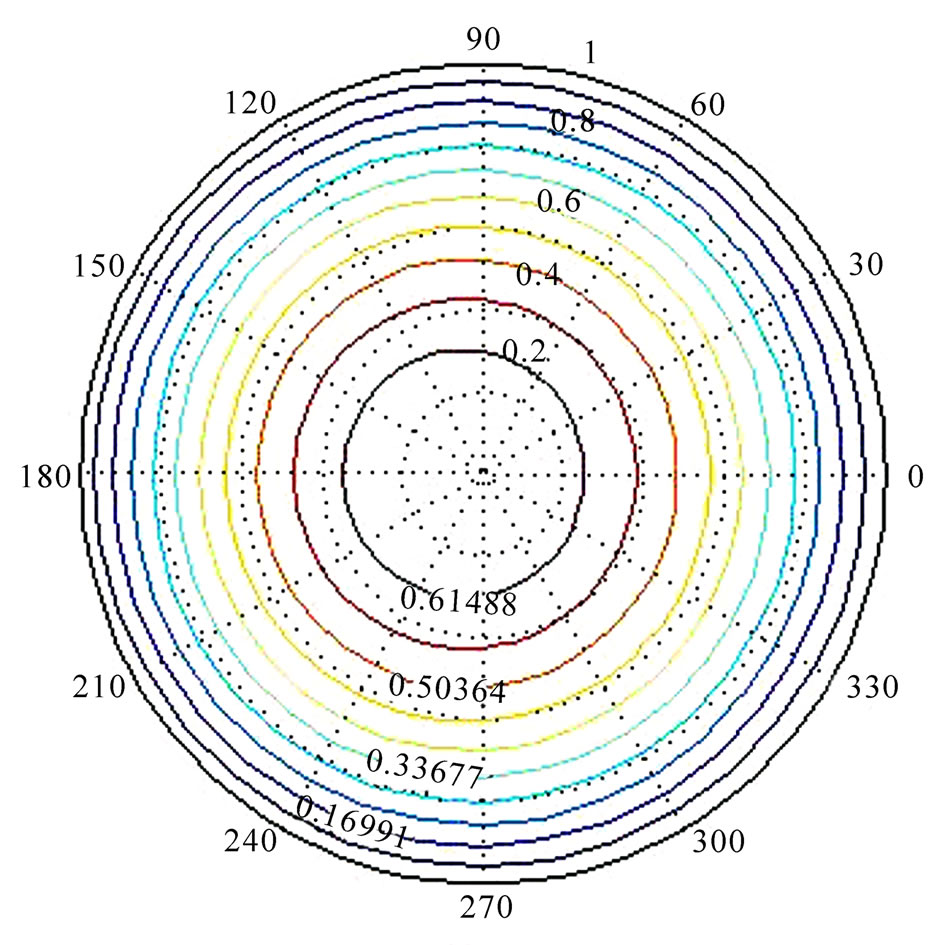
Figure 2. Deflections of the simply plate.
the strongly singular kernel are educed for the thermal bending problem of the plate supported at the boundary. he convolution formulae are utilized to get the solutions of deflection and slope directly for simple problems. As to complex problems, the Fourier series will be used to get the solutions with nice convergence velocity and computational accuracy. The calculating process is simple. accuracy. The calculating process is simple. The problems of other complicated loads can be solved with the similar method or by the superposition with the solutions of the above examples.
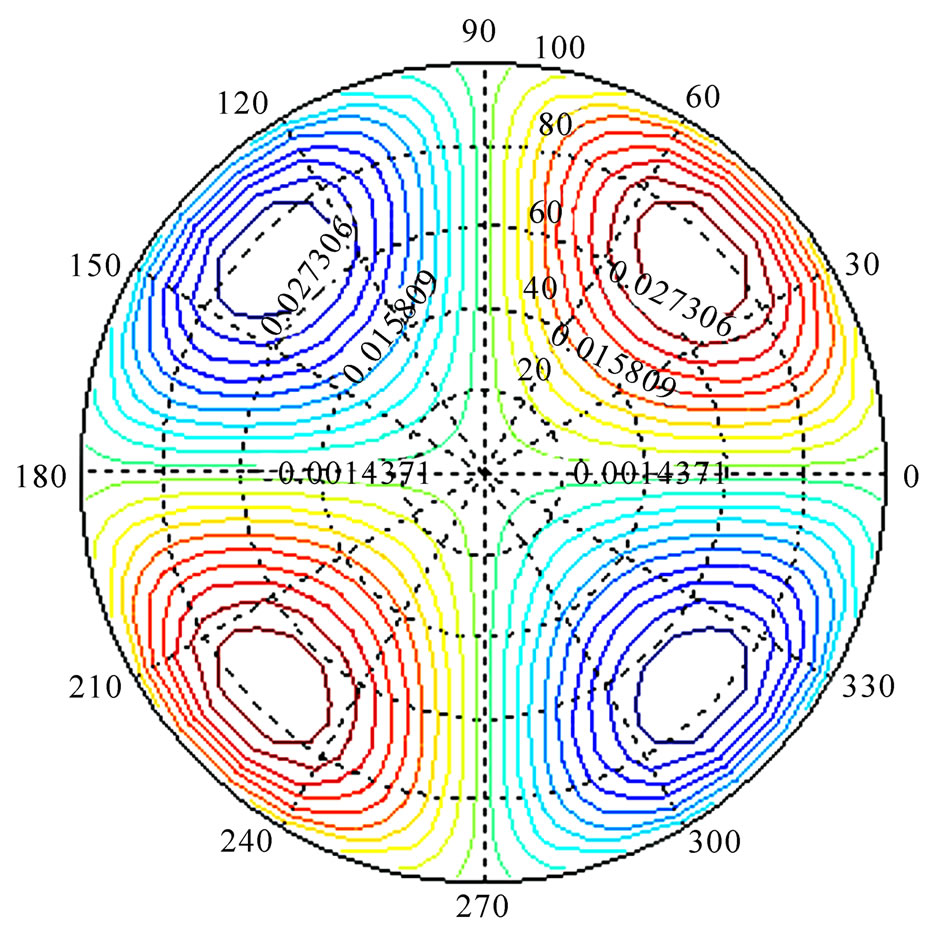
Figure 3. Deflections of circular plate.
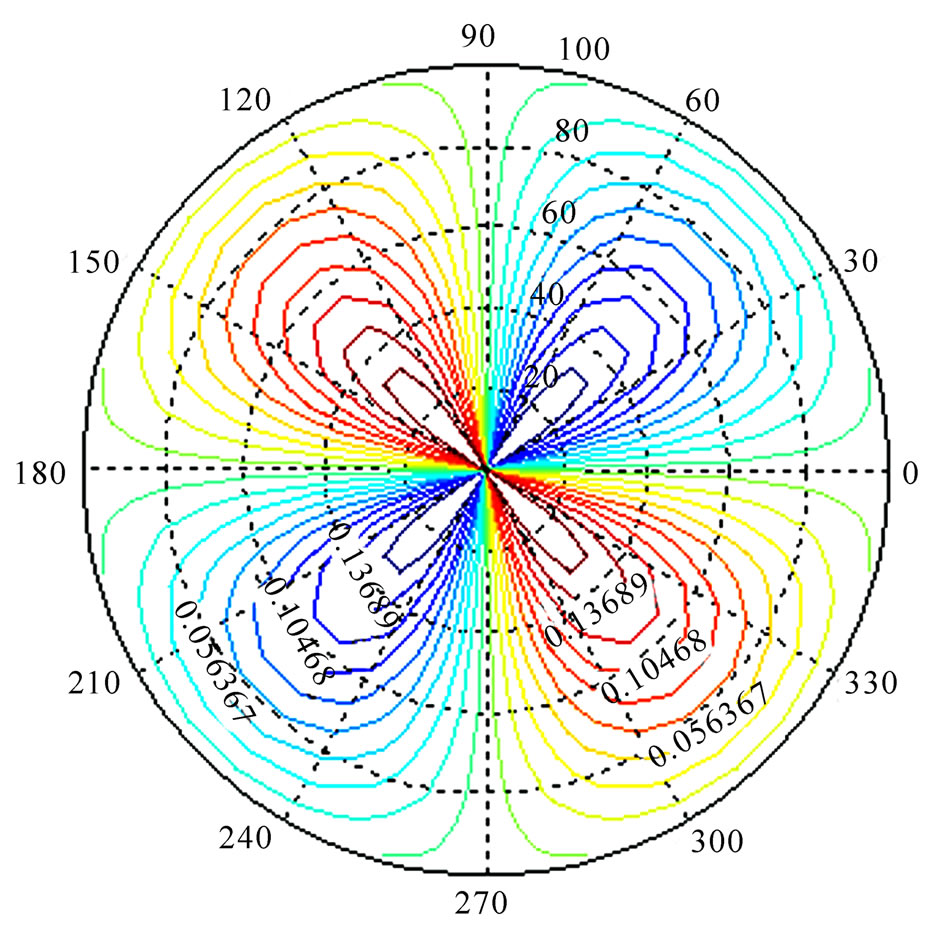
Figure 4. Mr of circular plate.
7. Acknowledgements
This work is supported by grants of National Basic Research Program of China, No. 2007CB209400 and Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), also supported by State Key Laboratory of Coal Resources and Safe Mining (CUMT) (SKLCRS08X04), supported by Foundation for National Doctoral Dissertation author of China (200760) and Program for New Century Excellent Talents in University (NCET-07-804).
REFERENCES
- S. P. Timoshengko and S. Woinowsky-Krieger, “Theory of Plates and Shells,” 2nd Edition, McGraw-Hill, New York, 1959.
- R. Szilard, “Theory and Analysis of Plates-Classical and Numerical Methods,” Prentice Hall, New Jersey, 1974.
- J. L. Zhu, “The Boundary Element Method for Elliptic Boundary Value Problems,” Science Press, Beijing, 1988.
- J. L. Zhu, “The Boundary Integral Equation Method for Solving Dirichelt Problem of Plane Biharmonic Equation,” Journal of Computational Mathematics, Vol. 6, No. 3, 1984, pp. 278-288.
- K. Chandrashekhara, “Theory of Plates,” University Press, Hyderabad, 2001, pp. 147-182.
- P. F. Hou, L. J. Guo and W. Lu, “Simply Supported Circular Plate under Uniform Thermo-Mechanical Coupling Loading,” Journal of Zhejiang University (Engineering Science), Vol. 41, No. 1, January 2007, pp. 104-108.
- Z. G. Zhao and P. R. Wang, “The Laplace Transform Finite Element Method for Dynamic Coupled Thermoelastic Bending Problems of Thin Plates,” Acta Mechanica Solida Sinica, Vol. 18, No. 2, 1997, pp. 183-187.
- Y. Sun and W. X. Zhong, “Finite Element Surface Stress Calculation,” Chinese Journal of Computational Mechanics, Vol. 27, No. 2, April 2010, pp. 177-181.
- I. Babuska and T. Stroubolis, “The Finite Element and Its Reliability,” Oxford University Press, London, 2001.
- B. L. Fu, “The New Bending Theorem of the Thin Plates on Reciprocal Method,” Science Press, Beijing, 2003.
- A. W. Wang, “Solution to Asymmetric Bending of Circular Plates under Single Load by Using Point-Source Function,” Acta Mechanica Sinica, Vol. 24, No. 3, 1992, pp. 381-387.
- X. S. Wang, “δ Function and Its Application in Mechanics,” Science Press, Beijing, 1993.
- D. H. Yu, “Mathematics Theory of National Boundary Element Method,” Science Press, Beijing, 1993.
- D. H. Yu, “Natural Boundary Integral Equations and Related Computational Methods ,” Journal of Yanshan University, Vol. 28, No. 2, March 2004, pp. 111-113.
- S. C. Li and Z. Z. Dong, “Natural Boundary Element Method to the Bending Problem of the Circular Plate under the Non-Continuous Loads,” Journal of Guangdong Industrial University, Vol. 16, No. 2, 2004, pp.83-88.
- S. C. Li, Z. Z. Dong and W. H. Xie, “Application of Natural Boundary Element Method to the Bending Problem of the Elastic Thin Plate,” Journal of Xuzhou Normal University, Vol. 20, No. 4, 2002, pp. 12-15.
- S. C. Li, Z. Z. Dong and W. H. Xie, “The Analytical Formulas of Bending Deflection for Infinite Plates with a Unit Circle under the Boundary Loads,” Journal of Gansu Sciences, Vol. 16, No. 2, 2004, pp. 83-88.
- I. M. Gel’fand and G. E. Shilov, “Generalized Functions,” Academic Press, New York, 1964.
- D. H. Yu, “Natural Boundary Integral Method and Its Applications,” Science Press & Kluwer Academic Publishers, Beijing, 2002.

