World Journal of Condensed Matter Physics
Vol.05 No.03(2015), Article ID:58589,9 pages
10.4236/wjcmp.2015.53016
Coexistence of Superconductivity and Antiferromagnetism in SmAsO1-xFxFe
Abera Mebrahtu, P. Singh
Department of Physics, Addis Ababa, Ethiopia
Email: kabeynabey@gmail.com, psinghgbpup@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 June 2015; accepted 2 August 2015; published 5 August 2015
ABSTRACT
Superconductivity and magnetism have been interesting topics in condensed mater physics and they have been studied experimentally and theoretically for many years. These two cooperative phenomena are antagonistic until the discovery of some rare earth ternary compounds that show the coexistence of superconductivity and magnetism. In some of the recently discovered iron-based layered superconductors, superconductivity and magnetism coexist. In the present work we examine the possibility of coexistence of antiferromagnetism and superconductivity in samarium arsenide oxide superconductor (SmAsO1-xFxFe). Using a model of the Hamiltonian and retarded double time Greens function formalism, we found expressions AFM order Parameter (η) and AFM transition temperature (Tm). We obtained the phase diagrams (Tc vs η) and(Tm vs η) to obtain the region where orders, i.e., superconductivity and AFM (antiferromagnetism), coexisted. The region under the intersection of the two merged graphs shows that superconductivity and AFM coexist in the system (SmAsO1-xFxFe).
Keywords:
Superconductivity, Antiferromagnetism, Cooper Pairs, Vortex State, Order Parameter, Random Phase Approximation, Nesting

1. Introduction
Superconductivity is the ability of certain materials to conduct electric current with practically zero resistance. This produces interesting and potentially useful effects. For a material to behave as a superconductor, low temperatures are required. Superconductivity was first observed in 1911 by H. K. Onnes, a Dutch physicist. His experiment was conducted with elemental mercury at 4 kelvin scale (approximately −452 degrees Fahrenheit), the temperature of liquid helium [1] [2] .
Most of the physical properties of superconductors vary from material to material, such as the heat capacity, the critical temperature, critical current density, and critical field at which superconductivity is destroyed. The coexistence of superconductivity and magnetism has been an interesting topic in condensed mater physics and it has been studied experimentally and theoretically for many years. These two cooperative phenomena are antagonistic. According to BCS (Bardeen, Cooper, Schreiffer) theory, a superconductor expels a magnetic field, which in turn destroys superconductivity. However, both superconductivity ordering and magnetic ordering have been seen in harmony (coexisting) in some of rare earth compounds. The coexistence of superconductivity and antiferromagnetism is quite peaceful and very weakly influences each other. Experiment has been revealed that superconducting and magnetic phases are interplayed in samarium iron pnictide superconductor (SmAsO1-xFxFe) with the long range of (0.1 ≤ x ≤ 0.15). In this paper we studied theoretical coexist of superconductivity and antiferromagnetism in SmAsO1-xFxFe.
The newly discovered iron-pnictid superconductor is unconventional superconductivity such as that in copper oxides. The reasons why unconventional pairing may be realized in iron pnictides are as follows: 1) Tc is very high, compared with conventional phonon-mediated BCS superconductors; 2) electron-phonon coupling is expected to be weak according to first-principles calculations [3] [4] . Mazin et al. argue that superconductivity realized in the iron-pnictide compounds is unconventional and mediated by antiferromagnetic spin fluctuations. Its pairing state is an extended s-wave pairing with a sign reversal of the order parameter among different Fermi surface sheets [5] [6] .
The superconductivity is also induced by the nesting-related antiferromagnetic spin fluctuations near the wave vectors connecting the electron and hole pockets. Kuroki et al. [7] [8] constructed a minimal model, where all the necessary five d-bands were included and calculated spin susceptibility and charge susceptibility within random phase approximation.
The most common way that a magnetic field destroys superconductivity is by disturbing the orbital effect, where the electrons in a pair orbit each other, acquiring more and more energy from the magnetic field. Once this energy becomes greater than that which unites the two electrons, the electron pairs break apart and superconductivity is suppressed. The other way magnetic fields can destroy superconductivity is when two electrons have what is called opposite spin; this is when in addition to the two electrons orbiting one another, they also are spinning like tops but in opposite directions, called s-wave spin. When the magnetic field is turned on, one electron gains energy while the other loses. “If the difference is bigger than the amount of energy holding the electrons together, then they fly apart and superconductivity has gone”, explained by Naughton [9] -[11] .
Experimental study on the newly discovered iron pnictide superconductor found that magnetism and superconductivity coexisted in the long rang doping in SmAsO1-xFxFe (0.1 ≤ x ≤ 0.15) [12] [13] .
2. Model System Hamiltonian
In order to study the coexistence of antiferromagnetism and superconductivity in superconducting SmAsO1- xFxFe theoretically in general and to find the expressions for transition temperature and order parameters in particular, systems of conduction and localized electrons have been considered. The model system Hamiltonian can be formulated as follows.
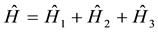 (1)
(1)
where
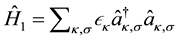
Is the Hamiltonian or energy of mobile (conduction) electrons. Here, the operators  are the creation (annihilation) operators for conduction electrons with the wave vector k and the spin projection on z-axis σ = ↑ or ↓.
are the creation (annihilation) operators for conduction electrons with the wave vector k and the spin projection on z-axis σ = ↑ or ↓. 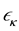 is the one electron kinetic energy measured relative to the chemical potential.
is the one electron kinetic energy measured relative to the chemical potential.  Is the interaction (electron-electron) through boson (phonon) exchange and is given by,
Is the interaction (electron-electron) through boson (phonon) exchange and is given by,
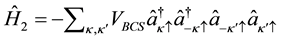
where VBCS defines the matrix element of the interaction potential.  Is the interaction term between conduction electrons and localized electrons due to some unspecified mechanism with some coupling constant (α) and is expressed as,
Is the interaction term between conduction electrons and localized electrons due to some unspecified mechanism with some coupling constant (α) and is expressed as,
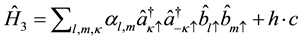
Putting all the three Hamiltonian together we obtain
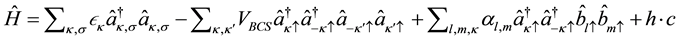 (2)
(2)
3. Equation of Motion for Mobile (Conduction) Electrons
The retarded double-time Green function is defined as
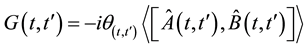 (3)
(3)
To obtain the equation of motion of the Green’s function we differentiate the above equation with respect to time t as,
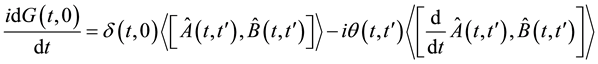 (4)
(4)
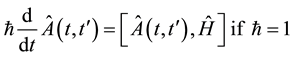
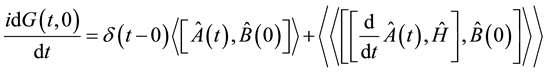 (5)
(5)
To solve this equation it is convenient to work with Fourier transform. A careful analysis shows that the function depends on t and 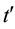 through
through . Thus we can write
. Thus we can write 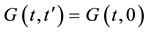 let
let 



The Dirac 

Therefore Equation (5) becomes



Now, let us solve the following commutation relation,

From which we obtain,

Following similar procedure as above, we get,

and

Substituting Equations (12), (13) and (14) into the equation of motion,

where 
One can also obtain the equation of motion for the expression 

For



Now, using Equations (16) and (17), the equation of motion becomes,
From which we obtain,

Using the relation for ∆, given by,

And by changing the summation into integration and by introducing the density of states at the Fermi level, 

Now, changing

Now, using Equation (22) in Equation (21), we get,

where

We can write Equation (23) as,

Let

3.1. Effect of Temperature on Superconducting Order Parameter (∆) and Magnetic Order Parameter (η)
Now, let us study Equation (25) by considering different cases.
Case (I): As

Hence, Equation (25) becomes,

Using the integral

Simplifying that we obtain

For


Case (II): At


where
λ = 0.3 - 0.9;
η = 0.05 - 7;
a = 0.00000067.
By substituting these values into the above equation we can calculate theoretical value for the critical temperature for SmAsFeO0.85F0.15 Tc = 55.5 k.
These are taken from the experimental data.
3.2. Equation of Motion for Localized Electrons
Using Green’s function formalism, the equation of motion for the localized electrons is obtained to be,

Now, using the Hamiltonian given in Equation (1), we evaluated the commutation 


where
Applying similar procedure as above and assuming


Now, from Equations (31) and (32), we get,

From which we get,

3.3. Correlation between Conduction and Mobile Electrons
The equation of motion that shows the correlation between the conduction and localized electrons can be demonstrated. Using similar definition as for ∆, we can write the magnetic ordering parameter, η as,

Changing the summation into integration and by introducing the density of states, 

Using the Matsubara frequency, 
Equation (36) becomes,

where 

Now, let us first solve the following expression.

Using Laplace’s transform and Matsubara frequency, Equation (38) becomes,
where

and

Then,

Since ∆l is very small, 
From which we get,

4. Results and Discussions
In this chapter, we examined the effect of magnetic order parameter η on superconducting transition temperature (Tc) and on AFM (antiferromagnetism) transition temperature (Tm) in SmAsO1-xFxFe. In chapter three, using the model of the Hamiltonian and retarded double time temperature dependent Greens function formalism; we obtained mathematical expressions the magnetic order parameter (η), and antiferromagnetism transition temperature (Tm). From Equation (27) we have got the superconducting transition (critical) temperature for the superconductor SmAsO1-xFxFe. Using this Tc value and Equation (28) we plotted the phase diagram of Tc versus η as shown in Figure 1. This figure indicates, as the magnetic order parameter (η) increases the superconducting transition temperature (Tc) decreases. The phase diagram of magnetic ordering temperature (Tm) versus magnetic ordering (η) also plotted as demonstrated in Figure 2, based on Equation (43). As we observed from this graph the magnetic transition temperature is increases (directly Proportional) as the magnetic order parameter increases. And finally, we merged Figure 1 and Figure 2 to obtain coexistence of superconductivity and antiferromagnetism.
5. Conclusions
In this work, we have studied the possible co-existence of antiferromagnetism and superconductivity in SmAsO1-xFxFe. Using a model Hamiltonian and Greens function formalism we obtained mathematical expression magnetic order parameter (η), critical temperature (Tc), and antiferromagnetism transitional temperature (Tm). Based on these mathematical expressions we plotted the graphs Tc vs. η as shown in Figure 1 and Tm vs. η also demonstrated in Figure 2. Finally the last two graphs Tc vs. η and Tm vs. η shown in Figure 3 were merged to obtain the coexistence of superconductivity and antiferromagnetism in SmAsO1-xFxFe.
Figure 1. Superconducting critical temperature vs. magnetic order parameter indicates, as the magnetic order parameter (η) increases the superconducting transition temperature Tc decreases.
Figure 2. Antiferromagnetism transition temperature (Tm) vs. magnetic order parameter (η).
Figure 3. The superconducting critical temperature and AFM (antiferromagnetism) transition temperature vs. magnetic order parameter.
The results of our work describe:
a) When magnetic order parameter increases, the critical temperature decreases;
b) The magnetic order parameter increases with the antiferromagnetism transitional temperature. Moreover, the region under the intersection of the two merged graphs demonstrated in Figure 3 shows that superconductivity and AFM coexist in SmAsO1-xFxFe.
Cite this paper
AberaMebrahtu,P.Singh, (2015) Coexistence of Superconductivity and Antiferromagnetism in SmAsO1-xFxFe. World Journal of Condensed Matter Physics,05,138-147. doi: 10.4236/wjcmp.2015.53016
References
- 1. Kamerlingh Onnes, H. (1911) Akad. WetenSchapp (Amsterdam), 14, 113.
- 2. Bednorz, J.G. and Muller, K.A. (1986) Possible high Tc Superconductivity in the Ba-La-Cu-O system. Zeitschrift für Physik B Condensed Matter, 64, 189-193. http://dx.doi.org/10.1007/BF01303701
- 3. Nomura, T.T. (2009) arXiv: 0811.2462v2 [cond-mat.supr-con].
- 4. Che, R.C., Wang, L., Chen, Z., Ma, C., Liang, C.Y., Lu, J.B., Shi, H.L., Yang, H.X. and Li, J.Q. (2008) Superconductivity in (La1-xCex)(O0.9F0.1)FeAs and La1-xPbx)OFeAs. EPL, 83, Article ID: 66005.
www.epljournal.org - 5. Mazin, I.I., Singh, D.J., Johannes, M.D. and Du, M.H. (2008) Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1-xFx. Physical Review Letters, 101, Article ID: 057003. http://dx.doi.org/10.1103/PhysRevLett.101.057003
- 6. Kamihara, Y., Watanabe, T., Hirano, M. and Hosono, H. (2008) Iron-Based Layered Superconductor La[O1-xFx]FeAs (x = 0.05 - 0.12) with Tc = 26 K. Journal of the American Chemical Society, 130, 3296-3297. http://dx.doi.org/10.1021/ja800073m
- 7. Kuroki, K., Onari, S., Arita, R., Usui, H., Tanaka, Y., Kontani, H. and Aoki, H. (2008) Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1-xFx. Physical Review Letters, 101, Article ID: 087004. http://dx.doi.org/10.1103/PhysRevLett.101.087004
- 8. Fujita, S. and Godoy, S. (1996) Quantum Statistical Theory of Superconductivity. Plenum Press, New York.
- 9. http://superconductors.org/UBNews.htm
- 10. Kordyuk, A.A. (2012) Iron-Based Superconductors: Magnetism, Superconductivity, and Electronic Structure. Low Temperature Physics, 38, 1119-1134. http://dx.doi.org/10.1063/1.4752092
- 11. Vorontsov, A.B., Vavilov, M.G. and Chubukov, A.V. (2010) Superconductivity and Spin-Density Waves in Multiband Metals. Physical Review B, 81, Article ID: 174538.
http://dx.doi.org/10.1103/PhysRevB.81.174538 - 12. Bardeen, J., Cooper, L.N. and Schrieffer, J.R. (1957) Theory of Superconductivity. Physical Review, 108, 1175. http://dx.doi.org/10.1103/PhysRev.108.1175
- 13. Drew, A.J., Niedermayer, Ch., Baker, P.J., Pratt, F.L., Blundell, S.J., Lancaster, T., Liu, R.H., Wu, G., Chen, X.H., Watanabe, I., Malik, V.K., Dubroka, A., Rssle, M., Kim, K.W., Baines, C. and Bernhard, C. (2009) www.nature.com/naturematerials












