World Journal of Condensed Matter Physics
Vol.05 No.02(2015), Article ID:56780,7 pages
10.4236/wjcmp.2015.52011
Electronic and Optical Properties of Rare Earth Oxides: Ab Initio Calculation
Sezen Horoz1, Sevket Simsek2, Selami Palaz3, Amirullah M. Mamedov4,5*
1Institute of Natural Sciences, Cukurova University, Adana, Turkey
2Department of Material Science and Engineering, Hakkari University, Hakkari, Turkey
3Department of Physics, Faculty of Science and Letters, Harran University, Sanliurfa, Turkey
4Nanotechnology Research Center (NANOTAM), Bilkent University, Ankara, Turkey
5International Scientific Center, Baku State University, Baku, Azerbaijan
Email: *mamedov@bilkent.edu.tr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 April 2015; accepted 25 May 2015; published 29 May 2015
ABSTRACT
In this work, we have investigated the electronic and optical properties of the technologically important rare earth oxide compounds―X2O3 (X: Gd, Tb) using the density functional theory within the GGA. The band structure of X2O3 have been calculated along high symmetry directions in the first brillouin zone. The real and imaginary parts of dilectric functions and the other optical responses such as energy-loss function, the effective number of valence electrons and the effective optical dielectric constants of the rare earth sesquioxides (Gd2O3 and Tb2O3) were calculated.
Keywords:
Rare Earth Oxides, Ab Initio Calculation, Electronic Structure, Optical Properties

1. Introduction
X2O3 (X:Gd, Tb) are the interesting materials from both fundamental and industrial perspectives and have a wide range of applications. They are thermodynamically stable, making them useful for corrosion resistive coating [1] -[5] . Additionally, their high refractive indices lead to applications in optics, such as antireflection coatings, switches, filters and modulators [1] [4] . The most recent interest of them is due to their high dielectric constants and electrical stability, making them good candidates for a new class of gate oxides in metal-oxide semiconductor field-effect transistors [1] . In addition, many properties of rare-earth sesquioxides are determined by their semicore f-levels. While being mainly localized on the rare-earth atoms and usually not participating in bonding and electronic conduction, f-shell electrons are available for optical transition and can establish strong magnetic order [1] . So far as we know, no ab initio general potential calculation of the optical properties of the rare-earth sesquioxides has been reported. The main purpose of this work is to provide some additional information to the existing features of Gd2O3 and Tb2O3 by using density functional theory. Therefore, in this work, we have investigated the electronic and optical properties of Gd2O3 and Tb2O3 compounds.
2. Method of Calculation
In the present paper, all calculations have been carried out using the ab-initio total-energy and molecular-dy- namics program VASP (Vienna ab-initio simulation program) developed at the Faculty of Physics of the University of Vienna [6] - [9] within the density functional theory (DFT) [10] . The exchange-correlation energy function is treated within the GGA (generalized gradient approximation) by the density functional of Perdew et al. [11] . We get a good convergence using a 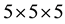 Monkhorst-Pack [12] mesh grid for the total-energy calculation with a cutoff energy of 510 eV for both compunds. The electronic iterations convergence is
Monkhorst-Pack [12] mesh grid for the total-energy calculation with a cutoff energy of 510 eV for both compunds. The electronic iterations convergence is 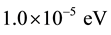 using the Normal (blocked Davidson) algorithm and reciprocal space projection operators. These values were found to be sufficient for studying the electronic and optical properties of X2O3 crystals.
using the Normal (blocked Davidson) algorithm and reciprocal space projection operators. These values were found to be sufficient for studying the electronic and optical properties of X2O3 crystals.
3. Results and Discussion
3.1. Structural and Electronic Properties
In the first step of our calculations, we have carried out the equilibrium lattice constants of Gd2O3, and Tb2O3 by minimizing the ratio of the total energy of the crystal to its volume using the experimental data [13] [15] . We have compared the present results for lattice parameters of X2O3 with previous experimental values [13] - [29] and are given in Table 1. These results are within the accuracy range of calculations based on density functional theory.
Table 1. The calculatedequilibriumlattice parameters and direct band gaps together with the available experimental values for Gd2O3 and Tb2O3.
The investigation of electronic band structure for understanding the electronic and optical properties of X2O3 is very useful. The band structures of the X2O3 were calculated using GGA. The electronic band structures were calculated along the special lines connecting the high-symmetry points Г, H, N, and P for X2O3 in the k-space. The electronic band structure of Gd2O3, and Tb2O3 along the high symmetry directions have been calculated by using the equilibrium lattice constants and are given in Figure 1 and Figure 2.
As can be seen in Figure 1, the Gd2O3 compound has a direct band gap semiconductor with the value 3.86 eV (in Г-high symmetry point). The band gap with the value 3.82 eV of Tb2O3 compound has the same character of that of Gd2O3 (Figure 2). The band gap values obtained for X2O3 are good agreement with the earlier theoretical resuts, but is less than the estimated experimental results [1] [3] [5] . In these figures (Figure 1 and Figure 2), the lowest valance bands that occur between 0 and −3.5 eV (72 energy states) are dominated by O 2p states while the valence bands that occur between −14 eV and −16.5 eV (24 energy states) are dominated by Gd 6s and Tb 6s states. The lowest occupied valance bands are essentially dominated by O 2s (−19 eV and −21.5 eV and include 48 energy states).
3.2. Optical Properties
It is well known that the effect of the electric field vector, 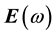 , of the incoming light is to polarize the material. At the level of a linear response, this polarization can be calculated using the following relation [29] :
, of the incoming light is to polarize the material. At the level of a linear response, this polarization can be calculated using the following relation [29] :
Figure 1. The calculated electronic band structure and Density of State for Gd2O3.
Figure 2. The calculated electronic band structure Density of State for Tb2O3.
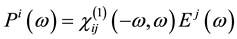 (1)
(1)
where 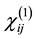 is the linear optical susceptibility tensor and it is given by [30]
is the linear optical susceptibility tensor and it is given by [30]
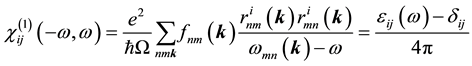 (2)
(2)
where 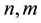 denote energy bands,
denote energy bands, 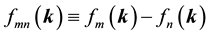 is the Fermi occupation factor,
is the Fermi occupation factor, 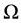 is the normalization volume.
is the normalization volume. 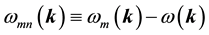 are the frequency differences,
are the frequency differences, 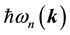 is the energy of band n at wave vector
is the energy of band n at wave vector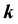 . The
. The 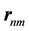 are the matrix elements of the position operator [30] .
are the matrix elements of the position operator [30] .
As can be seen in Equation (2), the dielectric function 



The real part of

cause the Kohn-Sham equations determine the ground state properties, the unoccupied conduction bands as calculated, have no physical significance.
The known sum rules [30] can be used to determine some quantitative parameters, particularly the effective number of the valence electrons per unit cell




where 


Further information on the role of the core and semi-core bands may be obtained by computing the contribution that the various bands make to the static dielectric constant,

One can therefore define an “effective” dielectric constant, that represents a different mean of the interband transitions from that represented by the sum rule, Equation (5), according to the relation

The physical meaning of 

interband transitions in the energy range from zero to
We first calculated the real and imaginary parts of the linear dielectric function of the Gd2O3, and Tb2O3 compounds (Figure 3 and Figure 4). In order to calculate the optical response by using the calculated band structure, we have chosen a photon energy range of 0 - 65 eV and have seen that a 0 - 40 eV photon energy range is sufficient for most optical functions. We first calculated the real and imaginary parts of linear dielectric function of the Gd2O3 and Tb2O3 compounds (Figure 4 and Figure 5). All the Gd2O3 and Tb2O3 compounds
Figure 3. The real and imaginary parts of the linear dielectric function and Electron energy-loss spectrum of Gd2O3.
Figure 4. The real and imaginary parts of the linear dielectric function and Electron energy-loss spectrum of Tb2O3.
studied so far have ε1 are equal to zero in the energy region between 9 eV and 40 eV for decreasing 


the energy region 4 eV and 30 eV. Some of the principal features and singularities of the 
The peaks of the correspond to the optical transitions from the valence band to the conduction band and are in agreement with the previous results. The maximum peak values of for Gd2O3 and Tb2O3 are around 9.31 eV and 9.49 eV, respectively.
The corresponding energy-loss functions, 


The calculated effective number of valence electrons 

Figure 5. The calculated (a) effective number of electrons participating in the interband transitions and (b) effective optical dielectric constant.
Table 2. The energy values at the zero point of real part of dielectric function for Gd2O3 and Tb2O3.
Table 3. The maximum peak values of the imaginary part of the dielectric function for Gd2O3 and Tb2O3.
about 30 eV (Gd2O3) and 35 eV (Tb2O3). This means that deep-lying valence orbitals participate in the interband transitiond as well (see Figure 1 and Figure 2). The effective optical dielectric constant, 
The curves of 



4. Conclusion
In the present work, we have made a detailed investigation of the electronic, and frequency-dependent linear optical properties of the X2O3 (X: Gd and Tb) crystals using the density functional methods. The result of the structural optimization implemented using the GGA are in good agreement with the experimental and theoretical results. We have examined photon-energy dependent dielectric functions, some optical properties such as the energy-loss function, the effective number of valance electrons and the effective optical dielectric constants for both materials.
Acknowledgements
This work is supported by the projects DPT-HAMIT, DPT-FOTON, NATO-SET-193 and TUBITAK under Project Nos., 113E331, 109A015, 109E301.
References
- Adachi, G., Imanaka, N. and Kang, Z.C. (2004) Binary Rare Earth Oxides. Kluwer Academic Publishers, New York.
- Frank, G., Tatsuro, W. and Wolfgang, B. (2010) Rare Earth oxide Alloys and Stacked Layers: An ab Initio Study. Thin Solid Films, 518, 4747-4749. http://dx.doi.org/10.1016/j.tsf.2009.12.074
- Gerald, L. (2006) Band Edge Electronic Structure of Transition Metal/Rare Earth Oxide Dielectrics. Applied Surface Science, 253, 311-321. http://dx.doi.org/10.1016/j.apsusc.2006.06.001
- Wang, J.J., Ji, T., Zhu, Y.Y., Fang, Z.B. and Ren, W.Y. (2012) Band Gap and Structure Characterization of Tm2O3 Films. Journal of Rare Earths, 30, 233-235. http://dx.doi.org/10.1016/S1002-0721(12)60029-5
- Roland, G., Stewart, J.C. and John, R. (2013) Nature of the Electronic Band Gap in Lanthanide Oxides. Physical Review B, 87, 125116-125122. http://dx.doi.org/10.1103/PhysRevB.87.125116
- Kresse, G. and Hafner, J. (1993) Ab Initio Molecular Dynamics for Liquid Metals. Physical Review B, 47, 558-561. http://dx.doi.org/10.1103/PhysRevB.47.558
- Kresse, G. and Furthmüller, J. (1996) Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Computational Materials Science, 6, 15-50. http://dx.doi.org/10.1016/0927-0256(96)00008-0
- Kresse, G. and Joubert, D. (1999) From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Physical Review B, 59, 1758-1775. http://dx.doi.org/10.1103/PhysRevB.59.1758
- Kresse, G. and Furthmüller, J. (1996) Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Physical Review B, 54, 11169-11186. http://dx.doi.org/10.1103/PhysRevB.54.11169
- Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, B864-B871. http://dx.doi.org/10.1103/physrev.136.b864
- Perdew, J.P., Burke, S. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868. http://dx.doi.org/10.1103/PhysRevLett.77.3865
- Monkhorst, H.J. and Pack, J.D. (1976) Special Points for Brillouin-Zone Integrations. Physical Review B, 13, 5188- 5192. http://dx.doi.org/10.1103/PhysRevB.13.5188
- Bartos, A., Lieb, K.P., Uhrmacher, M. and Wiarda, D. (1993) Refinement of Atomic Positions in Bixbyite Oxides Using Perturbed Angular Correlation Spectroscopy. Acta Crystallographica Section B Structural Science, 49, 165-169. http://dx.doi.org/10.1107/S0108768192007742
- Post, B., Moskowitz, D. and Glaser, F.W. (1956) Borides of Rare Earth Metals. Journal of the American Chemical Society, 78, 1800-1802. http://dx.doi.org/10.1021/ja01590a007
- Andreeva, A.F. and Gil’man, I.Y. (1978) Polymorphic Transitions in Rare Earth Oxides Obtained by Reactive Evaporation. Inorganic Materials, 14, 384-390. (İn Russian)
- Adachi, G.Y., Kawahito, T., Matsumoto, H. and Shiokawa, J. (1970) The Reactions of Lanthanide Oxides and Antimony Oxides. Journal of Inorganic and Nuclear Chemistry, 32, 681-686. http://dx.doi.org/10.1016/0022-1902(70)80278-0
- Hirosaki, N., Ogata, S. and Kocer, C. (2003) Ab İnitio Calculation of the Crystal Structure of the Lanthanide Ln2O3 Sesquioxides. Journal of Alloys and Compounds, 351, 31-34. http://dx.doi.org/10.1016/S0925-8388(02)01043-5
- Scavini, M., Coduri, M., Allieta, M., Brunelli, M. and Ferrero, C. (2012) Probing Complex Disorder in Ce1-xGdxO2-x/2 Using the Pair Distribution Function Analysis. Chemistry of Materials, 24, 1338-1345. http://dx.doi.org/10.1021/cm203819u
- Zhang, F.X., Lang, M., Wang, W., Becker, U. and Ewing, R.C. (2008) Structural Phase Transitions of Cubic Gd2O3 at High Pressures. Physical Review B, 78, Article ID: 064114. http://dx.doi.org/10.1103/PhysRevB.78.064114
- Pires, A.M., Davolos, M.R., Paiva, S.C.O., Stucchi, E.B. and Flor, J. (2003) New X-Ray Powder Diffraction Data and Rietveld Refinement for Gd2O3 Monodispersed Fine Spherical Particles. Journal of Solid State Chemistry, 171, 420- 423. http://dx.doi.org/10.1016/S0022-4596(02)00224-4
- Kennedy, B.J. and Avdeev, M. (2011) The Structure of C-Type Gd2O3: A Powder Neutron Diffraction Study Using Enriched 160Gd. Australian Journal of Chemistry, 64, 119-121. http://dx.doi.org/10.1071/CH10310
- Zachariasen, W.H. (1928) Skrifter utgitt av det Norske Videnskaps Akademi i Oslo 1: Matematisk Naturvidenskapelig Klasse.
- Pavlyuk, V.V., Rozycka, S.E., Marciniak, B., Paul B.V. and Dorogova, M. (2011) The Structural, Magnetic, Hydrogenation and Electrode Properties of REMg2Cu9−xNix Alloys (RE=La, Pr, Tb). Central European Journal of Chemistry, 9, 1133-1142. http://dx.doi.org/10.2478/s11532-011-0099-2
- Finkel’shtein, L.D., Samsonova, N.D. and Bazuev, G.V. (1980) Neighboring Structure of X-Ray Absorption in Determination of Europium-Oxygen Average Distances in Compunds with Improper Polyhedrons. Russian Journal of Inorganic Chemistry, 25, 1124-1128.
- Glushkova, V.B., Adylov, G.T., Yusupova, S.G., Sigalov, L.H., Kravchinskaya, M.V. and Rakhimov, R.K. (1988) Phase Rations in YO1.5-TbO1.5 and YO1.5-TbOx Systems. Inorganic Materials, 24, 665-669.
- Kunzmann, P. and Eyring, L. (1975) On the Crystal Structures of the Fluorite-Related İntermediate Rare-Earth Oxides. Journal of Solid State Chemistry, 14, 229-237. http://dx.doi.org/10.1016/0022-4596(75)90027-4
- McCarthy, G.J. (1971) Crystal Data on C-Type Terbium Sesquioxide (Tb2O3). Journal of Applied Crystallography, 4, 399-400. http://dx.doi.org/10.1107/S0021889871007295
- Gasgnier, M., Schiffmacher, G., Caro, P.E. and Eyring, L. (1986) The Formation of Rare Earth Oxides Far from Equilibrium. Journal of the Less Common Metals, 116, 31-42. http://dx.doi.org/10.1016/0022-5088(86)90214-6
- Levine, Z.H. and Allan, D.C. (1989) Linear Optical Response in Silicon and Germanium including Self-Energy Effects. Physical Review Letters, 63, 1719-1722. http://dx.doi.org/10.1103/PhysRevLett.63.1719
- Philipp, H.R. and Ehrenreich, H. (1963) Optical Properties of Semiconductors. Physical Review, 129, 1550-1560. http://dx.doi.org/10.1103/PhysRev.129.1550
NOTES
*Corresponding author.








