World Journal of Condensed Matter Physics
Vol.05 No.01(2015), Article ID:54131,9 pages
10.4236/wjcmp.2015.51004
Coexistence of Superconductivity and Ferromagnetism in Superconducting HoMo6S8
Tadesse Desta1, Gebregziabher Kahsay2
1Department of Physics, Addis Ababa University, Addis Ababa, Ethiopia
2Department of Physics, College of Science, Bahir Dar University, Bahir Dar, Ethiopia
Email: tad4jju@gmail.com, michige_90@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2015; accepted 13 February 2015; published 16 February 2015
ABSTRACT
This work focuses on the theoretical investigation of the coexistence of superconductivity and ferromagnetism in the superconducting HoMo6S8. By developing a model Hamiltonian for the system and using the Green’s function formalism and equation of motion method, we have obtained expressions for superconducting transition temperature (Tc), magnetic order temperature (Tm), superconductivity order parameter (D) and magnetic order parameter (η). By employing the experimental and theoretical values of the parameters in the obtained expressions, phase diagrams of energy gap parameter versus transition temperature, superconducting transition temperature versus magnetic order parameter and magnetic order temperature versus magnetic order parameter are plotted separately. By combining the phase diagrams of superconducting transition temperature versus magnetic order parameter and magnetic order temperature versus magnetic order parameter, we have demonstrated the possible coexistence of superconductivity and ferromagnetism in superconducting HoMo6S8.
Keywords:
Superconductivity, Ferromagnetism, Coexistence, Green’s Function, HoMo6S8

1. Introduction
Superconductivity was discovered in 1911 by Kamerlingh Onnes [1] when a so-called “Blue Boy” noticed that the resistivity of Hg metal vanished abruptly at a temperature of about 4.2 K. Ferromagnetism is a phenomenon by which a material can exhibit a spontaneous magnetization and is one of the strongest forms of magnetism. It is responsible for most of the magnetic behaviors encountered in everyday life and is the basis for all permanent magnets (as well as the metals that are noticeably attracted to them). In particular, a material is ferromagnetic in narrower sense only if all of its magneticions add a positive contribution to the net magnetization. If some of the magneticions subtract from the net magnetization, that is, if they are partially anti-aligned, then the material is ferrimagnetic. If the ions anti-align completely so as to have zero netmagnetization, despite the magnetic ordering, then it is an antiferromagnet. Thus, ferromagnetic materials exhibit parallel alignment of moments resulting in large net magnetization even in the absence of a magnetic field.
Superconductivity in Ferromagnetic must result from a different type of electronpairing mechanisms. In these materials, electrons with spins pointing in the same direction team up with each other to form Cooper pairs with one unit of spin resulting in a triplet superconductivity. In contrast, conventional superconductivity also known as s-wave singlet superconductivity occurs when electrons with oppositespins bind together to form Cooper pairs with zero momentum and spin.
The coexistence of superconductivity and ferromagnetism has been studied theoretically and experimentally. The coexistence of ferromagnetism and superconductivity was first addressed theoretically by Ginzburg in 1957 [2] and experimental investigation was made by Matthias et al. [3] . The interplay between superconducting and ferromagnetic long range order has been recently attracting new interest due to the discovery of superconductivity in ferromagnetic compounds such as UGe2 [4] , URhGe [5] , ZrZn2 [6] , and in RuSr2RECu2O8 compounds (with RE = Eu or Gd) [7] . The relationship between magnetism and superconductivity has received renewed attention since the discovery of ternary superconducting materials which also achieved long-range magnetic ordering at low temperatures. Ferromagnetic alignment can be expected to be strongly opposed by superconductivity. Such a long-period magnetic ordering was actually found in HoMo6S8 and in ErRh4B4. In ErRh4B4, Sinha et al. [8] carried out a detailed study on a single crystal in order to characterize this phase. For HoMo6S8, the study was done by Lynn et al. [9] only on polycrystalline samples.
In HoMo6S8, the ferromagnetic state destroys the superconductivity at sufficiently low temperatures. Recently, an experiment on HoMo6S8 [10] has shown that, the superconducting ordering parameter has a distinct maximum between some critical temperatures Tc1 and Tc2 (lower and upper superconducting critical temperatures), respectively and vanishes for T < Tc1 and T > Tc2.
Among the “Chevrel phases”, HoMo6S8 has been extensively studied in recent years [11] . HoMo6S8 becomes superconducting at Tc1 ≌ 1.82 K, but at a lower temperature Tc2 ≌ 0.64 K, it re-enters the normal state at the onset of long range ferromagnetic order. In a narrow temperature range Tc2 < T < Tm, superconductivity coexists with a modulated magnetic structure [12] .
2. Model System Hamiltonian
In order to study the coexistence of ferromagnetism and superconductivity in superconducting HoMo6S8 theoretically in general and to find the expressions for transition temperature and order parameters in particular, a system of conduction and localized electrons have been considered. The exchange interaction acts between the conduction and the localized electrons. Thus, within the frame work of the BCS model [13] , the model system Hamiltonian can be formulated as follows.
 (1)
(1)
where
 (2)
(2)
and is the Hamiltonian or energy of mobile (conduction) electrons and localized electrons respectively.
Here, the operators

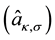 and
and

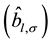 are the creation (annihilation) operators for conduction
are the creation (annihilation) operators for conduction
and localized electrons respectively with the wave vector
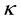 and the spin projection on z-axis σ = ↑ or ↓.
and the spin projection on z-axis σ = ↑ or ↓.
 is the one electron kinetic energy measured relative to the chemical potential.
is the one electron kinetic energy measured relative to the chemical potential.
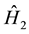 is the interaction (electron- electron) through boson (phonon) exchange and is given by,
is the interaction (electron- electron) through boson (phonon) exchange and is given by,
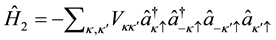 (3)
(3)
where
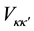 defines the matrix element of the interaction potential.
defines the matrix element of the interaction potential.
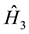 is the interaction term between con-
is the interaction term between con-
duction electrons and localized electrons due to some unspecified mechanism with some coupling constant (α) and is expressed as,
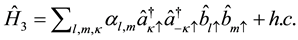 (4)
(4)
3. Equation of Motion for Mobile (Conduction) Electrons
Now, let us evaluate the following commutation relation,
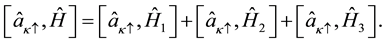 (5)
(5)
From which we obtain,
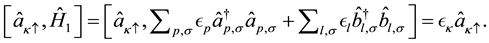 (6)
(6)
Following similar procedure as above, we get,
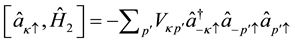 (7)
(7)
and

Substituting Equations (6), (7) and (8) into the equation of motion given by,

we obtain,

In general, we have to write the higher order Green’s function into lower order Green’s function by using Wick’s theorem. Thus, we have,

Now, substituting Equation (11) into Equation (10), we get,

where

One can also obtain the equation of motion for the expression


For




Now, using Equations (12) and (14), the equation of motion becomes,
From which we obtain,

Using the relation for ∆, given by,

and by changing the summation into integration and by introducing the density of states at the Fermi level, (N(0)), we get,

Now, changing

Now, using Equation (18) in Equation (17), we get,

where


We can write Equation (19) as,

Let

3.1. Effect of Temperature on Superconducting Order Parameter (∆) and Magnetic Order Parameter (η)
Now, let us study equation (21) by considering different cases.
Case (I): As

Hence, Equation (21) becomes,

Using the integral




For

This implies that,

For

The experimental value of HoMo6S8 is, Tc ≈ 1.82 K.
Thus,


Case (II): At


Now, employing Equation (27) and the experimental value of Tc for the superconducting HoMo6S8 and plausible approximations for other parameters, we plotted the transition temperature (Tc) versus magnetic ordering parameter (η) as shown in Figure 1.
For η = 0, we get the expression for Tc to be,

Figure 1. Transition temperature (Tc) versus magnetic order parameter (η) for superconducting HoMo6S8.
3.2. Equation of Motion for Localized Electrons
Using Green’s function formalism, the equation of motion for the localized electrons is obtained to be,

Now, using the Hamiltonian given in Equation (1), we evaluated the commutation



where
Applying similar procedure as above and assuming


Now, from Equations (31) and (32), we get,

From which we get,

3.3. Correlation between Conduction and Mobile Electrons
The equation of motion that shows the correlation between the conduction and localized electrons can be demonstrated. Using similar definition as for ∆, we can write the magnetic ordering parameter, η as,

Changing the summation into integration and by introducing the density of states, N(0), we get,

Using the Matsubara frequency,
Equation (36) becomes,

where

Now, let us first solve the following expression.

Using Laplace’s transform and Matsubara frequency, Equation (38) becomes,
where

and

Then,

Since ∆l is very small,

From which we get,

Using Equation (42) and the experimental value, Tm ≈ 0.67 K for HoMo6S8 and some plausible approximations for other parameters in the equation, we plot the magnetic order temperature (Tm) versus magnetic order parameter as shown in Figure 2.
Figure 2. Magnetic order temperature (Tm) versus magnetic order parameter (η) for superconducting HoMo6S8.
3.4. Equation of Motion for Pure Superconducting System
For pure superconducting system, that is, when magnetic order cannot appear or magnetic effect is zero, we can ignore η and our previous calculation gives the following results which is similar to the well-known BCS model.
As T → 0, η → 0 and tanh(βE/2) → 1, Equation (21) reduces to,

From which we obtain,

Furthermore, for T → Tc, η = 0 and for low temperature, i.e.
From which we get,

To obtain the temperature dependency of energy gap in Equation (21), we used the same techniques to solve the integral,

But from the BCS model

For
Using the relation
From which we can get,

Equation (47) shows how the superconducting order parameter, ∆(T) varies with temperature when η = 0 and is similar to the BCS model.
Using the experimental value, Tc ≈ 1.82 K for HoMo6S8 and some plausible approximations, we plot ∆ versus Tc as shown in Figure 3.
Now, by combining Figure 1 and Figure 2, we demonstrated the possible coexistence of superconductivity and ferromagnetism in HoMo6S8 as shown in Figure 4.
4. Results and Discussion
In this section, we describe the results which are obtained using the model Hamiltonian developed. We obtain the expressions for the superconducting ordering parameter (∆) and magnetic order parameter (η) with respect to
Figure 3. Energy gap parameter (∆) versus transition temperature (Tc) for superconducting HoMo6S8.
Figure 4. Coexistence of superconductivity and ferromagnetism in superconducting HoMo6S8.
superconducting transition temperature (Tc) and magnetic order temperature (Tm) respectively. First, using Equation (27) and the experimental value of Tc for the superconducting HoMo6S8 and plausible approximations for other parameters, we plotted the transition temperature (Tc) versus magnetic order parameter (η) as shown in Figure 1. As can be seen from the figure, when the magnetic order parameter increases the superconducting transition temperature decreases. Second, by employing Equation (42) and the experimental value, Tm ≈ 0.67 K for HoMo6S8 and some suitable approximations for the other parameters in the equation, we plotted the magnetic order temperature versus magnetic order parameter as demonstrated in Figure 2. From the figure, it is vivid that, as the magnetic order parameter increases the magnetic order temperature also increases. Furthermore, the superconducting order parameter (∆) is expressed as a function of the transition temperature (Tc) and is plotted in Figure 3. The expression we obtained for the pure superconductor in Equation (47) is in agreement with the BCS model for η = 0. It is clear that from Figure 3, the superconducting order parameter, which is the measure of pairing energy decreases with increasing temperature and vanishes at the transition temperature (Tc). From Figure 4, we observe that, Tc decreases with increasing η, whereas Tm increases with increasing η and there is a small region of temperature where both superconductivity and ferromagnetism coexist in HoMo6S8. Our finding is in agreement with the experimental observation [15] .
5. Conclusion
In the present work, we have demonstrated the basic concepts of superconductivity with special emphasis on the BCS model and Cooper pair focusing on the interaction between superconductivity and ferromagnetism which are closely connected to the particular crystal of superconducting HoMo6S8. Employing the double time temperature dependent retarded Green’s functions formalism, we developed the model Hamiltonian for the system and derived equations of motion for conduction electrons, localized electrons and for pure superconducting system and carried out various correlations by using suitable decoupling procedures. In developing the model Hamiltonian, we considered spin triplet pairing mechanism and obtained expressions for superconducting order parameter, magnetic order parameter, superconducting transition temperature and magnetic order temperature. By using appropriate experimental values and considering suitable approximations, we plotted figures using the equations developed. As is well-known, superconductivity and ferromagnetism are two cooperative phenomena which are mutually antagonistic since superconductivity is associated with the pairing of electron states related to time reversal while in the magnetic states the time reversal symmetry is lost. Because of this, there is a strong competition between the two phases. This competition between superconductivity and magnetism made coexistence unlikely to occur. However, the model we employed in this work, shows that, there is a small region of temperature where both superconductivity and ferromagnetism can coexist in superconducting HoMo6S8.
Cite this paper
TadesseDesta,GebregziabherKahsay, (2015) Coexistence of Superconductivity and Ferromagnetism in Superconducting HoMo6S8. World Journal of Condensed Matter Physics,05,27-36. doi: 10.4236/wjcmp.2015.51004
References
- 1. Onnes, H.K. (1911) Akad. van Wetenschappen (Amsterdam), 14, 113.
- 2. Ginzburg, V.L. (1957) Ferromagnetic Superconductors. Soviet Physics—JETP, 4, 153.
- 3. Matthias, B.T., Suhl, H. and Corenzwit, E. (1958) Spin Exchange in Superconductors. Physical Review Letters, 1, 92.
http://dx.doi.org/10.1103/PhysRevLett.1.92 - 4. Saxena, S.S., Agarwal, P., Ahilan, K., Grosche, F.M., Haselwimmer, R.K.W., Steiner, M.J., Pugh, E., Walker, I.R., Julian, S.R., Monthoux, P., Lonzarich, G.G., Huxley, A., Sheikin, I., Braithwaite, D. and Flouquet, J. (2000) Superconductivity on the Border of Itinerant-Electron Ferromagnetism in UGe2 Superconductivity. Nature, 406, 587.
http://dx.doi.org/10.1038/35020500 - 5. Aoki, D., Huxley, A., Ressouche, E., Braithwaite, D., Flouquet, J., Brison, J.P., Lhote, E. and Paulsen, C. (2001) Coexistence of Superconductivity and Ferromagnetism in URhGe. Nature, 413, 613-616.
http://dx.doi.org/10.1038/35098048 - 6. Pfleiderer, C., Uhlarz, M., Hayden, S.M., Vollmer, R., Lohneysen, H.V., Bernhoeft, N.R. and Lonzarich, G.G. (2001) Coexistence of Superconductivity and Ferromagnetism in the d-Band Metal ZrZn2. Nature, 412, 58.
http://dx.doi.org/10.1038/35083531 - 7. Cuoco, M., Gentile, P. and Noce, C. (2003) Coexistence of Ferromagnetism and Singlet Superconductivity via Kinetic Exchange. Physical Review Letters, 91, Article ID: 197003.
http://dx.doi.org/10.1103/PhysRevLett.91.197003 - 8. Sinha, S.K., Crabtree, G.W., Hinks, D.G., Mook, H.A. and Pringle, O.A. (1983) Neutron Scattering Studies of Magnetic Superconductors. Journal of Magnetism and Magnetic Materials, 31-34, 489.
http://dx.doi.org/10.1016/0304-8853(83)90545-0 - 9. Lynn, J.W., Raggazoni, A., Pynn, R. and Joffrin, J. (1981) Observation of Long Range Magnetic Order in the Reentrant Superconductor HoMo6S8. Journal de Physique Lettres, 42, 45-49.
http://dx.doi.org/10.1051/jphyslet:0198100420204500 - 10. Morales, F., Escudero, R., Briggs, A., Monceau, P., Horyn, R., Le Berre, F. and Pena, O. (1996) Point Contact Spectroscopy on the Ferromagnetic Superconductor HoMo6S8. Physica, 218B, 193.
http://dx.doi.org/10.1016/0921-4526(95)00591-9 - 11. (1982) Superconductivity in Ternary Compounds II. In: Maple and Fischer, Eds., Springer-Verlag, Berlin.
- 12. Lynn, J.W., Shirane, G., Thomlinson, W., Shelton, R.N. and Moncton, D.E. (1981) Magnetic Properties of the Reentrant Ferromagnetic Superconductor HoMo6S8. Physical Review B, 24, 3817.
http://dx.doi.org/10.1103/PhysRevB.24.3817 - 13. Bardeen, J., Cooper, L.N. and Schrieffer, J.R. 1957) Theory of Superconductivity. Physical Review, 108, 1175.
http://dx.doi.org/10.1103/PhysRev.108.1175 - 14. Zubarev, D.N. (1960) Double-Time Green Functions in Statistical Physics. Soviet Physics Uspekhi, 3, 320.
http://dx.doi.org/10.1070/PU1960v003n03ABEH003275 - 15. Ishikawa, M., Fischer, O. and Muller, J. (1978) Long Range Magnetic Order in the Superconducting State of Heavy Rare Earth Molybdenum Sulfides and Their Pseudo Ternary Compounds. Journal de Physique, 39, C6-1379.



















